运筹学论文及案例
运筹学案例

运筹学案例
嘿,朋友们!今天咱就来聊聊超级有意思的运筹学案例。
比如说,咱们出去旅游的时候要怎么规划路线呢,这可就是个典型的运筹学问题呀!
想象一下,你要去一个陌生的城市玩三天。
你是不是得考虑第一天去哪儿玩能让自己尽快熟悉这个城市,第二天怎么安排才能玩得尽兴又不那么累,第三天又怎样利用时间去一些特别的地方呢?这就像在下一盘棋,每一步都得精心谋划。
再看看快递行业,他们怎么做到让包裹那么快就送到我们手里呢。
这不就跟物流公司要给货车司机规划最优路线一样嘛!要让货车像赛车一样在公路上飞驰,又快又稳地把东西送到目的地。
“哎呀,要是没有运筹学,咱们得等多久才能收到快递呀!”
还有那些大工厂,生产线上的安排也是一门学问呢!怎么让工人和机器配合默契,高效地生产出产品呢。
“这要是没安排好,那不得乱套啦!”
运筹学在我们生活中的应用简直无处不在呀!从小小的旅行计划,到庞大的物流网络,再到复杂的工业生产。
它就像是一个神奇的魔法,让一切都变得井井有条。
咱就说,运筹学是不是超级重要啊!它让我们的生活变得更有序,更高效,也让我们能更好地享受这个美好的世界呀!所以呀,别小看这看似深奥的运筹学,它可是大有用处呢!。
运筹学经典案例

摘要
• 利用整数规划方法解决了场主在现有条件下,如何分配有 限的现金和劳动力使明年年底能够拥有最多的现金的问题 。得出结论: • 1.在明年种植414亩大豆,42亩玉米,100亩小麦;饲养 42头牛,2000只鸡可获得最大货币资产102811.0美元 。 • 2.通过分情况讨论,发现不管天气情况如何,购买尽可能 多的牛能赚更多的钱。所以普拉夫家族应该购买牛至42头 (最大容量);至于作物的种植量,普拉夫家族可以先去咨 询当地的气象站再根据实际情况作出决定,当得知未来可 能发生某种灾害天气时,就可以参考分析结果 ,进行资金 和劳动力的分配;如果未来的天气情况无法预测,为了尽 可能减少未来可能存在的损失,普拉发家族应该走一个稳 健的种植路线:种植更多小麦,同时也可以购进一些鸡。 • 3.使用lingo做敏感性分析之后可以看出资金的影子价格为 0,因此不需要贷款。
• • •
• • • • • • • • • • • • • • •
用lingo进行求解 在lingo输入界面输入 Max = 70*x1+60*(x2-x4)+40*(x3-0.05*x5) +850*x4+4.25*x5+(35000+1500*(x4-30))*1.1+ (5000+3*(x52000))*0.75+5*(4000-x1-0.9*x2-0.6*x3-6*10*x4-6*0.05*x5 ) +5.5*(45001.4*x1-1.2*x2-0.7*x3-6*10*x4-6*0.05*x5)+20000-1500*(x4-30)-3*(x52000)-40000; x1+x2+x3+2*x4<=640; x4<=42; x5<=5000; x4>=30; x5>=2000; x4<=x2; 0.05*x5<=x3; 1500*(x4-30)+3*(x5-2000) <=20000; @gin(x1); @gin(x2); @gin(x3); @gin(x4); @gin(x5); 经过计算得出最优解为X*=(414,42,100,42,2000);目标函数最大值 Z*=102811.0 即在明年种植414亩大豆,42亩玉米,100亩小麦;饲养42头牛,2000只鸡 可获得最大货币资产102811.0美元
管理运筹学案例分析

【案例1】某厂排气管车间生产计划的优化分析
1.问题的提出 排气管作为发动机的重要部件之一,极大地影响发动机的性能。某
发动机厂排气管车间长期以来,只生产一种四缸及一种六缸发动机的排 气管。由于其产量一直徘徊不前,致使投资较大的排气管生产线,一直 处于吃不饱状态,造成资源的大量浪费,全车间设备开动率不足50%。
税收
15 16 14.8 17 16.5 14.5 15.6 15.5
售价
150 160.1 149 172 166 145.6 157.8 155.8
利润
13.545 14.00114.99 15.56 15.312 12.8735 15.892 13.74
(元)
注:表中售价为含税价。
表C-3 设备加工能力一览表
【案例2】配料问题
某饲料公司生产肉用种鸡配合饲料,每千克饲料所需营养质量要求如表
C-4所示。
表C-4
营养成分 肉用种鸡国家标准 肉用种鸡公司标准
产蛋鸡标准
代谢能
2.7~2.8Mcal/kg
≥2.7Mcal/kg
≥2.65Mcal/kg
粗蛋白
135 ~145g/kg
135 ~145g/kg
≥151g/kg
x6 菜饼 0.32 1.62 360 113 8.1 7.1 5.3 8.4
x7 鱼粉 1.54 2.80 450 0 29.1 11.8 63 27
x8 槐叶粉 0.38 1.61 170 108 10.6 2.2 4.0 4.0
x9 DL-met 23.0
980
x10 骨粉 0.56
300 140
8.摇臂钻床 4.1 4.0 4.0 4.3 4.2 3.8 4.3 4.3
运筹学论文

运筹学论文摘要本论文主要探讨了运筹学在管理决策中的应用。
首先介绍了运筹学的基本概念和相关理论,然后分析了运筹学在企业管理中的实际应用案例,最后总结了运筹学的优势和局限性,并对未来运筹学研究方向进行了展望。
1. 引言随着企业管理的复杂性和竞争的加剧,越来越多的企业开始重视运筹学在管理决策中的应用。
运筹学作为一门应用数学学科,通过运筹学方法和技术来解决企业面临的各种问题,帮助企业高效运营和优化决策。
本文将从运筹学的基本概念、实际应用案例和研究展望三个方面展开论述。
2. 运筹学基本概念2.1 定义运筹学是一门研究如何对复杂系统进行优化决策的学科。
它以数学为基础,涉及多个学科领域,如线性规划、整数规划、图论、排队论等。
2.2 运筹学方法运筹学通过建立数学模型来描述和分析问题,然后采用优化算法和技术对模型进行求解,得到最优解或近似最优解。
常用的运筹学方法包括线性规划、整数规划、动态规划、启发式算法等。
3. 运筹学在企业管理中的应用案例3.1 生产调度优化运筹学可以帮助企业优化生产调度,提高生产效率和资源利用率。
通过建立生产调度模型,运用线性规划、整数规划等方法,可以实现最优生产调度方案的确定,使得生产过程更加高效。
3.2 配送路径优化对于物流企业来说,配送路径的优化是提高物流效率和降低成本的关键。
运筹学可以通过图论、整数规划等方法,确定最优的配送路径,减少行驶里程和时间,达到节约成本的目的。
3.3 库存管理优化运筹学可以帮助企业优化库存管理,减少库存成本和缺货风险。
通过建立库存模型,根据需求、供应、存储成本等因素,利用线性规划、动态规划等方法,确定最优的库存策略,实现库存成本的最小化和保证供应的可靠性。
4. 运筹学的优势与局限性4.1 优势 - 运筹学可以提供量化的决策支持,帮助企业从数据驱动的角度优化决策; - 运筹学方法和技术可以快速求解大规模、复杂的优化问题; - 运筹学可以提供全局最优解或近似最优解,并具有较高的准确性和可信度。
运筹学论文

运筹学论文1. "运筹学在制造业中的应用案例分析"这篇论文可以研究运筹学在制造业中的应用案例,探讨如何运用运筹学方法来优化制造流程、减少生产成本、提高生产效率等方面的实践经验。
2. "运筹学在物流管理中的应用及挑战"这篇论文可以研究运筹学在物流管理中的应用,分析运筹学方法在物流优化、路线规划、货物配送等方面的应用,并讨论实施这些方法面临的挑战和解决方案。
3. "基于运筹学的供应链管理优化研究"这篇论文可以研究基于运筹学的供应链管理优化方法,分析如何利用运筹学方法来改善供应链的效率和响应能力,以及解决供应链中的库存管理、订单分配等问题。
4. "运筹学在项目管理中的应用研究"这篇论文可以研究运筹学在项目管理中的应用,探讨如何利用运筹学方法来优化项目进度安排、资源分配、风险管理等方面的实践经验,并探讨这些方法在项目管理中的效果和局限性。
5. "基于运筹学的决策支持系统研究"这篇论文可以研究基于运筹学的决策支持系统的开发和应用,分析如何利用运筹学方法来辅助决策制定,提供精确的数据分析和模型建立,以及讨论这些系统在实际决策中的应用效果和局限性。
6. "运筹学在金融风险管理中的应用研究"这篇论文可以研究运筹学在金融风险管理中的应用,分析如何利用运筹学方法来评估和控制金融风险,包括市场风险、信用风险等方面,以及讨论这些方法的优点和局限性。
7. "运筹学在医疗资源优化中的应用研究"这篇论文可以研究运筹学在医疗资源优化中的应用,探讨如何利用运筹学方法来优化医疗资源的配置、排班安排、手术室管理等方面,以提高医疗服务的效率和质量。
8. "基于运筹学的环境保护决策研究"这篇论文可以研究基于运筹学的环境保护决策方法,分析如何利用运筹学方法来评估不同环境保护措施的效果,并对环境保护决策进行优化,以达到经济、社会和环境的可持续发展。
生活中运筹学案例分析

生活中运筹学案例分析
运筹学是一门研究如何做出最优决策的学科,它在生活中有着广泛的应用。
从
日常生活中的购物决策到企业的生产计划,都可以看到运筹学的影子。
在本文中,我们将通过一些生活中的案例来分析运筹学的应用。
首先,让我们来看一个购物决策的案例。
假设你需要购买一件衣服,而且你有
多个选择。
每件衣服的价格、品质、风格都不同,你需要在这些选择中做出最优的决策。
这时,你可以运用运筹学的方法,比如成本效益分析、决策树分析等,来帮助你做出最佳选择,从而在有限的预算内获得最大的满意度。
其次,让我们来看一个企业生产计划的案例。
假设一个工厂需要生产多种产品,并且有限的资源,比如人力、原材料、机器等。
在这种情况下,工厂需要合理安排生产计划,以最大化产出并降低成本。
这就需要运用运筹学的方法,比如线性规划、排程算法等,来优化生产计划,使得工厂能够以最有效的方式进行生产。
此外,运筹学还可以应用于交通运输、物流配送、金融投资等方面。
比如,在
交通运输中,如何合理安排车辆的路线,以最小化时间和成本;在物流配送中,如何优化仓储和配送流程,以提高效率和降低成本;在金融投资中,如何构建最佳的投资组合,以最大化收益和降低风险。
综上所述,运筹学在生活中有着广泛的应用,可以帮助我们在各种决策中做出
最优选择。
通过分析一些生活中的案例,我们可以更好地理解和应用运筹学的方法,从而提高我们的决策能力和生活质量。
希望本文能够对读者有所启发,让大家在生活中更加注重运筹学的应用。
运筹学案例分析
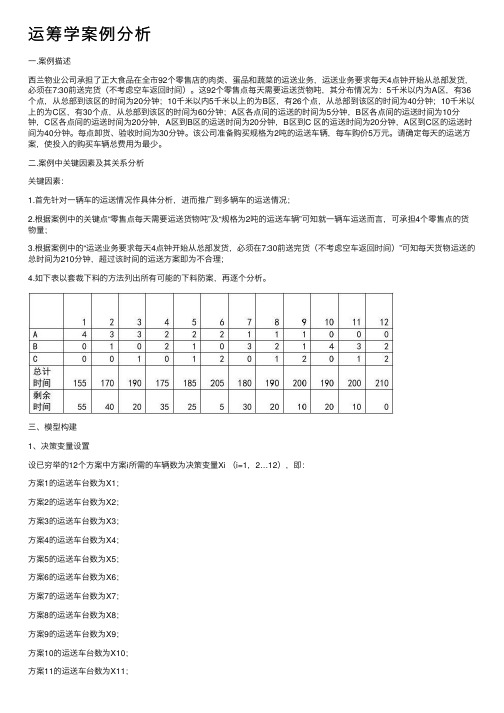
运筹学案例分析⼀.案例描述西兰物业公司承担了正⼤⾷品在全市92个零售店的⾁类、蛋品和蔬菜的运送业务,运送业务要求每天4点钟开始从总部发货,必须在7:30前送完货(不考虑空车返回时间)。
这92个零售点每天需要运送货物吨,其分布情况为:5千⽶以内为A区,有36个点,从总部到该区的时间为20分钟;10千⽶以内5千⽶以上的为B区,有26个点,从总部到该区的时间为40分钟;10千⽶以上的为C区,有30个点,从总部到该区的时间为60分钟;A区各点间的运送的时间为5分钟,B区各点间的运送时间为10分钟,C区各点间的运送时间为20分钟,A区到B区的运送时间为20分钟,B区到C 区的运送时间为20分钟,A区到C区的运送时间为40分钟。
每点卸货、验收时间为30分钟。
该公司准备购买规格为2吨的运送车辆,每车购价5万元。
请确定每天的运送⽅案,使投⼊的购买车辆总费⽤为最少。
⼆.案例中关键因素及其关系分析关键因素:1.⾸先针对⼀辆车的运送情况作具体分析,进⽽推⼴到多辆车的运送情况;2.根据案例中的关键点“零售点每天需要运送货物吨”及“规格为2吨的运送车辆”可知就⼀辆车运送⽽⾔,可承担4个零售点的货物量;3.根据案例中的“运送业务要求每天4点钟开始从总部发货,必须在7:30前送完货(不考虑空车返回时间)”可知每天货物运送的总时间为210分钟,超过该时间的运送⽅案即为不合理;4.如下表以套裁下料的⽅法列出所有可能的下料防案,再逐个分析。
三、模型构建1、决策变量设置设已穷举的12个⽅案中⽅案i所需的车辆数为决策变量Xi (i=1,2…12),即:⽅案1的运送车台数为X1;⽅案2的运送车台数为X2;⽅案3的运送车台数为X3;⽅案4的运送车台数为X4;⽅案5的运送车台数为X5;⽅案6的运送车台数为X6;⽅案7的运送车台数为X7;⽅案8的运送车台数为X8;⽅案9的运送车台数为X9;⽅案10的运送车台数为X10;⽅案11的运送车台数为X11;⽅案12的运送车台数为X12。
管理运筹学案例设计

管理运筹学案例设计管理运筹学是管理科学中一个重要的分支,通过运用数学、统计学和计算机科学等方法,对管理中的决策问题进行建模、分析和优化。
本文将介绍几个管理运筹学的案例,以帮助读者更好地理解其在实际管理中的应用。
案例一:生产调度优化某工厂生产多个产品,每个产品的生产需要不同的资源和时间。
工厂需要合理安排生产顺序,使得生产效率最大化,成本最小化。
通过管理运筹学的方法,可以建立数学模型来优化生产调度。
首先,我们需要确定每个产品的生产时间和资源需求。
然后,可以使用线性规划等数学方法,设计一个优化模型,以最小化总生产成本为目标函数,同时满足资源约束和交付期限。
案例二:库存管理优化某零售商经营多种商品,需要合理管理库存以满足需求,同时最小化库存成本。
通过管理运筹学的方法,可以建立库存管理模型来优化库存水平。
一种常见的方法是使用动态规划来确定最佳订货数量和补货时机,以最小化库存持有成本和缺货成本的总和。
通过对需求的预测和货架管理的优化,可以实现库存管理的最优化。
案例三:运输路线优化一家物流公司需要合理安排货物的运输路线,以最小化运输成本和时间。
通过管理运筹学的方法,可以设计运输路线优化模型,来寻找最佳的配送方案。
运输路线优化模型可以利用图论和网络优化方法,来确定最短路径和最优运输方案。
通过考虑货物的数量、目的地和运输方式等因素,可以制定最佳的运输策略,实现成本和效率的最优平衡。
结语管理运筹学是管理决策中的重要工具,可以帮助管理者在复杂的环境中做出最佳决策。
通过上述案例的介绍,我们可以看到管理运筹学在生产调度、库存管理和运输路线优化等方面的实际应用。
希望本文能够帮助读者更好地理解管理运筹学的概念和方法,从而在实际管理中取得更好的效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学课程论文与案例分析专业:姓名:学号:指导老师:运筹学课程论文与案例分析摘要:运筹学主要研究经济活动和军事活动中能用数量来表达的有关策划、管理方面的问题。
运筹学思想贯穿了企业管理的始终,它在企业战略管理、生产计划、市场营销、运输问题、库存管理、人事管理、财务会计等各个方面都具有重要的作用。
本文主要通过对运筹学的分析,结合企业管理,浅谈了运筹学对企业管理的影响。
掌握运筹学的基本概念、基本原理、基本方法和解题技巧,对于一些简单的问题可以根据实际问题建立运筹学模型及求解模型。
关键词:管理运筹学线性规划正文:现在普遍认为,运筹学是近代应用数学的一个分支,主要是将生产、管理等事件中出现的一些带有普遍性的运筹问题加以提炼,然后利用数学方法解决。
运筹学主要研究经济活动和军事活动中能用数量来表达的有关策划、管理方面的问题。
从最直观、明了的角度将运筹学定义为:“通过构建、求解数学模型规划、优化有限资源的合理利用,为科学决策提供量化一句的系统知识体系。
”运筹学的具体内容包括:规划论,包括线性规划、非线性规划、整数规划和动态规划、库存论、图论、决策论、对策论、排队论、可靠性理论等。
而《应用运筹学》作为运筹学的一部分,则重点介绍了管理运筹的思想与建模方法。
具体包括了线性规划及扩展问题模型、图与网络分析模型、项目管理技术、决策分析技术、库存模型和排队模型等运筹学的重要分支。
其主要特点是注重运筹学原理及方法在解决实际管理问题时应用,突出了管理问题的分析和运筹模型的构建过程,淡化了模型的理论推导和数学计算。
借助于十分普及的Excel软件来求解模型,使得运筹学模型的应用更加简明直观。
线性规划是运筹学的一个重要分支。
线性规划解决的是,在资源有限的条件下,为达到预期目标最优,而寻找资源消耗最少的方案。
其数学模型有目标函数和约束条件组成。
解决线性规划问题的关键是找出他的目标函数和约束方程,并将它们转化为标准形式。
简单的设计2个变量的线性规划问题可以直接运用图解法得到。
但是往往在现实生活中,线性规划问题涉及到的变量很多,很难用作图法实现,但是运用单纯形法记比较方便。
单纯形法的发展很成熟应用也很广泛,在运用单纯形法时,需要先将问题化为标准形式,求出基可行解,列出单纯形表,进行单纯形迭代。
当所有的变量检验数不大于零,且基变量中不含人工变量,计算结束。
将所得的量的值代入目标函数,得出最优值。
图论是一个古老的但又十分活跃的分支,它是网络技术的基础。
在日常生活和生产中,人们会经常碰到各种各样的图,如零件加工图、公路或铁路交通图、管网图等。
图论中图是上述各种类型图的抽象和概括,它用点表示研究对象,用边表示这些对象之间的联系。
而图与网络分析是近几十年来运筹学领域中发展迅速、而且十分灵活的一个分支。
由于它对实际问题的描述具有直观性,故广泛应用与物理学、化学、信息论、控制论、计算机科学、社会科学、以及现代经济管理科学等许多科学领域。
项目管理技术就是在时间、成本、质量、风险、合同、采购、人力资源等各个方面对项目进行的计划和控制。
其中项目管理的核心思想是对进度的管理和成本的控制。
决策分析技术是属决策论的一部分。
主要是在研究决策问题。
所谓决策就是根据客观可能性,借助一定的理论、方法和工具科学地选择最优方案的过程。
决策问题是由决策者和决策域构成的,而决策域又由决策空间、状态空间和结果函数构成。
研究决策理论与方法的科学就是决策科学。
库存模型则主要是对库存论的一种实际应用。
库存论是一种研究物质最优存储及存储控制的理论,物质存储时工业生产和经济运转的必然现象。
如果物质存储过多,则会占用大量仓储空间,增加保管费用,使物质过时报废从而造成经济损失。
如果存储过少,则会因失去销售时机而减少利润,或因原料短缺而造成停产。
因而如何寻求一个恰当的采购,存储方案就成为库存论研究的对象。
学习理论的目的就是为了解决实际问题。
图论为计算机领域也奠定了基础,运筹学的计算方法可以借用计算机来完成。
线性规划的理论对我们的实际生活指导意义很大。
当我们遇到一个问题,需要认真考察该问题。
如果它适合线性规划的条件,那么我们就利用线性规划的理论解决该问题。
但是很多时候我们遇到的问题用线性规划解决耗时、准确度低或者根本无法用线性规划解决。
那么我们就要寻找别的理论方法来解决问题。
通过对此次对应用运筹学的学习我掌握了运筹学的基本概念、基本原理、基本方法和解题技巧,对于一些简单的问题可以根据实际问题建立运筹学模型及求解模型。
应用运筹学对我们以后的生活也讲有不小的影响,将应用运筹学运用到实际问题上去学以致用。
案例分析:案例1:运输问题某公司经销甲产品。
它下设三个加工厂。
每日的产量分别是:A1为7吨,A2为4吨,A3为9吨。
该公司把这些产品分别运往四个销售点。
各销售点每日销量为:B1为3吨,B2为6吨,B3为5吨,B4为6吨。
已知从各工厂到各销售点的单位产品的运价为表3-3所示。
问该公司应如何调运产品,在满足各销点的需要量的前提下,使总运费为最少。
表1、单位运价表:表2、产销平衡表:解:其总运输费用为:3*3+4*11+2*9+2*2+3*10+6*5=135案例2:职场规划在职场上,职业生涯中的“五个坎”可被列为•第一坎:“青黄不接”阶段;•第二坎:“职业塑造”阶段;•第三坎:“职业锁定”阶段;•第四坎:“事业开拓”阶段;•第五坎:“事业平稳”阶段。
针对这五个阶段,你应该怎样规划自己?给出你的最佳职场规划方案。
职业生涯规划没有梦想对于每个人来说是非常可怕的一件事情,如同无头苍蝇似的到处碰壁。
很多人现代社会由于商品经济的发展变化发展很快,很难对自己的人生进行一个长期的规划。
佛家有云:“缘自性空”、“空无自性”。
的确在现代社会,人们的生活节奏加快,社会更新换代发展非常快。
如果如我们柔弱的个体,不加紧自己的脚步,跟随时代的步伐,不断学习,将很难有一个长足的进步。
一、前言:在今天这个人才竞争的时代,职业生涯规划开始成为在人争夺战中的另一重要利器。
对企业而言,如何体现公司“以人为本”的人才理念,关注员工的人才理念,关注员工的持续成长,职业生涯规划是一种有效的手段;而对每个人而言,职业生命是有限的,如果不进行有效的职业生涯规划,势必会造成生命和时间的浪费。
作为当代大学生,若是带着一脸茫然,踏入这个拥挤的社会怎能满足社会的需要,使自己占有一席之地?因此,我试着为自己拟定一份职业生涯规划,将自己的未来好好的设计一下。
有了目标,才会有动力。
二、自我盘点:我是一个本科生,是家里最大的希望。
成为有用之才是所有亲朋好友的希望。
我性格外向、开朗、活泼,业余时间爱交友、听音乐、外出散步,还有上网。
喜欢看小说、名人传记,尤其爱看杂志类的书籍,心中偶像是周恩来和吴仪,平时与人友好相处。
蒙受亲人、朋友、教师关爱,喜欢创新,动手能力较强做事认真、投入,但缺乏毅力、恒心,以致成绩不太理想,有时又多愁善感。
但总感觉有时缺乏自信心,并且不喜欢别人在背后评论自己。
有时候有点任性,有些小霸道。
三、解决自我盘点中的劣势和缺点:虽然恒心不够,毅力不够,但可凭借自身那份积极向上的热情鞭策自己,久而久之,我想就会慢慢培养起来的。
并且要充分利用一直关心支持我的庞大亲友团的优势,真心向同学、老师、朋友请教,及时请他们指出自身存在的各种不同缺点,并制定出相应计划以针对改正。
经常锻炼,增强体质,增加自信心,使自己更好表现。
虽然性格是很难改变的,但我要学会控制自己,给别人留下一个好印象,为自己的成功铺平道路。
四、未来人生职业生涯规划:根据自己的兴趣和所学专业,在未来应该会向检测和食品两方面发展。
围绕这两个方面,本人对未来7年作初步职业生涯规划如下:1、2010-2014年完成学业并争取学有所成。
充分利用校园环境及条件优势,认真学好专业知识,培养学习、工作、生活能力,全面提高个人综合素质,并作为就业准备。
2、2014-2016年,熟悉适应期:利用2年左右的时间,经过不断的尝试努力,争取找到合适自身发展的工作环境、岗位。
充分利用自身的工作条件扩大社交圈、重视同学交际圈、重视和每个人的交往,不论身份贵贱和亲疏程度。
3、2016-2019年,在自己的工作岗位上,踏踏实实的贡献自己的力量,拥有一个完美的家庭,使自己家庭事业两不误。
完成主要内容:(1)学历、知识结构:提升自身知识层次,从学校走向社会。
专业技能熟练,英语四、六级争取通过、普通话过级,且拿到英语口语等级证书及驾照。
开始接触社会、工作、熟悉工作环境。
(2)个人发展、人际关系:在这一期间,主要做好职业生涯的基础工作,加强沟通,虚心求教。
(3)生活习惯、兴趣爱好:适当交际的环境下,尽量形成比较有规律的良好个人习惯,并参加健身运动,如散步、打篮球等。
养成良好的锻炼、饮食、生活习惯。
每天保证睡眠6-8小时,每周锻炼三次以上。
五、成功标准:我的成功标准是个人事务、职业生涯、家庭生活的协调发展。
只要自己尽心尽力,能力也得到了发挥,每个阶段都有了切实的自我提高,即使目标没有实现,我也不会觉得失败,给自己太多的压力本身就是一件失败的事情。
六、结束语:计划固然好,但更重要的在于具体实践并取得成效。
任何目标,只说不做到头来都会是一场空。
然而,现实是未知多变的,定出的目标计划随时都可能遭遇问题,要求有清醒的头脑。
其实,每个人心中都有一座山峰,雕刻着理想、信念、追求、抱负;每个人心中都有一片森林,承载着收获、芬芳、失意、磨砺。
一个人,若要获得成功,必须拿出勇气,付出努力、拼搏、奋斗。
成功,不相信眼泪;成功,不相信颓废;成功不相信幻影,未来,要靠自己去打拼。
职业规划肯定要有,但是我觉得职业规划不可能现在就定下来,周围的环境随时在变,而且自己随着不断的成熟和接触不同的东西,也会变。
我以前想当官,后来想当外企白领,现在想创业,所以我觉得这个很难就定下来,更何况是在校大学生,没有任何社会阅历。
但是,虽然可能没有成型的职业规划,但是我觉得每个阶段的前进方向和短期目标要有,比如这段时间我要好好补习功课以迎接考试。
如果没有努力的方向和短期的目标,那就容易虚度光阴,浪费青春。
为我加油吧!。
