高考数学大一轮复习第九章平面解析几何第5节第1课时椭圆及其标准方程课件文新人教A版

合集下载

2021版高考数学一轮复习第9章解析几何第5节椭圆课件文新人教A版

4．(选修 2－1P49A 组 T6 改编)已知点 P 是椭圆x52＋y42＝1 上 y 轴右侧的一点，且以点 P 及焦点 F1，F2 为顶点的三角形的面积等于 1，则点 P 的坐标为________．
解析：设 P(x，y)，由题意知 c2＝a2－b2＝5－4＝1，
所以 c＝1，则|F1F2|＝2.由题意可得，点 P 到 x 轴的距离为 1，所以 y＝±1，把 y＝±1 代入x52＋y42＝1，
其数学表达式：集合 P＝{M||MF1|＋|MF2|＝2a}， |F1F2|＝2c，其中 a>0，c>0，且 a，c 为常数：
(1)若 4 __a_>_c_____，则集合 P 为椭圆； (2)若 5 __a_＝__c____，则集合 P 为线段； (3)若 6 __a_<_c_____，则集合 P 为空集．
)
解析：(1)由椭圆的定义知，当该常数大于|F1F2|时，其轨迹才是椭圆，而常数等于|F1F2|
时，其轨迹为线段 F1F2，常数小于|F1F2|时，不存在这样的图形．
(2)因为 e＝ac＝ a2a－b2＝
1－ba2，所以 e 越大，则ba越小，椭圆就越扁．
答案：(1)× (2)× (3)√ (4)√
得 x＝± 215，又 x>0，所以 x＝ 215，
所以 P 点坐标为
215，1或
215，－1.
答案：
215，1或
215，－1
三、易错自纠 5．若方程5－x2m＋m＋y2 3＝1 表示椭圆，则 m 的取值范围是________．
解析：由方程表示椭圆知5m－＋m3>>00，， 5－m≠m＋3，
解得－3<m<5 且 m≠1.
A1(0，－a)，A2(0，a)， B1(－b，0)，B2(b，0)

高考数学一轮复习椭圆及其性质课件

30
D [由椭圆的定义，知|AF1|＋|AF2|＝2a，|BF1|＋|BF2|＝2a，所以 △AF1B 的周长为|AF1|＋|AF2|＋|BF1|＋|BF2|＝4a＝12，所以 a＝3.因为椭圆的离心率 e＝ac＝23，所以 c＝2，所以 b2＝a2－c2＝5，所以椭圆 C 的方程为x92＋y52＝1，故选 D.]
)
[答案](1)× (2)× (3)× (4)√
10
二、教材改编
1．设 P 是椭圆2x52 ＋1y62 ＝1 上的点，若 F1，F2 是椭圆的两个焦点，
则|PF1|＋|PF2|等于( )
A．4
B．5
C．8
D．10
D [依椭圆的定义知：|PF1|＋|PF2|＝2×5＝10.]
11
2．已知中心在原点的椭圆 C 的右焦点为 F(1,0)，离心率等于12，
9
一、思考辨析(正确的打“√”，错误的打“×”)
(1)平面内到两个定点 F1，F2 的距离之和等于常数的点的轨迹是
椭圆．
()
(2)椭圆的离心率 e 越大，椭圆就越圆．
()
(3)ay22＋bx22＝1(a≠b)表示焦点在 y 轴上的椭圆．
()
(4)ax22＋by22＝1(a＞b＞0)与ay22＋bx22＝1(a＞b＞0)的焦距相等．(
则椭圆 C 的方程是( )
A.x32＋y42＝1
B.x42＋ y23＝1
C.x42＋y22＝1
D.x42＋y32＝1
12
D [设椭圆的标准方程为ax22＋by22＝1(a＞b＞0)．
因为椭圆的一个焦点为
F(1,0) ，离心率
e
＝
1 2
，
所
以

2020版高考数学总复习第九章平面解析几何第5节椭圆(第1课时)椭圆及简单几何性质课件文北师大版

2.椭圆的标准方程和几何性质
标准方程
ax22＋by22＝1 (a>b>0)
图形
ay22＋bx22＝1 (a>b>0)
范围
－a≤x≤a －b≤y≤b
－b≤x≤b －a≤y≤a
对称性
对称轴：坐标轴；对称中心：原点
顶点性质
A1(－a，0)，A2(a，0)， A1(0，－a)，A2(0，a)，
B1(0，－b)，B2(0，b)
解得
m－2>10－m，
6<m<10.因为焦距为 4，所以 c2＝m－2－10＋m＝4，解得 m＝8.
答案 A
角度2 椭圆的离心率
【例 3－2】 (2018·全国Ⅱ卷)已知 F1，F2 是椭圆 C 的两个焦点，P 是 C 上的一点．若
解析 (1)由椭圆的方程得 a＝ 3.设椭圆的另一个焦点为 F，则由椭圆的定义得|BA| ＋|BF|＝|CA|＋|CF|＝2a，所以△ABC 的周长为|BA|＋|BC|＋|CA|＝|BA|＋|BF|＋|CF|＋ |CA|＝(|BA|＋|BF|)＋(|CF|＋|CA|)＝2a＋2a＝4a＝4 3. (2)由椭圆的方程可知 F2(3，0)，由椭圆的定义可得|PF1|＝2a－|PF2|，∴|PM|－|PF1| ＝|PM|－(2a－|PF2|)＝|PM|＋|PF2|－2a≥|MF2|－2a，当且仅当 M，P，F2 三点共线时取得等号，又|MF2|＝（6－3）2＋（4－0）2＝5，2a＝10，∴|PM|－|PF1|≥5－10 ＝－5，即|PM|－|PF1|的最小值为－5. 答案 (1)C (2)－5
(2)(一题多解)若椭圆经过两点(2，0)和(0，1)，则椭圆的标准方程为_____________.

高考数学一轮复习第九章平面解析几何 9.5 椭圆文

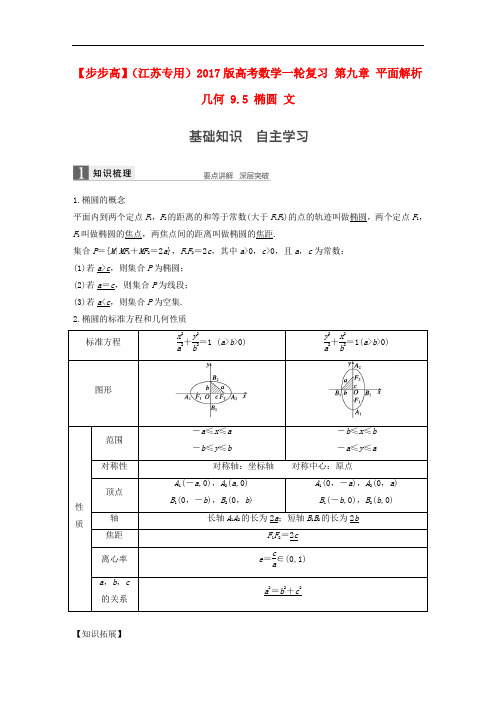
【步步高】（江苏专用）2017版高考数学一轮复习第九章平面解析几何 9.5 椭圆文1.椭圆的概念平面内到两个定点F1，F2的距离的和等于常数(大于F1F2)的点的轨迹叫做椭圆，两个定点F1，F2叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距.集合P＝{M|MF1＋MF2＝2a}，F1F2＝2c，其中a>0，c>0，且a，c为常数：(1)若a>c，则集合P为椭圆；(2)若a＝c，则集合P为线段；(3)若a<c，则集合P为空集.2.椭圆的标准方程和几何性质标准方程x2a2＋y2b2＝1 (a>b>0)y2a2＋x2b2＝1(a>b>0) 图形性质范围－a≤x≤a－b≤y≤b－b≤x≤b－a≤y≤a 对称性对称轴：坐标轴对称中心：原点顶点A1(－a,0)，A2(a,0)B1(0，－b)，B2(0，b)A1(0，－a)，A2(0，a)B1(－b,0)，B2(b,0) 轴长轴A1A2的长为2a；短轴B1B2的长为2b焦距F1F2＝2c离心率e＝ca∈(0,1)a，b，c的关系a2＝b2＋c2【知识拓展】点P (x 0，y 0)和椭圆的关系(1)点P (x 0，y 0)在椭圆内⇔x 20a 2＋y 20b 2<1.(2)点P (x 0，y 0)在椭圆上⇔x 20a 2＋y 20b 2＝1.(3)点P (x 0，y 0)在椭圆外⇔x 20a 2＋y 20b2>1.【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)平面内与两个定点F 1，F 2的距离之和等于常数的点的轨迹是椭圆.( × )(2)椭圆上一点P 与两焦点F 1，F 2构成△PF 1F 2的周长为2a ＋2c (其中a 为椭圆的长半轴长，c 为椭圆的半焦距).( √ )(3)椭圆的离心率e 越大，椭圆就越圆.( × )(4)方程mx 2＋ny 2＝1(m >0，n >0，m ≠n )表示的曲线是椭圆.( √ )(5)y 2a 2＋x 2b 2＝1 (a ≠b )表示焦点在y 轴上的椭圆.( × ) (6)x 2a 2＋y 2b 2＝1 (a >b >0)与y 2a 2＋x 2b2＝1(a >b >0)的焦距相等.( √ )1.(教材改编)椭圆x 210－m ＋y 2m －2＝1的焦距为4，则m ＝________.答案 4或8解析当焦点在x 轴上时，10－m >m －2>0， 10－m －(m －2)＝4，∴m ＝4. 当焦点在y 轴上时，m －2>10－m >0，m －2－(10－m )＝4，∴m ＝8.2.(2015·广东)已知椭圆x 225＋y 2m2＝1(m >0)的左焦点为F 1(－4,0)，则m ＝________.答案 3解析由题意知25－m 2＝16，解得m 2＝9，又m >0，所以m ＝3.3.已知椭圆C ：x 2a 2＋y 2b 2＝1 (a >b >0)的左、右焦点为F 1、F 2，离心率为33，过F 2的直线l 交C于A 、B 两点，若△AF 1B 的周长为43，则C 的方程为______________.答案x 23＋y 22＝1 解析 ∵△AF 1B 的周长为43，∴4a ＝43， ∴a ＝3，∵离心率为33，∴c ＝1， ∴b ＝a 2－c 2＝2，∴椭圆C 的方程为x 23＋y 22＝1.4.如果方程x 2＋ky 2＝2表示焦点在y 轴上的椭圆，那么实数k 的取值范围是________. 答案 (0,1)解析将椭圆方程化为x 22＋y 22k＝1，因为焦点在y 轴上，则2k>2，即k <1，又k >0，所以0<k <1.5.(教材改编)已知点P 是椭圆x 25＋y 24＝1上y 轴右侧的一点，且以点P 及焦点F 1，F 2为顶点的三角形的面积等于1，则点P 的坐标为__________________. 答案 ⎝⎛⎭⎪⎫152，1或⎝ ⎛⎭⎪⎫152，－1 解析设P (x ，y )，由题意知c 2＝a 2－b 2＝5－4＝1，所以c ＝1，则F 1(－1,0)，F 2(1,0)，由题意可得点P 到x 轴的距离为1，所以y ＝±1，把y ＝±1代入x 25＋y 24＝1，得x ＝±152，又x >0，所以x ＝152，∴P 点坐标为⎝ ⎛⎭⎪⎫152，1或⎝ ⎛⎭⎪⎫152，－1.题型一椭圆的定义及标准方程命题点1 椭圆定义的应用例1 如图所示，一圆形纸片的圆心为O ，F 是圆内一定点，M 是圆周上一动点，把纸片折叠使M 与F 重合，然后抹平纸片，折痕为CD ，设CD 与OM 交于点P ，则点P 的轨迹是________.答案椭圆解析由条件知PM ＝PF .∴PO ＋PF ＝PO ＋PM ＝OM ＝R >OF . ∴P 点的轨迹是以O ，F 为焦点的椭圆. 命题点2 利用待定系数法求椭圆方程例2 (1)已知椭圆以坐标轴为对称轴，且长轴是短轴的3倍，并且过点P (3,0)，则椭圆的方程为________________________________________________________________________. (2)已知椭圆的中心在原点，以坐标轴为对称轴，且经过两点P 1(6，1)，P 2(－3，－2)，则椭圆的方程为__________________________________________________________. 答案 (1)x 29＋y 2＝1或y 281＋x 29＝1(2)x 29＋y 23＝1 解析 (1)若焦点在x 轴上，设方程为x 2a 2＋y 2b 2＝1(a >b >0)，∵椭圆过P (3,0)，∴32a 2＋02b2＝1，即a ＝3，又2a ＝3×2b ，∴b ＝1，方程为x 29＋y 2＝1. 若焦点在y 轴上，设方程为y 2a 2＋x 2b2＝1(a >b >0).∵椭圆过点P (3,0).∴02a 2＋32b2＝1，即b ＝3.又2a ＝3×2b ，∴a ＝9，∴方程为y 281＋x 29＝1.∴所求椭圆的方程为x 29＋y 2＝1或y 281＋x 29＝1.(2)设椭圆方程为mx 2＋ny 2＝1(m >0，n >0且m ≠n ). ∵椭圆经过点P 1，P 2，∴点P 1，P 2的坐标适合椭圆方程.则⎩⎪⎨⎪⎧6m ＋n ＝1， ①3m ＋2n ＝1， ②①②两式联立，解得⎩⎪⎨⎪⎧m ＝19，n ＝13.∴所求椭圆方程为x 29＋y 23＝1. 思维升华 (1)求椭圆的方程多采用定义法和待定系数法，利用椭圆的定义定形状时，一定要注意常数2a >F 1F 2这一条件.(2)求椭圆标准方程的基本方法是待定系数法，具体过程是先定形，再定量，即首先确定焦点所在位置，然后再根据条件建立关于a ，b 的方程组.如果焦点位置不确定，要考虑是否有两解，有时为了解题方便，也可把椭圆方程设为mx 2＋ny 2＝1 (m >0，n >0，m ≠n )的形式.(1)已知圆(x ＋2)2＋y 2＝36的圆心为M ，设A 为圆上任一点，且点N (2,0)，线段AN 的垂直平分线交MA 于点P ，则动点P 的轨迹是__________.(2)过点(3，－5)，且与椭圆y 225＋x 29＝1有相同焦点的椭圆的标准方程为____________.(3)(2014·安徽)设F 1，F 2分别是椭圆E ：x 2＋y 2b2＝1(0<b <1)的左，右焦点，过点F 1的直线交椭圆E 于A ，B 两点.若AF 1＝3F 1B ，AF 2⊥x 轴，则椭圆E 的方程为______________. 答案 (1)椭圆 (2)y 220＋x 24＝1 (3)x 2＋32y 2＝1解析 (1)点P 在线段AN 的垂直平分线上，故PA ＝PN ，又AM 是圆的半径， ∴PM ＋PN ＝PM ＋PA ＝AM ＝6>MN ，由椭圆定义知，P 的轨迹是椭圆.(2)方法一椭圆y 225＋x 29＝1的焦点为(0，－4)，(0,4)，即c ＝4.由椭圆的定义知，2a ＝3－02＋－5＋42＋3－02＋－5－42，解得a ＝2 5.由c 2＝a 2－b 2可得b 2＝4.∴所求椭圆的标准方程为y 220＋x 24＝1.方法二 ∵所求椭圆与椭圆y 225＋x 29＝1的焦点相同， ∴其焦点在y 轴上，且c 2＝25－9＝16.设它的标准方程为y 2a 2＋x 2b2＝1(a >b >0).∵c 2＝16，且c 2＝a 2－b 2，故a 2－b 2＝16.① 又点(3，－5)在所求椭圆上， ∴－52a 2＋32b 2＝1，即5a2＋3b2＝1.②由①②得b 2＝4，a 2＝20，∴所求椭圆的标准方程为y 220＋x 24＝1.(3)设点B 的坐标为(x 0，y 0).∵x 2＋y 2b2＝1，∴F 1(－1－b 2，0)，F 2(1－b 2，0).∵AF 2⊥x 轴，∴可取A (1－b 2，b 2). ∵AF 1＝3F 1B ，∴AF 1→＝3F 1B →，∴(－21－b 2，－b 2)＝3(x 0＋1－b 2，y 0). ∴x 0＝－531－b 2，y 0＝－b 23.∴点B 的坐标为⎝ ⎛⎭⎪⎫－531－b 2，－b 23.将B ⎝ ⎛⎭⎪⎫－531－b 2，－b 23代入x 2＋y 2b 2＝1，得b 2＝23.∴椭圆E 的方程为x 2＋32y 2＝1.题型二椭圆的几何性质例3 (1)已知点F 1，F 2是椭圆x 2＋2y 2＝2的左，右焦点，点P 是该椭圆上的一个动点，那么|PF 1→＋PF 2→|的最小值是________.(2)(2015·浙江)椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的右焦点F (c ，0)关于直线y ＝bcx 的对称点Q 在椭圆上，则椭圆的离心率是________. 答案 (1)2 (2)22解析 (1)设P (x 0，y 0)，则PF 1→＝(－1－x 0，－y 0)，PF 2→＝(1－x 0，－y 0)，∴PF 1→＋PF 2→＝(－2x 0，－2y 0)，∴|PF 1→＋PF 2→|＝4x 20＋4y 20 ＝22－2y 20＋y 20 ＝2－y 20＋2.∵点P 在椭圆上，∴0≤y 20≤1， ∴当y 20＝1时，|PF 1→＋PF 2→|取最小值2.(2)方法一设椭圆的另一个焦点为F 1(－c,0)，如图，连结QF 1，QF ，设QF 与直线y ＝b cx 交于点M .由题意知M 为线段QF 的中点，且OM ⊥FQ .又O 为线段F 1F 的中点， ∴F 1Q ∥OM ，∴F 1Q ⊥QF ，F 1Q ＝2OM . 在Rt△MOF 中，tan∠MOF ＝MF OM ＝bc，OF ＝c ，可解得OM ＝c 2a ，MF ＝bca，故QF ＝2MF ＝2bc a ，QF 1＝2OM ＝2c2a.由椭圆的定义得QF ＋QF 1＝2bc a ＋2c2a＝2a ，整理得b ＝c ，∴a ＝b 2＋c 2＝2c ，故e ＝c a ＝22. 方法二设Q (x 0，y 0)，则FQ 的中点坐标⎝⎛⎭⎪⎫x 0＋c 2，y 02，k FQ＝y 0x 0－c ，依题意⎩⎪⎨⎪⎧y 02＝b c ·x 0＋c2，y 0x 0－c ·b c ＝－1，解得⎩⎪⎨⎪⎧x 0＝c 2c 2－a 2a 2，y 0＝2bc2a 2，又因为(x 0，y 0)在椭圆上，所以c 22c 2－a 22a 6＋4c4a4＝1，令e ＝c a，则4e 6＋e 2＝1，∴离心率e ＝22. 思维升华 (1)利用椭圆几何性质的注意点及技巧 ①注意椭圆几何性质中的不等关系：在求与椭圆有关的一些量的范围，或者最大值、最小值时，经常用到椭圆标准方程中x ，y 的范围，离心率的范围等不等关系. ②利用椭圆几何性质的技巧：求解与椭圆几何性质有关的问题时，要结合图形进行分析，当涉及顶点、焦点、长轴、短轴等椭圆的基本量时，要理清它们之间的内在联系. (2)求椭圆的离心率问题的一般思路求椭圆的离心率或其范围时，一般是依据题设得出一个关于a ，b ，c 的等式或不等式，利用a 2＝b 2＋c 2消去b ，即可求得离心率或离心率的范围.(1)已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)与双曲线x 2m 2－y 2n2＝1(m >0，n >0)有相同的焦点(－c,0)和(c,0)，若c 是a 、m 的等比中项，n 2是2m 2与c 2的等差中项，则椭圆的离心率是________. (2)已知椭圆x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1(－c,0)、F 2(c,0)，若椭圆上存在点P使a sin∠PF 1F 2＝csin∠PF 2F 1，则椭圆的离心率的取值范围为______.答案 (1)12(2)(2－1,1)解析 (1)在双曲线中m 2＋n 2＝c 2，又2n 2＝2m 2＋c 2，解得m ＝c2，又c 2＝am ，故椭圆的离心率e ＝c a ＝12. (2)依题意及正弦定理，得PF 2PF 1＝ac (注意到P 不与F 1，F 2共线)，即PF 22a －PF 2＝ac，∴2aPF 2－1＝c a，∴2aPF 2＝c a ＋1>2a a ＋c，即e ＋1>21＋e ，∴(e ＋1)2>2.又0<e <1，因此2－1<e <1.题型三直线与椭圆的综合问题命题点1 由直线与椭圆的位置关系研究椭圆的性质例4 (2015·重庆)如图，椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)的左、右焦点分别为F 1、F 2，过F 2的直线交椭圆于P ，Q 两点，且PQ ⊥PF 1.(1)若PF 1＝2＋2，PF 2＝2－2，求椭圆的标准方程；(2)若PQ ＝λPF 1，且34≤λ＜43，试确定椭圆离心率e 的取值范围.解 (1)由椭圆的定义，2a ＝PF 1＋PF 2＝(2＋2)＋(2－2)＝4，故a ＝2. 设椭圆的半焦距为c ，由已知PF 1⊥PF 2，因此2c ＝F 1F 2＝PF 21＋PF 22 ＝2＋22＋2－22＝23，即c ＝3，从而b ＝a 2－c 2＝1. 故所求椭圆的标准方程为x 24＋y 2＝1.(2)如图，连结F 1Q ，由PF 1⊥PQ ，PQ ＝λPF 1，得QF 1＝PF 21＋PQ 2＝1＋λ2PF 1.由椭圆的定义，PF 1＋PF 2＝2a ，QF 1＋QF 2＝2a ，进而PF 1＋PQ ＋QF 1＝4a ，于是(1＋λ＋1＋λ2)PF 1＝4a ，解得PF 1＝4a 1＋λ＋1＋λ2，故PF 2＝2a －PF 1＝2aλ＋1＋λ2－11＋λ＋1＋λ2. 由勾股定理得PF 21＋PF 22＝F 1F 22＝(2c )2＝4c 2，从而⎝ ⎛⎭⎪⎫4a 1＋λ＋1＋λ22＋⎝ ⎛⎭⎪⎫2a λ＋1＋λ2－11＋λ＋1＋λ22＝4c 2. 两边除以4a 2，得41＋λ＋1＋λ22＋λ＋1＋λ2－121＋λ＋1＋λ22＝e 2.若记t ＝1＋λ＋1＋λ2，则上式变成 e 2＝4＋t －22t 2＝8⎝ ⎛⎭⎪⎫1t －142＋12.由34≤λ＜43，并注意到t ＝1＋λ＋1＋λ2关于λ的单调性，得3≤t ＜4，即14＜1t ≤13. 进而12＜e 2≤59，即22＜e ≤53.命题点2 由直线与椭圆的位置关系研究直线的性质例5 (2015·江苏)如图，在平面直角坐标系xOy 中，已知椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)的离心率为22，且右焦点F 到左准线l 的距离为3.(1)求椭圆的标准方程；(2)过F 的直线与椭圆交于A ，B 两点，线段AB 的垂直平分线分别交直线l 和AB 于点P ，C ，若PC ＝2AB ，求直线AB 的方程.解 (1)由题意，得c a ＝22且c ＋a 2c＝3，解得a ＝2，c ＝1，则b ＝1，所以椭圆的标准方程为x 22＋y 2＝1.(2)当AB ⊥x 轴时，AB ＝2，又CP ＝3，不合题意.当AB 与x 轴不垂直时，设直线AB 的方程为y ＝k (x －1)，A (x 1，y 1)，B (x 2，y 2)，将AB 的方程代入椭圆方程，得(1＋2k 2)x 2－4k 2x ＋2(k 2－1)＝0，则x 1,2＝2k 2±21＋k21＋2k2，C 的坐标为⎝ ⎛⎭⎪⎫2k 21＋2k 2，－k 1＋2k 2，且AB ＝x 2－x 12＋y 2－y 12＝1＋k2x 2－x 12＝221＋k 21＋2k2.若k ＝0，则线段AB 的垂直平分线为y 轴，与左准线平行，不合题意. 从而k ≠0，故直线PC 的方程为 y ＋k1＋2k 2＝－1k ⎝ ⎛⎭⎪⎫x －2k 21＋2k 2，则P 点的坐标为⎝ ⎛⎭⎪⎫－2，5k 2＋2k 1＋2k 2，从而PC ＝23k 2＋11＋k2|k |1＋2k2. 因为PC ＝2AB ，所以23k 2＋11＋k 2|k |1＋2k 2＝421＋k21＋2k2，解得k ＝±1.此时直线AB 的方程为y ＝x －1或y ＝－x ＋1.思维升华解决直线与椭圆的位置关系的相关问题，其常规思路是先把直线方程与椭圆方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题.涉及弦中点的问题时用“点差法”解决，往往会更简单.(2015·北京)已知椭圆C ：x 2＋3y 2＝3，过点D (1,0)且不过点E (2,1)的直线与椭圆C 交于A ，B 两点，直线AE 与直线x ＝3交于点M . (1)求椭圆C 的离心率；(2)若AB 垂直于x 轴，求直线BM 的斜率；(3)试判断直线BM 与直线DE 的位置关系，并说明理由. 解 (1)椭圆C 的标准方程为x 23＋y 2＝1，所以a ＝3，b ＝1，c ＝ 2. 所以椭圆C 的离心率e ＝c a ＝63. (2)因为AB 过点D (1,0)且垂直于x 轴，所以可设A (1，y 1)，B (1，－y 1)，直线AE 的方程为y －1＝(1－y 1)(x －2)，令x ＝3，得M (3,2－y 1)，所以直线BM 的斜率k BM ＝2－y 1＋y 13－1＝1.(3)直线BM 与直线DE 平行，证明如下：当直线AB 的斜率不存在时，由(2)可知k BM ＝1. 又因为直线DE 的斜率k DE ＝1－02－1＝1，所以BM ∥DE ，当直线AB 的斜率存在时，设其方程为y ＝k (x －1)(k ≠1)，设A (x 1，y 1)，B (x 2，y 2)，则直线AE 的方程为y －1＝y 1－1x 1－2(x －2).令x ＝3，得点M ⎝⎛⎭⎪⎫3，y 1＋x 1－3x 1－2，由⎩⎪⎨⎪⎧x 2＋3y 2＝3，y ＝k x －1，得(1＋3k 2)x 2－6k 2x ＋3k 2－3＝0，所以x 1＋x 2＝6k 21＋3k 2，x 1x 2＝3k 2－31＋3k2，直线BM 的斜率k BM ＝y 1＋x 1－3x 1－2－y 23－x 2，因为k BM －1 ＝k x 1－1＋x 1－3－k x 2－1x 1－2－3－x 2x 1－23－x 2x 1－2＝k －1[－x 1x 2＋2x 1＋x 2－3]3－x 2x 1－2＝k －1⎝ ⎛⎭⎪⎫－3k 2＋31＋3k 2＋12k 21＋3k 2－33－x 2x 1－2＝0，所以k BM ＝1＝k DE ，所以BM ∥DE . 综上可知，直线BM 与直线DE 平行.8.高考中求椭圆的离心率问题典例 (1)(2015·福建)已知椭圆E ：x 2a 2＋y 2b2＝1(a ＞b ＞0)的右焦点为F ，短轴的一个端点为M ，直线l ：3x －4y ＝0交椭圆E 于A ，B 两点.若AF ＋BF ＝4，点M 到直线l 的距离不小于45，则椭圆E 的离心率的取值范围是__________.(2)(2014·江西)设椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左，右焦点为F 1，F 2，过F 2作x 轴的垂线与C相交于A ，B 两点，F 1B 与y 轴相交于点D ，若AD ⊥F 1B ，则椭圆C 的离心率等于________. 解析 (1)如图，设左焦点为F 0，连结F 0A ，F 0B ，则四边形AFBF 0为平行四边形.∵AF ＋BF ＝4， ∴AF ＋AF 0＝4， ∴a ＝2.设M (0，b )，则4b 5≥45，∴1≤b ＜2.离心率e ＝ca ＝c 2a 2＝a 2－b 2a 2＝ 4－b 24∈⎝⎛⎦⎥⎤0，32. (2)直线AB ：x ＝c ，代入x 2a 2＋y 2b 2＝1，得y ＝±b 2a .∴A (c ，b 2a )，B (c ，－b 2a).∴kBF 1＝－b 2a －0c －－c ＝－b 2a 2c ＝－b 22ac .∴直线BF 1：y －0＝－b 22ac (x ＋c ).令x ＝0，则y ＝－b 22a，∴D (0，－b 22a )，∴k AD ＝b 2a ＋b 22ac ＝3b 22ac .由于AD ⊥BF 1，∴－b 22ac ·3b 22ac＝－1，∴3b 4＝4a 2c 2，∴3b 2＝2ac ，即3(a 2－c 2)＝2ac ， ∴3e 2＋2e －3＝0， ∴e ＝－2±4－4×3×－323＝－2±423.∵e >0，∴e ＝－2＋423＝223＝33.答案 (1)⎝ ⎛⎦⎥⎤0，32 (2)33 温馨提醒离心率是椭圆的重要几何性质，是高考重点考查的一个知识点.这类问题一般有两类：一类是根据一定的条件求椭圆的离心率；另一类是根据一定的条件求离心率的取值范围.无论是哪类问题，其难点都是建立关于a ，b ，c 的关系式(等式或不等式)，并且最后要把其中的b 用a ，c 表达，转化为关于离心率e 的关系式，这是化解有关椭圆的离心率问题难点的根本方法.[方法与技巧]1.椭圆的定义揭示了椭圆的本质属性，正确理解、掌握定义是关键，应注意定义中的常数大于F 1F 2，避免了动点轨迹是线段或不存在的情况.2.求椭圆方程的方法，除了直接根据定义外，常用待定系数法.当椭圆的焦点位置不明确而无法确定其标准方程时，设方程为x 2m ＋y 2n＝1 (m >0，n >0，且m ≠n )可以避免讨论和烦琐的计算，也可以设为Ax 2＋By 2＝1 (A >0，B >0，且A ≠B )，这种形式在解题中更简便. 3.讨论椭圆的几何性质时，离心率问题是重点，求离心率的常用方法有以下两种： (1)求得a ，c 的值，直接代入公式e ＝c a求得；(2)列出关于a ，b ，c 的齐次方程(或不等式)，然后根据b 2＝a 2－c 2，消去b ，转化成关于e 的方程(或不等式)求解. [失误与防范]1.判断两种标准方程的方法为比较标准形式中x 2与y 2的分母大小.2.注意椭圆的范围，在设椭圆x 2a 2＋y 2b2＝1 (a >b >0)上点的坐标为P (x ，y )时，则|x |≤a ，这往往在求与点P 有关的最值问题中用到，也是容易被忽略而导致求最值错误的原因.A 组专项基础训练 (时间：40分钟)1.设F 1，F 2分别是椭圆x 225＋y 216＝1的左，右焦点，P 为椭圆上一点，M 是F 1P 的中点，OM ＝3，则P 点到椭圆左焦点的距离为________. 答案 4解析由题意知，在△PF 1F 2中，OM ＝12PF 2＝3，∴PF 2＝6，∴PF 1＝2a －PF 2＝10－6＝4.2.椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右顶点分别是A 、B ，左、右焦点分别是F 1、F 2，若AF 1，F 1F 2，F 1B 成等比数列，则此椭圆的离心率为________.答案55解析由题意知AF 1＝a －c ，F 1F 2＝2c ，F 1B ＝a ＋c ，且三者成等比数列，则F 1F 22＝AF 1·F 1B ，即4c 2＝a 2－c 2，a 2＝5c 2，所以e 2＝15，所以e ＝55.3.已知F 1(－1,0)，F 2(1,0)是椭圆C 的两个焦点，过F 2且垂直于x 的直线与椭圆C 交于A ，B两点，且AB ＝3，则C 的方程为______________. 答案x 24＋y 23＝1 解析设椭圆C 的方程为x 2a 2＋y 2b 2＝1(a >b >0)，则c ＝1.因为过F 2且垂直于x 轴的直线与椭圆交于A ，B 两点，且AB ＝3，所以b 2a ＝32，b 2＝a 2－c 2，所以a 2＝4，b 2＝a 2－c 2＝4－1＝3，椭圆的方程为x 24＋y 23＝1.4.已知椭圆x 24＋y 22＝1上有一点P ，F 1，F 2是椭圆的左，右焦点，若△F 1PF 2为直角三角形，则这样的点P 有______个. 答案 6解析当∠PF 1F 2为直角时，根据椭圆的对称性知，这样的点P 有2个；同理当∠PF 2F 1为直角时，这样的点P 有2个；当P 点为椭圆的短轴端点时，∠F 1PF 2最大，且为直角，此时这样的点P 有2个.故符合要求的点P 有6个.5.已知圆M ：x 2＋y 2＋2mx －3＝0(m <0)的半径为2，椭圆C ：x 2a 2＋y 23＝1的左焦点为F (－c,0)，若垂直于x 轴且经过F 点的直线l 与圆M 相切，则a 的值为________. 答案 2解析圆M 的方程可化为(x ＋m )2＋y 2＝3＋m 2，则由题意得m 2＋3＝4，即m 2＝1(m <0)， ∴m ＝－1，则圆心M 的坐标为(1,0). 由题意知直线l 的方程为x ＝－c ，又∵直线l 与圆M 相切，∴c ＝1，∴a 2－3＝1，∴a ＝2.6.已知P 为椭圆x 225＋y 216＝1上的一点，M ，N 分别为圆(x ＋3)2＋y 2＝1和圆(x －3)2＋y 2＝4上的点，则PM ＋PN 的最小值为________. 答案 7解析由题意知椭圆的两个焦点F 1，F 2分别是两圆的圆心，且PF 1＋PF 2＝10，从而PM ＋PN 的最小值为PF 1＋PF 2－1－2＝7.7.已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的离心率等于13，其焦点分别为A 、B 、C 为椭圆上异于长轴端点的任意一点，则在△ABC 中，sin A ＋sin Bsin C 的值等于________.答案 3解析在△ABC 中，由正弦定理得sin A ＋sin B sin C ＝CB ＋CAAB ，因为点C 在椭圆上，所以由椭圆定义知CA ＋CB ＝2a ，而AB ＝2c ，所以sin A ＋sin B sin C ＝2a 2c ＝1e＝3.8.已知F 1(－c,0)，F 2(c,0)为椭圆x 2a 2＋y 2b2＝1(a >b >0)的两个焦点，P 为椭圆上一点，且PF 1→·PF 2→＝c 2，则此椭圆离心率的取值范围是________________________. 答案 ⎣⎢⎡⎦⎥⎤33，22 解析设P (x ，y )，则PF 1→·PF 2→＝(－c －x ，－y )·(c －x ，－y )＝x 2－c 2＋y 2＝c 2，①将y 2＝b 2－b 2a2x 2代入①式解得x 2＝2c 2－b2a 2c 2＝3c 2－a2a 2c 2，又x 2∈[0，a 2]，∴2c 2≤a 2≤3c 2， ∴e ＝c a ∈⎣⎢⎡⎦⎥⎤33，22.9.如图，在平面直角坐标系xOy 中，椭圆C ：x 2a 2＋y 2b2＝1 (a >b >0)的右准线方程为x ＝4，右顶点为A ，上顶点为B ，右焦点为F ，斜率为2的直线l 经过点A ，且点F 到直线l 的距离为255.(1)求椭圆C 的标准方程；(2)将直线l 绕点A 旋转，它与椭圆C 相交于另一点P ，当B ，F ，P 三点共线时，试确定直线l 的斜率.解 (1)由题意知，直线l 的方程为y ＝2(x －a )，即2x －y －2a ＝0，所以右焦点F 到直线l 的距离为|2c －2a |5＝255，所以a －c ＝1.又因为椭圆C 的右准线为x ＝4，即a 2c ＝4，所以c ＝a 24，代入上式解得a ＝2，c ＝1，所以b 2＝3，所以椭圆C 的方程为x 24＋y 23＝1.(2)由(1)知B (0，3)，F (1,0)，所以直线BF 的方程为y ＝－3(x －1)，联立方程组⎩⎪⎨⎪⎧y ＝－3x －1，x 24＋y 23＝1，解得⎩⎨⎧x ＝0，y ＝3(舍去)或⎩⎪⎨⎪⎧x ＝85，y ＝－335.所以P ⎝ ⎛⎭⎪⎫85，－335，所以直线l 的斜率k ＝0－⎝ ⎛⎭⎪⎫－3352－85＝332.10.(2015·安徽)设椭圆E 的方程为x 2a 2＋y 2b2＝1(a >b >0)，点O 为坐标原点，点A 的坐标为(a,0)，点B 的坐标为(0，b )，点M 在线段AB 上，满足BM ＝2MA ，直线OM 的斜率为510. (1)求E 的离心率e ；(2)设点C 的坐标为(0，－b )，N 为线段AC 的中点，证明：MN ⊥AB .(1)解由题设条件知，点M 的坐标为⎝ ⎛⎭⎪⎫23a ，13b ，又k OM ＝510，从而b 2a ＝510. 进而a ＝5b ，c ＝a 2－b 2＝2b ，故e ＝c a ＝255.(2)证明由N 是AC 的中点知，点N 的坐标为⎝ ⎛⎭⎪⎫a2，－b 2，可得NM →＝⎝ ⎛⎭⎪⎫a 6，5b 6，又AB →＝(－a ，b )，从而有AB →·NM →＝－16a 2＋56b 2＝16(5b 2－a 2).由(1)的计算结果可知a 2＝5b 2，所以AB →·NM →＝0，故MN ⊥AB .B 组专项能力提升(时间：30分钟)11.从椭圆x 2a 2＋y 2b2＝1(a >b >0)上一点P 向x 轴作垂线，垂足恰为左焦点F 1，A 是椭圆与x 轴正半轴的交点，B 是椭圆与y 轴正半轴的交点，且AB ∥OP (O 是坐标原点)，则该椭圆的离心率是________. 答案22解析由题意可设P (－c ，y 0)(c 为半焦距)，k OP ＝－y 0c ，k AB ＝－ba，由于OP ∥AB ，∴－y 0c ＝－b a ，y 0＝bc a，把P ⎝ ⎛⎭⎪⎫－c ，bc a 代入椭圆方程得－c 2a 2＋⎝ ⎛⎭⎪⎫bc a 2b 2＝1，∴⎝ ⎛⎭⎪⎫c a 2＝12，∴e ＝c a ＝22.12.如图，已知椭圆C 的中心为原点O ，F (－25，0)为C 的左焦点，P 为C 上一点，满足OP ＝OF ，且PF ＝4，则椭圆C 的方程为__________.答案x 236＋y 216＝1 解析设椭圆的标准方程为x 2a 2＋y 2b2＝1(a >b >0)，焦距为2c ，右焦点为F ′，连结PF ′，如图所示.因为F (－25，0)为C 的左焦点，所以c ＝2 5.由OP ＝OF ＝OF ′知，∠PFF ′＝∠FPO ，∠OF ′P ＝∠OPF ′，所以∠PFF ′＋∠OF ′P ＋∠FPO ＋∠OPF ′＝180°，知∠FPO ＋∠OPF ′＝90°，即FP ⊥PF ′.在Rt△PFF ′中，由勾股定理，得PF ′＝FF ′2－PF 2＝452－42＝8.由椭圆定义，得PF ＋PF ′＝2a ＝4＋8＝12，从而a ＝6，得a 2＝36，于是b 2＝a 2－c 2＝36－(25)2＝16，所以椭圆的方程为x 236＋y 216＝1.13.椭圆x 24＋y 2＝1的左，右焦点分别为F 1，F 2，点P 为椭圆上一动点，若∠F 1PF 2为钝角，则点P 的横坐标的取值范围是________________. 答案 (－263，263)解析设椭圆上一点P 的坐标为(x ，y )，则F 1P →＝(x ＋3，y )，F 2P →＝(x －3，y ). ∵∠F 1PF 2为钝角，∴F 1P →·F 2P →<0，即x 2－3＋y 2<0，①∵y 2＝1－x 24，代入①得x 2－3＋1－x 24<0，34x 2<2，∴x 2<83. 解得－263<x <263，∴x ∈(－263，263).14.(2014·江苏)如图，在平面直角坐标系xOy 中，F 1，F 2分别是椭圆x 2a 2＋y 2b2＝1(a >b >0)的左，右焦点，顶点B 的坐标为(0，b )，连结BF 2并延长交椭圆于点A ，过点A 作x 轴的垂线交椭圆于另一点C ，连结F 1C .(1)若点C 的坐标为⎝ ⎛⎭⎪⎫43，13，且BF 2＝2，求椭圆的方程； (2)若F 1C ⊥AB ，求椭圆离心率e 的值.解设椭圆的焦距为2c ，则F 1(－c,0)，F 2(c,0). (1)因为B (0，b )，所以BF 2＝b 2＋c 2＝a . 又BF 2＝2，故a ＝ 2.因为点C ⎝ ⎛⎭⎪⎫43，13在椭圆上，所以169a 2＋19b 2＝1，解得b 2＝1.故所求椭圆的方程为x 22＋y 2＝1.(2)因为B (0，b )，F 2(c,0)在直线AB 上，所以直线AB 的方程为x c ＋y b＝1.解方程组⎩⎪⎨⎪⎧x c ＋yb＝1，x 2a 2＋y2b 2＝1，得⎩⎪⎨⎪⎧x 1＝2a 2c a 2＋c2，y 1＝bc 2－a 2a 2＋c 2，⎩⎪⎨⎪⎧x 2＝0，y 2＝b .所以点A 的坐标为⎝ ⎛⎭⎪⎫2a 2c a 2＋c 2，b c 2－a 2a 2＋c 2. 又AC 垂直于x 轴，由椭圆的对称性，可得点C 的坐标为⎝ ⎛⎭⎪⎫2a 2c a 2＋c 2，b a 2－c 2a 2＋c 2. 因为直线F 1C 的斜率为b a 2－c 2a 2＋c 2－02a 2c a 2＋c 2－－c ＝b a 2－c 23a 2c ＋c3，直线AB 的斜率为－b c，且F 1C ⊥AB ，所以b a 2－c 23a 2c ＋c 3·⎝ ⎛⎭⎪⎫－b c ＝－1. 又b 2＝a 2－c 2，整理得a 2＝5c 2.故e 2＝15，因此e ＝55.15.(2015·山东)在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为32，且点⎝ ⎛⎭⎪⎫3，12在椭圆C 上.(1)求椭圆C 的方程；(2)设椭圆E ：x 24a 2＋y 24b 2＝1，P 为椭圆C 上任意一点，过点P 的直线y ＝kx ＋m 交椭圆E 于A ，B 两点，射线PO 交椭圆E 于点Q .(ⅰ)求OQ OP的值；(ⅱ)求△ABQ 面积的最大值.解 (1)由题意知3a 2＋14b 2＝1.又a 2－b 2a ＝32，解得a 2＝4，b 2＝1.所以椭圆C 的方程为x 24＋y 2＝1.(2)由(1)知椭圆E 的方程为x 216＋y 24＝1.(ⅰ)设P (x 0，y 0)，OQ OP ＝λ (λ>0)，由题意知Q (－λx 0，－λy 0).因为x 204＋y 20＝1，－λx 0216＋－λy 024＝1，即λ24⎝ ⎛⎭⎪⎫x 204＋y 20＝1，所以λ＝2，即OQ OP ＝2.(ⅱ)设A (x 1，y 1)，B (x 2，y 2).将y ＝kx ＋m 代入椭圆E 的方程，可得(1＋4k 2)x 2＋8kmx ＋4m 2－16＝0，由Δ＞0，可得m 2＜4＋16k 2，①则有x 1＋x 2＝－8km 1＋4k 2，x 1x 2＝4m 2－161＋4k2. 所以|x 1－x 2|＝416k 2＋4－m 21＋4k2. 因为直线y ＝kx ＋m 与y 轴交点的坐标为(0，m )，所以△OAB 的面积S ＝12|m ||x 1－x 2|＝216k 2＋4－m 2|m |1＋4k2 ＝216k 2＋4－m 2m 21＋4k 2＝2⎝ ⎛⎭⎪⎫4－m 21＋4k 2m 21＋4k 2. 设m 21＋4k 2＝t ，将y ＝kx ＋m 代入椭圆C 的方程，可得(1＋4k 2)x 2＋8kmx ＋4m 2－4＝0，由Δ≥0，可得m 2≤1＋4k 2.②由①②可知0＜t ≤1，因此S ＝24－t t ＝2－t 2＋4t ，故S ≤23，当且仅当t ＝1，即m 2＝1＋4k 2时取得最大值2 3.由(ⅰ)知，△ABQ 面积为3S ，所以△ABQ 面积的最大值为6 3.。

2021版高考数学一轮复习第九章平面解析几何第5讲椭圆第1课时椭圆及其性质教案文新人教A版

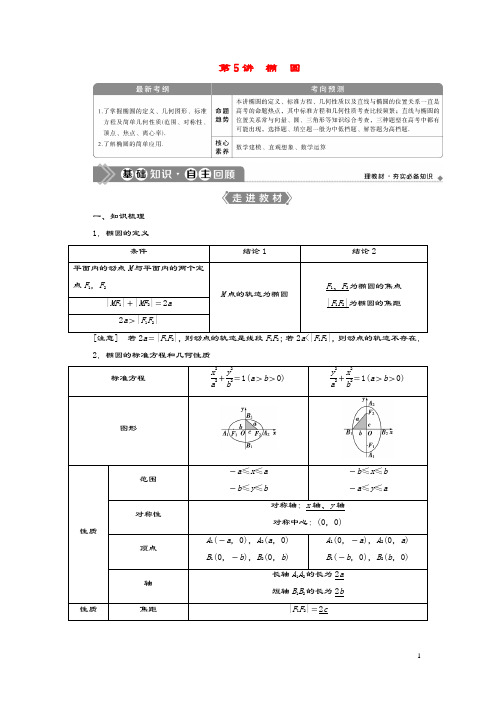
第5讲椭圆一、知识梳理1．椭圆的定义条件结论1结论2 平面内的动点M与平面内的两个定点F1，F2M点的轨迹为椭圆F1、F2为椭圆的焦点|F1F2|为椭圆的焦距|MF1|＋|MF2|＝2a2a＞|F1F2|a F1F2F1F2a F1F2 2．椭圆的标准方程和几何性质标准方程x2a2＋y2b2＝1(a＞b＞0)y2a2＋x2b2＝1(a＞b＞0)图形性质范围－a≤x≤a－b≤y≤b－b≤x≤b－a≤y≤a对称性对称轴：x轴、y轴对称中心：(0，0)顶点A1(－a，0)，A2(a，0)B1(0，－b)，B2(0，b)A1(0，－a)，A2(0，a)B1(－b，0)，B2(b，0) 轴长轴A1A2的长为2a短轴B1B2的长为2b性质焦距|F1F2|＝2c离心率e ＝ca，e ∈(0，1) a ，b ，c 的关系c 2＝a 2－b 21．点P (x 0，y 0)和椭圆的位置关系(1)点P (x 0，y 0)在椭圆内⇔x 20a 2＋y 20b 2<1.(2)点P (x 0，y 0)在椭圆上⇔x 20a 2＋y 20b 2＝1.(3)点P (x 0，y 0)在椭圆外⇔x 20a 2＋y 20b2>1.2．椭圆的常用性质(1)椭圆上的点到焦点距离的最大值为a ＋c ，最小值为a －c . (2)过椭圆的焦点且垂直于长轴的弦长为2b2a.(3)已知过焦点F 1的弦AB ，则△ABF 2的周长为4a .(4)设P ，A ，B 是椭圆上不同的三点，其中A ，B 关于原点对称，直线PA ，PB 斜率存在且不为0，则直线PA 与PB 的斜率之积为定值－b 2a2.二、习题改编1．(选修11P40例4改编)椭圆16x 2＋25y 2＝400的长轴的长，离心率．答案：10 352．(选修11P41练习T3改编)已知中心在原点的椭圆C 的右焦点为F (1，0)，离心率等于12，则C 的方程是．答案：x 24＋y 23＝13．(选修11P36练习T3改编)椭圆C ：x 225＋y 216＝1的左、右焦点分别为F 1，F 2，过F 2的直线交椭圆C 于A 、B 两点，则△F 1AB 的周长为，△AF 1F 2的周长为．答案：20 16一、思考辨析判断正误(正确的打“√”，错误的打“×”)(1)平面内与两个定点F 1，F 2的距离之和等于常数的点的轨迹是椭圆．( ) (2)椭圆的离心率e 越大，椭圆就越圆．( )(3)椭圆既是轴对称图形，又是中心对称图形．( )(4)y 2a 2＋x 2b 2＝1(a ≠b )表示焦点在y 轴上的椭圆．( ) (5)x 2a 2＋y 2b 2＝1(a >b >0)与y 2a 2＋x 2b2＝1(a >b >0)的焦距相同．( ) 答案：(1)× (2)× (3)√ (4)× (5)√ 二、易错纠偏常见误区(1)忽视椭圆定义中的限制条件； (2)忽视椭圆标准方程焦点位置的讨论．1．平面内一点M 到两定点F 1(0，－9)，F 2(0，9)的距离之和等于18，则点M 的轨迹是．解析：由题意知|MF 1|＋|MF 2|＝18，但|F 1F 2|＝18，即|MF 1|＋|MF 2|＝|F 1F 2|，所以点M 的轨迹是一条线段．答案：线段F 1F 22．已知椭圆的长轴长为10，其焦点到中心的距离为4，则这个椭圆的标准方程为．答案：x 225＋y 29＝1或y 225＋x 29＝1第1课时椭圆及其性质椭圆的定义及应用(典例迁移)(1)(2020·黑龙江哈尔滨六中二模)设椭圆C ：x 24＋y 2＝1的左焦点为F ，直线l ：y ＝kx (k ≠0)与椭圆C 交于A ，B 两点，则|AF |＋|BF |的值是( )A ．2B ．2 3C ．4D ．4 3(2)(2020·徐州模拟)已知F 1、F 2是椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的两个焦点，P 为椭圆C 上的一点，且PF 1⊥PF 2，若△PF 1F 2的面积为9，则b ＝．【解析】 (1)设椭圆的右焦点为F 1，连接AF 1，BF 1，因为OA ＝OB ，OF ＝OF 1，所以四边形AFBF 1是平行四边形．所以|BF |＝|AF 1|，所以|AF |＋|BF |＝|AF |＋|AF 1|＝2a ＝4，故选C. (2)设|PF 1|＝r 1，|PF 2|＝r 2，则⎩⎪⎨⎪⎧r 1＋r 2＝2a ，r 21＋r 22＝4c 2，所以2r 1r 2＝(r 1＋r 2)2－(r 21＋r 22)＝4a 2－4c 2＝4b 2，所以S △PF 1F 2＝12r 1r 2＝b 2＝9，所以b ＝3.【答案】 (1)C (2)3【迁移探究】 (变条件)本例(2)中增加条件“△PF 1F 2的周长为18”，其他条件不变，求该椭圆的方程．解：由原题得b 2＝a 2－c 2＝9，又2a ＋2c ＝18，所以a －c ＝1，解得a ＝5，故椭圆的方程为x 225＋y 29＝1.椭圆定义的应用主要有两个方面：一是确认平面内与两定点有关的轨迹是否为椭圆；二是当P 在椭圆上时，与椭圆的两焦点F 1，F 2组成的三角形通常称为“焦点三角形”，利用定义可求其周长，利用定义和余弦定理可求|PF 1|·|PF 2|，通过整体代入可求其面积等．1．已知椭圆x 225＋y 216＝1上一点P 到椭圆一个焦点F 1的距离为3，则P 到另一个焦点F 2的距离为( )A ．2B ．3C ．5D ．7解析：选D.因为a 2＝25，所以2a ＝10，所以由定义知，|PF 1|＋|PF 2|＝10，所以|PF 2|＝10－|PF 1|＝7.2．(2020·贵州六盘水模拟)已知点F 1，F 2分别为椭圆C ：x 24＋y 23＝1的左、右焦点，若点P 在椭圆C 上，且∠F 1PF 2＝60°，则S △F 1PF 2＝．解析：由|PF 1|＋|PF 2|＝4，|PF 1|2＋|PF 2|2－2|PF 1|·|PF 2|·cos 60°＝|F 1F 2|2，得3|PF 1|·|PF 2|＝12，所以|PF 1|·|PF 2|＝4，则S △F 1PF 2＝12|PF 1|·|PF 2|sin ∠F 1PF 2＝12×4sin60°＝ 3.答案： 3椭圆的标准方程(师生共研)(1)(一题多解)过点(3，－5)，且与椭圆y 225＋x 29＝1有相同焦点的椭圆的标准方程为( )A.x 220＋y 24＝1B.x 225＋y 24＝1 C.y 220＋x 24＝1 D ．x 24＋y 225＝1(2)若直线x －2y ＋2＝0经过椭圆的一个焦点和一个顶点，则该椭圆的标准方程为．【解析】 (1)法一(定义法)：椭圆y 225＋x 29＝1的焦点为(0，－4)，(0，4)，即c ＝4.由椭圆的定义知，2a ＝（3－0）2＋（－5＋4）2＋（3－0）2＋（－5－4）2，解得a ＝2 5.由c 2＝a 2－b 2，可得b 2＝4. 所以所求椭圆的标准方程为y 220＋x 24＝1. 法二(待定系数法)：设所求椭圆方程为y 225－k ＋x 29－k＝1(k <9)，将点(3，－5)的坐标代入，可得（－5）225－k ＋（3）29－k ＝1，解得k ＝5或k ＝21(舍去)，所以所求椭圆的标准方程为y 220＋x 24＝1.法三(待定系数法)：设所求椭圆方程为y 2a 2＋x 2b2＝1(a >b >0)．由题意得⎩⎪⎨⎪⎧5a 2＋3b 2＝1a 2－b 2＝16，解得⎩⎪⎨⎪⎧a 2＝20b 2＝4，所以所求椭圆的标准方程为y 220＋x 24＝1.(2)直线与坐标轴的交点为(0，1)，(－2，0)，由题意知当焦点在x 轴上时，c ＝2，b ＝1，所以a 2＝5，所求椭圆的标准方程为x 25＋y 2＝1.当焦点在y 轴上时，b ＝2，c ＝1，所以a 2＝5，所求椭圆的标准方程为y 25＋x 24＝1.【答案】 (1)C (2)x 25＋y 2＝1或x 24＋y 25＝1(1)用定义法求椭圆的标准方程先根据椭圆的定义确定a 2，b 2的值，再结合焦点位置求出椭圆的方程．其中常用的关系有：①b 2＝a 2－c 2；②椭圆上任意一点到椭圆两焦点的距离之和等于2a ； ③椭圆上一短轴顶点到一焦点的距离等于长半轴长a . (2)用待定系数法求椭圆的标准方程的步骤[提醒] 当椭圆焦点位置不明确时，可设为x 2m ＋y 2n＝1(m >0，n >0，m ≠n )，也可设为Ax2＋By 2＝1(A >0，B >0，且A ≠B )．1．已知动点M 到两个定点A (－2，0)，B (2，0)的距离之和为6，则动点M 的轨迹方程为( )A.x 29＋y 2＝1 B.y 29＋x 25＝1 C.y 29＋x 2＝1 D ．x 29＋y 25＝1解析：选D.由题意有6>2＋2＝4，故点M 的轨迹为焦点在x 轴上的椭圆，则2a ＝6，c ＝2，故a 2＝9，所以b 2＝a 2－c 2＝5，故椭圆的方程为x 29＋y 25＝1.故选D.2．设椭圆x 2m 2＋y 2n 2＝1(m >0，n >0)的右焦点为(2，0)，离心率为22，则此椭圆的方程为．解析：椭圆的右焦点为(2，0)，所以m 2－n 2＝4，e ＝22＝2m，所以m ＝22，代入m 2－n 2＝4，得n 2＝4，所以椭圆方程为x 28＋y 24＝1.答案：x 28＋y 24＝13．已知椭圆C 的中心在原点，一个焦点F (－2，0)，且长轴长与短轴长的比是2∶3，则椭圆C 的方程是．解析：设椭圆C 的方程为x 2a 2＋y 2b2＝1(a >b >0)．由题意知⎩⎨⎧a 2＝b 2＋c 2，a ∶b ＝2∶3，c ＝2，解得a 2＝16，b 2＝12.所以椭圆C 的方程为x 216＋y 212＝1.答案：x 216＋y 212＝1椭圆的几何性质(多维探究) 角度一椭圆的长轴、短轴、焦距(2020·泉州质检)已知椭圆x 2m －2＋y 210－m＝1的长轴在x 轴上，焦距为4，则m等于( )A ．8B ．7C ．6D ．5【解析】因为椭圆x 2m －2＋y 210－m＝1的长轴在x 轴上，所以⎩⎪⎨⎪⎧m －2>0，10－m >0，m －2>10－m ，解得6<m <10.因为焦距为4，所以c 2＝m －2－10＋m ＝4，解得m ＝8. 【答案】 A角度二求椭圆离心率的值(范围)(1)(2018·高考全国卷Ⅱ)已知F 1，F 2是椭圆C 的两个焦点，P 是C 上的一点．若PF 1⊥PF 2，且∠PF 2F 1＝60°，则C 的离心率为( )A ．1－32B ．2－ 3C.3－12D ．3－1(2)在平面直角坐标系xOy 中，点P 为椭圆C ：y 2a 2＋x 2b2＝1(a >b >0)的下顶点，M ，N 在椭圆上，若四边形OPMN 为平行四边形，α为直线ON 的倾斜角，若α∈⎝ ⎛⎭⎪⎫π6，π4，则椭圆C 的离心率的取值范围为( )A.⎝ ⎛⎭⎪⎫0，63 B.⎝ ⎛⎭⎪⎫0，32 C.⎝⎛⎭⎪⎫63，32 D ．⎝⎛⎭⎪⎫63，223【解析】 (1)由题设知∠F 1PF 2＝90°，∠PF 2F 1＝60°，|F 1F 2|＝2c ，所以|PF 2|＝c ，|PF 1|＝3c .由椭圆的定义得|PF 1|＋|PF 2|＝2a ，即3c ＋c ＝2a ，所以(3＋1)c ＝2a ，故椭圆C 的离心率e ＝ca＝23＋1＝3－1.故选D.(2)因为OPMN 是平行四边形，所以MN ∥OP 且MN ＝OP ，故y N ＝a 2，代入椭圆方程可得x N ＝3b 2，所以k ON ＝3a3b＝tan α. 又α∈⎝ ⎛⎭⎪⎫π6，π4，所以33<3a 3b <1，所以a <3b ，a 2<3(a 2－c 2)，解得0<c a <63，故选A. 【答案】 (1)D (2)A求椭圆离心率或其取值范围的方法(1)求出a ，b 或a ，c 的值，代入e 2＝c 2a 2＝a 2－b 2a 2＝1－⎝ ⎛⎭⎪⎫b a 2直接求．(2)先根据条件得到关于a ，b ，c 的齐次等式(不等式)，结合b 2＝a 2－c 2转化为关于a ，c 的齐次等式(不等式)，然后将该齐次等式(不等式)两边同时除以a 或a 2转化为关于e 或e 2的方程(不等式)，再解方程(不等式)即可得e (e 的取值范围)．角度三与椭圆性质有关的最值问题已知P 在椭圆x 24＋y 2＝1上，A (0，4)，则|PA |的最大值为( )A.2183B.763C ．5D ．2 5【解析】设P (x 0，y 0)，则由题意得x 2＝4(1－y 2)，所以|PA |2＝x 20＋(y 0－4)2＝4(1－y 20)＋y 20－8y 0＋16 ＝－3y 2－8y 0＋20＝－3⎝⎛⎭⎪⎫y 0＋432＋763，又－1≤y 0≤1，所以当y 0＝－1时，|PA |2取得最大值25，即|PA |的最大值为5.故选C. 【答案】 C求解最值、取值范围问题的技巧(1)与椭圆几何性质有关的问题要结合图形进行分析，即使画不出图形，思考时也要联想到一个图形．(2)椭圆的范围或最值问题常常涉及一些不等式．例如，－a ≤x ≤a ，－b ≤y ≤b ，0<e <1，在求椭圆的相关量的范围时，要注意应用这些不等关系．(3)最值问题，将所求列出表达式，构造基本不等式或利用函数单调性求解．1．已知椭圆x 2a 2＋y 2b2＝1(a >b >0)的一个焦点是圆x 2＋y 2－6x ＋8＝0的圆心，且短轴长为8，则椭圆的左顶点为( )A ．(－3，0)B ．(－4，0)C ．(－10，0)D ．(－5，0)解析：选D.因为圆的标准方程为(x －3)2＋y 2＝1，所以圆心坐标为(3，0)，所以c ＝3.又b ＝4，所以a ＝b 2＋c 2＝5. 因为椭圆的焦点在x 轴上，所以椭圆的左顶点为(－5，0)．2．若点O 和点F 分别为椭圆x 24＋y 23＝1的中心和左焦点，点P 为椭圆上的任意一点，则OP →·FP →的最大值为( )A ．2B ．3C ．6D ．8解析：选C.由椭圆x 24＋y 23＝1可得F (－1，0)，点O (0，0)，设P (x ，y )(－2≤x ≤2)，则OP →·FP →＝x 2＋x ＋y 2＝x 2＋x ＋3⎝ ⎛⎭⎪⎫1－x 24＝14x 2＋x ＋3＝14(x ＋2)2＋2，－2≤x ≤2，当且仅当x ＝2时，OP →·FP →取得最大值6.3．已知椭圆x 2a 2＋y 2b2＝1(a >b >0)，F 是椭圆的右焦点，A 为左顶点，点P 在椭圆上，PF ⊥x轴，若|PF |＝14|AF |，则椭圆的离心率为．解析：因为点P 在椭圆上，且PF ⊥x 轴，所以|PF |＝b 2a，又因为|AF |＝a ＋c ，|PF |＝14|AF |，所以4(a 2－c 2)＝a (a ＋c )，即4(a －c )＝a ，则3a ＝4c ，即c a ＝34. 答案：34[基础题组练]1．已知正数m 是2和8的等比中项，则圆锥曲线x 2＋y 2m＝1的焦点坐标为( )A ．(±3，0)B ．(0，±3)C ．(±3，0)或(±5，0)D ．(0，±3)或(±5，0)解析：选B.因为正数m 是2和8的等比中项，所以m 2＝16，即m ＝4，所以椭圆x 2＋y 24＝1的焦点坐标为(0，±3)，故选B.2．(2019·高考北京卷)已知椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为12，则( )A ．a 2＝2b 2B ．3a 2＝4b 2C ．a ＝2bD ．3a ＝4b解析：选B.由题意得，c a ＝12，所以c 2a 2＝14，又a 2＝b 2＋c 2，所以a 2－b 2a 2＝14，b 2a 2＝34，所以4b 2＝3a 2.故选B.3．曲线x 2169＋y 2144＝1与曲线x 2169－k ＋y 2144－k ＝1(k <144)的( )A ．长轴长相等B ．短轴长相等C ．离心率相等D ．焦距相等解析：选D.曲线x 2169－k ＋y 2144－k ＝1中c 2＝169－k －(144－k )＝25，所以c ＝5，所以两曲线的焦距相等．4．(2020·郑州模拟)已知椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1，F 2，离心率为23，过F 2的直线l 交C 于A ，B 两点，若△AF 1B 的周长为12，则C 的方程为( )A.x 23＋y 2＝1 B.x 23＋y 22＝1 C.x 29＋y 24＝1 D ．x 29＋y 25＝1解析：选D.由椭圆的定义，知|AF 1|＋|AF 2|＝2a ，|BF 1|＋|BF 2|＝2a ，所以△AF 1B 的周长为|AF 1|＋|AF 2|＋|BF 1|＋|BF 2|＝4a ＝12，所以a ＝3.因为椭圆的离心率e ＝c a ＝23，所以c＝2，所以b 2＝a 2－c 2＝5，所以椭圆C 的方程为x 29＋y 25＝1，故选D.5．(2020·昆明市诊断测试)已知F 1，F 2为椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点，B为C 的短轴的一个端点，直线BF 1与C 的另一个交点为A ，若△BAF 2为等腰三角形，则|AF 1||AF 2|＝( )A.13B.12C.23D ．3解析：选A.如图，不妨设点B 在y 轴的正半轴上，根据椭圆的定义，得|BF 1|＋|BF 2|＝2a ，|AF 1|＋|AF 2|＝2a ，由题意知|AB |＝|AF 2|，所以|BF 1|＝|BF 2|＝a ，|AF 1|＝a 2，|AF 2|＝3a2.所以|AF 1||AF 2|＝13.故选A.6．若椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的短轴长等于焦距，则椭圆的离心率为．解析：由题意可得b ＝c ，则b 2＝a 2－c 2＝c 2，a ＝2c ，故椭圆的离心率e ＝c a ＝22. 答案：227．(2020·贵阳模拟)若椭圆x 2a 2＋y 2b 2＝1(a >b >0)的离心率为32，短轴长为4，则椭圆的标准方程为．解析：由题意可知e ＝c a ＝32，2b ＝4，得b ＝2，所以⎩⎪⎨⎪⎧c a ＝32，a 2＝b 2＋c 2＝4＋c 2，解得⎩⎨⎧a ＝4，c ＝23，所以椭圆的标准方程为x 216＋y 24＝1.答案：x 216＋y 24＝18．(2019·高考全国卷Ⅲ)设F 1，F 2为椭圆C ：x 236＋y 220＝1的两个焦点，M 为C 上一点且在第一象限．若△MF 1F 2为等腰三角形，则M 的坐标为．解析：通解：由椭圆C ：x 236＋y 220＝1，得c ＝a 2－b 2＝4，不妨设F 1，F 2分别为左、右焦点，则由题意知|MF 1|＝|F 1F 2|＝2c ＝8，于是由椭圆的定义得|MF 1|＋|MF 2|＝12，所以|MF 2|＝12－|MF 1|＝4，易知△MF 1F 2的底边MF 2上的高h ＝|F 1F 2|2－⎝ ⎛⎭⎪⎫12|MF 2|2＝82－22＝215，所以12|MF 2|·h ＝12|F 1F 2|·y M ，即12×4×215＝12×8×y M ，解得y M ＝15，代入椭圆方程得x M ＝－3(舍去)或x M ＝3，故点M 的坐标为(3，15)．优解：不妨设F 1，F 2分别为左、右焦点，则由题意，得|MF 1|＝|F 1F 2|＝8，由椭圆的焦半径公式得|MF 1|＝ex M ＋6＝23x M ＋6＝8，解得x M ＝3，代入椭圆方程得y M ＝15，故点M 的坐标为(3，15)．答案：(3，15)9．已知椭圆的长轴长为10，两焦点F 1，F 2的坐标分别为(3，0)和(－3，0)． (1)求椭圆的标准方程；(2)若P 为短轴的一个端点，求△F 1PF 2的面积．解：(1)设椭圆的标准方程为x 2a 2＋y 2b2＝1(a >b >0)，依题意得⎩⎪⎨⎪⎧2a ＝10，c ＝3，因此a ＝5，b ＝4，所以椭圆的标准方程为x 225＋y 216＝1.(2)易知|y P |＝4，又c ＝3，所以S △F 1PF 2＝12|y P |×2c ＝12×4×6＝12.10．分别求出满足下列条件的椭圆的标准方程．(1)与椭圆x 24＋y 23＝1有相同的离心率且经过点(2，－3)； (2)已知点P 在以坐标轴为对称轴的椭圆上，且P 到两焦点的距离分别为5，3，过P 且与长轴垂直的直线恰过椭圆的一个焦点．解：(1)由题意，设所求椭圆的方程为x 24＋y 23＝t 1或y 24＋x 23＝t 2(t 1，t 2＞0)，因为椭圆过点(2，－3)，所以t 1＝224＋（－3）23＝2，或t 2＝（－3）24＋223＝2512.故所求椭圆的标准方程为x 28＋y 26＝1或y 2253＋x 2254＝1.(2)由于焦点的位置不确定，所以设所求的椭圆方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)或y 2a 2＋x 2b2＝1(a＞b ＞0)，由已知条件得⎩⎪⎨⎪⎧2a ＝5＋3，（2c ）2＝52－32，解得a ＝4，c ＝2，所以b 2＝12. 故椭圆的方程为x 216＋y 212＝1或y 216＋x 212＝1. [综合题组练]1．(2020·合肥市第二次质量检测)已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1，F 2，右顶点为A ，上顶点为B ，以线段F 1A 为直径的圆交线段F 1B 的延长线于点P ，若F 2B ∥AP ，则该椭圆的离心率是( )A.33B.23C.3 2D．22解析：选D.如图，由题意知，P为以F1A为直径的圆上一点，所以F1P⊥AP，结合F2B∥AP知F1P⊥F2B.又|F1B|＝|F2B|，所以△BF1F2为等腰直角三角形，所以|OB|＝|OF2|，即b＝c，所以a2＝b2＋c2＝2c2，即a＝2c，所以椭圆的离心率e＝ca＝22，故选D.2．(2019·高考全国卷Ⅰ)已知椭圆C的焦点为F1(－1，0)，F2(1，0)，过F2的直线与C交于A，B两点．若|AF2|＝2|F2B|，|AB|＝|BF1|，则C的方程为( )A.x22＋y2＝1 B.x23＋y22＝1C.x24＋y23＝1 D．x25＋y24＝1解析：选B.由题意设椭圆的方程为x2a2＋y2b2＝1(a>b>0)，连接F1A，令|F2B|＝m，则|AF2|＝2m，|BF1|＝3m.由椭圆的定义知，4m＝2a，得m＝a2，故|F2A|＝a＝|F1A|，则点A为椭圆C 的上顶点或下顶点．令∠OAF2＝θ(O为坐标原点)，则sin θ＝1a.在等腰三角形ABF1中，cos 2θ＝a23a2＝13，所以13＝1－2(1a)2，得a2＝3.又c2＝1，所以b2＝a2－c2＝2，椭圆C的方程为x23＋y22＝1.故选B.3．已知椭圆C：x2＋2y2＝4.(1)求椭圆C的离心率；(2)设O为原点．若点A在直线y＝2上，点B在椭圆C上，且OA⊥OB，求线段AB长度的最小值．解：(1)由题意，椭圆C的标准方程为x24＋y22＝1.所以a2＝4，b2＝2，从而c2＝a2－b2＝2.因此a＝2，c＝ 2.故椭圆C 的离心率e ＝c a ＝22. (2)设点A ，B 的坐标分别为(t ，2)，(x 0，y 0)，其中x 0≠0. 因为OA ⊥OB ，所以OA →·OB →＝0，即tx 0＋2y 0＝0，解得t ＝－2y 0x 0.又x 20＋2y 20＝4，所以|AB |2＝(x 0－t )2＋(y 0－2)2＝⎝⎛⎭⎪⎫x 0＋2y 0x 02＋(y 0－2)2＝x 2＋y 20＋4y 20x 20＋4＝x 20＋4－x 202＋2（4－x 20）x 20＋4＝x 202＋8x 20＋4(0<x 20≤4)．因为x 202＋8x 20≥4(0<x 20≤4)，当且仅当x 20＝4时等号成立，所以|AB |2≥8.故线段AB 长度的最小值为2 2.4．(2019·高考全国卷Ⅱ)已知F 1，F 2是椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的两个焦点，P 为C 上的点，O 为坐标原点．(1)若△POF 2为等边三角形，求C 的离心率；(2)如果存在点P ，使得PF 1⊥PF 2，且△F 1PF 2的面积等于16，求b 的值和a 的取值范围．解：(1)连接PF 1.由△POF 2为等边三角形可知在△F 1PF 2中，∠F 1PF 2＝90°，|PF 2|＝c ，|PF 1|＝3c ，于是2a ＝|PF 1|＋|PF 2|＝(3＋1)c ，故C 的离心率e ＝ca＝3－1.(2)由题意可知，满足条件的点P (x ，y )存在当且仅当 12|y |·2c ＝16，y x ＋c ·y x －c ＝－1，x 2a 2＋y 2b 2＝1，即c |y |＝16，①x 2＋y 2＝c 2，② x 2a 2＋y 2b 2＝1.③ 由②③及a 2＝b 2＋c 2得y 2＝b 4c 2，又由①知y 2＝162c2，故b ＝4.由②③得x 2＝a 2c2(c 2－b 2)，所以c 2≥b 2，从而a 2＝b 2＋c 2≥2b 2＝32，故a ≥4 2.当b ＝4，a ≥42时，存在满足条件的点P .所以b＝4，a的取值范围为[42，＋∞)．。

高考数学新增分大一轮复习第九章平面解析几何9.5椭圆第1课时讲义含解析0411137.docx

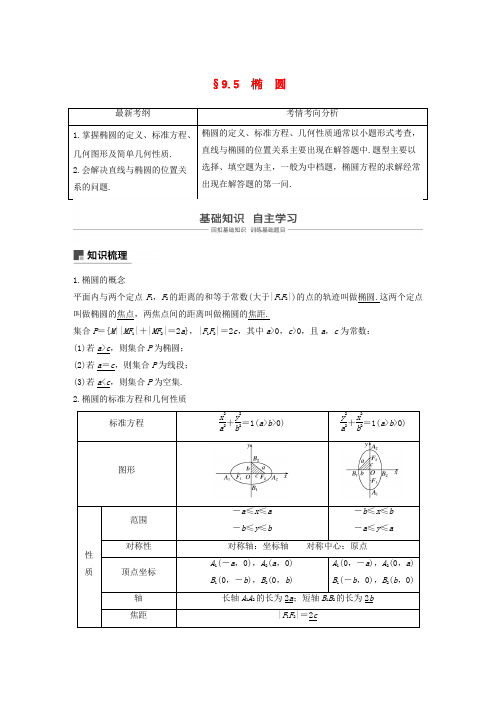
§9.5椭圆1.椭圆的概念平面内与两个定点F1，F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距.集合P＝{M||MF1|＋|MF2|＝2a}，|F1F2|＝2c，其中a>0，c>0，且a，c为常数：(1)若a>c，则集合P为椭圆；(2)若a＝c，则集合P为线段；(3)若a<c，则集合P为空集.2.椭圆的标准方程和几何性质概念方法微思考1.在椭圆的定义中，若2a ＝|F 1F 2|或2a <|F 1F 2|，动点P 的轨迹如何？提示当2a ＝|F 1F 2|时动点P 的轨迹是线段F 1F 2；当2a <|F 1F 2|时动点P 的轨迹是不存在的. 2.椭圆的离心率的大小与椭圆的扁平程度有怎样的关系？提示由e ＝c a＝1－⎝ ⎛⎭⎪⎫b a2知，当a 不变时，e 越大，b 越小，椭圆越扁；e 越小，b 越大，椭圆越圆.3.点和椭圆的位置关系有几种？如何判断. 提示点P (x 0，y 0)和椭圆的位置关系有3种(1)点P (x 0，y 0)在椭圆内⇔x 20a 2＋y 20b 2<1.(2)点P (x 0，y 0)在椭圆上⇔x 20a 2＋y 20b 2＝1.(3)点P (x 0，y 0)在椭圆外⇔x 20a 2＋y 20b2>1.4.直线与椭圆的位置关系有几种？如何判断？提示直线与椭圆的位置关系有三种：相离、相切、相交.判断方法为联立直线与椭圆的方程，求联立后所得方程的判别式Δ. (1)直线与椭圆相离⇔Δ<0. (2)直线与椭圆相切⇔Δ＝0. (3)直线与椭圆相交⇔Δ>0.题组一思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)椭圆上一点P 与两焦点F 1，F 2构成△PF 1F 2的周长为2a ＋2c (其中a 为椭圆的长半轴长，c 为椭圆的半焦距).( √ )(2)方程mx 2＋ny 2＝1(m >0，n >0，m ≠n )表示的曲线是椭圆.( √ )(3)y 2a 2＋x 2b 2＝1(a ≠b )表示焦点在y 轴上的椭圆.( × ) (4)x 2a 2＋y 2b 2＝1(a >b >0)与y 2a 2＋x 2b2＝1(a >b >0)的焦距相等.( √ )题组二教材改编 2.[P49T4]椭圆x 210－m ＋y 2m －2＝1的焦距为4，则m 等于( ) A.4B.8C.4或8D.12 答案 C解析当焦点在x 轴上时，10－m >m －2>0， 10－m －(m －2)＝4，∴m ＝4.当焦点在y 轴上时，m －2>10－m >0，m －2－(10－m )＝4，∴m ＝8.∴m ＝4或8. 3.[P80T3(1)]过点A (3，－2)且与椭圆x 29＋y 24＝1有相同焦点的椭圆的方程为( )A.x 215＋y 210＝1B.x 225＋y 220＝1C.x 210＋y 215＝1 D.x 220＋y 215＝1 答案 A解析由题意知c 2＝5，可设椭圆方程为x 2λ＋5＋y 2λ＝1(λ>0)，则9λ＋5＋4λ＝1，解得λ＝10或λ＝－2(舍去)， ∴所求椭圆的方程为x 215＋y 210＝1.4.[P49T6]已知点P 是椭圆x 25＋y 24＝1上y 轴右侧的一点，且以点P 及焦点F 1，F 2为顶点的三角形的面积等于1，则点P 的坐标为__________________. 答案 ⎝⎛⎭⎪⎫152，1或⎝ ⎛⎭⎪⎫152，－1 解析设P (x ，y )，由题意知c 2＝a 2－b 2＝5－4＝1，所以c ＝1，则F 1(－1，0)，F 2(1，0).由题意可得点P 到x 轴的距离为1，所以y ＝±1，把y ＝±1代入x 25＋y 24＝1，得x ＝±152，又x >0，所以x ＝152，所以P 点坐标为⎝⎛⎭⎪⎫152，1或⎝ ⎛⎭⎪⎫152，－1. 题组三易错自纠5.(2018·浙江余姚中学质检)已知方程x 2m 2＋y 22＋m＝1表示焦点在x 轴上的椭圆，则m 的取值范围是( )A.m >2或m <－1B.m >－2C.－1<m <2D.m >2或－2<m <－1答案 D解析 ∵椭圆的焦点在x 轴上， ∴m 2>2＋m >0，解得m >2或－2<m <－1.6.椭圆x 29＋y 24＋k ＝1的离心率为45，则k 的值为( )A.－21B.21C.－1925或21D.1925或21 答案 C解析若a 2＝9，b 2＝4＋k ，则c ＝5－k ，由c a ＝45，即5－k 3＝45，得k ＝－1925；若a 2＝4＋k ，b 2＝9，则c ＝k －5，由c a ＝45，即k －54＋k ＝45，解得k ＝21. 7.已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1，F 2，离心率为33，过F 2的直线l交C 于A ，B 两点，若△AF 1B 的周长为43，则C 的方程为( ) A.x 23＋y 22＝1B.x 23＋y 2＝1 C.x 212＋y 28＝1 D.x 212＋y 24＝1 答案 A解析 ∵△AF 1B 的周长为43，∴4a ＝43， ∴a ＝3，∵离心率为33，∴c ＝1，∴b ＝a 2－c 2＝2， ∴椭圆C 的方程为x 23＋y 22＝1.故选A.第1课时椭圆及其性质题型一椭圆的定义及应用1.如图所示，一圆形纸片的圆心为O ，F 是圆内一定点，M 是圆周上一动点，把纸片折叠使M 与F 重合，然后抹平纸片，折痕为CD ，设CD 与OM 交于点P ，则点P 的轨迹是( )A.椭圆B.双曲线C.抛物线D.圆答案 A解析由条件知|PM |＝|PF |，∴|PO |＋|PF |＝|PO |＋|PM |＝|OM |＝R >|OF |. ∴P 点的轨迹是以O ，F 为焦点的椭圆.2.已知△ABC 的顶点B ，C 在椭圆x 23＋y 2＝1上，顶点A 是椭圆的一个焦点，且椭圆的另外一个焦点在BC 边上，则△ABC 的周长是( ) A.23B.6C.43D.12 答案 C解析由椭圆的方程得a ＝ 3.设椭圆的另一个焦点为F ，则由椭圆的定义得|BA |＋|BF |＝|CA |＋|CF |＝2a ，所以△ABC 的周长为|BA |＋|BC |＋|CA |＝|BA |＋|BF |＋|CF |＋|CA |＝(|BA |＋|BF |)＋(|CF |＋|CA |)＝2a ＋2a ＝4a ＝4 3.3.椭圆x 24＋y 2＝1的左、右焦点分别为F 1，F 2，过F 1作垂直于x 轴的直线与椭圆相交，一个交点为P ，则|PF 2|等于( ) A.72B.32C.3D.4 答案 A解析 F 1(－3，0)，∵PF 1⊥x 轴，∴P ⎝ ⎛⎭⎪⎫－3，±12，∴|PF 1|＝12，∴|PF 2|＝4－12＝72. 4.设F 1，F 2分别是椭圆x 225＋y 216＝1的左、右焦点，P 为椭圆上任意一点，点M 的坐标为(6，4)，则|PM |－|PF 1|的最小值为________.答案－5解析由椭圆的方程可知F 2(3，0)，由椭圆的定义可得|PF 1|＝2a －|PF 2|.∴|PM |－|PF 1|＝|PM |－(2a －|PF 2|)＝|PM |＋|PF 2|－2a ≥|MF 2|－2a ，当且仅当M ，P ，F 2三点共线时取得等号，又|MF 2|＝(6－3)2＋(4－0)2＝5，2a ＝10，∴|PM |－|PF 1|≥5－10＝－5，即|PM |－|PF 1|的最小值为－5.思维升华椭圆定义的应用技巧(1)椭圆定义的应用主要有：求椭圆的标准方程，求焦点三角形的周长、面积及弦长、最值和离心率等.(2)通常定义和余弦定理结合使用，求解关于焦点三角形的周长和面积问题.题型二椭圆的标准方程命题点1 定义法例1 (1)(2019·丽水调研)已知两圆C 1：(x －4)2＋y 2＝169，C 2：(x ＋4)2＋y 2＝9，动圆M 在圆C 1内部且和圆C 1内切，和圆C 2外切，则动圆圆心M 的轨迹方程为( ) A.x 264－y 248＝1 B.x 248＋y 264＝1 C.x 248－y 264＝1 D.x 264＋y 248＝1 答案 D解析设圆M 的半径为r ，则|MC 1|＋|MC 2|＝(13－r )＋(3＋r )＝16>8＝|C 1C 2|，所以M 的轨迹是以C 1，C 2为焦点的椭圆，且2a ＝16，2c ＝8，即a ＝8，c ＝4，b ＝a 2－c 2＝43，故所求的轨迹方程为x 264＋y 248＝1.(2)在△ABC 中，A (－4，0)，B (4，0)，△ABC 的周长是18，则顶点C 的轨迹方程是( ) A.x 225＋y 29＝1(y ≠0) B.y 225＋x 29＝1(y ≠0) C.x 216＋y 29＝1(y ≠0) D.y 216＋x 29＝1(y ≠0) 答案 A解析由|AC |＋|BC |＝18－8＝10>8知，顶点C 的轨迹是以A ，B 为焦点的椭圆(A ，B ，C 不共线).设其方程为x 2a 2＋y 2b2＝1(a >b >0)，则a ＝5，c ＝4，从而b ＝3.由A ，B ，C 不共线知y ≠0.故顶点C 的轨迹方程是x 225＋y 29＝1(y ≠0).命题点2 待定系数法例2 (1)已知椭圆的中心在原点，以坐标轴为对称轴，且经过两点⎝ ⎛⎭⎪⎫－32，52，(3，5)，则椭圆的标准方程为__________. 答案y 210＋x 26＝1 解析设椭圆的方程为mx 2＋ny 2＝1(m ，n >0，m ≠n ). 由⎩⎪⎨⎪⎧⎝ ⎛⎭⎪⎫－322m ＋⎝ ⎛⎭⎪⎫522n ＝1，3m ＋5n ＝1，解得m ＝16，n ＝110.∴椭圆方程为y 210＋x 26＝1.(2)一个椭圆的中心在原点，坐标轴为对称轴，焦点F 1，F 2在x 轴上，P (2，3)是椭圆上一点，且|PF 1|，|F 1F 2|，|PF 2|成等差数列，则椭圆的标准方程为____________. 答案x 28＋y 26＝1 解析 ∵椭圆的中心在原点，焦点F 1，F 2在x 轴上，∴可设椭圆方程为x 2a 2＋y 2b2＝1(a >b >0)，∵P (2，3)是椭圆上一点，且|PF 1|，|F 1F 2|，|PF 2|成等差数列， ∴⎩⎪⎨⎪⎧4a 2＋3b 2＝1，2a ＝4c ，又a 2＝b 2＋c 2，∴a ＝22，b ＝6，c ＝2，∴椭圆的标准方程为x 28＋y 26＝1.思维升华 (1)求椭圆的标准方程多采用定义法和待定系数法.(2)利用定义法求椭圆方程，要注意条件2a >|F 1F 2|；利用待定系数法要先定形(焦点位置)，再定量，也可把椭圆方程设为mx 2＋ny 2＝1(m >0，n >0，m ≠n )的形式. 跟踪训练1(1)已知椭圆G 的中心在坐标原点，长轴在x 轴上，离心率为32，且椭圆G 上一点到两个焦点的距离之和为12，则椭圆G 的方程为( ) A.x 236＋y 29＝1 B.x 29＋y 236＝1 C.x 24＋y 29＝1 D.x 29＋y 24＝1 答案 A解析依题意设椭圆G 的方程为x 2a 2＋y 2b2＝1(a >b >0)，∵椭圆上一点到两焦点的距离之和为12，∴2a ＝12，∴a ＝6，∵椭圆的离心率为32，∴e ＝ca ＝1－b 2a 2＝32，即1－b 236＝32，解得b 2＝9，∴椭圆G 的方程为x 236＋y 29＝1，故选A. (2)过点(3，－5)，且与椭圆y 225＋x 29＝1有相同焦点的椭圆的标准方程为________________.答案y 220＋x 24＝1 解析 ∵所求椭圆与椭圆y 225＋x 29＝1的焦点相同，∴其焦点在y 轴上，且c 2＝25－9＝16.设它的标准方程为y 2a 2＋x 2b2＝1(a >b >0).∵c 2＝16，且c 2＝a 2－b 2，故a 2－b 2＝16.① 又点(3，－5)在所求椭圆上， ∴(－5)2a 2＋(3)2b 2＝1，即5a 2＋3b2＝1.②由①②得b 2＝4，a 2＝20，∴所求椭圆的标准方程为y 220＋x 24＝1.题型三椭圆的几何性质命题点1 求离心率的值(或范围)例3 (1)设椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1，F 2，P 是C 上的点，PF 2⊥F 1F 2，∠PF 1F 2＝30°，则C 的离心率为( ) A.36B.13C.12D.33答案 D解析方法一如图，在Rt△PF 2F 1中，∠PF 1F 2＝30°，|F 1F 2|＝2c ，∴|PF 1|＝2c cos30°＝43c 3，|PF 2|＝2c ·tan30°＝23c3.∵|PF 1|＋|PF 2|＝2a ，即43c 3＋23c 3＝2a ，可得3c ＝a . ∴e ＝c a ＝33. 方法二 (特殊值法)：在Rt△PF 2F 1中，令|PF 2|＝1，∵∠PF 1F 2＝30°，∴|PF 1|＝2，|F 1F 2|＝ 3. ∴e ＝2c 2a ＝|F 1F 2||PF 1|＋|PF 2|＝33.(2)椭圆x 2a 2＋y 2b2＝1(a >b >0)，F 1，F 2为椭圆的左、右焦点，O 为坐标原点，点P 为椭圆上一点，|OP |＝24a ，且|PF 1|，|F 1F 2|，|PF 2|成等比数列，则椭圆的离心率为( ) A.24B.23C.63D.64答案 D解析设P (x ，y )，则|OP |2＝x 2＋y 2＝a 28，由椭圆定义得|PF 1|＋|PF 2|＝2a ， ∴|PF 1|2＋2|PF 1||PF 2|＋|PF 2|2＝4a 2，又∵|PF 1|，|F 1F 2|，|PF 2|成等比数列， ∴|PF 1|·|PF 2|＝|F 1F 2|2＝4c 2，则|PF 1|2＋|PF 2|2＋8c 2＝4a 2，∴(x ＋c )2＋y 2＋(x －c )2＋y 2＋8c 2＝4a 2，整理得x 2＋y 2＋5c 2＝2a 2，即a 28＋5c 2＝2a 2，整理得c 2a 2＝38， ∴椭圆的离心率e ＝ca ＝64. (3)(2018·杭州调研)已知椭圆x 2a 2＋y 2b2＝1(a >b >c >0，a 2＝b 2＋c 2)的左、右焦点分别为F 1，F 2，若以F 2为圆心，b －c 为半径作圆F 2，过椭圆上一点P 作此圆的切线，切点为T ，且|PT |的最小值不小于32(a －c )，则椭圆的离心率e 的取值范围是__________.答案 ⎣⎢⎡⎭⎪⎫35，22解析因为|PT |＝|PF 2|2－(b －c )2(b >c )，而|PF 2|的最小值为a －c ，所以|PT |的最小值为(a －c )2－(b －c )2. 依题意，有(a －c )2－(b －c )2≥32(a －c )，所以(a －c )2≥4(b －c )2，所以a －c ≥2(b －c )，所以a ＋c ≥2b ，所以(a ＋c )2≥4(a 2－c 2)，所以5c 2＋2ac －3a 2≥0，所以5e 2＋2e －3≥0.① 又b >c ，所以b 2>c 2，所以a 2－c 2>c 2，所以2e 2<1.② 联立①②，得35≤e <22.命题点2 求参数的值(或范围)例4 (2017·全国Ⅰ)设A ，B 是椭圆C ：x 23＋y 2m＝1长轴的两个端点.若C 上存在点M 满足∠AMB＝120°，则m 的取值范围是( ) A.(0，1]∪[9，＋∞) B.(0，3]∪[9，＋∞) C.(0，1]∪[4，＋∞) D.(0，3]∪[4，＋∞)答案 A解析方法一设椭圆焦点在x 轴上，则0<m <3，点M (x ，y ).过点M 作x 轴的垂线，交x 轴于点N ，则N (x ，0).故tan∠AMB ＝tan(∠AMN ＋∠BMN )＝3＋x |y |＋3－x|y |1－3＋x |y |·3－x|y |＝23|y |x 2＋y 2－3.又tan∠AMB ＝tan120°＝－3，且由x 23＋y 2m ＝1，可得x 2＝3－3y 2m，则23|y |3－3y 2m＋y 2－3＝23|y |⎝ ⎛⎭⎪⎫1－3m y 2＝－ 3. 解得|y |＝2m3－m.又0<|y |≤m ，即0<2m3－m ≤m ，结合0<m <3解得0<m ≤1.对于焦点在y 轴上的情况，同理亦可得m ≥9. 则m 的取值范围是(0，1]∪[9，＋∞). 故选A.方法二当0<m <3时，焦点在x 轴上，要使C 上存在点M 满足∠AMB ＝120°，则a b≥tan60°＝3，即3m≥3，解得0<m ≤1.当m >3时，焦点在y 轴上，要使C 上存在点M 满足∠AMB ＝120°，则a b≥tan60°＝3，即m3≥3，解得m ≥9.故m 的取值范围为(0，1]∪[9，＋∞). 故选A.思维升华 (1)求椭圆离心率或其范围的方法解题的关键是借助图形建立关于a ，b ，c 的关系式(等式或不等式)，转化为e 的关系式，常用方法如下：①直接求出a ，c ，利用离心率公式e ＝c a求解. ②由a 与b 的关系求离心率，利用变形公式e ＝1－b 2a2求解. ③由椭圆的定义求离心率，e ＝c a ＝2c2a，而2a 是椭圆上任意一点到两焦点的距离之和，2c 是焦距，从而与焦点三角形联系起来.④构造a ，c 的齐次式.离心率e 的求解中可以不求出a ，c 的具体值，而是得出a 与c 的关系，从而求得e ，一般步骤如下：(ⅰ)建立方程：根据已知条件得到齐次方程Aa 2＋Bac ＋Cc 2＝0；(ⅱ)化简：两边同时除以a 2，化简齐次方程，得到关于e 的一元二次方程A ＋Be ＋Ce 2＝0； (ⅲ)求解：解一元二次方程，得e 的值；(ⅳ)验算取舍：根据椭圆离心率的取值范围e ∈(0，1)确定离心率e 的值. 若得到齐次不等式，可以类似求出离心率e 的取值范围. (2)椭圆几何性质的应用技巧①与椭圆的几何性质有关的问题要结合图形进行分析，即使不画出图形，思考时也要联想到图形.②椭圆相关量的范围或最值问题常常涉及一些不等式.例如，－a ≤x ≤a ，－b ≤y ≤b ，0<e <1，三角形两边之和大于第三边，在求椭圆相关量的范围或最值时，要注意应用这些不等关系.跟踪训练2 (1)已知椭圆x 24＋y 2b2＝1(0<b <2)的左、右焦点分别为F 1，F 2，过F 1的直线l 交椭圆于A ，B 两点，若|BF 2|＋|AF 2|的最大值为5，则b 的值是________. 答案3解析由椭圆的方程可知a ＝2，由椭圆的定义可知，|AF 2|＋|BF 2|＋|AB |＝4a ＝8，所以|AB |＝8－(|AF 2|＋|BF 2|)≥3，由椭圆的性质可知2b2a＝3.所以b 2＝3，即b ＝ 3.(2)(2018·温州高考适应性测试)椭圆x 2a 2＋y 2b2＝1(a >b >0)中，F 为右焦点，B 为上顶点，O 为坐标原点，直线y ＝b ax 交椭圆于第一象限内的点C ，若S △BFO ＝S △BFC ，则椭圆的离心率等于( ) A.22＋17 B.22－17C.22－13D.2－1答案 A解析联立直线y ＝b a x 与椭圆x 2a 2＋y 2b 2＝1，得在第一象限的交点为C ⎝ ⎛⎭⎪⎫22a ，22b ，又因为S △BFO＝S △BFC ，所以直线BF 与直线y ＝bax 的交点为线段OC 的中点，即线段OC 的中点⎝⎛⎭⎪⎫24a ，24b 在直线BF ：x c ＋y b ＝1上，则24a c ＋24b b ＝1，化简得椭圆的离心率e ＝c a ＝22＋17，故选A.(3)(2018·温州高考适应性测试)正方形ABCD 的四个顶点都在椭圆x 2a 2＋y 2b2＝1上，若椭圆的焦点在正方形的内部，则椭圆的离心率的取值范围是( ) A.⎝ ⎛⎭⎪⎫5－12，1B.⎝ ⎛⎭⎪⎫0，5－12 C.⎝⎛⎭⎪⎫3－12，1D.⎝⎛⎭⎪⎫0，3－12 答案 B解析由椭圆的对称性可知，正方形的四个顶点为直线y ＝±x 与椭圆的交点，即⎝ ⎛⎭⎪⎫±ab a 2＋b 2，±ab a 2＋b 2，因为椭圆的焦点在正方形的内部，所以c <ab a 2＋b2，化简得a 4－3a 2c 2＋c 4>0，所以e 4－3e 2＋1>0，又0<e <1，解得e 2<3－52，即0<e <5－12.1.(2018·浙江省金华东阳中学期中)如果方程x 2a 2＋y 2a ＋6＝1表示焦点在x 轴上的椭圆，则实数a 的取值范围是( ) A.a >3 B.a <－2C.a >3或a <－2D.a >3或－6<a <－2答案 D解析 ∵椭圆的焦点在x 轴上， ∴a 2>a ＋6>0，解得a >3或－6<a <－2. 2.(2018·绍兴质检)已知椭圆Γ：x 2m ＋6＋y 2m ＋2＝1(m >－2)上的动弦EF 过Γ的一个焦点(动弦不在x 轴上)，若Γ的另一个焦点与动弦EF 所构成的三角形的周长为20，则椭圆Γ的离心率为( ) A.15B.12C.25D.45 答案 C解析由椭圆的定义，得4a ＝20，解得a ＝5.又c 2＝a 2－b 2＝m ＋6－(m ＋2)＝4，所以c ＝2，所以椭圆的离心率e ＝c a ＝25，故选C.3.(2018·浙江省高考模拟试卷)已知椭圆的方程为x 212＋y 24＝1，矩形ABCD 的四个顶点都在椭圆上，若椭圆的焦点在矩形的内部，则矩形的长与宽的比值的取值范围为( ) A.(1，2) B.(1，3) C.(6，＋∞) D.(1，6)答案 C解析根据椭圆与矩形的对称性知，矩形的相邻两边分别平行于x 轴，y 轴，且椭圆与矩形都以原点O 为对称中心，如图是矩形的边过焦点时的情形，由椭圆方程x 212＋y 24＝1，知当x ＝22时，y ＝±233，故A ⎝ ⎛⎭⎪⎫22，233，此时，矩形的长与宽的比值为6，由于焦点在矩形的内部，所以矩形的长与宽的比值大于6，故选C. 4.设椭圆x 216＋y 212＝1的左、右焦点分别为F 1，F 2，点P 在椭圆上，且满足PF 1→·PF 2→＝9，则|PF 1|·|PF 2|的值为( ) A.8B.10C.12D.15 答案 D解析由椭圆方程x 216＋y 212＝1，可得c 2＝4，所以|F 1F 2|＝2c ＝4，而F 1F 2――→＝PF 2→－PF 1→，所以|F 1F 2――→|＝|PF 2→－PF 1→|，两边同时平方，得|F 1F 2――→|2＝|PF 1→|2－2PF 1→·PF 2→＋|PF 2→|2，所以|PF 1→|2＋|PF 2→|2＝|F 1F 2――→|2＋2PF 1→·PF 2→＝16＋18＝34，根据椭圆定义，得|PF 1|＋|PF 2|＝2a ＝8，(|PF 1|＋|PF 2|)2＝|PF 1|2＋|PF 2|2＋2|PF 1|·|PF 2|＝64，所以34＋2|PF 1|·|PF 2|＝64，所以|PF 1|·|PF 2|＝15.故选D.5.2016年1月14日，国防科工局宣布，嫦娥四号任务已经通过了探月工程重大专项领导小组审议通过，正式开始实施.如图所示，假设“嫦娥四号”卫星将沿地月转移轨道飞向月球后，在月球附近一点P 变轨进入以月球球心F 为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在P 点第二次变轨进入仍以F 为一个焦点的椭圆轨道Ⅱ绕月飞行.若用2c 1和2c 2分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用2a 1和2a 2分别表示椭圆轨道Ⅰ和Ⅱ的长轴长，给出下列式子：①a 1＋c 1＝a 2＋c 2；②a 1－c 1＝a 2－c 2；③c 1a 1<c 2a 2；④c 1a 2>a 1c 2. 其中正确式子的序号是( ) A.①③B.①④C.②③D.②④答案 D解析观察图形可知a 1＋c 1>a 2＋c 2，即①式不正确；a 1－c 1＝a 2－c 2＝|PF |，即②式正确；由a 1－c 1＝a 2－c 2>0，c 1>c 2>0知，a 1－c 1c 1<a 2－c 2c 2，即a 1c 1<a 2c 2，从而c 1a 2>a 1c 2，c 1a 1>c 2a 2，即④式正确，③式不正确.故选D.6.(2018·浙江省金华十校期末)椭圆M ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1，F 2，P 为椭圆M 上任一点，且|PF 1|·|PF 2|的最大值的取值范围是[2b 2，3b 2]，椭圆M 的离心率为e ，e －1e的最小值是( )A.－22 B.－ 2C.－66D.－63答案 A解析由椭圆的定义可知|PF 1|＋|PF 2|＝2a ， ∴|PF 1|·|PF 2|≤⎝ ⎛⎭⎪⎫|PF 1|＋|PF 2|22＝a 2，∴2b 2≤a 2≤3b 2，即2a 2－2c 2≤a 2≤3a 2－3c 2， ∴12≤c 2a 2≤23，即22≤e ≤63. 令f (e )＝e －1e ，则f (e )在⎣⎢⎡⎦⎥⎤22，63上是增函数，∴当e ＝22时，e －1e 取得最小值22－2＝－22. 7.(2018·浙江七彩阳光联盟联考)已知椭圆的方程为x 29＋y 24＝1，过椭圆中心的直线交椭圆于A ，B 两点，F 2是椭圆的右焦点，则△ABF 2的周长的最小值为________，△ABF 2的面积的最大值为________. 答案 10 2 5解析设F 1是椭圆的左焦点.如图，连接AF 1.由椭圆的对称性，结合椭圆的定义知|AF 2|＋|BF 2|＝2a ＝6，所以要使△ABF 2的周长最小，必有|AB |＝2b ＝4，所以△ABF 2的周长的最小值为10.2ABF S ＝12AF F S＝12×2c ×|y A |＝5|y A |≤25，所以△ABF 2面积的最大值为2 5.8.设F 1，F 2为椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点，经过F 1的直线交椭圆C 于A ，B 两点，若△F 2AB 是面积为43的等边三角形，则椭圆C 的方程为__________. 答案x 29＋y 26＝1 解析 ∵△F 2AB 是面积为43的等边三角形，∴AB ⊥x 轴，∴A ，B 两点的横坐标为－c ，代入椭圆方程，可求得|F 1A |＝|F 1B |＝b 2a.又|F 1F 2|＝2c ，∠F 1F 2A ＝30°，∴b 2a ＝33×2c .①又2F AB S ＝12×2c ×2b2a＝43，②a 2＝b 2＋c 2，③由①②③解得a 2＝9，b 2＝6，c 2＝3， ∴椭圆C 的方程为x 29＋y 26＝1.9.已知椭圆C 1：x 2a 2＋y 2b 2＝1(a >b >0)与椭圆C 2：y 2a 2＋x 2b2＝1(a >b >0)相交于A ，B ，C ，D 四点，若椭圆C 1的一个焦点为F (－2，0)，且四边形ABCD 的面积为163，则椭圆C 1的离心率e 为________. 答案22解析联立⎩⎪⎨⎪⎧x 2a 2＋y 2b 2＝1，y 2a 2＋x2b 2＝1，两式相减得x 2－y 2a 2＝x 2－y 2b 2，又a ≠b ，所以x 2＝y 2＝a 2b 2a 2＋b2，故四边形ABCD 为正方形，4a 2b 2a 2＋b 2＝163，(*)又由题意知a 2＝b 2＋2，将其代入(*)式整理得3b 4－2b 2－8＝0，所以b 2＝2，则a 2＝4，所以椭圆C 的离心率e ＝22. 10.已知A ，B ，F 分别是椭圆x 2＋y 2b2＝1(0<b <1)的右顶点、上顶点、左焦点，设△ABF 的外接圆的圆心坐标为(p ，q ).若p ＋q >0，则椭圆的离心率的取值范围为______________. 答案 ⎝ ⎛⎭⎪⎫0，22 解析如图所示，线段FA 的垂直平分线为x ＝1－1－b 22，线段AB 的中点为⎝ ⎛⎭⎪⎫12，b 2.因为k AB ＝－b ，所以线段AB 的垂直平分线的斜率k ＝1b，所以线段AB 的垂直平分线方程为y －b 2＝1b ⎝ ⎛⎭⎪⎫x －12.把x ＝1－1－b 22＝p 代入上述方程可得y ＝b 2－1－b 22b ＝q .因为p ＋q >0，所以1－1－b 22＋b 2－1－b22b >0，化为b >1－b 2. 又0<b <1，解得12<b 2<1，即－1<－b 2<－12，所以0<1－b 2<12，所以e ＝c a＝c ＝1－b 2∈⎝ ⎛⎭⎪⎫0，22. 11.已知点P 是圆F 1：(x ＋1)2＋y 2＝16上任意一点(F 1是圆心)，点F 2与点F 1关于原点对称.线段PF 2的垂直平分线m 分别与PF 1，PF 2交于M ，N 两点.求点M 的轨迹C 的方程. 解由题意得F 1(－1，0)，F 2(1，0)，圆F 1的半径为4，且|MF 2|＝|MP |，从而|MF 1|＋|MF 2|＝|MF 1|＋|MP |＝|PF 1|＝4>|F 1F 2|，所以点M 的轨迹是以F 1，F 2为焦点的椭圆，其中长轴长为4，焦距为2，则短半轴长为3，所以点M 的轨迹方程为x 24＋y 23＝1.12.已知椭圆x 2＋(m ＋3)y 2＝m (m >0)的离心率e ＝32，求m 的值及椭圆的长轴和短轴的长、焦点坐标、顶点坐标.解椭圆方程可化为x 2m ＋y 2mm ＋3＝1，m >0.∵m －mm ＋3＝m (m ＋2)m ＋3>0，∴m >m m ＋3， ∴a 2＝m ，b 2＝mm ＋3，c ＝a 2－b 2＝m (m ＋2)m ＋3. 由e ＝32，得m ＋2m ＋3＝32，∴m ＝1. ∴椭圆的标准方程为x 2＋y 214＝1，∴a ＝1，b ＝12，c ＝32.∴椭圆的长轴长和短轴长分别为2a ＝2和2b ＝1，焦点坐标为F 1⎝ ⎛⎭⎪⎫－32，0，F 2⎝ ⎛⎭⎪⎫32，0，四个顶点的坐标分别为A 1(－1，0)，A 2(1，0)，B 1⎝ ⎛⎭⎪⎫0，－12，B 2⎝⎛⎭⎪⎫0，12.13.(2018·浙江省台州适应性考试)已知椭圆C 的中心为原点O ，F (－5，0)为椭圆C 的左焦点，P 为椭圆C 上一点，且满足|OP |＝|OF |，|PF |＝6，则椭圆C 的标准方程为( ) A.x 249＋y 224＝1B.x 224＋y 249＝1C.x 249＋y 225＝1 D.x 225＋y 249＝1 答案 A解析如图，设椭圆C 的标准方程为x 2a 2＋y 2b2＝1(a >b >0)，椭圆C 的右焦点为M ，连接PM ，则|FM |＝2|OF |＝10，由|OP |＝|OF |＝|OM |知，FP ⊥PM ，又|PF |＝6，所以|PM |＝102－62＝8，所以2a ＝|PF |＋|PM |＝14，所以a ＝7，又c ＝5，所以b 2＝a 2－c 2＝49－25＝24，所以椭圆C 的标准方程为x 249＋y 224＝1.14.(2018·浙江省镇海中学模拟)设椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的右焦点为F ，椭圆C 上的两点A ，B 关于原点对称，且满足FA →·FB →＝0，|FB |≤|FA |≤2|FB |，则椭圆C 的离心率的取值范围是( ) A.⎣⎢⎡⎦⎥⎤22，53 B.⎣⎢⎡⎭⎪⎫53，1 C.⎣⎢⎡⎦⎥⎤22，3－1 D.[3－1，1)答案 A解析如图，作出椭圆的左焦点F ′，分别连接AB ，AF ′，BF ′，由椭圆的对称性可知，四边形AFBF ′为平行四边形.由FA →·FB →＝0，知FA ⊥FB ，所以四边形AFBF ′为矩形，所以|AB |＝|FF ′|＝2c .设|AF ′|＝m ，|AF |＝n ，则由椭圆的定义知m ＋n ＝2a ，① 在Rt△AF ′F 中，m 2＋n 2＝4c 2.②由①②，得mn ＝2(a 2－c 2)，则m n ＋n m ＝2c2a 2－c 2.令n m ＝t ，得t ＋1t ＝2c 2a 2－c 2. 由|FB |≤|FA |≤2|FB |，得nm＝t ∈[1，2]，所以t ＋1t ＝2c 2a 2－c 2∈⎣⎢⎡⎦⎥⎤2，52，即2≤2e 21－e 2≤52，解得22≤e ≤53，故选A.15.(2018·嘉兴测试)椭圆x 2a 2＋y 2b 2＝1(a >b >0)，直线l 1：y ＝－12x ，直线l 2：y ＝12x ，P 为椭圆上任意一点，过P 作PM ∥l 1且与l 2交于点M ，作PN ∥l 2且与l 1交于点N ，若|PM |2＋|PN |2为定值，则椭圆的离心率为________. 答案32解析设P (x 0，y 0)，则直线PM 的方程为y ＝－12x ＋x 02＋y 0，直线PN 的方程为y ＝12x －x 02＋y 0，分别与直线l 2，l 1的方程联立可得M ⎝ ⎛⎭⎪⎫x 02＋y 0，x 04＋y 02，N ⎝ ⎛⎭⎪⎫x 02－y 0，－x 04＋y 02，从而|PM |2＋|PN |2＝58x 20＋52y 20.又点P (x 0，y 0)在椭圆上，所以b 2x 20＋a 2y 20＝a 2b 2.又|PM |2＋|PN |2为定值，所以b 2a 2＝5852＝14，从而e 2＝a 2－b 2a 2＝34，从而e ＝32.16.已知椭圆x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1(－c ，0)，F 2(c ，0)，若椭圆上存在点P 使1－cos2∠PF 1F 21－cos2∠PF 2F 1＝a 2c 2，求该椭圆的离心率的取值范围.解由1－cos2∠PF 1F 21－cos2∠PF 2F 1＝a 2c 2，得c a ＝sin∠PF 2F 1sin∠PF 1F 2.又由正弦定理得sin∠PF 2F 1sin∠PF 1F 2＝|PF 1||PF 2|，所以|PF 1||PF 2|＝c a ，即|PF 1|＝c a |PF 2|.又由椭圆定义得|PF 1|＋|PF 2|＝2a ，所以|PF 2|＝2a 2a ＋c ，|PF 1|＝2ac a ＋c ，因为PF 2是△PF 1F 2的一边，所以有2c －2ac a ＋c <2a 2a ＋c <2c ＋2aca ＋c，即c 2＋2ac －a 2>0，所以e 2＋2e －1>0(0<e <1)，解得椭圆离心率的取值范围为(2－1，1).精美句子1、善思则能“从无字句处读书”。

2021高考数学一轮复习统考第9章平面解析几何第5讲椭圆课件北师大版

解析
考向三椭圆的几何性质
例 3 (1)(2019·云南保山期末)椭圆ax22＋by22＝1(a>b>0)的一个焦点为 F1，若椭圆上存在一点 P，满足以椭圆短轴为直径的圆与线段 PF1 相切于该线段的中点，则椭圆的离心率为( )
A．
2 2
B．23
C．95
D．
5 3
答案
解析设线段 PF1 的中点为 M，另一个焦点为 F2，由题意知，|OM|＝b，又 OM 是△F2PF1 的中位线，∴|OM| ＝12|PF2|＝b，|PF2|＝2b，由椭圆的定义知|PF1|＝2a－|PF2| ＝2a－2b.
解析答案
4．已知中心在原点的椭圆 C 的右焦点为 F(1,0)，离心率等于13，则椭圆
C 的方程是( )
A．x42＋y32＝1
B．x42＋ y23＝1
C．x42＋y22＝1
D．x92＋y82＝1
c＝1，
解析依题意，设椭圆方程为ax22＋by22＝1(a>b>0)，所以ac＝13，
c2＝a2－b2，
解析取 MN 的中点为 G，点 G 在椭圆 C 上．设点 M 关于椭圆 C 的焦点 F1 的对称点为 A，点 M 关于椭圆 C 的焦点 F2 的对称点为 B，则有|GF1| ＝12|AN|，|GF2|＝21|BN|，所以|AN|＋|BN|＝2(|GF1|＋|GF2|)＝4a＝12.
解析
考向二椭圆的标准方程
例 2 (1)(2019·全国卷Ⅰ)已知椭圆 C 的焦点为 F1(－1,0)，F2(1,0)，过
F2 的直线与 C 交于 A，B 两点．若|AF2|＝2|F2B|，|AB|＝|BF1|，则 C 的方程
为( )
A．x22＋y2＝1

高考数学一轮复习第九章解析几何9.5椭圆课件文北师大版

B1(0,-b),B 2(0,b)
长轴 A1A 2 的长为 2a
|F1F2|=2c

e= ∈(0,1)

c2=a2-b2
第四页，共48页。
y2
a2
+
x2
b2
=1(a>b>0)
-b≤x≤b
-a≤y≤a
对称中心:原点
A1(0,-a),A2(0,a)
B1(-b,0),B 2(b,0)
;短轴 B 1B2 的长为 2b

2
1+4
解得 k
2
5
=16,故
√5
k=± 4 .
第十五页，共48页。
--1616
考点
(kǎo
diǎn)1
考点(kǎo
diǎn)2
考点(kǎo
diǎn)3
解题心得1.在利用椭圆定义解题的时候,一方面要注意到常数
2a>|F1F2|这个条件;另一方面要熟练掌握由椭圆上任一点与两个焦点
所组成的焦点三角形中的数量关系.
25
16
第十七页，共48页。
-18-18
考点
(kǎo
diǎn)2
考点
(kǎo
diǎn)1
考点(kǎo
diǎn)3
解析: (1)如图,设椭圆的左焦点为F',
则|AF|= 22 + (2√3)2 =4=|AF'|,
|PF|+|PF'|=2a=6.
∵|PA|-|PF'|≤|AF'|,
∴△APF的周长=|AF|+|PA|+|PF|=|AF|+|PA|+6-|PF'|≤4+6+4=14,当且仅

(全国通用版)2019版高考数学大一轮复习第九章平面解析几何第5节第1课时椭

第1课时椭圆及其标准方程最新考纲 1.了解椭圆的实际背景，了解椭圆在刻画现实世界和解决实际问题中的作用； 2.掌握椭圆的定义、几何图形、标准方程及简单几何性质.知识梳理1.椭圆的定义在平面内与两定点F1，F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距.其数学表达式：集合P＝{M||MF1|＋|MF2|＝2a}，|F1F2|＝2c，其中a＞0，c＞0，且a，c为常数：(1)若a＞c，则集合P为椭圆；(2)若a＝c，则集合P为线段；(3)若a＜c，则集合P为空集.2.椭圆的标准方程和几何性质标准方程x2a2＋y2b2＝1(a>b>0)y2a2＋x2b2＝1(a>b>0)图形性质范围－a≤x≤a －b≤y≤b －b≤x≤b －a≤y≤a 对称性对称轴：坐标轴；对称中心：原点顶点A1(－a，0)，A2(a，0)，B1(0，－b)，B2(0，b)A1(0，－a)，A2(0，a)，B1(－b，0)，B2(b，0) 轴长轴A1A2的长为2a；短轴B1B2的长为2b焦距|F1F2|＝2c离心率e＝ca∈(0，1)a，b，c的关系c2＝a2－b2 [常用结论与微点提醒]1.过椭圆的一个焦点且与长轴垂直的弦的长为2b2a，称为通径.2.椭圆离心率e＝ca＝a2－b2a＝1－b2a2.3.应用“点差法”时，要检验直线与圆锥曲线是否相交.诊断自测1.思考辨析(在括号内打“√”或“×”）(1)平面内与两个定点F1，F2的距离之和等于常数的点的轨迹是椭圆.( )(2)椭圆的离心率e越大，椭圆就越圆.( )(3)方程mx2＋ny2＝1(m>0，n>0，m≠n)表示的曲线是椭圆.( )(4)x2a2＋y2b2＝1(a>b>0)与y2a2＋x2b2＝1(a>b>0)的焦距相同.( )解析(1)由椭圆的定义知，当该常数大于|F1F2|时，其轨迹才是椭圆，而常数等于|F1F2|时，其轨迹为线段F1F2，常数小于|F1F2|时，不存在这样的图形.(2)因为e＝ca＝a2－b2a＝1－ba2，所以e越大，则ba越小，椭圆就越扁.答案(1)×(2)×(3)√(4)√2.(2017·浙江卷)椭圆x29＋y24＝1的离心率是( )A.133B.53C.23D.59解析由已知，a＝3，b＝2，则c＝9－4＝5，所以e＝ca＝53.答案 B3.(2018·张家口调研)椭圆x216＋y225＝1的焦点坐标为( )A.(±3，0)B.(0，±3)C.(±9，0)D.(0，±9)解析根据椭圆方程可得焦点在y轴上，且c2＝a2－b2＝25－16＝9，∴c＝3，故焦点坐标为(0，±3)，故选 B.答案 B4.已知中心在原点的椭圆C的右焦点为F(1，0)，离心率等于12，则椭圆C的方程是( )A.x23＋y24＝1 B.x24＋y23＝1C.x24＋y22＝1 D.x24＋y23＝1。

高考数学一轮复习第九章平面解析几何第5讲椭圆课件理

解析 (1)由条件知 PM＝PF. ∴PO＋PF＝PO＋PM＝OM＝R＞OF. ∴P 点的轨迹是以 O，F 为焦点的椭圆. (2)由椭圆的方程得 a＝ 3.设椭圆的另一个焦点为 F，则由椭圆的定义得 BA＋BF＝CA＋CF＝2a，所以△ABC 的周长为 BA＋ BC＋CA＝BA＋BF＋CF＋CA＝(BA＋BF)＋(CF＋CA)＝2a＋2a ＝4a＝4 3.
2.(2015·广
东
卷
改
编
)
已
知
椭
圆
x2 25
＋
y2 m2＝1(m来自0)的左焦
点
为
F1(－4，0)，则 m＝________.
解析依题意有25－m2＝16，∵m>0，∴m＝3.
答案 3
3.已知椭圆 C：ax22＋by22＝1(a＞b＞0)的左、右焦点为 F1，F2，
离心率为 33，过 F2 的直线 l 交 C 于 A，B 两点.若△AF1B 的周长为 4 3，则 C 的方程为________. 解析由椭圆的定义可知△AF1B 的周长为 4a，所以 4a＝4 3，故 a＝ 3，又由 e＝ac＝ 33，得 c＝1，所以 b2＝a2－c2＝2，则 C 的方程为x32＋y22＝1. 答案 x32＋y22＝1
第5讲椭圆
考试要求 1.椭圆的实际背景，椭圆在刻画现实世界和解决实际问题中的作用，A级要求；2.椭圆的定义，几何图形，标准方程及简单几何性质，B级要求.
知识梳理
1.椭圆的定义
(1)第一定义：在平面内与两定点F1，F2的距离的和等于常数 (大于F1F2)的点的轨迹叫做椭圆 .这两定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距 . 集合P＝{M|MF1＋MF2＝2a}，F1F2＝2c，其中a＞0，c＞0，且a，c为常数： ①若 a＞c ，则集合P为椭圆； ②若 a＝c ，则集合P为线段； ③若 a＜c ，则集合P为空集.

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A.(±3，0)
B.(0，±3)
C.(±9，0)
D.(0，±9)
解析根据椭圆方程可得焦点在y轴上，且c2＝a2－b2＝25－16
＝9，∴c＝3，故焦点坐标为(0，±3)，故选B.
答案 B
基础诊断
考点突破
@《创新设计》
4.已知中心在原点的椭圆 C 的右焦点为 F(1，0)，离心率等于12，则椭圆 C 的方程是( )
A.5
B.6
C.7
D.8
解析 (1)连接QA.由已知得|QA|＝|QP|.
所以|QO|＋|QA|＝|QO|＋|QP|＝|OP|＝r.
又因为点A在圆内，所以|OA|＜|OP|，根据椭圆的定义，点Q的
轨迹是以O，A为焦点，r为长轴长的椭圆.
(2)由椭圆定义知点P到另一个焦点的距离是10－2＝8.
答案 (1)A (2)D
＝±
215，又 x＞0，所以 x＝
215，∴P
点坐标为
215，1或
215，－1.
答案
215，1或
215，－1
基础诊断
考点突破
@《创新设计》
第1课时椭圆及其标准方程
基础诊断
考点突破
@《创新设计》
考点一椭圆的定义及其应用【例1】 (1)(选修1－1P42A7改编)如图，圆O的半径为定长r，
基础诊断
考点突破
@《创新设计》
规律方法 1.椭圆定义的应用主要有：判定平面内动点的轨迹是否为椭圆、求椭圆的标准方程和离心率等. 2.椭圆的定义式必须满足2a＞|F1F2|.
基础诊断
考点突破
@《创新设计》
【训练 1】(1)设定点 F1(0，－3)，F2(0，3)，动点 P 满足条件|PF1|＋|PF2|＝a＋9a(a>0)，
A是圆O内一个定点，P是圆上任意一点，线段AP的垂直平分线l和半径OP相交于点Q，当点P在圆上运动时，点Q的轨迹是( )
A.椭圆 C.抛物线
B.双曲线 D.圆
基础诊断
考点突破
@《创新设计》
(2)椭圆2x52＋y2＝1 上一点 P 到一个焦点的距离为 2，则点 P 到另一个焦点的距离为
()
@《创新设计》
基础诊断
考点突破
@《创新设计》
诊断自测 1.思考辨析(在括号内打“√”或“×”)
(1)平面内与两个定点 F1，F2 的距离之和等于常数的点的轨迹是椭圆.( ) (2)椭圆的离心率 e 越大，椭圆就越圆.( ) (3)方程 mx2＋ny2＝1(m>0，n>0，m≠n)表示的曲线是椭圆.( ) (4)ax22＋by22＝1(a>b>0)与ay22＋bx22＝1(a>b>0)的焦距相同.( )
考点突破
2.椭圆的标准方程和几何性质
标准方程
ax22＋by22＝1(a>b>0)
ay22＋bx22＝1(a>b>0)
图形
@《创新设计》
基础诊断
考点突破
@《创新设计》
范围
－a≤x≤a － b≤y≤b
－b≤x≤b － a≤y≤a
对称性对称轴：坐标轴；对称中心：原点
A1(－a，0)，A2(a， A1(0，－a)，A2(0，
则点 P 的轨迹是( )
A.椭圆
B.线段
C.不存在
D.椭圆或线段
(2)与圆 C1：(x＋3)2＋y2＝1 外切，且与圆 C2：(x－3)2＋y2＝81 内切的动圆圆心 P
的轨迹方程为________.
基础诊断
考点突破
@《创新设计》
解析 (1)∵a＋9a≥2 a·9a＝6，当且仅当 a＝9a，即 a＝3 时取等号， ∴当a＝3时，|PF1|＋|PF2|＝6＝|F1F2|，点P的轨迹是线段F1F2；当a>0，且a≠3时，|PF1|＋|PF2|>6＝|F1F2|，点P的轨迹是椭圆. (2)设动圆的半径为r，圆心为P(x，y)，则有|PC1|＝r＋1，|PC2| ＝9－r.
及焦点 F1，F2 为顶点的三角形的面积等于 1，则点 P 的坐标为________. 解析设 P(x，y)，由题意知 c2＝a2－b2＝5－4＝1，所以 c＝1，则 F1(－1，0)，F2(1， 0)，由题意可得点 P 到 x 轴的距离为 1，所以 y＝±1，把 y＝±1 代入x52＋y42＝1，得 x
0)，
a)，
性质
顶点
B1(0，－b)，B22(0a， B1(－b，0)，2Bb2(b，
b)
2c 0)
轴焦距
长轴A1A2的长为 (0，；1短) 轴B1B2的长为
___a_2_－__b2
|F1F2|＝_______
基础诊
考点突
断
破
[常用结论与微点提醒] 1.过椭圆的一个焦点且与长轴垂直的弦的长为2ab2，称为通径. 2.椭圆离心率 e＝ac＝ a2a－b2＝ 1－ab22. 3.应用“点差法”时，要检验直线与圆锥曲线是否相交.
基础诊断
考点突破
2.(2017·浙江卷)椭圆x92＋y42＝1 的离心率是( )
13
5
2
5
A. 3
B. 3
C.3
D.9
解析
由已知，a＝3，b＝2，则 c＝
9－4＝
5，所以
e＝ac＝
5 3.
答案 B
@《创新设计》
基础诊断
考点突破
@《创新设计》
3.(2018·张家口调研)椭圆1x62＋2y52＝1 的焦点坐标为( )
基础诊断
考点突破
@《创新设计》
解析 (1)由椭圆的定义知，当该常数大于|F1F2|时，其轨迹才是椭圆，而常数等于|F1F2|时，其轨迹为线段F1F2，常数小于 (|F2)1因F为2|时e＝，ac＝不a存2a－在b2＝这样1－的ba图2，形所.以 e 越大，则ba越小，椭圆就越扁. 答案 (1)× (2)× (3)√ (4)√
的轨迹叫做椭圆.这两定点叫做椭圆的焦点
，两
焦点间的距离焦叫距做椭圆的
.
其数学表达式：集合P＝{M||MF1|＋|MF2|＝2a}，|F1F2|＝2c，其中a＞0，c＞0，且a，c为常数：
(1)若 a＞c ，则集合P为椭圆；
(2)若 a=c ，则集合P为线段；
(3)若 a<c ，则集合P为空集.
基础诊断
A.x32＋y42＝1
B.x42＋ y23＝1
C.x42＋y22＝1
D.x42＋y32＝1
解析由题意知 c＝1，e＝ac＝12，所以 a＝2，b2＝a2－c2＝3.故所求椭圆 C 的方程为 x42＋y32＝1.
答案 D
基础诊断
考点突破
@《创新设计》
5.(选修 1－1P42A6 改编)已知点 P 是椭圆x52＋y42＝1 上 y 轴右侧的一点，且以点 P
@《创新设计》
第5节椭圆
基础诊断
考点突破
@《创新设计》
最新考纲 1.了解椭圆的实际背景，了解椭圆在刻画现实世界和解决实际问题中的作用；2.掌握椭圆的定义、几何图形、标准方程及简单几何性质.
基础诊断
考点突破@《创新设 Fra bibliotek》知识梳
1.椭圆的定义
理
在平面内与两定点F1，F2的距离的和等于常数(大于|F1F2|)的点