《管理运筹学》第四版 第5章 单纯形法 课后习题解析
《管理运筹学》第四版课后习题解析(上)演示教学

《管理运筹学》第四版课后习题解析(上)《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解1x =127,2157x =;最优目标函数值697。
图2-12.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6x x =⎧⎨=⎩,函数值为3.6。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
(6)有唯一解 1220383x x ⎧=⎪⎪⎨⎪=⎪⎩,函数值为923。
3.解:(1)标准形式12123max 32000f x x s s s =++++1211221231212392303213229,,,,0x x s x x s x x s x x s s s ++=++=++=≥(2)标准形式1212min 4600f x x s s =+++12112212121236210764,,,0x x s x x s x x x x s s --=++=-=≥(3)标准形式12212min 2200f x x x s s ''''=-+++ 1221122122212212355702555032230,,,,0x x x s x x x x x x s x x x s s '''-+-+=''''-+=''''+--=''''≥4.解:标准形式1212max 10500z x x s s =+++1211221212349528,,,0x x s x x s x x s s ++=++=≥松弛变量(0,0)最优解为 1x =1,x 2=3/2。
5.解:标准形式12123min 118000f x x s s s =++++121122123121231022033184936,,,,0x x s x x s x x s x x s s s +-=+-=+-=≥剩余变量(0, 0, 13)最优解为 x 1=1,x 2=5。
管理运筹学课后习题

第一章思考题、主要概念及内容1、了解运筹学的分支,运筹学产生的背景、研究的内容和意义。
2、了解运筹学在工商管理中的应用。
3、体会管理运筹学使用相应的计算机软件,注重学以致用的原则。
第二章思考题、主要概念及内容图解法、图解法的灵敏度分析复习题1. 考虑下面的线性规划问题:max z=2x1+3x2 ;约束条件:x1+2x2 <65x1+3x2 < 15x1, x2 >0(1) 画出其可行域.(2) 当z=6 时,画出等值线2x1+3x2=6 .(3) 用图解法求出其最优解以及最优目标函数值.2. 用图解法求解下列线性规划问题,并指出哪个问题具有惟一最优解、无穷多最优解、无界解或无可行解.(1) min f=6x1+4x2 ;约束条件:2x1+x2 >1,3x1+4x2 >3,x1 ,x2 >0(2) max z=4x1+8x2 ;约束条件:2x1+2x2 < 1,0-x1+x2 >8,x1,x2 >0(3) max z=3x1-2x2 ;约束条件:x1+x2 <1,2x1+2x2 >4,x1 ,x2 >0(4) max z=3x1+9x2 ;约束条件:x1+3x2 w 22-x1+x2 <4x2w6,2x1-5x2 <0x1, x2 >03. 将下述线性规划问题化成标准形式:(1) max f=3x1+2x2 ;约束条件:9x1+2x2 < 303x1+2x2 < 132x1+2x2 <9x1 ,x2 >0.(2) min f=4x1+6x2 ;约束条件:3x1-x2>6x1+2x2 < 107x1-6x2=4 ,x1 ,x2 >0.(3) min f=-x1-2x2 ;约束条件:3x1+5x2 < 70,-2x1-5x2=50 ,-3x1+2x2 > 30x1 O, x2(提示:可以令x ' 1=1,这样可得x' 1 >同样可以令x '-2" 2=x2其中x 2 x" 2>0可见当x' 2>册,2 x2 >0当x ' 2<册,2 x2 <0即-x2 这样原线性规划问题可以化为含有决策变量x' ,1x ' ,2 x" 2的线性规划问题,这里决策变量x',1x',2 x" 2>.0 )4. 考虑下面的线性规划问题:min f=11x1+8x2 ;约束条件:10x1+2x2 > 2203x1+3x2 > 1284x1+9x2 > 326x1 2 x2 >0.(1) 用图解法求解.(2) 写出此线性规划问题的标准形式.(3) 求出此线性规划问题的三个剩余变量的值.5. 考虑下面的线性规划问题:max f=2x1+3x2 ;约束条件:x1+x2 < 1202x1+x2 >42x1+3x2 w 242x1+x2 w 16x1, x2 >0(1) 用图解法求解.(2) 假定c2值不变,求出使其最优解不变的cl值的变化范围.(3) 假定cl值不变,求出使其最优解不变的c2值的变化范围.(4) 当cl值从2变为4, c2值不变时,求出新的最优解.(5) 当cl值不变,c2值从3变为1时,求出新的最优解.(6) 当cl值从2变为2 5, c2值从3变为2 5时,其最优解是否变化?为什么?6. 某公司正在制造两种产品,产品I和产品H,每天的产量分别为30个和120个,利润分别为500元/个和400元/个•公司负责制造的副总经理希望了解是否可以通过改变这两种产品的数量而提高公司的利润.公司各个车间的加工能力和制造单位产品所需的加工工时如表2-4 (25页)所示.表2-4(1) 假设生产的全部产品都能销售出去,用图解法确定最优产品组合,即确定使得总利润最大的产品I和产品n的每天的产量.(2) 在(1)所求得的最优产品组合中,在四个车间中哪些车间的能力还有剩余?剩余多少?这在线性规划中称为剩余变量还是松弛变量?(3) 四个车间加工能力的对偶价格各为多少?即四个车间的加工能力分别增加一个加工时数时能给公司带来多少额外的利润?(4) 当产品I的利润不变时,产品n的利润在什么范围内变化,此最优解不变?当产品n的利润不变时,产品I的利润在什么范围内变化,此最优解不变?⑸当产品I的利润从500元/个降为450元/个,而产品n的利润从400元/个增加为430元/ 个时,原来的最优产品组合是否还是最优产品组合?如有变化,新的最优产品组合是什么?第三章思考题、主要概念及内容管理运筹学"软件的操作方法管理运筹学”软件的输出信息分析复习题1. 见第二章第7题,设x1为产品I每天的产量,x2为产品n每天的产量,可以建立下面的线性规划模型:max z=500x1+400x2 ;约束条件:2x1 < 30Q3x2 < 5402x1+2x2 < 4401.2x1+1.5x2 W 300x1, x2 >0使用管理运筹学”软件,得到的计算机解如图3-5)所示根据图3-5回答下面的问题:(1)最优解即最优产品组合是什么?此时最大目标函数值即最大利润为多少?⑵哪些车间的加工工时数已使用完?哪些车间的加工工时数还没用完?其松弛变量即没用完的加工工时数为多少?(3) 四个车间的加工工时的对偶价格各为多少?请对此对偶价格的含义予以说明.(4) 如果请你在这四个车间中选择一个车间进行加班生产,你会选择哪个车间?为什么?⑸目标函数中x1的系数cl,即每单位产品I的利润值,在什么范围内变化时,最优产品的组合不变?⑹目标函数中x2的系数C2,即每单位产品n的利润值,从400元提高为490元时,最优产品组合变化了没有?为什么?(7) 请解释约束条件中的常数项的上限与下限.(8) 第1车间的加工工时数从300增加到400时,总利润能增加多少?这时最优产品的组合变化了没有?(9) 第3车间的加工工时数从440增加到480时,从图3-5中我们能否求得总利润增加的数量?为什么?(10) 当每单位产品I的利润从500元降至475元,而每单位产品n的利润从400元升至450元时,其最优产品组合(即最优解)是否发生变化巧青用百分之一百法则进行判断.(11) 当第1车间的加工工时数从300增加到350,而第3车间的加工工时数从440降到380时,用百分之一百法则能否判断原来的对偶价格是否发生变化?如不发生变化,请求出其最大利润.2. 见第二章第8题(2),仍设xA为购买基金A的数量,xB为购买基金B的数量,建立的线性规划模型如下:max z=5xA+4xB ;约束条件:50xA+100xB < 1 200 000100xB > 300 000xA , xB>0.使用管理运筹学”软件,求得计算机解如图3-7所示.JI Iftff胭IB£轉■23DG0<0fit 嗾鼾1 c■ W■]i!I ifcTK LO出JW TW Mil] jxaaa mUQD SISl D3KXXU imno根据图3-7,回答下列问题:(1) 在这个最优解中,购买基金A和基金B的数量各为多少?这时获得的最大利润是多少?这时总的投资风险指数为多少?(2) 图3-7中的松弛/剩余变量的含义是什么?(3) 请对图3-7中的两个对偶价格的含义给予解释.(4) 请对图3-7中的目标函数范围中的上、下限的含义给予具体说明,并阐述如何使用这些信息.(5) 请对图3-7中的常数项范围的上、下限的含义给予具体说明,并阐述如何使用这些信息.⑹当投资总金额从1 200 000元下降到600 000元,而在基金B上至少投资的金额从300 000 元增加到600 000元时,其对偶价格是否发生变化?为什么?3. 考虑下面的线性规划问题:min z=16x1+16x2+17x3 ;约束条件:x1+x3 < 300 5x1-x2+6x3 > 153x1+4x2- x3 > 20x1, x2, x3 >0其计算机求解结果如图3-9所示.* n*Am4an1 Bill II ! ■"T " L 'KM詁 1 2T D0TO35蜩&的!ft20 SIU-s m3口7F上・3 <li馬;F W35 MT9ft17IK盘袒品斟■Ttt MA9 IN n无二2as a LI zs3唸5w根据图3-9,回答下列问题:(1)第二个约束方程的对偶价格是一个负数(为-3 622),它的含义是什么?⑵x2的相差值为0 703,它的含义是什么?⑶当目标函数中x1的系数从16降为15,而x2的系数从16升为18时,最优解是否发生变化?(4) 当第一个约束条件的常数项从30减少到15,而第二个约束条件的常数项从15增加到80时,你能断定其对偶价格是否发生变化吗?为什么?第四章思考题、主要概念及内容人力资源的分配问题; 生产计划的问题;套裁下料问题;配料问题;投资问题。
《管理运筹学》第四版课后习题答案
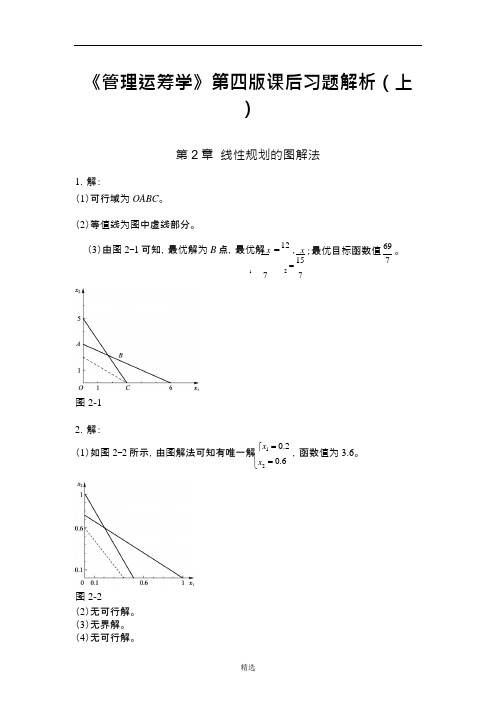
精选⎨= 0.6《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解 x =12, x = 15 1727图2-1;最优目标函数值 69。
72.解:(1)如图2-2所示,由图解法可知有唯一解 ⎧x 1 = 0.2,函数值为3.6。
⎩x 2图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
⎨ (5)无穷多解。
⎧x = (6)有唯一解 ⎪ 1⎪ 203 ,函数值为 92 。
8 3 x = ⎪⎩ 2 33.解: (1)标准形式max f = 3x 1 + 2x 2 + 0s 1 + 0s 2 + 0s 39x 1 + 2x 2 + s 1 = 303x 1 + 2x 2 + s 2 = 13 2x 1 + 2x 2 + s 3 = 9x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f = 4x 1 + 6x 2 + 0s 1 + 0s 23x 1 - x 2 - s 1 = 6 x 1 + 2x 2 + s 2 = 10 7x 1 - 6x 2 = 4x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式min f = x 1' - 2x 2' + 2x 2'' + 0s 1 + 0s 2-3x 1 + 5x 2' - 5x 2'' + s 1 = 70 2x 1' - 5x 2' + 5x 2'' = 50 3x 1' + 2x 2' - 2x 2'' - s 2 = 30 x 1', x 2' , x 2'' , s 1, s 2 ≥4.解: 标准形式max z = 10x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4x 2 + s 1 = 9 5x 1 + 2x 2 + s 2 = 8 x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
《管理运筹学》第四版课后习题解析(上)之欧阳引擎创编

《管理运筹学》第四版课后习题解析(上)欧阳引擎(2021.01.01)第2章线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解1x =127,2157x =;最优目标函数值697。
图2-12.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6x x =⎧⎨=⎩,函数值为3.6。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
(6)有唯一解1220383x x ⎧=⎪⎪⎨⎪=⎪⎩,函数值为923。
3.解:(1)标准形式(2)标准形式(3)标准形式4.解:标准形式松弛变量(0,0)最优解为1x =1,x2=3/2。
5.解:标准形式剩余变量(0, 0, 13)最优解为x1=1,x2=5。
6.解:(1)最优解为x1=3,x2=7。
(2)113c <<。
(3)226c <<。
(4)1264x x ==。
(5)最优解为x1=8,x2=0。
(6)不变化。
因为当斜率12113c c ---≤≤,最优解不变,变化后斜率为1,所以最优解不变。
7.解:设x ,y 分别为甲、乙两种柜的日产量,目标函数z=200x +240y , 线性约束条件:⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+006448120126y x y x y x 即 ⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+00162202y x y x y x 作出可行域.解⎩⎨⎧=+=+162202y x y x 得)8,4(Q 答:该公司安排甲、乙两种柜的日产量分别为4台和8台,可获最大利润2720元.8.解:设需截第一种钢板x 张,第二种钢板y 张,所用钢板面积zm2.目标函数z=x +2y , 线性约束条件:作出可行域,并做一组一组平行直线x +2y=t .解⎩⎨⎧=+=+12273y x y x 得)2/15,2/9(E.但E 不是可行域内的整点,在可行域的整点中,点)8,4(使z 取得最小值。
ch5 单纯形法.ppt

下面通过第二章例1来解释这些概念:
max z 50x1 100x2
s.tx1 x2 300 x1 x2 4j 1, 2.
管理运筹学
首先将其变为如下的标准型:
max z 50x1 100x2
s.tx1 x1 x2
x2 x4
管理运筹学
max z 50x1 100x2
max z 25000+50x1-100x5
s.tx1 x1 x2
x2 x4
x3
300 400
x2
250-x5
s.tx1 x3-x5 50 x1 x4 -x5 150
x2 x5 250
x2 x5 250
xj 0, j 1, 2,L 5.
管理运筹学
由于原非基变量在目标函数中的 系数均大于零,所以,对应的目标函 数值就会增大。
从经济意义上讲,若安排生产甲 产品或乙产品,就可使企业的利润指 标增加。
管理运筹学
所以只要目标函数的表达式中 不含基变量(此时变量的系数称为 检验数),而且还有正系数的非基 变量,就表示目标函数值还有改进 的可能。
x3
300 400
x2 x5 250
xj 0,j 1, 2,L 5.
管理运筹学
它的系数矩阵为:
1 1 1 0 0
A
(
p1,
p2
,
p3 ,
p4
,
p5
)
2
1
0
1
0
0 1 0 0 1
其中pj为系数矩阵A第j列的向量。A的 秩为3,A的秩m小于此方程组的变量的 个数n,
管理运筹学
在此例中我们不妨以下列矩阵为 为A的一个基,
管理运筹学
单纯形法的几种特殊情况

达不到最优解。
下面一个是由E.Beale给出的循环的例子。
例5
目标函数
min f =-(3/4)x4+20x5-(1/2)x6+6x7.
约束条件:x1+(1/4)x4-8x5-x6+9x7=0,
x2+(1/2)x4-12x5-(1/2)x6+3x7=0,
x3+x6=1,
x1,x2,x3,x4,x5,x6,x7≥0.
50 150 250
12500
50/1 150/2 —
50 50 250
15000
— 50/1 250/1
8
§4 几种特殊情况
这样我们求得了最优解为x1=50,x2=250,s1=0,s2=50,s3=0,此线性规划的 最优值为15000。这个最优解是否是惟一的呢?由于在第2次迭代的检验数
中除了基变量的检验数 1,2,4 等于零外,非基变量s3的检验数也等
30 0 20 1 -M 0
1
1/10
-3/10
0
0
0
-7/10
-1
1
zj
20
30
3+M/10 11+7M/10
M
-M
cj-zj
0
0
-3-M/10 -11-7M/10
-M
0
管理运筹学
b
比值
150 30 40
-40M
150/10 — 40/1
15
15/(3/10)
30
30/1
25
25/(7/10)
例4.用单纯形表,求解下列线性规划问题。
解:加上松驰变量s1,s2,s3化为标准形式后,
运筹学教材编写组《运筹学》课后习题-线性规划与单纯形法(圣才出品)

= =
8 −3
x1, x2, x3, x4 0
解:在第二个约束条件两边同时乘以-1,得到该线性规划问题的系数矩阵
4 / 28
圣才电子书 十万种考研考证电子书、题库视频学习平台
A
=
(
P1,
P2
,
P3
,
P4
)
=
2 −1
3 2
−1 −6
−4
7
①因为 P1 、 P2 线性无关,故有
令非基变量
x2
=
x3
=
0 ,解得
x1
=
34 , 5
x4
=
7 5
,故有基可行解
X
(3)
=
34 5
, 0, 0,
7 5
T
,
z3
=
117 5
。
④因为 P2 、 P3 线性无关,故有
32xx22
− −
x3 = 8 − 2x1 6x3 = 3+ x1
+ −
4x4 7x4
令非基变量
x1
=
x4
= 0,解得
x2
最优解或称为无界解。
(4) max z = x1 + x2 s.t. 3x1x1−−x2x20−3
x1, x2 0
解:如图 l-4 所示,该问题的可行域为空集,因此该线性规划无可行解。
2 / 28
圣才电子书 十万种考研考证电子书、题库视频学习平台
1.2 将下列线性规划问题变换成标准型,并列出初始单纯形表。
取得最小值,求解方程组
x1 x1
+ +
3x2
=
3
《管理运筹学》第四版课后习题解析(上)之欧阳德创编

《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1.解: (1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解1x =127,2157x =;最优目标函数值697。
图2-12.解:(1)如图2-2所示,由图解法可知有唯一解120.20.6x x =⎧⎨=⎩,函数值为3.6。
图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
(5)无穷多解。
(6)有唯一解1220383x x ⎧=⎪⎪⎨⎪=⎪⎩,函数值为923。
3.解:(1)标准形式(2)标准形式(3)标准形式4.解:标准形式松弛变量(0,0)最优解为1x =1,x2=3/2。
5.解:标准形式剩余变量(0, 0, 13)最优解为x1=1,x2=5。
6.解:(1)最优解为x1=3,x2=7。
(2)113c <<。
(3)226c <<。
(4)1264x x ==。
(5)最优解为x1=8,x2=0。
(6)不变化。
因为当斜率12113c c ---≤≤,最优解不变,变化后斜率为1,所以最优解不变。
7.解:设x ,y 分别为甲、乙两种柜的日产量,目标函数z=200x +240y , 线性约束条件:⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+006448120126y x y x y x 即 ⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+00162202y x y x y x 作出可行域.解⎩⎨⎧=+=+162202y x y x 得)8,4(Q 答:该公司安排甲、乙两种柜的日产量分别为4台和8台,可获最大利润2720元.8.解:设需截第一种钢板x 张,第二种钢板y 张,所用钢板面积zm2.目标函数z=x +2y , 线性约束条件:作出可行域,并做一组一组平行直线x +2y=t .解⎩⎨⎧=+=+12273y x y x 得)2/15,2/9(E.但E 不是可行域内的整点,在可行域的整点中,点)8,4(使z 取得最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《管理运筹学》第四版课后习题解析
第5章单纯形法
1.解:
表中a 、c 、e 、f 是可行解,f 是基本解,f 是基本可行解。
2.解:
(1)该线性规划的标准型如下。
max 5x 1+9x 2+0s 1+0s 2+0s 3 s.t. 0.5x 1+x 2+s 1=8 x 1+x 2-s 2=10
0.25x 1+0.5x 2-s 3=6 x 1,x 2,s 1,s 2,s 3≥0
(2)至少有两个变量的值取零,因为有三个基变量、两个非基变量,非基变量取零。
(3)(4,6,0,0,-2)T (4)(0,10,-2,0,-1)
T (5)不是。
因为基本可行解要求基变量的值全部非负。
(6)略 3.解:
令33
3x x x ''-'=,z f -=改为求f max ;将约束条件中的第一个方程左右两边同时乘以-1,并在第二和第三个方程中分别引入松弛变量5x 和剩余变量6x ,将原线性规划问题化为如下标准型:
j x '、j x ''不可能在基变量中同时出现,因为单纯性表里面j x '、j x ''相应的列向量是相同的,只有符号想法而已,这时候选取基向量的时候,同时包含两列会使
选取的基矩阵各列线性相关,不满足条件。
4.解: (1) 表5-1
0,,,,,, 24423 1863 1334 7234max 65433
21633
21543321433
214
321≥'''=-''+'--=++''+'-+-=+''+'---++-=x x x x x x x x x x x x x x x x x x x x x x x x x x x f 约束条件:
(2)线性规划模型如下。
max 6x 1+30x 2+25x 3 s.t. 3x 1+x 2+s 1=40 2x 2+x 3+s 2=50 2x 1+x 2-x 3+s 3=20 x 1,x 2,x 3,s 1,s 2,s 3 ≥0
(3)初始解的基为(s 1,s 2,s 3)
T ,初始解为(0,0,0,40,50,20)T ,对应的目标函数值为0。
(4)第一次迭代时,入基变量时x 2,出基变量为s 3。
6. 解:
(1)当现行解为可行解,并且对应的非基变量检验数均小于0时,该线性规划问题才有唯一最优解,即01≥k ,03<k ,05<k ;
(2)当某个非基变量的检验数为0时,该线性规划问题有多重最优解。
所以若满足现行解为最优解,并且有多重最优解即满足:或者01≥k ,03=k ,05≤k ;
或者01≥k ,03≤k ,05=k ;;或者01≥k ,03=k ,0
5=k (3)01≥k 可以保证该线性规划问题有可行解。
若此时该线性规划问题目标函数无界,也就是说一定存在某个检验数为正时,对应的列的系数向量元素全部非正,即50k >且04≤k ;
(4)由表中变量均为非人工变量,则01≤k 且02≥k ,由于变量的非负性条件,第一个约束方程变为矛盾方程,从而该问题无可行解;
7. 解:
(1)7,1,0,0,0,1,0,7========h g f e d c b a ; (2)表中给出的解是最优解。
8.解:
最优解为(2.25,0)
T ,最优值为9。
图5-1
单纯形法如表5-2所示。
9.解:
(1)最优解为(2,5,4)
T ,最优值为84。
(2)最优解为(0,0,4)T,最优值为−4。
10.解:
有无界解。
11.解:
(1)无可行解。
(2)最优解为(4,4)T,最优值为28。
(3)有无界解。
(4)最优解为(4,0,0)T,最优值为8。
12. 解:
,0,5( ,最优值为-12。
该线性规划问题的最优解为T)1。
