广东省中山市普通高中高一数学1月月考试题04
广东省江门市普通高中高一数学1月月考试题07(new)
高一数学1月月考试题07一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
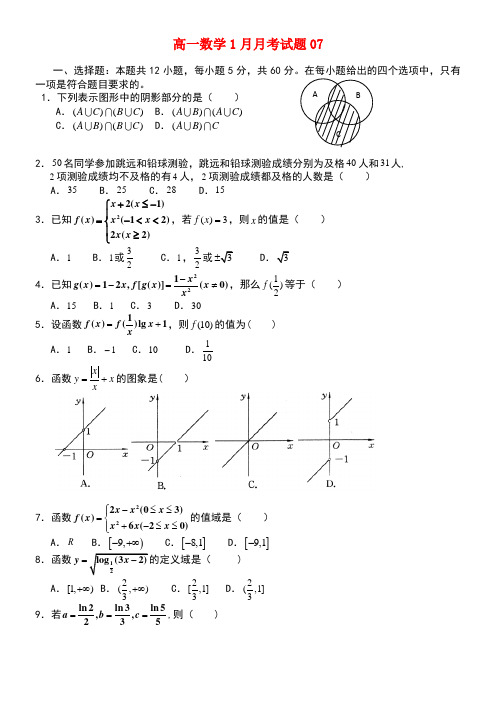
1.下列表示图形中的阴影部分的是( )A .()()A CBC B .()()A B A CC .()()A B B CD .()A B C2.50名同学参加跳远和铅球测验,跳远和铅球测验成绩分别为及格40人和31人, 2项测验成绩均不及格的有4人,2项测验成绩都及格的人数是( )A .35B .25C .28D .153.已知22(1)()(12)2(2)x x f x x x x x +≤-⎧⎪=-<<⎨⎪≥⎩,若()3f x =,则x 的值是( )A .1B .1或32C .1,32或3± D .34.已知221()12,[()](0)x g x x f g x x x-=-=≠,那么)21(f 等于( ) A .15 B .1 C .3 D .30 5.设函数1()()lg 1f x f x x=+,则(10)f 的值为( ) A .1 B .1- C .10 D .101 6.函数x x x y +=的图象是( )7.函数222(03)()6(20)x x x f x x x x ⎧-≤≤⎪=⎨+-≤≤⎪⎩的值域是( ) A .R B .[)9,-+∞ C .[]8,1- D .[]9,1-8.函数12log (32)y x =- )A .[1,)+∞B .2(,)3+∞C .2[,1]3D .2(,1]39.若ln 2ln 3ln 5,,235a b c ===,则( ) A B CA .a b c <<B .c b a <<C .c a b <<D .b a c <<10.若22521,(),4,1,(1),,(1)2x x y x y y x y x y x y x y a a ====+=-==>上述函数是幂函数的个数是( )A .0个B .1个C .2个D .3个11.若函数234y x x =--的定义域为[0,]m ,值域为25[4]4--,,则m 的取值范围是( ) A .(]4,0 B .3[]2,4 C .3[3]2, D .3[2+∞,)12.若函数()f x 唯一的一个零点同时在区间(0,16)、(0,8)、(0,4)、(0,2)内,那么 下列命题中正确的是( )A .函数()f x 在区间(0,1)内有零点B .函数()f x 在区间(0,1)或(1,2)内有零点C .函数()f x 在区间[)2,16内无零点D .函数()f x 在区间(1,16)内无零点二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题纸中的横线上。
广东省中山市普通高中高一数学11月月考试题04(new)

上学期高一数学11月月考试题04一.填空题:(每小题3分,共42分)1. 集合{1,2,3,4}A =的非空子集的个数为 15 ;2. 若,0,0<>>c b a 则a c > bc ; 3.已知集合}2,2{2a a a -为数集,求实数a 的取值范围是 0≠a 且4≠a ;4.若集合{}0132=++x kx x 中至多有一个元素,则k 的取值范围是 0=k 或49≥ ; 5.写出命题“已知a 、b 、c 是实数,如果0<ac ,那么()002≠=++a c bx ax 有实数根”的否命题 已知a 、b 、c 是实数,如果0≥ac ,那么()002≠=++a c bx ax 没有实数根” ;6.写出0x <的一个充分不必要的条件 1-<x (答案不唯一) ;7.设{}{}2,2,1,,4,2,1m Q m P ==,则满足P Q P =的实数m 的值为 0,2- ; 8。
集合{|24},{|0}A x x B x x a =-<<=-<,当A B =∅时,实数a 的取值范围是 2-≤a ;9.设全集R U =,集合{|11},{|02}A x x B x x =-≤≤=<<,则()B A C U ⋃= {}21≥-<x x x 或 ;10.若{}R x x x x A ∈<--=,0432,则N A = {}3,2,1,0 ;11.已知全集{}{}{}4,1,2,5,4,3,2,1===B A C B A U U ,则=B {}4,2,1 ; 12.设集合2{|43},{|2}A y y x x a B y y ==--++=<,若A B ⊂≠,则实数a 的取值范围是 5-<a ;13.设集合⎭⎬⎫⎩⎨⎧∈∈-=Z x Z x x A ,36,试用列举法表示集合A = {}9,3,6,0,5,1,4,2- ;14.给出下列条件p 与q :① 1:=x p 或2=x ;11:-=-x x q .② :p 一元二次方程02=++m x x 有实数解;41:<m q .③ x p :是6的倍数;x q :是2的倍数.④ :p 一个四边形是矩形;:q 四边形的对角线相等.其中p 是q 的必要不充分条件的序号为 ② ;二.选择题(每小题3分共12分)15.若0,0<<>>d c b a ,则下列不等式恒成立的是 ( C )()22ad bc A < ()33ad bc B < ()c b d a C < ()db c a D < 16.下列命题为真命题的是 ( D ) ()A 若A B =∅,则B A ,至少有一个为空集;()B 若集合(){}(){}1,,1,2--==+-==x y y x B x y y x A ,则{}1,2-=B A ;()C 任何集合必有一个真子集;()D 若{}{}22,x y x Q x y y P ====,则Q P ⊆;17.若不等式012>-+bx ax 的解集是{}43<<x x ,则实数b a +的值为 ( A ) ()21A ()2B ()41C ()31D 18.条件M 是N 的充要条件的为 ( D )()A 22:;:bc ac N b a M >> ()B c b d a N d c b a M ->->>:;,:()C bd ac N d c b a M >>>>>:;0,0: ()D 0:;:≤+=-ab N b a b a M三.解答题(共46分)19.(满分7分)已知0>>b a ,试比较2222b a b a -+与ba b a -+的值的大小. 解:因为2222222b a ab b a b a ba b a --=-+--+,又因为0>>b a ,所以002222>-⇒>>b a b a 且0<-ab , 即02222222<--=-+--+b a ab b a b a b a b a ,所以2222b a b a -+<ba b a -+. 20.(满分9分)若{}x U ,1,0=,{}1,0=A ,且U x ∈2,求A C U .解:因为U x ∈2,则有02=x 或12=x 或x x =2.解得0=x 或1±=x ,由集合元素的互异性知1-=x ,则{}1,1,0-=U ,故{}1-=A C U21.(满分10分)已知31:,421:≤≤+≤≤+x m x m βα,若α是β的必要条件,求实数m 的取值范围. 解:设{}421+≤≤+=m x m x A ,{}31≤≤=x x B .因为α是β的必要条件,所以A B ⊆,所以⎩⎨⎧+≤≤+42311m m 021≤≤-⇒m . 所以实数m 的取值范围是021≤≤-m . 22.(满分10分)设{}{},015,022=++==++=cx x x B b ax x x A又{}{}3,5,3==B A B A ,求c b a ,,的值.解:因为{}3=B A ,所以8015332-=⇒=++c c , 所以{}{},5,30152==++=cx x x B 由{},5,3=B A 可得{}3=A 或{}5,3=A ,而{}3=B A ,所以{}3=A .所以⎪⎩⎪⎨⎧=++=-=∆0330422b a ac a ⎩⎨⎧=-=⇒96b a , 所以8,9,6-==-=c b a .23.(满分10分)已知{}{}2,,1,21,1,1r r B d d A =++=,其中1,0≠≠r d ,问当r d ,满足什么条件时B A =?并求出这种情形下的集合A .解:由题意,有两种情形:⑴ ⎩⎨⎧=+=+②①2211r d r d ,由①得1-=r d ,代人②得0122=+-r r ,所以1=r ,与条件1≠r 矛盾,因此在这种情形下B A =不能成立.⑵ ⎩⎨⎧=+=+②①r d r d 2112,由①得12-=r d ,代人②得,0122=--r r()()0112=-+⇒r r ,由条件1≠r ,得21-=r ,代人②得43-=d .当21-=r ,43-=d 时,⎭⎬⎫⎩⎨⎧-==21,41,1B A .尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
高一数学第一次月考试题与答案

2017-2018学年度高一数学9月月考试卷本试卷分第Ⅰ卷和第Ⅱ卷两部分,共150分,考试时间120分钟。
学校:___________姓名:___________班级:___________考号:___________分卷I一、选择题(共12小题,每小题5.0分,共60分)1.已知集合M ={x ∈N +|2x ≥x 2},N ={-1,0,1,2},则(∁R M )∩N 等于( ) A . ∅ B . {-1} C . {1,2} D . {-1,0}2.已知集合P ={4,5,6},Q ={1,2,3},定义P ⊕Q ={x |x =p -q ,p ∈P ,q ∈Q },则集合P ⊕Q 的所有真子集的个数为( )A . 32B . 31C . 30D . 以上都不对3.定义A -B ={x |x ∈A ,且x ∉B },若A ={1,2,4,6,8,10},B ={1,4,8},则A -B 等于( ) A . {4,8} B . {1,2,6,10} C . {1} D . {2,6,10}4.下列各组函数中,表示同一个函数的是( ) A .y =x -1和y =B .y =x 0和y =1C .f (x )=x 2和g (x )=(x +1)2 D .f (x )=和g (x )=5.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图像是( )A .B .C .D .6.下列三个函数:①y =3-x ;②y =;③y =x 2+2x -10.其中值域为R 的函数有( ) A .0个 B .1个 C .2个 D .3个 7.一次函数g (x )满足g [g (x )]=9x +8,则g (x )是( ) A .g (x )=9x +8 B .g (x )=3x +8C .g (x )=-3x -4D .g (x )=3x +2或g (x )=-3x -4 8.下列函数中,在[1,+∞)上为增函数的是( ) A .y =(x -2)2 B .y =|x -1| C .y =D .y =-(x +1)2 9.若非空数集A ={x |2a + ≤x ≤3a -5},B ={x |3≤x ≤ },则能使A ⊆B 成立的所有a 的集合是( ) A . {a | ≤a ≤9} B . {a |6≤a ≤9} C . {a |a ≤9} D . ∅10.若函数f (x )= ,, , ,φ(x )=, , , ,则当x <0时,f (φ(x ))为( ) A . -x B . -x 2C .XD .x 2 11.若函数f (x )=的最小值为f (0),则实数m 的取值范围是( )A . [-1,2]B . [-1,0]C . [1,2]D . [0,2]12.已知函数f (x )=4x 2-kx -8在区间(5,20)上既没有最大值也没有最小值,则实数k 的取值范围是( )A. [160,+∞) B. (-∞,40]C. (-∞,4 ]∪[ 6 ,+∞) D. (-∞, ]∪[8 ,+∞)分卷II二、填空题(共4小题,每小题5.0分,共20分)13.已知M={2,a,b},N={2a,2,b2},且M=N,则有序实数对(a,b)的值为________.14.已知函数y=f(x2-1)的定义域为{x|-2<x<3},则函数y=f(3x-1)的定义域为____________.15.设函数f(x)=, ,, ,若f(f(a))=2,则a=_________.16.已知函数y=f(x)的定义域为{1,2,3},值域为{1,2,3}的子集,且满足f[f(x)]=f(x),则这样的函数有________个.三、解答题(共6小题,,共70分)17.(10分)用单调性的定义证明函数f(x)=2x2+4x在[-1,+∞)上是增函数.18(12分).根据下列函数解析式求f(x).(1)已知f(x+1)=2x2+5x+2;(2)已知f=x3+3-1;(3)已知af(x)+f(-x)=bx,其中a≠± 19(12分).已知集合A={x| ≤x<7},B={x|3<x<10},C={x|x<a}.(1)求A∪B,(∁R A)∩B;(2)若A∩C≠∅,求a的取值范围.20(12分).经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20-|t-10|.(1)试写出该种商品的日销售额y与时间t( ≤t≤ )的函数表达式;(2)求该种商品的日销售额y的最大值与最小值.21(12分).已知函数f(x)=(x-a)2-(a2+1)在区间[0,2]上的最大值为g(a),最小值为h(a)(a∈R).(1)求g(a)和h(a);(2)作出g (a )和h (a )的图像,并分别指出g (a )的最小值和h (a )的最大值各为多少?22(12分).已知函数f (x )的定义域是(0,+∞),当x >1时,f (x )>0,且f (x ·y )=f (x )+f (y ). (1)求f (1)的值;(2)证明:f (x )在定义域上是增函数;(3)如果f (3)=-1,求满足不等式f (x )-f (x - )≥ 的x 的取值范围.2017-2018学年度高一数学9月月考试卷答案解析1.【答案】D【解析】因为M ={1,2},所以(∁R M )∩N ={-1,0},故正确答案为D. 2.【答案】B【解析】由所定义的运算可知P ⊕Q ={1,2,3,4,5}, ∴P ⊕Q 的所有真子集的个数为25-1=31.故选B. 3.【答案】D【解析】A -B 是由所有属于A 但不属于B 的元素组成,所以A -B ={2,6,10}.故选D. 4.【答案】D【解析】A 中的函数定义域不同;B 中y =x 0的x 不能取0;C 中两函数的对应关系不同,故选D. 5.【答案】C【解析】考查四个选项,横坐标表示时间,纵坐标表示的是离开学校的距离,由此知,此函数图像一定是下降的,由此排除A ;再由小明骑车上学,开始时匀速行驶,可得出图像开始一段是直线下降型,又途中因交通堵塞停留了一段时间,故此时有一段函数图像与x轴平行,由此排除D,后为了赶时间加快速度行驶,此一段时间段内函数图像下降的比较快,由此可确定C正确,B不正确.故选C.6.【答案】B【解析】7.【答案】D【解析】∵g(x)为一次函数,∴设g(x)=kx+b,∴g[g(x)]=k(kx+b)+b=k2x+kx+b,又∵g[g(x)]=9x+8,∴9,8,解得3,或3,4,∴g(x)=3x+2或g(x)=-3x-4.故选D.8.【答案】B【解析】y=(x-2)2在[2,+∞)上为增函数,在(-∞,2]为减函数;y=|x-1|= , ,,在[1,+∞)上为增函数,故选B.9.【答案】B 10.【答案】B【解析】x<0时,φ(x)=-x2<0,∴f(φ(x))=-x2.11.【答案】D【解析】当x≤ 时,f(x)=(x-m)2,f(x)min=f(0)=m2,所以对称轴x=m≥ .当x>0时,f(x)=x++m≥ +m=2+m,当且仅当x=,即x=1时取等号,所以f(x)min=2+m.因为f(x)的最小值为m2,所以m2≤ +m,所以 ≤m≤ .12.【答案】C【解析】由于二次函数f(x)=4x2-kx-8在区间(5,20)上既没有最大值也没有最小值,因此函数f(x)=4x2-kx-8在区间(5,20)上是单调函数.二次函数f(x)=4x2-kx-8图像的对称轴方程为x=8,因此8≤5或8≥ ,所以k≤4 或k≥ 6 .13.【答案】(0,1)或(4,)【解析】∵M={2,a,b},N={2a,2,b2},且M=N,∴或即或或4当a=0,b=0时,集合M={2,0,0}不成立,∴有序实数对(a,b)的值为(0,1)或(4,),故答案为(0,1)或(4,).14.【答案】{x| ≤x<3}【解析】∵函数y=f(x2-1)的定义域为{x|-2<x<3},∴-2<x<3.令g(x)=x2-1,则- ≤g(x)<8,故- ≤3x-1<8,即 ≤x<3,∴函数y=f(3x-1)的定义域为{x| ≤x<3}.15.【答案】【解析】若a≤ ,则f(a)=a2+2a+2=(a+1)2+1>0,所以-(a2+2a+2)2=2,无解;若a>0,则f(a)=-a2<0,所以(-a2)2+2(-a2)+2=2,解得a=.故a=.16.【答案】10【解析】∵f[f(x)]=f(x),∴f(x)=x,①若f:{ , ,3}→{ , ,3},可以有f(1)=1,f(2)=2,f(3)=3,此时只有1个函数;②若f:{ , ,3}→{ },此时满足f(1)=1;同理有f:{ , ,3}→{ };f:{ , ,3}→{3},共有3类不同的映射,因此有3个函数;③首先任选两个元素作为值域,则有3种情况.例如选出1,2,且对应关系f:{ , ,3}→{ , },此时满足f(1)=1,f(2)=2.则3可以对应1或2,又有2种情况,所以共有3× =6个函数.综上所述,一共有1+3+6=10个函数.17.【答案】设x1,x2是区间[-1,+∞)上的任意两个实数,且x1<x2,则f(x1)-f(x2)=(2+4x1)-(2+4x2)=2(-)+4(x1-x2)=2(x1-x2)(x1+x2+2).∵- ≤x1<x2,∴x1-x2<0,x1+x2+2>0,∴f(x1)-f(x2)<0,即f(x1)<f(x2),∴f(x)在[-1,+∞)上是增函数.18.【答案】(1)方法一(换元法)设x+1=t,则x=t-1,∴f(t)=2(t-1)2+5(t-1)+2=2t2+t-1,∴f(x)=2x2+x-1.方法二(整体代入法)∵f(x+1)=2x2+5x+2=2(x+1)2+(x+1)-1,∴f(x)=2x2+x-1.(2)(整体代入法)∵f=x3+3-1=3-3x2·-3x·-1=3-3-1,∴f(x)=x3-3x-1(x≥ 或x≤-2).(3)在原式中以-x替换x,得af(-x)+f(x)=-bx,于是得+ - = ,- + =-消去f(-x),得f(x)=.故f(x)的解析式为f(x)=x(a≠± ).19.【答案】(1)因为A={x| ≤x<7},B={x|3<x<10},所以A∪B={x| ≤x<10}.因为A={x| ≤x<7},所以∁R A={x|x<2或x≥7},则(∁R A)∩B={x|7≤x<10}.(2)因为A={x| ≤x<7},C={x|x<a},且A∩C≠∅,所以a>2.20.【答案】(1)y=g(t)·f(t)=(80-2t)·( -|t-10|)=(40-t)(40-|t-10|)=3 4 , ,4 5 ,(2)当 ≤t<10时,y的取值范围是[1 200,1 225],在t=5时,y取得最大值1 225;当 ≤t≤ 时,y的取值范围是[600,1 200],在t=20时,y取得最小值600.综上,第5天,日销售额y取得最大值1 225元;第20天,日销售额y取得最小值600元.21.【答案】( )∵f(x)=(x-a)2-(a2+1),又x∈[ , ],∴当a≤ 时,g(a)=f(2)=3-4a,h(a)=f(0)=-1;当0<a≤ 时,g(a)=f(2)=3-4a,h(a)=f(a)=-(a2+1);当1<a<2时,g(a)=f(0)=-1,h(a)=f(a)=-(a2+1);当a≥ 时,g(a)=f(0)=-1,h(a)=f(2)=3-4a.综上可知g(a)=3 4h(a)=3 4(2)g(a)和h(a)的图像分别为:由图像可知,函数y=g(a)的最小值为-1,函数y=h(a)的最大值为-1.【解析】22.【答案】(1)解令x=y=1,得f(1)=2f(1),故f(1)=0.(2)证明令y=,得f(1)=f(x)+f()=0,故f()=-f(x).任取x1,x2∈( ,+∞),且x1<x2,则f(x2)-f(x1)=f(x2)+f()=f().由于>1,故f()>0,从而f(x2)>f(x1).∴f(x)在(0,+∞)上是增函数.(3)解由于f(3)=-1,而f(3)=-f(3),故f(3)=1.在f(x·y)=f(x)+f(y)中,令x=y=3,得f(9)=f(3)+f(3)=2.故所给不等式可化为f(x)-f(x- )≥f(9),∴f(x)≥f[9(x-2)],∴x≤94.又∴ <x≤94,∴x的取值范围是94.【解析】。
2018-2019学年广东省中山市东区中学高一数学文月考试题含解析

2018-2019学年广东省中山市东区中学高一数学文月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 下列函数中,在区间上是增函数的是A. B. C. D.参考答案:B2. 已知a>b,c>d,且c、d不为0,则下列不等式恒成立的是A.B.C.D.参考答案:D解:令a=2,b=-2,c=3,d=-6,则2×3<(-5)(-6)=30,可排除A2×(-6)<(-2)×3可排除B;2-3<(-2)-(-6)=4可排除C,∵a>b,c>d,∴a+c>b+d(不等式的加法性质)正确.故选D.3. 函数的一个对称中心是()A. B. C. D.参考答案:D略4. 设,且,则下列不等式恒成立的是()A. B.C. D.参考答案:D【分析】逐一分析选项,得到正确答案.【详解】由已知可知,可以是正数,负数或0,A.不确定,所以不正确;B.当时,两边同时乘以,应该,所以不正确;C.因为有可能等于0,所以,所以不正确;D.当时,两边同时乘以,,所以正确.故选D.【点睛】本题考查了不等式的基本性质,属于简单题型.5. 下列说法中,正确的个数是()①存在一个实数,使;②所有的质数都是奇数;③斜率相等的两条直线都平行;④至少存在一个正整数,能被5和7整除。
A.1B.2C.3D.4参考答案:C解析:①方程无实根;②2时质数,但不是奇数;③④正确。
6. 在三棱柱中,各棱长相等,侧掕垂直于底面,点是侧面的中心,则与平面所成角的大小是 ( )A. B. C. D.参考答案:C7. 已知为互不相等的正数,,则下列关系中可能成立的是()A.B.C.D.参考答案:C8. 的值是----------------------------------------()A.1B.0C.-1 D.参考答案:D9. 已知集合M={x|x<3},N={x|},则M∩N= ( )A.B.{x|0<x<3}C.{x|1<x<3} D.{x|2<x<3}参考答案:D略10. 若A为△ABC的内角,则下列函数中一定取正值的是()A. B. C. D.参考答案:A略二、填空题:本大题共7小题,每小题4分,共28分11. 已知正方形ABCD的边长为1,AP⊥平面ABCD,且AP=2,则PC =.参考答案:略12. 某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这1000名学生在该次自主招生水平测试中不低于分的学生数是.参考答案:60013. 在△ABC中,已知∠BAC=60°,∠ABC=45°,BC=,则AC=参考答案:14. 已知集合,,若,则实数m的取值范围是.参考答案:(-∞,3]①若,则②若,则应满足,解得综上得实数的取值范围是15. 已知,则的大小关系是.参考答案:略16. 已知函数满足:,,则:= .参考答案:2014略17. 设集合A={1, 2, 3}, B={2, 4, 5}, 则______________.参考答案:略三、解答题:本大题共5小题,共72分。
广东省深圳市深圳实验学校高中部2024-2025学年高一上学期第一次月考数学试题

广东省深圳市深圳实验学校高中部2024-2025学年高一上学期第一次月考数学试题一、单选题1.下列四个命题中真命题是( ) A .R x ∀∈,230+<x B .N x ∀∈,21x > C .Z x ∃∈,使31x <D .Q x ∃∈,23x =2.已知命题p :0R x ∀∈,20104x x -+≤,则命题p 的否定为( ) A .0x ∃∈R ,20104x x -+> B .0x ∃∈R ,20104x x -+< C .0R x ∀∈,2104x x -+≤D .0R x ∀∈,2104x x -+> 3.下列各组函数中,表示同一个函数的是( )A .2(),()x f x x g x x ==B .()(),()()f x x x R g x x x Z =∈=∈C .,0(),(),0x x f x x g x x x ≥⎧==⎨-<⎩D .2(),()f x x g x ==4.已知集合123M x x m m ⎧⎫==+∈⎨⎬⎩⎭Z ,,23N x x n n ⎧⎫==-∈⎨⎬⎩⎭Z ,,13P x x p p ⎧⎫==+∈⎨⎬⎩⎭Z ,,则下列,,M N P 的关系正确的是( ) A .M N = P B .M N P = C .M N PD .N P M5.小港、小海两人同时相约两次到同一水果店购买葡萄,小港每次购买50元葡萄,小海每次购买3千克葡萄,若这两次葡萄的单价不同,则( ) A .小港两次购买葡萄的平均价格比小海低 B .小海两次购买葡萄的平均价格比小港低C .小港与小海两次购买葡萄的平均价格一样D .丙次购买葡萄的平均价格无法比较 6.函数()()()252,2213,2a x x f x x a x a x ⎧---≥⎪=⎨+--<⎪⎩,若对任意1x ,()212R x x x ∈≠,都有()()()()12120x x f x f x --≤成立,则实数a 的取值范围为( )A .[]4,1--B .[]4,2--C .(]5,1--D .[]5,4--7.已知2()2a f x x ax =-+在区间[0,1]上的最大值为g (a ),则g (a )的最小值为( ) A .0B .12C .1D .28.已知函数()f x 的定义域为R ,对任意12x x <,有()()12121f x f x x x ->--,且(2)0f =,若()2211f x ax a x ax a --++≤++-对任意[1,1]a ∈-恒成立,则x 的取值范围为( )A .(2]-∞B .(,1]-∞-C .(,1][0,)-∞-+∞UD .[0,)+∞二、多选题9.设U 为全集,若A B A =U ,则( ) A .A B = B .B A ⊆C .A B B =ID .U UA B ⊆痧10.已知函数()26x f x x +=-,下列选项正确的是( ) A .若()2f x =,则14x = B .函数()f x 在定义域内是减函数 C .若[]2,8x ∈时,则()f x 的值域是[]1,5- D .若N x ∈,则函数()f x 有最小值也有最大值 11.下列说法正确的是( )A .若1x >,则311x y x +=-的最小值为B .已知1x >-,0y >,且21x y +=,则121x y ++的最小值为92C .已知正实数x 、y 满足2x y xy +=,则2xx y y++的最小值是4 D .若0x >,0y >、0z >,则22234x y z xy yz +++的最小值为25三、填空题 12.已知()1x f x -,则()f x 的定义域为13.已知14a b ≤+≤,12a b -≤-≤,则42a b -的取值范围为.14.设()()()2121f x a x a x =-+-+.若函数()f x 在区间[]3,6上的图象恒位于x 轴的上方,则实数a 的取值范围是.四、解答题15.给定函数()1f x x =+,()()21g x x =+,R x ∈.(1)在同一直角坐标系中画出函数()f x ,()g x 的图象; (2)观察图象,直接写出不等式()211x x +<+的解:(3)R x ∀∈,用()M x 表示()f x ,()g x 中的较大者,记为()()(){}max ,M x f x g x =.例如,当2x =时,()()(){}{}2max 2,2max 3,99M f g ===.请分别用图象法和解析法表示函数()M x .16.已知集合{}31A x x =-<,()(){}250B x x a x a =--<,R a ∈. (1)当0a >时,x A ∈是x B ∈的充分条件,求实数a 的取值范围; (2)若R B A ⊆ð,求实数α的取值范围.17.函数()22f x ax bx =++,,a b ∈R(1)若()0f x >的解集是{|1x x <或2}x >,求实数a ,b 的值; (2)当0a =时,若()()42f f x x =-,求实数b 的值;(3)a ∈R ,若()24f =,求()28f x x <-+的解集.18.某厂家拟定在2023年举行促销活动,经调查测算,该产品的年销量(即该厂的年产量)x 万件与年促销费用()0m m ≥万元满足32kx m =-+(k 为常数).如果不举行促销活动,该产品的年销量只能是1万件.已知2023年生产该产品的固定投入将为10万元,每生产1万件,该产品需要再投入16万元(再投入费用不包含促销费用),厂家将每件产品的销售价格定为“平均每件产品的固定投入与再投入”的32倍.(1)求k 的值;(2)将2023年该产品的利润y (万元)表示为年促销费用m (万元)的函数; (3)该厂家2023年约投入多少万元促销费用时,获得的利润最大,最大利润是多少?1.414,结果保留1位小数). 19.已知函数()221x f x x-=.(1)用单调性的定义证明函数()f x 在()0,∞+上为增函数;(2)是否存在实数λ,使得当()f x 的定义域为11,m n ⎡⎤⎢⎥⎣⎦(0m >,0n >)时,函数()f x 的值域为[]2,2m n λλ--.若存在.求出λ的取值范围;若不存在说明理由.。
普通高中高一数学1月月考试题03(2021学年)

广东省珠海市普通高中2017-2018学年高一数学1月月考试题03编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(广东省珠海市普通高中2017-2018学年高一数学1月月考试题03)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为广东省珠海市普通高中2017-2018学年高一数学1月月考试题03的全部内容。
上学期高一数学1月月考试题03一、选择题(每小题5分,共50分) 1.集合M= 集合N= 则( ) A.M =N B.M N C.M N D.M N 2。
下列四类函数中,具有性质“对任忌的x>0,y >o ,函数f(x )满足f (x+y)=f (x)f(y)”的是( )A。
幂函数 B .对数函数 C 。
指数函数 D .二次函数3。
若 = ,则 在( ) A 。
第一、三象限 B。
第一、二象限 C 。
第二、四象限 D 。
第三、四象限4。
a,b,c 均为正数,且2a = 则有( ) A 。
c 〈b 〈a B.c<a<b C.b 〈a 〈c D.a<b<c5。
f(x)= 若f(a)+f(1)=0,则a 的值等于( ) A 。
—3 B 。
—1 C.1 D.36。
定义在R上的奇函数f (x)满足:当x 〉0时,f(x )=2012x+log 2012x,则方程f(x)=0在R 上的实根个数是( )A 。
1B .2 C.3 D.47.若x 0是方程lg x+x=2的解,则x 0属于区间( )A。
(0,1) B.(1,1.25) C 。
(1。
25,1。
75) D 。
(1。
75,2)8.a〉1,对任意的x∈[a,2a]都有y ∈[a,a 2]满足方程log a x+log a y=3则a 的集合的( )A. B 。
高一数学上学期第一次月考试题(B卷)-人教版高一全册数学试题
2016-2017学年度万全中学第一次月考卷数学试卷(B 卷)考试X 围:第一章;考试时间:120分钟;注意事项:1.答题前填写好自己的某某、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题【共12个小题,每个题4分,共计48分】 1.已知R 是实数集,21xx ⎧⎫M =<⎨⎬⎩⎭,{}1y y x N ==-,则RN M =( )A .()1,2B .[]0,2C .∅D .[]1,2 2.满足条件M ∪{1}={1,2,3}的集合M 的个数是( ) A .1 B .2 C .3 D .43.设全集U ={1,2,3,4},集合S ={1,3},T ={4},则等于( )A 、{2,4}B 、{4}C 、ΦD 、{1,3,4}4.已知全集R U =,{}{}1,0)3(-<=<+=x x M x x x N ,则图中阴影部分表示的集合是( )A .{}13-<<-x x B.{}03<<-x x C.{}01<≤-x x D.{}3-<x5.设集合2{|1}P x x ==,那么集合P 的真子集个数是() A .3 B .4 C .7 D .86.函数y=x 2﹣2x ﹣1在闭区间[0,3]上的最大值与最小值的和是( ) A .﹣1 B .0 C .1 D .27.定义在R 上的函数()f x 对任意两个不相等实数,a b ,则必有( ) A.()f x 在R 上是增函数 B.()f x 在R 上是减函数 C.函数()f x 是先增加后减少 D.函数()f x 是先减少后增加 8.已知函数f(x)为奇函数,且当x>0时, f(x) =x 2f(-1)=( ) A .-2 B .0 C .1 D .29.下列函数中,既是奇函数又是增函数的为( ) A .1y x =+B .3y x =- C.||y x x = 10.若11x -≤≤时,函数()21f x ax a =++的值有正值也有负值,则a 的取值X 围是( )A .13a ≥-B .1a ≤-C .113a -<<-D .以上都不对 11.已知函数)(x f y =在R 上是增函数,且(21)(34)f m f m +>-,则m 的取值X 围是( ) A .(-)5,∞B .(5,)+∞C12.若定义在R 上的偶函数()f x 对任意12,[0,)∈+∞x x 12()≠x x ,有A .(3)(2)(1)<-<f f fB .(1)(2)(3)<-<f f fC .(1)(3)(2)<<-f f fD .(2)(3)(1)-<<f f f第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题【每小题4分,共计16分】13.已知全集U =R ,集合A ={x|x ≤-2,x ∈R},B ={x|x <1,x ∈R},则(∁U A)∩B =.14.已知集合}012|{2=+-=x ax x A 有且只有一个元素,则a 的值的集合..(.用列举法表示......).是. 15.2()24f x x x =-+的单调减区间是.16.若函数2122+-+=x )a (x y ,在(]4,∞-上是减少的,则a 的取值X 围是三、解答题17,18题每题10分,19,20,21每题12分,写出必要的解题和证明步骤。
广东省中山市普通高中高一数学11月月考试题07(new)
上学期高一数学11月月考试题07一、选择题:(本题共10题,每题3分,共30分。
)1、已知全集}5,4,3,2,1{=U ,且}4,3,2{=A ,}2,1{=B ,则=⋂)(B C A UA }2{B }5{C }4,3{D }5,4,3,2{2、下列函数中是偶函数且在),0(+∞上单调递增的是A x y =B 2x y -=C x y 2=D ||x y = 3、若1)21()22(1-=+-x x g ,则=)3(g A 1- B 21- C 43- D 87-4、函数1||2)(+-=x x f 的图像大致为5、已知函数⎩⎨⎧<≥+=0|,|0,12)(x x x x x f ,且3)(0=x f ,则实数0x 的值为A 3-B 1C 3-或1D 3-或1或3 6、若函数)(x f 是定义在R 上的偶函数,在]0,(-∞上是减函数,且0)2(=f ,则使得0)()1(<-x f x 的x 的取值范围是A (1,2))2,(⋃--∞B ),1()2,(+∞⋃--∞C ),1()1,(+∞⋃-∞D )2,1()1,(⋃-∞ 7、不等式0241>-++k x x 对R x ∈恒成立,则k 的取值范围是A 1-<kB 1->kC 0≤kD 0≥k8、函数)(x f 满足),)(()()()(4R y x y x f y x f y f x f ∈-++=,且41)1(=f ,0)0(≠f ,则下列等式不成立的是A 41)2()0(=+f f B 41)4()2(-=+f f C 41)2()3(-=-f f D 41)3()4(=-f f 9、函数||2x y =的定义域为],[b a ,值域为]16,1[,则点),(b a 表示的图形可以是10、定义函数B A f →:,其中}1,1{),,0()0,(-=+∞⋃-∞=B A ,且对于)0,(-∞中的任意一个x 都与集合B 中的1对应,),0(+∞中的任意一个x 都与集合B 中的1-对应,则)(2)()()(b a b a f b a b a ≠---+的值为 A a B b C b a ,中较小的数 D b a ,中较大的数二、填空题(本题共7题,每题3分,共21分。
高一数学下学期第一次月考试题含解析试题 2
创作人:
历恰面
日期:
2020年1月1日
考前须知:
1.在答题之前,先将本人的姓名、准考证号填写上在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的规定的正确位置。
2.选择题的答题:每一小题在选出答案以后,需要用2B铅笔把答题卡上对应题目之答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
232 321 230 023 123 021 132 220
231 130 133 231 331 320 122 233
由此可以估计,恰好第三次就停顿的概率为〔〕
A. B. C. D.
【答案】C
【解析】
【分析】
由题意知,经随机模拟产生了如下16组随机数,在16组随机数中恰好第三次就停顿的可以通过列举得到一共2组随机数,根据概率公式,得到结果.
零件数 /个
10
20
30
40
50
加工时间是
62
75
81
89
表中有一个数据模糊不清,请你推断出该数据的值是〔〕
A.66B.67C.68D.69
【答案】C
【解析】
【分析】
根据回归直线方程过样本中心点 ,计算 代入回归直线方程,解方程求得模糊不清的数据.
【详解】设模糊的数据为 , , ,由于回归直线方程过样本中心点 ,将 代入回归直线方程得 ,解得 ,应选C.
【详解】由题意知,经随机模拟产生了如下16组随机数,
在16组随机数中恰好第三次就停顿的有:021、130.
一共2组随机数,
∴所求概率为 .
应选:C.
【点睛】此题考察模拟方法估计概率,是一个根底题,解这种题目的主要根据是等可能事件的概率,注意列举法在此题的应用.
广东省中山市龙山中学2023-2024学年高一上学期10月月考数学试题
使得 g x2 f x1 ,则实数 a 的取值范围
.
四、解答题
17.设集合 A x∣ 2 x 2, B x∣1 m x 2m 2
(1)若 x A 是 x B 的充分条件,求实数 m 的取值范围; (2)若 A B B ,求实数 m 的取值范围. 18.已知 a 0,b 0 , a 2b 1 . (1)求 b 1 的最小值;
ab
试卷第 3页,共 5页
(2)求 a2 6ab 4b2 的最大值.
19.已知函数
f
x
2ax b x2 1
是定义在 1,1
上的奇函数,且
f
1 2
4 5
.
(1)求 a , b 的值;
(2)用定义法证明函数 f x 在1,1 上单调递增;
(3)若 f x m2 5mt 5 对于任意的 x 1,1 ,t 1,1 恒成立,求实数 m 的取值范围.
B.2, 4
C. 4,5
D. 2, 3
5.函数
y
x2 2x 的图像大致为( x2 2x 1
)
A.
B.
试卷第 1页,共 5页
C.
D.
6.已知 f (x) ax3 b 3 , f (4) 5,则 f 4 ( )
x
A.3
B.1
C.-1
D.-5
7.设函数 f (x) x2 x 16 (2 x a),其中实数 a 2 .若 f (x) 的值域为 [9,11] ,则 a x
①函数在整个定义域是严格增函数或严格减函数;
②存在区间a,b ,使得函数在区间a,b 上的值域为 a2 ,b2 ,则称函数 f x 是该定义
域上的“闭函数”.
试卷第 4页,共 5页
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省中山市普通高中2017-2018学年高一数学1月月考试题
第I卷(选择题)
一、选择题
1.如图,给出了偶函数yfx的局部图象,那么1f与3f 的大小关系正确的是
A.13ff B.13ff C.13ff D.13ff
2. 点(,)xy在映射“f”的作用下的象是(,2)xyxy,则在映射f作用下点(5,1)的原
象是( )
A.(2,3) B.(2,1) C. (3,4) D. (6,9)
3.设函数()yfx是R上的奇函数,且当[0,)x时,3()(1)fxxx,那么当
(,0]x时,()fx
( )
A.3(1)xx B.3(1)xx C.3(1)xx D.3(1)xx
4.函数12yxx的值域是( )
A.(,1] B.(,1] C.R D.[1,)
5.用“二分法”求函数3222fxxxx的一个正实数零点,其参考数据如下:
那么方程32220xxx的一个近似根(精确到0.1)为 ( )
A. 1.2 B. 1.3 C. 1.4 D. 1.5
6.对任意实数x规定y取14,1,(5)2xxx三个值中的最小值,则函数y( )
A.有最大值2,最小值1 B.有最大值2,无最小值
C.有最大值1,无最小值 D.无最大值,无最小值
12f 1.50.625f
1.250.984f
1.3750.260f 1.43750.162f
1.406250.054f
7.函数24()|3|3xfxx的图象关于( )
A.y轴对称 B.直线yx对称 C.坐标原点对称 D.x轴对称
8.函数8)(3xaxxxf)(Ra在区间],[nm上有最大值10,则函数)(xf在区间
],[mn
上有( )
A. 最大值-10 B. 最小值-10 C. 最小值—26 D. 最大值-26
9.已知集合|1,|21xMxxNx,则MN=( )
A. B.|0xx C.|1xx D.|01xx
10.已知0.312a,20.3b,12log2c,则,,abc的大小关系是( )
A.abc B.acb C.cba D.bac
11.下列对应法则f中,构成从集合A到集合B的映射是
A.2||:,},0|{xyxfRBxxA
B.2:},4{},2,0,2{xyxfBA
C.2:},1,0{},2,0{xyxfBA
D. 21:},0|{,xyxfyyBRA
12.设)(xf=ax12lg是奇函数,则)(xf<0的取值范围是( )
A.(-1,0) B.(0,1)
C.(-∞,0) D.(-∞, 0)∪(1,+∞)
第II卷(非选择题)
二、填空题
13.已知集合,Axy,0,1B,则从集合A到集合B的映射最多有 个.
14.偶函数()fx在[0,)上是增函数,则满足1(21)()3fxf的x的取值范围是_____.
15.下列几个命题
①方程2(3)0xaxa有一个正实根,一个负实根,则0a.
②函数2211yxx是偶函数,但不是奇函数.
③函数()fx的值域是[2,2],则函数(1)fx的值域为[3,1].
④ 设函数()yfx定义域为R,则函数(1)yfx与(1)yfx的图象关于
y
轴对称.
⑤一条曲线2|3|yx和直线 ()yaaR的公共点个数是m,则m的值不可能是1.
其中正确的有 ________.(把所有正确命题的序号都填上)
16.已知函数
1()log(2)()nfnnn
*
Ν
,定义:使)()2()1(kfff为整数的数
k
()k*N
叫作企盼数,则在区间1,10内这样的企盼数共有 个.
三、解答题
17.(本小题满分12分)
记函数1()2fxx的定义域为集合A,函数29)(xxg的定义域为集合B.
(1)求AB和AB;(2)若ACpxxC,}0|{,求实数p的取值范围.
18.(本小题满分12分)
已知集合}52|{xxP ,}121|{kxkxQ,若QP,
求实数k的取值范围.
19.(本小题满分12分)
已知函数52)(2axxxf.
(1)若)(xf的定义域和值域均是a,1,求实数a的值;
(2)若)(xf在区间2,上是减函数,且对任意的x1,1a,总有44xf,
求实数a的取值范围.
20.(本小题满分12分)
已知函数()fx满足对一切12,xxR都有1212()()()2fxxfxfx,且(1)0f,
当1x时有()0fx.
(1)求(1)f的值;
(2)判断并证明函数()fx在R上的单调性;
(3)解不等式:222[(2)]2(21)120fxxfxx.
21. 已知二次函数fx的顶点坐标为)1,1(,且(0)3f,
(1)求fx的解析式,
(2)x∈[1,1],()yfx的图象恒在221yxm的图象上方,
试确定实数m的取值范围,
(3)若fx在区间[,1]aa上单调,求实数a的取值范围.
22.已知函数33()(log)(log3)27xfxx
(1)若11[,]279x,求函数()fx最大值和最小值;
(2)若方程()0fxm有两根,,试求的值.
参考答案
1.D2.A3.D4.B5.C6.B7.C8.C9.D10.D11.C12.A
13.4
14.1233x
15.①⑤
16.2
17.(1)A∩B32|xx,A∪B=3|xx.(2)2p。
18.3(,)(6,)2。
19.(1)2a.(2) 32a.
20.⑴()fx在R上是减函数.
(2)略
⑶10,23xxx或.
21.(1)2()243fxxx;(2)1m;(3)0a或1a.
22.(1) maxmin()(3)12,()(2)5fxgfxg;(2)9
