2013 -2014 学年度第一学期
2013-2014学年第一学期课程表2013级
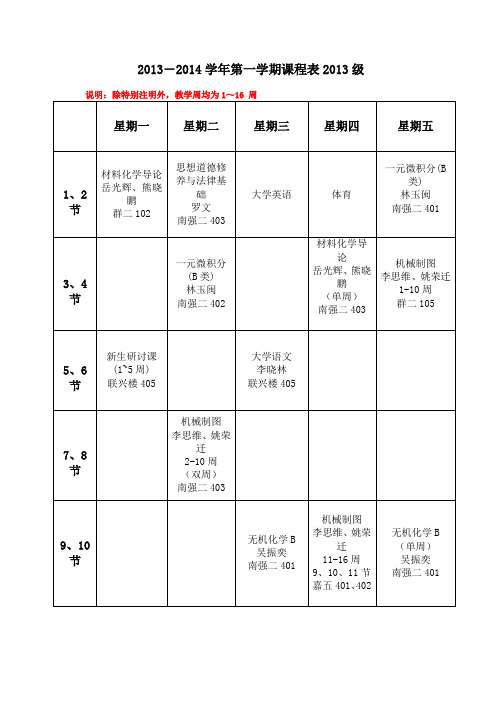
说明:除特别注明外,教学周均为1~16 周星期一星期二星期三星期四星期五1、2节材料化学导论岳光辉、熊晓鹏群二102思想道德修养与法律基础罗文南强二403大学英语体育一元微积分(B类)林玉闽南强二4013、4节一元微积分(B类)林玉闽南强二402材料化学导论岳光辉、熊晓鹏(单周)南强二403机械制图李思维、姚荣迁1-10周群二1055、6节新生研讨课(1~5周)联兴楼405大学语文李晓林联兴楼4057、8节机械制图李思维、姚荣迁2-10周(双周)南强二4039、10节无机化学B吴振奕南强二401机械制图李思维、姚荣迁11-16周9、10、11节嘉五401、402无机化学B(单周)吴振奕南强二401说明:【】为上课学生方向,无注明即通修;除特别注明外,教学周均为1~16 周星期一星期二星期三星期四星期五1、2节大学物理B(下)吕铁羽南强二109线性代数林玉闽南强二401大学物理B(下)黄凯南强二105纳米生物技术【选修】1-11周任磊南强二202纳米生物技术【选修】任磊1-11周(双周)南强二2023、4节大学物理B(下)黄凯南强二105大学物理B(下)吕铁羽南强二1095、6节C程序设计基础江弋南强二403冯少荣南强二401无机功能材料【选修】杨水源南强二4087、8节晶体学基础宓锦校(双周)联兴楼305C程序设计基础(双周)江弋嘉五601冯少荣嘉五501有机化学(上)邹友思(单周)南强二402晶体学基础宓锦校南强二402有机化学(上)邹友思南强二4039、10节大学英语说明:【】为上课学生方向,无注明即通修;除特别注明外,教学周均为1~16 周星期一星期二星期三星期四星期五1、2节有机化学实验B林敏5-16周仪器分析实验B【高分子】杨利民2-9周材料力学(下)【无机】张颖联兴楼305高分子化学【高分子】5-16周李磊、胡晓兰南强二504材料分析测试方法实验李思维、岳光辉、翁建5-16周3、4节材料物理与力学性能【无机】熊兆贤南强二302高分子化学【高分子】5-16周李磊、胡晓兰南强二504材料物理与力学性能【无机】(双周)熊兆贤南强二302材料科学基础(一)【无机】刘兴军南强二502高分子物理【高分子】(双周)熊晓鹏南强二3025、6节材料表面工程【选修】程璇南强二209固体物理基础【选修】彭栋梁南强二5077、8节材料科学基础(一)【无机】(单周)刘兴军南强二506高分子物理【高分子】熊晓鹏南强二3029、10节材料分析测试方法罗学涛、李锦堂(单周)联兴楼405材料分析测试方法罗学涛、李锦堂联兴楼405说明:生产实习:1-3周;【】为上课学生方向,无注明即通修;除特别注明外,教学周均为4~16 周星期一星期二星期三星期四星期五1、2节无机合成实验【无机】罗学涛、薛昊科学楼综合实验模块1 【高分子】白华、陈江溪;孙亚楠、林乃波综合实验模块2 【无机】李思维、卢勇;姜源、杨水源3、4节无机材料专业英语【无机】李锦堂南强二3015、6节7、8节合成材料【高分子】汪剑炜南强二201合成材料【高分子】(单周)汪剑炜南强二1039、10节。
北京市西城区2013—2014学年度高三年级第一学期期末数学理科
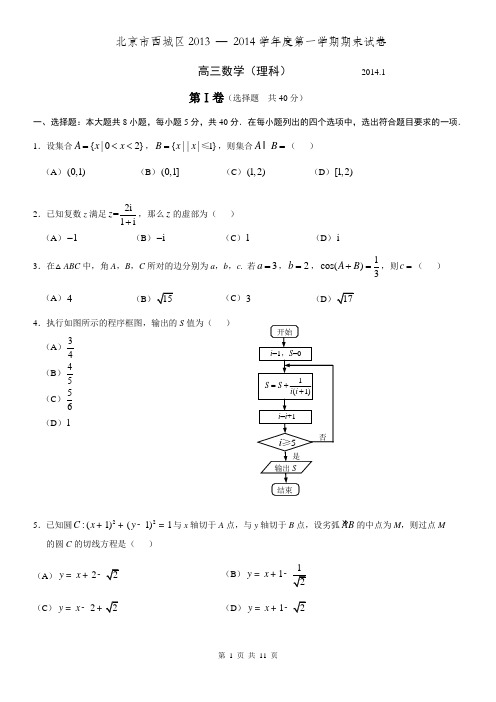
北京市西城区2013 — 2014学年度第一学期期末试卷高三数学(理科)2014.1第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.设集合{|02}A x x =<<,1{|||}B x x =≤,则集合A B = ( ) (A )(0,1)(B )(0,1](C )(1,2)(D )[1,2)3.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若3a =,2b =,1cos()3A B +=,则c =( ) (A )4(B(C )3(D4.执行如图所示的程序框图,输出的S 值为( ) (A )34 (B )45(C )56(D )12.已知复数z 满足2i=1iz +,那么z 的虚部为( ) (A )1-(B )i -(C )1(D )i5.已知圆22:(1)(1)1C x y ++-=与x 轴切于A 点,与y 轴切于B 点,设劣弧»AB 的中点为M ,则过点M 的圆C 的切线方程是( ) (A)2y x =+-(B)1y x =+-(C)2y x =-+(D)1y x =+-6. 若曲线221ax by +=为焦点在x 轴上的椭圆,则实数a ,b 满足( ) (A )22a b > (B )11a b< (C )0a b <<(D )0b a <<7.定义域为R 的函数()f x 满足(1)2()f x f x +=,且当(0,1]x ∈时,2()f x x x =-,则当[2,1]x ∈--时,()f x 的最小值为( ) (A )116-(B ) 18-(C ) 14-(D ) 08. 如图,正方体1111ABCD A B C D -的棱长为P 在对角线1BD 上,过点P 作垂直于1BD 的平面α,记这样得到的截面多边形(含三角形)的周长为y ,设BP =x , 则当[1,5]x ∈时,函数()y f x =的值域为( )(A) (B) (C) (D)第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9. 在平面直角坐标系xOy 中,点(1,3)A ,(2,)B k -,若向量OA AB ⊥,则实数k = ____. 10.若等差数列{}n a 满足112a =,465a a +=,则公差d =______;24620a a a a ++++= ______.11.已知一个正三棱柱的所有棱长均相等,其侧(左)视图如图所示,那么此三棱柱正(主)视图的面积为______.12.甲、乙两名大学生从4个公司中各选2个作为实习单位,则两人所选的实习单位中恰有1个相同的选法种数是______. (用数字作答)13. 如图,,B C 为圆O 上的两个点,P 为CB 延长线上一点,PA 为圆O 的切线,A 为切点. 若2PA =,3BC =,则PB =______;ACAB=______.1侧(左)视图14.在平面直角坐标系xOy 中,记不等式组220,0,2x y x y x y +⎧⎪-⎨⎪+⎩≥≤≤所表示的平面区域为D .在映射,:u x y T v x y =+⎧⎨=-⎩的作用下,区域D 内的点(,)x y 对应的象为点(,)u v . (1)在映射T 的作用下,点(2,0)的原象是 ; (2)由点(,)u v 所形成的平面区域的面积为______.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数()f x x ω=,π()sin()(0)3g x x ωω=->,且()g x 的最小正周期为π.(Ⅰ)若()2f α=[π,π]α∈-,求α的值; (Ⅱ)求函数()()y f x g x =+的单调增区间.16.(本小题满分13分)以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a 表示.(Ⅰ)若甲、乙两个小组的数学平均成绩相同,求a 的值; (Ⅱ)求乙组平均成绩超过甲组平均成绩的概率;(Ⅲ)当2a =时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为X ,求随机变量X 的分布列和数学期望.17.(本小题满分14分)如图,在多面体ABCDEF 中,底面ABCD 是边长为2的菱形, 60=∠BAD ,四边形BDEF 是矩形,平面BDEF ⊥平面ABCD ,BF =3, H 是CF 的中点.(Ⅰ)求证:AC ⊥平面BDEF ;(Ⅱ)求直线DH 与平面BDEF 所成角的正弦值; (Ⅲ)求二面角H BD C --的大小.甲组 乙组 891 a822 F CEHD18.(本小题满分13分)已知函数()()e xf x x a =+,其中e 是自然对数的底数,a ∈R . (Ⅰ)求函数)(x f 的单调区间;(Ⅱ)当1a <时,试确定函数2()()g x f x a x =--的零点个数,并说明理由.19.(本小题满分14分)已知,A B 是抛物线2:W y x =上的两个点,点A 的坐标为(1,1),直线AB 的斜率为k , O 为坐标原点. (Ⅰ)若抛物线W 的焦点在直线AB 的下方,求k 的取值范围;(Ⅱ)设C 为W 上一点,且AB AC ⊥,过,B C 两点分别作W 的切线,记两切线的交点为D ,求OD 的最小值.20.(本小题满分13分)设无穷等比数列{}n a 的公比为q ,且*0()n a n >∈N ,[]n a 表示不超过实数n a 的最大整数(如[2.5]2=),记[]n n b a =,数列{}n a 的前n 项和为n S ,数列{}n b 的前n 项和为n T . (Ⅰ)若114,2a q ==,求n T ; (Ⅱ)若对于任意不超过2014的正整数n ,都有21n T n =+,证明:120122()13q <<. (Ⅲ)证明:n n S T =(1,2,3,n =L )的充分必要条件为1,a q N N **挝.北京市西城区2013 — 2014学年度第一学期期末高三数学(理科)参考答案及评分标准2014.1一、选择题:本大题共8小题,每小题5分,共40分.1.B 2.C 3.D 4.B 5.A 6.C 7.A 8.D 二、填空题:本大题共6小题,每小题5分,共30分. 9.4 10.125511. 12.24 13.1 214.(1,1) π注:第10、13、14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)(Ⅰ)解:因为π()sin()(0)3g x x ωω=->的最小正周期为π, 所以2||ωπ=π,解得2ω=. ……………… 3分由 ()2f α=22α=, 即 cos 22α=, ……… 4分 所以 π22π4k α=±,k ∈Z . 因为 [π,π]α∈-, 所以7πππ7π{,,,}8888α∈--. ……………… 6分(Ⅱ)解:函数 π()()2sin(2)3y f x g x x x =+=+-ππ2sin 2cos cos 2sin 33x x x =+- ……………… 8分1sin 222x x =πsin(2)3x =+, ……………10分 由 2πππ2π2π232k k x -++≤≤, ………………11分 解得 5ππππ1212k k x -+≤≤. ………………12分所以函数()()y f x g x =+的单调增区间为5ππ[ππ]()1212k k k -+∈Z ,.…………13分16.(本小题满分13分)(Ⅰ)解:依题意,得 11(889292)[9091(90)]33a ++=+++, ……………… 2分解得 1a =. ……………… 3分 (Ⅱ)解:设“乙组平均成绩超过甲组平均成绩”为事件A , ……………… 4分依题意 0,1,2,,9a = ,共有10种可能. ……………… 5分 由(Ⅰ)可知,当1a =时甲、乙两个小组的数学平均成绩相同,所以当2,3,4,,9a = 时,乙组平均成绩超过甲组平均成绩,共有8种可能.… 6分 所以乙组平均成绩超过甲组平均成绩的概率84()105P A ==. ……………… 7分 (Ⅲ)解:当2a =时,分别从甲、乙两组同学中各随机选取一名同学,所有可能的成绩结果有339⨯=种, 它们是:(88,90),(88,91),(88,92),(92,90),(92,91),(92,92),(92,90),(92,91),(92,92), ……………… 9分则这两名同学成绩之差的绝对值X 的所有取值为0,1,2,3,4. ……………… 10分 因此2(0)9P X ==,2(1)9P X ==,1(2)3P X ==,1(3)9P X ==,1(4)9P X ==. ……………… 11分所以随机变量X 的分布列为:………………12分所以X 的数学期望221115()01234993993E X =⨯+⨯+⨯+⨯+⨯=.……………13分 17.(本小题满分14分)(Ⅰ)证明:因为四边形ABCD 是菱形,所以 AC BD ⊥. ……… 1分因为平面BDEF ⊥平面ABCD ,且四边形BDEF 是矩形,所以 ED ⊥平面ABCD , ……………… 2分 又因为 AC ⊂平面ABCD ,所以 ED AC ⊥. …………… 3分 因为 ED BD D = ,所以 AC ⊥平面BDEF . …………… 4分 (Ⅱ)解:设AC BD O = ,取EF 的中点N ,连接ON ,因为四边形BDEF 是矩形,,O N 分别为,BD EF 的中点,所以 //ON ED ,又因为 ED ⊥平面ABCD ,所以 ON ⊥平面ABCD ,由AC BD ⊥,得,,OB OC ON 两两垂直.所以以O 为原点,,,OB OC ON 所在直线分别为x 轴,y 轴,z 轴,如图建立空间直角坐标系. ……… 5分 因为底面ABCD 是边长为2的菱形,60BAD ∠= ,3BF =, 所以(0,A ,(1,0,0)B ,(1,0,0)D -,(1,0,3)E -,(1,0,3)F,C,13()22H . ………………6分因为 AC ⊥平面BDEF ,所以平面BDEF的法向量AC =. …………7分设直线DH 与平面BDEF 所成角为α,由33(,)222DH = , 得sin |cos ,|DH AC DH AC DH ACα⋅=<>=== ,所以直线DH 与平面BDEF. ………………9分 (Ⅲ)解:由(Ⅱ),得13()222BH =- ,(2,0,0)DB = .设平面BDH 的法向量为111(,,)x y z =n ,所以0,0,BH DB ⎧⋅=⎪⎨⋅=⎪⎩ n n ………………10分即111130,20,x z x ⎧-++=⎪⎨=⎪⎩ 令11z =,得(0,=n . ………………11分由ED ⊥平面ABCD ,得平面BCD 的法向量为(0,0,3)ED =-,则00(01(3)1cos ,232ED ED ED⋅⨯+⨯+⨯-<>===-⨯n n n . ………………13分 由图可知二面角H BD C --为锐角,所以二面角H BD C --的大小为60 . ………………14分18.(本小题满分13分)(Ⅰ)解:因为()()e xf x x a =+,x ∈R ,所以()(1)e x f x x a '=++. ……………… 2分 令()0f x '=,得1x a =--. ……………… 3分 当x 变化时,()f x 和()f x '的变化情况如下:……………… 5分故()f x 的单调减区间为(,1)a -∞--;单调增区间为(1,)a --+∞.………… 6分 (Ⅱ)解:结论:函数()g x 有且仅有一个零点. ……………… 7分理由如下:由2()()0g x f x a x =--=,得方程2e x ax x -=,显然0x =为此方程的一个实数解.所以0x =是函数()g x 的一个零点. ……………… 9分 当0x ≠时,方程可化简为e x ax -=.设函数()ex aF x x -=-,则()e 1x a F x -'=-,令()0F x '=,得x a =.当x 变化时,()F x 和()F x '的变化情况如下:即()F x 的单调增区间为(,)a +∞;单调减区间为(,)a -∞.所以()F x 的最小值min ()()1F x F a a ==-. ………………11分 因为 1a <,所以min ()()10F x F a a ==->, 所以对于任意x ∈R ,()0F x >, 因此方程e x a x -=无实数解.所以当0x ≠时,函数()g x 不存在零点.综上,函数()g x 有且仅有一个零点. ………………13分19.(本小题满分14分)(Ⅰ)解:抛物线2y x =的焦点为1(0,)4. ……………… 1分由题意,得直线AB 的方程为1(1)y k x -=-, ……………… 2分 令 0x =,得1y k =-,即直线AB 与y 轴相交于点(0,1)k -. ……………… 3分 因为抛物线W 的焦点在直线AB 的下方, 所以 114k ->, 解得 34k <. ……………… 5分 (Ⅱ)解:由题意,设211(,)B x x ,222(,)C x x ,33(,)D x y ,联立方程21(1),,y k x y x -=-⎧⎨=⎩ 消去y ,得210x kx k -+-=,由韦达定理,得11x k +=,所以 11x k =-. ……………… 7分 同理,得AC 的方程为11(1)y x k-=--,211x k =--. ……………… 8分对函数2y x =求导,得2y x '=,所以抛物线2y x =在点B 处的切线斜率为12x ,所以切线BD 的方程为21112()y x x x x -=-, 即2112y x x x =-. ……………… 9分 同理,抛物线2y x =在点C 处的切线CD 的方程为2222y x x x =-.………………10分联立两条切线的方程2112222,2,y x x x y x x x ⎧=-⎪⎨=-⎪⎩ 解得12311(2)22x x x k k +==--,3121y x x k k==-,所以点D 的坐标为111((2),)2k k k k---. ………………11分 因此点D 在定直线220x y ++=上. ………………12分因为点O 到直线220x y ++=的距离d ==所以5OD ≥,当且仅当点42(,)55D --时等号成立. ………………13分 由3125y k k =-=-,得k =.所以当k =OD………………14分20.(本小题满分13分)(Ⅰ)解:由等比数列{}n a 的14a =,12q =, 得14a =,22a =,31a =,且当3n >时,01n a <<. ……………… 1分所以14b =,22b =,31b =,且当3n >时,[]0n n b a ==. ……………… 2分即 ,6, 2,4, 17, 3.n n n T n ==⎧⎪=⎨⎪⎩≥ ……………… 3分(Ⅱ)证明:因为 201421()n T n n =+≤,所以 113b T ==,120142(2)n n n b T T n -=-=≤≤. ……………… 4分 因为 []n n b a =,所以 1[3,4)a ∈,2014[2,3)(2)n a n ∈≤≤. ……………… 5分 由 21a q a =,得 1q <. ……………… 6分 因为 201220142[2,3)a a q =∈,所以 20122223qa >≥,第 11 页 共 11 页 所以 2012213q <<,即 120122()13q <<. ……………… 8分 (Ⅲ)证明:(充分性)因为 1a N *Î,q N *Î, 所以 11n n a a q N -*= ,所以 []n n n b a a == 对一切正整数n 都成立.因为 12n n S a a a =+++L ,12n n T b b b =+++L ,所以 n n S T =. ……………… 9分 (必要性)因为对于任意的n N *Î,n n S T =,当1n =时,由1111,a S b T ==,得11a b =;当2n ≥时,由1n n n a S S -=-,1n n n b T T -=-,得n n a b =.所以对一切正整数n 都有n n a b =.由 n b Z Î,0n a >,得对一切正整数n 都有n a N *Î, ………………10分 所以公比21a q a =为正有理数. ………………11分 假设 q N *Ï,令p q r=,其中,,1p r r N *?,且p 与r 的最大公约数为1. 因为1a 是一个有限整数,所以必然存在一个整数()k k N Î,使得1a 能被k r 整除,而不能被1k r+整除. 又因为111211k k k k a p a a q r++++==,且p 与r 的最大公约数为1. 所以2k a Z +Ï,这与n a N *Î(n N *Î)矛盾.所以q *∈N .因此1a N *Î,q *∈N . ……………13分。
《国家公务员制度》A、B试卷及答案

2013—2014学年度第一学期行政管理专业《国家公务员制度》结业试卷(A)姓名:学号:成绩:一、选择题:(在每小题的四个备选答案中,选出所有正确的答案,并将正确答案的序号填在题干的括号内。
每选对一正确答案得1分,共24分)1、公务员制度是产生于国的制度。
( )A:英;人事管理 B:德;人事管理 C:中;人事管理 D:英;行政管理2、我国第一次使用“国家公务员"这一名称是在年.()A:1987 B:1988 C:1993 D:20053、国际公务员最早产生于。
()A:20世纪20年代 B:20世纪50年代C:20世纪40年代 D:20世纪70年代4、我国公务员范围分为两类,即:()A:各级政府的组成人员 B:学会、协会的成员C:除各级政府组成人员以外的公务员 D:事业单位人员5、我国选拔官吏制度经历了以下哪些阶段:()A:世袭制 B:军功制 C:科举制 D:政府分赃制6、公务员制度被德国政治社会学家韦伯概括为。
()A:官僚制 B:科举制 C:民主制 D:竞争制7、提出政治与行政的二分法的是:()A:古德诺 B:威尔逊 C:孟德斯鸠 D:克鲁兹8、西方行政学理论产生的代表作有:()A:《行政之研究》 B:《比较行政法》 C:《政治与行政》 D:《彭德尔顿文官法》9、公务员法律关系客体有:()A:行政行为 B:公务员行为 C:公务员精神财富 D:公务员人身10、我国公务员分为个等次,分别对应个级别.()A:10;8 B:12;8 C:10;15 D:12;1511、公务员受到撤职处分的,后终止处分。
()A:半年 B:1年 C:一年半 D:2年12、我国公务员的回避基本方式有:()A:职务回避 B:公务回避 C:地区回避 D:考试回避13、为使公务员培训工作正规化、制度化,我国政府于1994年9月在京成立了培养国家高级公务员的培训机构,即:( )A:国家行政学院 B:中国高级公务员培训中心C:管理干部院校 D:党校14、公务员辞退费发放,最长不超过月。
2013-2014学年度贵州省中小学开学及放假时间安排

2013-2014学年度贵州省中小学开学及放假时间安排一、2013--2014学年时间安排(一)义务教育阶段学校1、全学年52周,其中上课时间35周,学校机动时间2周,复习考试时间2周,寒暑假13周。
2、学校机动的2周时间,第一学期和第二学期各1周。
其中,第一学期机动的1周作为寒假增加到放寒假的时间中,第二学期机动的1周由学校视具体情况自行安排,可用于开展传统活动、文化节、运动会、夏令营等。
3、九年级第二学期毕业复习考试时间增加2周。
(二)普通高中学校1、全学年52周,其中教学时间40周;寒暑假11周,社会实践1周。
2、高一、高二全学年教学时间40周,其中授课35周,复习考试3周,社区服务和劳动技术教育2周。
3、高三全学年36周教学时间,其中授课22周,复习考试12周,社区服务和劳动技术教育2周。
二、开学及放假的具体时间安排2013--2014学年度第一学期开学及放假时间安排时间学段开学时间放假时间义务教育阶段1-6年级2013年9月2日(周一,农历七月二十七)2014年1月11日(周六,农历十二月十一)7-8年级2013年9月2日(周一,农历七月二十七)2014年1月11日(周六,农历十二月十一)9年级2013年8月26日(周一,农历七月二十)2014年1月18日(周六,农历十二月十八)高中阶段高一、高二年级2013年8月26日(周一,农历七月二十)2014年1月11日(周六,农历十二月十一)高三年级2013年8月19日(周一,农历七月十三)2014年1月25日(周六,农历十二月二十五)2013--2014学年度第二学期开学及放假时间安排时间学段开学时间放假时间义务教育阶段1-6年级2014年3月3日(周一,农历二月初三)2014年7月5日(周六,农历六月初九)7-8年级2014年3月3日(周一,农历二月初三)2014年7月12日(周六,农历六月十六)9年级2014年2月17日(周一,农历正月十八)中考结束后高中阶段高一、高二年级2014年2月24日(周一,农历正月二十五)2014年7月12日(周六,农历六月十六)高三年级2014年2月17日(周一,农历正月十八)高考结束后三、严格执行全省统一校历,将减负落到实处(一)中小学校历是根据国家有关规定,并结合我省中小学校工作实际确定的,各级教育行政部门和各级各类中小学校必须严格遵照执行,按照本通知要求妥善安排教育教学活动,不得提前开学或推迟放假。
北京市西城区2013-2014学年高一上学期期末考试数学试题(普通校试题

北京市西城区2013 — 2014学年度第一学期期末试卷高一数学 2014.1试卷满分:150分 考试时间:120分钟A 卷 [必修 模块4] 本卷满分:100分一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合要求的. 1.若sin 0<α,且cos 0>α,则角α是( ) (A )第一象限的角 (B )第二象限的角 (C )第三象限的角(D )第四象限的角2.已知向量1(1,0)=e ,2(0,1)=e ,那么122|+=|e e ( )(A )1(B (C )2(D 3.若角α的终边经过点(1,2)P -,则tan =α( )(A (B ) (C )2- (D )12-4.已知正方形ABCD 的边长为1,则AB AC ⋅=( )(A (B )1(C (D )25.在平面直角坐标系xOy 中,函数2sin()6y x π=-的图象( ) (A )关于直线6x π=对称 (B )关于直线6x π=-对称 (C )关于点(,0)6π对称(D )关于点(,0)6π-对称 6.已知非零向量,OA OB 不共线,且13BM BA =,则向量OM =( ) (A )1233OA OB +(B )2133OA OB +(C )1233OA OB -(D )1433OA OB -7.已知函数1()cos 22f x x x =+,则()12f π=( )(A )2(B )2(C )1(D 8.设a ,b 是两个非零向量,且+=-a b a b ,则a 与b 夹角的大小为( ) (A )120︒(B )90︒(C )60︒(D )30︒9.已知函数()sin cos f x x x =ωω在区间[,]63ππ-上单调递增,则正数ω的最大值是( ) (A )32(B )43(C )34 (D )2310.已知函数()cos(sin )f x x =,则下列结论中正确的是( ) (A )()f x 的定义域是[1,1]- (B )()f x 的值域是[1,1]- (C )()f x 是奇函数(D )()f x 是周期为π的函数二、填空题:本大题共6小题,每小题4分,共24分. 把答案填在题中横线上. 11. sin()6π-=______.12. 若sin =α,且(0,)∈πα,则α=______. 13. 已知向量(1,3)=a ,(2,)k =-b .若向量a 与b 共线,则实数k =_____. 14. 若tan 2=α,且32π∈(π,)α,则sin()2π+=α______. 15. 已知向量(cos ,sin )αα=a ,(cos ,sin )ββ=b .若π,3〈〉=a b ,则c o s ()-=αβ_____. 16. 定义在R 上的非常值函数()f x 同时满足下述两个条件:① 对于任意的x ∈R ,都有2()()3f x f x π+=; ② 对于任意的x ∈R ,都有()()66f x f x ππ-=+.则其解析式可以是()f x =_____.(写出一个满足条件的解析式即可)三、解答题:本大题共3小题,共36分.解答应写出文字说明,证明过程或演算步骤.17. (本小题满分12分)已知3tan 4=-α. (Ⅰ)求πtan()4-α的值;(Ⅱ)求2sin 3cos 3sin 2cos --αααα的值.18.(本小题满分12分)已知函数2()sin 22cos2f x x x x =⋅. (Ⅰ)求()f x 的最小正周期;(Ⅱ)若[,]84x ππ∈,求()f x 的最大值与最小值.19.(本小题满分12分)如图,正六边形ABCDEF 的边长为1.,M N 分别是,BC DE 上的动点,且满足BM DN =.(Ⅰ)若,M N 分别是,BC DE 的中点,求AM AN ⋅的值; (Ⅱ)求AM AN ⋅的取值范围.B 卷 [学期综合] 本卷满分:50分一、填空题:本大题共5小题,每小题4分,共20分.把答案填在题中横线上. 1. 已知集合2{|430}A x x x =-+>,{|02}B x x =<≤,那么A B =_____.2. 已知2log 3a =,32b=,21log 3c =.将,,a b c 按从小到大排列为_____. 3. 若函数2()2f x x x =-在区间(,)a +∞上是增函数,则a 的取值范围是_____. 4. 函数12()|21|xf x x =--的零点个数为_____.5. 给定数集A .若对于任意,a b A ∈,有a b A +∈,且a b A -∈,则称集合A 为闭集合.给出如下四个结论:① 集合{4,2,0,2,4}A =--为闭集合; ② 集合{|3,}A n n k k ==∈Z 为闭集合; ③ 若集合12,A A 为闭集合,则12AA 为闭集合;④ 若集合12,A A 为闭集合,且1A R Ø,2A R Ø,则存在c ∈R ,使得12()c A A ∉.其中,全部正确结论的序号是_____.二、解答题:本大题共3小题,共30分.解答应写出文字说明,证明过程或演算步骤. 6.(本小题满分10分)已知函数()log (2)1a f x x =+-,其中1a >.(Ⅰ)若()f x 在[0,1]上的最大值与最小值互为相反数,求a 的值; (Ⅱ)若()f x 的图象不经过第二象限,求a 的取值范围.7.(本小题满分10分)已知函数()|2|f x x x =-. (Ⅰ)解不等式()3f x <;(Ⅱ)设0a >,求()f x 在区间[0,]a 上的最大值.8.(本小题满分10分)设函数()f x ,()g x 的定义域分别为f g D D ,,且f g D D Ø.若对于任意f x D ∈,都有()()g x f x =,则称()g x 为()f x 在g D 上的一个延拓函数.给定2() 1 (01)f x x x =-<≤.(Ⅰ)若()h x 是()f x 在[1,1]-上的延拓函数,且()h x 为奇函数,求()h x 的解析式; (Ⅱ)设()g x 为()f x 在(0,)+∞上的任意一个延拓函数,且()g x y x=是(0,)+∞上的单调函数.(ⅰ)判断函数()g x y x=在(0,1]上的单调性,并加以证明; (ⅱ)设0s >,0t >,证明:()()()g s t g s g t +>+.北京市西城区2013 —2014学年度第一学期期末试卷一、选择题:本大题共10小题,每小题4分,共40分.1.D;2.D;3.C;4.B;5.C;6.A;7.A;8.B;9.C;10.D.二、填空题:本大题共6小题,每小题4分,共24分.11.12-;12.3π,或32π;13.6-;14.5-;15.12;16.sin3x等(答案不唯一).注:12题,得出一个正确的结论得2分.三、解答题:本大题共3小题,共36分.17.(Ⅰ)解:因为3 tan4=-α,所以πtan tanπ4tan()π41tan tan4--=+⋅ααα【3分】7=-. 【6分】(Ⅱ)解:因为3 tan4=-α,所以2sin3cos2tan33sin2cos3tan2--=--αααααα【9分】1817=. 【12分】18.(Ⅰ)解:1cos4()2cos22xf x x x-=⋅1cos4422xx-=+【2分】1sin(4)62xπ=-+.【4分】因为242Tππ==,所以()f x的最小正周期是2π.【6分】(Ⅱ)解:由(Ⅰ)得,1 ()sin(4)62f x xπ=-+.因为84x ππ≤≤, 所以 54366x πππ≤-≤, 【 8分】 所以 1sin(4)126x π≤-≤, 【 9分】所以 131sin(4)622x π≤-+≤. 【10分】所以,当6x π=时,()f x 取得最大值32;当4x π=时,()f x 取得最小值1.【12分】19.(本小题满分12分)(Ⅰ)解:如图,以AB 所在直线为x 轴,以A 为坐标原点建立平面直角坐标系. 【 1分】因为ABCDEF 是边长为1的正六边形,且,M N 分别是,BC DE 的中点,所以 5(,)44M ,1(2N , 【 3分】所以 5311848AM AN ⋅=+=. 【 4分】 (Ⅱ)解:设BM DN t ==,则[0,1]t ∈.【 5分】所以(1,)22t M +,(1N t -. 【 7分】 所以3(1)(1)22t AM AN t t ⋅=+⋅-+2112t t ++=-213(1)22t =--+ 【10分】 当0t =时,AM AN ⋅取得最小值1; 【11分】 当1t =时,AM AN ⋅取得最大值32. 【12分】一、填空题:本大题共5小题,每小题4分,共20分.1.{|01}x x <<;2.c b a <<;3. [1,)+∞;4. 2;5.②④. 注:5题,选出一个正确的序号得2分,有错选不给分.6.(Ⅰ)解:函数()log (2)1a f x x =+-的定义域是(2,)-+∞. 【 1分】因为 1a >,所以 ()log (2)1a f x x =+-是[0,1]上的增函数. 【 2分】 所以 ()f x 在[0,1]上的最大值是(1)log 31a f =-;最小值是(0)log 21a f =-.【 4分】 依题意,得 log 31(log 21)a a -=--, 【 5分】 解得a =【 6分】 (Ⅱ)解:由(Ⅰ)知,()log (2)1a f x x =+-是(2,)-+∞上的增函数. 【 7分】在()f x 的解析式中,令0x =,得(0)log 21a f =-, 所以,()f x 的图象与y 轴交于点(0,log 21)a -. 【 8分】 依题意,得(0)log 210a f =-≤, 【 9分】 解得 2a ≥. 【10分】 7.(Ⅰ)解:原不等式可化为22230x x x ≥⎧⎨--<⎩,,(1) 或22230.x x x <⎧⎨-+>⎩,(2) 【 1分】解不等式组(1),得 23x ≤<;解不等式组(2),得2x <. 【 3分】 所以原不等式的解集为{|3}x x <. 【 4分】(Ⅱ)解:222,2,()|2|2, 2.x x x f x x x x x x ⎧-≥⎪=-=⎨-+<⎪⎩ 【 5分】① 当01a <<时,()f x 是[0,]a 上的增函数,此时()f x 在[0,]a 上的最大值是2()2f a a a =-+. 【 6分】② 当12a ≤≤时,()f x 在[0,1]上是增函数,在[1,]a 上是减函数,此时()f x 在[0,]a 上的最大值是(1)1f =. 【 7分】③ 当2a >时,令()(1)(2)10f a f a a -=-->,解得1a >. 所以,当21a <≤此时()(1)f a f ≤,()f x 在[0,]a 上的最大值是(1)1f =;当1a >此时()(1)f a f >,()f x 在[0,]a 上的最大值是2()2f a a a =-.【 9分】记()f x 在区间[0,]a 上的最大值为()g a ,所以222,01,()1,112,1a a a g a a a a a ⎧-+<<⎪⎪=≤≤+⎨⎪->+⎪⎩ 【10分】8.(Ⅰ)解:当0x =时,由()h x 为奇函数,得(0)0h =. 【 1分】任取[10)x ∈-,,则(01]x -∈,, 由()h x 为奇函数,得22()()[()1]1h x h x x x =--=---=-+, 【 2分】所以()h x 的解析式为221,01,()0,0,1,10.x x h x x x x ⎧-<≤⎪==⎨⎪-+-≤<⎩【 3分】(Ⅱ)解:(ⅰ)函数()g x y x=是(0,1]上的增函数. 【 4分】证明如下:因为()g x 为()f x 在(0,)+∞上的一个延拓函数,所以当(01]x ∈,时,2()()1g x f x x ==-. 记()()1()g x f x k x x x x x===-,其中(0,1]x ∈. 任取12,(0,1]x x ∈,且12x x <,则210x x x ∆=->, 因为211221212112()(1)11()()()0x x x x y k x k x x x x x x x -+∆=-=---=>, 所以函数()g x y x=是(0,1]上的增函数. 【 6分】 (ⅱ)由()g x y x = 是(0,)+∞上的单调函数,且(0,1]x ∈时,()g x y x =是增函数,从而得到函数()g x y x= 是(0,)+∞上的增函数. 【 7分】因为 0s >,0t >, 所以 s t s +>,s t t +>, 所以()()g s t g s s t s+>+, 即 ()()()s g s t s t g s ⋅+>+⋅. 【 8分】 同理可得:()()()t g s t s t g t ⋅+>+⋅.将上述两个不等式相加,并除以s t +,即得 ()()()g s t g s g t +>+. 【10分】。
广东省汕头市龙湖区2013-14学年度第一学期教学质量监测789年级历史试卷及答案

2013~2014学年度第一学期初中质量监测试卷七年级历史说明:1.全卷考试用时为50分钟,满分100分。
2.答题前,考生必须将自己的姓名、座号按要求填写在密封线左边的空格内。
3.必须使用黑色钢笔或者签字笔在答题卷上作答,不能使用铅笔、红笔和涂改液。
一、选择题(本题有25小题,每小题3分,共75分。
每小题只有一个选项符合题意,请用2B铅笔在答题卡把所选选项按要求涂黑。
)1.“我来自元谋,自周口,牵起你毛茸茸的手,爱让我们直立行走。
”这是在网络上颇为流行的诗句。
下列远古人类,生活在云南省的是( )A. 元谋人B. 北京人C. 半坡人D. 河姆渡人2.历史老师在介绍我国一处早期文化遗址时,提到“长江流域”、“水稻”、“干栏式房屋”。
此文化遗址最有可能是( )A.元谋人遗址B.北京人遗址C.河姆渡遗址D.半坡遗址3.某台湾旅行团要来大陆拜祭中华民族的“人文初祖”,他们应该去( ) A.秦始皇陵B.中山陵C.大禹陵D.黄帝陵4.《礼记》记述说:“天子和诸侯都把世袭当作礼,用城郭、护城河来维护国家的稳固”。
第一个借助世袭之“礼”登上王位并治理国家的是( )A.尧B.舜C.禹D.启5.为巩固对周边的统治,西周实行的“授民授疆土”制度是( )A. 禅让制B. 分封制C. 世袭制D. 郡县制6.对右图表述正确的是( )A.著名的青铜器司母戊鼎B.造型奇特的四羊方尊C.三星堆青铜立人像D.戴枷的奴隶俑7.他对内整顿朝政,对外“尊王攘夷”,成为春秋时期的第一个霸主。
他是( )A.齐桓公B.秦穆公C.楚庄王D.晋文公8.农业是我国两千多年社会的立国之本,农业生产技术的革新历来受到重视。
下列哪一幅图片反映了我国农业发展史上的一次革命( )A.筒车B.铁农具 C.都江堰水利工程D.牛耕9.初一(2)班同学在学习“商鞅变法”时,排练了形象生动的历史课本剧。
下面是四位同学模拟发布的告示,其中不符合史实的一项是( )A.小周:土地属于私有,可以自由买卖B.小赵:出身贵族的人,爵位保持世袭C.小吴:努力耕种的人,可以免除徭役D.小代:军功卓著的人,授予爵位田宅10.400多年前意大利传教士翻译了记录孔子言行的书并带到欧洲,孔子学说开始西传,到目前全球已建成的孔子学院140所。
2013-2014学年高一数学上学期期中试题及答案(新人教A版 第39套)

淮北一中2013——2014学年度第一学期期中考试高一年级数学试卷满分150分 时间120分钟第Ⅰ卷(选择题 共50分)一,选择题:(本大题共10小题,每小题5分,共50分.在每小题所给的四个选项中,只有一项是符合题目要求的.)(1)设A 、B 为非空集合,定义集合A*B 为如图非阴影部分表示的集合,若{|},A x y ={|3,0},xB y y x ==>则A*B= ( )().0,2A (].1,2B [][).0,12,C ⋃+∞ []().0,12,D ⋃+∞(2).下列四组函数中,表示同一个函数的是 ( )()().1,A f x x g x =+=()()2.B f x g x =()()21.,11x C f x g x x x -==-+ ()2log .()2,x D f x g x x ==(3).若函数()()()2211log 1x x f x x x ⎧+≤⎪=⎨>⎪⎩,则[](2)f f = ( ) 2.log 5A .2B .1C .0D (4)函数y =()()(.1A -⋃ ()().2,11,2B -⋃ [)(].2,11,2C --⋃)(.1D ⎡-⋃⎣(5)下列函数中,同时具有性质:(1)图象过点(0,1);(2)在区间(0,+∞)上是减函数;(3)是偶函数.这样的函数是 ( )A.y =x 3+1B.y =log 2(|x |+2)C.y =(12)|x |D.y =2|x |(6)已知偶函数()f x 在区间[)0,+∞单调递减,则满足()()ln 1f x f >的x 取值范围是 ( )1.,1A e ⎛⎫ ⎪⎝⎭ ()1.0,1,B e ⎛⎫⋃+∞ ⎪⎝⎭ 1C.,e e ⎛⎫⎪⎝⎭()().0,1,D e ⋃+∞ (7)若关于x 的方程22350x x m ---+=有4个根,则m 的取值范围为 ( )A B().0,4A ().5,9B (].0,4C (].5,9D(8)在同一坐标系中,函数1()x y a=与log ()a y x =-(其中0a >且1a ≠)的图象 可能是 ( )(9)已知()()314,1log ,1aa x a x f x x x -+<⎧⎪=⎨≥⎪⎩是R 上的减函数,那么a 的取值范围是( )().0,1A 1.0,3B ⎛⎫ ⎪⎝⎭ 1.,17C ⎡⎫⎪⎢⎣⎭ 11.,73D ⎡⎫⎪⎢⎣⎭(10)已知一元二次不等式()<0f x 的解集为{1|<-1>}2x x x 或,则(10)>0x f 的解集为( ){.|<-1>lg2}A x x x 或 {}.|-1<<lg2B x x {}.|>-lg2C x x {}.|<-lg2D x x第Ⅱ卷(非选择题 共100分)二,填空题(本大题共5小题,每小题5分,共25分.把答案填在答题卡相应位置上.) (11)已知)1fx =+()f x =__________________(12)已知0.43a =,30.4b =,0.4log 3c =则,,c a b 的大小关系为________________ (13)函数212()log (32)f x x x =+-的单调递减区间为___________________(14)若函数(a 01)x y a a =>≠且在[]1,1-上的最大值与最小值的差是1,则a =_________ (15)在平面直角坐标系中,横坐标、纵坐标均为整数的点称为“格点”,如果函数()f x 的图像恰好通过()k k N *∈个格点,则称函数()f x 为“k 阶格点函数”。
2013-14(1)课表

周次 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 教学进程←军训→←————————————————————上课———————————————————→考试课程学时大学语文1 32 英语精读1 48 英语泛读1 32 英语口语1 32 英语听力1 32 英语语音1 32 大学体育1 32 思想道德修养与法律基础 32+16 大学计算机基础 24+24 公益劳动 1周军事训练及入学教育 2周星期专业班节次课程英语1301(40人)1302(40人)星期一1—2节英语精读1 5-19 邬磊23013—4节英语精读1 5-19 邬磊2301 5—6节大学计算机基础5-18 夏杰5303 大学计算机基础5-18 夏杰5303 7—8节大学计算机基础5-18 夏杰J102 大学计算机基础5-18 夏杰J102星期二1—2节英语泛读1 6-19 刘莹23013—4节英语听力1 6-19 张晓磊2408 英语泛读1 6-19 刘莹2301 5—6节英语口语1 6-19 Harris 2301 英语听力1 6-19 杨文静2408 7—8节英语口语1 6-19 Harris 2301星期三1—2节英语语音1 6-19 王姗姗2408 英语泛读1 6-7 刘莹2301 3—4节英语语音1 6-19 王姗姗2408 5—6节英语泛读1 6-7 刘莹2301 英语精读1 6-14 邬磊2302 7—8节星期四1—2节大学语文1 4-19 白云玲2301 大学语文1 4-19 白云玲2301 3—4节思想道德修养与法律基础4-19 11015—6节英语口语1 6-7 Harris 23017—8节英语口语1 6-7 Harris 2301星期五1—2节英语听力1 4-5 张晓磊2408英语精读1 6-15 邬磊2301英语听力1 10-11 杨文静2408 3—4节大学体育1 4-18 大学体育1 4-185—6节英语语音1 6-7 王姗姗2408 英语语音1 4-5 王姗姗2408 7—8节备注:1、公益劳动 1周时间由辅导员另行安排 2、军事训练及入学教育 2周周次 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 教学进程←———————————————————————上课———————————————————————→考试课程学时马克思主义基本原理 32+16 大学体育3 32 英语精读3 48 英语泛读3 32 英语听力3 40 英语口语3 40 第二外语1 64 英语写作1 32 英语语法2 32星期专业班节次课程英语1201(25人)1202(25人)星期一1—2节英语语法2 1-16 王金平2302 英语听力3 1-16 王晶2408 3—4节第二外语1(日语)26人1-16 张缦2302第二外语1(法语)24人1-16 李静宜23035—6节马克思主义基本原理1-16 罗晶晶12017—8节星期二1—2节英语听力3 1-17 王晶2408 英语口语3 1-19 Harris 2302 3—4节英语口语3 1-19 Harris 2302 英语精读3 2-9 龚莉2303 5—6节英语精读3 2-9 龚莉23037—8节星期三1—2节英语语法2 1-17 王金平2302 3—4节第二外语1(日语)26人1-17 张缦2302第二外语1(法语)24人1-17 李静宜23035—6节大学体育3 1-167—8节大学体育3 1-16星期四1—2节英语精读3 1-18 龚莉2202 英语泛读3 1-18 刘莹2303 3—4节英语泛读3 1-18 刘莹2303 英语精读3 1-18 龚莉2202 5—6节英语口语3 9-10 Harris 23017—8节英语口语3 9-10 Harris 2301星期五1—2节英语听力3 1-3 王晶2408 英语写作1 1-17 洪俊2302 3—4节英语写作1 1-17 洪俊2302 英语听力3 1-3 王晶2408 5—6节7—8节周次 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 教学进程←———————————————————————上课———————————————————————→考试课程学时高级英语1 64 第二外语3 64 英语笔译1 32 英语口译1 32 英语语言学概论 32 英国文学作品选读 32 英语写作3 32 英语国家概况32 跨文化交际 32星期专业班节次课程英语1101(44人)1102(44人)星期一1—2节英语写作3 1-16 邓欢2303 英语语言学概论1-16 张密23043—4节英语笔译1 1-16 李娟23045—6节英语语言学概论1-16 张密2301 英语笔译1 1-18 李娟23047—8节第二外语3(日语)30人1-17 张缦2302第二外语3(法语)14人1-16 李静宜2301第二外语3(日语)36人1-17 张缦2302第二外语3(法语)8人1-16 李静宜2301星期二1—2节英语国家概况1-17 陈义权2205 高级英语1 1-18 钱博洁2304 3—4节高级英语1 1-18 钱博洁2304 英国文学作品选读1-17 张越2205 5—6节英国文学作品选读1-17 张越23027—8节星期三1—2节英语写作3 1-17 邓欢23033—4节跨文化交际1-17 郑征2301 跨文化交际1-17 郑征23015—6节第二外语3(日语)30人1-17 张缦2202第二外语3(法语)14人1-17 李静宜2304第二外语3(日语)36人1-17 张缦2202第二外语3(法语)8人1-17 李静宜2304 7—8节星期四1—2节高级英语1 1-18 钱博洁23043—4节高级英语1 1-18 钱博洁2304 5—6节7—8节星期五1—2节英语口译1 1-17 徐利君2304 3—4节英语口译1 1-17 徐利君2304 英语国家概况1-17 陈义权2303 5—6节7—8节周次 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 教学进程←———————————————————————上课———————————————————————→考试课程学时英语文体学 32 英语论文写作 16 英语教学理论及方法 32 英语测试 16 商务英语写作 32 英文外贸函电 16星期专业班节次课程英语1001(44人)1002(43人)教育(22人)商务(22人)教育(13人)商务(30人)星期一1—2节英语教学理论及方法1-8 简丹2205英语教学理论及方法1-8 简丹22053—4节5—6节英文外贸函电1-8 张晓磊2303 英文外贸函电1-8 张晓磊2303 7—8节星期二1—2节英语文体学1-9 杨荣琦23033—4节英语教学理论及方法1-9 简丹2202商务英语写作1-9 龚芳2203英语教学理论及方法1-9 简丹2202商务英语写作1-9 龚芳2203 5—6节英语文体学1-9 杨荣琦23047—8节星期三1—2节英语论文写作1-9 杨文静22023—4节英语测试1-9 邓欢2202 英语测试1-9 邓欢22025—6节英语论文写作1-9 杨文静2303 7—8节星期四1—2节英语文体学1-9 杨荣琦23023—4节英语文体学1-9 杨荣琦2302 5—6节7—8节星期五1—2节3—4节商务英语写作1-9 龚芳2301 商务英语写作1-9 龚芳2301 5—6节7—8节备注:6-9周翻译/教学实习 10周期中结业性考试 11-18周毕业实习。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013 -2014 学年度第一学期
东莞市常平中学初中部中学体育艺术科组教研工作总结
执笔人:房勇
本学期体育艺术科组继续围绕学校实施精致教育的工作思路下,全面贯彻学
校教学计划,科组工作在学校的正确领导下和各部门的大力支持下,全体体艺科
组同事辛勤努力工作下,较好地完成了学校的体育艺术教学任务,现将2013-2014
学年度第一学期主要工作汇报如下:
一、本学期理论学习和提升教学理念方面
科组借助全校教学竞赛的契机。在科组掀起学习热潮。本次科组成员全部参
与比赛,大家互相听课评课。在科组参赛过程中,要求每一位教师都要按照学校
精致教育的理念来进行备课上课,通过大家一起备课研讨,每一位教师都在一定
程度上提高了自己的教研能力。本学期科组教师相互听课总数达到160节,校内
公开课11节。
本学期科组安排了全校体育教师赴黄江中学参加东莞市初中体育高效课堂展
示,听取专家报告,了解东莞市高效课堂进展情况。取得了不错的效果。其中房
勇老师参加东莞市体育骆云名师工作室跟岗学习。
二、教学常规管理
1 课堂常规管理
科组开学初就制定了本学期教学计划,要求每个教师按照计划进行教学,加
强体育艺术课程的范式推广,每个星期科组例会上都进行学习,按照教导处要求
积极开展精巧教学,科组要求每个老师教学设计要考虑精细,重视每个教学细节。
打造真正的高效课堂。每学期集中检查教师的教学设计,听课记录本以及集体备
课情况,力求科组成员步调一致。
2课余体育艺术训练方面
在发扬体育长期开展课余训练的优良传统之外,开展了艺术长期课余集训。
并制定了体育艺术训练考勤制度,使我校的体育艺术集训更加规范化和科学化。
体育艺术科组的老师牺牲了大量的业余休息时间,为学校的体育艺术工作做出了
贡献。
3 体育艺术竞赛方面
学校男女篮分别在东莞市中学生篮球比赛中取得团体第四名的好成绩。是最近
几年的最好成绩。学校田径队几年来第一次组队参赛,学生增长了见识。学校合
唱队参加东莞市中学合唱比赛获得优秀奖。学校艺术队多人数获得常平镇比赛名
次,队员们在比赛中展现的积极进取的拼搏精神充分展示了我校师生的精神风
貌。
4、校庆活动方面
本学期体育艺术科组承担学校校庆方面的工作,在时间紧任务重的情况下,
体育艺术科组全体成员共同努力下,顺利完成了任务,在本次校庆系列活动中,
每位老师都牺牲了大量时间,在今年的校庆活动中有很多做的很好的地方。例如
今年的校庆开幕式上一些班级的展示做的非常有创意,初三5班是本届运动会做
的突出的班级,多人打破学校运动会记录。学校校庆晚会也办的非常成功。
三、师资建设
1完善教学质量监管:形成质监组成员、学科组长、备课组长三位一体监管
机制,采取如下具体措施:
一查:查个人复备情况、查课堂集体备课落实情况、查知识落实情况;
二导:个别谈话导思想、找出问题导策略;
三思:通过听评课思考课堂教学实施的不足之处、通过与学生访谈反思教学
策略的不实之处;
四帮:面对实际问题找方法、面对工作难处多协助等工作进展情况。
2继续做好师资队伍的建设监管工作。
(1)本学期第4周举行新任教师汇报课,刘妍婷和邓翔宇老师分别上了一
节汇报课,得到了科组教师大量帮助。
(2)在本学期课堂教学竞赛中以学科课堂教学范式为衡量标准,每个老师
在科组上一节公开课。其中房勇老师获得一等奖,黄家伟黎业方老师获得二等奖。
(3)教师三年成长规划的落实、跟进工作。要求教师对照规划完成2013阶
段工作验收。
(4)体育美术科组编制完成校本课程。
3文科教学能手入围情况。
房勇老师经过努力,顺利已小组第一晋级教学能手决赛。
四、经验和教训
通过本学期体育艺术工作的开展,从中获得了很多启示和教训:体艺教学管
理有待加强检查和强化组织纪律性,科组成员之间的团结协作不够。学生的训练
水平有待提高。在期末考试中也暴露出一些科组成员之间沟通不够的问题。个别
裁判工作不认真的现象。
三、改进措施
全面实施精巧教育,在长期开展课余体育艺术训练的基础上,发扬优良传统,
健全和完善相关保障的规章制度,科组下学期推出量化考核条例,加强科组成员
之间沟通。要求科组教师要有大局意识,做到服从工作安排。在每学年度的各级
体育比赛和校园歌咏比赛、校庆晚会上,展示我校学生的风采和艺术水平。继续
规范教学范式和打造高效课堂努力。
回首一个学期的工作,是充满收获的一个学期,展望下一个学期的工作,我
们充满希望,我们坚信在学校精细化管理下,在精巧教学的指引下,体育艺术科
组一定会创造更大的辉煌!
