积的变化规律和商的变化规律
商的变化规律的口诀三条

商的变化规律的口诀三条
(1)被除数扩大(缩小)n倍,除数不变,商也相应的扩大(缩小)n倍。
(2)除数扩大(缩小)n倍,被除数不变,商相应的缩小(扩大)n 倍。
(3)被除数与除数同乘以来自或同除以一个数(零除外360问答),商不变。
扩展资料:
积的变化规律是指因数的变化所引起的积的变化。
(1)如一个因数扩大n倍,另一个因数不变,则积也扩大n倍。
(2)一个因数扩大n倍,另一个因数缩小n倍,则积不变。
除法运算肥天裂性质
(1)若某数除以(或乘)一个数,又乘(或除以)同一个数,则这个数
不变。
例如:68÷17×17=68(或68×17÷1绿钱规云歌投建以玉7=68)。
(2)一个数除以几个数的积兴得乡讲从养属得都花你,可以用这个
数依次除以积里的各个因数。
例如:320÷(2×5×8)=320÷2÷5÷8=4。
(3)几个数的积除以一个数,可以让积里的任何一致段机个因数除
以这个数,再与光其他的因数相乘。
例如:8×管苦洲视联72X4÷9=72÷9×8×4=256。
和差积商的变化规律

和差积商的变化规律一、和的变化规律(一)如果一个加数增加一个数,另一个加数不变,那么它们的和也增加同一个数.例如:3+5=8 a+b=c(3+2)+5=8+2 (a+m)+b=c+ma+(b+m)=c+m(二)如果一个加数减少一个数,另一个加数不变,那么,它们的和也减少同一个数.例如:8+6=14(8-4)+6=14-4a+b=c(a-m)+b=c-m(a≥m)a+(b-m)=c-m(b≥m)(三)如果一个加数增加一个数,另一个加数减少同样的加数,那么,它们的和不变.例如:8+3=11(8+2)+(3-2)=11(8-6)+(3+6)=11a+b=c(a+m)+(b-m)=c(b≥m)(a-m)+(b+m)=c(a≥m)(四)如果一个加数增加一个数m,另一个加数增加一个数n,那么,它们的和就增加(m+n).例如:5+3=8(5+2)+(3+7)=8+(2+7)a+b=c(a+m)+(b+n)=c+(m+n)(五)如果一个加数减少一个数m,另一个加数减少一个数n,那么,它们的和就减少(m+n).例如:30+18=48(30-15)+(18-9)=48-(15+9)a+b=c(a-m)+(b-n)=c-(m+n)(六)如果一个加数增加一个数m,另一个加数减少一个数n,当m>n时,它们的和就增加(m-n);当m<n时,它们的和就减少(n-m).例如:8+5=13(8+7)+(5-3)=13+(7-3)(8+2)+(5-4)=13-(4-2)a-b=c(a+m)+(b-n)=c+(m-n)(m>n)=c-(n-m)(n>m)二、差的变化规律(一)如果被减数增加或减少一个数,减数不变,那么它们的差也增加或减少同一个数.例如:9-5=4(9+3)-5=4+3(9-2)-5=4-2a-b=c(a+m)-b=c+m(a-m)-b=c-m(c≥m)(二)如果减数增加或减少一个数,被减数不变,那么,它们的差就减少或增加同一个数.例如:9-5=49-(5+3)=4-39-(5-3)=4+3a-b=ca-(b+m)=c-m(a≥b+m)a-(b-m)=c+m(b≥m)(三)如果被减数和减数同时增加或减少同一个数,那么,它们的差相等.例如:15-8=7(15+3)-(8+3)=7(15-5)-(8-5)=7a-b=c(a+m)-(b+m)=c(a-m)-(b-m)=c(a≥m b≥m)(四)如果被减数增加一个数m,减数减少一个数n,那么,它们的差就增加(m+n).例如:18-12=6(18+4)-(12-3)=6+(4+3)a-b=c(a+m)(b-n)=c+(m-n)(b≥n)(五)如果被减数减少一个数m,减数增加一个数n,那么,它们的差就减少(m+n)例如:18-12=6(18-2)-(12+1)=6-(2+1)a-b=c(a-m)-(b+n)=c-(m+n)(c≥m+n)(六)如果被减数增加一个数m,减数增加一个数n,那么,当m>n时,它们的差就增加(m+n);当m<n时,它们的差就减少(n-m).例如:20-12=8(20+5)-(12+3)=8+(5-3)(20+5)-(12+6)=8-(6-5)a-b=c(a+m)-(b+n)=c+(m-n)(m>n)(a+m)-(b+n)=c-(n-m)(m<n)(七)如果被减数减少一个数m,减数减少一个数n,那么,当m>n时,它们的差要减少(m-n);当 m<n时,它们的差要增加(n-m).例如:40-22=18(40-3)-(22-2)=18-(3-2)(40-5)-(22-7)=18+(7-5)a-b=c(a-m)-(b-n)=c-(m-n)(m>n)(a-m)(b-n)=c+(n-m)(n>m)三、积的变化规律(一)如果一个因数扩大m倍,另一个因数不变,那么,它们的积也扩大m倍.例如:8×5=40(8×3)×5=40×38×(5×4)=40×4a×b=c(a×m)×b=c×ma×(b×m)=c×m(二)如果一个因数缩小m倍,另一个因数不变,那么,它们的积也缩小m倍.如:25×4=100(25÷5)×4=100÷525×(4÷2)=110÷2a×b=c(a÷m)×b=c÷ma×(b÷m)=c÷m(三)如果一个因数扩大m倍,另一个因数缩小相同的倍数,那么它们的积不变.例如:45×10=450(45×2)×(10÷2)=450(45÷5)×(10×5)=450a×b=c(a×m)×(b÷m)=c (m≠0)(a÷m)×(b×m)=c(m≠0)(四)如果一个因数扩大m倍,另一个因数扩大n倍,那么,它们的积扩大(m×n)倍.例如:4×5=20(4×3)×(5×2)=20×(3×2)a×b=c(a×m)×(b×n)=c×(m×n)(m≠0,n≠0)(五)如果一个因数缩小m倍,另一个因数缩小n倍,那么,它们的积就缩小(m×n)倍.例如:20×8=160(20÷5)×(8÷4)=160÷(5×4)a×b=c(a÷m)×(b÷n)=c÷(m×n)(m≠0,n≠0)(六)如果一个因数扩大m倍,另一个因数缩小n倍,那么,当m>n时它们的积扩大(m÷n)倍,当m<n时,它们的积就缩小(n÷m)倍.例如:8×6=48(8×10)×(6÷2)=48×(10÷2)(8×2)×(6÷6)=48÷(6÷2)a×b=c(a×m)×(b÷n)=c×(m÷n)(m>n)(n≠0)(a×m)÷(b÷n)=c÷(n÷m)(m<n)(m≠0)四、商的变化规律(一)如果被除数和除数同时扩大或缩小相同的倍数,那么,它们的商不变.例如:42÷6=7(42×2)÷(6×2)=7(42÷3)÷(6÷3)=7a÷b=c(a×m)÷(b×m)=c(m≠0)(a÷m)÷(b÷m)=c(m≠0)(二)如果被除数扩大(或缩小)m倍,除数不变,那么,它们的商就扩大(或缩小)m倍.例如:16÷2=8(16×3)÷2=8×3(16÷2)÷2=8÷2a÷b=c(a×m)÷b=c×m(m≠0)(a÷m)÷b=c÷m (m≠0)(三)如果除数扩大或缩小m倍,被除数不变,那么,它们的商反而缩小或扩大m倍.例如:44÷11=444÷(11×2)=4÷244÷(11÷11)=4×11a÷(b×m)=c÷m(m≠0)a÷(b÷m)=c×m (m≠0)(四)如果被除数扩大m倍,除数缩小n倍,那么,它们的商就扩大(m×n)倍.例如:72÷9=8(72×2)÷(9÷3)=8×(2×3)a÷b=c(a×m)÷(b÷n)=c×(m×n)(m,n≠0)(五)如果被除数缩小m倍,除数扩大n倍,那么,它们的商就缩小(m×n)倍.例如:72÷6=12(72÷3)÷(6×2)=12÷(3×2)a÷b=c(a÷m)÷(b×n)=c÷(m×n)(m≠0 n≠0)(六)如果被除数扩大m倍,除数扩大n倍,当m>n时,它们的商就扩大(m÷n)倍,当m<n时,它们的商就缩小(n÷m)倍.例如:96÷24=4(96×4)÷(24×2)=4×(4÷2)(96×2)÷(24×4)=4÷(4÷2)a÷b=c(a×m)÷(b×n)=c×(m÷n)(m>n,n≠0)(a×m)÷(b×n)=c÷(n÷m)(m<n,m≠0)(七)如果被除数缩小m倍,除数缩小n倍,当m>n时,它们的商就缩小(m÷n)倍,当m<n时,它们的商就扩大(n÷m)倍.例如:64÷16=4(64÷4)÷(16÷2)=4÷(4÷2)(64÷2)÷(16÷4)=4×(4÷2)a÷b=c(a÷m)÷(b÷n)=c÷(m÷n)(m>n n≠0)(a÷m)÷(b÷n)=c×(n÷m)(m<n m≠0)加减法混合运算的性质(一)交换的性质在加减混合运算式题中,带着数字前的运算符号,变换加、减数的位置顺序进行计算,结果不变.如a+b-c=a-c+b (a≥c)=b-c+a (b≥c)(二)结合的性质在加减混合运算中,可以把加数、减数用括号括起来.当加号后面添括号时,原来的加数,减数都不变;当减号后面添括号时,则原来的减数变加数,加数变减数.如a-b+c-d+m=(a-b)+(c-d)+m (a≥b,c≥d)=a-(b-c)-(d-m) (b≥c,d≥m)=a+(m-b)+(c-d) (m≥b,c≥d)可以归纳为,括号前面是加号,去掉括号不变“号”;加号后面添括号,括号里面不变“号”,括号前面是减号,去掉括号要变“号”,减号后面填括号,括号里面要变“号”.(注:可编辑下载,若有不当之处,请指正,谢谢!)。
商的变化规律

商的变化规律【复习与巩固】积的变化规律1、一个因数不变,另一个因数乘(或除以)几,积乘(或除以)几。
若:24×25=600240×25= 24×250= 48×25= 24×50=若:48×50=240048×5= 24×50= 48×25= 48×(50÷4)=2、一个因数乘(或除以)几,另一个因数除以(或乘)几,积不变。
若:15×14=210(15÷3)×(14×3)= (15×3)×(14÷3)=(15×5)×(14 5)=210 (15 )×(14 )=210【知识点1】商的变化规律:(1)被除数、除数同时乘以(或除以)相同的数,商不变。
1、在()里填上适当的数,使计算简便。
490 ÷ 35 = 270 ÷ 18 = 350 ÷ 25 =×()×2 ÷()÷3 ×()×()÷ 70 ÷ 6 ÷840 ÷ 14 = 180 ÷ 15 = 140 ÷ 35 =÷()÷()×()×2 ÷()÷()÷÷ 30 ÷2、填空。
1)210÷30=(210×15)÷(30×)商的变化规律2)48÷12=(48×)÷(12 4)3)60÷12=(60 ÷)÷(12 ÷3)4)63÷7=(63÷10)÷(7÷)5)如果被除数和除数都乘100,那么商( )6)如果被除数和除数都除以20,那么商( )(2)除数不变,被除数乘以(或除以)几,商也要乘以(或除以)几。
四年级上册数学思维拓展题:和差积商变化规律

四年级上册数学思维拓展题:和差积商变化规律和的变化规律:如果一个加数增加(或减少)一个数(不为0),另一个加数不变,则它们的和也增加(或减少)同一个数。
如果一个加数增加一个数(不为0),另一个加数减少同一个数,和不变。
差的变化规律:如果一个被减数增加(或减少)一个数(不为0),减数不变,则差增加(或减少)同一个数。
如果一个被减数和减数同时增加(或减少)一个数(不为0),差不变。
如果被减数不变,一个减数增加(或减少)一个数(不为0),差也减少(或增加)同一个数。
积的变化规律:1.一个因数扩大(或缩小)若干倍,另一个因数不变,积也扩大(或缩小)相同的倍数。
2.一个因数扩大(或缩小)若干倍,而另一个因数缩小(或扩大)相同的倍数,它们的积不变。
3.一个因数乘以(或除以)a,另一个因数乘以(或除以)b,积就乘以(或除以)ab的积。
商的变化规律:1.被除数扩大(或缩小)若干倍,除数不变,商也扩大(或缩小)同样的倍数。
2.被除数不变,除数扩大(或缩小)若干倍,商反而缩小(或扩大)相同的倍数。
3.被除数乘以a,除数除以b,商就乘以ab的积。
4.被除数除以a,除数乘以b,商就除以ab的积。
参考答案:1、两个数相加,如果一个加数减少9,要使和增加9,另一个加数应该有什么变化?解题思路:一个加数减少9,假设另一个加数不变,和就减少了9;题目要求和增加9,所以另一个加数应该增加9+9=18。
2、两个数相减,如果被减数减少10,减数也减少10,差是否有变化?解题思路:被减数减少10,假设减数不变,差就减少10;假设被减数不变,减数减少10,和就增加10;差先减少10,再增加10,所以无变化。
3、被减数、减数、差相加得2076,差是减数的一半。
如果被减数不变,差增加42,减数应该变成多少?解题思路:减数与差的和即是被减数,2076里有2个被减数,被减数等于2076÷2=1038。
差是减数的一半,也就是说减数是差的2倍,差应该为1038÷(2+1)=346,减数为346×2=692。
积、商的变化规律(含答案)-

积、商的变化规律同学们好,在上一讲我们研究了和、差的变化规律,今天这一讲我们来研究,积、商的变化规律。
请同学们填出下表,说出什么发生了变化,积、商有没有发生变化,如果有变化是怎样变的,你能从中得出什么结论吗?规律:两个因数相乘,被乘数乘以(或除以)一个不为0的数,乘数不变,积也乘以(或除以)同一个数。
两个因数相乘,被乘数不变,乘数乘以(或除以)一个不为0的数,积也乘以(或除以)同一个数。
两个因数相乘,被乘数乘以(或除以)一个不为0的数,乘数同时除以(或乘以)同一个数,积不变。
规律:在除法里被除数乘以(或除以)一个不为0的数,除数不变,商也乘以(或除以)同一个数。
被除数不变,除数乘以(或除以)一个不为0的数,商反而除以(或乘以)同一个数。
被除数乘以(或除以)一个不为0的数,除数同时乘以(或除以)相同的一个数,商不变。
例1. 2584⨯=⨯⨯÷=⨯=()()254844100212100分析与解答:根据积的变化规律,一个因数扩大多少倍,另一个因数反而缩小相同的倍数,积不变的规律,使25×4,使84÷4,转化为100×21,这就很快计算出结果是2100。
例2. 12588⨯=⨯⨯÷=⨯=()()125888810001111000例3. 2250125÷=⨯÷⨯=÷=()()22508125818000100018分析与解答:根据商的变化规律,被除数和除数同时乘以或除以一个数(不为0)商不变的规律,可以使2250×8,使125×8,转化为18000÷1000,这样就能很快算出结果是18。
【模拟试题】(答题时间:45分钟)(一)尝试体验 1. 填一填1272244⨯⨯⨯⨯⨯⎫⎬⎪⎪⎪⎭⎪⎪⎪=÷÷÷÷÷⎫⎬⎪⎪⎪⎭⎪⎪⎪=()()()()()()()()()()()()()()()()()() 完成上面两组题后,每组后面的4个题与第一算式比较各部分是怎样变化的,才保证了使它们的和、差、积、商没发生变化? 2. 利用积、商变化规律,计算下面各题。
积商的变化规律练习题
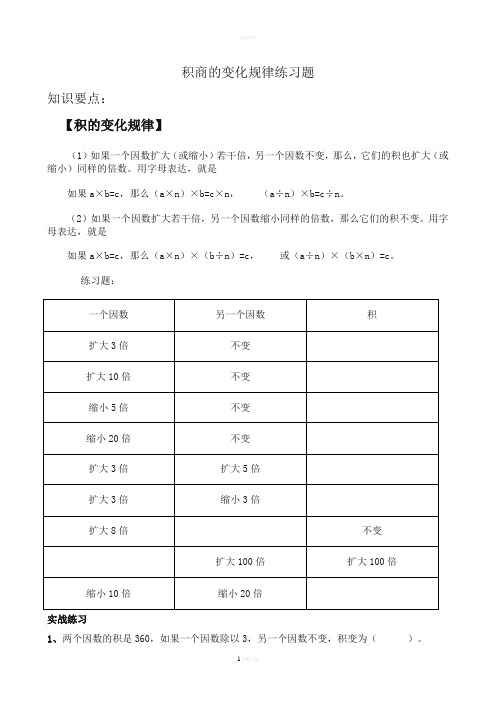
积商的变化规律练习题知识要点:【积的变化规律】(1)如果一个因数扩大(或缩小)若干倍,另一个因数不变,那么,它们的积也扩大(或缩小)同样的倍数。
用字母表达,就是如果a×b=c,那么(a×n)×b=c×n,(a÷n)×b=c÷n。
(2)如果一个因数扩大若干倍,另一个因数缩小同样的倍数,那么它们的积不变。
用字母表达,就是如果a×b=c,那么(a×n)×(b÷n)=c,或(a÷n)×(b×n)=c。
练习题:实战练习1、两个因数的积是360,如果一个因数除以3,另一个因数不变,积变为()。
2、两个因数相乘,一个因数乘6,另一个因数不变,那么积()。
3、两个因数相乘的积是5600,如果一个因数不变,另外一个因数除以10,那么积是()。
4、两个数相乘是75,如果一个因数乘7,另一个因数除以7,积是()。
5、已知A×B=400,如果A乘3,则积是(),如果B除以5,则积是()。
6、两个数相乘,一个因数乘10,另一个因数也乘10,积()。
7、两个因数的积是420,如果一个因数不变,另一个因数乘8,积是()。
8、两个数相乘的积是160,如果一个因数除以2,另一个因数也除以2,积是()。
【商或余数的变化规律】(1)如果被除数扩大(或缩小)若干倍,除数不变,那么它们的商也扩大(或缩小)同样的倍数。
用字母表达,就是如果a÷b=q,那么(a×n)÷b=q×n,(a÷n)÷b=q÷n。
(2)如果除数扩大(或缩小)若干倍,被除数不变,那么它们的商反而缩小(或扩大)同样的倍数。
用字母表达,就是如果a÷b=q,那么a÷(b×n)=q÷n,a÷(b÷n)=q×n。
六年级上册数学讲义-和、差、积、商的变化规律-人教版(含答案)

和、差、积、商的变化规律学生姓名年级学科授课教师日期时段核心内容和、差、积、商的变化规律课型一对一/一对N教学目标1.掌握和、差、积、商的变化规律2.学会根据规律进行速算重、难点根据积、商的变化规律速算课首沟通1、上讲回顾(错题管理);检查作业;2、询问学生加减乘除的运算公式知识导图课首小测1.两个数相加,一个加数增加25,另一个加数也增加15,和()。
2.两数相减,如果被减数减少18,减数减少8,差()。
3.两个因数相乘,如果一个因数缩小5倍,另一个因数扩大5倍,积()。
4.根据每组第一个算式的结果,直接写出第二、第三个算式的得数。
(1)18÷6=3(18×2)÷(6×2)= (18×3)÷(6×3)= (2)480÷10=48(480÷2)÷(10÷2)= (480÷5)÷(10÷5)= (3)420÷6=70(420×2)÷(6÷2)= (420÷5)÷(6×2)=知识梳理导学一:和的变化规律例 1. 按题目要求解答下列各题。
(1)两个数相加,一个数减8,另一个数加8,和是否变化?(2)两个数相加,一个数加3,另一个数也加3,和有什么变化?(3)两个数相加,一个数减6,另一个数减2,和有什么变化?例 2. 按要求解答下列各题。
(1)两个数相加,如果一个加数增加8,要使和增加15,另一个加数应有什么变化?(2)两个数相加,如果一个加数增加8,要使和减少15,另一个加数应有什么变化?例 3. 小华在计算两个数相加时,把一个加数个位上的1错误地写成7,把另一个加数十位上的3错误地写成8,所得的和是1996。
原来两个数相加的正确答案是多少?例 4. 两个加数都扩大了8倍,则和扩大()倍。
【学有所获】两个加数都乘以(或除以)同一个数(零除外),和也乘以(或除以)同一个数。
积的变化规律

“点线面”思维训练模式3——
从“积的变化规律”到“积不变的规律”
一、一个因数变化
【1】一个因数不变,另一个因数扩大了。
【结论】:一个因数不变,另一个因数扩大多少倍(0除外),积也跟着扩大相同的倍数。
【2】一个因数不变,另一个因数缩小。
【结论】:一个因数不变,另一个因数缩小多少倍(0除外),积也跟着缩小相同的倍数。
(一)、积的变化规律:
(1)、一个因数不变,另一个因数乘(或除以)几,积就相应的乘(或除以)几。
字母表示:如果axb=C,则
(ax3)×b=c×3
举例:axb=12如果(ax3)则积就是
12×3=36.
(2)、一个数乘一个比1大的数,积比原数大;
(3)、一个数乘一个比1小的数,积比原数小。
【3】积的变化规律:
【结论】:积与因数同向变化。
【4】同步应用
【5】能力提升
【6】拓展训练
二、积不变的规律
【结论】:一个因数扩大或缩小多少倍,另一个因数缩小或扩大相同的倍数(0除外),积不变。
两个因素反向变化,积不变。
(巧墨静好)
下一节内容:1.商的变化规律——商不变的规律——余数的变化规律
2、和、差、积、商的变化规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
积的变化规律和商的变化规律
以积的变化规律和商的变化规律为标题,本文将从数学的角度讨论积和商的变化规律,并探讨其应用领域。
一、积的变化规律
积是指两个或多个数相乘的结果。
在数学中,我们经常遇到各种形式的乘法运算,而积的变化规律是乘法运算的核心。
1.1 正数的乘积
当两个正数相乘时,积的结果也是正数。
这是因为正数表示具有一定数量的物体或数值,相乘后得到的仍然是正数的数量。
1.2 负数的乘积
当一个正数与一个负数相乘时,积的结果为负数。
这是因为正数表示具有一定数量的物体或数值,而负数表示缺少一定数量的物体或数值,相乘后得到的是缺少的数量,所以结果为负数。
1.3 零的乘积
任何数与零相乘,积的结果都为零。
这是因为零表示没有物体或数值,与任何数相乘都得到没有的数量。
1.4 小数的乘积
当两个小数相乘时,积的结果为更小的数。
这是因为小数表示比1小的数值,相乘后得到更小的数值。
1.5 科学计数法的乘积
科学计数法是一种表示大数或小数的方法,它将一个数表示为一个数值与10的幂的乘积。
当两个科学计数法相乘时,可以将指数相加,乘积的结果也是科学计数法形式的数。
二、商的变化规律
商是指一个数除以另一个数的结果。
在数学中,商的变化规律是除法运算的核心。
2.1 正数的商
当一个正数被另一个正数除时,商的结果为正数。
这是因为正数表示具有一定数量的物体或数值,被除数表示要将这一定数量的物体或数值平均分给除数,所以商的结果仍然为正数。
2.2 负数的商
当一个负数被一个正数除时,商的结果为负数。
这是因为负数表示缺少一定数量的物体或数值,被除数表示要将这缺少的数量的物体或数值平均分给除数,所以商的结果为缺少的数量,即负数。
2.3 零的商
任何数除以零是没有意义的,因为零表示没有物体或数值,不能将某一数量平均分给零个单位。
2.4 小数的商
当一个小数被一个大于1的数除时,商的结果为更小的数。
这是因为小数表示比1小的数值,被除数表示要将这一小部分的数量平均分给除数,所以商的结果更小。
2.5 科学计数法的商
当一个科学计数法被另一个科学计数法除时,可以将指数相减,商的结果也是科学计数法形式的数。
三、应用领域
积和商的变化规律在数学中有广泛的应用,也在生活中有一些实际的应用。
3.1 数学运算
积和商是数学中最基本的运算之一,它们在数学的各个分支中都有广泛的应用。
比如在代数中,我们常常需要进行多项式的乘法运算;在几何中,我们常常需要计算图形的面积和体积;在统计学中,我们常常需要计算概率和期望值等。
3.2 经济学
积和商的变化规律在经济学中也有应用。
比如在计算价格指数时,我们需要将某一年的价格与基准年的价格相除,得到价格指数;在计算经济增长率时,我们需要将某一年的国内生产总值与前一年的国内生产总值相除,得到经济增长率。
3.3 科学研究
在科学研究中,积和商的变化规律也有应用。
比如在物理学中,我们常常需要计算力与位移的乘积,得到功;在化学中,我们常常需要计算物质的摩尔质量;在生物学中,我们常常需要计算生物种群的增长率等。
积和商的变化规律是数学中最基本的运算之一,它们在数学的各个分支和生活的各个领域都有广泛的应用。
掌握积和商的变化规律,有助于我们理解和应用数学知识,解决实际问题。
