倍长中线法(初二)

合集下载

浙教版八年级数学上册全等三角形之手拉手模型、倍长中线-截长补短法

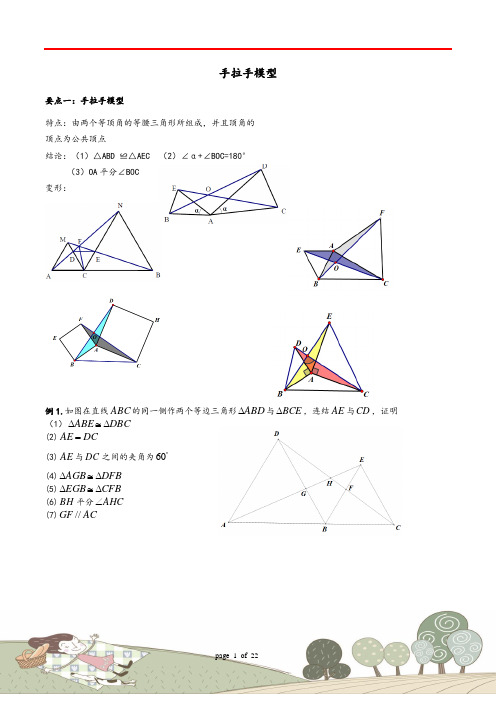
手拉手模型要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的顶点为公共顶点结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180° （3）OA 平分∠BOC 变形：例1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60 (4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)BH 平分AHC ∠ (7)AC GF //变式精练1：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ （2）DC AE =（3）AE 与DC 之间的夹角为︒60（4）AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2）DC AE =(3）AE 与DC 之间的夹角为︒60(4）AE 与DC 的交点设为H ,BH 平分AHC ∠例2：如图，两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H 问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例3：如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H 问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例4：两个等腰三角形ABD ∆与BCE ∆，其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ，问：（1）DBC ABE ∆≅∆是否成立？（2）AE 是否与CD 相等？（3）AE 与CD 之间的夹角为多少度？（4）HB 是否平分AHC ∠？例5：如图，点A. B. C 在同一条直线上，分别以AB 、BC 为边在直线AC 的同侧作等边三角形△ABD 、△BCE.连接AE 、DC ，AE 与DC 所在直线相交于F ，连接FB.判断线段FB 、FE 与FC 之间的数量关系，并证明你的结论。

初二数学倍长中线专题

初二数学倍长中线专题一．求边的数量关系分析：本题中，要求三角形一边的范围，不难想到在三角形三边关系中是有所涉及的。

但这里的AC与AB，AD不在同一三角形中，无法直接来求，必须进行适当转换．由于题目中明确给出中线，则倍长中线，构造全等，将AC转化至某一条线段，与AB、AD组成三角形．分析：本题中，要直接发现BE，EF，CF 间的大小关系，是很困难的，三条线段不在同一个三角形中．受上一题启发，可能有同学会想到倍长中线AD．但是，这样只能将AC转化至某一条线段，与CF没有关系，因此看到中点D，我们也要想到倍长“隐藏的”中线FD．再联系到DE，DF为角平分线，“邻补角的角平分线互相垂直”，∠EDF为90°，想到转化EF，以达到将三条线段转化至同一个三角形的目的．小结：以上两题，均是探究边之间的数量关系，借助倍长中线，构造旋转180°的SAS 型全等，将不是同一三角形的边转化，使之能构成三角形，从而求解．这对学生的思维能力要求还是比较高的．不光看到中线，有时，看到中点也要想到这种辅助线作法．二．证明边等分析：本题是经典老题，解法多样．显然图中△BDF和△ECF不全等，不能直接得到BD＝CE．那就需要对其中一条边进行转化．考虑到F为DE中点，加之有对顶角的存在，已经有一对边，一对角等，要构造全等很容易，可以再添一对角等，或者一对边等，这里提供2种方法．分析：要证边等，第一步分析能否直接通过证明全等得到，显然不能．想到AD为△ABC中线，则应该倍长中线，尝试将AC转化到与BF在同一三角形中．分析：本题其实是在上一题的基础上，去掉了边BF，即擦除了“中线”，只留了中点E，再多加了一条AD，所以方法应该不变．小结：例2和例3及变式，都是证明边等。

但都不能直接通过全等得到，需要用倍长中线进行转化。

而在证明过程中，其实都借助了双等腰三角形的八字形，有一组对顶角作为中间桥梁。

通过四个角等，最后得边等。

学而思初二数学秋季班第2讲.倍长中线与截长补短.提高班.教师版

1初二秋季·第2讲·提高班·教师版三角形9级全等三角形的经典模型（二）三角形8级全等三角形的经典模型（一）三角形7级倍长中线与截长补短倍长中线与截长补短满分晋级漫画释义2倍长中线与截长补短2初二秋季·第2讲·提高班·教师版定义示例剖析倍长中线：即延长三角形的中线，使得延长后的线段是原中线的两倍．其目的是构造一对对顶的全等三角形；其本质是转移边和角．EDABC其中BD CD =，延长AD 使得DE AD =，则BDE CDA △≌△．【例1】已知ABC △中，AD 平分BAC ∠，且BD CD =，求证：AB AC =．【解析】延长AD 到E ，使DE AD =，连接CE ．则CDE BDA △≌△，∴CE AB =，CED BAD ∠=∠， ∵AD 平分BAC ∠，∴BAD CAD ∠=∠， ∴CED CAD ∠=∠，∴CE AC =， ∴AB AC =．思路导航例题精讲知识互联网题型一：倍长中线EABCDABCD3初二秋季·第2讲·提高班·教师版【教师备选】教师可借用例1对等腰三角形三线合一性质的逆命题进行简单归纳：已知角平分线+中线证等腰三角形，如例1；已知角平分线+高证等腰三角形，如拓展1；已知中线+高证等腰三角形，如拓展2．【拓展1】已知△ABC 中，AD 平分∠BAC ，且AD ⊥BC ，求证：AB =AC ．【解析】∵AD 平分∠BAC ，∴∠BAD =∠CAD∵AD ⊥BC ，∴∠ADB =∠ADC =90° ∴△ABD ≌△ACD (SAS) ∴AB =AC ．【拓展2】已知△ABC 中，AD ⊥BC ，且BD CD =，求证：AB =AC ．【解析】∵AD ⊥BC ，且BD CD =∴AD 所在直线是线段BC 的垂直平分线根据垂直平分线上的点到线段两端点距离相等故AB =AC ．【例2】 ⑴如图，已知ABC △中，AB AC =，CE 是AB 边上的中线，延长AB 到D ，使BD AB =．给出下列结论：①AD =2AC ；②CD =2CE ；③∠ACE =∠BCD ；④CB 平分∠DCE ，则以上结论正确的是．【解析】 ①正确．∵AB AC =，BD AB =，∴AD =2AC ．②、④正确．延长CE 到F ，使EF CE =，连接BF ． ∵CE 是AB 的中线，∴AE EB =．在EBF △和EAC △中 AE BEAEC BEF CE FE =⎧⎪∠=∠⎨⎪=⎩典题精练ABDEDCBA4初二秋季·第2讲·提高班·教师版∴EBF EAC ≌△△∴BF AC AB BD ===，EBF EAC ∠=∠ ∴FBC FBE EBC A ACB DBC ∠=∠+∠=∠+∠=∠ 在FBC △和DBC △中 FB DB FBC DBC BC BC =⎧⎪∠=∠⎨⎪=⎩∴FBC DBC ≌△△∴2CD CF CE ==，∠FCB =∠DCB 即CD =2CE ，CB 平分∠DCE ．③错误．∵∠FCB =∠DCB ，而CE 是AB 边上中线而不是∠ACB 的角平分线故∠ACE 和∠BCD 不一定相等．⑵如图，在△ABC 中，点D 、E 为边BC 的三等分点，给出下列结论：①BD =DE =EC ；②AB +AE ＞2AD ；③AD +AC ＞2AE ；④AB +AC ＞AD +AE ，则以上结论正确的是．NM ED CBAEDCBA【解析】点D 、E 为边BC 的三等分点，∴BD =DE =CE 延长AD 至点M ，AE 至点N ，使得DM =AD ，EN =AE ，连接EM 、CN ，则可证明△ABD ≌△MED ，进而可得AB +AE ＞2AD ，再证明△ADE ≌△NCE ，进而可得AD +AC ＞2AE ，将两式相加可得到AB +AE +AD +AC ＞2AD +2AE ，即AB +AC ＞AD +AE ． ∴①②③④均正确．【例3】如图，已知在ABC △中，AD 是BC 边上的中线，E 是AD 上一点，延长BE 交AC 于F ，AF EF =，求证：AC BE =．FCAEBD5初二秋季·第2讲·提高班·教师版【解析】延长AD 到G ，使DG AD =，连接BG∵BD CD =，BDG CDA ∠=∠，AD GD = ∴ADC GDB △≌△， ∴AC GB =，G EAF ∠=∠ 又∵AF EF =，∴EAF AEF BED ∠=∠=∠ ∴G BED ∠=∠，∴BE BG =，∴AC BE =．【例4】在正方形ABCD 中，PQ ⊥BD 于P ，M 为QD 的中点，试探究MP 与MC 的关系．NABCDMPQ Q PMDCBA【解析】延长PM 至点N ，使PM =MN ，连结CP 、CN 、DN ．易证△PMQ ≌△NMD ， ∴PB =PQ =DN ，∠PQD =∠NDM ∴PQ ∥DN ，又∵∠BPQ =∠BDN= 90° ∴∠PBQ =∠BDC=∠NDC =45° 再证△BPC ≌△DNC (SAS) 易证△PCN 为等腰直角三角形，又∵PM =MN ，∴PM ⊥MC ,且PM =CM ．GFEDCBA FE D CBA6初二秋季·第2讲·提高班·教师版定义示例剖析截长：即在一条较长的线段上截取一段较短的线段DCBA在线段AB 上截取AD AC =补短：即在较短的线段上补一段线段使其和较长的线段相等AB C D延长AC ，使得AD AB =【例5】在ABC △中，A ∠的平分线交BC 于D ，AB AC CD =+，40B ∠=︒，求C ∠的大小．（希望杯培训题）D C B AED CB A【解析】在AB 上截取AE AC =，连接DE ．∵AE AC =，BAD CAD ∠=∠，AD AD =，∴ACD AED △≌△， ∴C AED ∠=∠，CD DE =，∵AB AC CD =+，AE AC =，∴CD BE DE == ∴40EBD EDB ∠=∠=︒，80C AED ∠=∠=︒例题精讲思路导航题型二：截长补短7初二秋季·第2讲·提高班·教师版D CB AEDCB AD CEBAE DCB A【例6】如图，在ABC △中，2B C ∠=∠，BAC ∠的平分线AD 交BC 于点D ．求证：AB BD AC +=．【解析】方法一：（截长）在AC 上截取AB AE =，连接DE ．在ABD △和AED △中AB AE =，BAD EAD ∠=∠，AD AD =∴ABD AED △≌△∴BD ED =，B AED ∠=∠又∵2AED EDC C B C ∠=∠+∠=∠=∠ ∴EDC C ∠=∠，∴ED EC =∴AB BD AC +=．方法二：（补短）延长AB 到点E 使得AC AE =，连接DE ．在AED △和ACD △中，AE AC =，EAD CAD ∠=∠，AD AD = ∴AED ACD △≌△，∴C E ∠=∠ 又∵22ABC E BDE C BDE ∠=∠+∠=∠=∠ ∴E BDE ∠=∠∴BE BD =，∴AB BD AC +=．方法三：（补短）延长DB 到点E 使得AB BE =，连接AE 则有EAB E ∠=∠，2ABC E EAB E ∠=∠+∠=∠ 又∵2ABC C ∠=∠，∴C E ∠=∠ ∴AE AC = EAD EAB BAD E DAC ∠=∠+∠=∠+∠C DAC ADE =∠+∠=∠∴AE DE =，∴AB BD EB BD ED AE AC +=+=== ∴AB +BD=AC若题目条件或求证结论中含有“a b c =+”的条件，需要添加辅助线时多考虑“截长补短”.建议教师此题把3种解法都讲一下，方便学生更加深刻理解这种辅助线添加方法.【例7】已知：在ABC △中，AB CD BD =-，AD BC ⊥，求证：2B C ∠=∠．【解析】方法一：在DC 上取一点E ，使BD DE =，如图1，在ABD △和AED △中，AD BC ⊥，BD ED =，AD AD =．典题精练DC BA8初二秋季·第2讲·提高班·教师版∴ABD AED △≌△． ∴AB AE =，B AED ∠=∠．又∵AE AB CD BD CD DE EC ==-=-= ∴C EAC ∠=∠，∴2C EAC AED C ∠+∠=∠=∠ ∴2B C ∠=∠．图1E AB CD图2EAB CD方法二：延长DB 到点E ，使BE AB =，如图2， ∴E EAB ∠=∠．∵AB CD BD =-，∴ED CD =．在AED △和ACD △中，AD BC ⊥，ED CD =，AD AD =． ∴AED ACD △≌△． ∴E C ∠=∠． ∵2ABD E ∠=∠ ∴2B C ∠=∠．【探究对象】截长补短法是几何证明题中十分重要的方法，通常来证明几条线段的数量关系，常见做辅助线方法有：截长法：⑴过某一点作长边的垂线；⑵在长边上截取一条与某一短边相同的线段，再证剩下的线段与另一短边相等。

初中数学倍长中线法课件模板.ppt

∴∠ ANF=∠ANE=90° AD⊥EF
E
N F
A
B
D
C
M
解题要点：延长中线AD，构造平行四边形。在证明全等三角形的基础上，运用转化思想，将位置关系转化为角的数量关系
13
实战演练——探究角的数量关系
例四：在平行四边形 ABCD中,AB=5,BC=10,F为AD 的中点,CE⊥AB 于E,设∠ABC=0(60°＜0<90°），是否存在正整数 k,使得∠EFD=k∠AEF?若存在,求出k 的值:若不存在,请说明理由。
例三: 已知AD是 △ABC 的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°, 试探究线段AD与EF 的位置关系,并加以证明
E
F A
B
D
C
11
实战演练
例三: 已知AD是 △ABC 的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°,
试探究线段AD与EF 的位置关系,并加以证明
E
A E
B
F
D
C
14
实战演练
G
A E
F
D
B
C
小结：倍长中线法只是解题的第一步！注重把握中点与直角三角形相关定理的结合，以及等边等角、对顶角相等相互转化的应用。
15
实战演练—— 一题多解
例五：已知在△ABC中，AB=AC，D在AB上，E在AC的延长线上，DE交BC于F，且DF=EF,求证：BD=CE A
A
想一想
B
①通过添加辅助线，还有哪些方式可以构造全等三角形？
D
C
②除了构造SAS全等三角形，可否构造AAS的全等三角形？
E
5
倍长中线法
A

初二上学期全等三角形专题之倍长中线与截长补短教案(有答案)

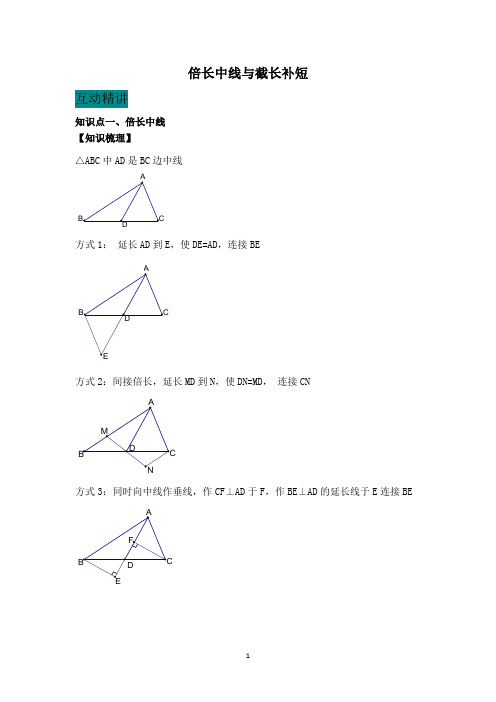
倍长中线与截长补短互动精讲知识点一、倍长中线【知识梳理】△ABC中AD是BC边中线方式1：延长AD到E，使DE=AD，连接BE方式2：间接倍长，延长MD到N，使DN=MD，连接CN方式3：同时向中线作垂线，作CF⊥AD于F，作BE⊥AD的延长线于E连接BE【例题精讲】例1、△ABC中，AB=5，AC=3，求中线AD的取值范围。

例2、已知：如图，在ABCDF//AB≠，D、E在BC上，且DE=EC，过D作BA ∆中，AC∠交AE于点F，DF=AC.求证：AE平分BAC【课堂练习】1、在△ABC中，AD是BC边上的中线，E是AD上一点，且BE＝AC，延长BE交AC 于F，求证：AF＝EF。

2、如图，△ABC中，E、F分别在AB、AC上，DE⊥DF，D是中点，试比较BE+CF 与EF的大小.ED F CBA知识点二、截长补短【知识梳理】截长补短的方法适用于求证线段的和差倍分关系。

截长，指在长线段中截取一段等于已知线段；补短，指将短线段延长，延长部分等于已知线段。

【例题精讲】例1、如图，AB∥CD，BE平分∠ABC，CE平分∠BCD，点E在AD上，求证：BC=AB+CD例2、已知：如图，ABCD是正方形，∠FAD=∠FAE. 求证：BE+DF=AE.【课堂练习】1、（1）如图1-1，△ABC 中，∠BAC=120°，AD ⊥BC 于D ，且AB+BD=DC ，则∠C=__20°．（2）如图1-2，正方形ABCD 的边长为1，P 、Q 分别是边BC 、CD 上的点，连接PQ ．若△CPQ的周长是2，则∠PAQ=___________．图1-1 图1-2课堂检测1、如图，ABC ∆中，AB AC =，108A ∠=︒，BD 平分ABC ∠交AC 于D 点．求证：BC AC CD =+．D C B AA B C DP QADB C2、已知CD=AB，∠BDA=∠BAD，AE是△ABD的中线，求证：∠C=∠BAE课后作业1、已知：△ABC中，AB=4cm ，BC=6cm ，BD是AC边上的中线，求BD的取值范围是。

倍长中线法

倍长中线法的变形可以根据具体问题的需要对倍长中线法进行变形以便更好地解决问题。
拓展学生的解题思路
倍长中线法在数学教育中的价值
培养学生的数学思维和创新能力
添加标题
添加标题
添加标题
添加标题
提高学生分析问题和解决问题的能力
促进数学教育的改革和发展
感谢您的耐心观看
汇报人：
证明倍长中线法的推论
推论：倍长中线法可以证明三角形中线定理
应用范围：适用于所有三角形包括等腰三角形、直角三角形等
添加标题
添加标题
添加标题
添加标题
证明过程：通过倍长中线法将三角形分为两个小三角形然后利用相似三角形的性质进行证明
注意事项：在应用倍长中线法时需要保证中线的长度足够长以便进行倍长操作
倍长中线法的几何意义
倍长中线法是利用中线的性质来证明线段相等的方法倍长中线法的几何意义在于将线段延长一倍从而证明线段相等倍长中线法在几何证明题中应用广泛是解决线段相等问题的重要方法之一倍长中线法可以通过构造辅助线来证明线段相等使证明过程更加简洁明了
倍长中线法的应用场景
定义：倍长中线法是一种几何证明方法通过延长线段来证明线段相等或三角形全等应用场景：证明线段相等、三角形全等、平行四边形性质等适用范围：适用于各种几何图形如三角形、四边形、圆等注意事项：在应用倍长中线法时需要仔细分析图形确定是否适用该方法
添加副标题
倍长中线法
汇报人：
目录
CONTENTS
01 添加目录标题
02 倍长中线法的定义
03 倍长中线法的证明
04 倍长中线法的应用
05 倍长中线法的拓展
添加章节标题
倍长中线法的定义
倍长中线法的概念

2024中考数学综合复习模型篇专题08 倍长中线法和截长补短法综合应用(解析版)

专题08倍长中线法和截长补短法综合应用倍长中线类型一：直接倍长中线△ABC 中AD 是BC 边中线方法：延长AD 到E ，使DE=AD ，连接BE类型二：间接倍长中线作CF ⊥AD 于F ，作BE⊥AD 的延长线于E 连接BE 。

延长MD 到N ，使DN=MD ，连接CN截长补短常见类型及常规解题思路：①a b c ±=可采取直接截长或补短，绕后进行证明。

或者化为类型②证明。

②a b kc±=可以将a b ±与c 构建在一个三角形中，然后证明这个三角形为特殊三角形，如等边三角形，等腰直角三角形，或一个角为30 的直角三角形等。

截长法常规辅助线：（1）过某一点作长边的垂线（2）在长边上截取一条与某一短边相同的线段，再证剩下的线段与另一短边相等。

补短法常规辅助线：（1）延长短边。

（2）通过旋转等方式使两短边拼合到一起类型一：倍长中线法【典例1】如图，在△ABC中，AB＝a，AC＝b，a，b均大于0，中线AD＝c，求c的取值范围．【解答】解：延长AD到E，使AD＝DE，连接BE，∵AD＝DE，∠ADC＝∠BDE，BD＝DC，∴△ADC≌△EDB（SAS），∴BE＝AC＝b，在△AEB中，AB﹣BE＜AE＜AB+BE，即a﹣b＜2AD＜a+b，∴＜c＜．【典例2】已知：在△ABC中，AD是BC边上的中线，E是AD上一点，且BE＝AC，延长BE交AC于F，求证：AF＝EF．【解答】证明：如图，延长AD到点G，使得AD＝DG，连接BG．∵AD是BC边上的中线（已知），∴DC＝DB，在△ADC和△GDB中，∴△ADC≌△GDB（SAS），∴∠CAD＝∠G，BG＝AC又∵BE＝AC，∴BE＝BG，∴∠BED＝∠G，∵∠BED＝∠AEF，∴∠AEF＝∠CAD，即：∠AEF＝∠FAE，∴AF＝EF．【典例3】如图，△ABC中，点D是BC的中点，点E、F分别在AB、AC上，且DE⊥DF，求证：BE+CF ＞EF．【解答】证明：如图，延长ED使得DM＝DE，连接FM，CM．∵BD＝DC，∠BDE＝∠CDM，DE＝DM，∴△BDE≌△CDM（SAS），∴BE＝CM，∵DE＝DM，DF⊥EM，∴FE＝FM，∵CM+CF＞FM，∴BE+CF＞EF．【变式1】如图，在△ABC中，AC＝3，AB＝5，点D为BC的中点，且AD⊥AC，则△ABC的周长为　．【解答】解：延长AD到E，使AD＝DE，连接BE，∵D为BC的中点，∴BD＝CD，∵∠ADC＝∠BDE，∴△ADC≌△EDB（SAS），∴AC＝BE＝3，∠DAC＝∠E，∵AD⊥AC，∴∠DAC＝90°，∴∠E＝90°，∴AE＝＝＝4，∴AD＝DE＝2，∴BD＝＝＝，∴BC＝2BD＝2，∴△ABC的周长为AB+AC+BC＝5+3+2＝8+2．故答案为：8+2．【变式2】如图，在△ABC中，点E是AB边的中点，D是BC延长线上一点，连接DE交AC于点F，且AF＝BD，若BD＝3，AC＝5，则CD的长为　．【解答】解：延长DE至H，使EH＝DE，连接AH，∵AF＝BD，BD＝3，AC＝5，∴CF＝AC﹣AF＝5﹣3＝2，在△BED和△AEH中，，∴△BED≌△AEH（SAS），∴AH＝BD，∠D＝∠H，∵AF＝BD，∴AH＝AF，∴∠AFH＝∠H，∴∠CFD＝∠D，∴CD＝CF＝2，故答案为：2．【变式3】如图，在Rt△ABC中，∠BAC＝90°，点D是BC的中点，E是AB边上一点，DF⊥DE交AC于点F，连接EF，若BE＝2，CF＝，则EF的长为　．【解答】解：如图，延长FD到G使GD＝DF，连接GE，BG，在△BDG和△CDF中，，∴△BDG≌△CDF（SAS），∴BG＝CF＝，∠GBD＝∠C，∴BG∥CA，∴∠EBG＝∠A＝90°，∵BE＝2，∴EG＝＝＝，∵DF⊥DE，DF＝DG，∴EF＝EG＝，故答案为：．【变式4】如图，在矩形ABCD中，AB＝8，BC＝9，点E为AB的中点，点F在BC上，且BF＝2FC，AF 与DE，DB分别交于点G，H，求GH的长．【解答】解：如图，过点F作FM⊥AD于M，交ED于O，则FM＝AB＝8，∵BF＝2FC，BC＝9，∴BF＝AM＝6，FC＝MD＝3，∴AF＝＝＝10，∵OM∥AE，∴，∵点E为AB的中点，∴OM ＝，∴OF ＝FM ﹣OM ＝8﹣＝，∵AE ∥FO ，∴△AGE ∽△FGO ，∴＝，∴AG ＝＝，∴GH=10-4-415=49【变式5】如图，四边形ABCD 为平行四边形，点E ，F 分别为BC ，AB 上的点，且点F 为AB 的中点，连接DF ，DE ．（1）如图①，若DF 平分∠ADE ，求证：AD +BE ＝DE ；（2）如图②，若四边形ABCD 是边长为4的正方形，当ED 平分∠FDC 时，求EC 的长．【解答】（1）证明：延长DF ，CB 交于G ，如图：∵四边形ABCD 为平行四边形，∴AD ∥CB ，∴∠ADG ＝∠G ，∵DF 平分∠ADE ，∴∠ADG＝∠EDG，∴∠G＝∠EDG，∴DE＝GE＝GB+BE，∵F是AB中点，∴AF＝BF，在△ADF和△BGF中，，∴△ADF≌△BGF（AAS），∴AD＝GB，∴DE＝AD+BE；（2）解：延长AB，DE交于H，如图：∵四边形ABCD是边长为4的正方形，点F为AB的中点，∴DF＝＝＝2，AB∥CD，∴∠CDE＝∠H，∵ED平分∠FDC，∴∠CDE＝∠FDE，∴∠FDE＝∠H，∴FH＝DF＝2，∴BH＝FH﹣BF＝2﹣2，∵∠C＝90°＝∠HBE，∠DEC＝∠HEB，∴△DCE∽△HBE，∴＝，即＝，解得CE＝2﹣2．∴EC的长为2﹣2．【变式6】阅读下面材料，并按要求完成相应的任务．如图①，圆内接四边形的对角线AC⊥BD，垂足为G，过点G作AD的垂线，垂足为E，延长EG交BC于点F，则点F为BC的中点．下而是部分证明过程：∵AC⊥BD，EF⊥AD，∴∠EGD+∠FGC＝90°，∠EGD+∠EDG＝90°，∴∠EDG＝∠FGC．∵∠ADB＝∠ACB，…任务一：请将上述过程补充完整；任务二：如图②，在△ABC中，把边AC绕点C顺时针旋转90°得到DC，把边BC绕点C逆时针旋转90°得到EC．连接DE，取AB的中点M，连接MC并延长交DE于点N．（1）求证：MN⊥DE；（2）若AC＝4，AB＝6，∠CAB＝30°，求DE的长．【解答】解：任务一：∵AC⊥BD，EF⊥AD，∴∠EGD+∠FGC＝90°，∠EGD+∠EDG＝∴∠EDG＝∠FGC．∵∠ADB＝∠ACB，∴∠ACB＝∠CGF，∴CF＝FD，同理BF＝FG，∴BF＝CF，∴点F为BC的中点；任务二：（1）证明：延长CM到F使MF＝CM，∵AM＝MB，∴ACBF是平行四边形，∴AF＝BC＝CE，AF∥BC，∴∠CAF+∠ACB＝180°，∠DCE+∠ACB＝180°，∴∠CAF＝∠DCE，∵DC＝AC，∴△DCE≌△CAF（SAS），∴∠D＝∠ACF，∵∠ACF+∠DCN＝90°，∴∠D+∠DCN＝90°，∴∠DNC＝90°，∴MN⊥DE；（2）解：作CG⊥AB于G，∵∠CAB＝30，AC＝4，∴CG＝2，AG＝2，∵AM＝AB＝3，∴GM＝，∵CM2＝CG2+GM2，∴CM2＝22+（）2，∴CM＝，∵△DCE≌△CAF，∴DE＝CF＝2．类型二：截长补短【典例4】模型分析当题目中出现线段的和差关系时，考虑用截长补短法，该类题日中常出现等腰三角形、角平分线等关键词句，采用截长补短法进行证明．问题：如图，在△ABC中，AD平分∠BAC交BC于点D，且∠B＝2∠C，求证：AB+BD＝AC．截长法：在AC上截取AE＝AB，连接DE，证明CE＝BD即可．补短法：延长AB至点F，使AF＝AC，连接DF，证明BF＝BD即可．请结合右边的证明结论．求证：AB+BD＝AC．请结合右边的【模型分析】证明结论．求证：AB+BD＝AC．【截长法】【补短法】【解答】证明：【截长法】在AC上截取AE＝AB，连接DE，∵AD平分∠BAC，∴∠BAD＝∠DAC，在△ABD和△AED中，，∴△ABD≌△AED（SAS），∴∠B＝∠AED，BD＝DE，又∠B＝2∠C，∴∠AED＝2∠C，而∠AED＝∠C+∠EDC＝2∠C，∴∠C＝∠EDC，∴DE＝CE，∴AB+BD＝AE+CE＝AC．证明：【补短法】延长AB到F，使BF＝BD，连接DF，∵BF＝BD，∴∠F＝∠BDF，∴∠ABC＝∠F+∠BDF＝2∠F，且∠ABC＝2∠C，∴∠C＝∠F，且∠CAD＝∠BAD，AD＝AD，∴△ADF≌△ADC（AAS）∴AC＝AF，∴AC＝AF＝AB+BF＝AB+BD．【变式1】如图，△ABC为等边三角形，D为△ABC外一点，连接AD，BD，CD，∠ADB＝∠ADC＝60°，求证：AD＝BD+CD．【解答】证明：在DA上截取DE＝DB，连接BE，如下图所示，∵∠ADB＝60°，DE＝DB，∴△ABD为等边三角形，∴∠EBD＝60°，BE＝BD，∵△ABC为等边三角形，∴∠ABC＝60°，BA＝BC，∴∠EBD﹣∠EBC＝∠ABC﹣∠EBC，∴∠ABE＝∠CBD，在△ABE和△CBD中，，∴△ABE≌△CBD（SAS），∴AE＝CD，∴AD＝AE+ED＝CD+BD．【变式2】如图，Rt△ABC中，AC＝BC，AD平分∠BAC交BC于点D，CE⊥AD交AD于F点，交AB于点E．求证：AD＝2DF+CE．【解答】证明：在AF上截取FG＝DF，连接CG，则DG＝2DF，∵∠ACB＝90°，∴∠DCF+∠ACF＝90°，又∵CF⊥AD，∴∠ACF+∠CAF＝90°，∴∠DCF＝∠CAF，∵AD平分∠CAE，∴∠CAF＝∠EAF，∵DF＝FG，CF⊥DG，∴CD＝CG，∴∠CDG＝∠CGD，∵∠DGC＝∠GAC+∠ACG，∠ADC＝∠B+∠BAD，∴∠B＝∠ACG，又∵AC＝BC，∴△ACG≌△CBE（ASA），∴AG＝CE，∴AD＝AG+DG＝CE+2DF．【变式3】如图，△ABC内接于⊙O，AC＝BC，CD是⊙O的一条弦，且＝，过点A作AP⊥CD，分别交CD，⊙O于点E，P，连接BP，若CD＝6，△ABP的周长为13，求AE的长．【解答】解：在AE上截取AF＝BP，连接CF，PC，∵AC＝BC，∠CAF＝∠CBP，∴△CAF≌△CBP，CF＝CP，∵CD⊥PA，∴EF＝PE，∴AE＝AF+FE＝PB+PE，∵AC＝BC，∴＝，∵＝，∴＝，∴AB＝CD＝6，∵△ABP的周长是13，∴AP+PB＝7，∵AE＝PE+PB，∴2AE＝AP+PB，∴AE＝．【变式4】如图，在△ABC中，AB＝AC，在AB左侧作∠BDC＝∠BAC＝α，过点A作AE⊥DC于点E．（1）当α＝90°时，①求证：AE＝DE；②若BD＝AE＝2，请求出△ABC的面积；（2）当α≠90°时，求证：BD+DE＝EC．【解答】（1）①证明：过点B作BF⊥AE，交AE的延长线于点F，∵AE⊥CD，∴∠DEF＝90°，又∵∠BDE＝90°，∴四边形BDEF为矩形，∴DE＝BF，∵∠BAC＝90°，∴∠BAF+∠EAC＝90°，又∵∠EAC+∠ACE＝90°，∴∠BAF＝∠ACE，又∵∠AEC＝∠BFA＝90°，AB＝AC，∴△ABF≌△CAE（AAS），∴BF＝AE，∴DE＝AE；②解：∵四边形BDEF为矩形，BD＝AE＝2，∴BD＝EF＝2，DE＝BF＝AE＝，∴AF＝AE+EF＝+2，∴BA2＝BF2+AF2＝＝8+4，∴S＝＝；△ABC（2）证明：过点A作AF⊥BD，交BD的延长线于F，连接AD，设CD与AB交于点O，∵∠BDC＝∠BAC，∠BOD＝∠AOC，∴∠ACO＝∠DOB，即∠ABF＝∠ACE，又∵∠AEC＝∠AFB＝90°，AC＝AB，∴△ACE≌△ABF（AAS），∴AE＝AF，BF＝CE，又∵AD＝AD，∴Rt△ADE≌Rt△ADF（HL），∴DE＝DF，∴CE＝BF＝BD+DF＝BD+DE．【变式5】【问题背景】如图①，在边长为1的正方形ABCD中，点E为射线BC上的一个动点（与点B，C不重合），连接AE，过点E作EF⊥AE，与正方形ABCD的外角∠DCG的平分线交于点F．李老师指出，当点E为线段BC 的中点时，AE＝EF．【初步探索】（1）如图②，当点E在线段BC的延长线上时，其他条件不变，那么结论“AE＝EF”是否仍然成立；【问题解决】（2）当点E在线段BC上时，设BE＝x，△ECF的面积为y，求y与x之间的函数关系式；【拓展延伸】（3）如图③，将正方形ABCD放在平面直角坐标系xOy中，点O与点B重合，点C在x轴正半轴上，当点E运动到某一点时，点F恰好落在直线y＝﹣2x+3上，求此时点E的坐标．【解答】解：【问题背景】如图1，取AB的中点H，连接EH，∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝90°＝∠BCD，∵CF平分∠DCG，∴∠DCF＝45°，∴∠ECF＝135°，∵E是BC的中点，∴BH＝BE＝AH＝CE，∴∠BHE＝∠BEH＝45°，∴∠AHE＝∠ECF＝135°，∵AE⊥EF，∴∠AEB+∠FEC＝90°，∵∠AEB+∠BAE＝90°，∴∠FEC＝∠BAE，∴△AHE≌△ECF（ASA），∴AE＝EF；【初步探索】（1）仍然成立，理由如下：如图2，在BA的延长线上取一点N，使AN＝CE，连接NE．∵AB＝BC，AN＝CE，∴BN＝BE，∴∠N＝∠FCE＝45°，∵四边形ABCD是正方形，∴AD∥BE，∴∠DAE＝∠BEA，∴∠NAE＝∠CEF，在△ANE和△ECF中，，∴△ANE≌△ECF（ASA），∴AE＝EF；【问题解决】（2）如图3，在BA上截取BH＝BE，连接HE，同理得：△AHE≌△ECF，∴y＝S＝AH•BE＝x（1﹣x）＝﹣x2+x（0≤x≤1）；△AHE【拓展延伸】（3）如图4，在BA上截取BH＝BE，连接HE，过点F作FM⊥x轴于M，设点E（a，0），∴BE＝a＝BH，∴HE＝a，由（1）可得△AHE≌△ECF，∴CF＝HE＝a，∵CF平分∠DCM，∴∠DCF＝∠FCM＝45°，∵FM⊥CM，∴∠CFM＝∠FCM＝45°，∴CM＝FM＝a，∴BM＝1+a，∴点F（1+a，a），∵点F恰好落在直线y＝﹣2x+3上，∴a＝﹣2（1+a）+3，∴a＝，∴点E（，0）．【典例5】如图1，在Rt△ABC中，AB＝BC，点D，E，F分别在AB，BC，AC边上，且DE＝EF，∠DEF ＝∠B，∠A＝45°．（1）试猜想CF与BE之间的数量关系，并证明；（2）自主探究：如图2，若将已知条件中含45°的直角三角形换成含30°的直角三角形，其余条件不变，试探究BE和CF的关系．【解答】解：（1）CF与BE之间的数量关系为：CF＝BE．理由：过点F作FH⊥BC于点H，如图，∵Rt△ABC中，AB＝BC，∠A＝45°，∴∠C＝45°，∠B＝90°．∵∠DEF＝∠B，∴∠DEF＝90°，∴∠DEB+∠FEH＝90°．∵∠BDE+∠DEB＝90°，∴∠BDE＝∠FEH．在△BDE和△HEF中，，∴△BDE≌△HEF（AAS），∴BE＝FH．∵FH⊥BC，∠C＝45°，∴△FHC为等腰直角三角形，∴FC＝FH，∴FC＝BE；（2）CF与BE之间的数量关系为：CF＝BE．理由：过点F作FH⊥BC于点H，如图，∵Rt△ABC中，∠A＝30°，∴∠C＝60°，∠B＝90°．∵∠DEF＝∠B，∴∠DEF＝90°，∴∠DEB+∠FEH＝90°．∵∠BDE+∠DEB＝90°，∴∠BDE＝∠FEH．在△BDE和△HEF中，，∴△BDE≌△HEF（AAS），∴BE＝FH．∵FH⊥BC，∠C＝60°，∴sin60°＝，∴FC＝FH，∴FC＝BE．【变式1】如图，在△ABC中，∠ABC＝45°，AD⊥BC于点D，点F是AC上一点，连接BF交AD于点E，且DE＝CD，连接DF，若AF＝4，DF＝2，则BF的长为　．【解答】解：如图，在BF上截取HF＝AF，连接AH，∵∠ABC＝45°，AD⊥BC，∴AD＝BD，∠ADB＝∠ADC＝90°，在△BDE和△ADC中，，∴△BDE≌△ADC（SAS），∴∠EBD＝∠CAD，∵∠BED＝∠AEF，∴∠AFE＝∠BDE＝90°，∴∠AHF＝∠HAF＝45°，∴AH＝AF，∴∠BAH＝∠DAF，∠AHB＝135°，∠AEF＝∠BED，∠AFE＝∠BDE＝90°，∴△AFE∽△BDE，∴＝，∵∠AEB＝∠FED，∴△AEB∽△FED，∴∠EAB＝∠EFD＝45°，∴∠AFD＝∠AFH+∠EFD＝90°+45°＝135°，∴∠AHB＝∠AFD，∴△AHB∽△AFD，∴＝＝，∴BH＝DF，∴BF＝BH+HF＝DF+AF＝2+4．故答案为：2+4．【变式2】如图，四边形ABCD内接于⊙O，BC是⊙O的直径，连接AC，BD，若AB＝AC，请探究AD，BD，DC之间的数量关系．【解答】解：作AE⊥AD交BD于E，∵BC是直径，∴∠BAC＝90°，∵∠BAE+∠EAC＝∠DAC+∠EAC＝90°，∴∠BAE＝∠CAD，∵∠ABD＝∠ACD，AB＝AC，∴△ABE≌△ACD（SAS），∴BE＝CD，∵△AED是等腰直角三角形，∴DE＝AD，∵BD＝DE+BE，∴BD＝AD+CD．【变式3】如图，在△ABC中，∠ACB＝120°，BC＞AC，点E在BC上，点D在AB上，CE＝CA，连接DE，∠ACB+∠ADE＝180°，CH⊥AB，垂足为点H．求证：DE+AD＝2CH．【解答】证明：如图，作∠FCD＝∠ACB，交BA延长线于F，∵∠FCA+∠ACD＝∠ACD+∠DCB，∴∠FCA＝∠DCB，∵∠ACB＝120°，∠ACB+∠ADE＝180°，∴∠EDB＝120°，∠EDA＝60°，∵∠FAC＝120°+∠B，∠CED＝120°+∠B，∴∠FAC＝∠CED，在△AFC和△EDC中，，∴△AFC≌△EDC（ASA），∴AF＝DE，FC＝CD，∵CH⊥FD，∴FH＝HD，∠FCH＝∠HCD＝60°，∴DH＝CH，∵AD+DE＝AD+AF＝FD＝2DH＝2CH，∴AD+DE＝2CH．【变式4】如图，在△ABC中，AB＝AC，∠BAC＝90°，点D是平面内一点，且AD⊥CD．点O是BC的中点，连接OA，OD．（1）如图①，若点D是BC下方一点，过点O作OE⊥OD分别交AC，AD于点E，F．①求证：∠OAF＝∠OCD；②若CD＝1，DF＝2，求BC的长；（2）如图②，若点D是AC右侧一点，试判断AD，CD，OD之间的数量关系，并说明理由．【解答】（1）①证明：∵AB＝AC，O为BC的中点，∴OA＝OB＝OC，OA⊥OC，∵OE⊥OD，∴∠AOC＝∠EOD＝90°，∴∠AOF＝∠COD，∵∠AOM＝∠MDC＝90°，∠AMO＝∠CMD，∴∠OAM＝∠MCD，∴△OAF≌△OCD（ASA），∴∠OAF＝∠OCD；②解：∵△OAF≌△OCD，∴AF＝CD＝1，∵DF＝2，∴AD＝AF+DF＝1+2＝3，∵AD⊥DC，∴∠ADC＝90°，∴AC＝＝＝，∵AC＝AB，∴BC＝AC＝＝2；（2）解：AD+CD＝OD．理由：过点O作OE⊥OD，交DA的延长线于点E，∵∠DOE＝∠AOC＝90°，∴∠AOE＝∠COD，∵∠ODC+∠+ODA＝90°，∠ODA+∠OEA＝90°，∴∠ODC＝∠OEA，又∵OA＝OC，∴△OCD≌△OAE（AAS），∴CD＝AE，OD＝OE，∴DE＝OD，∴AD+AE＝AD+CD＝OD．【变式5】【问题探究】如图，△ABC是等腰三角形，AB＝AC，点D是平面内一点，连接AD，BD，CD，且∠CAB＝∠CDB．（1）如图①，当∠CAB＝60°时，试探究BD，CD，AD之间的数量关系；（2）如图②，当∠CAB＝120°时，探究是否为定值，并说明理由；【问题解决】（3）如图③，在四边形ADBC中，AB＝AC，∠CAB＝∠CDB＝120°，若AD＝2，BD＝3，求CD的长．【解答】解：（1）BD，CD，AD之间的数量关系为：BD＝CD+AD，理由如下：在BD上取一点E，使BE＝CD，连接AE，设AC交BD于H，如图①所示：∵∠CAB＝∠CDB，∠AHB＝∠CHD，∴∠ABE＝∠ACD，在△ABE和△ACD中，，∴△ABE≌△ACD（SAS），∴AD＝AE，∠DAC＝∠EAB，∴∠DAC+∠CAE＝∠EAB+∠CAE＝∠CAB＝60°，∴△ADE是等边三角形，∴DE＝AD，∴BD＝BE+DE＝CD+AD；（2）是定值，理由如下：在BD上取一点E，使BE＝CD，连接AE，设AC交BD于H，过点A作AF⊥BD于F，如图②所示：∵∠CAB＝∠CDB，∠AHB＝∠CHD，∴∠ABE＝∠ACD，在△ABE和△ACD中，，∴△ABE≌△ACD（SAS），∴AD＝AE，∠DAC＝∠EAB，∴∠DAC+∠CAE＝∠EAB+∠CAE＝∠CAB＝120°，∴∠ADE＝∠AED＝（180°﹣120°）＝30°，∵AF⊥DE，∴DF＝EF，AF＝AD，在Rt△AFD中，由勾股定理得：DF＝＝＝AD，∴DE＝2DF＝AD，∵DE＝BD﹣BE＝BD﹣CD，∴BD﹣CD＝AD，∴＝，∴是定值；（3）在CD上取一点E，使CE＝BD，连接AE，设AB交CD于H，过点A作AF⊥CD于F，如图③所示：∵∠CAB＝∠CDB，∠AHC＝∠BHD，∴∠ACE＝∠ABD，在△ACE和△ABD中，，∴△ACE≌△ABD（SAS），∴AE＝AD，∠EAC＝∠DAB，∴∠EAC+∠BAE＝∠DAB+∠BAE＝∠CAB＝120°，∴∠ADE＝∠AED＝（180°﹣120°）＝30°，∵AF⊥DE，∴DF＝EF，AF＝AD，在Rt△AFD中，由勾股定理得：DF＝＝＝AD，∴DE＝2DF＝AD，∴CD＝CE+DE＝BD+AD＝3+×2＝3+2．。

初中数学几何模型之倍长中线模型

数学模型-倍长中线模型模型分析：倍长中线主要用于证明全等三角形，其主要是在全等三角形的判定过程中，给出中线，通过延长辅助线的方法证明三角形全等及其他，达到解题的目的．其主要的图形特征和证明方法如下图：已知：在三角形ABC 中，O 为BC 边中点，辅助线：延长AO 到点D 使AO=DO ，结论：△AOB ≌△DOC证明：延长AO 到点D 使AO=DO ，由中点可知，OB=OC ，在△AOB 和△DOC 中OA ODAOB DOC OB OC=⎧⎪∠=∠⎨⎪=⎩∴△AOB ≌△DOC同理下图中仍能得到△AOB ≌△DOC规律总结：由倍长中线法证明三角形全等的过程一般均是用SAS 的方法，这是由于作出延长线后出现的对顶角决定的．补充：关于倍长中线的其他模型①向中线做垂直，易证△BEO ≌△CDO步骤：延长AO 到点D ，过点B ，C 分别向AD 作垂线，垂足为E ，D ，易证△BEO ≌△CDO(AAS)②过中线做任意三角形证明全等，易证△BDO ≌△CEO步骤：AC 上任意选取一点E ，连接EO 并延长到点D ，使EO=DO ，连接BD ，易证△BDO ≌△CEO(SAS)实例精练：1. 如图，在平行四边形ABCD 中，28CD AD ==，E 为AD 上一点，F 为DC 的中点，则下列结论中正确的是（）A. 4BF =B. 2ABC ABF ∠>∠C. ED BC EB +=D. 2DEBC EFB S S =四边形【答案】D【解析】【分析】根据平行四边形的性质可以得到228CD AD BC ===，且F 为DC 的中点，所以4CF BC ==,由此可判断A 选项；再结合平行线的性质可以得到CFB FBA ∠=∠，由此可判断B 选项；同时延长EF 和BC 交于点P ，,,DF CF DFE PFC D FCP =∠=∠∠=∠ 可以证得DFE CFP ≅，所以ED BC CP BC BP +=+= 由此可以判断C 选项；由于DFE CFP ≅，所以BEP DEBC S S =四边形，由此可以判断D 选项；【详解】四边形ABCD 是平行四边形∴ 228CD AD BC ===∴ 4CF BC ==由于条件不足，所以无法证明4BF =,故A 选项错误；4CF BC ==∴ CFB FBC ∠=∠DC AB ∥∴ CFB FBC FBA ∠=∠=∠∴ 2ABC ABF ∠=∠故B 选项错误；同时延长EF 和BC 交于点PAD BP∴ D FCP ∠=∠∴ 在DFE △和CFP 中：()DF CF DFE PFC D FCP ASA ⎧=⎪∠=∠⎨⎪∠=∠⎩∴ DFE CFP ≅∴ ED BC CP BC BP +=+=由于条件不足，并不能证明BP BE =，故C 选项错误；DFE CFP ≅∴ BEP DEBC S S =四边形F 为DC 的中点∴ 2BEP BEF DEBC S S S ==四边形故D 选项正确；故选：D.【点睛】本题主要考查平行四边形的性质，以及全等三角形的判定，根据题意作出相应的辅助线是求解本题的关键.2. 如图，901,2,AB CD BCD AB BC CD E ∠=︒===，，为AD 上的中点，则BE ＝______．【解析】【分析】延长BE 交CD 于点F ，证ABE DFE ≌，则BE=EF=12BF ，故再在直角三角形BCF 中运用勾股定理求出BF 长即可.【详解】解：延长BE 交CD 于点F∵AB 平行CD ，则∠A=∠EDC ，∠ABE=∠DFE ，又E 为AD 上的中点，∴BE=EF,所以ABE DFE ≌. ∴1,12BE EF BF AB DF ==== ∴1CF =在直角三角形BCF 中，∴12BE BF ==. 【点睛】本题的关键是作辅助线，构造三角形全等，找到线段的关系，然后运用勾股定理求解.3. 如图，ABC ∆中，D 为BC 的中点，E 是AD 上一点，连接BE 并延长交AC 于F ，BE AC =，且9BF =，6CF =，那么AF 的长度为__．【答案】32；【解析】【分析】延长AD 至G 使AD DG =，连接BG ，得出ACD GBD ∆≅∆ 得出AC BG BE ==，所以得出AEF ∆是等腰三角形，根据已知线段长度建立等量关系计算．【详解】如图：延长AD 至G 使AD DG =，连接BG在ACD ∆和GBD ∆中：CD BD ADC BDG AD DG =⎧⎪∠=∠⎨⎪=⎩∴ACD GBD ∆≅∆∴,CAD G AC BG ∠=∠=∵BE AC =∴BE BG =∴G BEG ∠=∠∵BEG AEF ∠=∠∴AEF EAF ∠=∠∴EF AF =∴AF CF BF EF +=-即69AF EF +=- ∴32AF = 【点睛】倍长中线是常见的辅助线、全等中相关的角的代换是解决本题的关键． 4. 如图，平行四边形ABCD 中，CE AD ⊥于E ，点F 为边AB 中点，12AD CD =，40CEF ∠=︒，则AFE ∠=_________【答案】30【解析】【分析】延长EF 、CB 交于点G ，连接FC ，先依据全等的判定和性质得到FE FG =，依据直角三角形斜边上的中线等于斜边的一半，得到FC FE FG ==，依据平行四边形的对边相等及等量代换得到BF BC =，依据三角形等边对等角得到50FCG G ∠=∠=︒、50BFC FCG ∠=∠=︒，依据三角形内角和得到GFC ∠，通过作差即得所求.【详解】解：延长EF 、CB 交于点G ，连接FC ，∵平行四边形ABCD 中，∴//AD BC ，AB CD =,AD BC =,∴A GBF ∠=∠，AFE BFG ∠=∠，90GCE CED ∠==︒又∵点F 为边AB 中点，得12A FB A BF ==, ∴AFE △≌BFG (ASA)，0509C G EF ∠∠-==︒︒，∴FE FG =，∴FC FE FG ==，∴50FCG G ∠=∠=︒,∴18080GFC FCG G ∠=︒-∠-∠=︒, ∵12BF AB =,12AD CD = AB CD =,AD BC =, ∴BF BC =,∴50BFC FCG ∠=∠=︒,∴30BFG GFC BFC ∠=∠-∠=︒,∴30BFG AFE ∠∠==︒,故答案为：30.【点睛】本题考查了平行四边形的性质、全等的判定和性质、直角三角形斜边上的中线等于斜边的一半、三角形等边对等角、三角形内角和，解题的关键是构造直角三角形.5. 已知：如图所示，AD平分BAC，M是BC的中点，MF//AD，分别交CA延长线，AB于F、E．求证：BE=CF．【答案】见解析.【解析】【分析】过B作BN∥AC交EM延长线于N点，易证△BMN≌△CMF，可得CF＝BN，然后由MF//AD，AD平分∠BAC可得∠F＝∠DAC=∠BAD＝∠BEM，∠BEM ＝∠N，所以BE＝BN＝CF.【详解】证明：过B作BN∥AC交EM延长线于N点，∵BN∥AC，BM＝CM，∴∠BMN＝∠CMF，∠N＝∠F，∴△BMN≌△CMF，∴CF＝BN，又∵MF//AD，AD平分∠BAC，∴∠F＝∠DAC=∠BAD＝∠BEM，∴∠BEM＝∠N，∴BE＝BN＝CF.【点睛】本题考查了角平分线的定义，平行线的性质，全等三角形的判定和性质等知识，作辅助线构造出等腰三角形是解题的关键，也是本题的难点．6. 如图所示，在ABC ∆中，AD 交BC 于点D ，点E 是BC 中点，EF AD ∥交CA 的延长线于点F ，交AB 于点G ，若BG CF =，求证：AD 为BAC ∠的平分线.【答案】见解析【解析】【分析】延长FE ，截取EH =EG ，连接CH ，可证∴BEG ≌△CEH ，即可求得∠F =∠FGA ，即可求得∠CAD =∠BAD ，即可解题．【详解】证明：延长FE ，截取EH =EG ，连接CH ，∵E 是BC 中点，∴BE =CE ，∴∠BEG =∠CEH ，在∴BEG 和∴CEH 中，BE CE BEG CEH GE EH ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△BEG ≌△CEH （SAS ），∴∠BGE =∠H ，∴∠BGE =∠FGA =∠H ，∴BG =CH ，∵CF =BG ，∴CH =CF ，∴∠F =∠H =∠FGA ，∵EF ∥AD ，∴∠F =∠CAD ，∠BAD =∠FGA ，∴∠CAD =∠BAD ，∴AD 平分∠BAC ．【点睛】本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证∴BEG ≌△CEH 是解题的关键．7. 已知：如图所示，在ABC ∆中，AD 为中线，BF 交,AD AC 分别于,E F ，如果BE AC =，求证：AF EF = ．【答案】详见解析【解析】【分析】根据点D 是BC 的中点，延长AD 到点G ，得到BDE CDG ∆∆≌，利用全等三角形的对应角相等，对应边相等进行等量代换，得到△AEF 中的两个角相等，然后用等角对等边证明AE 等于EF ．【详解】证明：延长ED 至G ，使DG DE =，连结GC ，∵在ABC ∆中，AD 为中线，∴BD=CD ，在△ADC 和△GDB 中，BD CD BDE CDG DE DG =⎧⎪∠=∠⎨⎪=⎩∴BDE CDG ∆∆≌，BE CG ∴=，BED CGD ∠=∠，BE AC =，AC GC ∴=，AGC CAG ∴∠=．又BED AEF ∠=∠，∴AEF EAF ∠=∠，∴AF EF =.【点睛】本题考查全等三角形的判定与性质，解题的关键是通过作辅助线构建全等三角形．8. 如图所示，AD 为ABC ∆的角平分线，,E F 分别在,BD AD 上，DC DE =，若EF AB ∥．求证：EF AC =．【答案】详见解析【解析】【分析】延长FD 至G ，使DG DF =，连结CG ，可证DEF DCG ∆∆≌，则EF=CG ，利用全等三角形和角平分线以及平行线的性质可得GAC AGC ∠=∠ ，根据等角对等边得AC=CG ，即可得出结论.【详解】证明：延长FD 至G ，使DG DF =，连结CG ，∵DC=DE ，∠EDF=∠CDG ，DG DF =∴DEF DCG ∆∆≌，EF CG ∴=，EFG CGD ∠=∠EF AB ∥，EFG BAD ∴∠=∠，又BAD CAD ∠=∠，GAC AGC ∴∠=∠，AC GC ∴=，EF AC ∴=.【点睛】本题考查全等三角形的判定和性质，关键是证△EDF 与△CDG 全等． 9. 如图所示，在ABC ∆中，AD 为中线，90,2BAD AB AD ∠==，求DAC ∠的度数．【答案】45°【解析】【分析】延长AD 至E ，使DE AD =，连结CE ，则ADB EDC ∆∆≌，根据全等三角形的性质得EC=AB ，90E BAD ∠=∠=︒，由AB=2AD 可得EC=AE ，可得△AEC 是等腰直角三角形，即可得∠DAC 的度数．【详解】解：延长AD 至E ，使DE AD =，连结CE ，∵BD=CD ，∠ADB=∠EDC∴ADB EDC ∆∆≌，∴EC=AB ，90E BAD ∠=∠=︒，∵AB=2AD ，DE AD =∴AB=AE=EC∴△AEC 是等腰直角三角形，∴∠DAC=45°.故答案为45°.【点睛】本题考查全等三角形的判定与性质等腰直角三角形的性质，解题的关键是作辅助线构建全等三角形和等腰直角三角形.10. 已知：如图，在ABC ∆中，90C ∠=︒，D 为AB 的中点，E 、F 分别在AC 、BC 上，且ED FD ⊥于D .求证：222AE BF EF +=.【答案】详见解析【解析】【分析】通过倍长线段DE ，将AE 、BF 、EF 转化到BGF ∆中，再证BGF ∆为直角三角形.=，连结BG、FG，【详解】延长ED至G，使DG DE∠=∠，=，ADE BDGAD BD∴∆≅∆，ADE BDG∴=，A DBG∠=∠，AE BG∴，AC BG∴∠=︒，FBGC FBG180∴∠+∠=︒，90222∴+=，BG BF GF=，又ED FD⊥，ED GD∴=，EF GF222∴+=.AE BF EF【点睛】本题考查了全等三角形判定与性质，勾股定理，正确添加辅助线，熟练掌握相关知识是解题的关键.11. 阅读下面材料：数学课上，老师给出了如下问题：如图，AD为△ABC中线，点E在AC上，BE交AD于点F，AE＝EF．求证：AC ＝BF．经过讨论，同学们得到以下两种思路：以进一步证得∠G＝∠F AE＝∠AFE＝∠BFG，从而证明结论．思路二如图∴，添加辅助线后并利用AE＝EF可证得∠G＝∠BFG＝∠AFE＝∠F AE，再依据AAS可以进一步证得△ADC≌△GDB，从而证明结论．（1）∴思路一的辅助线的作法是：；∴思路二的辅助线的作法是：．（2）请你给出一种不同于以上两种思路的证明方法（要求：只写出辅助线的作法，并画出相应的图形，不需要写出证明过程）．【答案】（1）∴延长AD至点G，使DG＝AD，连接BG；∴作BG＝BF交AD的延长线于点G；（2）详见解析【解析】【分析】（1）∴依据SAS可证得△ADC≌△GDB，再利用AE＝EF可以进一步证得∠G＝∠F AE＝∠AFE＝∠BFG，从而证明结论．∴作BG＝BF交AD的延长线于点G．利用AE＝EF可证得∠G＝∠BFG＝∠AFE＝∠F AE，再依据AAS可以进一步证得△ADC≌△GDB，从而证明结论．（2）作BG∥AC交AD的延长线于G，证明△ADC≌△GDB（AAS），得出AC＝BG，证出∠G＝∠BFG，得出BG＝BF，即可得出结论．【详解】解：（1）∴延长AD至点G，使DG＝AD，连接BG，如图∴，理由如下：∵AD为△ABC中线，∴BD＝CD，在△ADC和△GDB中，=AD DGADC GD CD BDB ⎧=∠⎪∠⎪⎨⎩＝，∴△ADC≌△GDB（SAS），∴AC＝BG，∵AE＝EF，∴∠CAD＝∠EF A，∵∠BFG＝∠G，∠G＝∠CAD，∴∠G＝∠BFG，∴BG＝BF，∴AC＝BF．故答案为：延长AD至点G，使DG＝AD，连接BG；∴作BG＝BF交AD的延长线于点G，如图∴．理由如下：∵BG＝BF，∴∠G＝∠BFG，∵AE＝EF，∴∠EAF＝∠EF A，∵∠EF A＝∠BFG，∴∠G＝∠EAF，在△ADC和△GDB中，CAD GADC GCD BDDB ⎧⎪⎨⎪=⎩∠∠∠∠＝＝，∴△ADC≌△GDB（AAS），∴AC＝BG，∴AC＝BF；故答案为：作BG＝BF交AD的延长线于点G；（2）作BG∥AC交AD的延长线于G，如图∴所示：则∠G＝∠CAD，∵AD为△ABC中线，∴BD＝CD，在△ADC和△GDB中，CAD GADC GCD BDDB ⎧⎪⎨⎪=⎩∠∠∠∠＝＝，∴△ADC≌△GDB（AAS），∴AC＝BG，∵AE＝EF，∴∠CAD＝∠EF A，∵∠BFG＝∠EF A，∠G＝∠CAD，∴∠G＝∠BFG，∴BG＝BF，∴AC＝BF．【点睛】本题主要考查全等三角形的判定和性质、等腰三角形的性质、其中一般证明两个三角形全等共有四个定理：AAS、ASA、SAS、SSS，需要同学们灵活运用，解题的关键是学会做辅助线解决问题．12. 阅读∴1）阅读理解：如图①，在△ABC中，若AB=10∴AC=6，求BC边上的中线AD的取值范围．解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE（或将△ACD 绕着点D逆时针旋转180°得到△EBD），把AB∴AC∴2AD集中在△ABE中，利用三角形三边的关系即可判断．中线AD的取值范围是________∴∴2）问题解决：如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D∴DE交AB于点E∴DF交AC于点F，连接EF，求证：BE+CF∴EF∴∴3）问题拓展：如图③，在四边形ABCD中，∠B+∠D=180°∴CB=CD∴∠BCD=140°，以C为顶点作一个70°角，角的两边分别交AB∴AD于E∴F两点，连接EF，探索线段BE∴DF∴EF之间的数量关系，并加以证明．【答案】∴1∴2∴AD∴8∴∴2）证明见解析；（3∴BE+DF=EF；理由见解析.【解析】（1）延长AD至E，使DE=AD，由SAS证明∴ACD∴∴EBD，得出BE=AC=6，【分析】在∴ABE中，由三角形的三边关系求出AE的取值范围，即可得出AD的取值范围；（2）延长FD至点M，使DM=DF，连接BM、EM，同（1）得∴BMD∴∴CFD，得出BM=CF，由线段垂直平分线的性质得出EM=EF，在∴BME中，由三角形的三边关系得出BE+BM＞EM即可得出结论；（3）延长AB至点N，使BN=DF，连接CN，证出∴NBC=∴D，由SAS证明∴NBC∴∴FDC，得出CN=CF，∴NCB=∴FCD，证出∴ECN=70°=∴ECF，再由SAS 证明∴NCE∴∴FCE，得出EN=EF，即可得出结论．【详解】（1）解：延长AD至E，使DE=AD，连接BE，如图∴所示：∴AD是BC边上的中线，∴BD=CD，在∴BDE和∴CDA中，BD=CD，∴BDE=∴CDA，DE=AD，∴∴BDE∴∴CDA（SAS），∴BE=AC=6，在∴ABE中，由三角形的三边关系得：AB﹣BE＜AE＜AB+BE，∴10﹣6＜AE＜10+6，即4＜AE＜16，∴2＜AD＜8；故答案为2＜AD＜8；（2）证明：延长FD至点M，使DM=DF，连接BM、EM，如图∴所示：同（1）得：∴BMD∴∴CFD（SAS），∴BM=CF，∴DE∴DF，DM=DF，∴EM=EF，在∴BME中，由三角形的三边关系得：BE+BM＞EM，∴BE+CF＞EF；（3）解：BE+DF=EF；理由如下：延长AB至点N，使BN=DF，连接CN，如图3所示：∴∴ABC+∴D=180°，∴NBC+∴ABC=180°，∴∴NBC=∴D，在∴NBC和∴FDC中，BN=DF，∴NBC =∴D，BC=DC，∴∴NBC∴∴FDC（SAS），∴CN=CF，∴NCB=∴FCD，∴∴BCD=140°，∴ECF=70°，∴∴BCE+∴FCD=70°，∴∴ECN=70°=∴ECF，在∴NCE和∴FCE中，CN=CF，∴ECN=∴ECF，CE=CE，∴∴NCE∴∴FCE（SAS），∴EN=EF，∴BE+BN=EN，∴BE+DF=EF．考点：全等三角形的判定和性质；三角形的三边关系定理.13. 如图，在∴ABC中，AB=AC，D为线段BC的延长线上一点，且DB=DA，BE∴AD于点E，取BE的中点F，连接AF．(1)若，求BE的长；(2)在（1）的条件下，如果∴D=45°，求∴ABD的面积．(3)若∴BAC=∴DAF，求证：2AF=AD；【答案】（1）（2）9；（3）见详解【解析】【分析】（1）在Rt △AEB 中，利用勾股定理即可解决问题；（2）由∠D ＝45°可证得BE ＝DE ，再利用三角的面积公式计算即可；（3）如图，延长AF 至M 点，使AF ＝MF ，连接BM ，首先证明△AEF ≌△MFB ，再证明△ABM ≌△ACD 即可．【详解】（1）解：∵AB ＝AC ，AC∴AB∵BE ⊥AD ，AE，∴在Rt △AEB中，BE ===；（2）解：∵BE ⊥AD ，∠D ＝45°，∴∠EBD ＝∠D ＝45°，∴BE ＝DE＝∴AD ＝AE+DE=∴11922ABD S AD BE =⋅=⨯=；（3）证明：如图，延长AF 至M 点，使AF ＝MF ，连接BM ，∵点F 为BE 的中点，∴EF ＝BF ，在△AEF 和△MBF 中，AF FM AFE BFM EF BF =⎧⎪∠=∠⎨⎪=⎩∴△AEF ≌△MBF （SAS ），∴∠F AE ＝∠FMB ，∴AE ∥MB ，∴∠EAB +∠ABM ＝180°，∴∠ABM ＝180°﹣∠BAD ，又∵AB ＝AC ，DB ＝DA ，∴∠ABC ＝∠ACB ＝∠BAD ，∴∠ACD ＝180°﹣∠ACB ，∴∠ABM ＝∠ACD ．又∵∠BAC ＝∠DAF ，∴∠BAC ﹣∠MAC ＝∠DAF ﹣∠MAC ，∴∠1＝∠2．在△ABM 和△ACD 中，12AB ACABM ACD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABM ≌△ACD （ASA ），∴AM ＝AD ，又∴AM ＝AF +MF ＝2AF ，∴2AF ＝AD ．【点睛】本题考查全等三角形的判定和性质、等腰三角形的性质、勾股定理等知识，解题的关键是中线延长一倍，作出正确的辅助线构造全等三角形，属于常考题型．14. 阅读材料，解答下列问题．如图1，已知△ABC 中，AD 为中线．延长AD 至点E ，使 DE =AD ．在△ADC 和△EDB 中，AD =DE ，∠ADC =∠EDB ，BD =CD ，所以，△ACD ≌△EBD ，进一步可得到AC =BE ，AC //BE 等结论．在已知三角形的中线时，我们经常用“倍长中线”的辅助线来构造全等三角形，并进一步解决一些相关的计算或证明题．解决问题：如图2，在△ABC 中，AD 是三角形的中线，点F 为AD 上一点，且BF =AC ，连结并延长BF 交AC 于点E ，求证：AE =EF ．【答案】详见解析【解析】【分析】延长AD 到M ，使DM=AD ，连接BM ，根据SAS 推出△BDM ≌△CDA ，根据全等三角形的性质得出BM=AC ，∠CAD=∠M ，根据BF=AC 可得BF=BM ，推出∠BFM=∠M ，求出∠AFE=∠EAF 即可．【详解】如图，延长AD 至点M ，使得MD AD =，并连结BM ，∵AD 是三角形的中线，∴BD CD =，在MDB △和ADC △中，,,,BD CD BDM CDA DM DA =⎧⎪∠=∠⎨⎪=⎩∴MDB ADC △≌△，∴AC MB =，BMD CAD ∠=∠，∵BF AC =，∴BF BM =，∴BMD BFD ∠=∠，∵BFD EFA ∠=∠，BMD CAD ∠=∠，∴EFA EAF ∠=∠，即AE EF =．【点睛】本题考查了全等三角形的性质和判定，等腰三角形的性质和判定的应用，主要考查学生的运用性质进行推理的能力，关键是能根据“倍长中线”法作出辅助线来构造全等三角形．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

For personal use only in study and research; not for
commercial use

全等三角形的构造方法---常用辅助线
搞清了全等三角形的证题思路后，还要注意一些较难的一些证明问题，只要构造合适的
全等三角形，把条件相对集中起来，再进行等量代换，就可以化难为易了．下面举例说明几
种常见的构造方法，供同学们参考．

(一)倍长中线法:
题中条件若有中线，可延长一倍，以构造全等三角形，从而将分散条件集中在一个三
角形内。

例1．如图（1）AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF．
求证：AC=BF
证明：延长AD至H使DH=AD，连BH，∵BD=CD，
∠BDH=∠ADC，DH=DA，
∴△BDH≌△CDA，∴BH=CA，∠H=∠DAC，又∵AE=EF，
∴∠DAC=∠AFE，∵∠AFE=∠BFD，∴∠AFE= 图（1）
∠BFD=∠DAC=∠H，∴BF=BH，∴AC=BF．

小结：涉及三角形中线问题时，常采用延长中线一倍的办法，即倍长中线法。它
可以将分居中线两旁的两条边AB、AC和两个角∠BAD和∠CAD集中于同一个
三角形中，以利于问题的获解。

中线一倍辅助线作法
△ABC中方式1：延长AD到E，
AD是BC边中线使DE=AD，
连接BE
方式2：间接倍长

作CF⊥AD于F，延长MD到N，
作BE⊥AD的延长线于E 使DN=MD，
连接BE 连接CD

D
A
B
C

E
D

A
B
C

F
E
D
C
B

N
D
C
B

A
M

E
A
B
C
D

H
例2、△ABC中，AB=5，AC=3，求中线AD的取值范围
例3、已知在△ABC中，AB=AC，D在AB上，E在AC的延长线上，DE交BC于F，且
DF=EF，求证：BD=CE

课堂练习：已知在△ABC中，AD是BC边上的中线，E是AD上一点，且BE=AC，延长
BE交AC于F，求证：AF=EF

例4、已知：如图，在ABC中，ACAB，D、E在BC上，且DE=EC，过D作
BADF//
交AE于点F，DF=AC.
求证：AE平分BAC

课堂练习：已知CD=AB，∠BDA=∠BAD，AE是△ABD的中线，求证：∠C=∠BAE

F
E

B
C

第 1 题图
A
B
F
D
E
C

ED
A
B
C
作业：
1、在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线
相交于点F。试探究线段AB与AF、CF之间的数量关系，并证明你的结论

2、已知：如图，ABC中，C=90，CMAB于M，AT平分BAC交CM于D，交BC
于T，过D作DE//AB交BC于E，求证：CT=BE.

4：已知CD=AB，∠BDA=∠BAD，AE是△ABD的中线，求证：∠C=∠BAE
5、在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE=∠EAF，AF与DC的延长线
相交于点F。试探究线段AB与AF、CF之间的数量关系，并证明你的结论

F
E
A
B
C

D A B
C

T
E

ED
A
B
C

F
E
A
B
C

D
仅供个人用于学习、研究；不得用于商业用途。
For personal use only in study and research; not for commercial use.
Nur für den persönlichen für Studien, Forschung, zu kommerziellen Zwecken verwendet werden.
Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.
только для людей, которые используются для обучения, исследований и не должны
использоваться в коммерческих целях.

以下无正文
仅供个人用于学习、研究；不得用于商业用途。
For personal use only in study and research; not for commercial use.
Nur für den persönlichen für Studien, Forschung, zu kommerziellen Zwecken verwendet werden.
Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.
только для людей, которые используются для обучения, исследований и не должны
использоваться в коммерческих целях.

以下无正文
For personal use only in study and
research; not for commercial use