已知两同方向同频率的简谐振动的运动方程
大学物理振动与波练习题与答案
【解】:(1) y 5cos(20 4x) 厘米
(2) y 5cos(3t 11) 厘米
(3) y 5cos3(t 4 x 5) , c 3 (cm/ s)
33
4
(4) y 5cos(3t 9) , yI 15 sin(3t 9) 0
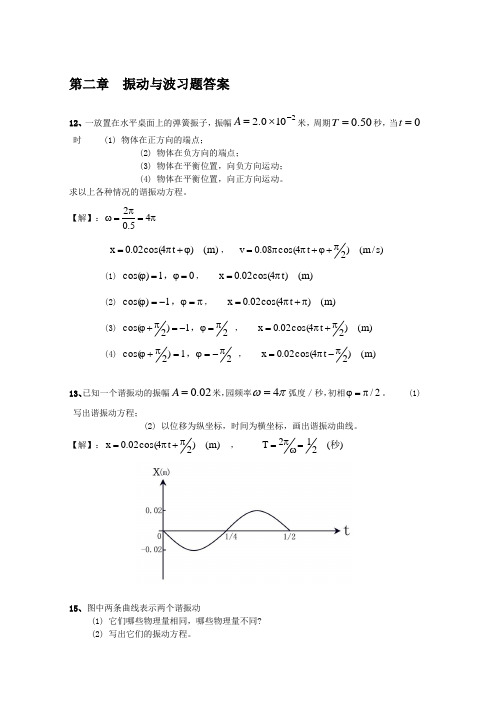
23、一平面简谐波沿 x 轴正方向传播,波速 c=8 m/s, 若 t=0 时的波形曲线如图 2-23 所示 (1)写出波动方程 (2)画出 t=1.25 s 时的波形曲线 【解】:
t=0 时,y=0, v>0 cm T=5s
所以 2 。 波长= 40
y 4.0 cos[0.4t ] (cm) 2
B 点的振动方程
yA
(t)
5 c os [10
(t
20) 300
2
]
5 c os (10t
7 6
)cm
(2)
A,B 相位相同
(3) 或 O 点的振动方程
yo
(t)
5
cos(10t
2
)
(cm)
O 点相位
o
2
OB,OA 间的相位差
oA
oB
2 3
O 比 A 超前
oA
o
A
2 3
A
7 6
同时 B 点
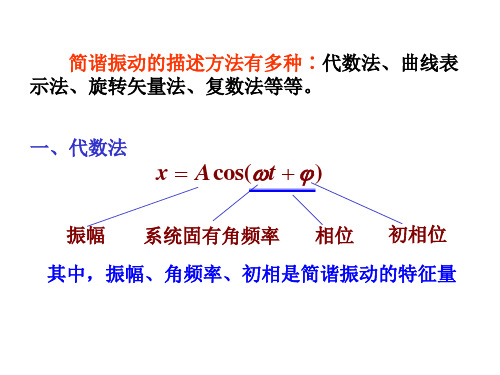
13、已知一个谐振动的振幅 A 0.02 米,园频率 4 弧度/秒,初相 / 2 。 (1)
写出谐振动方程; (2) 以位移为纵坐标,时间为横坐标,画出谐振动曲线。
【解】: x 0.02cos(4 t 2) (m) ,
T
2
1 2
简谐振动 旋转矢量法
2 1 2k π (k 0 , 1, 2,)
x
x
A
A2
A1
o
o
T
t
A A 1 A 2
A A A 2 A1 A2 cos( 2 1 ) 2)相位差 2 1 (2k 1)π (k 0 , 1, )
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M
A
P x
注意:旋转矢量在第 2 象限 速度v < 0
M P
A
x
注意:旋转矢量在第 2 象限 速度v < 0
M
P
A
x
注意:旋转矢量在第 3 象限 速度v 0
P M
A
<
x
注意:旋转矢量在第 3 象限 速度v 0
P x M
A
<
注意:旋转矢量在第 3 象限 速度v 0
( 1) 2 1 0, 称同相; (2) 2 1 , 称反相; (3) 2 1 0, 称振动2超前, 振动1落后; (4) 1 2 0, 称振动1超前, 振动2落后.
对于沿 x 轴振动的两个同频率的简谐振动:
用旋转矢量表示相位关系 同相位 反相位
对应关系
t
用旋转矢量图画简谐运动的
x t
图
T 2π (旋转矢量旋转一周所需的时间)
A
P
M
x
注意:旋转矢量在第 1 象限 速度v < 0
A
P
M
x
注意:旋转矢量在第 1 象限 速度v < 0
A
P
M x
普通物理学第十章 机械振动试题
第十章机械振动一、是非题1.简谐振动的能量与频率的平方成正比。
···········································()2.两个简谐振动的合振动仍然是一周期性振动。
·····································()3.两个简谐振动的合振动的振幅仅决定于两个分振动的振幅,与其他因素无关。
··········()4.物体作简谐振动,其动能随时间作周期性变化。
····································()6.两个同方向同频率简谐振动的合振动振幅在其相位差为π的奇数倍时取最小值。
大学物理振动波动例题习题

振动波动一、例题(一)振动1。
证明单摆是简谐振动,给出振动周期及圆频率.2. 一质点沿x 轴作简谐运动,振幅为12cm,周期为2s 。
当t = 0时, 位移为6cm ,且向x 轴正方向运动。
求: (1) 振动表达式;(2) t = 0.5s 时,质点的位置、速度和加速度;(3)如果在某时刻质点位于x =—0.6cm ,且向x 轴负方向运动,求从该位置回到平衡位置所需要的时间。
3。
已知两同方向,同频率的简谐振动的方程分别为:x 1= 0.05cos (10 t + 0.75π) 20.06cos(100.25)(SI)x t π=+求:(1)合振动的初相及振幅.(2)若有另一同方向、同频率的简谐振动x 3 = 0。
07cos (10 t +ϕ 3 ), 则当ϕ 3为多少时 x 1 + x 3 的振幅最大?又ϕ 3为多少时 x 2 + x 3的振幅最小?(二)波动1. 平面简谐波沿x 轴正方向传播,振幅为2 cm ,频率为 50 Hz ,波速为 200 m/s.在t = 0时,x = 0处的质点正在平衡位置向y 轴正方向运动,求:(1)波动方程(2)x = 4 m 处媒质质点振动的表达式及该点在t = 2 s 时的振动速度。
2. 一平面简谐波以速度m/s 8.0=u 沿x 轴负方向传播.已知原点的振动曲线如图所示.求:(1)原点的振动表达式;(2)波动表达式;(3)同一时刻相距m 1的两点之间的位相差.3. 两相干波源S 1和S 2的振动方程分别是1cos y A t ω=和2cos(/2)y A t ωπ=+.S 1距P 点3个波长,S 2距P 点21/4个波长。
求:两波在P 点引起的合振动振幅。
4。
沿X 轴传播的平面简谐波方程为:310cos[200(t )]200x y π-=- ,隔开两种媒质的反射界面A 与坐标原点O 相距2。
25m ,反射波振幅无变化,反射处为固定端,求反射波的方程.二、习题课(一)振动1. 一质点在x 轴上作简谐振动,振辐A = 4 cm,周期T = 2 s ,其平衡位置取作坐标原点.若t = 0时刻质点第一次通过x = -2 cm 处,且向x 轴负方向运动,则O 2.25m Ax t O A/2 -A x 1 x 2 质点第二次通过x = -2 cm 处的时刻为[ ](A) 1 s (B) (2/3) s (C ) (4/3) s (D ) 2 s2.已知某简谐振动的振动曲线如图所示,则此简谐振动的振动方程为(A ) ⎪⎭⎫ ⎝⎛+=3232cos 2ππt x ;(B ) ⎪⎭⎫ ⎝⎛-=332cos 2ππt x ;(C) ⎪⎭⎫ ⎝⎛+=3234cos 2ππt x ;(D ) ⎪⎭⎫ ⎝⎛-=334cos 2ππt x 。
大学物理A第九章 简谐振动

第九章 简谐振动一、填空题(每空3分)9-1 质点作简谐振动,当位移等于振幅一半时,动能与势能的比值为 ,位移等于 时,动能与势能相等。
(3:1,22A ±)9-2两个谐振动方程为()120.03cos (),0.04cos 2()x t m x t m ωωπ==+则它们的合振幅为 。
(0.05m )9-3两个同方向同频率的简谐振动的表达式分别为X 1=6.0×10-2cos(T π2t+4π) (SI) , X 2=4.0×10-2cos(T π2t -43π) (SI) ,则其合振动的表达式为______(SI).( X=2.0×10-2cos(T π2t+4π) (SI)) 9-4一质点作周期为T 、振幅为A 的简谐振动,质点由平衡位置运动到2A处所需要的最短时间为_________。
(12T) 9-5 有两个同方向同频率的简谐振动,其表达式分别为 )4cos(1πω+=t A x m 、)43cos(32πω+=t A x m ,则合振动的振幅为 。
(2 A)9-6 已知一质点作周期为T 、振幅为A 的简谐振动,质点由正向最大位移处运动到2A处所需要的最短时间为_________。
(6T) 9-7有两个同方向同频率的简谐振动,其表达式分别为 )75.010cos(03.01π+=t x m 、)25.010cos(04.02π-=t x m ,则合振动的振幅为 。
(0.01m )9-8 质量0.10m kg =的物体,以振幅21.010m -⨯作简谐振动,其最大加速度为24.0m s -⋅,通过平衡位置时的动能为 ;振动周期是 。
(-32.010,10s J π⨯) 9-9一物体作简谐振动,当它处于正向位移一半处,且向平衡位置运动,则在该位置时的相位为 ;在该位置,势能和动能的比值为 。
(3,1:3π)9-10质量为0.1kg 的物体,以振幅21.010m -⨯作谐振动,其最大加速度为14.0m s -⋅,则通过最大位移处的势能为 。
机械振动一章习题解答

T = 2π
所以应当选择答案(C)。
m ( k1 + k 2 ) m = 2π k k1 k 2
习题 12—4
一质点作简谐振动,周期为 T,当它由平衡位置向 X 轴正方向运动 ]
时,从二分之一最大位移处到最大位移处这段路程所需要的时间为: [ (A) T/4。 (B) T/12。 (C) T/6。 (D) T/8。
解: 单摆的振动满足角谐振动方程, 这里所给的 θ 是初始角位移,显然是从最大角位移处计时。由 旋转矢量法容易判断该单摆振动的初位相为 “0” , 因此,应当选择答案(C) 。 −θm
题解 12―1 图
习题 12—2
轻弹簧上端固定,下端系一质量为 m1 的物体,稳定后在 m1 下边又
系一质量为 m2 的物体,于是弹簧又伸长了 ∆x ,若将 m2 移去,并令其振动,则 振动周期为: [ (A) T = 2π ]
位相 ϕ = π 2 ,故振动方程为
x = 0.02 cos(1.5t +
π ) 2
(SI)
习题 12─17
两个同方向的简谐振动的振动方程分别为
1 , x 2 = 3 × 10 − 2 cos 2π (t + ) 4
1 x1 = 4 × 10 − 2 cos 2π (t + ) 8
(SI)
求:合振动方程。 解:设合振动方程为
X
习题 12─12
一质点作简谐振动,振动图
线如图所示,根据此图,它的周期
4 O –2
2
t (s)
T=
ϕ=
,用余玄函数描述时的初位相
习题 12―12 图
。 解:根据振动图线可画出旋转矢量图,可得
t=2
∴ ∴
简谐振动方程弹簧振子的振动理性化模型

1
常见的振动现象
合成
分解
复杂振动
若有两个同方向、同频率的简谐振动
x1 A t 1 ) 1 cos( x2 A2 cos(t 2 )
两个振动的合位移
x A cos(t )
合振动的振幅
A A A 2 A1 A2 cos( 2 1 )
2 1 2 2
x A cos(t )
2
x, v
简谐运动能量图
o
能量
x t
T
0 t x Acost v t v A sin t
1 E kA2 2 1 2 2 Ep kA cos t 2
o
T
T
3T
4
2
4
T
1 t Ek m 2 A2 sin 2 t 2
二、两个友 诉说了内心的忧虑.正在说话时,寺 院里的钟声响了,说来奇怪,磬也发 出了嗡嗡的响声.
共振的现象
和尚的朋友明白了原由,悄悄 用钢锉在磬上锉了几处. 从此之后, 磬再也不会无故发声了. 和尚以为 妖怪已被赶走,心事顿消,病也不 治而愈.
共振的原因
磬为什么会不敲自鸣呢?这是共振 引起的一种现象. 当一物体的振动频率 与另一物体的固有频率一致时,前者的 振动能引发后者的振动. 磬的频率偶然 地和钟的频率一样,因此每当钟响时, 磬也因共振而发出嗡嗡之声.
显然,和尚的朋友深通物理知识, 他不仅知道这是一种共振现象,而且知 道如何消除这种现象.他巧妙地在磬上锉 了几下,这就改变了磬的固有频率,使 磬与钟的频率不再一样,也就引 不起共鸣了.
医用物理学教学课件 第二节 两个简谐振动的合成

A12 A22 2A1A2[cos01 cos02 sin01 sin02]
A12 A22 2A1A2 cos(02 01)
A A12 A22 2A1A2 cos
[注:cos( ) cos cos sin sin ]
t4 t3
t2
t1 Y超前π /2
右旋振动
t1 t2
t3
t4 Y落后π /2
左旋振动
例七
一质点同时参与相互垂直的两个振动:
X
8c
os(
t
)
cm
36
Y 6cos( t ) cm
33
请你画出合振动运动轨迹图。
解:
36
2
2B ∵Y落后π/2,左旋振动
2
2
A0
cos
2
O
X
2 A0
cos 2
1
2
t
注: 2t 1t
1 2
(1
cos
)
cos
2
从角度可分析:
t
2
1
2
t
1t
AA
2 1 t
2
O
X
将A与ωt表达式代入 x Acost
x
2
A0
cos 1
∴画一个2A*2B的矩形,内切
画椭圆,标出左旋箭头即可
2A
(2) 2 m 的情况: 1 n
若频率不相等,但是整数比,则合振动的轨迹 是有规则的稳定的闭合曲线-------李萨如图形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知两同方向同频率的简谐振动的运动方程
振动和运动方程:
一、概念介绍:
1. 振动:振动是一种物体运动的现象,其特点是物体在经过一个完整
周期后回到本来的状态。
2. 简谐振动:简谐振动是振动运动的一种,其主要特征是,其经过一
定时间后位置会重复,而且运动曲线呈现正弦形。
3. 同方向同频率振动:所谓同方向同频率振动,是指两个振动运动轨
迹相同,在经过一定时间后有相同的重复次数,回到同一相对位置的
振动。
二、运动方程
1. 运动方程的表达式:x = A sin ( ω t ± φ )
A:振幅,表示振动的最大幅度;
ω:角速度,单位为弧度每秒;
t:时间,单位为秒;
φ:初相,单位为弧度。
2. 运动方程的解:
求取运动方程的解,即可求出振动在某一时间点的位置:x = A sin ( ω
t + φ )
3. 偏移量:
偏移量δ可表示振动的重复性,一般通过计算每一完整周期的时间来
求出:δ = 2π / ω
三、同方向同频率的简谐振动的运动方程应用
1. 实际应用
同方向同频率的简谐振动的运动方程在科学实验中得到了广泛的应用,
比如物理实验或机械测量中都会使用它来研究同方向同频率振动运动
在一个完整周期内的状态变化。
2. 探究原理
同方向同频率振动是一种动力学运动,它的运行表现出正弦形的曲线,
每一次的完整周期之后都会回到初始位置,而运动的曲线形状也很相
似,由此可以探究几何学曲线特点及动力学学说等原理。
3. 理论价值
理解简谐振动在力学上的价值和原理,是进行工程设计及研究的基础
知识,同方向同频率振动的相关研究,也为后期在实际应用中做出工
程上对抗谐振或抑制谐振等其他性质变化提供了基础理论。
