083925_2012年重庆中考数学复习专题训练(23题)
中考数学中档解答题(23~25)强化训练-含答案

中档解答题(23~25)强化训练(一)(限时:30分钟满分:30分) 23.借鉴我们已有研究函数的经验,探索函数y=|x2-2x-3|-2的图象与性质,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:其中,(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;(3)观察函数图象:①当方程|x2-2x-3|=b+2有且仅有两个不相等的实数根,根据函数图象直接写出b的取值范围为________;②在该平面直角坐标系中画出直线y=12x+2,根据图象直接写出该直线与函数y=|x2-2x-3|-2的图象的交点横坐标为________(结果保留一位小数).解(1)3,2.(2)图象如下:(3)①当方程|x2-2x-3|=b+2有且仅有两个不相等的实数根,即y1=|x2-2x-3|-2与y2=b有两个不同的交点.观察图象可知b的取值范围为b>2或b=-2.②图象如下,观察图象可知,直线y=12x+2与函数y=|x2-2x-3|-2的图象的交点横坐标分别为-1.7和4.2.24.暑期临近,重庆市某中学为了丰富学校的暑期文化生活,同时帮助孩子融洽亲子关系,增进亲子间的情感交流,计划组织学生去某景区参加为期一周的“亲子一家游”活动.若报名参加此次活动的学生人数共有56人,其中要求参加的每名学生都至少需要一名家长陪同参与.(1)假设参加此次活动的家长人数比参加的学生人数的2倍少2人.为了此次活动学校专门为每名学生和家长购买一件T 恤衫,家长的T 恤衫每购买8件赠送1件学生T 恤衫(不足8件不赠送),学生T 恤衫每件15元,学校购买服装的费用不超过3401元,请问每件家长T 恤衫的价格最高是多少元?(T 恤衫的价格为整数元)(2)已知该景区的成人票价每张100元,学生票价每张50元.为了支持此次活动,该景区特地推出如下优惠活动:每张成人票价格下调a %.学生票价格下调12a %.另外,经统计此次参加活动的家长人数比学生人数多a %.参加此次活动的购买票价总费用比未优惠前减少了67a %,求a 的值.解 (1)设每件家长T 恤衫的价格为x 元,根据题意得,(56×2-2)x +[56-(56×2)÷8+1]×15≤3401, 解得x ≤25355, ∵x 为正整数, ∴x ≤25.答:每件家长T 恤衫的价格最高是25元. (2)设y =a %,根据题意得,56(1+y )×100(1-y )+56×50×⎝ ⎛⎭⎪⎫1-12y =[56(1+y )×100+56×50]×⎝ ⎛⎭⎪⎫1-67y ,整理得4y 2-y =0,解得y=0.25或y=0(舍去),∴a%=0.25,a=25.答:a的值为25.25.已知,在平行四边形ABCD中,AE⊥BC,且E为BC的中点,AE=2BE,P为BC 上一点,连接DP,作EF⊥DP于点F,连接AF.(1)若AD=4,求AE的长;(2)求证:2AF+EF=DF.解(1)∵AE=2BE,E是BC的中点,∴AE=BC.又∵四边形ABCD是平行四边形,∴BC=AD=4,∴AE=BC=4.(2)证明:如图,作GA⊥AF,交DP于点G,∵AD∥BC,∴∠ADG=∠DPC,∵∠AEP=∠EFP=90°,∴∠PEF+∠EPF=∠PEF+∠AEF=90°,即∠ADG=∠AEF=∠EPF.又∵AE=AD,∠F AE=∠GAD=90°-∠EAG,∴△AFE≌△AGD,∴AF=AG,即△AFG是等腰直角三角形,且EF=DG,∴FG=2AF,且DF=DG+FG=EF+FG,∴2AF+EF=DF.。
【新课标】备战2012年重庆市中考数学综合解答题选编

2010年重庆市中考数学综合解答题选编
【重庆市潼南县】
五、解答题:(本大题2个小题,第25小题10分,第26小题12分,共22分)解答时每小题必须给出必要的演算过程或推理步骤.
25. (10分)某镇道路改造工程,由甲、乙两工程队合作20天可完成.甲工程队单独施工
比乙工程队单独施工多用30天完成此项工程.
(1)求甲、乙两工程队单独完成此项工程各需要多少天?
(2)若甲工程队独做a 天后,再由甲、乙两工程队合作 天(用含a 的代数式表示)可完成此项工程;
(3)如果甲工程队施工每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的工程,才能使施工费不超过64万元?
26.(12分)如图, 已知抛物线c bx x y ++=22
1与y 轴相交于C ,与x 轴相交于A 、B ,点A 的坐标为(2,0),点C 的坐标为(0,1-).
(1)求抛物线的解析式;
(2)点E 是线段AC 上一动点,过点E 作DE ⊥x 轴于点D ,连结DC ,当△DCE 的面积最大时,求点D 的坐标;
(3)在直线BC 上是否存在一点P ,使△ACP 为等腰三角形,若存在,求点P 的坐标,若不存在,说明理由.
题图26
备用图。
2012年重庆中考数学24

MH GB F E DC A重庆中考专题训练24题24.如图,在正方形ABCD 中,E 、F 分别为BC 、AB 上两点,且BE =BF ,过点B 作AE 的垂线交AC 于点G ,过点G 作CF 的垂线交BC 于点H ,延长线段AE 、GH 交于点M . (1)求证:∠BFC =∠BEA ;(2)求证:AM =BG +GM .24.如图正方形ABCD 中,E 为AD 边上的中点,过A 作AF ⊥BE ,交CD 边于F ,M 是AD 边上一点,且有BM =DM +CD . ⑴求证:点F 是CD 边的中点;⑵求证:∠MBC =2∠ABE .24.已知,ABC Rt ∆中,90,30.ACB CAB ∠=∠=分别以AB 、AC 为边,向形外作等边ABD ∆和等边.ACE ∆(1)如图1,连结线段BE 、CD .求证:BE =CD ;(2)如图2,连接DE 交AB 于点F .求证:F 为DE 中点.24、已知:正方形ABCD 中,E 是AB 的中点,F 是AD 上一点,且ED=FC ,ED 、FC 交于点G ,连接BG ,BH 平分∠GBC 交FC 于H ,连接DH 。
(1)求证:ED ⊥FC ;(2)求证:DGH ∆是等腰直角三角形M F E CD B A12.如图,AC 是正方形ABCD 的对角线,点O 是AC 的中点,点Q 是AB 上一点,连接CQ ,DP ⊥CQ 于点E ,交BC 于点P ,连接OP ,OQ ; 求证:(1)△BCQ ≌△CDP; (2)OP=OQ.13、已知如图,四边形ABCD 为平行四边形, AD a , AC 为对角线 ,BM ∥AC,过点D 作DE//CM ,交AC 的延长线于F ,交BM 的延长线于E. (1)求证:△AD F ≌△BCM ;(2)若AC=2CF ,∠ADC=60 o, A C ⊥DC,求四边形ABED 的面积(用含a 的代数式表示)。
24、已知,如图,在正方形ABCD 中,点E 、F 分别在AB 上和AD 的延长线上,且BE=DF ,连接EF ,G 为EF 的中点.求证:(1)CE=CF ;(2)DG 垂直平分AC .24、如图正方形ABCD 中,E为AD 边上的中点,过A 作AF ⊥BE,交CD 边于F ,M 是AD 边上一点,且有BM =DM +CD . ⑴求证:点F是CD 边的中点; ⑵求证:∠MBC =2∠ABE .C P M F E CDB A24、如图,在直角梯形ABCD 中,AD ⊥DC ,AB ∥DC ,AB=BC ,AD 与BC 延长线交于点F ,G 是DC 延长线上一点,AG ⊥BC 于E . (1)求证:CF=CG ;(2)连接DE ,若BE=4CE ,CD=2,求DE 的长.24、如图,梯形ABCD 中,AB ∥CD ,AD ⊥CD ,AC=AB ,∠DAC=30度.点E 、F 是梯形ABCD 外的两点,且∠EAB=∠FCB ,∠ABC=∠FBE,∠CEB=30°. (1)求证:BE=BF ;(2)若CE=5,BF=4,求线段AE 的长.24.如图,梯形ABCD中,AD ∥BC ,∠A =900,点E 为CD 边的中点,BE ⊥CD ,且∠FBE=2∠EBC .在线段AD 上取一点F ,在线段BE 上取一点G ,使得BF =BG ,连接CG . (1)若AB =AF ,EG =2,求线段CG 的长; (2)求证:∠EBC +31∠ECG =30°.24.如图,在四边形ABCD 中,AB=AD ,∠B AD =60°,∠BCD =120°,连接AC ,BD 交于点E .⑴若BC=CD=2,M 为线段AC 上一点,且AM :CM=1:2, 连接BM ,求点C 到BM 的距离. ⑵证明:BC+CD=AC .24.如图1,菱形ABCD 中,点E 、F 分别为AB 、AD 的中点,连接CE 、CF. (1)求证:CE=CF ;(2)如图2,若H 为AB 上一点,连接CH ,使2CHB ECB ∠=∠,求证:CH=AH+AB.A24题B CDE FGD CACAC24.已知:正方形ABCD 中,E 是AB 的中点,F 是AD 上一点,且ED=FC ,ED 、FC 交于点G ,连接BG ,BH 平分∠GBC 交FC 于H ,连接DH .(1)求证:ED ⊥FC ; (2)求证:DGH ∆是等腰直角三角形.24.在正方形ABCD 中,点E 、F 分别在BC 、CD 上,且∠BAE=︒30,∠DAF=︒15. (1)求证:EF=BE+DF ;(2)若AEF 的面积.24. 如图,在Rt ABC ∆中,90ACB ∠=,AC BC <,D 为AB 的中点,DE 交AC 于点E ,DF 交BC 于点F ,且DE DF ⊥,过A 作//AG BC 交FD 的延长线于点G . (1)求证:AG BF =;(2)若9,18AE BF ==,求线段EF 的长.24.如图,梯形ABCD 中,AD ∥BC ,∠ABC =90°,BF ⊥CD 于F ,延长BF 交AD 的延长线于E ,延长CD 交BA 的延长线于G ,且DG =DE ,AB =72,CF =6. (1)求线段CD 的长;(2)H 在边BF 上,且∠HDF =∠E ,连接CH ,求证:∠BCH =45°-21∠EBC .24题图FED CB A B CDE F H24题图G A。
2012中考数学综合题集训

2012中考数学综合题集训1.如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O 落在水平面上,对称轴是水平线OC 。
点A 、B 在抛物线造型上,且点A 到水平面的距离AC =4O 米,点B 到水平面距离为2米,OC =8米。
(1) 请建立适当的直角坐标系,求抛物线的函数解析式;(2)为了安全美观,现需在水平线OC 上找一点P ,用质地、规格已确定的圆形钢管制作两根支柱P A 、PB 对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省(支柱与地面、造型对接方式的用料多少问题暂不考虑)时的点P ?(无需证明) (3)为了施工方便,现需计算出点O 、P 之间的距离,那么两根支柱用料最省时点O 、P 之间的距离是多少?(请写出求解过程)【答案】解:(1)以点O 为原点、射线OC 为y 轴的正半轴建立直角坐标系………………1分设抛物线的函数解析式为2y ax =,………………2分由题意知点A 的坐标为(4,8)。
且点A 在抛物线上,………………3分 所以8=a×24,解得a=12,故所求抛物线的函数解析式为212y x =………………4分 (2)找法:延长AC,交建筑物造型所在抛物线于点D, ………………5分 则点A 、D 关于OC 对称。
连接BD 交OC 于点P ,则点P 即为所求。
………………6分 (3)由题意知点B 的横坐标为2,且点B 在抛物线上, 所以点B 的坐标为(2,2)………………7分又知点A 的坐标为(4,8),所以点D 的坐标为(-4,8)..................8 设直线BD 的函数解析式为 y=kx+b , (9)则有2248k b k b +=⎧⎨-+=⎩ (10)解得k=-1,b=4.故直线BD 的函数解析式为 y=-x+4,………………11 把x=0代入y=-x+4,得点P 的坐标为(0,4)两根支柱用料最省时,点O 、P 之间的距离是4米。
重庆中考数学第25题专题练习

重庆中考第25题专题练习 姓名1、已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-,与x 轴交于A B ,两点,与y 轴交于点C ,其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标.(3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE PC ∥交x 轴于点E .连接PD 、PE .设CD 的长为m ,PDE △的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.2、如图,在平面直角坐标系中,抛物线n mx x y ++=2经过A (3,0),B (0,-3)两点,点P 是直线AB 上一动点,过点P 作x 轴的垂线交抛物线于点M ,设点P 的横坐标为t , (1)分别求直线AB 和这条抛物线的解析式(2)若点P 在第四象限,连结BM 、AM ,当线段PM 最长时,求ABM ∆的面积。
(3)是否存在这样的点P ,使得以点P 、M 、B 、O 为顶点的四边形为平行四边形?若存在,请直接写出点P 的横坐标;若不存在,请说明理由。
A CxyBO (第25题图)3、.如图,在平面直角坐标系xOy 中,已知抛物线顶点N 的坐标为(-1.-92),此抛物线交y 轴于B (0,-4),交x 轴于A 、C 两点且A 点在C 点左边.(1)求抛物线解析式及A 、C 两点的坐标.(2)如果点M 为第三象限内抛物线上一个动点且它的横坐标为m ,设△AMB 的面积为S ,求S 关于m 的函数关系式并求出S 的最大值.(3)若点P 是抛物线上的动点,点Q 是直线y=x 上的动点,判断有几个位置使得以点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.4、如图,抛物线1417452++-=x x y 与y 轴突于A 点,过点A 的直线y =kx +l 与抛物线交于另一点B ,过点B 作BC ⊥x 轴,垂足为点C (3,0)(l )来直线AB 的函数关系式;(2)动点P 在线段OC 上从原点出发以每秒一个单位的速度向C 移动,过点产作PN ⊥x 轴,交直线AB 于点M ,交抛物线于点N ,设点P 移动的时间为t 秒,MN 的长度为s 个单位,求s 与t 的函数关系式,并求出线段MN 的最大值。
重庆市直属重点中学2012年中考数学模拟试题(含答案)

21(第4题)初2012级学生学业质量调研测试题数学试题读题卷(此卷不交)(本试题共五个大题,26个小题,满分150分,时间120分钟)参考公式:抛物线y =ax 2+bx +c(a ≠0)的顶点坐标为)44,2(2ab ac a b --,对称轴公式为a b x 2-=.一、选择题:(本大题共10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卷中对应的表格内.1.下列四个数中,最大的数是A .2B .1-C .0D .22.下列运算中,计算正确的是A .a 3·a 2=a 6B .824a a a ÷=C . ()422ab ab =D .236()a a =3.下列图形中,既是轴对称图形,又是中心对称图形的是4.如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=28o ,那么∠2的度数是 A.60° B.62°C.68°D.72°5.下列说法中正确的是A.了解长江中鱼的种类适合采用全面调查B.数据1,1,2,2,3的众数是3C.了解某饮料中所含色素宜采用抽样调查D.一组数据的波动越大,方差越小 6. 如图,已知OB 是⊙O 的半径,点C 、D 在⊙O 上,∠DCB =40°,则∠OBD =BACO(第6题)A AB CD俯视图左 视 图主视 图(第7题)A.80oB.50oC.40oD.60o7.一个几何体的三视图如图所示,这个几何体是 A .圆锥B .圆柱C .三棱锥D .三棱柱8. 如图,A 、B 、C 、D 为⊙O 的四等分点,动点P 从圆心O 出发,沿O C D O --- 路 线作匀速运动,设运动时间为t (秒),∠APB =y (度),则下列图象中表示y 与t 之间函数关系最恰当的是9.下图是由棋子组成的“正”字,则第6个图形需要棋子枚数为A .45B .46C .47D .4810.如图,为二次函数2y ax bx c =++的图象,给出的下列6个结论:①0ab <; ②方程20ax bx c ++=的根为1213x x =-=,; ③024<++c b a ; ④当1x >时,y 随x 值的增大而增大; ⑤当y >0时,―<x <3; ⑥a +b +c >0. 其中正确..的有 A .2个 B .3个 C .4个 D .5个初2012级学生学业质量调研测试题(第一次)数学试题 答题卷(此卷必须交)题号一二 三 四 五总 分总分人 复查人 1—1011—1617—2021—2425—26得分 评分人[机密]2012年 4月22日前(第8题) A B C D OPBty 045 90 Dty 045 90 Aty45 90 Cty45 90 (第10题)··· ····· · · (1)··· ··· ·· · (2) · ·· ····· ··· ··· · · (3) · ·· ···· ···· ·· · · · ………115233(第15题)一、选择题:(本大题共10个小题,每小题4分,共40分)题号 123 4 5678910 共对(个)答案二、填空题:(本题共6小题,每小题4分,共24分,请把下列各题的正确答案填写在横线上)11.全国两会期间,温家宝总理强调,“十二五”期间,将新建保障性住房36 000000套.这些住房将有力地缓解住房的压力,特别是解决中低收入和新参加工作的大学生住房的需求.把36000000用科学记数法表示应是 .12.两个相似多边形的面积比是9:16,其中较小多边形周长为36cm ,则较大多边形周长为cm .13.某校九年级二班50名学生的年龄情况如下表所示:年 龄 14岁 15岁 16岁 17岁 人 数720167则该班学生年龄的中位数为 .14.已知扇形的圆心角为120°,半径为6,则扇形面积是 .15.标有1,1,2,3,3,5六个数字的立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为x ,朝下一面的数为y ,得到平面直角坐标系中的一个点(x ,y ).已知小华前二次掷得的两个点所确定的直线经过点P (4,7),则他第三次掷得的点也在这条直线上的概率为 .16. 自行车轮胎安装在前轮上行驶6 000千米后报废,若安装在后轮上只能行驶4 000千米.为了行驶尽可能远的路程,如果采用当自行车行驶一定路程后将前、后轮胎调换使用的方法,那么安装在自行车上的一对新轮胎最多可行驶 千米.三、解答题:(本大题共4个小题,每小题6分,共24分)解答时每小题必须给出必要的演算过程或推理步骤.17.计算: 18.解分式方程: 1111x x x -=+-. 解不等式 3513+<-x x ,并 ()0122012931231π-⨯-⎪⎭⎫ ⎝⎛+-+--.19.已知:如图,AC =DF ,AD =BE ,BC =EF .求证:∠C =∠F .20.已知:如图,在3×3(单位:cm )的正方形网格中,图形的各个顶点都在格点上求:图中阴影部分的面积.四、解答题:(本大题共个4小题,每小题10分,共40分)解答时每小题必须给出必要的演算过程或推理步骤.21.先化简,再求值: 错误!未找到引用源。
2012重庆中考数学模拟训练5
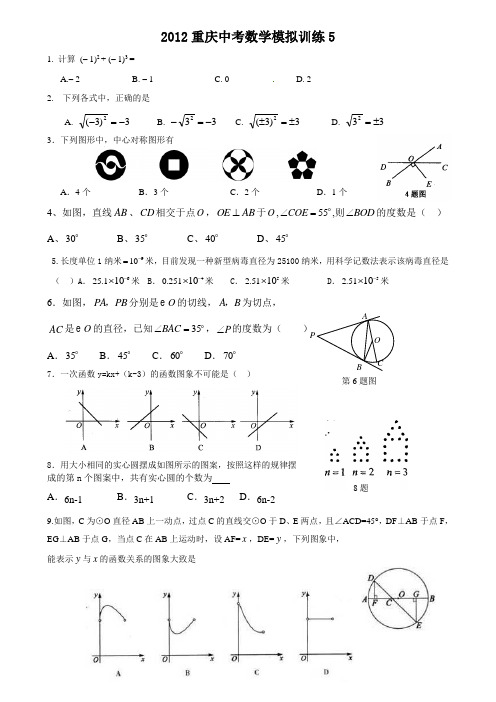
2012重庆中考数学模拟训练51. 计算 (– 1)2 + (– 1)3 =A.– 2B. – 1C. 0D. 2 2. 下列各式中,正确的是A.3)3(2-=- B. 332-=- C. 3)3(2±=± D. 332±=3.下列图形中,中心对称图形有A .4个B .3个C .2个D .1个4、如图,直线AB 、CD 相交于点O ,OE AB ⊥于O ,55COE ∠= ,则BOD ∠的度数是( ) A 、30B 、35C 、40D 、455.长度单位1纳米910-=米,目前发现一种新型病毒直径为25100纳米,用科学记数法表示该病毒直径是( )A .625.110-⨯米 B .40.25110-⨯米C .52.5110⨯米D .52.5110-⨯米6.如图,PA PB ,分别是O 的切线,A B ,为切点,AC 是O 的直径,已知35BAC ∠= ,P ∠的度数为( )A .35B .45C .60D .707.一次函数y=kx+(k-3)的函数图象不可能是( )8.用大小相同的实心圆摆成如图所示的图案,按照这样的规律摆 成的第n 个图案中,共有实心圆的个数为A .6n-1B .3n+1C .3n+2D .6n-29.如图,C 为⊙O 直径AB 上一动点,过点C 的直线交⊙O 于D 、E 两点,且∠ACD=45°,DF ⊥AB 于点F ,EG ⊥AB 于点G ,当点C 在AB 上运动时,设AF=x ,DE=y ,下列图象中,能表示y 与x 的函数关系的图象大致是第6题图8题10.如图,正方形ABCD 中,点E 是对角线 BD 上一点,点F 是边BC 上一点,点G 是边CD 上一 点,BE=2ED ,CF=2BF ,连接AE 并延长交 CD 于 G ,连接 AF 、EF 、FG .给出下列五个结论:①DG=GC ;②∠FGC=∠AGF ;③ABF FCG S S ∆∆=;④; ⑤∠AFB=∠AEB .其中正确结论的个数是 ( ) A .5 个 B .4个C .3 个D .2个11、一组数据2,6,4,7,8,5的中位数是_________12.如图1,在 Rt △ABC 中,∠B=90°.ED 是AC 的垂直平分线,交AC 于点D, 交BC 于点E,已知∠BAE=30°,则∠C 的度数为_____________13、若关于x 的方程1011--=--m xx x 有增根,则m 的值是 . 14.圆锥的侧面积为18πcm 2,其侧面张开图是半圆,则圆锥的底面半径是。
重庆中考初中数学专题训练(有答案)--15题训练

15题训练一、注意下面定律(要记住,考试时候节约许多计算时间):1、如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=m/n.2、互相独立的实验事件的概率求法:设A成功的概率是m,B成功的概率是n,两事件同时发生的概率是m×n.3、生活中的随机事件分为确定事件和不确定事件,确定事件又分为必然事件和不可能事件,其中必然事件发生的概率为1,即P(必然事件)=1;不可能事件发生的概率为0,即P(不可能事件)=0;如果A为不确定事件,那么0<P(A)<1二、选题1、从1,2,3,…,14,15这15个整数中任取一个数记作a,那么关于x的方程ax=15x-24的解为整数的概率为7/15考点:概率公式;一元一次方程的解.专题:计算题.分析:可将原方程变形为(a-15)x=-24,要使关于x的方程ax=15x-24的解为整数,a-15必须能被24整除,找到符合条件的数,再利用概率公式解答即可.解答:解:原方程可变形为(a-15)x=-24,∵关于x的方程ax=15x-24的解为整数,∴a-15能被24整除,∴a=3或7或9或11或12或13或14共7种可能.故答案为:7/15.2、3、在一个不透明的盒子里装有5个分别写有数字-2,-1,0,1,2的小球,它们除数字不同外其余全部相同.现从盒子里随机取出一个小球,将该小球上的数字作为字母b的值,将该数的平方作为字母c的值,则使抛物线y=-x2+bx+c经过第一象限的概率是()4、(2011•江津区)在一个袋子里装有10个球,其中6个红球,3个黄球,1个绿球,这些球除颜色外,形状、大小、质地等完全相同,充分搅匀后,在看不到球的条件下,随机从这个袋子中摸出一球,不是红球的概率是2/5考点:概率公式.分析:根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数.二者的比值就是其发生的概率的大小.解答:解:红球的概率:(3+1)÷10=2/5.5、6、在一个不透明的盒子里装有6个分别写有数字-1,0,1,2,3,5的小球,它们除数字不同外其余全部相同.现从盒子里随机取出一个小球,记下数字a后不放回,再取出一个记下数字b,那么点(a,b)在抛物线y=x2+1上的概率是()7、任意掷一枚骰子,5点朝上的概率是()偶数点朝上的概率是()大于2的点朝上的概率是()小于7的点朝上的概率是().8、抛掷三枚硬币,掷得“两正一反”的概率等于()这个概率值表示的意思是掷很多次,平均每8次有三次出现两正一反;不是“三个反面”的概率等于(),这个概率值表示的意思是()9、从8名男医生和7名女医生中选一人作为医疗小组的组长,是男医生的概率是(),是女医生的概率是()分析:男医生人数除以医生总人数即为所求的是男医生的概率;同理可得是女医生的概率.解答:解:从8名男医生和7名女医生中选一人作为医疗小组的组长,是男医生的概率是8/(8+7)=8/15,同理女医生的概率为7/15.点评:明确概率的意义是解答的关键,用到的知识点为:概率=所求情况数与总情况数之比.10、现在某实验室有A,B二项互相独立的实验,已知A成功的概率是1/2,B成功的概率是2/3,二项实验同时成功的概率是()11、下列说法:(1)事件发生的概率可以是任意正数;(2)不确定事件的概率大于0而小于1;(3)不确定事件发生的概率是不确定的;(4)事件发生的概率可以等于事件不发生的概率,其中正确的()A.1个B.2个C.3个D.4个解:(1)错,事件发生的概率不能大于1.(2)对,不可能事件的概率为0,必然事件的概率为1,不确定事件的概率大于0而小于1.(3)错,不确定事件的概率有一定的规律可以遵循.(4)对,例如随机抛硬币事件,出现正面和出现反面的概率都为0.5.正确的有2个,故选B.生活中的随机事件分为确定事件和不确定事件,确定事件又分为必然事件和不可能事件,其中必然事件发生的概率为1,即P(必然事件)=1;不可能事件发生的概率为0,即P(不可能事件)=0;如果A 为不确定事件,那么0<P(A)<112、(2007•十堰)掷一个质地均匀的骰子,出现的点数大于4的概率是1/3,出现的点数为偶数的概率是()让出现的点数大于4的情况数除以总情况数6;让出现的点数为偶数的情况数除以总情况数6即为所求的概率.解答:解:掷一个质地均匀的骰子,有6种情况,即1、2、3、4、5、6,出现的点数大于4的有2种,故其概率是1/3;出现的点数为偶数的有3种,故其概率是1/2.点评:本题考查的是概率的求法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=m/n.13、一年365天,任意翻一本日历,正好翻到你生日的概率是(),是2月的概率是()14、从一副扑克牌中任意抽取一张.(1)它是王牌的概率是()(2)它是Q的概率是();(3)它是草花的概率是()15、从一篮鸡蛋中取五个,如果其重量小于30克的概率是0.3,重量在大于30,小于40克的概率是0.5,那么其重量不大于40克的概率是()由题意可得,重量不大于40克的概率等于重量小于30克的概率加上重量在[30,40]克的概率,运算求得结果.解答:解:重量不大于40克的概率等于重量小于30克的概率加上重量在[30,40]克的概率,即0.3+0.5=0.8.故答案为0.8.点评:本题主要考查互斥事件的概率加法公式,属于基础题.16、甲乙两人下棋比赛,两人下成和棋的概率是1/2,乙获胜的概率是1/3,则乙不输的概率是()17、甲、乙两人下棋,甲获胜的概率为30%,和棋的概率为50%,那么乙不输的概率为()考点:概率公式.分析:等量关系为:甲获胜的概率,和棋的概率和乙获胜的概率的和是1,把相关数值代入即可求解.解答:解,根据题意,乙获胜的概率是1-30%-50%=20%,所以乙不输的概率为50%+20%=70%.点评:解答本题的关键是要判断出“甲获胜的概率,和棋的概率和乙获胜的概率的和是1”.18、三名同学站成一排,其中小明站在中间的概率是(),站在两端的概率是()考点:概率公式.分析:三个同学站成一排总共有3×2种情况,分别计算所求情况组合的个数,利用概率公式进行计算即可.解答:解:小明站在中间有2种情况,站在两端有4种情况.故小明站在中间的概率是2/6=13,站在两端的概率是4/6=2/3.点评:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A 的概率P(A)=m/n.19、有100件产品,其中有5件次品,现抽出1件产品,它是正品的概率是(),它是次品的概率是().考点:概率公式.分析:让正品数和次品数,分别除以总产品数即为所求的概率.解答:解:有100件产品,其中有5件次品,即95件正品;现抽出1件产品,它是正品的概率是95/100=19/20,它是次品的概率是5/100=1/20.点评:本题考查随机事件概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=m/n.20、(2011•宿迁)在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.(1)写出点M坐标的所有可能的结果;(2)求点M在直线y=x上的概率;(3)求点M的横坐标与纵坐标之和是偶数的概率.本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.15题目16、某城市有一段马路需要整修,这段马路的长不超过3500米.今有甲、乙、丙三个施工队,分别施工人行道、非机动车道和机动车道.他们于某天零时同时开工,每天24小时连续施工.若干天后的零时,甲完成任务;几天后的18时,乙完成任务,自乙队完成的当天零时起,再过几天后的8时,丙完成任务,已知三个施工队每天完成的施工任务分别为300米、240米、180米,问这段路面有多长?24、已知四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°,请说明:BC+DC=AC.分析:由AB=AD,∠BAD=60°可得△ABD是等边三角形;把△ADC绕点D逆时针旋转60°,点A与点B重合,点连接EC ,C 转到点E ,则△DCE 是等边三角形,∠BAD=60°,又因为∠BCD=120°,所以∠BAD+∠BCD=180°,故B 、C 、E 共线,得出最后结论.解答:解:∵AB=AD ,∠BAD=60°,∴△ABD 是等边三角形,把△ADC 绕点D 逆时针旋转60°,点A 与点B 重合,点连接EC ,C 转到点E ,则△DCE 是等边三角形,∴∠BAD=60°, 又∵∠BCD=120°,∴∠BAD+∠BCD=180°, 故B 、C 、E 共线,∴AC=BE=BC+CE=BC+DC .点评:本题考查了全等三角形的判定与性质及等边三角形的性质;可围绕结论寻找全等三角形,运用全等三角形的性质判定线段相等,共线的证明是正确解答本题的关键. 15.(本小题满分6分) 如图,O⑴ 写出O 上所有格点....的坐标: ___________________________________________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12012年重庆中考数学复习专题训练(23题)概率与统计专练【1】 某班有50名同学,男、女生人数各占一半,在本周操行评定中操行得分情况如图(1)统计表中所示,图(2)是该班本周男生操行得分的条形统计图:图(1) (1)补全统计表和条形统形图;(2)计算全班同学的操行平均得分;(3)若要在操行得分为5分的4名同学中选出两名 同学作“本周明星”,用画树状图或列表的方法求 出选为“本周明星”的正好是一名男同学和一名女 同学的概率。
【2】我校初三年级共1000人,初三上期为了进一步了解学生的身体素质情况,体育老师从全年级抽取了50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下图所示:请结合图表完成下列问题: (1)表中的a =_________;(2)请把频数分布直方图补充完整;(3)这个样本数据的中位数落在第_____组;(4)若初三年级学生一分钟跳绳次数(x )达标要求是:120<x 不合格;140120<≤x 为合格;160140<≤x 为良;160≥x 为优.根据以上信息,请你估算全年级学生一分钟跳绳次数为优的人数(要求写出计算过程).1分 2分 3分 4分 5分操行分图(2)2【3】 2009年4月28日,墨西哥爆发甲型流感(俗称猪流感)疫情,由于防范措施不当,疫情迅速蔓延全球,亚洲地区也不可幸免,截至北京时间5月16日17点,亚洲共有8个国家或地区被确诊有甲型流感病例(如图).其中韩国被确诊的人数占亚洲被确诊人数的1.8请你根据上面提供的信息解答下列问题:(1)请补全条形统计图,并填空:截至北京时间5月16日17点,亚洲一共有 人被确诊为甲型流感病例:这8个国家或地区被确诊病例人数的中位数是 人,众数是 人.(2) 2003年中国爆发非典疫情,现又爆发甲型流感疫情,请结合你所学过的知识,写出一条预防疫情的措施:【4】 某年级一班和二班的同学在老师的倡议下踊跃为希望工程捐款,据统计,捐款金额共有10元、20元、30元、40元和50元五种.各班捐款情况统计如下:(1)一班中,捐款30元的同学所占该班总人数的百分比为 ;平均每位同学捐款 元: (2)假如二班捐款30元的同学所占该班总人数的百分比等于一班捐款20元的同学所占该班总人数的百分比,求二班同学捐款30元的人数并补全二班同学捐款情况统计图;(写出求解过程) (3)二班同学捐款金额的中位数是 元.3【5】 小西和小恺做转盘游戏,现有甲、乙两个转盘,甲转盘被等分成4个扇形,分别标有数字3、4、7、8;乙转盘被等分成3个扇形,分别标有数字3、4、7.小西转动甲转盘,转盘停止转动时,指针所指的数字记为a ,小恺转动乙转盘,转盘停止转动时,指针所指的数字记为b ,(当指针指向两个扇形的交线时,重新转动转盘).(1)请你用画树状图或列表的方法,求(,a b )共有几种结果;(2)若a 、b 、5、6四个数字可以排成四个连续的整数(与顺序无关),则小西胜;否则小恺胜.判断上述游戏是否公平,若公平,请说明理由:若不公平,请说明理由并修改游戏规则,使游戏公平.【6】 随着我国人民生活水平和质量的提高,百岁寿星日益增多.某市是中国的长寿之乡,截至2009根据表格中的数据得到条形图如下:解答下列问题:(1)请把统计图中地区二和地区四中缺失的数据、图形补充完整;(2)填空:该市五个地区100周岁以上老人中,男性人数的极差是 人,女性人数的中位数是 人;(3)预计2015年该市100周岁以上的老人将比2009年2月的统计数增加100人,请你估算2015年地区一增加100周岁以上的男性老人多少人?地区一 地区二地区三 地区四(第22题)4【7】 现有两个纸箱,每个纸箱内各装有4个材质、大小都相同的乒乓球,其中一个纸箱内4个小球上分别写有1、2、3、4这4个数,另一个纸箱内4个小球上分别写有5、6、7、8这4个数,甲、乙两人商定了一个游戏,规则是:从这两个纸箱中各随机摸出一个小球,然后把两个小球上的数字相乘,若得到的积是2的倍数,则甲得1分,若得到积是3的倍数,则乙得2分.完成一次游戏后,将球分别放回各自的纸箱,摇匀后进行下一次游戏,最后得分高者胜出.。
(1)请你通过列表(或树状图)分别计算乘积是2的倍数和3的倍数的概率;(2)你认为这个游戏公平吗?为什么?若你认为不公平,请你修改得分规则,使游戏对双方公平.【8】某校学生会准备调查初中2010级同学每天(除课间操外)的课外锻炼时间.⑴ 确定调查方式时,甲同学说:“我到1班去调查全体同学”;乙同学说:“我到体育场上去询问参加锻炼的同学”;丙同学说:“我到初中2010级每个班去随机调查一定数量的同学”. 请你指出哪位同学的调查方式最为合理;⑵ 他们采用了最为合理的调查方法收集数据,并绘制出如图-1所示的条形统计图和如 图-2所示的扇形统计图,则他们共调查了多少名学生?请将两个统计图补充完整;⑶ 若该校初中2010级共有240名同学,请你估计该年级每天(除课间操外)课外锻炼时间不大于20分钟的人数.(注:图-2中相邻两虚线形成的圆心角为30°.)8题图-18题图-25【9】 某房产网站为了了解我市2009年第一季度购房消费需求情况,随机调查了200名有购房需求的人,以下是根据调查结果制作的两幅尚不完全的统计图.已知价格范围C 的人数是价格范围E 人数的5倍,请根据统计图中提供的信息回答下列问题: (1)被调查人员中,选择价格范围C 的人数为__________,选择价格范围E 的人数为___________; (2)补全条形统计图和扇形统计图;(3)如果2009年第一季度我市所有的有购房需求的人数为15000人,试估计这些有购房需求的人中可按受4500元/平方米以上的人数是_____________人.【10】 有两个可以自由转动的均匀转盘,.A B 转盘A 被平均分成4等份,分别标上-2,2,6,8四个数字;转盘B 被平均分成3等份,分别标上-1,-2,3三个数字.自由转动转盘A 与B ,转盘停止后,指针各指向一个数字,把A 转盘指针指向的数字作为被除数,B 转盘指针指向的数字作为除数,计算这两个数的商.(1)请你用画树状图或列表的方法,求这两数的商为分数的概率;(2)小贝和小晶想用以上两个转盘做游戏,规则是:若这两数的商为负整数,则小贝赢;若这两个数的商为正数,划小晶赢.你认为该游戏公平吗?请说明理由.如果不公平,请你修改游戏规则,使游戏公平.【11】 “无论多么大的困难除以13亿,都将是一个很小的困难”.在汶川特大地震发生后,我市某中学全体学生积极参加了“同心协力,抗震救灾”活动,九年级9班两位同学对本班捐款情况作了统计:全班50人共捐款900元,两位同学分别绘制了两幅不完整的统计图(注:每组含最小值,不含最大值).请你根据图中的信息,解答下列问题: (1)捐款金额在10-15元的人数有_____________人;610元~15元40%图2图115元~20元25元~30元20元~25元b%a%10%捐款人数扇形统计图金额(2)补全条形统计图,并计算扇形统计图a 、b 的值;(3)全校共有1268人,请你估计全校学生捐款的总金额大约是多少元.【12】 如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字.小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.(1)请你通过画树状图的方法求小颖获胜的概率.(2)你认为该游戏规则是否公平?若游戏规则公平,请说明理由;若游戏规则不公平,请你设计出一种公平的游戏规则.甲乙(12题图)【13】某班半期考试后,对数学学科进行了分析,随机抽取了16名同学的成绩(均为整数),小刚的成绩为x分,另外15名同学的成绩如下(单位:分):83,92,98,100,101,101,109,111,111,112,112,112,118,124,128.(1)请补全上面的表格和频数分布直方图;(2)小刚的成绩x属于第__________组;(3)该样本的中位数是__________分;(4)小明已求出了第一、二、四、五组同学的平均成绩是120111分,请你求出样本的平均成绩S的最小值.【14】如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字. 小亮和小华利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小华获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜. 如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.(1)请你通过画树状图或者列表的方法分别求出小华和小亮获胜的概率.(2)小华和小亮想用这两个转盘做游戏,他们规定:小华获胜时,小华得2分;小亮获胜时,小亮得3分. 这个游戏对双方公平吗?请说明理由;如果不公平,试修改得分规定,使游戏双方公平.甲乙14题图78【15】 在某校的体能测试中,九年级的480名女生参加了立定跳远测试,现从这480名女生的跳远距离中随机抽取10名女生的跳远距离绘制成如下条形统计图.(另附:九年级女生立定跳远的计分标准)(1)这10名女生在本次测试中:立定跳远距离..的极差是_________________cm ,中位数是______________cm ; 立定跳远得分..的众数是_________________分,平均数是______________分. (2)请你估计该校这次立定跳远中得满分的女生人数.【16】 某校初三年级音乐期末测试已结束,为了解全年级情况,以该年级(1)班学生的测试成绩为样本,按A ,B ,C ,D 四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:(说明:A 级:90分~100分(均含最小值、最大值,后同);B 级:75分~89分;C 级:60分~74分;D 级:60分以下)(1)请把条形统计图补充完整;(2)扇形统计图中D 级所在的扇形的圆心角度数是_______________; (3)样本中测试成绩的中位数落在__________级;(4)若该年级有1100名学生,请你用此样本估计音乐期末测试中A 级和B 级的学生人数约为____________人.等级 A D A B C D 20%9【17】 某校一课外活动小组为了解学生最喜欢的球类运动情况;随机抽查本校九年级的200名学生,调查的结果如图所示. 请根据该扇形统计图解答以下问题: (1)求图中的x 的值;(2)求最喜欢足球运动的学生人数;(3)若由2名最喜欢篮球运动的学生(用12,A A 表示),1名最喜欢乒乓球运动的学生(用B 表示),1名最喜欢足球运动的学生(用C 表示)组队外出参加一次联谊活动. 欲从中选出2人担任组长(不分正副),请用树状图或列表法列出所有可能情况,并求2人均是最喜欢篮球运动的学生的概率.【18】 在2010年5月1日世博会开幕的当天,某特许商品零售商张先生售出以下四种世博徽章,其价格如下:张先生对当天售出这四种徽章的个数进行统计,绘制成如下所示的统计图:缤纷世博徽章美好上海徽章16% 吉祥物金边徽章12% 国徽世博徽章当天各徽章售出个数占总数的百分比(1)请求出当天张老板共售出这四种徽章多少个,并求出这些徽章的平均价格;(2)补全扇形和条形统计图;(3)取缤纷世博徽章、吉祥物金边徽章、美好上海徽章、国旗世博徽章各一枚,分别记为,、、、A B C D在张先生店中的小明想从这4枚徽章中选出两枚购买,以留作纪念,求他刚好选中A和C的概率是多少?请用树状图或列表法求出.【19】在我校举办的课外活动中,有一项是小制作评比.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1. 第三组的件数是12. 请你回答:(1)本次活动共有__________件作品参赛;各组作品件数的中位数是_________件.(2)经评比,第四组和第六组分别有10件和2件作品获奖,(3)小制作评比结束后,组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示,请用树状图或列表法求出刚好展示B、D的概率.日期10。
