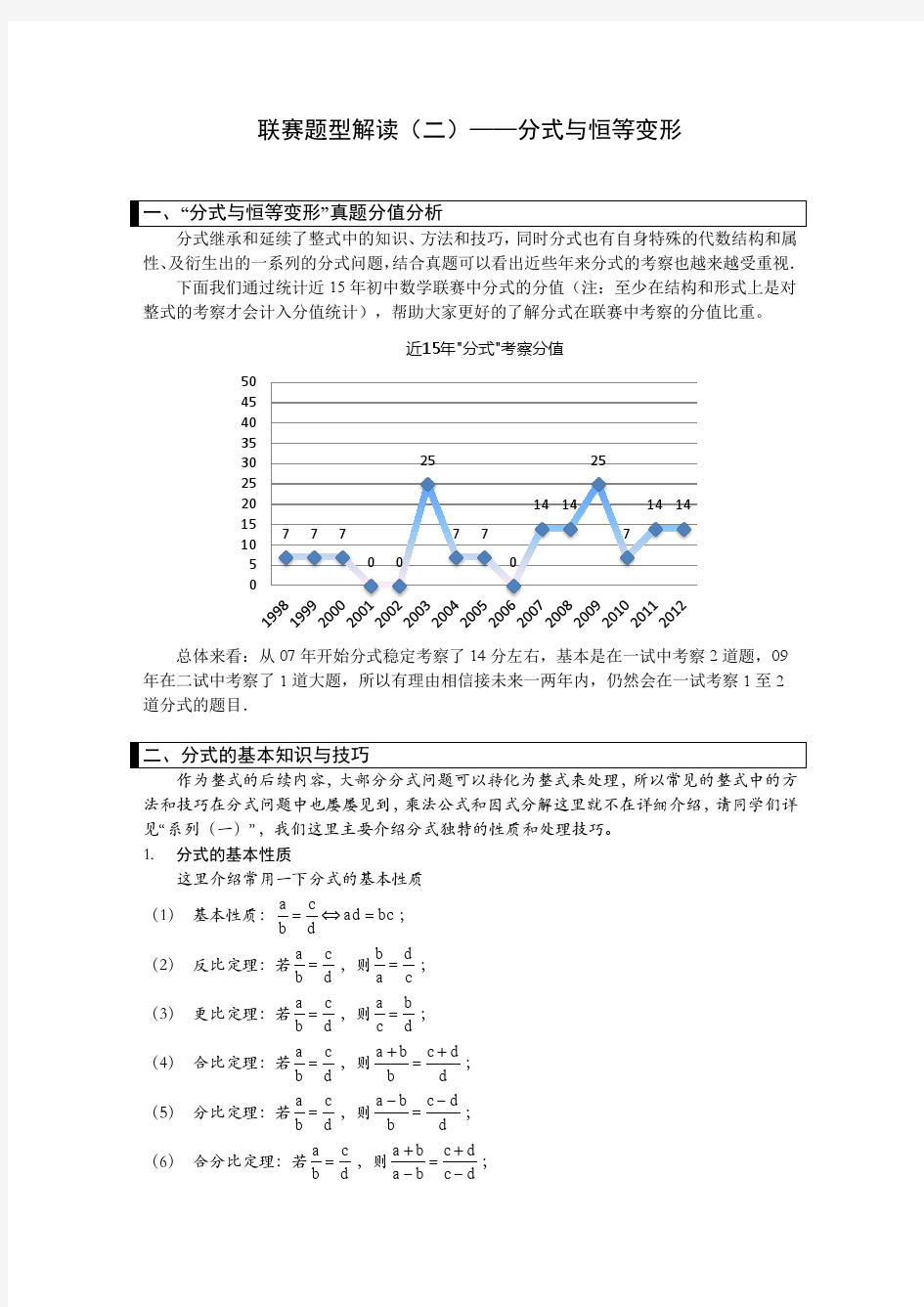
分式与恒等变形-初中数学联赛题型解读系列(二)

分式经典培优竞赛题[1]

1. 若，试判断是否有意义。 2. 计算： 3、解方程： 4. 已知与互为相反数，求代数式 的值。 5. 一列火车从车站开出，预计行程450千米，当它开出3小时后，因特殊任务多停一站，耽误30分钟，后来把速度提高了0.2倍，结果准时到达目的地，求这列火车的速度。 6. 已知，试用含x的代数式表示y，并证明。 6、中考原题： 例1．已知，则M＝__________。 例2．已知，那么代数式的值是_________。 1. 当x取何值时，分式有意义？

3. 计算： 4. 解方程： 5. 要在规定的日期内加工一批机器零件，如果甲单独做，刚好在规定日期内完成，乙单独做则要超过3天。现在甲、乙两人合作2天后，再由乙单独做，正好按期完成。问规定日期是多少天？ 6. 已知 ，求的值。 9、（6分）已知02 =-a a ，求1112421222-÷+--?+-a a a a a a 的值． 21、（6分）设23111 x A B x x ==+--，，当x 为何值时，A 与B 的值相等？ 3、计算（1）?? ? ??--++-y x x y x y x x 2121 (2)4214121111x x x x ++++++- 6、若25452310 A B x x x x x -+=-+--,试求A 、B 的值. 16、已知c b a -=+，求?? ? ??++??? ??++??? ??+b a c c a b c b a 111111的值 17、已知12 --x x =0，则5412x x x ++= 18、设1=abc ，则=++++++++1 11c ca c b bc b a ab a 19、已知20032=+x a ，20042=+x b ，20052=+x c ，且6012=abc ，求 c b a ab c ac b bc a 111---++的值 20、已知31=+b a ab ，41=+c b bc ，51=+c a ac ，求ac bc ab abc ++的值

新人教版八年级数学分式典型例题(供参考)

分式的知识点及典型例题分析 1、分式的定义： 例：下列式子中，y x +15、8a 2 b 、-239a 、y x b a --25、4322b a -、2-a 2、m 1、65xy x 1、21、212+x 、πxy 3、 y x +3、m a 1 +中分式的个数为（ ） （A ） 2 （B ） 3 （C ） 4 (D) 5 练习题：（1）下列式子中，是分式的有 . ⑴275x x -+； ⑵ 123 x -；⑶25a a -；⑷22x x π--；⑸22b b -；⑹22 2xy x y +. （2）下列式子，哪些是分式？ 5a -； 234x +；3 y y ； 78x π+；2x xy x y +-；145b -+. 2、分式有，无意义，总有意义： 例1：当x 时，分式 51 -x 有意义； 例2：分式x x -+212中，当____=x 时，分式没有意义 例3：当x 时，分式112-x 有意义。 例4：当x 时，分式1 2+x x 有意义 例5：x ，y 满足关系 时，分式 x y x y -+无意义； 例6：无论x 取什么数时，总是有意义的分式是（ ） A ． 122+x x B.12+x x C.133+x x D.2 5 x x - 例7：使分式2 +x x 有意义的x 的取值范围为（ ）A ．2≠x B ．2-≠x C ．2->x D ．2

分式的恒等变形教学提纲

分式的恒等变形

第二讲 分式的恒等变形 【专题知识点概述】 分式的恒等变形是代数式恒等变形的一种。它以整式恒等变形为基础，并结合分式自身的特点，因此更具有独特的复杂性和技巧性，在数学竞赛中常常出现有关这方面的命题。 分式的恒等变形涉及到的主要内容有：分式性质、概念的灵活应用，分式的各种运算、化简、求值及恒等证明等等。 一：基本知识 1.分式的运算规律 （1）加减法：)(同分母c b a c b c a ±=± )(异分母bc bd ac c d b a ±=± （2）乘法：bd ac d c b a =? （3）除法：bc ad d c b a =÷ （4）乘方：n n n b a b a =)( 2.分式的基本性质 （1）)0(,≠÷÷==m m b m a b a bm am b a （2）分子、分母与分式本身的符号，改变其中任何两个，分式的值不变。 3.比例的重要性质 （1）如果e f b a e f c d c d b a ===那么,（传递性） （2）如果bd ac c d b a ==那么（内项积等于外项积） （3）如果)(合比性质那么c d c b b a d c b a ±=±= （4）如果)()0(,合分比性质那么d b d b c a c a d b d c b a -+=-+≠-= （5）如果,0,≠+++==n d b n m d c b a 且 那么)(等比性质b a n d b m c a =++++++

4.倒数性质 （1）如果两个数互为倒数，那么这两个数的乘积为1。 （2）如果两个数互为倒数，那么这两个数的同次幂仍互为倒数。 （3）如果两个正数互为倒数，那么这两个正数的和不小于2。 二、有关分式的运算求值问题 乘法公式是进行整式恒等变形的常用的重要的工具，我们通过下面的例题来说明在整式的恒等变形中，如何灵活巧妙的运用乘法公式。 ? 例1.若a 、b 、c 均为非零常数，且满足 a c b a b c b a c c b a ++-=+-=-+， 又abc a c c b b a x ))()((+++=，且0

分式培优竞赛题

1. 若ab a b +--=10，试判断1111 a b -+，是否有意义。 2. 计算：a a a a a a 2211313 +-+--+- 3、解方程：11765556 222-++=-+-+x x x x x x 4. 已知a a 269-+与||b -1互为相反数，求代数式 ()42222222222a b a b ab a b a ab b a b ab b a -++-÷+-++的值。 5. 一列火车从车站开出，预计行程450千米，当它开出3小时后，因特殊任务多停一站，耽误30分钟，后来把速度提高了倍，结果准时到达目的地，求这列火车的速度。 6. 已知x y y =+-2332 ，试用含x 的代数式表示y ，并证明()()323213x y --=。 6、中考原题： 例1．已知M x y xy y x y x y x y 22222 2-=--+-+，则M ＝__________。 例2．已知x x 2 320--=，那么代数式()x x x --+-11132的值是_________。 1. 当x 取何值时，分式2111x x +-有意义 : 3. 计算：x y y x y x y y x ++-+-242442222 4. 解方程：x x x x x x x x ++-++=++-++21436587 5. 要在规定的日期内加工一批机器零件，如果甲单独做，刚好在规定日期内完成，乙单独做则要超过3天。现在甲、乙两人合作2天后，再由乙单独做，正好按期完成。问规定日期是多少天 6. 已知43602700x y z x y z xyz --=+-=≠，，，求x y z x y z +--+2的值。 9、（6分）已知02 =-a a ，求1112421222-÷+--?+-a a a a a a 的值． 21、（6分）设23111 x A B x x ==+--，，当x 为何值时，A 与B 的值相等

奥数-分式恒等变形学

分式恒等变形 方法一、通分：直接通分；逐步通分；移项通分；分组通分；分母因式分解再通分。 例1. 若22004a m +=，22003b m +=，22002c m +=且24abc =，求 111a b c bc ca ab a b c ++---的值。 例2. 若0abc ≠，0a b c ++=，求222 a b c bc ac ab ++的值。 例3. @ 例4. 求证： 2220()()()()()() a bc b a c c ba a b a c a b b c c b a c ---++=++++++ 例5. 设正数x ，y ，z 满足不等式 2222x y z xy +-+2222y z x yz +-+222 2z x y xz +->1,求证x ，y ，z 是某个三角形的三边长 例6. 求分式 24816 1124816 111111a a a a a a +++++ -+++++，当2a =时的值． ； 例7. 若1111a b c a b c ++= ++，求证：777777 1111 a b c a b c ++=++.

例8. 化简:()()()()()() a b b c c a a b b c c a a b b c c a a b b c c a ------+++++++++． ！ 例9. 计算：2132x x x -++262x x ---210 4 x x -- -． 例10. 化简22 32233223222244 113a b a b a a b ab b a a b ab b a b a b a b +++-- +++-+--+-． 例11. # 例12. 化简： () () () () () () 2222222 2 2 2 2 2 a b c b c a c a b a c b a b c b c a ------+ + +-+-+- 例13. 已知0a b c ++=，求证222222222 111 0b c a a c b b a c ++=+-+-+- 例14. 已知0a b c ++=，求222 222222a b c a bc b ac c ab +++++的值 … 例15. 已知1,2xyz x y z =++=， 22216 x y z ++=，求代数式 111 222xy z yz x zx y +++++的值。

初中数学竞赛指导：《分式》竞赛专题训练(含答案)

初中数学竞赛指导：《分式》竞赛专题训练 (含答案) -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN

《分式》竞赛专题训练 1 分式的概念 分母中含有字母的有理式叫做分式.分式的分母不能为零;只有当分式的分母不为零，而分式的分子为零时，分式的值为零. 经典例题 (1)当x 为何值时，分式22211x x --有意义? (2)当x 为何值时，分式22211x x --的值为零? 解题策略 (1) 要使分式22211x x --有意义，应有分母不为零这个分式有两个分母x 和11x -，它们都不为零，即0x ≠且110x -≠，于是当0x ≠且1x ≠时，分式22211x x --有意义， (2) 要使分式22211x x --的值为零，应有2220x -=且110x -≠，即1x =±且1x ≠，于是当1x =-时，分式22211x x --的值为零 画龙点睛 1. 要使分式有意义，分式的分母不能为零. 2. 要使分式的值为零，应有分式的分母不为零，而分式的分子等于零，以上两条，缺一不可. 举一反三 1. (1)要使分式24 x x -有意义的x 的取值范围是( ) (A)2x = (B) 2x ≠ ( C)2x =- (D)2x ≠-

(2)若分式的的值为零，则x 的值为( ) (A)3 (B)3或3- (C) 3- (D)0 2. (1)当x 时，分式 23(1)16x x -+-的值为零; (2) 当x 时，分式2101 x x +≥- 3. 已知当2x =-时，分式x b x a -+无意义;当4x =时，分式的值x b x a -+为零，求a b +. 融会贯通 4. 0≤，求a 值的范围. 2 分式的基本性质 分式的基本性质是:分式的分子和分母都乘以或除以同一个不等于0的整式，分式的值不变.分式的基本运算，例如改变分子、分母或分式的符号以及通分、约分等，都要用到这个性质.本节主要讲解它在解答一些分式计算综合题时的应用. 经典例题 若2731x x x =-+，求2421x x x ++的值 解题策略 因为 2731 x x x =-+，所以0x ≠ 将等式2731x x x =-+的左边分子、分母同时除以x ，得1713x x =-+，所以有

初中数学-八年级--分式习题(附答案)

1 / 6 分式 1、（1）当x 为何值时，分式2 122---x x x 有意义？ （2）当x 为何值时，分式2 122---x x x 的值为零？ 2、计算： （1）()212242-?-÷+-a a a a （2）222---x x x （3）x x x x x x 2421212-+÷??? ? ?-+-+ （4）x y x y x x y x y x x -÷????????? ??--++-3232 （5）4214121111x x x x ++++++- 3、计算（1）已知211222-=-x x ，求?? ? ??+-÷??? ??+--x x x x x 111112的值。 （2）当()00130sin 4--=x 、0 60tan =y 时，求y x y xy x y x x 3322122++-÷???? ??+-222y x xy x -++ 的值。 （3）已知0232 2=-+y xy x （x ≠0，y ≠0），求xy y x x y y x 2 2+--的值。 （4）已知0132 =+-a a ，求142 +a a 的值。 4、已知a 、b 、c 为实数，且满足()() 02)3(432222=---+-+-c b c b a ，求c b b a -+-11的值。 5、解下列分式方程：

（1）x x x x --=-+222； （2）41)1(31122=+++++x x x x （3）1131222=??? ??+-??? ??+x x x x （4）31 24122=---x x x x 6、解方程组：???????==-9 2 113111y x y x 7、已知方程 1 1122-+=---x x x m x x ，是否存在m 的值使得方程无解？若存在，求出满足条件的m 的值；若不存在，请说明理由。 8、某商店在“端午节”到来之际，以2400元购进一批盒装粽子，节日期间每盒 按进价增加20%作为售价，售出了50盒；节日过后每盒以低于进价5元作为售 价，售完余下的粽子，整个买卖过程共盈利350元，求每盒粽子的进价． 9、某书店老板去图书批发市场购买某种图书．第一次用1200元购书若干本， 并按该书定价7元出售，很快售完．由于该书畅销，第二次购书时，每本书的批 发价已比第一次提高了20%，他用1500元所购该书数量比第一次多10本．当按 定价售出200本时，出现滞销，便以定价的4折售完剩余的书．试问该老板这两 次售书总体上是赔钱了，还是赚钱了（不考虑其它因素）？若赔钱，赔多少？若 赚钱，赚多少？ 10、进入防汛期后，某地对河堤进行了加固．该地驻军在河堤加固的工程中出色完成了任务．这是记者 与驻军工程指挥官的一段对话:

奥数-分式恒等变形学

分式恒等变形 方法一、通分：直接通分；逐步通分；移项通分；分组通分；分母因式分解再通分。 例1. 若22004a m +=，22003b m +=，22002c m +=且24abc =，求 111 a b c bc ca ab a b c ++---的值。 例2. 若0abc ≠，0a b c ++=，求222 a b c bc ac ab ++的值。 例3. 求证： 2220()()()()()() a bc b a c c ba a b a c a b b c c b a c ---++=++++++ 例4. 设正数x ，y ，z 满足不等式 2222x y z xy +-+2222y z x yz +-+222 2z x y xz +->1,求证x ，y ，z 是某个三角形的三边长 例5. 求分式 24816 1124816 111111a a a a a a +++++ -+++++，当2a =时的值． 例6. 若1111a b c a b c ++= ++，求证：777777 1111 a b c a b c ++=++.

例7. 化简:()()()()()() a b b c c a a b b c c a a b b c c a a b b c c a ------+++++++++． 例8. 计算：2132x x x -++262x x ---210 4 x x -- -． 例9. 化简22 32233223222244 113a b a b a a b ab b a a b ab b a b a b a b +++-- +++-+--+-． 例10. 化简： () () () () () () 2222222 2 2 2 2 2 a b c b c a c a b a c b a b c b c a ------+ + +-+-+- 例11. 已知0a b c ++=，求证222222222 111 0b c a a c b b a c ++=+-+-+- 例12. 已知0a b c ++=，求222 222222a b c a bc b ac c ab +++++的值 例13. 已知1,2xyz x y z =++=， 22216 x y z ++=，求代数式 111 222xy z yz x zx y +++++的值。

【初中数学】有关分式的竞赛题

有关分式的竞赛题 1、（1997希望杯）已知≠x 0，化简x x x 31211++所得结果是 2、（1996希望杯）化简??? ? ??+-+????? ?? -+-y x xy y x y x xy y x 44的结果是（ ） A 、22x y - B 、22y x - C 、224y x - D 、224y x - 3、（1996希望杯）当2 22225816627123??? ? ?-+????? ??---+÷??? ??+-=a a a a a a a 时，代数式的值是 4、（1998希望杯）若a pm b am pm ab a ab m ---=22，则化简应得到 5、（2000希望杯）若a 为整数，且分式 ()()()()211812624422332-+-+--+--+-a a a a a a a a a a 的值是正整数，则a 的值等于 或等于 6、（1996希望杯）已知1111++++++++=c ac c b bc b a ab a abc ，则 的值是 7、（1997天津）已知 n n n n n n c b a c b a n c b a c b a ++=++++=++11111111为奇数时，，求证： 8、（第13届北京迎春杯）已知b a 、为整数。如果关于x 的一元一次方程()[]与21222-=---a x b x ()()[]327312+--=+-x b x b 的解相同，那么=ab 9、（第11届北京迎春杯）一辆汽车从甲地开往乙地，如果车速提高20%，可以比原定时间提前1小时到达，如果要提前2小时到达，那么车速应比原来车速提高 %。 10、（1997五羊杯）甲、乙、丙三人做某工作。甲独作所需时间为乙、丙合作所需时间的3倍，乙独作所需时间为甲、丙合作所需时间的2倍，则丙独作所需时间为甲、乙合作所需时间的 。， A 、 B 、1.5 C 、 D 、

人教版数学八年级培优和竞赛二合一讲炼教程13、分式总复习

3、分式总复习 【知识精读】 分式定义：（、为整式，中含有字母）性质通分：约分：分式方程定义：分母含有未知数的方程。如解法思想：把分式方程转化为整式方程方法：两边同乘以最简公分母依据：等式的基本性质 注意：必须验根应用：列分式方程解应用题及在其它学科中的应用A B A B A M B M M A B A M B M M x x A B B =??≠=÷÷≠???????-=+???????????????????????????????????????????()()005113【分类解析】 1. 分式有意义的应用 例1. 若，试判断是否有意义。ab a b +--=101111a b -+， 分析：要判断是否有意义，须看其分母是否为零，由条件中等式左边因1111 a b -+，式分解，即可判断与零的关系。 a b -+11， 解： ab a b +--=10 ∴+-+=a b b ()()110 即()()b a +-=110 或∴+=b 10a -=10 中至少有一个无意义。∴-+1111a b ， 2. 结合换元法、配方法、拆项法、因式分解等方法简化分式运算。 例2. 计算：a a a a a a 2211313 +-+--+-

分析：如果先通分，分子运算量较大，观察分子中含分母的项与分母的关系，可采取“分离分式法”简化计算。 解：原式=+-+--+-a a a a a a ()()111313 =-+-+-=- +--=--+++-=- -+-a a a a a a a a a a a a a 1113 1113311322 13(()() ()() ()() 例3. 解方程：11765556 222-++=-+-+x x x x x x 分析：因为，，所以最简公x x x x 27616++=++()()x x x x 25623-+=--()()分母为：，若采用去分母的通常方法，运算量较大。由于()()()()x x x x ++--1623故可得如下解法。x x x x x x x x x x 222225556561561156 -+-+=-+--+=--+ 解： x x x x x x 222561561156 -+--+=--+ 原方程变为11761156 22-++=--+x x x x ∴++=-+∴++=-+∴=176156 7656 2222x x x x x x x x x 经检验，是原方程的根。 x =0 3. 在代数求值中的应用 例4. 已知与互为相反数，求代数式a a 2 69-+||b -1的值。()42222222222 a b a b ab a b a ab b a b ab b a -++-÷+-++ 分析：要求代数式的值，则需通过已知条件求出a 、b 的值，又因为

代数式的恒等变形

代数式的恒等变形 一、常值代换求值法——“1”的妙用 例1 、 已知ab=1，求2 211 11b a +++的值 [解] 把ab=1代入，得 22 11 11b a +++ =22 b ab ab a ab ab +++ =b a a b a b ++ + =1 例2 、已知xyzt=1，求下面代数式的值： 分析 直接通分是笨拙的解法，可以利用条件将某些项的形式变一变． 解 根据分式的基本性质，分子、分母可以同时乘以一个不为零的式子，分式的值不变．利用已知条件，可将前三个分式的分母变为与第四个相同． 同理 练习：1 111,1=++++++++=c ca c b b c b a ab a abc 证明：若 二、配方法 例1、 若实数a 、b 满足a2b2+a2+b2-4ab+1=0，求b a a b + 之值。 [解] ∵a2b2+a2+b2-4ab+1 =(a2b2-2ab+1)(a2-2ab+b2) =(ab-1)2+(a-b)2 则有(ab-1)2+(a-b)2=0 ∴?? ?==-.1,0ab b a 解得?? ?==;1,1b a ?? ?-=-=.1,1b a 当a=1，b=1时，b a a b + =1+1=2 当a=-1，b=-1时， b a a b +=1+1=2 例1 设a 、b 、 c 、 d 都是整数，且m=a2+b2,n=c2+d2,mn 也可以表示成两个整数 的平方和，其形式是______. 解mn=(a2+b2)(c2+d2) =a2c2+2abcd+b2d2+a2d2+b2c2-2abcd =(ac+bd)2+(ad-bc)2

分式方程竞赛题(优.选)

第一讲 分式方程(组)的解法 分母中含有未知数的方程叫分式方程．解分式方程的基本思想是转化为整式方程求解，转化的基本方法是去分母、换元，但也要灵活运用，注意方程的特点进行有效的变形．变形时可能会扩大(或缩小)未知数的取值范围，故必须验根． 例1 解方程 222111++=011828138 x x x x x x +-+--- 解 令y ＝x 2＋2x －8，那么原方程为 111++=0915y y y y x +- 去分母得 y (y －15x )＋(y ＋9x )(y －15x )＋y (y ＋9x )＝0， y 2－4xy －45x 2＝0， (y ＋5x )(y －9x )＝0， 所以 y ＝9x 或y ＝－5x ． 由y ＝9x 得x 2＋2x －8＝9x ，即x 2－7x －8＝0，所以x 1＝－1，x 2＝8； 由y ＝－5x ，得x 2＋2x －8＝－5x ，即x 2＋7x －8＝0，所以x 3＝－8，x 4＝1． 经检验，它们都是原方程的根． 例2 解方程 224727218014x x x x x x +--+＋－＝＋272724x x x -+－18＝0 解 设y ＝241 x x x +-，则原方程可化为y ＋72y －18＝0 y 2－18y ＋72＝0，

所以 y 1＝6或y 2＝12． 当y ＝6时，24=61 x x x +-，x 2＋4x ＝6x －6，故x 2－2x ＋6＝0，此方程无实数根． 当y ＝12时，24=121 x x x +-，x 2＋4x ＝12x －12，故x 2－8x ＋12＝0,故x 2－8x ＋12＝0， 所以 x 1＝2或x 2＝6． 经检验，x 1＝2，x 2＝6是原方程的实数根． 例3 解方程 22631042101322 x x x x x x x x ++++-+=++++ 分析与解 我们注意到：各分式的分子的次数不低于分母的次数，故可考虑先用多项式除法化简分式．原方程可变为 25231+(3)201322 x x x x x --++-=++++， 整理得 253201232 x x x x x ---=++++， 去分母、整理得 x ＋9＝0，x ＝－9． 经检验知，x ＝－9是原方程的根． 例4 解方程 1625+=2736 x x x x x x x x ++++++++＋． 分析与解 方程中各项的分子与分母之差都是1，根据这一特点把每个分式化为整式和真分式之和，这样原方程即可化简．原方程化为

整式恒等变形

第8讲整式恒等变形 模块一恒等变形→降幂迭代与换元 基础夯实 题型一降幂迭代法与大除法 【例1】(第14届“希望杯”邀请赛试题)如果x2＋x－1＝0，那么x3＋2x2＋3＝__________． 【练1】(1990年第一届希望杯初二第一试) 已知3x2＋4x－7＝0，求6x4＋11x3－7x2－3x－7的值．

题型二 整体代入消元法 【例2】(第14届希望杯1试)若x ＋y ＝－1，求x 4＋5x 3y ＋x 2y ＋8x 2y 2＋xy 2＋5xy 3＋y 4的值． 【练2】当x －y ＝1时，求x 4－xy 3－x 3y －3x 2y ＋3xy 2＋y 4的值． 题型三 换元法 强化挑战 【例3】化简(y ＋z －2x )2＋(z ＋x －2y )2＋(x ＋y －2z )2－3(y －z )2－3(x －y )2－3(x －z )2． 【练3】已知x ，y ，z 为有理数(y －z )2＋(z －x )2＋(x －y )2＝(y ＋z －2x )2＋(x ＋z －2y )2＋(x ＋y －2z )2，求()()() ()()()222111111yz zx xy x y z ++++++的值． 模块二 恒等变形→因式分解与不定方程 题型一 因式分解 基础夯实 【例4】(1)已知a 5－a 4b －a 4＋a －b －1＝0，且2a －3b ＝1，则a 3＋b 3的值等于________． (2)若a 4＋b 4＝a 2－2a 2b 2＋b 2＋6，则a 2＋b 2＝________． 【练4】(1)若x 满足x 5＋x 4＋x ＝－1则x ＋x 2＋x 3＋…＋x 2012＝__________． (2)已知15x 2－47xy ＋28y 2＝0，求x y 的值． 强化挑战 【例5】已知：a 、b 、c 为三角形的三条边，且a 2＋4ac ＋3c 2－3ab －7bc ＋2b 2＝0，求证：2b ＝a ＋c ． 【练5】(1)在三角形ABC 中，a 2－16b 2－c 2＋6ab ＋10bc ＝0，其中a ，b ，c 是三角形的三边，求证：a ＋c ＝2b ．

分式方程竞赛题

分式方程竞赛题 Company number：【0089WT-8898YT-W8CCB-BUUT-202108】

第一讲 分式方程(组)的解法 分母中含有未知数的方程叫分式方程．解分式方程的基本思想是转化为整式方程求解，转化的基本方法是去分母、换元，但也要灵活运用，注意方程的特点进行有效的变形．变形时可能会扩大(或缩小)未知数的取值范围，故必须验根． 例1 解方程 解 令y ＝x 2＋2x －8，那么原方程为 去分母得 y (y －15x )＋(y ＋9x )(y －15x )＋y (y ＋9x )＝0， y 2－4xy －45x 2＝0， (y ＋5x )(y －9x )＝0， 所以 y ＝9x 或y ＝－5x ． 由y ＝9x 得x 2＋2x －8＝9x ，即x 2－7x －8＝0，所以x 1＝－1，x 2＝8； 由y ＝－5x ，得x 2＋2x －8＝－5x ，即x 2＋7x －8＝0，所以x 3＝－8，x 4＝1． 经检验，它们都是原方程的根． 例2 解方程 224727218014x x x x x x +--+＋－＝＋272724x x x -+－18＝0 解 设y ＝241 x x x +-，则原方程可化为y ＋72y －18＝0 y 2－18y ＋72＝0， 所以 y 1＝6或y 2＝12． 当y ＝6时，24=61 x x x +-，x 2＋4x ＝6x －6，故x 2－2x ＋6＝0，此方程无实数根．

当y ＝12时，24=121 x x x +-，x 2＋4x ＝12x －12，故x 2－8x ＋12＝0,故x 2－8x ＋12＝0， 所以 x 1＝2或x 2＝6． 经检验，x 1＝2，x 2＝6是原方程的实数根． 例3 解方程 分析与解 我们注意到：各分式的分子的次数不低于分母的次数，故可考虑先用多项式除法化简分式．原方程可变为 25231+(3)201322 x x x x x --++-=++++， 整理得 253201232 x x x x x ---=++++， 去分母、整理得 x ＋9＝0，x ＝－9． 经检验知，x ＝－9是原方程的根． 例4 解方程 1625+=2736 x x x x x x x x ++++++++＋． 分析与解 方程中各项的分子与分母之差都是1，根据这一特点把每个分式化为整式和真分式之和，这样原方程即可化简．原方程化为 111111112736 x x x x -+-=-+-++++， 即 11=(6)(7)(2)(3) x x x x ++++，

代数变形中常用的技巧

代数变形中常用的技巧 数学与应用数学专业 摘要：代数变形是为了达到某种目的或需要而采取的一种手段，是化归、转化和联想的准备阶段，它属于技能性的知识，当然存在着技巧和方法，也就需要人们在学习代数的实践中反复操练才能把握，乃至灵活应用。代数变形技巧是学习掌握代数的重要基础，这种变形能力的强弱直接关系到解题能力的发展。本文就初等代数变形中的解题技巧，作一些论述。关键词代数变形技巧 两个代数式A、B，如果对于其中所含字母的一切允许值它们对应的值都相等，则称这两个代数式恒等，记作A≡B或A=B，把一个代数式换成另一个和它恒等的代数式，叫做代数式的恒等变形。恒等变形是代数的最基本知识，是学好中学数学的基础，恒等变形的理论依据是运算律和运算法则，所以，恒等变形必须遵循各运算法则，并按各运算法则在其定义域内进行变形。 代数恒等变形技巧是学习与掌握代数的重要基础,这种变形能力的强弱直接关系到解题能力的发展。代数恒等变形实质上是为了达到某种目的或需要而采取的一种手段，是化归、转化和联想的准备阶段，它属于技能性的知识，当然存在着技巧和方法，也就需要人们在学习代数的实践中反复操练才能把握，乃至灵活与综合应用。中学生在平时的学习中不善于积累和总结变形经验，在稍复杂的问题面前常因变形方向不清，而导致常规的化归、转化工作难以实施，甚至失败，其后果直接影响着应试的能力及效率。 代数的恒等变形包括的内容较多，本文着重阐述代数运算和解题中常见的变形技巧及应用。 一、整式变形 整式变形包括整式的加减、乘除、因式分解等知识。这些知识都是代数中的最基础的知识。有关整式的运算与化简求值，常用到整式的变形。 例1：化简(y+z-2x)2+(z+x-2y)2+(x+y-2z)2-3(y-z)2-3(z-x)2-3(x-y)2 分析：此题若按常规方法先去括号，再合并类项来进行恒等变形的话，计算会繁杂。而通过观察发现此题是一个轮换对称多项式，就其特点而言，若用换元法会使变形简单，从而也说明了换元法是变形的一种重要方法。 解：设y-z=a, z-x=b, x-y=c,则a+b+c=0，y+z-2x=b-c, x+z-2y=c-a, x+y-2z=a-b。于是原式=(b-c)2+(c-a)2+(a-b)2-3a2-3b2-3c2 =b2-2ac+c2+c2-2ac+a2+a2-2ab+b2-3a2-3b2-3c2 =-a2 -b2-c2-2ac-2ab-2bc =-(a+b+c)2 =0 例2：分解因式 ①(1-x2)(1-y2)-4xy ②x4+y4+ x2y2 分析：本题的两个小题，若按通则变形，则困难重重，不知从何下手，但从其含平方的项来研究，考虑应用配方法会使变形迎刃而解。①题先将括号展开，并把-4xy拆成-2xy和-2xy，再分组就可以配成完全平方式。②题用添项、减项法加上x2y2再减去x2y2，即可配方，然后再进行变形分解。 解：①原式= 1-y2-x2+x2y2-2xy-2xy =(1-2xy+x2y2)-( x2+2xy+ y2)

数学八年级分式竞赛题

1.在x 1、21、212+x 、πxy 3、y x +3、m a 1+中分式的个数有（ ） A 、2个 B 、3个 C 、4个 D 、5个 2.当分式 2 3x -无意义时，x=______ 3.若12 13 x x x x +-÷--有意义，则x 的取值范围是______ 4.用科学记数法表示—0.000 000 0314= ． 5.已知13x x +=，则分式22 1 x x + = 6.下列函数中，是反比例函数的是（ ） A.y=x-1 B.2 8x y = C.x y 21= D.2=x y 7.若函数x k y 1 -= （k ≠1）在每一象限内，y 随x 的增大而减小，则k 的取值范围是（ ） A. k 〉1 B. k 〈1 C. k>0 D. k<0 8.请写出满足：在每一象限内，y 随x 的增大而增大的反比例函数解析式 9.点（1，6）在双曲线k y x =上，则k= 10.若函数()2 10 3k y k x -=+是反比例函数，则常数k= 11.如果点（2，3）和（-3，a ）都在反比例函数x k y =的图象上，则a= . 12.将点p(5,3)向下平移1个单位后，落在函数k y x =的图象上，则k 的值为 13.已知点A ()12,y -，B ()21.5,y -和C ()31,y 都在反比例函数2y x =-的图象上，则1y ，2y ，3y 的大小关系是 14.下列几组数中，不能作为直角三角形三边长度的是（ ）； A 、1.5，2，2.5 B 、3，4，5 C 、5，12，13 D 、20，30，40

15.直角三角形一直角边为cm 12，斜边长为cm 13，则它的面积为 ． 16.在Rt △ABC 中，∠C=90°，若a:b=3:4，c=20，则a= ，b= 。 17.已知一个直角三角形的两边长分别是3和4，则第三边为 。 18.在直角坐标系中，点P （-2，3）到原点的距离是 （ ） （A ）5 （B ）13 （C ）11 （D ）2 19.若将直角三角形的两直角边同时扩大2倍，则斜边扩大为原来的（ ）； A 、2倍 B 、3倍 C 、4倍 D 、5倍 20.如果正方形ABCD 的面积为9 2 ，则对角线AC 的长度为（ ）； A 、3 2 B 、9 4 C 、 3 2 D 、92 21.如图，在Rt △ABC 中，∠C=90°，D 为AC 上一点， 且DA=DB=5，又△DAB 的面积为10，那么DC 的长是（ ） A 、4 B 、3 C 、5 D 、4.5 22.如图，一圆柱高8cm ，底面半径2cm ，一只蚂蚁从点A 爬 到点B 处吃食，要爬行的最短路程（ 取3）是（ ）． A. 20cm B. 10cm C. 14cm D. 无法确定 23.直角三角形的两直角边分别为5、12，则斜边上的高为＿＿＿＿＿＿． 24.木工做一个长方形桌面，量的它的长为60cm,宽为40cm,对角线为70cm,这个桌面 （合格或不合格或无法判断） 25.利用图（1）或图（2）两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理，这个定理称为 ，该定理的结论其数学表达式是 ． A C B D

分式的恒等变形(一)

分式的恒等变形（一） （1）已知2202010a a -+=，则代数式2220202403911a a a -+++的值是__________。 【答案】由已知可得12020a a + =，原式()212202012120202019a a a a =-+++=-++= （2）已知2410a a ++=，则代数式42321912192a a a a a ++++的值是__________。 【答案】由已知可得14a a +=-，22114a a +=，原式22119333211219a a a a + +===++ （3）已知4x y +=-，12xy =-，则1111 y x x y +++++的值是__________。 【答案】由已知可得2240x y +=，原式()()()()()()22 11402423411412115y x x y ++++?-+===-++-+-+ （4）已知4ab x a b = +，则2222x a x b x a x b +++--的值是__________。 【答案】由已知可得()4ab a b x =+， 原式()()()()()()()()() 222222222228222224x a x b x b x a x a b x x ab x a x b x a b x ab x a b x +-++--+-====---++-+ （5）已知612ab a b bc b c ?=??-??=?-?，则ac a c -的值是_________。 【答案】取倒数后两式相加得 14a c ac -=，所以4ac a c =- （6）解方程： ()()()()()111333669218 x x x x x x x ++=++++++ 【答案】裂项相消，111339218x x x ??-= ?++??，解得2x =

分式的恒等变形精讲精练

一、化分式为部分分式的和 【例1】 （4级）(第10届华罗庚金杯决赛) 下面的等式成立：22465()()x y x y x y A x y B -+--=--++，求A 、B . 【例2】 （4级）若代数式(1)(2)(3)x x x x p ++++恰好能分解为两个二次整式的乘积(其中二次项系数均为1， 且一次项系数相同)，则p 的最大值是 . 【例3】 （5级）若213111 a M N a a a -=+ --+，求M 、N 的值. 【例4】 （3级）(06年宁波市重点中学提前考试招生试题)已知2a x +与2b x -的和等于244 x x -，求a ，b . 【例5】 （4级）(2004年第15届培训题)已知正整数,a b 满足111 4 a b +=，则a b +的最大值是 ． 【例6】 （4级）若对于3±以外的一切数，2 8339 m n x x x x -=+--均成立，求mn . 【例7】 （5级）若关于x 的恒等式 222Mx N c x x x a x b +=- +-++中，22 Mx N x x ++-为最简分式，且有a b >，a b c +=， 求N . 【例8】 （4级）将2 6 9 x -化为部分分式. 分式恒等变形（竞赛部分）

【例9】 （4级）化21 (1)(2) x x x ---为部分分式． 【例10】 （4级）将下列分式写成部分分式的和的形式：234 2 x x x +--. 【例11】 （4级）将下列分式写成部分分式的和的形式：32222361 (1)(3) x x x x x -++++. 【例12】 （5级）将下列分式写成部分分式的和的形式：322 41338 (1)(2)(1)x x x x x x -+++--. 【例13】 （4级）计算：2132x x x -++262x x ---2 10 4 x x ---． 【例14】 （4级）将下列分式写成部分分式的和的形式：4322231 (1)(1) x x x x x ++-+-. 二、分式的恒等证明 【例15】 （4级）（1994广东潮州市初中数学竞赛） 求证：()()3322222222 22a a a ab b a ab b a ab b a ab b a b a b ????++--+-=++-+ ???-+? ??? 【例16】 （5级）已知x 、y 、z 为三个不相等的实数，且111 x y z y z x +=+=+，求证：2221x y z =.

八年级数学培优辅导讲义竞赛训练导学案 分式的运算 分式的化简与求值 含答案解析

八年级数学培优辅导讲义竞赛训练导学案 分式的化简与求值 典例剖析 【例l 】 已知2 310a a -+=，则代数式3 61 a a +的值为 ． （“希望杯”邀请赛试题） 解题思路：目前不能求出a 的值，但可以求出13a a +=，需要对所求代数式变形含“1 a a +”． 【例2】 已知一列数1234567,,,,,,,a a a a a a a 且18a =，75832a =， 356 124234567 a a a a a a a a a a a a =====，则5a 为（ ） A ．648 B ．832 C ．1168 D ．1944 （五城市联赛试题） 解题思路：引入参数k ，把17a a 用k 的代数式表示，这是解决等比问题的基本思路． 【例3】 3(0)x y z a a ++=≠． 求 222 ()()()()()() ()()() x a y a y a z a z a x a x a y a z a --+--+---+-+-． （宣州竞赛试题） 解题思路：观察发现，所求代数式是关于x a y a z a ---、、的代数式，而条件可以拆成x a y a z a ---、、的等式，因此很自然的想到用换元法来简化解题过程． 【例4】 已知 1,2,3,xy yz zx x y y z z x ===+++求x 的值． （上海市竞赛试题） 解题思路：注意到联立等式得到的方程组是一个复杂的三元一次方程组，考虑取倒数，将方程组化为简单的形式．

【例5】 不等于0的三个正整数,,a b c 满足1111 a b c a b c ++= ++，求证：,,a b c 中至少有两个互为相反数． 解题思路：,,a b c 中至少有两个互为相反数，即要证明()()()0a b b c c a +++=． （北京市竞赛试题） 【例6】 已知,,a b c 为正整数，满足如下两个条件：①32;a b c ++= ② 1 4 b c a c a b a b c bc ac ab +-+-+-++= 解题思路：本题熟记勾股定理的公式即可解答． （全国初中数学联赛试题） 能力训练 1．若a b c d b c d a ===，则a b c d a b c d -+-+-+的值是 ． （“希望杯”邀请赛试题） 2．已知2 131 x x x =-+，则242 91x x x =-+ ． （广东竞赛试题） 3．若2 2 2 1998,1999,2000a x b x c x +=+=++=且24abc =，则111c a b ab bc ac a b c ++--- 的值为 ． （“缙云杯”竞赛试题） 4．已知 232325 x xy y x xy y +-=--，则11 x y -= ． 5．如果111,1a b b c + =+=，那么1 c a +=（ ）． A ．1 B ．2 C ．12 D ．1 4 （“新世纪杯”竞赛试题）