流体通过颗粒层的流动(20200903201203)
化工原理 第4章 流体通过颗粒层的流动 典型例题题解(2)

第4章 流体通过颗粒层的流动 典型例题
例1:固定床压降公式的应用 用20oC 、101.3KPa的空气通过某固定床脱硫塔,测得如下数据: 空床气速 0.3m/s 空床气速 0.8m/s 单位床层高度的压降 220 Pa/m 单位床层高度的压降 1270 Pa/m
试利用欧根公式估计甲烷在30oC 、0.7MPa下,以空床气速0.4m/s 通过该固定床 脱硫塔时,单位床层高度的压降为多少?已知在 30oC 、0.7MPa条件下,甲烷的 物性数据为: 0 . 012 mPa s ; 4 . 50 kg / m 3 解:欧根公式为
P L
4 . 17
例3:确定板框过滤机的生产条件 利用板框过滤机进行恒压过滤,滤饼可压缩性指数S=0.5,当操作 压力(表压)为P1时,滤框充满滤饼需要1.5hr,现悬浮液不变,滤饼 体积与滤液体积之比c值不变,生产要求框内充满可延长为3hr,则操 作压力P2应调节为原来的多少倍?(过滤介质阻力可忽略)
例4 :转筒真空过滤机的生产能力 某悬浮液,在过滤压力(表压)为3kgf/cm2时,k=5×105m2/s,q =0.01m3/m2,滤饼体积与滤液体积之比c=0.08m3/m3.现拟 e 采用真空过滤机进行过滤,过滤机的型号为GP20-2.6。G代表外 滤面真空过滤机,p代表普通用途。转筒直径2.6m,转筒宽度2.6m, 过滤面积20m2,转速0.13rpm-0.8rpm,浸入角度90º -133º ,生产中拟 采用的转速为0.13rpm,浸入角度130º ,操作真空度为0.7kgf/cm2.滤 饼的压缩性指数s=0.3,滤布阻力在压力改变时不起变化,试求生产 能力,以V滤饼m3/hr表示。并计算滤饼厚度为多少? 解:核算过滤面积, 吹松 洗 涤
第三章 流体流过颗粒和颗粒层的流动1

三、流体通过不规则颗粒
以不同 值,
C
~
D
Re
p
关系,
CD
Rep 2,CD=24 / Rep FD ,u
2、过渡区
2 Rep 1000,CD=15.8 / Re0p.6 FD u1.4, 0.6
3、湍流区 1000 Rep 2105,CD=0.44 FD u2形体曳力
4、湍流边界层区 Rep 2105,CD=0.1 (边界层分离点后移)
二维平面
D
N 2
D维客体,N最小数,σ截面积
第三章 流体通过颗粒及颗粒床层的流动
第一节 概述 第二节 流体通过颗粒的流动 第三节 颗粒在流体中的流动 第四节 流体通过颗粒床层流动 第五节 固体流态化
第二节 流体通过颗粒的流动
曳力和曳力系数
曳力:固体颗粒流动方向受到的力
FD = f (L,u,p,),u相对速度
第一节 概述
化工单元中经常遇到→多相流 固定床反应器 流化床反应器 过滤 吸附-离子交换 沉降 •••
一、单颗粒的特性及表征:
大小 颗粒的特性 表面积
形状 1、对于球形颗粒,只用直径dP 可以表征
V
6
d
3 p
S
d
2 p
aS 6 V dp
2、对于非球形颗粒: 当量直径 球形度
dev 3 6V /,des S /,dea 6 / a
圆柱0.874,一般在0.6~0.7之间
二、颗粒群的特性及表征
1、粒度分布
dp < dpi 的质量分率为Fi,
dpmax处 F=1.0(F:粒度分布函数)
Fi
d pi 0
f
d(dp )
0 f d(d p ) 1
流体经过固体颗粒床层时的三种状态

流体经过固体颗粒床层时的三种状态在流体经过固体颗粒床层时,咱们可以观察到三种有趣的状态。
嘿,想想看,当水流过一堆沙子时,事情可就变得妙趣横生。
那就让我们一起深挖一下吧!1. 流体的初始状态1.1 稳态流动首先,我们得说说“稳态流动”。
这可不是数学老师的公式,而是流体在颗粒床层里悠哉游哉的样子。
就像在沙滩上漫步,水流自顾自地经过沙粒,根本不受影响。
这个时候,颗粒的排列比较均匀,流体的速度也是比较稳定的,简直就像一条懒洋洋的河流,轻轻流过。
1.2 动态变化可是,要是你加点儿劲儿,流速突然提高,那就有意思了。
水流变得像火箭一样,带着冲劲儿穿过颗粒床层。
这个时候,颗粒之间的空隙会被迅速填满,流体会遇到更多的阻力,就像你在拥挤的地铁里,周围都是人,动都动不了。
于是,流体就开始发生变化,速度不再那么稳,流动变得有些“抖动”。
2. 颗粒的反应2.1 颗粒的挪动说到颗粒,那可是个有趣的群体。
它们就像是派对上的小伙伴,一开始有序地待在一起,等水流经过时,竟然开始摇摆起来!一部分颗粒可能会被冲得飞起,另一部分则紧紧抓住地盘,不肯动。
这样一来,流体的流动状态也跟着变化,形成了一种动态的平衡。
2.2 颗粒的沉降而随着时间的推移,颗粒还可能出现沉降现象。
有些颗粒因为流体的冲击,被迫降落到更深的地方,就像是夏天的西瓜,慢慢沉入冰凉的水中。
这一过程可以让我们看到流体和颗粒之间奇妙的互动,简直就是一场精彩的舞蹈。
3. 流体的最终状态3.1 临界点再说说当流体流动到一定程度时,可能会达到一个临界点。
这就像是在喝汽水,喝到最后那一口,泡沫一下子全冒出来,流体的状态会突然变化,可能会变得浑浊不清,或者变得更快,像是直升飞机一样冲出颗粒床层的束缚。
这时,流动的特征发生了翻天覆地的变化,颗粒和流体仿佛在一瞬间达成了一种默契,开始了一场新的冒险。
3.2 最终结果最终,流体经过固体颗粒床层后,留下的往往是一个新的平衡状态。
就像一场激烈的球赛,最后两队都累得不行,却依旧保持着和谐的氛围。
流体绕过颗粒及颗粒床层的流动

第一节流体绕过颗粒及颗粒床层的流动1.1颗粒、颗粒群及颗粒床层的特性一、单个颗粒的性质形状规则(球形)的颗粒:大小:用颗粒的某一个或某几个特征尺寸表示,如球形颗粒的大小用直径d p表示。
比表面积:单位体积颗粒所具有的表面积,其单位为m2/m3,对球形颗粒为:形状不规则(非球形)的颗粒:(1)颗粒的形状系数:表示颗粒的形状,最常用的形状系数是球形度Φs,它的定义式为:相同体积的不同形状颗粒中,球形颗粒的表面积最小,所以对非球形颗粒而言,总有Φs<1。
当然,对于球形颗粒,Φ=1。
(2) 颗粒的当量直径:a.等体积当量直径d evb.等比表面积当量直径d ea对于非球形颗粒,若体积当量直径为d e:二、颗粒群的特性粒度分布(Particle size distributions)粒度分布测定方法(筛分分析):常用筛分法,再求其相应的平均特性参数。
---泰勒(Tyler)标准筛(表3-1)颗粒粒度(Particle size)对于工业上常见的中等大小的混合颗粒,一般采用一套标准筛进行测量,这种方法称为筛分。
用表格表示:筛孔尺寸——颗粒质量;用图表示:颗粒尺寸——质量分率分布函数:质量分数w i(<d pi)与d pi频率函数:质量分数w i(d pi)与颗粒群的平均特性参数:颗粒群的平均粒径有不同的表示法,常用等比表面积当量直径来表示颗粒的平均直径,则混合颗粒的平均比表面积αm为:由此可得颗粒群的比表面积平均当量直径d m为:三、颗粒床层的特性(1)床层的空隙率:单位体积颗粒床层中空隙的体积(ε),即:ε是颗粒床层的一个重要特性,它反映了床层中颗粒堆集的紧密程度,其大小与颗粒的形状、粒度分布、装填方法、床层直径、所处的位置等有关。
一般颗粒床层的空隙率为0.47~0.7。
(2)床层的比表面积单位体积床层中颗粒的表面积称为床层的比表面积。
(忽略颗粒间的接触面积)影响αb的主要因素:颗粒尺寸。
一般颗粒尺寸越小,αb越大。
43 流体通过颗粒床层(固定床)的压降
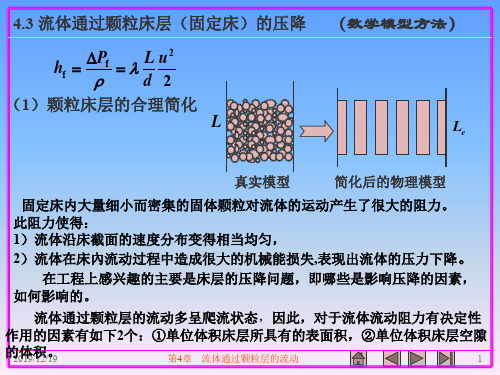
在工程上感兴趣的主要是床层的压降问题,即哪些是影响压降的因素, 如何影响的。
流体通过颗粒层的流动多呈爬流状态,因此,对于流体流动阻力有决定性
作用的因素有如下2个:①单位体积床层所具有的表面积,②单位体积床层空隙
的体积。
2019/12/19
第4章 流体通过颗粒层的流动
1
为保持简化后的物理模型与原真实模型的等效性,必须: 1)所有细管的内表面积等于颗粒床层的全部自由表面积; 2)所有细管的供流体流动的空间等于颗粒床层的空隙容积。
数学模型方法:立足于对所研究过程的深刻理解,按以下主要步骤 进行工作:
1.将复杂的真实过程本身简化成易于用数学方程式描述的物理模型
2.对所得到的物理模型进行数学描述,即建立数学模型;并将真实 过程中的参数引入数学模型;
3.通过实验对数学模型的合理性进行检验,并测定模型参数。
在过滤操作中,液体通过滤饼层 时的压降,就可应用康采尼常数 的压降计算式:
2019/12/19
第4章 流体通过颗粒层的流动
4
在定流义速:较R低e时' ,Rdee’<u12 , λ’=K’/Rue’ , K’=5.0 ,称为Kozeny常数
4 a 1
将λ‘ ,Re’代入单位床层压降的表达式 流体通过颗粒固定床时压降的计算式:
Pf
L
4.3 流体通过颗粒床层(固定床)的压降
hf
Pf
L u2 d2
(1)颗粒床层的合理简化 L
(数学模型方法)
Le
真实模型
简化后的物理模型
固定床内大量细小而密集的固体颗粒对流体的运动产生了很大的阻力。 此阻力使得: 1)流体沿床截面的速度分布变得相当均匀,
颗粒与流体之间的相对流动

第4章 颗粒与流体之间的相对流动4.1 流体绕过颗粒及颗粒床层的流动4.1.1 颗粒床层的特性单个颗粒的特性球形颗粒是最简单的一种颗粒,它的各有关特性均可用单一参数—直径d 全面表示。
体积 63d V π=;表面积 2d S π=; 比表面积 dV S a 6== (单位体积固体颗粒所具有的表面积称为颗粒的比表面积)对非球形颗粒,以当量直径d e 来表征其与球形颗粒在某些特性方面的等效。
(1)体积等效直径d ev 使当量球形颗粒的体积等于真实颗粒的体积V P 。
63ev P d V π=或36πPev V d =(2)表面积等效直径d es 使当量球形颗粒的表面积等于真实颗粒的表面积S P 。
2es P d S π=或πP es S d =(3)比表面积等效直径d ea 使当量球形颗粒的比表面积等于真实颗粒的比表面积a 。
ea P P d V S a 6==或PP ea S V d 6= 球形度φS :体积相同时球形颗粒的表面积与实际颗粒的表面积之比。
相同V PS S S )(=φ 0≤φs ≤1。
颗粒群的特性由大量单个颗粒组成的集合—颗粒群。
(1) 粒度分布不同粒径范围内所含粒子的个数或质量称为粒度分布。
一般用粒度表征颗粒的大小,球形颗粒的粒度就是其直径。
颗粒粒度的测量方法有筛分法、显微镜法、沉降法等。
筛分法通常采用一套标准筛进行测量。
常用的泰勒标准筛以筛号(目数)表示筛孔的大小。
目数:每英寸长度上的孔数。
(2)颗粒群的平均直径pm d :以比表面积相等为原则的球形颗粒群的平均直径pm d :∑=Pi i Pm d x d 1式中:x i —第i 筛号上的筛余量质量分数; 21Pipi Pi d d d +=-。
床层特性(1) 床层的空隙率ε:床层中空隙的体积与床层总体积之比。
ε=床层空隙体积/床层总体积=(床层体积-颗粒所占体积)/床层总体积(2)床层的各向同性各向同性的一个重要特点:床层横截面上可供流体通过的空隙面积(即自由截面)与床层截面之比在数值上等于空隙率ε。
流体的颗粒运动和颗粒流动
流体的颗粒运动和颗粒流动流体的颗粒运动和颗粒流动是流体力学中的重要概念。
它们描述了在流体中颗粒的移动方式和流动行为。
加深对流体的颗粒运动和颗粒流动的理解,对于各个领域的工程和科学研究都具有重要意义。
一、颗粒运动流体的颗粒运动是指在流体中个体颗粒沿着预定轨迹运动的过程。
颗粒运动的特征对于研究流体的性质和行为具有重要影响。
在实际运动过程中,颗粒主要受到流场中的力的作用,如浮力、重力、摩擦力等。
根据颗粒大小和浓度的不同,流体的颗粒运动分为单颗粒运动和多颗粒运动。
单颗粒运动是指一个颗粒在流体中的运动情况。
在单颗粒运动中,颗粒受到流场的作用力,其移动过程可以用牛顿第二定律描述。
此外,流体的物理性质如粘度、密度等也会对颗粒的运动产生影响。
多颗粒运动是指多个颗粒在流体中的相互作用和运动。
在多颗粒运动中,颗粒之间存在相互干扰和相互作用,这些因素会使颗粒的运动变得更加复杂。
二、颗粒流动颗粒流动是指颗粒在流体中按照一定规律的方式流动的现象。
颗粒流动通常在一定空间范围内进行,其速度和方向可能会随时间和空间的变化而变化。
在颗粒流动中,颗粒之间的相互作用和碰撞等因素起着至关重要的作用。
颗粒流动可以分为两种类型:层流和湍流。
层流是指颗粒按照有序且平行的方式流动,颗粒之间的相互作用影响较小。
湍流是指颗粒间流动速度剧烈变化的一种现象,颗粒之间的相互作用十分复杂。
在实际的流体系统中,层流和湍流常常同时存在,并且相互转变。
颗粒流动的性质和行为会受到多种因素的影响,如流体的粘度、流速、颗粒的浓度和大小等。
为了更好地描述和研究颗粒流动,科学家们提出了不同的模型和理论。
其中最著名的是斯托克斯流和牛顿流体模型,它们对于描述颗粒流动的行为具有重要意义。
在工程和科学的研究中,颗粒运动和颗粒流动的研究可以应用于各种领域,如颗粒分离、颗粒传输、颗粒混合等。
例如,在化工领域中,颗粒流动的研究可以帮助优化粉状物料的输送和搅拌过程,提高生产效率。
在生物医学领域中,对血液中红细胞的颗粒运动和流动的研究,有助于理解血液的循环和输送机制。
4 颗粒在流体中的流动 (2)
坏使颗粒形成的网架结构,这个刚好能够破坏颗粒网架结构的切
应力就是屈服切应力τ0。宾汉流体的流变曲线可用下式表达。
du
0
D dy
例如:牙膏、泥浆、血浆等 。
(2)假塑性流体
假塑性流体的流变特点:粘度随切应力的增大而减小。 第一种解释适合于高分子聚合物溶液,这类物质都是亲液性
的,能吸收溶剂而膨胀,最后以大分子状态溶解。如将切向 力施加于此种溶液,则大分子发生定向排列。逐渐将长轴转 成沿流动方向,如切向力越大,转向也越加彻底,因此流动 时粘滞阻力也变得越小了。 第二种解释适用于加有适量凝聚剂的溶胶系统,可用图4-4 的示意图来说明,原有的絮状胶粒因切向力而拆散,切向力 越大,则拆散得越彻底,粘度也降低得越多,如被完全拆散 则粘应不再降低。
(3)在层流流态和紊流流态之间存 在过渡流态,在过渡流态中,粘性力 和惯性力共同控制流体的运动。
图4-6 介质绕流球体的流态 (a) 层流 (b) 紊流
20
为了定性反映惯性力与粘性力的相对大小,常用一个无 量纲数来表示惯性力与粘性力的比值,这个无量纲数称为 雷诺数,用Re表示。对于球形颗粒在流体中的运动,雷诺 数定义:
1. 流体的分类方法
服从牛顿内摩擦定律的流体称为牛顿流体,不服 从牛顿内摩擦定律的流体都称为非牛顿流体。
a)根据切应力τ对剪切速率du/dy的关系曲线特征分类: 图4-2给出了五种类型流体,即牛顿流体(曲线1)、宾汉 流体(曲线2)、 假塑性流体(曲线3)、胀塑性流体(曲 线4)和屈服假塑性流体(曲线5)。
27
间的曲线,得出的阻力公式称为阿连公式。
4. 通用阻力系数公式
阿伯拉罕(F. F. Abraham, 1970)运用边界层的概念分 析球体的阻力,得出非常简洁与适用的阻力系数公式:
流体动力学中的颗粒-粒子流动
流体动力学中的颗粒-粒子流动导言流体动力学是研究流体力学和动力学性质的科学分支。
在流体动力学中,颗粒-粒子流动则是一个重要的研究方向。
颗粒-粒子流动是指在流体中存在着一些离散的颗粒或粒子,在流体的作用下发生运动和相互作用的现象。
颗粒-粒子流动广泛应用于颗粒物料输送、颗粒物料分散、颗粒物料混合等领域。
颗粒-粒子流动的基本概念在流体动力学中,颗粒-粒子流动指的是由流体中的颗粒或粒子组成的流动体系。
颗粒-粒子流动体系不仅包括了流体的流动特性,还包括颗粒或粒子的运动和相互作用。
在颗粒-粒子流动体系中,流体与颗粒或粒子之间存在着复杂的相互作用力,如颗粒-粒子之间的接触力、流体对颗粒或粒子的拖曳力等。
颗粒-粒子流动体系的运动和相互作用规律受到多个因素的影响,包括颗粒或粒子的物理性质、流体的性质以及流动条件等。
颗粒-粒子流动体系的运动可以分为两个方面,一是颗粒或粒子相对于流体的运动,二是颗粒或粒子间的相互作用。
颗粒-粒子流动体系的相互作用力包括接触力、摩擦力、颗粒或粒子对流体的扰动力等。
颗粒-粒子流动的研究方法研究颗粒-粒子流动的方法有多种,包括实验方法、数值模拟方法和理论分析方法等。
实验方法是最直接的研究颗粒-粒子流动行为的方法,通过设计合适的实验装置和测量手段,可以获得颗粒-粒子流动的实际情况。
数值模拟方法则通过建立颗粒-粒子流动的数学模型,利用计算机进行数值求解,得到流体和颗粒或粒子的运动和相互作用的信息。
理论分析方法则是从理论角度出发,通过对颗粒-粒子流动体系的基本方程进行推导和分析,来揭示颗粒-粒子流动的规律和特性。
在实验方法中,常用的手段包括粒子追踪技术、颗粒图像测速技术等。
粒子追踪技术通过跟踪颗粒或粒子的运动轨迹来获得颗粒-粒子流动的信息。
颗粒图像测速技术则是利用高速相机对流体中的颗粒或粒子进行拍摄,然后根据图像处理技术来获得颗粒-粒子流动的速度和位置信息。
数值模拟方法是研究颗粒-粒子流动的重要手段之一,可以对流体动力学和颗粒或粒子运动进行数值计算,揭示流体和颗粒或粒子的运动规律。
流体动力学中的颗粒流动研究
流体动力学中的颗粒流动研究1. 引言流体动力学是研究流体运动规律的一门学科。
在流体动力学中,颗粒流动是一个重要的研究领域。
颗粒流动是指固体颗粒在流体中的运动过程,广泛应用于工程领域,如粉体冶金、环境工程、生物工程等。
研究颗粒流动对于提高工程领域中的生产效率,减少能源消耗具有重要意义。
本文将从颗粒流动的基本原理、数值模拟方法和实验技术等方面探讨流体动力学中颗粒流动的研究进展。
2. 颗粒流动的基本原理2.1 颗粒流动的定义颗粒流动是指在流体中存在大量固体颗粒的流动情况。
颗粒流动的特点是颗粒之间存在相互作用力,并且颗粒与流体之间存在相互作用。
颗粒流动的研究对象主要包括颗粒的运动规律、堆积规律和颗粒与流体之间的相互作用。
2.2 颗粒流动的分类根据颗粒流动过程中颗粒的排列方式和动力学行为,颗粒流动可以分为离散颗粒流动和连续颗粒流动两种情况。
离散颗粒流动是指流体中的颗粒之间存在间隙,并且颗粒之间具有相互作用力。
颗粒在流体中的运动是分离的,并且存在碰撞和摩擦等相互作用。
连续颗粒流动是指流体中的颗粒之间没有间隙,并且颗粒之间的相互作用力可以忽略。
颗粒在流体中的运动是连续的,并且以流体速度为主导。
2.3 颗粒流动的数学描述颗粒流动可以通过欧拉方程和拉格朗日方程进行数学描述。
欧拉方程是基于流体动力学的宏观描述,将流体看作一个连续的介质进行研究。
拉格朗日方程是基于颗粒动力学的微观描述,关注于个别颗粒的运动规律。
3. 颗粒流动的数值模拟方法3.1 离散元法离散元法是一种常用的颗粒流动数值模拟方法,它基于颗粒之间的相互作用力和动量守恒原理,采用离散的数值方法来模拟颗粒的运动过程。
离散元法可以用于研究颗粒在不同流动条件下的堆积、分散、流动和输运等过程。
3.2 欧拉-拉格朗日方法欧拉-拉格朗日方法是将欧拉和拉格朗日方程耦合起来,通过求解欧拉方程来获得流场信息,再通过求解拉格朗日方程来获得颗粒动力学信息。
这种方法可以考虑颗粒与流体之间的相互作用,适用于研究颗粒在复杂流动环境中的运动特性。
