考点 空间基本图形的关系与公理
立体几何公理及定理

立体几何公理及定理一、空间点、线、面之间的关系1、两条直线的位置关系有:2、两个平面的位置关系有:公理1、如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
公理2、过不在一条直线上的三点,有且只有一个平面。
推论1、一组平行直线确定唯一一个平面。
推论2、一条直线及直线外一点确定唯一一个平面。
公理3、如果有两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
公理4(平行公理)、平行于同一直线的两直线平行。
二、平行关系直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
直线与平面平行的性质定理:一条直线与一个平面平行,则过这条直线的任意平面与此平面的交线与该直线平行。
平面与平面平行的判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
平面与平面平行的性质定理:1、如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
2、两平面平行,其中一个平面内的任一直线平行于另一个平面。
3、夹在两个平行平面间的平行线段相等。
4、平行于同一平面的两个平面平行。
三、垂直关系直线与平面垂直的判定定理:一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直。
直线与平面垂直的性质定理:1、垂直于同一个平面的两条直线互相平行。
2、如果一条直线垂直一个平面,那么这条直线垂直于平面内的所有直线。
平面与平面垂直的判定定理:如果一个平面过另一个平面的垂线,那么这两个平面垂直。
平面与平面垂直的性质定理:如果两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
三角公式汇总一、任意角的三角函数1. ①与α终边相同的角的集合(角α与角β的终边重合):{}Z k k ∈+⨯=,360|αββ ②终边在x 轴上的角的集合: {}Z k k ∈⨯=,180| ββ③终边在y 轴上的角的集合:{}Z k k ∈+⨯=,90180| ββ ④终边在坐标轴上的角的集合:{}Z k k ∈⨯=,90| ββ⑤ 若角α与角β的终边在一条直线上,则角α与角β的关系:βα+=k 180 2. 角度与弧度的互换关系:360°=2π 180°=π弧度与角度互换公式: 1rad =π180°≈57.30° 1°=180π3、弧长公式:r l ⋅=||α. 扇形面积公式:211||22s lr r α==⋅扇形 4、三角函数在各象限的符号:(一全二正弦,三切四余弦)正切、余切余弦、正割正弦、余割5、在角α的终边上任取..一点),(y x P ,记:22y x r +=,正弦:r y =αsin 余弦:r x =αcos 正切:xy=αtan 二、同角三角函数的基本关系式 商数关系:αααcos sin tan = 平方关系:1cos sin22=+αα,2211tan cos αα+=,212sin cos (sin cos )αααα+=+ 212sin cos (sin cos )αααα-=-三、诱导公式⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
72空间图形的基本关系与公理
年级:高三科目:数学授课人:
课题
空间图形的基本关系与公理
第72课时
教学
目标
1了解可以作为推理依据的公理和定理.
2.能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题.
重点
证明所作的角是异面直线所成的角.
中心发言人
难点
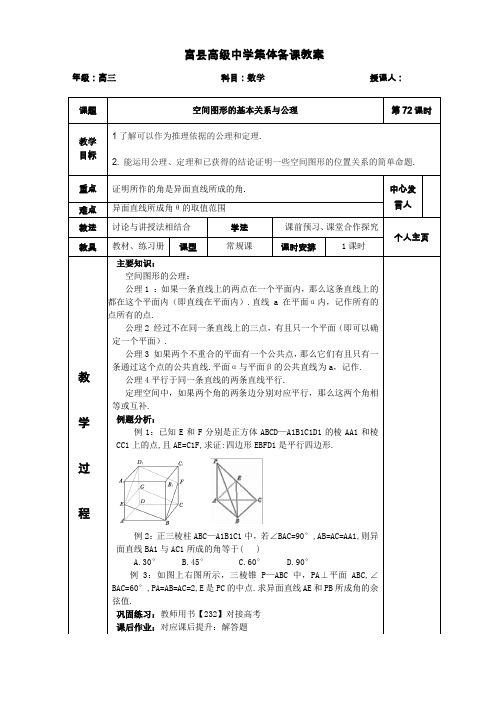
异面直线所成角θ的取值范围源自教法讨论与讲授法相结合例2:正三棱柱ABC—A1B1C1中,若∠BAC=90°,AB=AC=AA1,则异面直线BA1与AC1所成的角等于()
A.30°B.45°C.60°D.90°
例3:如图上右图所示,三棱锥P—ABC中,PA⊥平面ABC,∠BAC=60°,PA=AB=AC=2,E是PC的中点.求异面直线AE和PB所成角的余弦值.
学法
课前预习、课堂合作探究
个人主页
教具
教材、练习册
课型
常规课
课时安排
1课时
教
学
过
程
主要知识:
空间图形的公理:
公理1:如果一条直线上的两点在一个平面内,那么这条直线上的都在这个平面内(即直线在平面内).直线a在平面α内,记作所有的点所有的点.
公理2经过不在同一条直线上的三点,有且只一个平面(即可以确定一个平面).
巩固练习:教师用书【232】对接高考
课后作业:对应课后提升:解答题
教
后
反
思
备课组长签字:年月日
公理3如果两个不重合的平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.平面α与平面β的公共直线为a,记作.
公理4平行于同一条直线的两条直线平行.
定理空间中,如果两个角的两条边分别对应平行,那么这两个角相等或互补.
【优化方案】高三数学一轮复习 第8章8.3空间图形的基本关系及公理课件 文 北师大版

4.(2010年西安调研)已知a、b是异面直线,下 列命题: ①存在一个平面α,使a∥α,且b∥α;②存在一 个平面α,使a⊥α且b⊥α;③存在一个平面α, 使a⊂α,且b与α相交;④存在一个平面α,使a, b到平面α的距离相等. 其中正确命题是________. 答案:①③④
5.如图所示,在正方体ABCD-A1B1C1D1中, AB1与C1B所成的角是________.
意时,应仔细分析问题中每一句话的含义.
三点共线与三线共点问题 利用两平面交线的惟一性,证明诸点在两平面的 交线上是证明空间诸点共线的常用方法.证明点 共线的方法从另一个角度讲也就是证明三线共点 的方法. 证明线共点,基本方法是先确定两条直线的交点, 再证交点在第三条直线上,也可将直线归结为两 平面的交线,交点归结为两平面的公共点,由公 理2证明点在直线上.
课前热身 1.(教材习题改编)如图所示,将无盖正方体纸盒 展开,直线AB,CD在原正方体中的位置关系是 ( )
A.平行
B.垂直
C.相交成60°
D.异面成60°
答案:D
2.若三个平面两两相交,且三条交线相交于一 点,则这三个平面把空间分成( )部分. A.5 B.6 C.7 D.8 答案:D
3.下列四个命题中,正确命题的个数是( ) ①空间不同三点确定一个平面; ②垂直于同一直线的两直线平行; ③一条直线和两平行线中的一条相交,也必和另 一条相交; ④两组对边相等的四边形是平行四边形. A.0 B. 1 C.2 D.3 答案:A
1 中点,得 GH 綊 AD,易得 BC 綊 GH,从而四 2 边形 BCHG 是平行四边形. (2)证明 D 点在 EF、CH 确定的平面内.
【解】
(1)证明:由已知 FG=GA, 1 FH=HD,可得 GH 綊 AD. 2 1 又 BC 綊 AD, 2 ∴GH 綊 BC, ∴四边形 BCHG 为平行四边形.
届数学一轮复习第七章立体几何第三节空间图形的基本关系与公理课时规范练文含解析

第七章立体几何第三节空间图形的基本关系与公理课时规范练A组—-基础对点练1.若直线a⊥b,且直线a∥平面α,则直线b与平面α的位置关系是()A.bαB.b∥αC.bα或b∥αD.b与α相交或bα或b∥α解析:b与α相交或bα或b∥α都可以.答案:D2.(2020·江西景德镇模拟)将图①中的等腰直角三角形ABC沿斜边BC上的中线折起得到空间四面体ABCD(如图②),则在空间四面体ABCD中,AD与BC的位置关系是()A.相交且垂直B.相交但不垂直C.异面且垂直D.异面但不垂直解析:在题图①中,AD⊥BC,故在题图②中,AD⊥BD,AD⊥DC,又因为BD∩DC=D,所以AD⊥平面BCD,又BC平面BCD,D不在BC上,所以AD⊥BC,且AD与BC异面,故选C。
答案:C3.(2020·湖北荆州模拟)设α,β是两个不同的平面,a,b是两条不同的直线,则下列命题正确的是()A.若a⊥b,b⊥α,则a∥αB.若aα,bβ,α∥β,则a与b是异面直线C.若a⊥α,b⊥β,a⊥b,则α⊥βD.若α∩β=b,a∥b,则a∥α且a∥β解析:选项A,a可能在α内,故A错;选项B,a与b可能平行可能异面,故B错;选项D,a可能在α或β内,故D错.故选C.答案:C4.(2020·安徽安庆模拟)在正方体ABCD。
A1B1C1D1中,点P是线段BC1上任意一点,则下列结论中正确的是()A.AD1⊥DP B.AC1⊥DPC.AP⊥B1C D.A1P⊥B1C解析:在正方体ABCD。
A1B1C1D1中,∵B1C⊥BC1,B1C⊥AB,BC1∩AB=B,∴B1C⊥平面ABC1D1,∵点P是线段BC1上任意一点,∴AP平面ABC1D1,∴AP⊥B1C.故选C.答案:C5.(2020·河北模拟)若a,b是不同的直线,α,β是不同的平面,则下列命题中正确的是()A.若a∥α,b∥β,a⊥b,则α⊥βB.若a∥α,b∥β,a∥b,则α∥βC.若a⊥α,b⊥β,a∥b,则α∥βD.若a∥α,b⊥β,a⊥b,则α∥β解析:∵a∥b,a⊥α,∴b⊥α,又b⊥β,∴α∥β.故选C.答案:C6. (2020·广东东莞模拟)如图,在三棱柱ABC.A1B1C1中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC的中点,则下列叙述正确的是()A.CC1与B1E是异面直线B.AC⊥平面ABB1A1C.AE,B1C1为异面直线,且AE⊥B1C1D.A1C1∥平面AB1E解析:因为CC1与B1E都在平面CC1B1B内,且CC1与B1E是相交直线,所以选项A错误.假设AC⊥平面ABB1A1,则AC⊥AB,即∠CAB=90°,从而可得∠C1A1B1=90°,这与题设“底面三角形A1B1C1是正三角形”矛盾,故假设错误,即选项B错误.因为点B1∉AE,直线B1C1交平面AEB1于点B1,所以AE,B1C1为异面直线;由题意可知△ABC是正三角形,又E是BC的中点,所以AE⊥BC,结合BC∥B1C1可得AE⊥B1C1,故选项C正确.因为直线AC交平面AB1E于点A,又AC∥A1C1,所以直线A1C1与平面AB1E相交,故选项D错误.综上,选C。
高中数学 第一章 立体几何初步 1234 空间图形的基本关系与公理导学案(无答案)北师大版必修2 学

4空间图形的基本关系与公理【教学目标】1.理解空间中点、线、面的位置关系;2.理解空间中平行直线、相交直线、异面直线、平行平面、相交平面等概念;3.掌握三个公理及推论,并能运用它们去解决有关问题;4.会用集合语言来描述点、直线和平面之间的关系以及图形的性质.【重点难点】掌握三个公理及推论,并能运用它们去解决有关问题【教法教具】以讲学稿为依托的探究式教学方法,多媒体教学【教学课时】 2课时【教学流程】自主学习(课前完成,含独学和质疑)1.空间点与直线的位置关系(1)如果点P在直线a,记作P∈a.(2)如果点P在直线a,记作P∉a.2.空间点与平面的位置关系(1)如果点P在平面α,记作P∈α.(2)如果点P在平面α,记作P∉α.3.空间两条直线的位置关系(1)平行直线:如果直线a和b在同一个平面内,但没有,这样的两条直线叫作平行直线,记作a∥b.(2)相交直线:如果直线a和b有且只有公共点P,这样的两条直线叫作相交直线,记作a∩b=P.(3)异面直线:如果直线a和b不同在平面内,这样的两条直线叫作异面直线.4.空间直线与平面的位置关系(1)直线在平面内:如果直线a与平面α有个公共点,我们称直线a在平面α内,记作aα.(2)直线与平面相交:如果直线a与平面α有且只有公共点P,我们称直线a与平面α相交于点P,记作a∩α=P.(3)直线与平面平行:如果直线a与平面α没有,我们称直线a与平面α平行,记作a∥α.5.空间平面与平面的位置关系(1)平行平面:如果平面α与平面β没有,我们称平面α与平面β是平行平面,记作α∥β.(2)相交平面:如果平面α和平面β不重合,但有,我们称平面α与平面β相交于直线l,记作α∩β=l.6.公理1如果一条直线上的在一个平面内,那么这条直线上所有的点都在这个平面内(即直线在平面内).7.公理2经过的三点,有且只有一个平面.或简单说成:不共线的三点确定一个平面.8.公理3如果两个的平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.9.公理2的推论推论1:经过一条直线和这条,有且只有一个平面;推论2:经过两条直线,有且只有一个平面;推论3:经过两条直线,有且只有一个平面.合作探究:(对学、群学)探究点一空间点、线、面的位置关系导引观察下面三个长方体回答下列问题.思考 1 观察长方体,你能发现长方体有多少个顶点?多少条棱?多少个面?棱所在的直线,以及侧面、底面之间的位置关系吗?例1 将下面用符号语言表示的关系用文字语言予以叙述,并用图形语言予以表示:α∩β=l,A∈l,ABα,ACβ.跟踪训练1 根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:(1)A∈α,B∉α;(2)lα,m∩α=A,A∉l;(3)P∈l,P∉α;Q∈l,Q∈α.探究点二空间图形的公理思考1 实际生活中,我们有这样的经验:把一根直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.从经验中我们能得到什么结论呢?思考2 如何用符号语言表示公理1?公理1有怎样的用途?思考3 生活中经常看到用三角架支撑照相机;测量员用三角架支撑测量用的平板仪;有的自行车后轮旁只安装一只撑脚.上述事实和类似经验可以归纳出平面怎样的性质?思考4 如何用符号语言表示公理2?公理2有怎样的用途?思考5 如图所示,直线BC外一点A和直线BC能确定一个平面吗?为什么?思考6 如图所示,两条相交直线能不能确定一个平面?为什么?思考7 如图所示,两条平行直线能不能确定一个平面?为什么?思考8 我们已经看到各种棱柱、棱锥的每两个相交的面之间的交线都是直线段,由此你能总结出怎样的结论?思考9 如何用符号语言表示公理3?公理3有怎样的用途?例2 已知a∥b∥c,l∩a=A,l∩b=B,l∩c=C.求证:a,b,c和l共面.跟踪训练2 已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.求证:直线l1、l2、l3在同一平面内.探究点三共线问题例3 已知△ABC在平面α外,AB∩α=P,AC∩α=R,BC∩α=Q,如图所示.求证:P、Q、R三点共线.跟踪训练3 如图所示,在正方体ABCD—A1B1C1D1中,E为AB的中点,F为AA1的中点.求证:CE、D1F、DA三线交于一点.【达标拓展】(检测、拓展)1.若A∈平面α,B∈平面α,C∈直线AB,则( )A.C∈αB.C αC.ABαD.AB∩α=C2.平行六面体ABCD—A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( )A.3 B.4 C.5 D.63.若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成________部分.4.如图,已知D,E是△ABC的边AC,BC上的点,平面α经过D,E两点,若直线AB与平面α的交点是P,则点P与直线DE的位置关系是________.【学后反思】【练案】一、基础过关1.下列图形中,不一定是平面图形的是( )A.三角形B.菱形C.梯形D.四边相等的四边形2.空间中,可以确定一个平面的条件是( )A.两条直线B.一点和一条直线C.一个三角形 D.三个点3.如图所示,用符号语言可表示为( )A.α∩β=m,nα,m∩n=AB.α∩β=m,n∈α,m∩n=AC.α∩β=m,nα,A m,A nD.α∩β=m,n∈α,A∈m,A∈n4.已知平面α与平面β、γ都相交,则这三个平面可能的交线有( ) A.1条或2条B.2条或3条C.1条或3条 D.1条或2条或3条5.给出以下命题:①和一条直线都相交的两条直线在同一平面内;②三条两两相交的直线在同一平面内;③有三个不同公共点的两个平面重合;④两两平行的三条直线确定三个平面.其中正确命题的个数是________.6.已知α∩β=m,aα,bβ,a∩b=A,则直线m与A的位置关系用集合符号表示为________.7.如图,梯形ABDC中,AB∥CD,AB>CD,S是直角梯形ABDC所在平面外一点,画出平面SBD和平面SAC的交线,并说明理由.二、能力提升8.空间不共线的四点,可以确定平面的个数是( )A.0B.1C.1或4D.无法确定9.空间中A,B,C,D,E五个点,已知A,B,C,D在同一平面内,B,D,C,E在同一平面内,那么这五点( )A.共面B.不一定共面C.不共面D.以上都不对10.已知α、β为平面,A、B、M、N为点,a为直线,下列推理错误的是________.①A∈a,A∈β,B∈a,B∈β⇒aβ;②M∈α,M∈β,N∈α,N∈β⇒α∩β=MN;③A∈α,A∈β⇒α∩β=A;④A、B、M∈α,A、B、M∈β,且A、B、M不共线⇒α、β重合.11.如图,在长方体ABCD-A1B1C1D1中,O1是A1C1与B1D1的交点,长方体体对角线A1C交截面AB1D1于点P.求证:O1,P,A三点在同一条直线上.12.已知a,b,c,d是两两相交且不共点的四条直线,求证:a,b,c,d共面.三、探究与拓展13.在四面体ABCD中,E,G分别为BC,AB的中点,F在CD上,H在AD上,且有DF∶FC=DH∶HA=2∶3.求证:EF,GH,BD交于一点.。
【优化方案】2012高考数学总复习 第8章§8.3空间图形的基本关系及公理精品课件 理 北师大版

如图所示, 如图所示,已知空间四边形 ABCD 中, E,H 分别是边 AB,AD 的中点,F,G 分别是 , 的中点, , , CF CG 2 上的点, 边 BC,CD 上的点,且CB=CD= , , 3 (1)求证:三条直线 EF,GH,AC 交于一点. 求证: 交于一点. 求证 , , AE CF AH CG (2)若在本题中, = =2, 若在本题中, 若在本题中 EB FB , HD=GD=3, , 其他条件不变. 求证: EH, FG, 三线共点. BD 其他条件不变. 求证: , , 三线共点.
AE CF (2)因为 = =2, 因为EB FB ,
所以 EF∥AC. ∥ AH CG 又HD=GD=3, , ∴HG∥AC, ∥ ,
∴EF∥HG,且EF>HG. ∥ , 所以四边形EFGH为梯形. 为梯形. 所以四边形 为梯形 交于点P, 设EH与FG交于点 , 与 交于点 则P∈平面 ∈平面ABD,P∈平面 , ∈平面BCD, , 所以P在两平面的交线 上 所以 在两平面的交线BD上, 在两平面的交线 所以EH、 、 三线共点 三线共点. 所以 、FG、BD三线共点. 【易错警示】 易错警示】 缺乏理论依据. 缺乏理论依据. 证明线共点时, 证明线共点时,两条直线相交可能
(4) 空 间 直 线 和 平 面 的 位 置 关 系 有 三 种 : 直线在平面内 __________________ 、 直 线 和 平 面 相 交 、 直线与平面平行 . _______________. (5) 空 间 两 平 面 的 位 置 关 系 有 两 种 : 两平面平行和两平面相交 _____________________________. . 思考感悟 直线吗? 直线吗? 若aα,b β,则a,b就一定是异面 , , , 就一定是异面
高中数学高考第3节 空间点、直线、平面之间的位置关系 课件

主
回 顾
c∥b,从而a∥b,这与a与b是异面直线矛盾,故①正确.
课 后
对于②,a与b可能异面垂直,故②错误.
限 时
集
课 堂
对于③,由a∥b可知a∥β,又α∩β=c,从而a∥c,故③正
训
考
点 确.
探
究
返 首 页
41
课
前
自
主 回
(2)图①中,直线GH∥MN;图②中,G,H,N三点共面,但M 课
顾
∉平面GHN,因此直线GH与MN异面;图③中,连接MG(图略),
探
究 _有__且__只__有__一__条___过该点的公共直线.
返 首 页
5
课
前 自
(4)公理2的三个推论
主
回 顾
推论1:经过一条直线和这条直线外的一点,有且只有一个平 课 后
面.
限 时
集
课 堂
推论2:经过两条相交直线,有且只有一个平面.
训
考
点
推论3:经过两条平行直线,有且只有一个平面.
探
究
返 首 页
后 限
些点都是这两个平面的公共点,再根据基本公理3证明这些点都在
时 集
课
训
堂 考
交线上;②同一法:选择其中两点确定一条直线,然后证明其余点
点
探 也在该直线上.
究
返 首 页
25
课 前
(2)证明线共点问题:先证两条直线交于一点,再证明第三条直
自
主 线经过该点.
回
课
顾
(3)证明点、直线共面问题:①纳入平面法:先确定一个平面,
探
究
返 首 页
43
1.下列结论中正确的是 ( )
1.4.1__空间图形基本关系的认识__1.4.2__空间图形的公理(公理1、2、3)

C 共点B′,经过点B有且只有一条过该点的
公共直线B′C′.
公理3
如果两个不重合的平面有一个公共点,那么
它们有且只有一条通过这个点的公共直线.
P l , 且P l
P
l
作用: ①判断两个平面相交的依据. ②判断点在直线上.
1、如图,用符号表示下列图形中点、直线、平面之间 的位置关系.
(5)空间平面与平面的位置关系有两种: I 如图②中,平面α和平面β没有公共点,这样
的两个平面叫作平行平面,记作:α∥β; II 如图③中,平面α和平面β不重合,但有公共点,
这样的两个平面叫作相交平面.
思考交流
1. 观察图①②③所示的长方体,再举出一些点、线、面
的位置关系的例子.
2.
观察你周围的一些实物,指出一些点、线、面的位置
关系.
课堂探究2
空间图形的公理 思考1:如果直线 l 与平面α有一个公共点P,直线 l 是 否在平面α内?
思考2:如果直线l与平面α 有两个公共点,直线l是否在
平面α 内?
实际生活中,我们有这样的经验:把一根直尺边缘 上的任意两点放到桌面上,可以看到,直尺的整个边缘 就落在了桌面上.
公理1
如果一条直线上的两点在一个平面内,那么这
条直线上所有的点都在这个平面内(即直线在平面内).
A
l B
A l ,B l ,A ,B l
作用:
在生产、生活中, 人们经过长期观察与实 践,总结出关于平面的 一些基本性质,我们把 它作为公理.这些公理 是进一步推理的基础.
判定直线是否在平面内.
思考3:我们知道,两点确定一条直线.那么怎样确定一个
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间基本图形的关系与公理
1.已知平面外一点P 和平面内不共线三点A 、B 、C ,A ′、B ′、C ′分别在P A 、PB 、PC 上,若延长A ′B ′、B ′C ′、A ′C ′与平面分别交于D 、E 、F 三点,则D 、E 、F 三点( )
A .成钝角三角形
B .成锐角三角形
C .成直角三角形
D .在一条直线上
2.已知α、β是两个不同的平面,直线a ⊂α,直线b ⊂β,命题p :a 与b 没有公共点,命题q :α∥β,则p 是q 的( )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
3.若P 是两条异面直线l 、m 外的任意一点,则( )
A .过点P 有且仅有一条直线与l 、m 都平行
B .过点P 有且仅有一条直线与l 、m 都垂直
C .过点P 有且仅有一条直线与l 、m 都相交
D .过点P 有且仅有一条直线与l 、m 都异面
4. l 1,l 2,l 3是空间三条不同的直线,则下列命题正确的是( )
A .l 1⊥l 2,l 2⊥l 3⇒l 1∥l 3
B .l 1⊥l 2,l 2∥l 3⇒l 1⊥l 3
C .l 1∥l 2∥l 3⇒l 1,l 2,l 3共面
D .l 1,l 2,l 3共点⇒l 1,l 2,l 3共面
5.设P 表示一个点,a 、b 表示两条直线,α、β表示两个平面,给出下列四个命题,其中正确的命题是( )
①P ∈a ,P ∈α⇒a ⊂α; ②a ∩b =P ,b ⊂β⇒a ⊂β
③a ∥b ,a ⊂α,P ∈b ,P ∈α⇒b ⊂α; ④α∩β=b ,P ∈α,P ∈β⇒P ∈b
A .①②
B .②③
C .①④
D .③④
6.平面α∩β=l ,点A ∈α,点B ∈α,且C ∉l ,C ∈β,又AB ∩l =R ,如图所示,过A 、B 、C 三点确定的平面为γ,则β∩γ是( )
A .直线AC
B .直线B
C C .直线CR
D .直线AR
7. 已知a,b 是异面直线,直线c∥直线a,则c 与b( )
A.一定是异面直线
B.一定是相交直线 C .不可能是平行直线 D.不可能是相交直线
8.以下四个命题中,正确命题的个数是( )
①不共面的四点中,其中任意三点不共线;
②若点A 、B 、C 、D 共面,点A 、B 、C 、E 共面,则A 、B 、C 、D 、E 共面;
③若直线a 、b 共面,直线a 、c 共面,则直线b 、c 共面;
④依次首尾相接的四条线段必共面.
9.已知直线l ,若直线m 同时满足以下三个条件:m 与l 是异面直线;m 与l 的夹角为
3
(定值);m 与l 的距离为π.那么,这样的直线m 的条数为( )
A.0
B.2
C.4
D.无穷
10.如图,E、F是AD上互异的两点,G、H是BC上互异的两点,由图可知,①AB与CD互为异面直线;②FH分别与DC、DB 互为异面直线;③EG与FH互为异面直线;④EG与AB互为异面直线.其中叙述正确的是( )
A.①③
B.②④
C.①④
D.①②
11.如图,在正方体ABCD—A1B1C1D1中,E、F分别是A1B1、CC1的中点,则异面直线AE与BF所成角的余弦值为( )
1342
....
A B C D
5555
12.在空间四边形ABCD中,各边边长均为1,若BD=1,则AC的取值范围是________.
13.如图,正方体ABCD—A1B1C1D1中,M是DD1的中点,O是底面正方形ABCD的中心,P为棱A1B1上任意一点,则直线OP 与直线AM所成角的大小等于________.
14.如图所示,正方体ABCD-A1B1C1D1中,给出下列五个命题:
①直线AC1在平面CC1B1B内;
②设正方形ABCD与A1B1C1D1的中心分别为O、O1,则平面AA1C1C与平面BB1D1D的交线为OO1;
③由点A、O、C可以确定一个平面; ④由A、C1、B1确定的平面是ADC1B1;
⑤若直线l是平面AC内的直线,直线m是平面D1C内的直线;若l与m相交,则交点一定在直线CD上.
其中真命题的序号是________.
15.如图,正方体ABCD—A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:
①直线AM与CC1是相交直线; ②直线AM与BN是平行直线;
③直线BN与MB1是异面直线; ④直线AM与DD1是异面直线.
其中正确的结论为________(注:把你认为正确的结论的序号都填上).
16.在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是________(写出所有正确结论的编号).
①矩形;②不是矩形的平行四边形;
③有三个面为等腰直角三角形,另一个面为等边三角形的四面体;
④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.
17.a,b,c是空间中的三条直线,下面给出五个命题:
①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a∥c;
③若a与b相交,b与c相交,则a与c相交;④若a⊂平面α,b⊂平面β,则a,b一定是异面直线;⑤若a,b与c成等角,则a∥b.
上述命题中正确的命题是________(只填序号).
18.在图中,G、H、M、N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH、MN是异面直线的图形有________.(填上所有正确答案的序号)
19.已知E和F分别是正方体ABCD-A1B1C1D1的棱AA1和棱CC1上的点,且AE=C1F,求证:四边形EBFD1是平行四边形.
20.在正方体AC1中,E是CD的中点,连结AE并延长与BC的延长线交于点F,连结BE并延长交AD的延长线于点G,连结FG.
求证:直线FG⊂平面ABCD且直线FG∥直线A1B1.
21..空间四边形ABCD中,AB=CD且AB与CD所成的角为30°,E、F分别是BC、AD的中点,求EF与AB所成角的大小.
22.如图所示,S是正三角形ABC所在平面外一点,SA=SB=SC,且∠ASB=∠BSC=∠CSA=90°,M、N分别是AB和SC的中点,求异面直线SM和BN所成角的余弦值.。
