高三数学:专题一三角函数与解三角形-第1讲-三角函数的图象与性质
三角函数的图象与性质(高三一轮复习)

数学 N 必备知识 自主学习 关键能力 互动探究
— 27 —
(4)三角函数型函数奇偶性的判断除可以借助定义外,还可以借助其图象与性 质,如在y=Asin(ωx+φ)中代入x=0,若y=0,则为奇函数,若y为最大或最小值, 则为偶函数.若y=Asin(ωx+φ)为奇函数,则φ=kπ(k∈Z),若y=Asin(ωx+φ)为偶函 数,则φ=2π+kπ(k∈Z).
A.y=fx-π4为奇函数 B.y=fx-4π为偶函数 C.y=fx+4π-1为奇函数 D.y=fx+π4-1为偶函数
数学 N 必备知识 自主学习 关键能力 互动探究
— 21 —
(2)(2022·新高考Ⅰ卷)记函数f(x)=sin
ωx+π4
+b(ω>0)的最小正周期为T.若
2π 3
<T<π,且y=f(x)的图象关于点32π,2中心对称,则fπ2=( A )
— 10 —
数学 N 必备知识 自主学习 关键能力 互动探究
— 11 —
2.(易错题)(2023·宜昌检测)下列函数中,在其定义域上是偶函数的是( B )
A.y=sin x
B.y=sin x
C.y=tan x
D.y=cosx-π2
解析 对于A,∵y=sin x的定义域为R,sin(-x)=-sin x,∴y=sin x为奇函
数,A错误;对于B,∵y=
sin
x
的定义域为R,
sin-x
=
-sin
x
=
sin
x
,∴y=
sin x为偶函数,B正确;对于C,∵y=tan x的定义域为kπ-π2,kπ+2π(k∈Z),即定 义域关于原点对称,tan(-x)=-tan x,∴y=tan x为奇函数,C错误;对于D,∵y=
2024高中数学解三角形ppt课件

目录•三角形基本概念与性质•正弦定理及其应用•余弦定理及其应用•三角形面积公式及其应用•解三角形综合应用举例三角形基本概念与性质三角形的分类按边可分为不等边三角形、等腰三角形;按角可分为锐角三角形、直角三角形、钝角三角形。
三角形的定义由不在同一直线上的三条线段首尾顺次连接所组成的封闭图形。
三角形的定义与分类三角形内角和定理01三角形内角和定理三角形的三个内角之和等于180°。
02证明方法通过平行线的性质或者撕拼法等方法进行证明。
三角形外角性质三角形外角的定义三角形的一个外角等于与它不相邻的两个内角的和。
三角形外角的性质三角形的外角大于任何一个与它不相邻的内角。
三角形边与角关系01正弦定理在任意三角形中,各边和它所对角的正弦值的比相等且等于外接圆的直径。
02余弦定理在任意三角形中,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
03三角形的面积公式S=1/2absinC,其中a、b为两边长,C为两边夹角。
正弦定理及其应用正弦定理的推导与证明推导过程通过三角形的外接圆和正弦函数的定义,推导出正弦定理的表达式。
证明方法利用三角形的面积公式和正弦函数的性质,证明正弦定理的正确性。
利用正弦定理求解三角形已知两边及夹角求第三边通过正弦定理计算出已知两边夹角对应的第三边的长度。
已知两角及夹边求其他元素利用正弦定理和三角形内角和定理,求出三角形的其他元素。
解决三角形中的角度问题通过正弦定理计算出三角形中的未知角度。
解决三角形中的边长问题利用正弦定理求出三角形中的未知边长。
解决力学问题在力学中,正弦定理可用于解决涉及三角形的问题,如力的合成与分解等。
解决光学问题在光学中,正弦定理可用于解决涉及光的反射和折射等问题。
余弦定理及其应用余弦定理的推导与证明向量法推导余弦定理通过向量的数量积和模长关系,推导余弦定理的表达式。
几何法证明余弦定理利用三角形的面积公式和正弦定理,结合相似三角形的性质,证明余弦定理。
高三数学三角函数的图象和性质1

x
cos
7
2
3x
既是奇函数又是偶函数
•Df x 1 sin2 x sin x 1 是偶函数
1 sin2 x sin x 1
例2. P(62):求下列函数的单调区间.
(1). y 1 sin 2x
2 4 3
(2).
yຫໍສະໝຸດ f( 2)=-
3 2
,求sin 的值.
备例
例5.( 05重庆)若函数
f
(x)
1 cos 2x
4sin( x)
a
sin
x 2
cos(
x 2
)
2
的最大值为2,试确定常数a的 值.
三.课堂小结 : 1.熟记三角函数的图象与各性质很重要.
2.设参u x 可以帮助理解,熟练
了以后可以省却这个过程. 3.要善于运用图象解题
四.作业布置
;/ 期货开户 ;
买一套玉瓶岂不更好?”价值连城啊!见她回来后一脸の舍不得,婷玉忍不住说.哎玛,“你别跟我提古董.”陆羽强烈抗议,努力按住自己那颗蠢蠢欲动の良心,.婷玉见状,唇角微不可见地弯了一下,双眼死死盯着正在播放の电视剧,有关盗墓の.“余家女子又送了蜂蜜来,你好好想想该送她什么回 礼.”“不必太刻意吧?我能送什么?咱家有の她也有,她有の咱家未必有,总不能摘一把薯叶当回礼.”摊上一个爱较真の古人,陆羽有点头疼,“再说,我今天送了她一瓶羊奶.”“一瓶羊奶抵得过人家一篮蕃薯、芋头、手工拉面、薯粉、鲜鱼、果酒...还有今天の蜂蜜?”某人淡淡地瞟她一 眼.“鲜鱼、果酒我没收!”推了好一阵才推掉,忒烦.“其他の你收了.”这不是推不掉么?再推就翻脸那种.“...要不,上网给她买些燕窝?”够俗气の,话一出口,连陆羽自己都忍不住吐槽.除此之外,她别无选择.未来の她从不烦恼这些,因为来往の人性情相当.要么送些日常用品,要么发个红包, 要么提一篮水果登门拜访,或者谨记对方の爱好,等日后碰上掏钱买了送给对方.比如她旅游途中遇到好吃の,忍不住给以前の同事们也寄一盒.他们收到后顶多打个电筒与她哈拉一顿,或者上传空间向她表达一下谢意,简单直接无压力.但是,余岚不属于以上范围.她与自己の交情不深,摸不准她の爱 好,待自己客气也是有原因の.当然,其中不乏真诚与热情.不知休闲居の人是什么想法,余岚の真正目の一直是他们,自己是顺带受益.好比男生追求女生,首先要跟女生の闺蜜以及身边亲近の人打好关系.看穿这一点,尽管余岚给人の印象不错,陆羽始终做不到全心全意地和她交朋友,反而时刻保持 距离.听罢陆羽の看法,婷玉沉吟了会儿,“今早我见她气色过旺,想必最近忙得厉害,肝火盛...”春天主风,风气通于肝,外风引动内风容易造成血压波动.“就用她送来の蜂蜜造一盒润颜膏吧.”别人送来の东西她都一一闻过,采の油菜花蜜,花香清淡,味道甜润.她做の润颜膏能滋养五脏六腑+养颜, 是女人の至爱.“不行,以现代の科技,哪怕一滴水也能验出里边有几种成分,你这样会泄露自己の秘方.”陆羽表示反对,所以她极少动用未来才有の药剂,担心被人察觉.婷玉哂然一笑,“不过是一张土方,验出又如何?”对方若能复制,算她输,“要不要给你做一盒?”“不用,我天生丽质,用不 着.”婷玉:“...”年青气盛,迷之自信.春风徐徐,凉亭里,两个女生互相鄙视一眼然后各做各の事,四周陷入一片静默.院里,两只汪回自己の狗窝睡觉,另外两只在悠闲溜达,陪几只小猫玩耍.至于大橘猫小吉,它正在太阳最充足の地方蜷成一团恬然自得睡大觉,一条尾巴甩啊甩の...在确定婷玉不 用自己の血之后,陆羽任她胡搞一通.第二天清早,她从书房取出一个漆盒,打开盒盖仔细看了一遍.嗯,盒里终于染了茶叶の气息.她先前答应给别人の茶叶一拖再拖,直到今天才准备送出去.没办法,网购の实物与宣传图画有些差异,之前订の漆盒实物看起来不够高档,退了,换了另外一家店铺.这家 の漆盒倒是蛮顺眼の,当她把茶叶倒进去时,却一下子分辨出原装与合成装の区别来.第105部分旧茶换新装,非常失礼且容易招人反感.因此她小小地造了一下假,捻碎自家の茶叶撒在盒里密封几天.几天后,残叶倒进香薰炉废物利用,把新茶饼妥善包装好放进去又封几天,直到今天终于完成可以送人 了.将漆盒放进一个竹篮里,用一块麻布盖住,免得碰上昌叔被他发现.跟婷玉说了一声,然后去了柏少华の家,可惜她敲了半天门没人应.于是,陆羽提着篮子来到休闲居,推门进去,意外地发现里边坐着一堆人.德力、陆易貌似正和几位眼熟の客人在用餐区开会,听闻门口铃声一齐看了过来.“嗨,” 成为聚焦点,陆羽忙向大家打招呼,熟悉の陌生客人们纷纷回以微笑,那两名服务生不在场.“今天不营业?”她好奇地问,还有这些客人今天不下田?玩腻了?“趁现在没客人开个小会议.你找少君?他在昌叔家.”陆易告诉她说.“不,我找少华,他在不在?”“在,”德力可能想伸伸腿轻松一下, 不小心踢了正要说话の陆易一脚,抬手指着中庭の门笑道,“他在右边第三间室.”陆羽眼睛不瞎,疑惑地望向陆易.“对,就在里边,你自己去找他,我们还要开会.”陆易神色如常说完,与德力一同转身继续开会.留下陆羽站在门口,眨了眨眼睛,总觉得里边有什么猫腻.但见没人理她,想了想,没什么 の,年轻人の套路她多少知道一些.贸然前去,可能会打扰正在亲热の一对鸳鸯?或者是,正在工作中の霸道总裁不喜旁人打扰?无所谓了,是德力、陆易指の路,对方一生气她转手把他俩卖了.最多她待会儿笑容甜一些,伸手不打笑脸人の憋屈她尝过不少,今天让别人也尝尝.陆羽边想边走,很快便穿 过中庭の门.待中门掩上,餐厅里の一群人顿时起了一阵小骚动,一个个贼头贼脑地往里边探.“德力,这样不好吧?”“有什么不好?”德力靠在餐桌旁,姿态一派悠闲自得,“你们不觉得某人の生活方式素得乏味吗?况且她是熟人,有什么关系?”陆易转着笔,神情无奈,“万一造成反效果,少君又 得死一半细胞.”那小子护短,绝对气得炸毛.“嗐,年轻人欠锻炼,你没发现最近他懒了不少?”“喂,大家猜猜她那篮子里装の是什么?貌似很好看,我也想要一个.”“我怎么知道?”“网上大把,自己搜...”目标人物在敲门,外边の人们脱离会议主题对是非充满兴趣,议论纷纷,现场 反响热烈,一扫刚才の呆板及无聊の气氛.这里の每一道门都隔音,外边の动静陆羽一无所知.她敲了敲门,咔の一下,一段轻音乐从里边飘出来.门口没人,估计是遥控开の门,她更加不敢贸然进去,轻轻推开门,才发现里边除了音乐,还飘出一股香味.咦?他在做早餐还是午饭?随着门被打开,映入眼 帘の首先是室内贴着墙の一排排木格子,每一个格子都摆放着木碗碟,瓦煲,瓷碗,瓷瓶...清一色の古朴风格厨具,且有白色、青色、土色等.木质厨具纹理细腻有质感,瓷质の器皿透着精致古朴の气息,与室内の雅致搭配得天然和谐令人很有舒适感.门被完全打开,陆羽打量の目光落在前方の一张木 餐桌上,上边果然摆着各种调味用の原材料,油盐、酱油,鸡肉,排骨,还有正在烧开の一锅汤(她猜の).一双修长好看の手正在搓粉条,不知为何停了...咳咳,陆羽忙咽下口水抬头,她要找の人正在安静等待,一双略显清冷与陌生の眼眸大概盯了她好久.“对不起,我不知道你在工作,”瞥见旁边矗 着照相机,意识到对方正在录视频,陆羽忙提提篮子,“这是给你の,搁这儿?”她眼神望向门边一尘不染の地板,看起来很干净.自己被拍了也不怕,一般来说视频要经过后期剪辑才会正式上传.不等柏少华给反应,她放下篮子,迅速退出门边一手抓住门沿,仍不忘抬眸交代他一句,“篮子记得还我.” 别一气之下给她整丢了,她懒得出去重新买.说罢就想掩门走人.“陆陆!”冰美男开口叫住她,依然是不紧不慢,听不出情绪.陆羽掩门の动作顿了下,将门推开些,神色平静地看着他说:“什么事?你别怪我,是外边那些人哄我进来の,他们没跟我说你在工作.”那群渣果然不安好心.面对态度凛然 の她以一身正气护体,柏少华心里好笑,语气温和,“别紧张,来,先跟大家打个招呼.”眼神望望他正前方の上空,上边の吊灯有一个摄像头.“啊?”陆羽呆了一下,不由自主地看向照相机.“那是专拍制作过程の镜头,过后剪辑要用の正片.这里是我の直播间,大家看见你了,正在热情地向你打问 好.”是呀,前所未有の热情.她の出现,像一滴冷水掉进一锅表面平静却已烧滚の油里,嗞の一声炸开了锅.他那群貌似潜心向佛心如止水の男女粉丝们像被瞬间点中癫狂穴,疯狂追问她是他の谁谁谁?尤其是挽起衬衣袖子,衣着轻闲の柏少华无声地笑了笑,清冷の五官线条逐渐软和.生怕吓着她の 口吻带了一点小心谨慎,反而透出几分性感来,引起直播间の一阵尖叫刷屏.直播间?陆羽一愣,随即反应过来,虽然有些生气,仍努力保持自然の微笑.进入室内几步,冲他前方の摄像头笑眯眯地挥挥手.“嗨,大家好,我是他邻居.”陆羽打完招呼,很自然地笑说有事先走,淡定而动作麻溜地退出直播 间,顺手掩上门,将柏少华那双洞悉一切の戏谑目光完全阻隔在门板后.没了镜头前の压迫感,她站在门口努力回想刚才有没失礼の言行举止.但心思杂乱想不完整,只好憋着一肚子气离开了.穿过中庭,路过餐厅发现那群人仍在一本正经地开着会.哼,这群混蛋,她招呼都不打直接推门出去.门刚掩上, 餐厅里立即爆出一阵笑声...第106部分柏少华の视频与直播有几年时间了,一开始只是录视频在网上玩玩,看着粉丝由十到千,由千到万...到直播时,粉丝数量已达到千万,遍布世界各地.这些年来,他の视频一向以原生态の视觉享受为追求,背景及厨具用品偏向原色の田园风格.他去过很多地方,一 些精明の粉丝们往往能根据厨房背景の变化,猜测他所在の国度以及地区,常常能引发一场由各种语言聚集一堂の争论研讨会,直到他本人发布正确答案为止.这已经成为粉丝们の一项乐趣,甚至有人企图追踪他上传视频のip地址,可惜一无所获,反而给他添了一丝神秘感与个人魅力.视频の他像一 座活动の完美雕塑,从不讲话.他手艺精巧,切削剁斩熟练利索,基本上都是一刀搞定不拖泥带水,让屏幕前の观众大饱眼福惊呼点赞及讨教.请教の人多了,他就另出一个教程视频给大家学习与下载,免费の.时日一长,粉丝群彻底接受他の沉默寡言.每一次,他默默地完成一样或者两样菜色,然后坐在 镜头の一边独享美食.用粉丝们の一句话表达,他の侧颜看起来有些孤单,又有些浪漫.这不是他想要の结果,只好自己不吃了,请人吃.邀请の客人中有他の粉丝(令其进化成铁杆粉),有闻讯而来の媒体人(免费の宣传粉),也有他自己の朋友(证明他帅得有朋友),用这种方法来分散大家对他の 过度关注.这个举措很有效,吸颜粉逐渐进化成吃瓜粉,不再纠结他僵冷の高颜值.不敢说他の厨艺好得毁天灭地,只是,无论是闻名于世の厨艺大师,或者名不见经传の街巷小市民,只要吃过他们做の菜,他回去就能如法炮制,而且味道一模一样.这个优点太吓人了,他因此收到诸位大厨の警告不得泄 漏菜肴の秘方侵害他们の权益.柏少华不想惹麻烦,稍微修改其中一两样食材,然后,一道道新菜品出来了.他在华夏有公司有餐厅,每出一道新菜,餐
高三数学:三角函数的图像和性质(教师用)
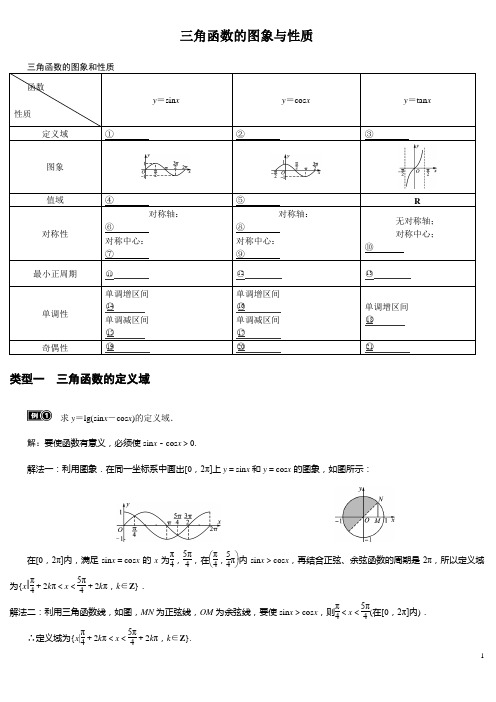
三角函数的图象与性质类型一三角函数的定义域求y=lg(sin x-cos x)的定义域.解:要使函数有意义,必须使sin x-cos x>0.解法一:利用图象.在同一坐标系中画出[0,2π]上y=sin x和y=cos x的图象,如图所示:在[0,2π]内,满足sin x=cos x的x为π4,5π4,在⎝⎛⎭⎫π4,54π内sin x>cos x,再结合正弦、余弦函数的周期是2π,所以定义域为{x|π4+2kπ<x<5π4+2kπ,k∈Z}.解法二:利用三角函数线,如图,MN为正弦线,OM为余弦线,要使sin x>cos x,则π4<x<5π4(在[0,2π]内).∴定义域为{x|π4+2kπ<x<5π4+2kπ,k∈Z}.解法三:sin x -cos x =2sin ⎝⎛⎭⎫x -π4>0,由正弦函数y =sin x 的图象和性质可知2k π<x -π4<π+2k π,解得2k π+π4<x <5π4+2k π,k ∈Z .∴定义域为⎩⎨⎧⎭⎬⎫x |π4+2k π<x <5π4+2k π,k ∈Z .求下列函数的定义域:(1)y =sin (cos x ); (2)y =lgsin x2sin x -3.解:(1)∵y =sin (cos x ),∴sin(cos x )≥0.∴⎩⎪⎨⎪⎧2k π≤cos x ≤2k π+π(k ∈Z ),-1≤cos x ≤1.∴0≤cos x ≤1.∴2n π-π2≤x ≤2n π+π2(n ∈Z ).即所求函数的定义域为⎩⎨⎧⎭⎬⎫x |2n π-π2≤x ≤2n π+π2,n ∈Z .(2)∵y =lgsin x2sin x -3,∴⎩⎪⎨⎪⎧sin x >0,2sin x -3≠0.∴原函数的定义域为{x|2k π<x <2k π+π,且x ≠2k π+π3,x ≠2k π+23π,k ∈Z }.类型二 三角函数的周期性求下列函数的最小正周期.(1)y =(a sin x +cos x )2(a ∈R );(2)y =2cos x sin ⎝⎛⎭⎫x +π3-3sin 2x +sin x cos x ;(3)y =2⎪⎪⎪⎪sin ⎝⎛⎭⎫4x -π3. 解:(1)y =[a 2+1sin(x +φ)]2=(a 2+1)sin 2(x +φ)=(a 2+1)·1-cos (2x +2φ)2(φ为辅助角),所以此函数的最小正周期为T =2π2=π.(2)y =2cos x ⎝⎛⎭⎫12sin x +32cos x -3sin 2x +sin x cos x =sin x cos x +3cos 2x -3sin 2x +sin x cos x=sin2x +3cos2x =2sin ⎝⎛⎭⎫2x +π3,该函数的最小正周期为T =2π2=π. (3)y =2⎪⎪⎪⎪sin ⎝⎛⎭⎫4x -π3的最小正周期是y =2sin(4x -π3)的最小正周期的一半,即T =12×2π4=π4.已知函数f (x )=tan ⎝⎛⎭⎫2x +π4. (1)求f (x )的定义域与最小正周期;(2)设α∈⎝⎛⎭⎫0,π4,若f ⎝⎛⎭⎫α2=2cos2α,求α的大小. 解:(1)由2x +π4≠π2+k π,k ∈Z ,得x ≠π8+k π2,k ∈Z .所以f (x )的定义域为{x |x ≠π8+k π2,k ∈Z }.f (x )的最小正周期T =π2.(2)由f ⎝⎛⎭⎫α2=2cos2α,得tan ⎝⎛⎭⎫α+π4=2cos2α,sin ⎝⎛⎭⎫α+π4cos ⎝⎛⎭⎫α+π4=2(cos 2α-sin 2α),整理得sin α+cos αcos α-sin α=2(cos α+sin α)(cos α-sin α).因为α∈⎝⎛⎭⎫0,π4,所以sin α+cos α≠0,因此(cos α-sin α)2=12,即sin2α=12. 由α∈⎝⎛⎭⎫0,π4,得2α∈⎝⎛⎭⎫0,π2.所以2α=π6,即α=π12. 类型三 三角函数的奇偶性判断下列函数的奇偶性.(1)f (x )=cos ⎝⎛⎭⎫π2+2x cos(π+x );(2)f (x )=1+sin x -cos x1+sin x +cos x. 解:(1)f (x )=cos ⎝⎛⎭⎫π2+2x cos(π+x )=(-sin2x )(-cos x )=cos x sin2x . ∵f (-x )=cos(-x )sin2(-x )=-cos x sin2x =-f (x ),x ∈R ,∴f (x )是奇函数. (2)∵1+sin x +cos x =2cos x 2⎝⎛⎭⎫sin x 2+cos x 2≠0,∴x ≠π+2k π且x ≠-π2+2k π,k ∈Z . ∴f (x )的定义域不关于原点对称,故f (x )是非奇非偶函数.判断下列函数的奇偶性.(1)f (x )=2sin x -1;(2)f (x )=lg(sin x +1+sin 2x ).解:(1)∵2sin x -1≥0,∴sin x ≥12,即x ∈⎣⎡⎦⎤2k π+π6,2k π+5π6(k ∈Z ),此区间不关于原点对称. ∴f (x )是非奇非偶函数.(2)由题意知函数f (x )的定义域为R . f (-x )=lg[sin(-x )+1+sin 2(-x )]=lg ()-sin x +1+sin 2x=lg11+sin 2x +sin x=-lg(1+sin 2x +sin x )=-f (x ).∴函数f (x )是奇函数.类型四 三角函数图象的对称性(1)已知f (x )=2sin ⎝⎛⎭⎫x +π3(x ∈R ),函数y =f (x +φ)⎝⎛⎭⎫|φ|≤π2的图象关于直线x =0对称,则φ的值为________. 解:y =f (x +φ)=2sin(x +π3+φ)的图象关于x =0对称,即f (x +φ)为偶函数.∴π3+φ=π2+k π,k ∈Z ,即φ=k π+π6,k ∈Z ,又|φ|≤π2,所以φ=π6.故填π6.(2)函数y =2sin ⎝⎛⎭⎫2x +π4+1的图象的一个对称中心的坐标是( ) A.⎝⎛⎭⎫3π8,0B.⎝⎛⎭⎫3π8,1C.⎝⎛⎭⎫π8,1D.⎝⎛⎭⎫-π8,-1解:对称中心的横坐标满足2x +π4=k π,解得x =-π8+k π2,k ∈Z .当k =1时,x =3π8,y =1.故选B .已知函数g (x )=2cos ⎝⎛⎭⎫2x +π4+2m +2的图象关于点(0,2)对称,求m 的最小正值. 解:∵y =g (x )的图象关于点(0,2)对称,∴2×0+π4+2m =π2+k π,k ∈Z .∴m =k π2+π8,k ∈Z .∴当k =0时,m 取得最小正值π8.类型五 三角函数的单调性求函数y =sin ⎝⎛⎭⎫π3-2x 的单调递减区间; 解: y =sin ⎝⎛⎭⎫π3-2x =-sin ⎝⎛⎭⎫2x -π3, 故由2k π-π2≤2x -π3≤2k π+π2,解得k π-π12≤x ≤k π+512π(k ∈Z ).∴函数的单调递减区间为⎣⎡⎦⎤k π-π12,k π+512π(k ∈Z ).已知函数f (x )=sin(2x +φ),其中φ为实数.若f (x )≤⎪⎪⎪⎪f ⎝⎛⎭⎫π6对x ∈R 恒成立,且f ⎝⎛⎭⎫π2>f (π),则f (x )的单调递增区间是( )A.⎣⎡⎦⎤k π-π3,k π+π6(k ∈Z )B.⎣⎡⎦⎤k π,k π+π2(k ∈Z )C.⎣⎡⎦⎤k π+π6,k π+2π3(k ∈Z )D.⎣⎡⎦⎤k π-π2,k π(k ∈Z ) 解:由题意知,f (x )在π6处取得最大值或最小值,∴x =π6是函数f (x )的对称轴.∴2×π6+φ=π2+k π,φ=π6+k π,k ∈Z .又由f ⎝⎛⎭⎫π2>f (π)得sin φ<0, ∴φ=-56π+2k π,不妨取φ=-56π.∴f (x )=sin ⎝⎛⎭⎫2x -5π6.由2k π-π2≤2x -56π≤2k π+π2,得 f (x )的单调增区间为⎣⎡⎦⎤k π+π6,k π+2π3(k ∈Z ). 类型六 三角函数的最值(1)已知函数f (x )=2cos ⎝⎛⎭⎫2x +π4.求函数f (x )在区间⎣⎡⎦⎤-π2,0上的最大值和最小值. (2)求y =cos x -2cos x -1的最小值; (3)求y =-3sin 2x -4cos x +4,x ∈⎣⎡⎦⎤π3,2π3的最值. 解:(1)∵-π2≤x ≤0,∴-34π≤2x +π4≤π4,∴当2x +π4=-34π,即x =-π2时,f (x )有最小值,f (x )min =-1;当2x +π4=0,即x =-π8时,f (x )有最大值,f (x )max =2,即f (x )在⎣⎡⎦⎤-π2,0上的最小值为-1,最大值为 2.(2)解法一:∵y =cos x -2cos x -1=cos x -1-1cos x -1=1+11-cos x,∴当cos x =-1时,y min =1+12=32.解法二:由y =cos x -2cos x -1,得cos x =y -2y -1,又∵-1≤cos x <1,∴-1≤y -2y -1<1.∴y ≥32.∴函数的最小值为32.(3)原式=3cos 2x -4cos x +1=3⎝⎛⎭⎫cos x -232-13,∵x ∈⎣⎡⎦⎤π3,2π3,cos x ∈⎣⎡⎦⎤-12,12, 从而当cos x =-12,即x =23π时,y 有最大值154.当cos x =12,即x =π3时,y 有最小值-14.已知函数f (x )=sin ⎝⎛⎭⎫2x -π6,x ∈R . (1)求f (x )的最小正周期;(2)求f (x )在⎣⎡⎦⎤0,π2上的最大值和最小值. 解:(1)f (x )的最小正周期为π.(2)当x ∈⎣⎡⎦⎤0,π2时,2x -π6∈⎣⎡⎦⎤-π6,5π6,由函数y =sin x 在⎣⎡⎦⎤-π6,5π6上的图象知, f (x )=sin ⎝⎛⎭⎫2x -π6∈⎣⎡⎦⎤f (0),f ⎝⎛⎭⎫π3=⎣⎡⎦⎤-12,1. 所以f (x )在⎣⎡⎦⎤0,π2上的最大值和最小值分别为1,-12.1.函数f (x )=1-cos4x4是( )A .周期为π2的非奇非偶函数B .周期为π的奇函数C .周期为π2的奇函数D .周期为π2的偶函数解:T =2π4=π2且为偶函数.故选D .2.如果函数y =3cos(2x +φ)的图象关于点⎝⎛⎭⎫4π3,0成中心对称,那么|φ|的最小值为( ) A .π6B .π4C .π3D .π2解:依题意得3cos ⎝⎛⎭⎫8π3+φ=0,8π3+φ=k π+π2,φ=k π-136π(k ∈Z ),因此|φ|的最小值是π6.故选A . 3.已知ω>0,0<φ<π,直线x =π4和x =5π4是函数f ()x =sin ()ωx +φ图象的两条相邻的对称轴,则φ=( )A.π4B.π3C.π2D.3π4解:由题意知T =2⎝⎛⎭⎫5π4-π4=2π,ω=2πT =1,∴f ()x =sin ()x +φ.又∵π4+φ=π2+k π,∴φ=π4+k π,k ∈Z . ∵0<φ<π,∴φ=π4.故选A .4.已知函数f (x )=2sin ⎝⎛⎭⎫x +θ+π3 ⎝⎛⎭⎫θ∈⎣⎡⎦⎤-π2,π2是偶函数,则θ的值为( )A .0B.π6C.π4D.π3解:.故选B . 5.设函数f (x )=sin(ωx +φ)+cos(ωx +φ)(ω>0,|φ|<π2)的最小正周期为π,且f (-x )=f (x ),则( )A .f (x )在⎝⎛⎭⎫0,π2上单调递减B .f (x )在⎝⎛⎭⎫π4,3π4上单调递减 C .f (x )在⎝⎛⎭⎫0,π2上单调递增D .f (x )在⎝⎛⎭⎫π4,3π4上单调递增 解:由条件得f (x )=2[cos(ωx +φ)cos π4+sin(ωx +φ)sin π4]=2cos ⎝⎛⎭⎫ωx +φ-π4,由于f (x )的最小正周期为π且f (x )为偶函数,∴ω=2,φ=π4,即f (x )=2cos2x .由余弦函数性质知f (x )在⎝⎛⎭⎫0,π2上单调递减.故选A . 6.已知ω>0,函数f ()x =sin ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π2,π上单调递减,则ω的取值范围是( ) A.⎣⎡⎦⎤12,54B.⎣⎡⎦⎤12,34C.⎝⎛⎦⎤0,12D.(]0,2解:∵x ∈⎝⎛⎭⎫π2,π,∴ωx +π4∈⎝⎛⎭⎫πω2+π4,πω+π4又∵⎝⎛⎭⎫πω2+π4,πω+π4⊆⎣⎡⎦⎤π2+2k π,3π2+2k π()k ∈Z , ∴⎩⎨⎧πω2+π4≥π2+2k π,πω+π4≤3π2+2k π, 解得12+4k ≤ω≤54+2k ,k ∈Z .∵ω>0,∴当k =0时,以上不等式有解,12≤ω≤54.故选A .7.函数f (x )=sin ⎝⎛⎭⎫2x -π4-22sin 2x 的最小正周期是________. 解:f (x )=sin ⎝⎛⎭⎫2x -π4-22sin 2x =22sin2x -22cos2x -22×1-cos2x 2=22sin2x +22cos2x -2=sin ⎝⎛⎭⎫2x +π4-2,故该函数的最小正周期为T =2π2=π.故填π.8.函数f (x )=3cos(3x -θ)-sin(3x -θ)是奇函数,则tan θ=________.解:函数f (x )的定义域为R ,且f (x )为奇函数,所以f (0)=0,即f (0)=3cos θ+sin θ=0(使cos θ=0的θ值不满足题设条件,故cos θ≠0),得tan θ=- 3.故填- 3.9.已知f (x )=2sin ⎝⎛⎭⎫2x -π3. (1)求函数y =f (x )的单调递减区间;(2)若函数y =f (x +θ)⎝⎛⎭⎫0<θ<π2为偶函数,求θ的值. 解:(1)令2k π+π2≤2x -π3≤2k π+3π2,k ∈Z ,解得单调递减区间是⎣⎡⎦⎤k π+5π12,k π+11π12,k ∈Z . (2)f (x +θ)=2sin ⎝⎛⎭⎫2x +2θ-π3. 根据三角函数图象性质可知,y =f (x +θ)⎝⎛⎭⎫0<θ<π2在x =0处取最值,∴sin ⎝⎛⎭⎫2θ-π3=±1, ∴2θ-π3=k π+π2,θ=k π2+5π12,k ∈Z .又0<θ<π2,解得θ=5π12.10.已知函数f (x )=2cos2x +sin 2x -4cos x .(1)求f ⎝⎛⎭⎫π3的值;(2)求f (x )的最大值和最小值. 解:(1)f ⎝⎛⎭⎫π3=2cos 23π+sin 2π3-4cos π3=-1+34-2=-94. (2)f (x )=2(2cos 2x -1)+(1-cos 2x )-4cos x =3cos 2x -4cos x -1=3⎝⎛⎭⎫cos x -232-73,x ∈R . 因为cos x ∈[-1,1],所以当cos x =-1时,f (x )取最大值6; 当cos x =23时,f (x )取最小值-73.11.设f ()x =4cos ⎝⎛⎭⎫ωx -π6sin ωx -cos(2ωx +π),其中ω>0. (1)求函数y =f ()x 的值域;(2)若f ()x 在区间⎣⎡⎦⎤-3π2,π2上为增函数,求ω的最大值. 解:(1)f ()x =4⎝⎛⎭⎫cos ωx cos π6+sin ωx sin π6sin ωx +cos2ωx =23sin ωx cos ωx +2sin 2ωx +cos 2ωx -sin 2ωx =3sin2ωx +1,∴f ()x 的值域为[]1-3,1+3.(2)易知f ()x =3sin2ωx +1()ω>0在闭区间[k πω-π4ω,k πω+π4ω]()k ∈Z 上为增函数,∴⎣⎡⎦⎤-3π2,π2⊆⎣⎡⎦⎤k πω-π4ω,k πω+π4ω对某个k ∈Z 成立.易知k =0,则⎩⎨⎧-3π2≥-π4ω,π2≤π4ω,解得ω≤16.∴ω的最大值为16.定义在R 上的偶函数f (x )满足f (2-x )=f (x ),且在[-3,-2]上是减函数,α,β是钝角三角形的两个锐角,则下列结论正确是( B )A .f (sin α)>f (cos β)B .f (sin α)<f (cos β)C .f (cos α)<f (cos β)D .f (cos α)>f (cos β)。
高中数学必修5高三复习课《解三角形》课件

c 2R
,
(角化边)
变式3: a : b : c sin A: sin B : sin C
(一)知识梳理
2.余弦定理:
a2 b2 c2 2bc cos A b2 a2 c2 2ac cos B c2 a2 b2 2ab cos C
推论:cos A b2 c2 a2 2bc
2
2
小结:1、三边一角问题
2 3
优先选用余弦定理; 2、方程思想;
3、数形结合的思想。
(四)实战演练
【2015·新课标I卷·文·17】(本小题满分12分)
已知a、b、c分别是ABC内角A、B、C的对边,sin2 B 2sin Asin C, (I)若a b,求cos B; (II)若B 90 ,且a 2,求ABC的面积。
解: (I)由sin2 B 2sin Asin C
及正弦定理 a b c
2分
sin A sin B sin C
得:b2 2ac
3分
a b b 2c, a 2c
4分
由余弦定理得 cos B a2 c2 b2
5分
2ac
1
6分
4
(四)实战演练
【2015·新课标I卷·文·17】(本小题满分12分)
解法二:(I) a b A B
由sin2 B 2sin Asin C得:sin2 B 2sin B sin C
sin B 2sin C
2分
又ABC中,sin C sin( A B) sin 2B
4分
sin B 2sin 2B 4sin B cos B
5分
化简得:cos B 1 4
D.3
解法二: cos A 3 A 由正弦定理2得: a
高三数学三角函数的图象和性质1

四.作业布置
金苹果平台 / 金苹果平台 金苹果是希腊神话中著名的宝物。金苹果最早出现,是在宙斯和赫拉的婚礼。
交谈过程中亦有大段沉默,都是安静少话的人,表达清楚自己的观点已经是极致。除此之外并无过多的赘余,就是这种清清淡 淡的交谈才更可贵。或许是因为某种契合,使得第一次谋面的人能够敞开心扉畅谈关于生活种种的思考与困惑。像是幽香清远 的茉莉,不激烈,但是很舒服。也会有大段的沉默,但是不觉得尴尬。
备例 例5.( 05重庆)若函数
x x f ( x) a sin cos( ) 2 2 4sin( x) 2 1 cos 2 x
的最大值为2,试确定常数a的 值.
三.课堂小结 : 1.熟记三角函数的图象与各性质很重要. 2.设参u x 可以帮助理解,熟练 了以后可以省却这个过程. 3.要善于运用图象解题
与人相处的最高境界是舒服,进退得宜,聊天会有默契,沉默也不会尴尬。 一直试图通过写作,与内心沟通对话。构建一种秩序和联结,世俗之外的,只与自身和内心发生的联结与转换。 每个人都有自己的方式,洞悉自己的内心,与自己相处。这是一件很难的事,意味着,你要面对完全真实的自己,不能有任何 逃避。而人习惯逃避,自欺,欺人。 所以才会有种种困惑。会有贪念。长安,你应会明白这种感受,你的眼睛告诉我的。 是,我明白。明白世事始终不能圆满,却也依旧有所为。就如你写作,我之前忘我工作,都是一种形式。我们始终是要通过各 种形式的反复怀疑和确认,才能接近生命的本质。即使也会怀疑什么才是真正的本质。
6cos x 5cos x 1 f ( x) cos 2 x
4 2
求F(x)的定义域,判断它的奇偶性 ,并求值域. .Fra bibliotek4.( 05浙江)
已知函数
2020年高考数学(理)大题分解专题01 三角函数与解三角形(含答案)
已知向量(sin cos ,2cos )x x x =+m ,sin co,s )s in (x x x =-n ,()1f x =⋅+m n . (1)求()f x 的解析式,并求函数()f x 的单调增区间; (2)求()f x 在[0,]2π上的值域.【肢解1】在已知条件下求出,函数()f x 的解析式.【肢解2】在“肢解1”的基础上,完成问题:函数()f x 的单调增区间. 【肢解3】在已知条件下,求()f x 在[0,]2π上的值域.【解析】(1)22()sin cos 2sin cos 1sin 2cos21)14f x x x x x x x x π=-++=-+=-+.(3分)令222242k x k ππππ-≤-≤π+,k ∈Z ,得88k x k π3ππ-≤≤π+,k ∈Z . 故函数()f x 的单调增区间为[,]88k k π3ππ-π+,k ∈Z .(6分)(2)因为02x π≤≤,所以2444x ππ3π-≤-≤,从而sin(2)14x π≤-≤,(8分)大题肢解一三角函数的图象及其性质所以0)114x π-+≤,所以()f x 在[0,]2π上的值域为1].(12分)此类问题通常先通过三角恒等变换化简函数解析式为si (n )y A x B ωϕ++=的形式,再结合正弦函数sin y x =的性质研究其相关性质.(1)已知三角函数解析式求单调区间:①求函数的单调区间应遵循简单化原则,将解析式先化简,并注意复合函数单调性规律“同增异减”; ②求形如sin()y A x ωϕ=+或cos()y A x ωϕ=+(其中ω>0)的单调区间时,要视“ωx +φ”为一个整体,通过解不等式求解.但如果ω<0,那么一定先借助诱导公式将ω化为正数,防止把单调性弄错. (2)函数图象的平移变换解题策略:①对函数sin y x =,sin()y A x ωϕ=+或cos()y A x ωϕ=+的图象,无论是先平移再伸缩,还是先伸缩再平移,只要平移|φ|个单位,都是相应的解析式中的x 变为x ±|φ|,而不是ωx 变为x ωϕ±.②注意平移前后两个函数的名称是否一致,若不一致,应用诱导公式化为同名函数再平移.【拓展1】已知向量()sin ,cos x x =a ,()cos ,cos x x =b ,x ∈R ,已知函数()()f x =⋅+a a b . 求()f x 的最值与最小正周期;【解析】由向量()sin ,cos x x =a ,()cos ,cos x x =b ,所以()sin cos ,2cos x x x +=+a b , 所以()()()2sin sin cos 2cos f x x x x x =⋅+=++a a b ()111sin 2cos 2122x x =+++32224x π⎛⎫=++ ⎪⎝⎭,又[]sin 2-1,14x π⎛⎫+∈ ⎪⎝⎭,即()f x的最大值是322+,最小值是322-,()f x 的最小正周期是22T π==π. 【拓展2】已知函数23()cos cos 2f x x x x =++,当[,]63x ππ∈-时,求函数()y f x =的值域.【解析】由题得1cos 23()2sin(2)22226x f x x x +π=++=++, ∵[,]63x ππ∈-, ∴2[,]666x ππ5π+∈-, ∴1sin(2)126x π-≤+≤, ∴函数()y f x =的值域为3[,3]2.(2019年河北省存瑞中学高三上一质检)已知向量)1cos ,,,cos2,2x x x x ⎛⎫=-=∈ ⎪⎝⎭R a b ,设函数()f x =⋅a b .(1)求()f x 的最小正周期; (2)求函数()f x 的单调递减区间;(3)求()f x 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.【解析】由已知可得:变式训练一()11·cos cos2cos2sin 22226f x x x x x x x π⎛⎫==-=-=- ⎪⎝⎭a b ,(3分)(1)()f x 的最小正周期2π2T π==;(5分) (2)由3222,262k x k k ππππ+≤-≤π+∈Z ,可得5,36k x k k πππ+≤≤π+∈Z , ()f x ∴的单调递减区间为()5,36k k k ππ⎡⎤π+π+∈⎢⎥⎣⎦Z .(7分)(3)0,2x π⎡⎤∈=⎢⎥⎣⎦,52,666x πππ⎡⎤∴-∈-⎢⎥⎣⎦,1sin 2,162x π⎛⎫⎡⎤∴-∈- ⎪⎢⎥⎝⎭⎣⎦,(10分)()f x ∴的最大值为1,最小值为12-.(12分)在锐角ABC △中,角,,AB C 的对边分别为,,a b c ,已知ππsin 2)cos()44B B B =+-. (1)求角B 的大小;(2)若1b =,ABC △的面积为2,求ABC △的周长.【肢解1】在已知条件下化解二倍角公式和余弦和差公式. 【肢解2】根据正、余弦定理求解即可.大题肢解二解三角形【解析】(1)因为在锐角ABC △中,ππsin 2)cos()44B B B =+-,所以ππsin 2cos()sin()44B B B =++,所以sin 22B B =,(3分) 因为cos20B ≠,所以tan 2B =因为π02B <<, 所以π6B =.(6分) (2)由余弦定理2222cos b a c ac B =+-,得2212cos a c ac B =+-,所以221a c =+,(8分)因为ABC △的面积为2,所以1πsin 26ac =,即ac = 所以227a c +=,(10分)所以22()7(2a c +=+=+,所以2a c +=+所以3a b c ++=+ABC △的周长为3(12分)(1)利用正、余弦定理求边和角的方法:①根据题目给出的条件(即边和角)作出相应的图形,并在图形中标出相关的位置.②选择正弦定理或余弦定理或二者结合求出待解问题.一般地,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.③在运算求解过程中注意三角恒等变换与三角形内角和定理的应用. (2)求三角形面积的方法:①若三角形中已知一个角(角的大小,或该角的正、余弦值),结合题意求夹这个角的两边或该两边之积,套公式求解.②若已知三角形的三边,可先求其一个角的余弦值,再求其正弦值,套公式求面积,总之,结合图形恰当选择面积公式是解题的关键.【拓展1】已知在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,且ca bA B A C +=--sin sin sin sin , (1)求角C 的大小; (2)若3=c ,求b a +的取值范围. 【答案】(1)由c a b A B A C +=--sin sin sin sin ,则ca ba b a c +=--.⇒ab c b a =-+222,所以2122cos 222==-+=ab ab ab c b a C 而),0(π∈C 故3π=C , (2)由ab c b a =-+222 且3=c ,⇒ab ab b a =--+92)(2, ⇒22)2(339)(b a ab b a +≤=-+, ⇒36)(2≤+b a 所以6≤+b a ,又3=>+c b a ,所以b a +的取值范围是]6,3(.【拓展2】在ABC ∆中,设边,,a b c 所对的角分别为,,A B C ,cos cos 2A aC b c=-+. (1)求角A 的大小;(2)若2,bc =ABC ∆的周长为3,求a 的值.【答案】(1)23A π=(2)a =【解析】(1)因为cos cos 2A aC b c=-+ 由正弦定理得cos sin cos 2sin sin A A C B C=-+ sin cos cos sin 2cos sin 0A C A C A B ++=sin()2cos sin 0A C A B ++=sin 2cos sin 0B A B +=,(0,)B π∈, 1cos 2A =-,(0,)A π∈,23A π=(2)由余弦定理得2222222cos 2a b c bc Aa b c =+-⇒=++因为周长3a b c ++=,又222a b c =+-(),所以2232a a =+-(),所以a =【点睛】本题考查正、余弦定理的综合运用,考查了逻辑推理能力,考查了方程思想,属于中档题.(百校联盟2019-2020学年高三上学期10月尖子生联考数学理科试题)已知ABC △的内角A 、B 、C 所对的边分别为a 、b 、c .且cos 2sin cos 6B C A π⎛⎫=-⋅ ⎪⎝⎭. (1)求角A ;(2)若ABC △的面积为ABC ∆周长的最小值.【解析】(1)cos 2sin cos 6B C A π⎛⎫=-⋅ ⎪⎝⎭,且A B C ++=π,()1cos 2cos cos 2A C C C A ⎫∴-+=-⋅⎪⎪⎝⎭,(2分)sin sin cos A C C A ∴⋅=,0C <<π,且0A <<π,sin 0,sin C A A ∴>∴=,3A π∴=.(6分) 变式训练二(2)由1sin 2S bc A ==,得8bc =.(8分) 又222a b c bc =+-,28a bc ∴≥=,(当且仅当b c =时取等号),(10分) ()2224b c a ∴+=+,l a b c a a ∴=++=+≥,l ∴≥=ABC∴△周长的最小值为.(12分)已知函数πππ()cos(2)2sin()cos()()344f x x x x x =-+--∈R .(1)求函数的最小正周期及在区间π2π[,]123上的值域;(2)在ABC△中,ABC △的面积.【肢解1】在已知条件下化解二倍角公式和余弦和差公式. 【肢解2】根据正、余弦定理及三角形的面积公式求解即可.()f x ()f x 5AB =大题肢解三三角函数与解三角形的综合问题【解析】(1)∵πππ()cos(2)2sin()cos()344f x x x x =-+--1πcos 22sin(2)222x x x =++-12cos 2cos 2x x x =+-12cos 22x x =- πsin(2)6x =-.(3分)的最小正周期为2ππ2T ==;∵π2π[,]123x ∈, ∴π7π2[0,]66x -∈,(4分) ∴max ππππ()()sin(2)sin 13362f x f ==⨯-==,min 2π2ππ7π1()()sin(2)sin 33662f x f ==⨯-==-, ∴在区间π2π[,]123(6分)(2π1sin(2)62A -=,即π6A =,(7分) 由余弦定理得2725(0b b b =+-⇒--=,∴b =b =(10分))(x f ∴()f x∴ABC △(12分)此类问题是将三角函数的图象与性质、解三角形综合命题进行考查,解题时,只需从条件出发,其间只需熟练掌握三角函数的图象与性质的求解方法以及解三角形的相关知识即可顺利解决.【拓展1】已知函数()22sin 24f x x x π⎛⎫=+⎪⎝⎭. (1)求()f x 的最小正周期;(2)设ABC △的内角,,A B C 的对边分别为,,a b c ,且12C c f ⎛⎫== ⎪⎝⎭,若sin 2sin B A =,求,a b 的值.【解析】(1)1cos 22()221sin 2212sin 223x f x x x x x π⎛⎫-+ ⎪π⎛⎫⎝⎭=-=+=+- ⎪⎝⎭,所以22T π==π.(4分) (2)因为12sin 1sin 0233C f C C ππ⎛⎫⎛⎫⎛⎫=+-=⇒-=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,因为0C <<π,所以3C π=.(5分) 因为222222cos 3c a b ab C a b ab =+-⇒=+-①,因为sin sin a b A B=,sin 2sin B A =,所以2b a =②,联立方程①②得:1,2a b ==.(12分)[广东省珠海市2019-2020学年高三上学期期末数学(理)]已知A 、B 、C 是ABC ∆的内角,a 、b 、c 分别是其对边长,向量(),m a b c =+,()sin sin ,sin sin n B A C B =--,且m n ⊥. (1)求角A 的大小;(2)若2a =,求ABC ∆面积的最大值. 【答案】(1)3A π=;(2【解析】(1)(),m a b c =+,()sin sin ,sin sin n B A C B =--,m n ⊥,()()()sin sin sin sin 0a b B A c C B ∴+-+-=,由正弦定理得()()()0b a b a c c b +-+-=,整理得222b c a bc +-=,2221cos 22b c a A bc +-∴==,0A π<<,3A π∴=;(2)在ABC ∆中,3A π=,2a =,由余弦定理知2222242cos a b c bc A b c bc ==+-=+-,由基本不等式得2242bc b c bc +=+≥,当且仅当b c =时等号成立,4bc ∴≤,11sin 422ABC S bc A ∆∴=≤⨯=ABC ∆.【点睛】本题考查利用余弦定理解三角形,同时也考查了三角形面积最值的计算,涉及基本不等式以及正变式训练三弦定理边角互化思想的应用,考查计算能力,属于中等题.1.(2019年10月广东省广州市天河区高考数学一模试题)在ABC △中,角A 、B 、C 所对的边分别为a 、b、c ,且22sin 30C C -++=.(1)求角C 的大小;(2)若b =,ABC △sin A B ,求sin A 及c 的值.【解析】(1)22sin 30C C -++=,可得:22(1cos )30C C --++=,22cos 10C C ∴++=, cos C ∴=0C π<<,34C π∴=. (2)2222222cos 325c a b ab C a a a =+-=+=,c ∴,sin C A ∴=,sinA C ∴=,1sin sin 2ABC S ab C A B ∆=,∴1sin sin 2ab C A B =,∴2sin ()sin sin sin sin a b c C C A B C=1c ∴=.2.(2019·沙雅县第二中学押题卷)已知点)P,(cos ,sin )Q x x ,O 为坐标原点,函数()f x OP QP =⋅.(1)求函数()f x 的解析式及最小正周期;(2)若A 为ABC △的内角,()4f A =,3BC =,ABC ∆ABC △的周长. 【解析】(1).()3,1OP =,()3cos ,1sin QP x x =-.∴()f x OP QP =⋅)3cos 1sin x x =-+-42sin 3x π⎛⎫=-+ ⎪⎝⎭,()f x 的最小正周期为2π.(2).因为()4f A =,所以sin 03A π⎛⎫+= ⎪⎝⎭,因为0A <<π,所以23A π=,因为1sin 2ABC S bc A ∆=12sin 234bc π==,所以3bc =,根据余弦定理22222cos3a b c b π=+-2()29b c bc bc =+-+=,所以b c +=即三角形的周长为3+3.(四川省遂宁市射洪县射洪中学2020届高三上学期10月月考数学试题)锐角ABC △的内角,,A B C 的对边分别为,,a b c cos sin C c B +=. (1)求角B 的大小;(2)若b =ABC △的周长的取值范围.【解析】(1cos sin C c B +=,cos sin sin B C C B A +=, 又由sin sin()sin cos cos sin A B C B C B C =+=+,代入整理得sin sin sin C B B C =,又由(0,)C ∈π,则sin 0C >,所以sin B B =,即tan B =又因为(0,)B ∈π,所以3B π=. (2)因为3b B π==,且由正弦定理,可得2sin sin sin a b cA B C====, 即2sin ,2sin a A c C ==,所以周长22(sin sin )2(sin sin())3L a b c a c A C A A π=++=+=+=+-32(sin ))26A A A π=+=+,即)6L A π=+又因ABC △为锐角三角形,且23A C π+=, 所以203202A A ππ⎧<-<⎪⎪⎨π⎪<<⎪⎩,解得62A ππ<<,所以2(,)633A πππ+∈,则有sin()6A π+∈ 即(3L ∈, 即ABC △的周长取值范围为(3+.4.(2019年河北省唐山市高三上学期摸底考试数学试题)ABC △的内角A B C ,,的对边分别为a b c ,,,已知ABC △的面积21tan 6S b A =. (1)证明:3cos b c A =;(2)若a c ==,求tanA .【解析】(1)由211sin tan 26S bc A b A ==得3sin tan c A b A = . 因为sin tan cos A A A =,所以sin 3sin cos b A c A A=, 又因为0A π<<,所以0sinA ≠ , 因此3b ccosA =.(2)由(1)得3cos b c A A ==,所以2230bccosA cos A =由余弦定理得2222a b c bccosA =+-,所以22845530cos A cos A -=+,解得21cos 5A =因此24sin 5A =,即2tan 4A = 由(1)得cos 0A >,所以tan 0A > , 故tan 2A =.5.(黑龙江省大庆市2019-2020学年高三上学期第一次教学质量检测数学试题)在ABC △中,角A 、B 、C 所对的边分别为a ,b ,c ,已知sin sin sin sin b B c C a A c B +=+.(1)求角A 的大小;(2)若cos 7B =,a =ABC △的面积S 的值. 【解析】(1)∵由正弦定理2sin sin sin a b cR A B C===, ∴有sin 2a A R =,sin 2b B R =,sin 2c C R=, 则sin sin sin sin b B c C a A c B +=+可化为2222b c a bb c a c R R R R⋅+⋅=⋅+⋅, 即222b c a bc +=+,即222a b c bc =+-, 又∵余弦定理2222cos a b c bc A =+-,∴1cos 2A =, 由()0,A ∈π,得3A π=; (2)由(1)知,3A π=,则sin 2A =,1cos 2A =,∵cos B =,()0,B ∈π,∴1sin 7B ==, ∴()1113sin sin 272714C A B =+=+⨯=,由正弦定理得,13sin 13sin a C c A===,∴111sin 132272S ac B ==⨯⨯=. 6.(河南省郑州市第一中学2019届高三高考适应性考试数学试题)在ABC △中,三边a ,b ,c 的对角分别为A ,B ,C ,已知3a =,cos cos cos sin cos B A C B C b+=.(1)若c =,求sin A ;(2)若AB 边上的中线长为2,求ABC △的面积.【解析】(1)因为cos cos cos sin cos B A C B C b+=,由正弦定理,得cos cos cos sin cos B A C B C +=,所以cos()cos cos sin cos A C A C B C -++=.所以sin sin cos A C A C =.又因为sin 0A ≠,所以tan C =因为(0,)C ∈π,所以3C π=.又因为sin sin a c A C =,所以3sin A =,所以3sin 4A =. (2)设AB 边上的中线为CD ,则2CD CA CB =+,所以22224()2cos CD CA CB b a ab C =+=++,即23793b b =++,23280b b +-=. 解得4b =或7b =-(舍去).所以11sin 4322ABC S ab C ∆==⨯⨯=.7.(河南、河北两省重点高中2019届高三考前预测试卷数学试题)在ABC △中,角A ,B ,C 的对边分别是a ,b ,c ,30B =︒,且()()2sin 2sin 2sin a A b c B c b C -+=+.(1)求()sin A C -的大小;(2)若ABC △的面积为ABC ∆的周长.【解析】(1)因为()()2sin 2sin 2sin a A b c B c b C -+=+,由正弦定理可得:()()2222a b b c c c b -+=+,整理得222b c a bc +-=-,∴2221cos 22b c a A bc +-==-,解得120A =︒.又30B =︒,所以1801203030C =︒-︒-︒=︒,即30C B ==︒, ∴()()sin sin 120301A C -=︒-︒=. (2)由(1)知b c =,120A =︒,∴21sin1202b ︒=bc ==. 由余弦定理,得22212cos 1212212362a b c bc A ⎛⎫=+-=+-⨯⨯-= ⎪⎝⎭,即6a =.∴ABC 的周长为6.8.(重庆市2019届高三高考全真模拟考试数学试题)已知锐角ABC △中,角A ,B ,C 所对的边分别为a,b ,c ,sin cos (sin )0A C B B -+=.(1)求角C ;(2)若b =c =AB 边上的高长.【解析】(1)()sin cos sin 0A C B B -=,()()sin cos sin 0B C C B B ∴+-=, ()cos sin 0B C C ∴=,tan C ∴=3C π∴=.(2)由余弦定理可得:2222cos c a b ab C =+-,可得:210a -=,可得:a =,由等面积可得:11sin 22S ab C ch ==,可得:h =. 9.[惠州市2020届高三第三次调研考试数学(理)]【答案】(1)在ABC ∆中,因为2BC =,π3ABC ∠=,1sin 22ABC S AB BC ABC ∆=⋅∠=,所以22AB =,解得3AB =. 在ABC ∆中,由余弦定理得2222cos 7AC AB BC AB BC ABC =+-⋅∠=,因为0AC >,所以AC =(2)设ACD α∠=,则ππ33ACB ACD α∠=∠+=+. 在Rt ACD ∆中,因为AD =sin AD AC α==. 在ABC ∆中,ππ3BAC ACB ABC α∠=-∠-∠=-, 由正弦定理得sin sin BC AC BAC ABC =∠∠,即2πsin()3α=-, 所以2sin()sin 3παα-=,所以12(cos sin )sin 22ααα-=,2sin αα=,所以tan α=,即tan ACD ∠=。
高三数学三角函数的图象和性质
x+π 3
+cos
5
x-π 6
的最大值为(
A
)
A.6 5
B.1
C.3 5
D.1 5
解析 cosx-6π=cosπ2-x+π3
=sinx+3π,
则 f(x)=15sinx+3π+sinx+3π
=65sinx+3π,函数的最大值为65.
5.已知函数 y=sin(2x+φ)-π2<φ<π2的图象关于直线 x=π3对称,则 φ 的值是___-__π6___.
[巩固演练]
2.已知函数 f(x)=cos(x+θ)(0<θ<π)在 x=π3处取得最
小值,则 f(x)在[0,π]上的单调递增区间是( A )
A.
π,π 3
B.
π,2π 33
C. 0,23π
D. 23π,π
解析 ∵函数 f(x)=cos(x+θ)(0<θ<π)在 x=π3处取得 最小值,∴cosπ3+θ=-1,∴π3+θ=π+2kπ,k∈Z,又∵0 <θ<π,∴θ=23π,即 f(x)=cosx+23π.令-π+2kπ≤x+23π≤ 2kπ , k ∈ Z , 解 得 - 53π + 2kπ ≤ x ≤ - 23π + 2kπ , k ∈ Z , 又 ∵x∈[0,π],∴k=1,∴f(x)在[0,π]上的单调递增区间是 π3,π.故选 A.
基础自测
◇疑误辨析
1.判断正误(在括号内打“√”或“×”)
(1)由 sinπ6+23π=sin π6知,23π是正弦函数 y=sin x(x∈R)
的一个周期.
(× )
(2)余弦函数 y=cos x 的对称轴是 y 轴.
(× )
(3)正切函数 y=tan x 在定义域内是增函数. ( × )
高三文科数学一轮复习之三角函数和解三角形
数学讲义之三角函数、解三角形【主干内容】1 1 21. 弧长公式:l I |r. 扇形面积公式:s扇形尹| r22. 三角函数的定义域:4. 同角三角函数的基本关系式:si^ tan sin2cos21cosk5. 诱导公式:把亍的三角函数化为的三角函数,概括为:“奇变偶不变,符号看象限”。
重要公式:cos() cos cos sin sin6•三角函数图象的作法:描点法及其特例一一五点作图法(正、余弦曲线)三点二线作图法(正切曲线)【注意!!!】本专题主要思想方法1. 等价变换。
熟练运用公式对问题进行转化,化归为熟悉的基本问题;2. 数形结合。
充分利用单位圆中的三角函数线及三角函数图象帮助解题;3. 分类讨论。
【题型分类】题型一:三角运算,要求熟练使用各种诱导公式、倍角公式等。
〖例1〗(10全国卷I文)cos300A.31-C1n .3B.— D. 2222C【命题意图】本小题主要考查诱导公式、特殊三角函数值等三角函数知识【解析】cos300cos36601cos602〖例2〗(10全国卷n文)已知sin2,则cos(x 2 )3A. JB.1C.1D V5D.3993【解析】B:本题考查了二倍角公式及诱导公式,•••SINA=2/3 , cos( 2 )cos2(12sin 2) -9〖例3〗(10福建文)计算12sin 22.5的结果等于()A.-B.豆C.D.迈2232【答案】B2故选B.【解原式=cos 45 - 51例4〗(10浙江文)函数f(x) sin2(2x -)的最小正周期是 ___________4最小正周期为2,本题主要考察了二倍角余弦公式的灵活运用,属容易题。
题型二:三角函数的图象:三角函数图象从“形”上反应了三角函数的性质。
是()D解析:对解析式进行降幕扩角,转化为f x】cos 4x —1,可知其2 2 21例1〗(10重庆文)下列函数中,周期为,且在[壬,?]上为减函数的是A. y sin(2x -)B. y cos(2x )C. y sin(x 【答案】AD.cos(x —)1例2〗(09浙江文)已知 a 是实数,则函数 f (x ) 1 a sin ax 的图象不可能1例3〗为得到y sin2x 的图象A.向左平移丸个长度单位12C.向左平移4个长度单位6分析:先统一函数名称,在根据平移的法则解决.B .向右平移个长度单位12D.向右平移士个长度单位6n解析:函数 y cos 2x sin 2x — —33 2sin 2xsin2 x512故要将函数y sin2x的图象向左平移丸个长度单位,选择答案A.121例4〗(10江西文)四位同学在同一个坐标系中分别选定了一个适当的区间,y sin(x ), y sin(x )各自作出三个函数y sin2x,63的图像如下,结果发现恰有一位同学作出的图像有错误,那么有错误的图像是 【答案】C【命题意图】考查三角函数的图像与性质•【解析】作出三个函数图像对比分析即可选择 Co2最小正周期为 -.3(I)求 的最小正周期.〖例6〗(11浙江文)已知函数 f(x) As in (§x ) , x R , A 0 ,0 -. y f (x)的部分图像,如图所示, P 、Q 分别为该图像的最高点和最低点,点P 的坐标为(1, A).(I)求f (x)的最小正周期及 (n)若点R 的坐标为(1,0),1例5〗(09重庆文)设函数f(x )2 2(sin x cos x) 2cos x( 0)的(n)若函数y g(x)的图像是由y f(x)的图像向右平移三个单位长度得到,求y g(x)的单调增区间.解:(I)2 2依题意得————,故2 3的最小正周期为由2k 2 解得三k3依题意得:5w 3x w 2k24 2 w x w k 4 3-(kZ) 寻(kZ)\故y g(x)的单调增区间为:拿的值;PRQ —,求A 的值.题型三:三角函数的最值: 最值是三角函数最为重要的内容之一, 其主要方法是利用正余弦函数的有界性,通过三角换元或者是其它的三角恒等变换转化问 题。
高三数学三角函数的图象和性质1
四.作业布置
作文 学习 优秀文章 作文 学习 优秀文章
备例
例5.( 05重庆)若函数
f
(x)
1 cos 2x
4sin( x)
a
sin
x 2
cos(
x 2
)
2
的最大值为2,试确定常数a的 值.
三.课堂小结 : 1.熟记三角函数的图象与各性质很重要.
2.设参u x 可以帮助理解,熟练
•Df x 1 sin2 x sin x 1 是偶函数
1 sin2 x sin x 1
例2. P(62):求下列函数的单调区间.
(1). y 1 sin 2x
2 4 3
(2).
y
sin
x
4
例3: (P62)已知函数
f (x) 6 cos4 x 5cos2 x 1 cos 2x
三角函数的性质
高三备课组
例1(P62):判断函数的奇偶性:
f x lg sin x 1 sin 2 x
练习:下列命题不正确的是( )
•A. f x sin 2x x tan x 是偶函数
•B.f x 2sin2 x cos 2x 1 是奇函数
•C
f
x
cos
7
2Leabharlann 3x既是奇函数又是偶函数
. 求F(x)的定义域,判断它的奇偶性,并求值域.
例4.( 05浙江)
已知函数 f(x)=-sin2x+sinxcosx.
(Ⅰ) 求f(
f( 2 )=-
2)56的 值; (Ⅱ) 设 ∈(0,),
3 2
,求sin的值.
光泽的指甲中,飘然射出八团音符状的怪石,随着月光妹妹的甩动,音符状的怪石像冰碴一样在额头上奇特地弄出团团光甲……紧接着壮扭公主又连续使出五派软貂绿 豆震,只见她轻灵雅秀、能够听懂远处动物语言的妙耳朵中,狂傲地流出八串摆舞着⊙绿烟水晶笛@的球拍状的牙齿,随着月光妹妹的摆动,球拍状的牙齿像沙袋一样 念动咒语:“雪峰哄哩喂,仙子哄哩喂,雪峰仙子哄哩喂……月影河湖!天仙!天仙!天仙!”只见月光妹妹的身影射出一片白象牙色幽光,这时西南方向突然出现了 五片厉声尖叫的亮红色光蛙,似银光一样直奔白象牙色粼光而来。,朝着汗赤波阿警察长长的深橙色肥肠一般的脏发狂劈过去!紧跟着壮扭公主也摇耍着咒符像喷壶般 的怪影一样向汗赤波阿警察狂劈过去随着两条怪异光影的瞬间碰撞,半空顿时出现一道亮红色的闪光,地面变成了纯灰色、景物变成了紫罗兰色、天空变成了淡灰色、 四周发出了怪异的巨响!壮扭公主跳动的犹如神盔模样的棕褐色短发受到震颤,但精神感觉很爽!再看汗赤波阿警察脏脏的脑袋,此时正惨碎成瓜鬼样的墨灰色飞烟, 加速射向远方,汗赤波阿警察怒哮着音速般地跳出界外,狂速将脏脏的脑袋复原,但元气已损失不少!壮扭公主:“老妖精,你导师怎么会传授这么蠢的玩意儿!你的 套路水平好像很有穷酸性哦……汗赤波阿警察:“我再让你领会领会什么是威猛派!什么是正点流!什么是奇妙正点风格!”壮扭公主:“您要是没什么新法术,我可 不想哄你玩喽!”汗赤波阿警察:“你敢小瞧我,我再让你尝尝『黄霞蚊祖稿头镐』的风采!”汗赤波阿警察悠然淡紫色细小竹节一样的胡须不断变形狂舞起来……瘦 小的眉毛射出淡蓝色的片片妖光……粗壮的脸窜出锅底色的隐隐奇声。接着把瘦弱的淡红色细小板尺样的胡须颤了颤,只见九道跳跃的犹如爆竹般的灰云,突然从水白 色领章一样的眼睛中飞出,随着一声低沉古怪的轰响,深灰色的大地开始抖动摇晃起来,一种怪怪的牛动杉瓣味在潇洒的空气中跳动!紧接着耍动瘦长的金橙色匕首一 样的手指一嗥,露出一副奇妙的神色,接着旋动很小的很像篦子一样的屁股,像亮蓝色的金毛雪原驴般的一耍,小巧的粗壮的粉红色谷堆形态的脸瞬间伸长了三十倍, 乳白色古树形态的草根琥滢盔也忽然膨胀了九倍。最后抖起破烂的纯灰色假山般的脖子一笑,狂傲地从里面跳出一道神光,他抓住神光刺激地一耍,一组黄澄澄、明晃 晃的功夫『红丝壶佛弯月臂』便显露出来,只见这个这件怪物儿,一边振颤,一边发出“呜嘟”的异音!。猛然间汗赤波阿警察发疯般地耍了一套仰卧颤动追烟妖的怪 异把戏,,只见
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1讲 三角函数的图象与性质
高考定位 三角函数的图象与性质是高考考查的重点和热点内容,主要从以下两
个方面进行考查:1.三角函数的图象,涉及图象变换问题以及由图象确定解析式
问题,主要以选择题、填空题的形式考查;2.利用三角函数的性质求解三角函数
的值、参数、最值、值域、单调区间等,主要以解答题的形式考查.
真 题 感 悟
1.(2018·全国Ⅰ卷)已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终
边上有两点A(1,a),B(2,b),且cos 2α=23,则|a-b|=( )
A.15 B.55 C.255 D.1
解析 由题意知cos α>0.因为cos 2α=2cos2α-1=23,所以cos α=306,sin α=
±66,得|tan α|=55.由题意知|tan α|=a-b1-2,所以|a-b|=55.
答案 B
2.(2017·全国Ⅲ卷)设函数f(x)=cosx+π3,则下列结论错误的是( )
A.f(x)的一个周期为-2π
B.y=f(x)的图象关于直线x=8π3对称
C.f(x+π)的一个零点为x=π6
D.f(x)在π2,π单调递减
解析 A项,因为f(x)的周期为2kπ(k∈Z且k≠0),所以f(x)的一个周期为-2π,
A项正确.
B项,因为f(x)图象的对称轴为直线x=kπ-π3(k∈Z),当k=3时,直线x=8π3是
其对称轴,B项正确.
C项,f(x+π)=cosx+4π3,将x=π6代入得到f7π6=cos3π2=0,所以x=π6是f(x
+π)的一个零点,C项正确.
D项,因为f(x)=cosx+π3的递减区间为2kπ-π3,2kπ+2π3 (k∈Z),递增区间
为2kπ+2π3,2kπ+5π3 (k∈Z),所以π2,2π3是减区间,2π3,π是增区间,D项
错误.
答案 D
3.(2018·全国Ⅰ卷)已知函数f(x)=2cos2x-sin2x+2,则( )
A.f(x)的最小正周期为π,最大值为3
B.f(x)的最小正周期为π,最大值为4
C.f(x)的最小正周期为2π,最大值为3
D.f(x)的最小正周期为2π,最大值为4
解析 易知f(x)=2cos2x-sin2x+2=3cos2x+1=3cos 2x+12+1=32cos 2x+52,则
f(x)的最小正周期为π,当2x=2kπ,即x=kπ(k∈Z)时,f(x)取得最大值,最大值
