论洛必达法则.doc
洛必达法则

2. 型
1 1 00 . 步骤: 0 0 00
例8 求 lim (
x 0
1 1 ). sin x x
()
解
x 0,
x sin x x sin x 原式 lim lim x 0 x sin x x 0 x2
1 cos x sin x lim lim 0. x 0 x 0 2x 2
那么
f ( x) f ( x ) A (或 ) lim lim x x0 g ( x) x x0 g ( x )
将x x0改为x x0 , x x0 , x , x , x 时,同样适用 . 说明:
ln x 例4 求 lim . x x
极限不存在
不能使用洛必塔法则. 改用其它方法求极限. sin x 1 x sin x x 1 lim lim x x x sin x sin x 1 x
注意:洛必达法则不能滥用!
二、 0 , ,0 ,1 , 型未定式
0 0
关键: 将其它类型未定式化为洛必达法则可
第二节 洛必达法则
0 一、 型未定式 0 二、 型未定式
三、0 、 、0 0 、1 、 0 型未定式
四、小结
思考题
回顾:
0 0
x 1 lim 2 lim x 0 x x 0 x
sin 3 x lim 3 x 0 x
4x3 x 2 lim 2 x 2 x 2 x 4
2 sec x 1 tan x x lim 原式 lim 3 x0 x 0 3 x2 x
tan 2 x x2 1 lim lim 2 . 2 x 0 3 x x 0 3 x 3
32洛必达法则共9页word资料
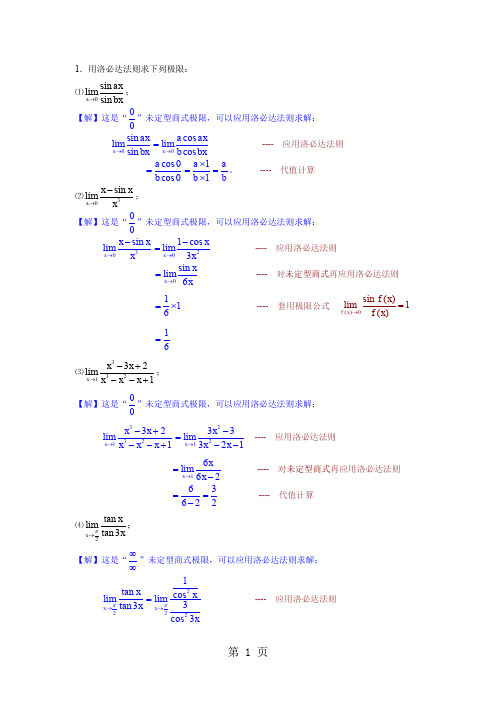
1.用洛必达法则求下列极限:⑴0sin limsin x axbx→;【解】这是“00”未定型商式极限,可以应用洛必达法则求解:0sin lim sin x ax bx →0cos limcos x a axb bx→= ---- 应用洛必达法则 cos 0cos 0a b =11a b ⨯=⨯ab=。
---- 代值计算 ⑵30sin lim x x x x→-; 【解】这是“00”未定型商式极限,可以应用洛必达法则求解:30sin lim x x x x →-201cos lim3x xx →-= ---- 应用洛必达法则 0sin lim6x xx→= ---- 对未定型商式再应用洛必达法则 116=⨯ ---- 套用极限公式 ()0sin ()lim1()f x f x f x →= 16=⑶332132lim 1x x x x x x →-+--+; 【解】这是“”未定型商式极限,可以应用洛必达法则求解: 332132lim 1x x x x x x →-+--+22133lim 321x x x x →-=-- ---- 应用洛必达法则 16lim62x xx →=- ---- 对未定型商式再应用洛必达法则63622==- ---- 代值计算 ⑷2tan limtan 3x xxπ→; 【解】这是“∞∞”未定型商式极限,可以应用洛必达法则求解: 2tan lim tan 3x xx π→2221cos lim 3cos 3x x xπ→= ---- 应用洛必达法则222cos 3lim3cos x xx π→= ---- 整理繁分式 22cos3(sin 3)3lim32cos (sin )x x x x x π→⋅-⋅=⋅⋅- ---- 对未定型商式再应用洛必达法则2sin 6limsin 2x xxπ→= ---- 化简复杂分式 26cos6lim2cos 2x xxπ→= ---- 对未定型商式再应用洛必达法则3cos3cos ππ=---- 代值计算3=⑸2(ln )lim x x x→+∞; 【解】这是“∞∞”未定型商式极限,可以应用洛必达法则求解: 2(ln )limx x x→+∞12ln lim 12x x x x→+∞⋅= ---- 应用洛必达法则 4ln limx xx→+∞= ---- 化简繁分式14lim 12x x x→+∞= ---- 对未定型商式再应用洛必达法则 8limx x→+∞= ---- 化简繁分式 0=⑹2ln()2lim tan x x x ππ+→-; 【解】这是“∞∞”未定型商式极限,可以应用洛必达法则求解:2ln()2lim tan x x x ππ+→-2212lim 1cos x x xππ+→-= ---- 应用洛必达法则 22cos lim 2x x x ππ+→=----- 化简繁分式22cos (sin )lim 1x x x π+→-= ---- 对未定型商式再应用洛必达法则2cossin22ππ=-0= ---- 代入计算⑺212lim x x x e →;【解】这是“0⨯∞”未定型极限,应化为商式极限后应用洛必达法则求解:212lim xx x e →2102lim 1x x e x →= ---- 化为商式后,成为“∞∞”未定型商式极限 212021()'lim1()'x x e x x→= ---- 应用洛必达法则 2211lim x x e →+∞= ---- 化简繁分式 =+∞ ---- 代入计算⑻0lim cot x x x →;【解】这是“0⨯∞”未定型极限,应化为商式极限后应用洛必达法则求解:lim cot x x x →0limtan x xx →= ---- 化为商式后,成为“∞∞”未定型商式极限021lim 1cos x x →= ---- 应用洛必达法则 20limcos x x →= ---- 化简繁分式2cos 01== ---- 代入计算⑼2lim(sec tan )x x x π→-;【解】这是“∞-∞”未定型极限,应化为商式极限后应用洛必达法则求解:2lim(sec tan )x x x π→-21sin lim()cos cos x x x xπ→=- ---- 为通分化为商式作准备 21sin limcos x xx π→-= ---- 成为“00”未定型商式极限2cos limsin x xxπ→-=- ---- 应用洛必达法则cos 20sin2ππ== ---- 代入计算⑽11lim()1ln x x x x→--; 【解】这是“∞-∞”未定型极限,应化为商式极限后应用洛必达法则求解:11lim()1ln x x x x→--1ln (1)lim(1)ln x x x x x x →--=- ---- 通分化为商式,成为“00”未定型 1ln 11lim1ln x x x x x→+-=-+---- 应用洛必达法则1ln limln 1x x xx x x →=+- ---- 化简繁分式,成为“00”未定型 1ln 1limln 11x x x →+=++ ---- 应用洛必达法则 011022+==+ ---- 代入计算 ⑾tan 0lim xx x +→;【解】这是“00”幂指函数未定型极限,应化为商式极限后应用洛必达法则求解: 【解法一】应用对数法,令tan xy x=,则tan ln ln ln tan ln cot xxy xx x x===, 于是,00ln lim ln lim cot x x xy x ++→→= ---- 成为“∞∞”未定型021lim 1sin x x x+→=- ---- 应用洛必达法则20sin lim x x x +→= ---- 化简繁分式,成为“00”未定型 02sin cos lim 1x x x+→= ---- 应用洛必达法则2sin0cos00== ---- 代入计算得到 0l i m l n 0x y +→=,亦即0ln lim 0x y +→=, 从而有 0l i m 1x y e +→==,亦即tan 0lim 1xx x +→=。
经典洛必达法则

即 f ( ) 0
例 设0 a b,证明b a ln b b a .
b
aa
证明: 设f ( x) ln x,
f ( x)在[a,b]上满足拉格朗日中值定理的条件,
所以, (a,b),使 f (b) f (a) f ( )(b a),
因为f ( x) 1 ,上式即为
拉格朗日(Lagrange)中值定理(1)如果函数 f(x)在 闭区间[a, b]上连续(,2)在开区间(a, b)内可导,那末在 (a, b)内至少有一点(a b),使等式
f (b) f (a) f ' ()(b a) 成立.
推论 如果函数 f ( x) 在区间 I 上的导数恒为零, 那末 f ( x) 在区间 I 上是一个常数.
lim sin x sin
x 1
2
2
1.
2
例
求
lim
x0
cos
x
x3
1
x
.
(
0 0
)
sin x 1
解 原式 lim x0
2 3x2
1 x
.
例
求
lim
x1
x
x3 3
x
3x 2
x
2
1
.
(0) 0
解:
×
正解:
重难突破微专题(十) 洛必达法则

温馨提示:此套题为Word 版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word 文档返回原板块。
重难突破微专题(十)洛必达法则一、洛必达法则的具体内容1.洛必达法则:设函数f (x ),g (x )满足:(1)lim x →a f (x )=lim x →ag (x )=0; (2)在x =a 附近,f ′(x )和g ′(x )都存在,且g ′(x )≠0;(3)lim x →a f ′(x )g ′(x ) =A (A 可为实数,也可以是±∞).则lim x →a f (x )g (x ) =lim x →a f ′(x )g ′( =A .(可循环使用)注意:①使用洛必达法则时,是对分子、分母分别求导,而不是对它们的商求导,求导之后再求极限得最值.②0·∞型∞·∞型可转化为00 型或∞∞ 型.二、洛必达法则的简单应用【典例1】求lim x →01-cos x 3x 2 的值. 【解析】因为将x =0代入1-cos x 3x 2 的分母分子都为0,即典型的00 型.则lim x →0 1-cos x 3x 2 =lim x →0 (1-cos x )′(3x 2)′=lim x →0 sin x 6x =16 (循环使用洛必达法则,对分式的分子分母连续求导).本例中的代数式“1-cos x 3x 2 ”改为“e 2x -13x ”结果如何?【解析】因为将x =0代入e 2x -13x 的分母分子都为0,即典型的00 型.则lim x →0 e 2x -13x =lim x →02e 2x 3 =23 .【典例2】计算极限lim x →+∞ln x x α (α>0). 【解析】此极限满足洛必达法则,于是得lim x →+∞ ln x x α =lim x →+∞ 1xαxα-1 =lim x →+∞ 1αx α =0. 在使用洛必达法则时应注意以下几点:①洛必达法则只适用于00 型或∞∞ 型的极限.②如果lim f ′(x )g ′(x ) 仍是00 型或∞∞ 型,则可继续使用洛必达法则.③如果lim f ′(x )g ′(x ) 不存在且不是∞,并不表明lim f (x )g (x )不存在,只表明洛必达法则失效,这时应用其他方法求解. 三、洛必达法则的综合应用【典例3】已知函数f (x )=mx -sin x ,g (x )=ax cos x -2sin x (a >0).(1)若函数y =f (x )是(-∞,+∞)上的单调递增函数,求实数m 的最小值;(2)若m =1,且对任意x ∈⎣⎢⎡⎦⎥⎤0,π2 ,都有不等式f (x )≥g (x )成立,求实数a 的取值范围.【解析】(1)因为函数f (x )=mx -sin x 在R 上单调递增,所以f ′(x )≥0恒成立,所以f ′(x )=m -cos x ≥0,即m ≥cos x ,所以m min =1.(2)因为m =1,所以函数f (x )=x -sin x ,由f (x )≥g (x )对任意x ∈⎣⎢⎡⎦⎥⎤0,π2 都成立,得 x +sin x -ax cos x ≥0恒成立.即ax cos x ≤x +sin x 恒成立.①当x =0时,0≤0恒成立;②当x =π2 时,0≤π2 +1恒成立;③当0<x <π2 时,a ≤x +sin x x cos x 恒成立;令h (x )=x +sin x x cos x ,则h ′(x )=(1+cos x )x cos x -(x +sin x )(cos x -x sin x )(x cos x )2 =x +x 2sin x -12sin 2x(x cos x )2=12(2x -sin 2x )+x 2sin x (x cos x )2 >0,所以h (x )=x +sin x x cos x 在x ∈⎝ ⎛⎭⎪⎫0,π2 上单调递增; 所以a <h (0)=00 (行不通,洛必达法则),lim x →0 h (x )=lim x →0 1+cos xcos x -x sin x=1+11 =2, 所以0<a ≤2初等方法解决:因为m =1,所以函数f (x )=x -sin x ,因为f (x )≥g (x ),所以x +sin x -ax cos x ≥0.对于任意x ∈⎣⎢⎡⎦⎥⎤0,π2 ,令H (x )=x +sin x -ax cos x ,则H ′(x )=1+cos x -a (cos x -x sin x )=1+(1-a )cos x +ax sin x①当1-a ≥0,即0<a ≤1时,H ′(x )=1+(1-a )cos x +ax sin x ≥0,所以H (x )在⎣⎢⎡⎦⎥⎤0,π2 上为单调递增函数, 所以H (x )≥H (0)=0,符合题意,所以0<a ≤1.②当1-a <0,即a >1时,令h (x )=1+(1-a )cos x +ax sin x ,于是h ′(x )=(2a -1)sin x +ax cos x . 因为a >1,所以2a -1>0,所以h ′(x )≥0,所以h (x )在⎣⎢⎡⎦⎥⎤0,π2 上为单调递增函数, 所以h (0)≤h (x )≤h ⎝ ⎛⎭⎪⎫π2 ,即2-a ≤h (x )≤π2 a +1,所以2-a ≤H ′(x )≤π2 a +1. (ⅰ)当2-a ≥0,即1<a ≤2时,H ′(x )≥0,所以H (x )在⎣⎢⎡⎦⎥⎤0,π2 上为单调递增函数,于是H (x )≥H (0)=0,符合题意, 所以1<a ≤2.(ⅱ)当2-a <0,即a >2时,存在x 0∈⎝ ⎛⎭⎪⎫0,π2 ,使得当x ∈(0,x 0)时,有H ′(x )<0,此时H (x )在(0,x 0)上为单调递减函数,从而H (x )<H (0)=0,不能使H (x )>0恒成立,综上所述,实数a 的取值范围为0<a ≤2.【典例4】设函数f (x )=e x -1-x -ax 2;(1)若a =0,求f (x )的单调区间;(2)若当x ≥0时f (x )≥0,求a 的取值范围.【解析】(1)当a =0时,f (x )=e x -1-x ,f ′(x )=e x -1.当x ∈(-∞,0)时,f ′(x )<0;当x ∈(0,+∞)时,f ′(x )>0.故f (x )在(-∞,0)上单调递减,在(0,+∞)上单调递增.(2)f ′(x )=e x -1-2ax .由(1)知e x ≥1+x ,当且仅当x =0时等号成立. 故f ′(x )≥x -2ax =(1-2a )x ,从而当1-2a ≥0,即a ≤12 时,f ′(x )≥0(x ≥0),而f (0)=0,于是当x ≥0时,f (x )≥0.由e x >1+x (x ≠0),可得e -x >1-x (x ≠0).从而当a >12 时,f ′(x )<e x -1+2a (e -x -1)=e -x (e x -1)(e x -2a ),故当x ∈(0,ln 2a )时,f ′(x )<0,而f (0)=0,于是当x ∈(0,ln 2a )时,f (x )<0.综合得a 的取值范围为⎝⎛⎦⎥⎤-∞,12 . 原题的解析在处理第(2)问时用到的不等式放缩较难想到,现应用洛必达法则处理如下:(2)方法一:当x ≥0时,f (x )≥0,即e x -1-x ≥ax 2.①当x =0时,a ∈R ;②当x >0时,e x -1-x ≥ax 2等价于a ≤e x -1-x x 2 .记g (x )=e x -1-x x 2 则g ′(x )=(x -2)e x +x +2x 3. 记h (x )=(x -2)e x +x +2,x ∈(0,+∞),则h ′(x )=(x -1)e x +1,当x ∈(0,+∞)时,h ″(x )=x e x >0,所以h ′(x )=(x -1)e x +1在(0,+∞)上单调递增,且h ′(x )>h ′(0)=0, 所以h (x )=(x -2)e x +x +2在(0,+∞)上单调递增,且h (x )>h (0)=0,因此当x ∈(0,+∞)时,g ′(x )=h (x )x 3 >0,从而g (x )=e x -1-x x 2 在(0,+∞)上单调递增.由洛必达法则有,lim x →0 g (x )=lim x →0 e x -1-x x 2 =limx →0 e x -12x =lim x →0 e x 2 =12 , 即当x →0时,g (x )→12 ,所以当x ∈(0,+∞)时,所以g (x )>12 ,因此a ≤12 .综上所述,当a ≤12 且x ≥0时,f (x )≥0成立.方法二:f ′(x )=e x -1-2ax ;①当a ≤12 时,f ′(x )=e x -1-2ax ≥e x -1-x ≥0(e x -1-x ≥0,求导易证);所以y =f (x )在x ∈[0,+∞)上单调递增,从而f (x )≥f (0)=0,命题是成立的.>12 -1-2ax ,易得f ′(0)=0,f ″(x )=e -2a ,其中2a >1,可得y =f ′(x )在x ∈(0,ln 2a )上单调递减,在x ∈(ln 2a ,+∞)上单调递增.且f ′(0)=0,所以当x ∈(0,ln 2a )时,f ′(x )<f ′(0)=0;所以y =f (x )在x ∈(0,ln 2a )上单调递减,故f(x)<f(0)=0,此时命题不成立.故得正确答案是a≤12.1.对恒成立问题中的求参数取值范围,参数与变量分离较易理解,但有些题中求分离出来的函数式的最值有点麻烦,利用洛必达法则可以较好地处理它的最值,是一种值得借鉴的方法.2.对于不能分离参数或分离参数后求最值较困难的问题,我们可以把含参不等式整理成f(x,a)>0或f(x,a)≥0的形式,然后从研究函数的性质入手,转化为讨论函数的单调性和极值.在解题过程中常常要用到如下结论:(1)如果f(x,a)有最小值g(a),则f(x,a)>0恒成立⇔g(a)>0,f(x,a)≥0恒成立⇔g(a)≥0;(2)如果f(x,a)有最大值g(a),则f(x,a)<0恒成立⇔g(a)<0,f(x,a)≤0恒成立⇔g(a)≤0.关闭Word文档返回原板块。
洛必达法则

6 cos 6 x 3. = = lim π x → 2 cos 2 x
2
注意:洛必达法则是求未定式的一种有效方法, 注意:洛必达法则是求未定式的一种有效方法, 但与其它求极限方法结合使用,效果更好. 但与其它求极限方法结合使用,效果更好. 例6 解
tan x x . 求 lim 2 x → 0 x tan x
0 ( ) 0
(tan x )′ sec2 x = 1. 原式 = lim = lim x →0 x→0 → ( x )′ 1
x3 3 x + 2 . 例2 求 lim 3 2 x →1 x x x + 1
0 ( ) 0
3 x2 3 6x 3 解 原式 = lim 2 = lim = . x →1 3 x 2 x 1 x →1 6 x 2 2
2
1 ln(1 + ) x ; 2, 2, lim x → +∞ arctan x
3,lim x cot 2 x ;
x →0
2 1 ); 4, 4,lim( 2 x →1 x 1 x 1
1 tan x 6, 6, lim ( ) ; x → +0 x
5, lim x
x → +0
sin x
;
2 7, lim ( arctan x) x . x → +∞ π
sec 2 x 1 tan x x = lim 原式 = lim 2 3 x →0 x →0 3x x tan x 1 2 sec 2 x tan x 1 = lim = lim = . x →0 6x 3 x →0 x 3
0 二, ∞ , ∞ ∞ ,0 ,1 , ∞ 型未定式解法
0 0
∞
关键:将其它类型未定式化为洛必达法则可解决 关键: 的类型 ( 0 ), ( ∞ ) .
第二节洛必达法则

称为
0 0
型不定式.
例如, lim tan x , x0 x
0 0
目录 上一页 下一页 退 出
定理1 设f x,g x满足:
(1) lim f x 0, lim g x 0;
x x0
x x0
(2) 在U x0 内可导,且g x 0;
lim (tan x) x0 ( x)
lim sec2 x0 1
x
1.
例2
求
lim
x1
x
x3 3
x
3x 2
x
2
1
.
0 0
解
原式
3x2 3
lim
x1
3
x2
2
x
1
lim 6x x1 6 x 2
3. 2
目录 上一页 下一页 退 出
例3
求
二、1、 1; 8
6、1;
2、1;
7、e
2 π
.
3、1 ; 2
4、 1 ; 5、1; 2
三、连续.
目录 上一页 下一页 退 出
二、用洛必达法则求下列极限:
1、
lim
x
lnsin x ( 2x)2
;
2
1
ln(1 )
2、 lim
x;
x arctan x
3、lim x cot 2x ; x0
4、lim( x1
x
2 2
1
x
1
); 1
5、 lim x sin x ; x0
6、lim ( 1 )tan x ; x0 x
洛必达法则

f ( x) f '( ) 即•• g ( x) g '( )
( 在x与a之间)
下页
由于当x→a时,ξ→a,对上式两边取极限得
f ( x) f ( ) lim lim x a g ( x) x a g ( ) f ( x) f ( x) 即•• lim lim x a g ( x) x a g ( x )
注:每次使用罗必达法则之前,必须分析所求极限 是否满足法则条件,若不满足,应停止使用,改用 其他方法。
下页
“零比零”型未定式的定值法 x sin x lim 例 2 例 3 求 3 x 0 x x sin x lim1 cos x lim sin x 1 解 lim 解 x 0 x 0 3x 2 x 0 6 x 6 x3 例 例 43 求 lim 2
2
x e sin x 1 e sin x 1 lim lim 2 2 x 0 x 0 (sin x) x
2
x
e cos x e x sin x 1 lim lim x 0 x 0 2x 2 2
x
e x 1 sin x 例11 求极限 lim x x 0 (e 1)sin x
f (sin x) 1 f (sin x) 1 lim lim x 0 x 0 f ( x) 1 ln f ( x)
f (sin x) f (0) x lim x 0 sin x 0 f ( x) f (0)
所以不能用洛必达法则 但其极限是存在的 lim x sin x lim (1 sin x ) 1 x x x x
例14
e cos x lim 求 x 0 x sin x
洛必达法则的几何意义

洛必达法则的几何意义洛必达法则,又称为洛伦兹变换,是狭义相对论中最基本的公式,描述了质点在相对运动时的物理量的变化规律,成为研究时空变化的基础。
然而,很少有人关注到它的几何意义,本文将从几何的角度来探讨洛必达法则的含义。
首先,我们来看洛必达法则的表达式:$\begin{cases}x'=\dfrac{x-vt}{\sqrt{1-\dfrac{v^2}{c^2}}}\\[2ex]t'=\dfrac{t-\frac{vx}{c^2}}{\sqrt{1-\dfrac{v^2}{c^2}}}\end{cases}$其中,$x,t$表示观察者S所测量到的事件的时空坐标,$v$表示S'和S之间的相对速度,$x',t'$表示S'所测量到的事件的时空坐标,$c$表示光速。
这个公式看上去十分熟悉,因为它就是我们在熟悉的平面直角坐标系中的坐标变换公式。
事实上,狭义相对论中的时空坐标系也可以看作是一个四维的“坐标系”,我们通常称之为闵可夫斯基时空。
在平面直角坐标系中,坐标变换的几何意义是什么?我们以二维平面为例,设有两个坐标系,一个是$x-y$坐标系,另一个是$x'-y'$坐标系,假设$x'-y'$坐标系在$x-y$坐标系的左下方以$\theta$度的角度旋转。
那么,我们如何从$x-y$坐标系中的点$(x,y)$求出在$x'-y'$坐标系中的坐标呢?对于一个向量$\vec{V}$而言,它的坐标变换可以看作是它在两个坐标系中的向量的点积:$\vec{V}\cdot\vec{n}=V_xn_x+V_yn_y=V_{x'}n_{x'}+V_{y'}n_{y'}$其中,$\vec{n}$表示$x-y$坐标系的基向量,在$x'-y'$坐标系中的坐标就是$n_{x'},n_{y'}$,$V_x,V_y$表示$\vec{V}$在$x-y$坐标系中的投影,$V_{x'},V_{y'}$表示$\vec{V}$在$x'-y'$坐标系中的投影。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
例13、 ,
但若用法则,则 不存在。
所以,洛必达法则失效时要寻求别的方法来求解极限。
连续多次使用法则时,每次都要检查是否满足定理条件,只有未定式方可使用此法则,否则就会得出错误的结果。
例14、 (不是未定式) .
事实上, .
对 型进行转化时,哪个放分子,哪个放分母也是有讲究的。
例15、 极限反倒变复杂了,如果变换形式,
摘要
在数学分析中,求极限的方法是多种多样的,其中利用导数转化求极限是洛必达法则的一大特色。在使用洛必达法则求极限的过程中,一定要检验是否满足洛必达法则的三个条件,但法则成立的条件是比较苛刻的。实际上,洛必达法则在解决实际问题中有着广泛的作用。本文只从:①法则适用函数极限的类型;②将法则的应用推广至求数列极限以扩大法则的适用范围;③对法则的不足(失效)之处和使用误区等方面进行了探讨和研究。并将该法则推广到了多元函数及其复变函数和差分形式当中去。显示了该法则在极限计算中的重要作用。
(2) f (x)=0与 g (x)=0;
(3) ,
则 =
洛必达法则2:若函数f (x)与g(x)满足下列条件:
(1) A>0,在 与 可导,且g '(x)≠0;
(2) f (x)=0与 g (x)=0;
(3)
则 =
2
洛必达法则3:若函数f (x)与g(x)满足下列条件:
(1)在a的某去心邻域 可导,且g '(x)≠0;
解
例6、 .
解 .
可见利用洛必达法则能够解决很多函数极限问题,而且可以将法则和其他求极限方法结合起来同时使用。
3.
例7、求 .
解此问题可归类到 型未定式极限,但由于题目中变量为 正整数,对这些孤立点 无法求导,故不能直接利用洛必达法则求解。应先将极限式中的 换成连续变量 ,求函数 极限,再由归结原则知原数列极限值。
则 .
极限存在的因子可先从极限式中分离出来,这样求导时就变得简单些。
运用洛必达法则时常结合等价无穷小代换求极限。如例12.
3.3
近年来的高考数学试题常与大学数学知识有机接轨,以高考数学为背景的命题形式成为了热点。许多省市的高考试卷的压轴题都是导数应用问题,其中求参数的取值范围就是一类重点考察的题型。这类题目容易让学生想到用分离参数的方法,但其中有部分题在高中范围内用分离参数的方法常常需要复杂的讨论,学生掌握起来非常困难。研究发现,利用分离参数的方法难以解决这部分问题的原因是出现了 型的式子,而这就是大学中的不定式问题,解决这类问题最有效的方法就是利用洛必达法则。
解法2、 ,
若 ,则上式等于0,与已知条件矛盾;
若 ,则 是 型未定式,可用洛必达法则求解。即
.
根据以上从右至左,多次应用法则得 .
解法2求出 后,讨论了其存在性,排除了 的情形后,得出了 ;此时 是 型未定式,继续应用洛必达法则进行求解,从而避免了武断上述极限存在的错误。
该问题的关键是讨论 的存在性,只有它存在才能使用洛必达法则。
第三章
3.1
3.
在自变量的某变化过程中,对上述两种基本类型可直接应用法则求极限。
Hale Waihona Puke 例2、求数列极限 .解:先求函数极限 .取对数后的 极限为:
所以, .
注:在求极限时,如果 还是 型未定式,且 , 仍满足洛必达法则条件,则可继续使用该法求极限。另外,要分辨是否是数列极限,是数列极限则不能直接使用洛必达法则。
例17、(2010年全国新课标理)设函数 。
(1)若 ,求 的单调区间;
(2)若当 时 ,求 的取值范围。
现用洛必达法则处理第(2)题如下:
解:(2)当 时, ,对任意实数 ,均存在 。
当 时, ,等价于 ,
令 ,则 ,
令 ,则 ,
知 在 上为增函数, ,知 在 上为增函数,
,所以 在 上为增函数。
例10、求极限 .
分析:这问题是 型未定式,但分子分母分别求导后,变成 ,而 与 当 时极限均不存在。但原极限存在,可用如下方法求得。
.
即此时法则失效。
例11、求
解 (振荡),法则失效,但原函数极限存在,
.
3
例12、求 .
解 ,
求导两次后极限式出现循环现象,故洛必达法则失效,不能使用。
但原式极限存在,可用下面方法求得:
对于 型,可通过通分化为 型未定式计算;
对于 , , 型,可先化为以e为底的指数函数的极限,再利用指数函数的连续性,转为直接求指数的极限,而指数的极限形式为 型,再转化为 型或 型计算。
例4、求 .
解:此题属 型未定式。讲原式中的 写在分母上,使其变为 型后,应用洛必达法则,即 .
例5、求 ( 型).
例16、(2011年全国新课标理)已知函数曲线 在点 处的切线方程为 。
(1)求 的值;
(2)如果当 ,且 时, ,求 的取值范围。
现用洛必达法则处理第(2)题如下:
解:(2)由题设可得,当 时, 恒成立。
令 ,则 ,
再令 ,
则 ,易知 在 上为增函数,且 ,故当 时, 当 时, 。
所以 在 上为减函数,在 上为增函数,故 ,所以 在 上为增函数。因为 ,所以当 时, ,当 时, ,
求函数极限是高等数学中的一项重要内容,是研究微积分学的工具。在众多求极限方法中,洛必达法则因其使用简单方便又可解决绝大部分极限问题而备受青眯,但如果使用不当也容易产生误区,得出错误结果。
第二章
2.
2
洛必达法则1:若函数f (x)与g(x)满足下列条件:
(1)在a的某去心邻域 可导,且g '(x)≠0;
(2) f (x)= 与 g (x)= ;
(3) ,
则 =
2
从定理知道,无论是“ ”型还是“ ”型都必须具备一个重要条件,即在自变量的同一过程中, 存在(或为 )时,才有 存在(或为 ),且 = ,但是此条件却不便先验证后使用。所以连续多次使用该法则时,每次都要验证它是否为“ ”型或“ ”型。
其使用程序如下: , ,…, ,若 存在(或为 ),那么才有式子 = = = = 成立,而上式成立是基于 , ,…, 都是“ ”型未定式,而且从右到左依次相等。但为了书写方便,在应用此法求极限时,总是习惯从右到左写。这样,如果忽略了对条件的验证,就有可能出错。
所以当 时, ,当 时, ,所以 在 上为减函数,在 上为增函数,
因为由洛必达法则知, ,
所以 ,即 的取值范围为 。
本题由已知很容易想到用分离变量的方法把参数 分离出来,然后对分离出来的函数 求导,研究其单调性、极值。此时遇到了“当 时,函数 值没有意义”这一问题,很多考生会陷入困境。如果考前对优秀的学生讲洛必达法则的应用,再通过强化训练就能掌握解决此类难题的这一有效方法。
,
故由归结原则得, .
该法则尽管求极限很方便,但也并不是万能的,而且使用时也要谨慎,否则容易出错。
3.
在求极限时若能灵活地将法则和其他求极限方法结合起来使用,则计算往往变得更为简单、方便。
例8、求 .
解显然,当 时, , ,
故 .
该法则是通过计算函数的导数,利用导数的极限求出原函数的极限,故只适用于函数极限的求解。然而在应用时,对 型及 型数列极限也可间接应用。
关键词洛必达法则极限应用推广
Abstract
In mathematical analysis, a variety of ways to limit, derivative into the limit of which is a major feature l ' hospital rule. Los Bida rule limiting process, must be tested meets the three conditions which Los Bida, but rule conditions are more demanding. In fact, Los Bida law has a broader role in solving practical problems. This article from: ① principles applicable limit of function types; ② apply the rule extension to sequence limit in order to expand the scope of the law; ③ insufficient to rule (fail) and errors are discussed and studied. And the rule was extended to functions of several variables, with its complex functions and differential forms. Shows the law is important in limit calculation.
3.
有时极限式并不满足法则条件,如用法则求解,就会得到错误的结果,主要有三种情形。
3
例9、求 .
解:事实上,此题可以直接利用函数连续性得到结果。
如果运用洛必达法则, .
由于本题不是未定式 型,而上面错误地应用了洛必达法则,从而得出错误的结论。.
3
特别当 时,函数式中含有 或 ;或当 时,函数式中含有 或 时,用法则求极限时出现极限震荡,此时法则失效。
例1、问a,b取何值时,下式成立?
=1,a>0.
解:解法1、 =
而 ,由此可以得到 ,于是b=1,所以有 ,即a=4.根据以上从左到右推导顺序.问题出在式 ,即 的存在性并没有论证.根据洛必达法则的条件,只有当 存在时,式 才能成立.这种问题往往在求极限时被忽视.因此后面的做法就是去了根基.所以上述解法1错误。
