哈工大能源学院材料力学讲课课件第9章.ppt
合集下载
材料力学第9章-压杆稳定3第8章-能量法1
l
iz
1.3 7 m 55.2103 m
165
9.5 压杆的合理设计 由图9.11查得，Q235钢压杆相应的稳定因数为
＝0.262。
显然，前面假设的＝0.5这个值过大，需重新假设 值再来 试算；重新假设的 值大致上取以前面假设的＝0.5和所得 的＝0.262的平均值为基础稍偏于所得 的值。
重新假设＝0.35，于是有
例 用能量法求两端球铰的压杆的临界压力。
设压杆微弯曲时的挠曲线方程为：
y
y
a
x
l
2
l
2
解：
2 2
C
该挠曲线满足位移边界条件： A
y
y0 yl 0
则任一截面上的弯矩为：
x l
B Fx
M
x
Fcr
y
Fcr
a
x
l 2
2
l 2
2
M 2 EI dx
由：
Fcr
l
y '2 dx
1、分析法/解析法
平衡方程——静力平衡关系 几何方程——变形几何关系 物理方程——应力应变关系
2、能量法
利用应变能的概念，解决与弹性体系变形有关的问题的 方法。
在求解组合变形、曲杆或杆系以及超静定问题时，能量 法是一种非常有效的方法，是结构分析的基础。
能量法/基本概念
能量法有关的几个基本概念 1、外力功:线弹性体系在外力的作用下产生变形，每个外力
在与它相对应的位移上所作的功 W。
2、应变能:弹性体受外力作用下产生变形而储存了能量，这个
被储存的能量即为应变能或变形能 U。
2l
代入上式有，
yq
x
x
M
材料力学第九章超静定系统
第九章 超静定系统9-1 图示悬臂梁32750,3010.l mm EI N m ==⨯。
弹簧刚度317510/k N m =⨯。
若梁与弹簧的间隙 1.25mm δ=，求力450P N =作用时弹簧的受力。
解：若按一般悬臂梁，则有作用点处挠度32.11 1.253Pl f mm mm EIδ==>= 可见梁在实际变形下触及弹簧。
设弹簧的弹力为N ，问题一次超静定；挠度设为P δ，则弹簧被压缩量为P δδ-，对梁而言3()3P l P N EIδ=-； 对弹簧而言N=k(-)P δδ以上两式得3()3l NP N EI Kδ-=+，解得82.7N =牛顿 所以，弹簧受力为82.7牛顿。
题9-1图 题9-2图9-2 图示悬臂梁的自由端刚好与光滑斜面接触，求温度升高t ∆时梁的最大弯矩。
已知A a E I 、、、，且不计轴力对弯曲变形的影响。
解：斜面光滑，则B 处（自由端）所受力为垂直于斜面向上，以B R 代替。
问题一次超静定，协调条件为：垂直于斜面方向上的位移分量为0（沿B R 方向） 升温时，l t l α∆=∆⋅，则分量为cos45t l δ=∆⋅︒B R 作用下：(),cos45R B B BM x M Nl Ndx N R EI P EA R δ∂∂=⋅+⋅=⋅︒∂∂⎰362B B R R l R lEI EAδ=+ （沿B R 向斜上方），t δ与R δ方向相反，则：0R t δδ-=解出23B R t Al Iα=∆+，则max 23cos 453B EIAl M R l t Al I α=︒=∆+9-3 图示桁架中各杆的抗拉压刚度相同。
试求桁架各杆的内力。
解：假设1杆受拉力N 。
由于杆1实际上是连续的，因而切口处的相对位移应等于零。
于是变形协调条件为：10δ=。
应用莫尔定理01i i ii N N l EA δ=∑，11N N =，31N N =，5612N N N ==-，341N N P ==-，00131N N ==，00562N N ==-，0034N N ==∴116+(180N δ=-+=，31N N ==（拉力），56N N ==24N N ==q题9-3图 题9-4图 题9-5图9-4 设刚架的抗弯刚度EI 为常量。
材料力学 第九章 压杆稳定
cr s p
cr s cr a b
cr
小柔度杆 中柔度杆
O
π2 E
2
大柔度杆
2
1
l
i
大柔度杆—发生弹性失稳 中柔度杆—发生非弹性失稳 小柔度杆—不发生失稳，而发生强度失效
Fuzhou University
杆类型
大柔度杆
定义
1
临界力
π EI Fcr ( l ) 2
n 0,1, 2
取
n 1
π 2 EI Fcr 2 l
细长压杆的临界载荷的欧 拉公式 (两端铰支)
Fuzhou University
材料力学课件
w A sin kx B co s kx
kl n , n 0,1, 2
F x l w F x
取 n 1
π 2 EI Fcr 2 l
2
临界应力
cr π2E性质Fra bibliotek2
稳定 稳定 强度
中柔度杆 2 1 Fcr A(a b ) 小柔度杆
cr a b
2
Fcr A s
cr s
l
i
1 π
i
E
I A
1.0, 0.5, 0.7, 2.0
a s 2 b
Fcr
Fcr
π 2 EI
2l
2
π 2 EI
0.7l
2
π 2 EI Fcr 2 (l )
欧拉公式的普遍形式
Fuzhou University
材料力学课件 讨论：
π 2 EI Fcr ( l )2
cr s cr a b
cr
小柔度杆 中柔度杆
O
π2 E
2
大柔度杆
2
1
l
i
大柔度杆—发生弹性失稳 中柔度杆—发生非弹性失稳 小柔度杆—不发生失稳，而发生强度失效
Fuzhou University
杆类型
大柔度杆
定义
1
临界力
π EI Fcr ( l ) 2
n 0,1, 2
取
n 1
π 2 EI Fcr 2 l
细长压杆的临界载荷的欧 拉公式 (两端铰支)
Fuzhou University
材料力学课件
w A sin kx B co s kx
kl n , n 0,1, 2
F x l w F x
取 n 1
π 2 EI Fcr 2 l
2
临界应力
cr π2E性质Fra bibliotek2
稳定 稳定 强度
中柔度杆 2 1 Fcr A(a b ) 小柔度杆
cr a b
2
Fcr A s
cr s
l
i
1 π
i
E
I A
1.0, 0.5, 0.7, 2.0
a s 2 b
Fcr
Fcr
π 2 EI
2l
2
π 2 EI
0.7l
2
π 2 EI Fcr 2 (l )
欧拉公式的普遍形式
Fuzhou University
材料力学课件 讨论：
π 2 EI Fcr ( l )2
材料力学 9组合变形精品PPT课件
解：(1) 外力分析 P
(2) 内力分析
N M
N=P， M=Pe
d
属拉弯组合变形
e
P
e
P
(3) 应力分析
(3) 应力分析
maxMN
d
M N
Wz A
N M
32dP3e4dP2
讨论：当e=d时，
e
max3d2P2 4dP2
P
9N
例题4 正方形截面立柱的中间处开一个槽，使截面
面积为原来截面面积的一半。求开槽后立柱的的最大压
2F / a2 F / 4a2
8
斜弯曲（双向弯曲） ①. 矩形截面梁的斜弯曲: a . 危险点:
a MmaYxmaxM ZZmmaIxaZxYm [ ax]
IY
b . 中性轴及其方程:
任意点的正应力
MZY0 MYZ0 0
IZ
IY
MZYMY Z
IZ
IY
M Z IY Y 0 M YIZZ 0 0
B+ ：
m a x M WB Z 11.67MP[a]
梁的强度满足！
§8－ 3、拉（压）弯组合变形问题的扩充
1. 偏心拉伸(压缩)
+
危险点属单
向应力状态
m axW PZePA
讨论：1)若P点不在y和z轴上,应力又如何计算呢？
2)若要使截面上的正应力都是压力,P力作 用在什么范围？
例3. 图示链条中的一个链环，受拉力P作用，已知： d，e，试求最大应力。
PX=P cos PY=P sin
2.分组：属拉弯组合变形
3.内力分析： 找出危险截面 (作相关的内力图)
固定端截面为危险截面
N=
Px A
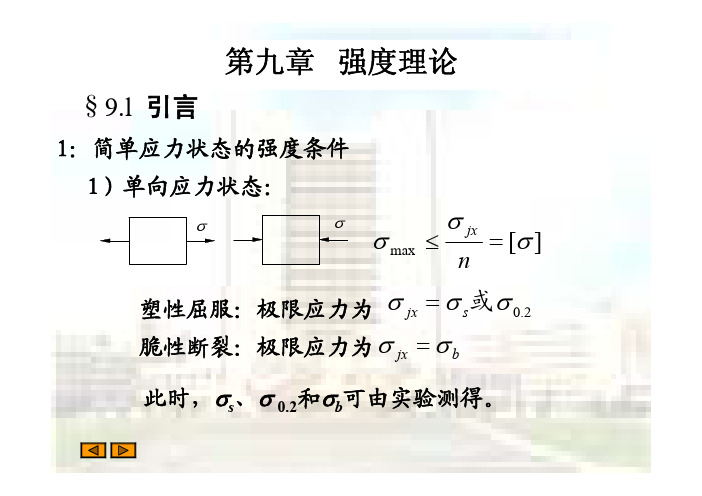
材料力学第9章 强度理论
解：
max
2 2 2
2
1 ＋ 2 2 2
2
min
－ 2 2 2
2
2 0
3 2 2 2
2
1 ＋ 2 2 2
（3）单元体（c）
σ1 80MPa σ 2 -70MPa
σ3 -140MPa
70 MPa
σr 3 220MPa
（4）单元体（d）
σr 4 195MPa
140 MPa （c） 80 MPa
max 70 30 94.72 70 30 2 2 ( ) 40 2 2 min 5.28 30MPa
2.强度理论
是关于“构件发生强度失效起因”的假说.
根据材料在复杂应力状态下破坏时的一些现象与形式 ,进行分 析,提出破坏原因的假说。在这些假说的基础上,可利用材料在单 向应力状态时的试验结果 , 来建立材料在复杂应力状态下的强度 条件。 基本观点 构件受外力作用而发生破坏时,不论破坏的表面现象如何复 杂,其破坏形式总不外乎几种类型,而同一类型的破坏则可能是某 一个共同因素所引起的。
120 MPa
110 MPa
（a ）
70 MPa 30MPa
（ b）
40MPa 70MPa
140 MPa
80 MPa 50MPa （c）
（ d）
解：（1）单元体（a）
120 MPa
σ1 0
σ 2 σ 3 120MPa
（a ）
120 MPa
σr 3 σ1 σ 3 0 ( 120) 120MPa
r2 1 u 2 3
哈尔滨工程大学力学基础课件第9章
o
a1 = a 0 45o
（e）
最大、最小剪应力所在截面和主平 0 a 、 a 90 面 0 0 面成45°。
例1 构件中某点的原始单元体 及其应力如图所示，试求主应力及 主单元体位置，最大最小剪应力及 其所在的截面的倾角。 解:由图知
s x = 100MPa s y = 20MPa
x
100MPa
t max 100 - 20 2 2 = ( ) 40 = 56.6MPa t min 2
100MPa
40MPa 20MP a (a)
x
22.5°
56.6MPa 60MPa
相对应的正应力为
116.6 3.4 s= = 60MPa 2
(c)
例2 如图，一处于横力弯曲下的梁，其截面 mn上的弯矩为M，剪力为Q，可求得截面上 一点A处的 s 和 t 分别为 s = -70MPa t = 50MPa 试确定A点的主应力及主平面的方位，并讨论 同一截面上其他点的应力状态。
m m
A
s
t
a
l
(a)
n
(b)
x
解：A点处截取的单元体放大后 如图c所示，由s = -70MPa t = 50MPa 选定x的方向垂直向上。 得
sx = 0
s y = -70MPa
2t xy
txy
s1
s3
70MPa 50MPa
(c)
t xy = -50MPa
tan 2a 0 = -
2 (-50) == 1.429 s x -s y 0 - (-70)
o
o
2a 0 = 55
a 0 = 27.5
或
2a 0 = 235o
a 0 = 117.5o
a1 = a 0 45o
（e）
最大、最小剪应力所在截面和主平 0 a 、 a 90 面 0 0 面成45°。
例1 构件中某点的原始单元体 及其应力如图所示，试求主应力及 主单元体位置，最大最小剪应力及 其所在的截面的倾角。 解:由图知
s x = 100MPa s y = 20MPa
x
100MPa
t max 100 - 20 2 2 = ( ) 40 = 56.6MPa t min 2
100MPa
40MPa 20MP a (a)
x
22.5°
56.6MPa 60MPa
相对应的正应力为
116.6 3.4 s= = 60MPa 2
(c)
例2 如图，一处于横力弯曲下的梁，其截面 mn上的弯矩为M，剪力为Q，可求得截面上 一点A处的 s 和 t 分别为 s = -70MPa t = 50MPa 试确定A点的主应力及主平面的方位，并讨论 同一截面上其他点的应力状态。
m m
A
s
t
a
l
(a)
n
(b)
x
解：A点处截取的单元体放大后 如图c所示，由s = -70MPa t = 50MPa 选定x的方向垂直向上。 得
sx = 0
s y = -70MPa
2t xy
txy
s1
s3
70MPa 50MPa
(c)
t xy = -50MPa
tan 2a 0 = -
2 (-50) == 1.429 s x -s y 0 - (-70)
o
o
2a 0 = 55
a 0 = 27.5
或
2a 0 = 235o
a 0 = 117.5o
材料力学-第9章 能量法
材料力学里的虚功原理： 变形体受力处于平衡状态时，外力在虚位移上所作的功 （外力虚功）等于内力在虚变形上作的功（内力虚功）
外力q在虚位移 上作功
q
=
应力 在虚应变 上作用 * 若外力虚功不等于内力虚功，则外力作功未完全转化为结构 应变能，受力不平衡
材料力学－第9章 能量法
§9-3 虚功原理、内力虚功
材料力学－第9章 能量法
§9-1 功与应变能的基本概念
轴向拉压
dx
对于拉伸和压缩杆件，微段的应变能为
FN
FN
dVε
1 FN d 2
Vε＝
dx+dδ
l 1 l 1 l 1 F 1 FN d FN dx FN dx FN N dx 0 2 0 2 0 2 0 2 E EA l
材料力学－第9章 能量法
§9-2 互等定理
思考题：
根据功的互等定理和位移互等定理对下列结构完成等式
?=?
材料力学－第9章 能量法
§9-2 互等定理
思考题：
根据功的互等定理和位移互等定理对下列结构完成等式
?=?
材料力学－第9章 能量法
§9-2 互等定理
思考题：
根据功的互等定理和位移互等定理对下列结构完成等式
?=?
材料力学－第9章 能量法
§9-2 互等定理
例题
A
Me
B
l
图示静不定梁，承受弯矩作用。利用功的互等 定理确定B端的支反力。设弯曲刚度EI为常数。
材料力学－第9章 能量法
§9-2 互定理
解：
Me A B FR M e
将支座B解除，代以支反力FR
。
将力偶Me和支反力FR作为一组力， 另外施加力F作为第二组力
材料力学：第九章 强度理论
不论材料处于何种应力状态，只要最大拉应力σ1 达到材料单向拉 伸断裂时的最大拉应力 σ1u (即σb)，材料即发生断裂
－材料的断裂条件
强度条件
σ1 － 构件危险点处的最大拉应力 [σ] － 材料单向拉伸时的许用应力
最大拉应变理论（第二强度理论）
理论要点
引起材料断裂的主要因素－最大拉应变 e1
e1 e1u
宜用第一强度理论考虑强度问题
一种常见应力状态的强度条件
单向、纯剪切联合作用
塑性材料 强度条件：
纯剪切许用应力
单向、纯剪 切联合作用
纯剪切情况下（s = 0）
塑性材料强度条件:
[σ] τmax 2
[σ] τmax 3
强度理论的应用
使用强度理论进行强度校核的步骤：
(1)画剪力图、弯矩图，确定危险截面； (2)据应力公式，确定截面上的危险点； (3)求最大应力； (4)根据材料性质, 选择合适的强度理论,
当
时, 材料屈服
强度条件
－材料的屈服条件
s1 , s2 , s3 － 构件危险点处的工作应力 [s] － 材料单向拉伸时的许用应力
例题 例2-1 铸铁构件危险点处受力如图,
试校核强度，[s]=30 MPa
解： (1) 列出已知条件
(2) 计算应力最大值
(3) 选择强度理论, 进行校核 （压应力 < 拉应力）
承压薄壁圆筒应力分析
三种应力: 轴向x, 周向y, 径向z
承压薄壁圆筒应力分析
(1) 轴向应力 筒底压力
筒壁应力
(2) 周向应力
1
(3) 径向应力
径向应力/周向应力
很小的量
故 s r 很小, 忽略不计
承压薄壁圆筒强度条件
－材料的断裂条件
强度条件
σ1 － 构件危险点处的最大拉应力 [σ] － 材料单向拉伸时的许用应力
最大拉应变理论（第二强度理论）
理论要点
引起材料断裂的主要因素－最大拉应变 e1
e1 e1u
宜用第一强度理论考虑强度问题
一种常见应力状态的强度条件
单向、纯剪切联合作用
塑性材料 强度条件：
纯剪切许用应力
单向、纯剪 切联合作用
纯剪切情况下（s = 0）
塑性材料强度条件:
[σ] τmax 2
[σ] τmax 3
强度理论的应用
使用强度理论进行强度校核的步骤：
(1)画剪力图、弯矩图，确定危险截面； (2)据应力公式，确定截面上的危险点； (3)求最大应力； (4)根据材料性质, 选择合适的强度理论,
当
时, 材料屈服
强度条件
－材料的屈服条件
s1 , s2 , s3 － 构件危险点处的工作应力 [s] － 材料单向拉伸时的许用应力
例题 例2-1 铸铁构件危险点处受力如图,
试校核强度，[s]=30 MPa
解： (1) 列出已知条件
(2) 计算应力最大值
(3) 选择强度理论, 进行校核 （压应力 < 拉应力）
承压薄壁圆筒应力分析
三种应力: 轴向x, 周向y, 径向z
承压薄壁圆筒应力分析
(1) 轴向应力 筒底压力
筒壁应力
(2) 周向应力
1
(3) 径向应力
径向应力/周向应力
很小的量
故 s r 很小, 忽略不计
承压薄壁圆筒强度条件