数学建模 减肥模型
关于减肥计划的数学模型

2011第一学期数学建模选修课期末作业名称:减肥计划学号:1008054311系别:计算机系姓名:宛笛上课时间:周四晚上是否下学期上课:是减肥计划摘要:近年来,随着人们生活水平的提高,肥胖现象也日趋普遍,越来越多的人开始关注和解决肥胖问题,与此同时,各类减肥食品充斥市场,却达不到好的效果,或者不能维持,有的还会对消费者的身体带来一定损害.本文中,我们建立了节食与运动的模型,通过控制饮食和适当的运动,在不伤害身体的前提下,达到减轻体重并维持下去的目标.关键字:肥胖节食运动不伤害减轻体重1问题重述当今社会,人们对于健康越来越重视,而肥胖也成为困扰很多人的健康问题,肥胖者通过各种方式减肥,但很多人收效甚微,本文通过制定合理的节食和运动计划科学的直到肥胖者减肥.2 问题分析(1) 体重变化由体内能量守恒破坏引起;(2)人体通过饮食(吸收热量)引起体重增加;(3)代谢和运动(消耗热量)引起体重减少3符号说明1)K: 表示第几周;2)ω(k):表示第k周的体重;3)C(k):表示第k周吸收的热量;4)α:表示热量转换系数[α =1/8000(kg/kcal)];5)β:表示代谢消耗系数(因人而异);6) β’:表示通过运动代谢消耗系数在原有的基础上增加,即可表为β’=β+β1, β1有运动形式和时间决定.4模型假设1)体重增加正比于吸收的热量——每8000千卡增加体重1千克;2)代谢引起的体重减少正比于体重——每周每公斤体重消耗200千卡 ~ 320千卡(因人而异),相当于70千克的人每天消耗2000千卡 ~ 3200千卡;3)运动引起的体重减少正比于体重,且与运动形式有关;4)为了安全与健康,每周体重减少不宜超过1.5千克,每周吸收热量不要小于10000千卡。
5 减肥计划事例:某甲体重100千克,目前每周吸收20000千卡热量,体重维持不变。
现欲减肥至75千克。
1)在不运动的情况下安排一个两阶段计划。
第一阶段:每周减肥1千克,每周吸收热量逐渐减少,直至达到下限(10000千卡);第二阶段:每周吸收热量保持下限,减肥达到目标2)若要加快进程,第二阶段增加运动,试安排计划。
减肥计划模型建立

数学建模期末大作业减肥计划的模型第十小组摘要:随着社会的发展和人们生活水平的逐步提高,越来越多的意识到健身的重要性,运动减肥是健身运动的一个重要组成部分。
本文是通过建立减肥模型寻求合理的减肥方法,并从饮食和运动两方面来具体分析。
根据不同运动消耗的能量不同, BMI定义为体重(单位:kg)除以身高(单位:m)的平方,是联合国世界卫生组织颁布的体重指数,规定BMI在18.5至25为正常,大于25为超重,超过30则为肥胖。
我国有关部门针对东方人特点,拟将上述规定中的25、30分别改为24、29。
本文为改善肥胖者体重,建立数学模型,通过分段法(降重、保重、加速等阶段),制定出减肥计划供肥胖者参考。
最终确定最佳减肥方案。
关键词:运动饮食饮食热量转换代谢消耗合理减肥 MATLAB问题分析:某甲身高1.7m,体重100kg,BMI值高达34.6。
目前每周吸收20000kcal热量,现为其制定减肥计划,令其体重减至75kg并且维持下去。
计划如下:1.降重阶段:在不运动条件下,每周体重减少1kg,每周吸收热量逐渐减少,直至达到安全的下限(10000kcal)。
2.保重阶段:在不运动条件下,每周吸收热量保持下限,减肥达到目标(75kg)。
模型假设:1.体重增加正比于吸收的热量,平均每8000kcal增加体重1kg。
2.正常代谢引起的体重减少正比于体重,每周每kg体重消耗热量一般在200kcal至320kcal之间,且因人而异。
3.运动引起的体重减少正比于体重,且与运动形式有关。
4.为了安全与健康,每周体重减少不宜超过1.5kg,每周吸收热量不要小于10000kcal。
模型建立:记第k周末体重为W(k),吸收热量为C(k);热量转换系数为:a=1/8000 (kg/kcal);代谢消耗系数为:b;体重每周减少B=1kg;在不考虑运动的情况下体重变化的基本方程为:W(k+1)=W(k)-b*W(k)+a*C(k+1) (k=0,1,2…) (1式)则当某甲减肥前体重不变时,由(1式)得:W=W-b*W+a*C (A式)1.降重:要求体重每周减少B,吸收热量减至下限C0,即:W(k)-W(k+1)=B (2式)W(k)=W(0)-B*k (3式)由(1式)得:W(k)-W(k+1)=b*W(k)-a*C(k+1) (B式)将(2、3式)代入上式得:B=b*[W(0)-B*k]-a*C(k+1)即得:C(k+1)=(b/a)*W(0)-(B/a)*(1+b*k)2.保重:要求每周吸收热量保持下限C0由(1式)得:W(k+1)=W(k)-b*W(k)+a*C0将上式递推得:W(k+1)=(1-b)^n*W(k)+a*C0*[1+(1-b)+…+(1-b)^(n-1)] =(1-b)^n*[W(k)-a*C0/b]+a*C0/b (C式) 模型求解:(A式)function work1(W0,a,C)b=a*C/W0;b>>work1(100,1/8000,20000)b =0.0250(B式)function work2(W0,B,a,b,C0)k=[(b*W0-a*C0)/B-1]/b;k>>work2(100,1,1/8000,0.025,10000)k =10% 可知按照此种方式,可使体重每周减少1kg,第10周达到90kg.由(C式)以及以下数据:W(k)=90kg;W(k+1)=75kg;a=1/8000 kg/kcal;b=0.025;C0=10000kcal 解得:n=19即每周吸收热量保持下限C0=10000kcal,再有19周体重可减至75kg。
2018电子科技大学数学建模校内赛A题:健身计划制定,女性身体形态数学建模设想
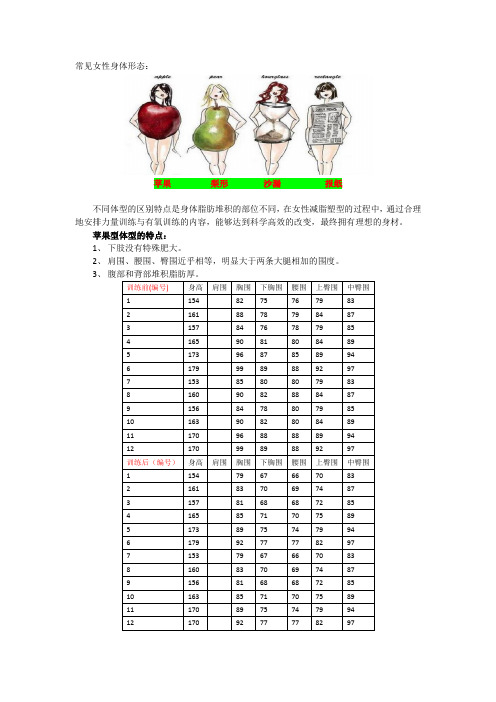
常见女性身体形态:
苹果梨形沙漏报纸
不同体型的区别特点是身体脂肪堆积的部位不同,在女性减脂塑型的过程中,通过合理地安排力量训练与有氧训练的内容,能够达到科学高效的改变,最终拥有理想的身材。
苹果型体型的特点:
1、下肢没有特殊肥大。
2、肩围、腰围、臀围近乎相等,明显大于两条大腿相加的围度。
3、
梨形体型的特点:
1、肩围小于胸围和腰围臀围。
2、胸围小于腰围,腰围小于臀围。
3、臀围是整个身体最肥大的地方。
1、胸部饱满。
2、腰部纤细。
3
1、整体很瘦削。
2、肩围、胸围、腰围、臀围相差不大。
数学建模减肥计划

减肥计划——节食与运动摘要:肥胖已成为公众日益关注的卫生健康问题。
肥胖是与目前严重危害人类健康疾病,如糖尿病、高血压、冠心病、血脂异常、胆囊疾病、痛风、骨关节病、阻塞性睡眠呼吸暂停、某些癌症等的发病有明显相关的危险因素之一。
但是实际情况确是违禁广告屡禁不止。
之所以造成这种情况的原因很多,但是有一个重要原因就是科学素质低,不知道应该从生理机理,特别是从数学模型的角度来考虑和认识问题。
数学模型的优点是科学的解释了肥胖的机理,引导群众合理科学的减肥。
关键词:减肥饮食合理运动一、问题重述联合国世界卫生组织颁布的体重指数(简记BMI)定义为体重(单位:kg)除以身高(单位:m)的平方,规定BMI在18.5至25为正常,大于25为超重,超过30则为肥胖。
据悉,我国有关机构对东方人的特点,拟将上述规定中的25改为24,30改为29。
在国人初步过上小康生活以后,不少自感肥胖的人纷纷奔向减肥食品的柜台。
可是大量事实说明,多数减肥食品达不到减肥的目标,或者即使能减肥一时,也难以维持下去。
许多医生和专家的意见是,只有通过控制饮食和适当的运动,才能在不伤害身体的条件下,达到减轻体重并维持下去的目的。
肥胖是与目前严重危害人类健康疾病,如糖尿病、高血压、冠心病、血脂异常、胆囊疾病、痛风、骨关节病、阻塞性睡眠呼吸暂停、某些癌症等的发病有明显相关的危险因素之一。
肥胖也是身体健康的晴雨表,反映着体内多方面的变化。
很多人在心理上害怕自己变得肥胖,追求苗条,因而减肥不仅是人们经常听到的话题,更有人花很多的时间和金钱去付诸实践的活动,从而也就造成了各种减肥药、器械和治疗方法的巨大的市场。
各种假药或对身体有害的药品和治疗方法、夸大疗效的虚假广告等等就应运而生了,对老百姓造成了不应有的伤害。
情况的严重使得国家广电总局、新闻出版总署等不得不发出通知,命令所有电视台自2006年8月1日起停止播出丰胸、减肥等产品的电视购物节目。
但是实际情况确是违禁广告屡禁不止。
数学建模减肥计划

减肥计划——节食与运动摘要:肥胖已成为公众日益关注的卫生健康问题。
肥胖是与目前严重危害人类健康疾病,如糖尿病、高血压、冠心病、血脂异常、胆囊疾病、痛风、骨关节病、阻塞性睡眠呼吸暂停、某些癌症等的发病有明显相关的危险因素之一。
但是实际情况确是违禁广告屡禁不止。
之所以造成这种情况的原因很多,但是有一个重要原因就是科学素质低,不知道应该从生理机理,特别是从数学模型的角度来考虑和认识问题。
数学模型的优点是科学的解释了肥胖的机理,引导群众合理科学的减肥。
关键词:减肥饮食合理运动一、问题重述联合国世界卫生组织颁布的体重指数(简记BMI)定义为体重(单位:kg)除以身高(单位:m)的平方,规定BMI在18.5至25为正常,大于25为超重,超过30则为肥胖。
据悉,我国有关机构对东方人的特点,拟将上述规定中的25改为24,30改为29。
在国人初步过上小康生活以后,不少自感肥胖的人纷纷奔向减肥食品的柜台。
可是大量事实说明,多数减肥食品达不到减肥的目标,或者即使能减肥一时,也难以维持下去。
许多医生和专家的意见是,只有通过控制饮食和适当的运动,才能在不伤害身体的条件下,达到减轻体重并维持下去的目的。
肥胖是与目前严重危害人类健康疾病,如糖尿病、高血压、冠心病、血脂异常、胆囊疾病、痛风、骨关节病、阻塞性睡眠呼吸暂停、某些癌症等的发病有明显相关的危险因素之一。
肥胖也是身体健康的晴雨表,反映着体内多方面的变化。
很多人在心理上害怕自己变得肥胖,追求苗条,因而减肥不仅是人们经常听到的话题,更有人花很多的时间和金钱去付诸实践的活动,从而也就造成了各种减肥药、器械和治疗方法的巨大的市场。
各种假药或对身体有害的药品和治疗方法、夸大疗效的虚假广告等等就应运而生了,对老百姓造成了不应有的伤害。
情况的严重使得国家广电总局、新闻出版总署等不得不发出通知,命令所有电视台自2006年8月1日起停止播出丰胸、减肥等产品的电视购物节目。
但是实际情况确是违禁广告屡禁不止。
减肥数学建模

减肥数学建模
在当今社会,减肥已经成为了很多人关注的话题。
人们希望通过科学的方法和
合理的方式来减肥,以达到健康和美丽的目的。
而数学建模作为一种科学的分析方法,可以帮助我们更好地理解减肥过程中的变化规律,从而找到更有效的减肥方案。
首先,我们可以通过数学建模来分析减肥的基本原理。
减肥的过程实际上是一
个能量平衡的问题,即摄入的能量和消耗的能量之间的关系。
我们可以用数学模型来描述这个过程,通过方程式来表示能量的变化和平衡,进而找到减肥的最佳方案。
其次,数学建模还可以帮助我们分析减肥过程中的身体变化。
比如,我们可以
通过建立数学模型来研究减肥对身体各项指标的影响,比如体重、体脂率、肌肉量等。
通过数学模型的分析,我们可以更好地了解减肥过程中身体的变化规律,从而找到更科学的减肥方法。
另外,数学建模还可以帮助我们优化减肥方案。
通过建立数学模型,我们可以
对不同的减肥方案进行模拟和比较,找到最适合自己的减肥方案。
比如,我们可以通过数学模型来分析不同饮食和运动方案对减肥效果的影响,从而找到最有效的减肥方案。
除此之外,数学建模还可以帮助我们预测减肥的效果。
通过建立数学模型,我
们可以根据自己的减肥计划和实际情况,预测未来的减肥效果,从而更好地调整和优化减肥方案,提高减肥的效果和成功率。
总的来说,数学建模在减肥过程中发挥着重要的作用。
通过数学建模,我们可
以更好地理解减肥的原理和规律,优化减肥方案,预测减肥效果,从而找到更有效的减肥方法。
因此,我们可以将数学建模应用到减肥过程中,以帮助我们更科学、更有效地减肥,达到健康和美丽的目标。
数学模型课程设计_减肥模型
1 引言随着社会的进步和发展,人们的生活水平不断提高。
由于饮食营养摄入量的不断改善和提高,“肥胖”已经成为全社会关注的一个重要的问题。
肥胖是与目前严重危害人类健康疾病,如糖尿病、高血压、冠心病、血脂异常、胆囊疾病、痛风、骨关节病、阻塞性睡眠呼吸暂停、某些癌症等的发病有明显相关的危险因素之一。
肥胖也是身体健康的晴雨表,反映着体内多方面的变化。
很多人在心理上害怕肥胖,追求苗条,因而减肥并不是口头话题,更有人花很多时间和金钱去实施减肥。
这也造成了各种减肥药、减肥器械和治疗方法的巨大市场。
各种假药或对身体有害的药品,夸大疗效的虚假广告等等也就应应运而生理念,对老百姓造成了不必要的伤害。
所以,如何正确对待减肥是我们必须考虑的问题。
于是了解减肥的机理成为关键。
2模型的提出2.1背景知识根据中国生理科学会修订并建议的我国人民的每日膳食指南可知:(1) 每日膳食中,营养素的供给量是作为保证正常人身体健康而提出的膳食质量标准。
如果人们在饮食中摄入营养素的数量低于这个数量,将对身体产生不利的影响。
(2)人体的体重是评定膳食能量摄入适当与否的重要标志。
(3)人们热能需要量的多少,主要决定于三个方面:维持人体基本代谢所需的能量、从事劳动和其它活动所消耗的能量以及食物的特殊动力作用(将食物转化为人体所需的能量)所消耗的能量。
(4)一般情况下,成年男子每一千克体重每小时平均消耗热量为4200焦耳。
(5)一般情况下,食用普通的混合膳食,食物的特殊动力作用所需要的额外的能量消耗相当于基础代谢的10%。
2.2模型分析通常,当体内能量守恒被破坏时就会引起体重的变化。
人们通过饮食吸收热量,一部分用于代谢和运动消耗,若有剩余则转化为脂肪存储起来,导致体重的增加。
如果要想体重减少,必须使吸收的热量小于消耗的热量,从而使机体代谢存储的脂肪。
这可以通过减少摄入和增加消耗来实现,即减少进食量,增加运动量。
但每天的进食不仅提供能量,还提供人体必需的营养物质,所以进食量不能过少。
分方程模型减肥模型
随着社会的进步和发展,人们的生活水平不断 提高。 由于饮食营养摄入量的不断改善和提高,“肥 胖”已经成为全社会关注的一个重要的问题。 如何正确对待减肥是我们必须考虑的问题。于 是了解减肥的机理成为关键。
微分方程模型实例4——减肥模型
5.3.5 减肥模型
一. 背景知识
根据中国生理科学会修订并建议的我国人民的每日膳食指南可知: (1) 每日膳食中,营养素的供给量是作为保证正常人身体健康而提出的膳食
二. 问题分析与模型假设
(4) 不同的活动对能量的消耗是不同的,例如:体重分别为50千克和100千 克的人都跑1000米,所消耗的能量显然是不同的。可见,活动对能量的 消耗也不是一个简单的问题,但考虑到减肥的人会为自己制订一个合理 且相对稳定的活动计划,我们可以假设在单位时间(1日)内人体活动 所消耗的能量与其体重成正比,记B为每1千克体重每天因活动所消耗的 能量。
虑能量的摄入和消耗所引起的体重的变化。
根据能量的平衡原理,任何时间段内由于体重的改变所引起的人体内能量的变化
应该等于这段时间内摄入的能量与消耗的能量的差。
考虑时间区间[t,t t]内能量的改变,根据能量平衡原理,有
t t
t t
B为每1千克体重每天 因活动所消耗的能量。
D[w(t t) w(t)] At B
质量标准。如果人们在饮食中摄入营养素的数量低于这个数量,将对身 体产生不利的影响。 (2) 人体的体重是评定膳食能量摄入适当与否的重要标志。 (3) 人们热能需要量的多少,主要决定于三个方面:维持人体基本代谢所需 的能量、从事劳动和其它活动所消耗的能量以及食物的特殊动力作用 (将食物转化为人体所需的能量)所消耗的能量。 (4) 一般情况下,成年男子每一千克体重每小时平均消耗热量为4200焦耳。 (5) 一般情况下,食用普通的混合膳食,食物的特殊动力作用所需要的额外 的能量消耗相当于基础代谢的10%。
数学建模-人体重变化
一、人体重变化某人的食量是10467焦/天,最基本新陈代谢要自动消耗其中的5038焦/天。
每天的体育运动消耗热量大约是69焦/(千克•天)乘以他的体重(千克)。
假设以脂肪形式贮存的热量100% 地有效,而1千克脂肪含热量41868焦。
试研究此人体重随时间变化的规律。
一、问题分析人体重W(t)随时间t变化是由于消耗量和吸收量的差值所引起的,假设人体重随时间的变化是连续变化过程,因此可以通过研究在△t时间内体重W的变化值列出微分方程。
二、模型假设1、以脂肪形式贮存的热量100%有效2、当补充能量多于消耗能量时,多余能量以脂肪形式贮存3、假设体重的变化是一个连续函数4、初始体重为W0三、模型建立假设在△t时间内:体重的变化量为W(t+△t)-W(t);身体一天内的热量的剩余为(10467-5038-69*W(t))将其乘以△t即为一小段时间内剩下的热量;转换成微分方程为:d[W(t+△t)-W(t)]=(10467-5038-69*W(t))dt;四、模型求解d(5429-69W)/(5429-69W)=-69dt/41686W(0)=W0解得:5429-69W=(5429-69W0)e(-69t/41686)即:W(t)=5429/69-(5429-69W0)/5429e(-69t/41686)当t趋于无穷时,w=81;摘要:本文对数序建模实验课本上第一章中有关体重增长的课后习题进行了解答。
并且在该基础上提出了一些对该模型的修改想法,同时参考了比较成熟的生物数学中的生物体重增长模型作为扩展。
关键词:数学建模实验;体重增长;模型修改意见问题陈述某动物从食物中每天得到2500卡的热量,其中1200卡用于基本的新陈代谢,每天每千克的体重需要再消耗16卡。
假如它每增加1kg的体重需要10000卡的热量,问该动物的体重将会如何变化。
问题分析该数学问题如果单纯从所需要的知识来讲,其难度只能算是初中数学问题。
但是如果把该问题看成是一个研究体重增长的简化数学模型的话,那其意义就不会停留在初中数学应用题的水平上了。
2015年数学建模讲座 4月20日
2025届甘肃省武威市高一化学第一学期期末考试模拟试题注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每题只有一个选项符合题意) 1、下列气体中不能用排空气法收集的是( ) A .H 2B .CO 2C .NOD .NO 22、分离氯化钾和二氧化锰混合物,不需要的实验操作是( ) A .过滤 B .溶解 C .蒸发 D .称量3、下列有关试剂的保存或配制说法错误的是( ) A .少量金属钠可以保存在水中B .漂白粉不能长期放置于敞口烧杯中C .配制硫酸亚铁溶液时,要加入少量铁粉D .新制氯水放在棕色试剂瓶中 4、一定条件下,下列不能用勒夏特列原理解释的是 A .合成氨时将氨液化分离,可提高原料的利用率 B .H 2、I 2、HI 混合气体加压后颜色变深 C .实验室常用排饱和NaCl 溶液的方法收集Cl 2 D .新制氯水中,滴加硝酸银溶液,溶液颜色变浅 5、下列反应属于非氧化还原反应的是( )A .10Al +3V 2O 5高温6V+5Al 2O 3B .2Mg +CO 2点燃2MgO +CC .N 2+3H 2Δ催化剂2NH 3D .SiO 2+CaO高温CaSiO 36、下列物质中不能..用化合反应的方法生成的是 ①Fe 3O 4 ②H 2SiO 3 ③Fe(OH)3 ④Cu(OH)2 ⑤FeCl 2 ⑥CaSiO 3 A .①③④⑥B .②④C .②④⑤D .①②④7、化学与生活密切相关,下列说法错误的是 A .Na 2CO 3用于制胃酸中和剂 B .FeSO 4用于制补铁剂 C .硬铝合金用于制造飞机和宇宙飞船D .14C 用于测定文物年代8、设N A 代表阿伏加德罗常数,下列说法正确的是( ) A .5.6g 铁与足量盐酸反应转移的电子数为0.3N AB.常温常压下,11.2L甲烷中含有的氢原子数为2N AC.标准状况下,22.4L氦气与22.4L氟气所含原子数均为2N AD.常温下,2.7g铝与足量的盐酸反应,失去的电子数为0.3N A9、相同质量的SO2和SO3它们之间的关系是()A.所含硫原子的物质的量之比为1:1B.氧原子的物质的量之比为3:2C.硫元素的质量比为4:5D.氧元素的质量比为5:610、下列有关金属及其合金的说法不正确的是()A.目前我国流通的硬币是由合金材料制造的B.生铁、普通钢和不锈钢中的碳含量依次增加C.镁在空气中燃烧发出耀眼的白光,可用于制作照明弹D.日用铝制品表面覆盖着氧化膜,对内部金属起保护作用11、下列说法正确的是()A.浓硝酸和浓硫酸都应保存在棕色试剂瓶中B.氢氧化钠溶液用带有橡胶塞的试剂瓶保存C.工业制得的浓盐酸、浓硝酸所带黄色都是Fe3+所致D.铝制或铁制容器可贮运浓硫酸、浓硝酸和浓盐酸这三大强酸12、下列表格中各项分类都正确的一组是类别A.A B.B C.C D.D13、用固体NaOH配制一定物质的量浓度的NaOH溶液,下列操作正确的是A.称量时,将固体NaOH直接放在天平左盘上B.将称量好的固体NaOH放入容量瓶中,加蒸馏水溶解C.定容时如果加水超过了刻度线,用胶头滴管直接吸出多余部分D.将烧杯中溶解固体NaOH所得溶液,冷却到室温后转移至容量瓶中14、关于氧化还原反应,下列说法正确的是A.被还原的物质是还原剂B.氧化剂被还原,还原剂被氧化C.失去电子,化合价降低的物质是还原剂D.氧化剂失去电子,化合价升高15、配制一定物质的量浓度的NaOH溶液,下列操作会造成结果偏高的是()A.称量固体NaOH时,有潮解现象B.溶解后移液至容量瓶中,未冷却溶液C.未将洗涤烧杯的水转移至容量瓶中D.定容时仰视读数16、下列反应不属于氧化还原反应的是A.4HCl(浓)+MnO2 加热MnCl2+Cl2↑+2H2O B.H2SO4+Zn=ZnSO4+H2↑C.3Cu+8HNO3=3Cu(NO3)2+2NO↑+4H2O D.NH4HCO3加热NH3↑+ H2O +CO2↑二、非选择题(本题包括5小题)17、A、B、C、W均为中学常见的物质,它们之间有如图所示的转化关系(其他产物及反应条件已略去,反应可以在水溶液中进行)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有一人体重110kg,身高180cm,制定减肥计划使其BMI降到25以下
目前人们公认的评测体重的标准是联合国世界卫生组织颁布的体重指数BMI,定义为BMI=h/L^2其中h是体重(单位是kg),L是身高(单位是m)。
模型分析:
在正常情况下,人体通过食物摄入的热量与代谢和运动消耗的热量会影响体重的变化,摄入的热量大于消耗的热量会使人增肥,反之会使人体重降低,因此需要从人体对热量的吸收与消耗两方面进行分析,在适当的假设下建立模型,减肥计划应以不伤害人体健康为目标,所以吸收热量不应过少减重体重不要过快来限制,同时增大运动量也是减肥的关键,也应加以考虑,通常,制定减肥计划以周为时间单位比较方便,所以这里用离散时间模型——差分方程来讨论。
模型假设:
根据上述分析,参考有关生理数据,做出以下假设:
1、体重增加正比于吸收的热量,平均每8000kcal增加体重1kg。
(kcal是非国际单位制单位,1kcal=4.5kJ);
2、身体正常代谢引起的体重减少正比于体重,每周每千克体重消耗热量一般在200kcal至320kcal之间,且因人而异,这相当于体重110kg的人每天消耗约3413kcal至5029kcal之间;
3、运动引起的体重减少正比于体重,且与运动形式和运动时间有关;
4、为了健康考虑,每周吸收热量不能少于10 000kcal,且每周减少量不能超过1 000kcal每周体重减少不能超过1kg;
5、假设此人身体健康,没有肠胃方面的毛病;
通过调查资料得知各种食物的每百克所含的大卡热量供参考(假设食物重量如表中一样重),如下表
基本模型:
记第k周(初)体重为w(k)(kg),第k周吸收热量为c(k)(kcal),k=1,2,……。
设热量转换(体重的)系数为α,身体代谢消耗系数为β,根据模型假设,正常
情况下(不考虑运动)体重变化的基本方程为α(1)
w
k
(k
)1
k
c
wβ
k
w
(
k
-
+
=
⋯
⋯
)
=
(
)
(
+,2,1
),
由假设1,α=1/8000kg/kcal,当确定了个人的代谢消耗系数β后,就可按照(1)式由每周吸收的热量c(k)推导出他的体重w(k)的变化。
增加运动时,只需将β改为β+β1,β1由运动的形式和时间决定。
减肥计划的提出:
有一人体重110kg,身高180cm,BMI达到33.95。
假设此人目前每周吸收30 000kcal热量,体重长期不变,现在制定减肥计划使其BMI降到25既是体重减至81kg并维持下去:
1、在正常代谢情况下安排一个两阶段计划,第一阶段:吸收热量由20 000kcal 每周减少500kcal,直至达到安全下限(每周10 000kcal);第二阶段:每周吸收热量保持下限,直至达到减肥目标。
2、为加快进程而增加运动,重新安排两阶段计划。
3、给出达到目标后维持体重不变的方案。
减肥计划的制定:
首先我们应先将此人的热量吸收降至安全下限,制定的此人的第一周的食谱如下:
此后只需要每周每天中午的米饭减少25g,鸡胸肉减少20g,下午的米饭减少25g,牛肉减少20g,坚持10周就可以达到每周吸收热量安全下限10 000kcal 了,十周之后食谱如下不再改变:
然后确定这个人的代谢消耗系数β,根据他每周吸收的c=20 000kcal 热量,体重为w=110kg 不变,在(1)式中另w(k+1)=w(k)=w,c(k)=c ,得
w=w+αc -βw
于是
w c /αβ= 得出β=0.023 (2)
相当于每周每千克体重消耗热量181.8kcal ,可以看出,此人消化不行以。
1、正常代谢情况下有两个阶段,第一个阶段要求吸收热量由20 000kcal 降到10 000kcal ,达到下线kcal c 10000min =,即
c(k)=20 000-1 000k ,k=1,2,……,10 (3)
将c(k)及α=1/8000,β=0.023代入(1)式,可得
w(k+1)=(1-β)w(k)+α(20000-500k)=0.977w(k)+2.5-0.0625k,
K=1,2,……,20 (4)
(4)式虽是一阶线性常系数差分方程,但因右端含有时间变量k ,不能直接应用基础知识6-1的求解方程,更方便的是以w(1)=110kg 为初始值,编一个程序计算第21周的体重为w(21)=98.1182kg.
第二阶段要求每周吸收热量保持下限m in c ,由(1)式可得
25.1)(977.0)()1()1(min +=+-=+k w c k w k w αβ,k=21,22, (5)
以第一阶段的终值w(21)为第二阶段的初值,再按照程序计算直到w(21+n)<=81kg 为止,可得w(21+22)=80.5816kg ,即每周吸收热量保持下限10 000kcal ,再有22周体重可减至81kg ,两阶段共需42周。
但是经过检验,第二阶段的每周体重减少超过了1kg ,所以我们应该增加每周热量吸收下限,使下限10000min =c 变为10500min =c ,这个时候仍然保持每周降低热量吸收为500,第一个阶段为19周,w(20)=99.1486kg,之后再经过25周,w(20+25)=80.5872kg ,两阶段共经历44周,并且每周体重减少不超过1kg 。
2、为加快进程而增加运动,记表3中热量消耗为γ,每周运动时间为t h ,在(1)式中将β改为β+αγt ,即
)()()()()1(k w t k c k w k w αγβα+-+=+ (6) 试取007.0=t αγ,则03.0=+t αγβ,(4)、(5)式分别变成为
w(k+1)=0.97w(k)+2.5-0.0625k , k=1,2,……,19 (7) w(k+1)=0.97w(k)+1.3125, k=20,21,…… (8) 类似的计算可得,w(20)=88.2973kg,w(20+6)=80.8567kg ,即若增加007.0=t αγ的运动,就可以将第二阶段的时间缩短为6周,但是经过检验可得第二个阶段每周的体重减少超过1kg ,所以我们在第二个阶段取003.0=t αγ,则026.0=+t αγβ
(7) 、(8)式分别变成
W(k+1)=0.974w(k)+2.5-0.0625k ,k=1,2,……,19 (9) W(k+1)=0.974w(k)+1.3125, k=20,21,…… (10) 计算可得w(20)=88.2973kg,w(20+9)=80.3148kg,即第二阶段若增加003.0=t αγ的运动 就可以将不训练时第二阶段的时间缩短为9周,稍加训练的话可以28周到达目标,由1/8000=α可知,第一阶段增加的运动内容应满足56=t γ,第二阶段增加的运动内容应满足24=t γ,如第一阶段每周步行7h 加乒乓球4h 加跑步2h 加一小时自行车(中速),第二阶段乒乓球4h 加步行2h 。
增加运动的效果非常明显。
3、达到目标后维持体重不变的方案,最简单的是寻求每周吸收热量保持某常数
值c,使体重w=81kg不变,在(6)式中令w(k+1)=w(k)=w,c(k)=c,得
w=w+αc-(β+αγt)w
于是
β/
α
αγ
t
=(11)
c+
(w
)
由(11)式,在正常代谢情况下(γ=0)可算出c=14904kcal,若第一阶段增加56
tγ
=
运动可算出c=19440kcal,第二阶段增加24
tγ运动可算出c=16848kcal。
=
17041102
丁典。
