计算连续曲线梁桥的有限段法
连续曲线梁桥设计浅谈
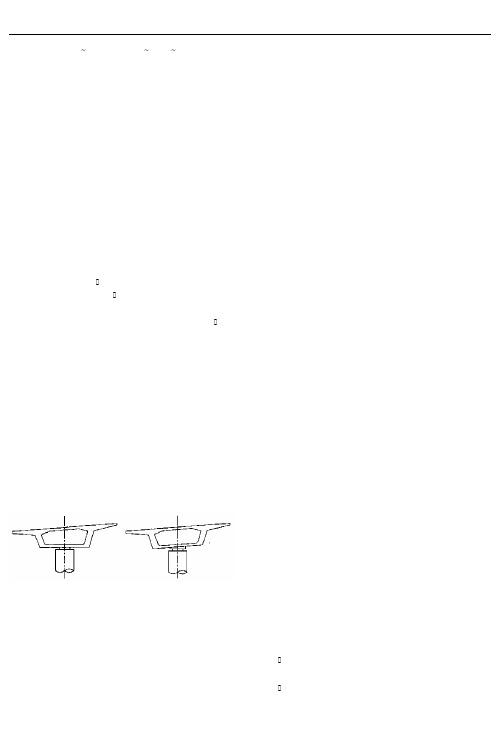
的超高布置方式
曲线梁桥结构受力特点
梁体的弯扭耦合作用 曲梁 在外荷载 的作用下会 同时 产生弯矩和扭矩, 并且互 相影 响, 使梁 截面处 于弯 扭耦合 作 用的状态, 其 截面主拉应 力往 往比 相应的 直梁 桥大得 多, 这 是曲梁独有的受力 特点。曲 线梁 桥由 于受到 强大 的扭矩 作 用, 产生扭 转变形, 其 曲线外 侧的 竖向 挠度大 于同 跨径的 直 桥; 由于弯扭耦合作 用, 在梁端可能出 现翘曲; 当梁端横 桥向 约束较弱时, 梁体有向弯道外侧 “ 爬移” 的趋势 。
结构设计与研究应用 � � � � � 《 四川建材》 年第 期
【文章编号】 : ( ) -
连 续 曲 线 梁 桥 设 计 浅 谈
欧阳尚贤
(佛山市顺德区规划设计院有限公司)
【摘 要】 : 本文 介绍了曲 线桥梁 的受力 特点, 分析了 曲 内 梁和外 梁受力 不均 在曲线 梁桥中, 由于 存在较 大
曲线梁桥的结构设计
直梁桥受 “弯、 剪” 作用, 而曲线 梁桥处 于 “ 弯、 剪、 扭” 的 复合受力状态, 故上 、 下部结构必须构成有利于 抵抗 “ 弯、 剪、 扭” 的措施。 ( ) 曲线梁桥的弯扭刚度比对结构的受力状态和变 形状 态有着直接的关系: 弯扭 刚度 比越 大, 由 曲率 因素 而导致 的 扭转弯形越大, 因 此, 对于曲 线梁 桥而言 在满 足竖 向变形 的 前提下, 应尽可 能减 小抗 弯刚度、 增 大抗扭 刚度。所 以在 曲 线桥梁中, 宜选用 低高度梁和抗扭惯矩较大的箱形截面。 ( ) 在曲线梁桥截 面设计时, 要 在桥跨范 围内 设置一 些 横隔板, 以加强横 桥向刚度并保持全桥稳 定性。在截面 发生 较大变化的位置, 要设渐变段过渡, 减小应力集中效应。 ( ) 在进行配筋设 计时要充 分考虑 扭矩效 应, 弯梁应 在 腹板侧面布置较多受力钢筋, 其截面上下缘钢 筋也比同 等跨 径的直桥多, 且应 配置较多的抗扭箍筋。 ( ) 城市立交桥中的弯箱梁桥中墩多布置成独柱支 承构
无伸缩缝曲线箱梁桥剪力滞效应有限段法分析与试验研究

簋 关敬 l 计 相系 I
l I
衣次令单元 的两 端结点位移基 本未知量产 生单位位移 ,从 i i i
导到各 自的积分 常数A A  ̄ 并将积分常数代 入相关公式 , 求 得变形函数及 单元荷载列 阵
l 对 入 ” 成 刚 矩 I“ 号 座 形 总 度 I
G
—
G
图 8 测试截面沿桥纵 向分布示意 图
1
.
2
.
3
.
4
.
5
.
6
.
7
.
8
9
.
.
内侧 1
l T
1
l i
1
外侧
图 1 曲线 箱 梁 模 型 工 况 六 加 载 ( 片 ) 1 照
图 9 应 变 片 横 向 分 布 示 意 图
在各工况试验过 程中控制箱梁模型处于线弹性 阶段 。
响较大的位置 。根据 以下几个 因素来确定测试断面 。
本试验共进行六种加 载工况 。如下表 1 所示
表 1 模 型 加 载 工 况
工况 加载截面
—
() 1理论计算 初步结果 ;2 梁 上受 约束 部位 及直接 施加 () 集 中荷载断面处 ;3 连续梁 正负弯矩区域 。 ()
模型试验实测 了七 个断 面 。如 图 8所示 , 中 A~A截 其 面为 1 #桥台附近处 , —B D—D截 面分别 为 1 B 、 #跨 的两个 14 / 跨处 , C—C截面在 1 #跨跨 中截 面处 ,E —E截 面表示 近 中跨 内支座截面 , —F表示 中跨距 内支座 的 14跨处 , F / G—G
—
( —G r 、 C—C
预应力混凝土连续梁桥的计算

预应力混凝土连续梁桥的计算1 绪论本毕业设计主要是关于大跨度预应力混凝土延续梁桥结构的设计,预应力混凝土延续梁桥以结构受力功用好、变形小、伸缩缝少、行车平顺温馨、外型繁复美观、养护工程量小、抗震功用强等而成为最富有竞争力的主要桥型之一。
与同等跨径的简支梁桥相比,延续梁桥的截面控制弯距得以增加,同时由于采用平衡悬臂施工方法,使桥梁单跨跨径得以增大,从而在近二十余年来延续梁桥失掉普遍的运用。
因此,本次毕业设计关于延续梁桥的设计对今后的走上任务单位有着极端重要的意义。
本设计主要为渭河特大桥的设计,其中桥梁跨度为40+64+40 m,全长144 m,桥面宽6.9 m。
设计荷载规范:铁路中--活荷载;桥面纵坡:0% (平坡);桥面横坡:±1.5%;桥轴平面线型:曲线。
主梁采用悬臂挂篮对称施工,共划分为五个阶段。
第一阶段:在支架上施工中间墩顶0#块和1#块;第二阶段:在0#、1#块上张拉预应力钢筋并装置好挂篮,然后悬臂向外依次浇筑2#块、3#块……并张拉预应力钢筋,直到最大悬臂,同时在悬臂浇筑行将完成的时分,在两端搭支架浇筑边跨部位的4个单元;第三阶段:边跨合拢;第四阶段:中跨合拢,撤除挂篮,由边跨向跨中对称停止桥面铺装;第五阶段:完工验收,交付运营运用阶段。
本桥设4个支座,其中第一个支座为固定铰支座,其他为活动铰支座。
在本设计进程中我们主要停止了以下几个方面的任务:1、依据设计资料初步拟定主梁截面尺寸;2、停止内力〔恒载内力、活载内力〕计算;3、力筋的计算与布置;4、预应力损失及有效预应力的计算;5、关于预加力惹起的结构次内力讨论;6、主梁截面强度计算;7、主梁抗裂性检算;8、弹性阶段应力的计算与验算。
由于本次毕业设计选用的是变截面的延续梁,计算十分烦琐,故在计算时采用电算。
设计中一切顺序均没有在注释中详细给出,而是直接输入计算结果。
另外本次设计的计算数据与桥梁设计软件桥梁博士,计算一切失掉的数据停止比拟,以反省正确性。
钢结构课件连续体系梁桥的设计与计算

计算分析
根据桥梁设计规范,对该桥进行了 静力、动力和稳定性分析,计算了 主梁和桥墩的承载能力、位移和应 力分布等。
施工方案
根据计算结果和施工条件,制定了 详细的施工方案,包括钢构件的制 作、运输、拼装和焊接等。
某大桥的施工过程与监控
施工监控
在施工过程中,对该桥进行了全 面的施工监控,实时监测桥梁的 变形、位移和应力等参数,确保
钢结构课件连续体系 梁桥的设计与计算
目录
• 引言 • 连续体系梁桥的设计 • 钢结构的计算与分析 • 案例研究 • 结论与展望
01
引言
背景介绍
随着我国交通事业的不断发展,对桥 梁的需求不断增加,对桥梁的质量和 性能要求也越来越高。
钢结构连续体系梁桥作为一种新型的 桥梁结构形式,具有结构稳定、承载 能力强、施工方便等优点,被广泛应 用于各类桥梁工程中。
施工方法设计
施工方法选择
根据工程条件和要求,选 择合适的施工方法,如预 制拼装、整体吊装或常规 浇筑等。
施工顺序设计
合理安排施工顺序,确保 施工过程中的结构安全和 稳定性。
施工监控
采用先进的施工监控技术, 实时监测施工过程中的结 构变形和应力状态,确保 施工安全和质量。
桥面铺装设计
铺装材料选择
根据桥梁使用环境和荷载要求,选择合适的 铺装材料,如耐磨耐压沥青混凝土、耐久性 好且防滑性能良好的耐磨耐压混凝土等。
01
02
03
结构形式选择
根据桥梁跨度、荷载要求 和地形条件,选择适合的 结构形式,如简支梁、连 续梁和悬臂梁等。
截面设计
根据桥梁承载能力和稳定 性要求,设计钢结构的截 面类型和尺寸,以满足强 度、刚度和稳定性要求。
平曲线段内大跨径连续刚构桥梁的设计计算

平曲线段内大跨径连续刚构桥梁的设计计算发表时间:2016-11-16T16:42:38.980Z 来源:《基层建设》2016年18期作者:韦雨强[导读] 摘要:本文以某工程为例,从主梁方面简要分析了大跨径连续钢构桥梁的主桥构造,并从曲线梁特点以及静力分析两方面探讨了如何对平曲线段内大跨径连续刚够桥梁设计进行计算,以期保证设计人员设计方案的精准性,进而保证工程的实际质量。
广西建川投资管理有限责任公司广西壮族自治区 530001摘要:本文以某工程为例,从主梁方面简要分析了大跨径连续钢构桥梁的主桥构造,并从曲线梁特点以及静力分析两方面探讨了如何对平曲线段内大跨径连续刚够桥梁设计进行计算,以期保证设计人员设计方案的精准性,进而保证工程的实际质量。
关键词:平曲线段内;大跨径;连续钢构桥;设计引言如今,大跨径连续钢构桥梁的数量不断增加,人们对该类型桥梁的设计质量也有了更高的要求。
为此,设计单位必须提高设计人员的设计水平,以便保证该类型桥梁的使用质量。
平曲线段部分设计工作是大跨径连续钢构桥梁整体设计的重要环节,直接关系到钢构桥梁的工程质量。
而且由于影响曲线梁的因素较多,导致设计难度较大。
故而,设计人员应更为注重该环节的设计工作,不断提高自身设计水平,以确保设计图纸的精准度以及工程质量。
1工程实例设定某铁路横跨黄河干流,所用桥梁类型即为大跨径连续钢构桥。
桥址部分主河槽宽度达到300m。
主流偏向左岸,而左岸为山崖,且较为陡峭,相对高度差值为30m。
右岸滩区域较为宽阔且地势平坦,高于主河道,两者差值为8m。
河道长期存在流水。
通常情况下,水深处于4m至6m之内。
桥址占据黄河流域部分区域,共计220000km2,设计所参考的流量值为:Q1%=6500M3/s,Q0.33%=7340M3/s。
线路法线同黄河主槽内部泓线所形成的夹角角度为2°,主桥使用跨径为(80+2×120+80)m的预应力混凝土连续钢构,整体位于R=800m的平曲线之上。
连续梁桥—内力计算课件

连续梁桥的内力计算实例
简单连续梁桥的内力计算
简单连续梁桥的受力特点 在简单连续梁桥中,上部结构通过支座与下部结构相连, 形成多跨连续梁。这种结构的受力特点是在支座处产生负 弯矩,跨中产生正弯矩。
内力计算方法 对于简单连续梁桥,通常采用整体式桥墩和分离式桥墩两 种形式。根据不同形式,可以采用不同的方法进行内力计 算。
计算示例
假设一跨40m的连续梁桥,采用整体式桥墩,通过计算可 得在跨中处的弯矩为179.1kN·m。
复杂连续梁桥的内力计算
复杂连续梁桥的受力特点
复杂连续梁桥通常具有多跨、多支座、多转向等特点,其受力情况比简单连续梁桥更为复 杂。
内力计算方法
对于复杂连续梁桥,需要采用更精确的方法进行内力计算,如有限元法、有限差分法等。
设计标 准
连续梁桥的设计标准主要包括设计荷载、设计速度、设计年限等,根据不同的 桥梁类型和用途,设计标准会有所不同。
连续梁桥的内力计算方法
静力法
定义:静力法是一种通过施加等效荷载 来模拟结构受力的方法。在连续梁桥的 内力计算中,静力法通常用于计算恒载
作用下结构的内力。
静力法通过将结构自重和其他恒载施加 到结构上,并考虑结构边界条件和支撑 条件,来求解结构的内力。该方法通常 采用弯矩和剪力等力学指标来表示结构
连续梁桥—内力计算课件
• 连续梁桥概述
连续梁桥概述
连续梁桥的定义与特点
定义
连续梁桥是一种具有连续刚构的 桥梁,主要由混凝土构建,包括 主梁、桥墩和基础等部分。
特点
连续梁桥具有结构刚度较大、变 形较小、抗风性能好、养护简单 等优点,同时其造型美观,适用 于不同地形和跨度。
连续梁桥的分类与结构形式
分类
先简支后连续梁桥的特点和计算方法
先简支后连续梁桥的特点和计算方法作者:李会军来源:《广东科技》 2014年第10期李会军(福建省路港交通咨询中心,福建福州 350011)摘要:简支转连续法在中等跨径装配式预应力混凝土连续梁桥中应用很广泛。
它具有变形小、伸缩缝少、工期短的优点。
以政和县石屯大桥危桥改建工程采用的4×25m+4×25m先简支后连续预应力混凝土T梁为例,简要介绍先简支后连续梁桥的特点和计算方法。
关键词:连续梁桥;先简支后连续;T梁0 引言简支转连续法在中等跨径装配式预应力混凝土连续梁桥中应用很广泛。
它具有变形小、伸缩缝少、工期短的优点。
先简支后连续梁桥具体的施工过程为:先在场地进行梁的预制,再吊装至墩台上就位,此时为一般简支体系,然后通过浇筑支点连接段混凝土,张拉负弯矩区域的预应力钢束,更换支座(体系转换)后形成结构连续梁体系。
本文结合政和县石屯大桥危桥改建工程采用的4×25m+4×25m预应力混凝土先简支后连续T梁,简要介绍先简支后连续梁桥的特点和计算方法。
1 设计基本资料1.1 工程概况石屯大桥位于政和县石屯镇旧石屯大桥处,是将旧石屯大桥拆除后,在原址新建。
它是石屯镇与工业园区的连接桥梁,中心桩号K0+557.5,桥孔为8×25m预应力钢筋混凝土T梁,下部采用肋板式桥台、桩式基础,矩形盖梁柱式桥墩、钻孔灌注桩。
大桥长207m。
在0#台、8#台处各设置一道D80型伸缩缝,4#墩处设置一道D160型伸缩缝。
本桥位于直线段内,桥面横坡为双向坡1.5%。
石屯大桥设计荷载为公路-Ⅱ级;桥面宽度为2m(护栏+人行道)+11m(行车道)+2m(人行道+护栏)=15m,双向两车道;桥面横坡为1.5%;设计行车速度为40km/h。
1.2 主要材料预制T梁、桥面现浇连续段均采用C50混凝土;桥面铺装采用C50防水混凝土;预应力钢束采用技术性能符合国家标准《预应力筋用钢绞线》(GB/T5224-2003)规定的高强度低松驰7丝钢绞线,公称直径为15.2mm,公称面积139mm2,标准强度fpk=1860MPa,弹性模量Ep=1.95×105MPa,1000h后应力松驰率不大于2.5%。
基于MIDAS_CIVIL的连续弯桥梁格法计算分析
基于MIDAS/CIVIL的连续弯桥梁格法计算分析发布时间:2021-06-09T07:20:04.992Z 来源:《建筑学研究前沿》2021年6期作者:祝宇瑶[导读] 采用MIDAS/CIVIL有限元软件,建立了一座两跨连续梁模型,跨径均为50m,基于梁格法原理建立模型,讨论在恒载作用下,不同曲率半径对曲梁的变形、内力影响。
对在工程应用中,为减小弯桥弯扭耦合的影响提出合理化建议重庆交通大学重庆市 400000摘要:采用MIDAS/CIVIL有限元软件,建立了一座两跨连续梁模型,跨径均为50m,基于梁格法原理建立模型,讨论在恒载作用下,不同曲率半径对曲梁的变形、内力影响。
对在工程应用中,为减小弯桥弯扭耦合的影响提出合理化建议。
关键词:弯箱梁桥;弯扭耦合;梁格法;有限元1、引言中国社会发展至今,国家对路网覆盖范围不断增大,在此之间必然会限于地形、地貌,或出于路线整体线性连续性和城市美化等因素而考虑搭建曲线线性的梁桥。
且现阶段的曲线梁桥因其能较为完美地达到设计和使用要求而日益得到广泛应用(如天津中山门桥、北京四元桥、上海莘庄立交桥等)。
2、弯箱梁桥的弯扭耦合作用及其影响因素曲线梁桥区别于直线桥梁,在发生竖向弯曲时,由于曲率的影响,必然产生扭转,而这种扭转又将导致梁的挠曲变形,这种特有的受力现象被称为弯扭耦合作用。
人类研究曲梁过程中发现,影响曲梁弯扭耦合效应的因素最为关键的参数是:圆心角、桥宽与曲率半径之比、弯扭刚度比等。
1)圆心角。
主梁的弯曲程度是影响弯桥受力特性最主要的因素,它是跨长与半径的比值,反映了与跨径有关的相对弯曲关系。
如果桥梁跨长一定,主梁圆心角的大小就代表了梁的曲率。
圆心角越大,曲率半径就越小,所显示的曲线梁桥的受力特点就越明显。
2)桥梁宽度与曲率半径之比。
偏心布置在桥面上的汽车荷载将产生扭矩,由于弯扭耦合作用又将产生弯矩。
偏心荷载对曲线梁桥的内力有较大影响,因此在进行曲线梁桥计算时,除了考虑圆心角外,还应充分考虑桥梁宽度的因素。
曲线连续梁桥的结构设计
许 传 贵
( 辽 宁乾成工程设计 咨询有限公 司, 辽宁 沈阳 1 1 0 0 0 3 ) 摘 要: 曲线梁桥是高速公路和城市立交中普遍应用的一种桥型。文章根据曲线梁桥的结构受力特点, 论述 了曲线梁桥在施工及成 桥 运 营阶段 出现 病 害的原 因 , 论述 了曲线 梁桥 在设 计 中应 注意的 问题 , 并提 出 了该 类型桥 梁设 计 中的一 些经验做 法 和解 决方案 。 关键 词 : 曲 线 梁桥 ; 结构 设 计 ; 受力 特点 考虑扭矩对整体结构的影响,曲线梁不仅应在腹板侧面布置较 目前在 高等 级公 路及 城市 立 交 中曲线 梁桥 的应 用得 到 了普 遍 的 多 受力 钢筋 , 而 且其 截 面上 下缘 钢 筋也 比 同等跨 径 的 直桥 多 , 同 时配 认可, 尤其 在城 市 立交 匝道设 计 中最为广 泛 。曲线梁桥 的设 计 中常采 置较 多 的抗 扭 箍筋 。 用 箱型 截面 , 因其 具 有材 料用 量少 、 结 构 自重小 、 抗 扭刚 度大 、 整 体稳 3 . 4下 部支 撑方式 的选 用 定性好 、 截面应力分配合理等优点 , 而在曲线梁桥中应用非常普遍。 曲线梁桥下部支撑方式的选取 ,直接影响桥梁整体结构内力的 现阶段 曲线梁桥的设计和理论研究已经取得了很多成果 ,但由 分 布情况 。 对于 曲线 梁桥 , 中间支 承一般 分 为两种类 型 : 抗 扭型 支承 和 于 曲线 梁桥 结 构受 力复 杂 、 施工 过程 中标 高不 能 准确 的控制 , 由于设 单支点铰支承。根据以往的设计经验下部支撑方式的选用可参照以 计 的原 因导致 在项 目的施工 或 使用 过程 中已多 次发 生过 事故 。常见 下 原则 : 问题 主要 为 : 曲梁 内侧支 座 脱空 ; 主梁 横 向侧 移 量 过大 ; 横 向刚 度不 3 . 4 . 1对 于 宽度较 宽 、 曲线 半径 较大 的 曲线梁 桥 ( 桥宽 B > 1 2 r n 、 半 足 引起 扭 曲变 形 ; 固结 墩墩 身开 裂 ; 梁 体 的外移 和 翻转 进一 步导 致支 径 R > 1 0 0 m) , 主梁所受的扭转作用小 、 桥体宽度较大及横 向连接来增 座、 伸缩 缝 的剪切 破坏 和平 曲线超 高 的丧失 等 。 故在 曲线 梁桥 的设计 加 横 向的稳 定性 ,故 在 中墩位 置采 用具 有抗 扭较 强 的多柱 或 多支座 与施工过程中应充分考虑结构 的弯 、 剪、 扭受力特性 , 对结构 内力进 的支承 方式 , 亦 可采用 墩 柱与梁 固结 的支 承形式 , 即抗扭 型支 承 。 行准确分析及合理优化, 消除设计带来 的不安全隐患。 3 . 4 . 2 对 于宽 度 较窄 、 曲线 半径 较 小 的 曲线 梁 桥 ( 桥宽 B ≤1 2 m、 2 曲线 梁桥 受力 特点 半径 R ≤1 0 0 m) , 主梁 所受扭 转作 用大 , 尤其是 预应 力钢束 径 向力作 用 2 . 1“ 弯一 扭” 耦 合作 用 所 产生 的主 梁横 向扭矩 , 导致扭 转 变形很 大 。由于 桥窄 因此宜 采用 独 曲梁 由于 自身 及外 荷载 的作用 下会 同 时产生弯 矩 和扭矩 , 并且 相 柱墩 , 但 应视 墩柱 高度 的不 同来 选用 支承 结构形 式 。较高 的 中墩 可采 互作 用 。表 现为 曲梁 内外 侧尺 寸不 同 、 支座 反力 不等 、 外荷 载偏 心 及 用墩柱 与梁 固结 的结构 支承 形式 , 较 低 的 中墩 可采用 具有 较弱 抗扭 能 预应力径向作用共同引起较大的扭矩, 使梁截面处于“ 弯一 扭” 耦合作 力 的单点 支 承的方 式 。这样 可有 效 降低墩 柱 的弯矩 和减 小 主梁 的横 用 的状 态, 其 截 面主 拉应 力 比相 应 的直 梁桥 大得 多 , 这 是 曲梁 所独 有 向扭转变形 。但这两种支承方式都需对横向支座偏心进行调整。 的受力 特点 。 3 . 5墩柱截面的合理选用 在变形方面, 强大的扭矩作用致使 曲线梁桥产生扭转变形; 曲线 正如以上所述 ,当采用墩柱与梁固结的支承形式且墩柱较矮的 外侧的竖向挠度要大于同等跨径的直桥 ; 由于“ 弯一 扭” 耦合作用, 在梁 情况 下 , 宜 采用 矩形截 面墩 柱 。因为矩形 截面沿 主梁 纵 向抗 弯 刚度较 端可能出现“ 翘 曲” ; 当梁端处横桥 向约束较弱时, 梁体有 向曲线外侧 小, 而沿主梁横 向抗弯刚度较大, 这样不仅减小了主梁横向扭转变形 , 而且 较少 了墩 柱 的配筋 。针 对整 体结 构 的受力 特点 拟定 构造 和 配置 “ 爬 移” 的趋 势 。 在 受 力方 面 , 由于存 在较 大 的 扭矩 , 通 常 会 使外 梁 超 载 、 内 梁卸 钢筋 , 使整 个设计 更加 合理 安全 。 载, 尤其 当活 载偏置 时 , 内侧支 座甚 至会 出现负 反力 , 如果 支 座不 能承 3 . 6支 座形式 的合 理选用 受 拉力 , 就会 出现梁 体与 支座 发生 脱离 的现象 , 即“ 支 座脱 空 ” 现象 , 这 根据 以上 所介 绍 的结构 受力 特 点及设 计 中的 经验做 法来 选 取相 种 现象 在小 半径 的宽桥 中特 别 明显 。 对应 的支座类 型 , 具体 如下 : 2 . 2下部 墩台受 力复 杂 3 . 6 . 1曲线连续 梁桥 选用 中墩 支座 时, 尽 可能 横桥 向位 移 固定 , 限 曲梁 内外侧 支 座反 力相 差较 大 ,导致 各 墩柱 所受 垂直 力有 较 大 制 主梁 横 向侧 移, 可 采用盆 式或 普通板 式橡 胶支座 。 差 异 。 曲线桥墩 顶 水平 力不 仅 由制 动力 、 温度 变化 引起 的 内力 、 地震 3 . 6 . 2 当桥 长大 于 1 0 0 m 时, 梁 端支 座可 采 用盆 式橡 胶 支座 及 带 力等 产生 外 , 还有 汽车 离心 力 和预应 力 张拉 产生 的径 向力 , 这也 是 比 有 横桥 向位 移 固定装 置 的 四氟板 橡胶 支座 ,保证 桥梁 顺桥 向 自由滑 直线桥 墩顶 受力 复杂 之处 。 动、 横桥 向位 移 固定 ; 当桥 长小 于 1 0 0 m时 , 梁端 支座 可 以采 用普 通 板 故 在 曲线 梁 桥结 构设 计 中, 应 进行 全 面的 三维 空间受 力分 析 , 只 式橡胶支座。对于曲线梁桥支座设计 , 选用“ 梁端设普通板式橡胶支 采用横向分布等简化计算方法, 不能满足设计要求 。必须对其在承受 座 、 所有 中墩设 横 桥 向 自由滑 动 的盆 式 支座 ” 是 非常 危险 的, 应 引起 设 纵 向弯 曲 、 扭转 和翘 曲作用 下, 结 合 自重 、 预应 力 和汽 车活 载等 荷载 进 计者 的重视 。 行详 细 的受力 分析 , 充 分考 虑其 结构 的空 间受力 特点 才能 保证 结构 设 3 . 6 . 3当 曲线梁 桥较宽 时, 桥 梁整 体升 降温 变化 在墩 顶产 生 的横 桥 向水平力 会较 大, 尤 其是 当所有 中墩 支座均 为横 桥 向位 移 固定 时 , 计 的安 全性 。 3 曲线 梁桥 的结构设 计 水平力 增加 更为 明显 , 整 体计 算时应 关 注水平力 变化 情况 。 直 线梁 桥在 设计 中主要 考 虑梁 的“ 弯、 剪” 作用 , 而 曲线 梁 桥结 构 4结束 语 曲线 梁桥 由于其结 构受 力 的特殊 性 ,较 同等跨 径 的直梁 桥要 复 处于“ 弯、 剪、 扭” 的复合受力状态, 故桥梁整体要以抵抗复合受力状态 进行 结 构设计 , 并在 构造设 计 中加强 抵抗 措施 。 杂得 多 , 因此 在进 行设计 和计 算 时应 引起 足够 的重 视 。 通过 对 曲线 梁 3 . 1弯扭 刚度 比 桥结 构受 力 特点 的分析 及设 计 中存在 问题 的总结 ,并提 出了 曲线 梁 曲线梁 桥 的弯扭 刚 度 比对结 构 的受力 状态 和变 形状 态有 着 直接 桥设 计 中 的一些 经验做 法 和解决 方 案 ,对 同类 桥梁 的设 计具 有 一定 的关系: 弯扭刚度比越大 由曲率因素而导致的扭转变形越大。 故在曲 的参 考价 值 。 参考 文献 线梁桥设计时, 满足曲梁竖 向变形 的同时, 应尽可能减小抗弯刚度 、 增大抗扭刚度, 来抵抗对整体结构产生的不利影响。 所以在曲线梁桥 『 1 ] 姚玲 森曲 线梁『 M1 . 北 京: 人 民交通 出版社 , 1 9 8 9 中. 抗扭惯矩较大的箱形截面和低高度梁的应用最为广泛。 『 2 1 邵容 光 , 夏 淦等 . 混凝 土弯 梁桥 『 M 1 . 人 民交通 出版社, 1 9 9 4 . 『 3 1 吴 西伦. 弯梁桥设 计『 M] . 人 民 交通 出版 社 , 1 9 9 0 . 3 . 2截 面设计 孙 广华 . 曲线 梁桥 计 算f M 1 . 人 民交通 出版社, 1 9 9 5 . 曲线箱梁桥截面设计 时, 要在桥跨范围内设置一些横隔板, 并且 1 5 1 何 维 力. 独柱 支承 的曲线 梁桥 设 计【 J J . 北京 建筑 工程 学院学报 , 2 0 0 1 . 要比相应的直梁桥有所加强 , 增加横桥向刚度并保持全桥稳定性 。 在 『 『 6 1 赵巧燕. 多跨 混凝 土 弯 梁桥 若 干 问题研 究[ J 】 . 北京 工 业 大 学工 学硕 截 面发生 较 大变化 的位 置, 要设 渐变 段过 渡, 减小 应力 集 中效 �
第三章 连续梁桥内力次内力计算
• 实体截面:用于小跨度的桥梁(现浇)
• 空心板截面:常用于1530m的连续梁桥 (现浇)
• 肋式截面:常用跨度在1530m范围内, 常采用预制架设施工,并在梁段安装完 成之后,经体系转换形成连续梁。鱼腹 式
• 特点:构造简单,施工方便,适用于中、 小跨度的连续梁桥。
9
第三章 连续梁桥 第一节 概述
7
第三章 连续梁桥 第一节 概述
混凝土连续梁桥概述-布置
(2)梁高的选择
等高度连续梁
变高度连续梁
等截面连续梁
VS
变截面连续梁
➢梁高不变。具有构造、制造和施 工简便的特点。适用于中等跨度 (4060m左右)的、较长的桥梁。 可按等跨或不等跨布置。长桥多采
用等跨布置,以简化构造,统一模
式,便于施工。
➢更能适应结构的内力分布规律。受 力状态与其施工时的内力状态基本吻 合。梁高变化规律可以是斜(直)线、 圆弧线或二次抛物线。箱型截面的底 板、腹板和顶板可作成变厚度,以适 应梁内各截面的不同受力要求。
箱内外,配以横隔板、转向块等构
特点-减小截
造,对梁体施加预应力。
面尺寸;提高混
凝土浇筑质量;
无须预留孔道,
减少孔道压浆等
工序;施工方便
迅速,钢束便于
更换;钢束线形
容易调整,减小
预应力损失;但
其对力筋防护和
结构构造等的要
求较高,抗腐蚀、
耐疲劳性能有待
提高。
在桥梁工程中
有所应用(新桥
设计和既有桥梁
加固)。
37
第三章 连续梁桥 第一节 概述
混凝土连续梁桥概述-设计实例
38
第三章 连续梁桥 第一节 概述
混凝土连续梁桥概述-设计实例
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第22卷第4期佛山科学技术学院学报(自然科学版)VOl.22NO.4
2004年12月JOurnalOfFOShanUniverSity(NaturalScienceEditiOn)Dec::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::.2004
文章编号:1008-0171(2004)04-0051-04
计算连续曲线梁桥的有限段法杜嘉斌1 罗旗帜2 张学文1
(1.华南理工大学土木工程系 广东广州510640;2.佛山科学技术学院学校办公室 广东佛山528000)摘要:导出平面曲线梁桥有限段法分析的单元刚度矩阵 利用功能原理得到了荷载列阵 编制计算程序 对连续曲线梁桥进行静力计算G给出了算例 并将力法和传递矩阵法的结果作了比较 证明本文方法的正确性G
关键词:连续曲线梁桥;有限段法;位移模式中图分类号:U448.215文献标识码:A
平面曲线梁桥的静力计算问题 许多学者已经做了大量工作[1-5] 但计算连续曲线梁桥时由于超静定次数的增加而变得很困难G它的分析诚然可以采用通用的有限元技术 这种方法计算量大 在工程中难以推广和运用G本文运用能量变分法得到的曲线梁平衡微分方程的齐次解作为位移模式 利用直接刚度法导出了单元刚度矩阵 利用功能原理得到了荷载列阵G编制了平面曲线梁桥的静力计算程序G对两跨连续曲线梁桥进行了静力计算 且将传递矩阵法[1]和力法[2]的结果进行了比较 证明了本文方法的正确性G本文方法既简单又实用 与通用有限元相比 运行时间及数据处理大为减少G
1微分方程和边界条件
由文献[1]得到体系的总势能为H=U +V =12El S0(U~2-2gU~R+g2R2)dz+12GKT S0(g/2+2Rg/U/+U/2R2)dz-
S0gyUdz- S0mzgdz+[MU/]\S0-[OU]\S0-[Tg]\S0 (1)
式中 El GKT分别表示梁的抗弯刚度~抗扭刚度;U g分别为竖向变形~扭转变形;O M T分别代表截面的剪力~弯矩~扭矩;gy mz分别代表竖向分布荷载~径向分布扭矩G
由8H=0 得
ElU~~-GKTR2U~-El+GKTRg~=gy -El+GKTRU~-GKTg~+ElR2g=mzG(2)ElUW-El+GKTRg/-GKTR2[]U/+O(z)8US0=0
ElU~-ElR[]g+M(z)8U/S0=0 GKT
RU/+GKT[]g/-T(z)8gS0< L=0G
(3)
式(2)是由变分得到的曲梁基本微分方程 式(3)是变分所要求的自然边界条件G
收稿日期:2004-08-30
基金项目:国家自然科学基金资助项目(50378019);广东省自然科学基金资助项目(034066)
作者简介:杜嘉斌(1979-) 男 广东佛山人 华南理工大学与佛山科学技术学院联合培养硕士研究生G2单元刚度矩阵和荷载列阵2. 位移模式在有限元中,单元的位移模式一般采用多项式作为近似函数0本文的位移模式与此不同,采用的是微分方程的齐次解作为位移模式{6]0为了编写程序的方便,各量正负号的规定如图 所示0
图 符号及正负号的规定对于平面曲线梁桥, 个结点取3个位移基本未知量
(挠度)~ /(转角)及 (扭转角),对应的结点力为 (剪力)~ (弯矩)及T(扭矩)0曲线梁桥的单元如图2所示0为了导出单元刚度系数,令gy=0,mz=0,即微分方程
(2)的齐次解为图2结点位移
(z)=A -A2z-A3RcOszR-A4(YsinzR-RzcOszR)-A RsinzR-A6(YcOszR-RzsinzR), (z)=A3cOszR-A4zcOszR-A sinzR-A6zsinzR ,(4)
式中,Y=2EIR2/(EI-GKT),A ~A6为积分常数0
2.2单元刚度矩阵根据刚度法原理,单元刚度方程为{ ]e{6 }e={P }e,即
2 3 4 6 2 22 23 24 2 26 3 32 33 34 3 36 4 42 43 44 4 46 2 3 4 6 6 62 63 64 6 66 / =
T
T 0( )
为求出各刚度系数,令 = ,其他的未知数为零,由边界条件,可以列出如下的线性方程组A -A3R-A6Y= ,A2-A4(Y/R-R)-A =0,A3=0,
A -A2S-A3RcOsSR-A4(YsinSR-RScOsSR)-A RsinSR-
A6(YcOsSR-RSsinSR=0,
A2-A3sinSR-A4(YcOsSRR-SsinSR-RcOsSR)-A cOsSR-A6(ScOsSR-RsinSR-YsinSRR=0,A3cOsSR-A4ScOsSR-A cOsSR-A6SsinSR =00
(6)
解线性方程组(6)即可确定当 发生单位位移时的积分常数A ~A6,由此,当该结点发生单位位移时的
2 佛山科学技术学院学报(自然科学版)第22卷单元变形被解出O依次让未知数U/ { Uj U/j {j分别发生单位位移 即得到6个线性方程组 可以确定各自状态下的积分常数和单元变形(由于篇幅所限 这里没有给出Al~A6的具体算术表达式)O
由式(3)可知 与位移对应的力分别为
(z)=-ElU"-El-GKTR{/-GKT
RZU/
M(z)=-ElU"-ElR{ T(z)=GKTRU/-GKT<(L{/O(7)
由刚度系数的物理含义可得各刚度系数的计算式为 l =ElU"-El-GKTR{/-GKTRZ U/z=0 Z =-ElU"-ElR {z=0 3 =-GKTRU/-GKT {/z=0 4 =-ElU"-El-GKTR{/-GKTRZ U/z=S 5 =-ElU"-ElR {z=S 6 =GKTRU/-GKT {/z=S
<(LO(8)
当依次令未知量U U/ { Uj U/j {j发生单位位移时 取l~6 U U/ {为相应位移下的单元变形O
Z.3单元荷载列阵曲线梁桥4种代表性荷载指集中力P~集中扭矩T~均布荷载g和均布扭矩m 下面只简单介绍其中两种情况O
(l)曲线梁桥上作用集中力P 受力如图3所示O由虚功原理可得P U( p)- l=0 即 =-P U( p)=0O其中
U( p)=Al-AZ p-AZRcOs pR-A4(ysin pR-R pcOs pR)-A5Rsin
p
R
-A6(ycOs pR-R psin pR)O(9)(Z)曲线梁桥上作用均布荷载g 受力如图4所示O由虚功原理可得g U( p)- l=0 即 =-g U( p)=0O其中
U( p)= p0 Al-AZz-A3RcOszR-A4(ysinzR-RzcOszR)-A5RsinzR-A6(ycOszR-RzsinzR dzO(l0)
图3曲线梁上作用P图4曲线梁上作用g
式(9) (l0)中Al~A6均为U 发生单位位移时的积分常数O同理可以求出M T j Mj及Tj 只
是Al~A6是未知数U/ { Uj U/j {j分别发生单位位移时对应的积分常数O同理可以求出均布集中扭矩T与均布扭矩m作用下的荷载列阵O
值得注意的是 以上求得的各种荷载下的结点等效荷载 单元两端荷载列阵只需在前加负号即可O
35第4期杜嘉斌等:计算连续曲线梁桥的有限段法3结果比较3.1算例如图5所示的两等跨连续曲梁(具有刚性扭转约束)
求给定荷载下各支承点的变形和内力(假定El/GK
T=1)G
3.2计算比较根据上述平面曲线梁桥的计算公式编写了计算程序 以图5中截面2-2左侧为例进行计算 得出的结果与文献 1 和力法 2 的比较如表1所示G图5两等跨连续曲梁表1几种方法的结果比较
变形与内力文献 1 方法力法
2
本文方法
分2个单元分20个单元
(2)左0000 (2)左(/El)-437.3198-437.3223-437.3210-437.3210
@(2)左0000
@(2)左-6.0514-6.0514-6.0514-6.0514
M(2)左33.030433.030433.030333.0303
T(2)左10.732810.733510.733510.7355
从表1可以看出:(1)本文的计算结果与文献 1 和文献 2 的计算结果吻合较好 证明了本文方法的正确性和可靠性;(2)本文方法分2个单元的结果跟20个单元的结果完全一样 这说明本文方法的收敛速度很快 体现了本文所采用的位移模式的优越性 使得计算量大大减少G
本文利用了曲线梁桥的微分方程的齐次解作为单元的位移模式 导出了刚度矩阵和荷载列阵G所得的计算结果 经与力法和传递矩阵法的结果比较 证明了本文方法的正确性和可靠性;本文方法与通用的有限元法相比计算简单 并可用于连续曲线梁桥的静力问题以及薄壁曲线箱梁剪力滞等问题的计算G
参考文献:
1 罗旗帜.计算曲线梁桥的传递矩阵法 J .中南公路工程 1990 (3):32-41.
2 岛田静雄 仓西茂.曲线梁的计算公式 M .北京:人民交通出版社 1981. 3 姚玲森.曲线梁 M .北京:人民交通出版社 1989. 4 李惠生.曲线梁桥法分析 M .北京:中国铁道出版社 1992. 5 孙广华.曲线梁桥计算 M .北京:人民交通出版社 1995. 6 罗旗帜.薄壁箱形梁剪力滞计算的梁段有限元法 J .湖南大学学报 1991 18(2):33-38.
Finitesegmentmethodforcalculatingcontinuous
curvedgirderbridges
DUJia-bin1 LUOOi-zhi2 ZHANGXue-wen1(1.CivilengineeringDepartment SouthChinaUniversityofTechnology Guangzhou510640 China;2.President sOffice FoshanUniversity Foshan528000 China)
Abstract:Thehomogeneoussolutionderivedfromthegoverningdifferentialeguationswasusedasthedisplacementpatternsoffinitesegment.Thestiffnessmatrixandloadcolumnmatrixesareobtainedintermsofdirectedstiffnessmethodandworkingenergyprinciple.Aprogramisdesignedtocalculatethecurvedgirderbridge.Anexamplewasgiven comparisonsbetweenforcemethodandthematrixdeliveringmethodarepresentedtotestifytheaccuracyoftheabovemethod.KeyWords:continuouscurvedgirder;finitesegmentmethod;displacementpattern
