Euler-Poincare' Characteristic and Phase Transition in the Potts Model
行测答题技巧:片段阅读之标题的选用专项练习

标题选用题其实就是根据文段选出一个适合的标题。
标题选择型的题目,一般在提问时,都会有“标题、题目”等比较明显的字眼,比如:“最适合做本段文宇标题的是”、“该段文字作为一则报纸上的新闻,最适合做该段文字题目的是”等。
方案专家提醒考生:解答这类题目,其实就两点:一,概括主要内容,就是说标题内容要涵盖全文,我们做题时先要根据文段概括出主旨。
二,浓缩主要内容,这是做题的第二步。
标题要简洁明了,要让人一目了然的知道中心内容,在做这类题的时候,一定要抓住了共性和个性,抓关键词,通过关键词简要明了的表述主要内容。
1. “80后”这个词,最早于2001年出现在网络论坛中,指的是一批活跃于网络论坛的出生于20世纪80年代的诗人。
2003年开始,它更多指的是一批被商业运作出名的生于1980年以后的写手。
2004年底,随着“80后作家”的批量涌现,这个词逐渐被用来指称整个20世纪80年代出生的年轻人群体。
最适合做这段文字标题的是:A. “充满希望”的一代B. “80后”的由来C. 用新视角理性看待“80后”D. “80后”引起社会的广泛关注2. 我国汽车工业现在面临缺乏完整的轿车开发能力和自己的品牌的困境,零部件制造体系并没有形成相应的规模,与国外同类行业相比还存在很大差距,虽然汽车工业在近年来有了长足发展,但落后的管理和服务体系在"入世"后国门大开的情况下,仍然成为了中国本行业的"瓶颈",因此,我们必须对这些问题加以认真研究。
以下标题符合上文意思的是( )。
A. 汽车工业的主要问题B. 如何应对汽车工业的"瓶颈"C. WTO与中国的汽车工业D. 汽车工业的喜人发展3. 手机垃圾短信息有“骚扰型”,多为恶作剧、“黄段子”、小道消息;有“陷阱型”,多是骗取用户钱财;有广告短信。
短信业务的确给运营商们带来了丰厚的利润,但有些短信正成为一种“信息公害”,让人不堪其扰。
poincare dulac定理

poincare dulac定理
Poincaré-Dulac定理是微分方程理论中的一个重要结果,它给出了某些特定类别的微分方程的简化方法。
该定理陈述:针对一个二维的自主系统(autonomous system)dx/dt = P(x,y)、dy/dt = Q(x,y),如果在某个区域内,存在一个实数函数 g(x,y) 使得下式成立,则伴随着适当的坐标变换,在变换后的坐标系中,微分方程可以简化为以下形式之一:
1. dx/dt = λx
dy/dt = μy
2. dx/dt = λx + h(x,y)
dy/dt = μy
其中λ, μ为仅与x, y有关的实函数,h(x, y)为高阶项(至少为二阶)的一部分。
这个定理实际上提供了一种将一般形式的二维自主系统简化为线性或带有一些高阶项的系统的方法。
它在应用中有着广泛的应用,尤其在动力学系统和混沌理论中经常被使用。
3态potts模型的普适序参量计算

3态potts模型的普适序参量计算
Potts模型(Potts Model)是一种有用的普适序参量计算,它可以用来表征各种类型的非常复杂的材料和系统。
Potts模型是一种统一的模型,它以不同的参数表征物质中的电子,就像态的相对论一样,它可以被用来描述变分方程的“本征”物态、能量依赖关系和宽带结构。
以下是Potts模型的常见参数:
1. 能量参数:它描述了原子和分子之间形成键的能量,同时确定了模型物质结构特性。
2. 休止基元:它是定义物质行为的约束,它可以对物质自由度进行限定和调节,可用于着色技术中。
3. 热力学参数:它可以帮助研究者更深入地理解物质的温度依赖性,并提供了控制材料多态之间的温度平衡的参数。
4. 广义库伦参数:它可以根据库伦定律计算出每个物质之间的能量以及相互作用的大小。
5. 物态参数:它定义了模型物质能量随物态变化及其它物理属性变化的转换,因此它可以用来说明物质的多态行为。
6. 平滑函数参数:它是Potts模型的基础,为不同的物态建立平滑函数,可以使模型更加可靠。
7. 广义Kitaev参数:它用于描述物质的一系列あ面特性,比如衰减函
数的指数,衰减函数的厚度,原子之间的定向性,多层次的多态结构,以及物质表面的微结构等。
8. 灰度参数:它可以用来表征分子性质,因为它描述了能量状态和不
同温度下分子的传输性能。
9. 非线性参数:它描述了系统物态与其它参量如熵,强度,热容等之
间完全相互作用的系统,并在不同的温度和压力下对这些参量的变化
进行模拟。
以上就是Potts模型的普适序参量计算,它可以帮助研究者弄清普适物
质的行为以及多态演化规律。
向涛-General Introduction

• Elementary interactions:
– el-el, el-ph, el-mag, …
• Elementary structures and phases:
• Development of theoretical methods
– Analytical: path integral, Green’s function, mean-field theory … – Numerical: density functional, Monte Carlo, DMRG, DMFT …
2. Band Theory
– 1900: 金属电导和热传导的经典自由电子理论(Drude) – 1924: 基于Fermi统计的自由电子理论(Pauli 和 Sommerfield) – 1907: 铁磁性相变的分子场理论(Weiss) – 金属导电的能带理论(Bloch)
Standard Picture of Metel and Insulator
Fermi Statistics:Foundation of Chemistry
Bosons have no Chemical Bonds
Fermions can form Chemical Bonds
“With a heavy heart, I have been converted to the idea that Fermi-Dirac, not Einstein-Bose is the correct statistics” (for electrons) Pauli, letter to Schrodinger, Dec 1926
漫谈微分几何、多复变函数与代数几何(Differential geometry, functions

漫谈微分几何、多复变函数与代数几何(Differential geometry, functions of complex variable and algebraic geometry)Differential geometry and tensor analysis, developed with the development of differential geometry, are the basic tools for mastering general relativity. Because general relativity's success, to always obscure differential geometry has become one of the central discipline of mathematics.Since the invention of differential calculus, the birth of differential geometry was born. But the work of Euler, Clairaut and Monge really made differential geometry an independent discipline. In the work of geodesy, Euler has gradually obtained important research, and obtained the famous Euler formula for the calculation of normal curvature. The Clairaut curve of the curvature and torsion, Monge published "analysis is applied to the geometry of the loose leaf paper", the important properties of curves and surfaces are represented by differential equations, which makes the development of classical differential geometry to reach a peak. Gauss in the study of geodesic, through complicated calculation, in 1827 found two main curvature surfaces and its product in the periphery of the Euclidean shape of the space not only depends on its first fundamental form, the result is Gauss proudly called the wonderful theorem, created from the intrinsic geometry. The free surface of space from the periphery, the surface itself as a space to study. In 1854, Riemann made the hypothesis about geometric foundation, and extended the intrinsic geometry of Gauss in 2 dimensional curved surface, thus developing n-dimensional Riemann geometry, with the development of complex functions. A group of excellentmathematicians extended the research objects of differential geometry to complex manifolds and extended them to the complex analytic space theory including singularities. Each step of differential geometry faces not only the deepening of knowledge, but also the continuous expansion of the field of knowledge. Here, differential geometry and complex functions, Lie group theory, algebraic geometry, and PDE all interact profoundly with one another. Mathematics is constantly dividing and blending with each other.By shining the charming glory and the differential geometric function theory of several complex variables, unit circle and the upper half plane (the two conformal mapping establishment) defined on Poincare metric, complex function theory and the differential geometric relationships can be seen distinctly. Poincare metric is conformal invariant. The famous Schwarz theorem can be explained as follows: the Poincare metric on the unit circle does not increase under analytic mapping; if and only if the mapping is a fractional linear transformation, the Poincare metric does not change Poincare. Applying the hyperbolic geometry of Poincare metric, we can easily prove the famous Picard theorem. The proof of Picard theorem to modular function theory is hard to use, if using the differential geometric point of view, can also be in a very simple way to prove. Differential geometry permeates deep into the theory of complex functions. In the theory of multiple complex functions, the curvature of the real differential geometry and other series of calculations are followed by the analysis of the region definition metric of the complex affine space. In complex situations, all of the singular discrete distribution, and in more complex situations, because of the famous Hartogsdevelopment phenomenon, all isolated singularities are engulfed by a continuous region even in singularity formation is often destroyed, only the formation of real codimension 1 manifold can avoid the bad luck. But even this situation requires other restrictions to ensure safety". The singular properties of singularities in the theory of functions of complex functions make them destined to be manifolds. In 1922, Bergman introduced the famous Bergman kernel function, the more complex function or Weyl said its era, in addition to the famous Hartogs, Poincare, Levi of Cousin and several predecessors almost no substantive progress, injected a dynamic Bergman work will undoubtedly give this dead area. In many complex function domains in the Bergman metric metric in the one-dimensional case is the unit circle and Poincare on the upper half plane of the Poincare, which doomed the importance of the work of Bergman.The basic object of algebraic geometry is the properties of the common zeros (algebraic families) of any dimension, affine space, or algebraic equations of a projective space (defined equations),The definitions of algebraic clusters, the coefficients of equations, and the domains in which the points of an algebraic cluster are located are called base domains. An irreducible algebraic variety is a finite sub extension of its base domain. In our numerical domain, the linear space is the extension of the base field in the number field, and the dimension of the linear space is the number of the expansion. From this point of view, algebraic geometry can be viewed as a study of finite extension fields. The properties of algebraic clusters areclosely related to their base domains. The algebraic domain of complex affine space or complex projective space, the research process is not only a large number of concepts and differential geometry and complex function theory and applied to a large number of coincidence, the similar tools in the process of research. Every step of the complex manifold and the complex analytic space has the same influence on these subjects. Many masters in related fields, although they seem to study only one field, have consequences for other areas. For example: the Lerey study of algebraic topology that it has little effect on layer, in algebraic topology, but because of Serre, Weil and H? Cartan (E? Cartan, eldest son) introduction, has a profound impact on algebraic geometry and complex function theory. Chern studies the categories of Hermite spaces, but it also affects algebraic geometry, differential geometry and complex functions. Hironaka studies the singular point resolution in algebraic geometry, but the modification of complex manifold to complex analytic space and blow up affect the theory of complex analytic space. Yau proves that the Calabi conjecture not only affects algebraic geometry and differential geometry, but also affects classical general relativity. At the same time, we can see the important position of nonlinear ordinary differential equations and partial differential equations in differential geometry. Cartan study of symmetric Riemann space, the classification theorem is important, given 1, 2 and 3 dimensional space of a Homogeneous Bounded Domain complete classification, prove that they are all homogeneous symmetric domains at the same time, he guessed: This is also true in the n-dimensional equivalent relation. In 1959, Piatetski-Shapiro has two counterexample and find the domain theory of automorphic function study in symmetry, in the 4 and 5dimensional cases each find a homogeneous bounded domain, which is not a homogeneous symmetric domain, the domain he named Siegel domain, to commemorate the profound work on Siegel in 1943 of automorphic function. The results of Piatetski-Shapiro has profound impact on the theory of complex variable functions and automorphic function theory, and have a profound impact on the symmetry space theory and a series of topics. As we know, Cartan transforms the study of symmetric spaces into the study of Lie groups and Lie algebras, which is directly influenced by Klein and greatly develops the initial idea of Klein. Then it is Cartan developed the concept of Levi-Civita connection, the development of differential geometry in general contact theory, isomorphic mapping through tangent space at each point on the manifold, realize the dream of Klein and greatly promote the development of differential geometry. Cartan is the same, and concluded that the importance of the research in the holonomy manifold twists and turns, finally after his death in thirty years has proved to be correct. Here, we see the vast beauty of differential geometry.As we know, geodesic ties are associated with ODE (ordinary differential equations), minimal surfaces and high dimensional submanifolds are associated with PDE (partial differential equations). These equations are nonlinear equations, so they have high requirements for analysis. Complex PDE and complex analysis the relationship between Cauchy-Riemann equations coupling the famous function theory, in the complex case, the Cauchy- Riemann equations not only deepen the unprecedented contact and the qualitative super Cauchy-Riemann equations (the number of variables is greater than the number of equations) led to a strange phenomenon. This makes PDE and the theory ofmultiple complex functions closely integrated with differential geometry.Most of the scholars have been studying the differential geometry of the intrinsic geometry of the Gauss and Riemann extremely deep stun, by Cartan's method of moving frames is beautiful and concise dumping, by Chern's theory of characteristic classes of the broad and profound admiration, Yau deep exquisite geometric analysis skills to deter.When the young Chern faced the whole differentiation, he said he was like a mountain facing the shining golden light, but he couldn't reach the summit at one time. But then he was cast as a master in this field before Hopf and Weil.If the differential geometry Cartan development to gradually change the general relativistic geometric model, then the differential geometry of Chern et al not only affect the continuation of Cartan and to promote the development of fiber bundle in the form of gauge field theory. Differential geometry is still closely bound up with physics as in the age of Einstein and continues to acquire research topics from physicsWhy does the three-dimensional sphere not give flatness gauge, but can give conformal flatness gauge? Because 3D balls and other dimension as the ball to establish flat space isometric mapping, so it is impossible to establish a flatness gauge; and n-dimensional balls are usually single curvature space, thus can establish a conformal flat metric. In differential geometry, isometry means that the distance between the points on the manifold before and after the mapping remains the same. Whena manifold is equidistant from a flat space, the curvature of its Riemann cross section is always zero. Since the curvature of all spheres is positive constant, the n-dimensional sphere and other manifolds whose sectional curvature is nonzero can not be assigned to local flatness gauge.But there are locally conformally flat manifolds for this concept, two gauge G and G, if G=exp{is called G, P}? G between a and G transform is a conformal transformation. Weyl conformal curvature tensor remains unchanged under conformal transformation. It is a tensor field of (1,3) type on a manifold. When the Weyl conformal curvature tensor is zero, the curvature tensor of the manifold can be represented by the Ricci curvature tensor and the scalar curvature, so Penrose always emphasizes the curvature =Ricci+Weyl.The metric tensor g of an n-dimensional Riemann manifold is conformally equivalent to the flatness gauge locally, and is called conformally flat manifold. All Manifolds (constant curvature manifolds) whose curvature is constant are conformally flat, so they can be given conformal conformal metric. And all dimensions of the sphere (including thethree-dimensional sphere) are manifold of constant curvature, so they must be given conformal conformal metric. Conversely, conformally flat manifolds are not necessarily manifolds of constant curvature. But a wonderful result related to Einstein manifolds can make up for this regret: conformally conformally Einstein manifolds over 3 dimensions must be manifolds of constant curvature. That is to say, if we want conformally conformally flat manifolds to be manifolds of constant curvature, we must call Ric= lambda g, and this is thedefinition of Einstein manifolds. In the formula, Ric is the Ricci curvature tensor, G is the metric tensor, and lambda is constant. The scalar curvature S=m of Einstein manifolds is constant. Moreover, if S is nonzero, there is no nonzero parallel tangent vector field over it. Einstein introduction of the cosmological constant. So he missed the great achievements that the expansion of the universe, so Hubble is successful in the official career; but the vacuum gravitational field equation of cosmological term with had a Einstein manifold, which provides a new stage for mathematicians wit.For the 3 dimensional connected Einstein manifold, even if does not require the conformal flat, it is also the automatic constant curvature manifolds, other dimensions do not set up this wonderful nature, I only know that this is the tensor analysis summer learning, the feeling is a kind of enjoyment. The sectional curvature in the real manifold is different from the curvature of the Holomorphic cross section in the Kahler manifold, and thus produces different results. If the curvature of holomorphic section is constant, the Ricci curvature of the manifold must be constant, so it must be Einstein manifold, called Kahler- Einstein manifold, Kahler. Kahler manifolds are Kahler- Einstein manifolds, if and only if they are Riemann manifolds, Einstein manifolds. N dimensional complex vector space, complex projective space, complex torus and complex hyperbolic space are Kahler- and Einstein manifolds. The study of Kahler-Einstein manifolds becomes the intellectual enjoyment of geometer.Let's go back to an important result of isometric mapping.In this paper, we consider the isometric mapping between M and N and the mapping of the cut space between the two Riemann manifolds, take P at any point on M, and select two non tangent tangent vectors in its tangent space, and obtain its sectional curvature. In the mapping, the two tangent vectors on the P point and its tangent space are transformed into two other tangent vectors under the mapping, and the sectional curvature of the vector is also obtained. If the mapping is isometric mapping, then the curvature of the two cross sections is equal. Or, to be vague, isometric mapping does not change the curvature of the section.Conversely, if the arbitrary points are set, the curvature of the section does not change in nature, then the mapping is not isometric mapping The answer was No. Even in thethree-dimensional Euclidean space on the surface can not set up this property. In some cases, the limit of the geodesic line must be added, and the properties of the Jacobi field can be used to do so. This is the famous Cartan isometry theorem. This theorem is a wonderful application of the Jacobi field. Its wide range of promotion is made by Ambrose and Hicks, known as the Cartan-Ambrose-Hicks theorem.Differential geometry is full of infinite charm. We classify pseudo-Riemannian spaces by using Weyl conformal curvature tensor, which can be classified by Ricci curvature tensor, or classified into 9 types by Bianchi. And these things are all can be attributed to the study of differential geometry, this distant view Riemann and slightly closer to the Klein point of the perfect combination, it can be seen that the great wisdom Cartan, here you can see the profound influence of Einstein.From the Hermite symmetry space to the Kahler-Hodge manifold, differential geometry is not only closely linked with the Lie group, but also connected with algebra, geometry and topologyThink of the great 1895 Poicare wrote the great "position analysis" was founded combination topology unabashedly said differential geometry in high dimensional space is of little importance to this subject, he said: "the home has beautiful scenery, where Xuyuan for." (Chern) topology is the beauty of the home. Why do you have to work hard to compute the curvature of surfaces or even manifolds of high dimensions? But this versatile mathematician is wrong, but we can not say that the mathematical genius no major contribution to differential geometry? Can not. Let's see today's close relation between differential geometry and topology, we'll see. When is a closed form the proper form? The inverse of the Poicare lemma in the region of the homotopy point (the single connected region) tells us that it is automatically established. In the non simply connected region is de famous Rham theorem tells us how to set up, that is the integral differential form in all closed on zero.Even in the field of differential geometry ignored by Poicare, he is still in a casual way deeply affected by the subject, or rather is affecting the whole mathematics.The nature of any discipline that seeks to be generalized after its creation, as is differential geometry. From the curvature, Euclidean curvature of space straight to zero, geometry extended to normal curvature number (narrow Riemann space) andnegative constant space (Lobachevskii space), we know that the greatness of non Euclidean geometry is that it not only independent of the fifth postulate and other alternative to the new geometry. It can be the founder of triangle analysis on it. But the famous mathematician Milnor said that before differential geometry went into non Euclidean geometry, non Euclidean geometry was only the torso with no hands and no feet. The non Euclidean geometry is born only when the curvature is computed uniformly after the metric is defined. In his speech in 1854, Riemann wrote only one formula: that is, this formula unifies the positive curvature, negative curvature and zero curvature geometry. Most people think that the formula for "Riemann" is based on intuition. In fact, later people found the draft paper that he used to calculate the formula. Only then did he realize that talent should be diligent. Riemann has explored the curvature of manifolds of arbitrary curvature of any dimension, but the quantitative calculations go beyond the mathematical tools of that time, and he can only write the unified formula for manifolds of constant curvature. But we know,Even today, this result is still important, differential geometry "comparison theorem" a multitude of names are in constant curvature manifolds for comparison model.When Riemann had considered two differential forms the root of two, this is what we are familiar with the Riemann metric Riemannnian, derived from geometry, he specifically mentioned another case, is the root of four four differential forms (equivalent to four yuan product and four times square). This is the contact and the difference between the two. But he saidthat for this situation and the previous case, the study does not require substantially different methods. It also says that such studies are time consuming and that new insights cannot be added to space, and the results of calculations lack geometric meaning. So Riemann studied only what is now called Riemann metric. Why are future generations of Finsler interested in promoting the Riemann's not wanting to study? It may be that mathematicians are so good that they become a hobby. Cartan in Finsler geometry made efforts, but the effect was little, Chern on the geometric really high hopes also developed some achievements. But I still and general view on the international consensus, that is the Finsler geometry bleak. This is also the essential reason of Finsler geometry has been unable to enter the mainstream of differential geometry, it no beautiful properties really worth geometers to struggle, also do not have what big application value. Later K- exhibition space, Cartan space will not become mainstream, although they are the extension of Riemannnian geometry, but did not get what the big development.In fact, sometimes the promotion of things to get new content is not much, differential geometry is the same, not the object of study, the more ordinary the better, but should be appropriate to the special good. For example, in Riemann manifold, homogeneous Riemann manifold is more special, beautiful nature, homogeneous Riemann manifolds, symmetric Riemann manifold is more special, so nature more beautiful. This is from the analysis of manifold Lie group action angle.From the point of view of metric, the complex structure is given on the even dimensional Riemann manifold, and the complexmanifold is very elegant. Near complex manifolds are complex manifolds only when the near complex structure is integrable. The complex manifold must be orientable, because it is easy to find that its Jacobian must be nonnegative, whereas the real manifold does not have this property in general. To narrow the scope of the Kahler manifold has more good properties, all complex Submanifolds of Kahler manifolds are Kahler manifolds, and minimal submanifolds (Wirtinger theorem), the beautiful results captured the hearts of many differential geometry and algebraic geometry, because other more general manifolds do not set up this beautiful results. If the first Chern number of a three-dimensional Kahler manifold is zero, the Calabi-Yau manifold can be obtained, which is a very interesting manifold for theoretical physicists. The manifold of mirrors of Calabi-Yau manifolds is also a common subject of differential geometry in algebraic geometry. The popular Hodge structure is a subject of endless appeal.Differential geometry, an endless topic. Just as algebraic geometry requires double - rational equivalence as a luxury, differential geometry requires isometric transformations to be difficult. Taxonomy is an eternal subject of mathematics. In group theory, there are single group classification, multi complex function theory, regional classification, algebraic geometry in the classification of algebraic clusters, differential geometry is also classified.The hard question has led to a dash of young geometry and old scholars, and the prospect of differential geometry is very bright.。
基因间距离
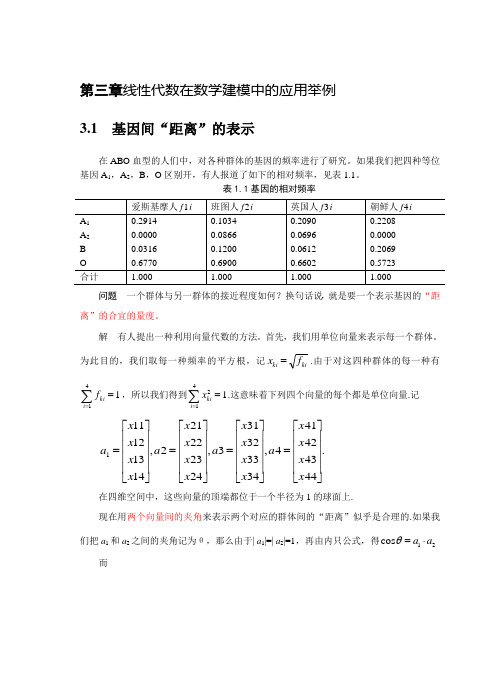
第三章线性代数在数学建模中的应用举例 3.1 基因间“距离”的表示在ABO 血型的人们中,对各种群体的基因的频率进行了研究。
如果我们把四种等位基因A 1,A 2,B ,O 区别开,有人报道了如下的相对频率,见表1.1。
表1.1基因的相对频率 爱斯基摩人f 1i 班图人f 2i 英国人f 3i 朝鲜人f 4i A 1 0.2914 0.1034 0.2090 0.2208 A 2 0.0000 0.0866 0.0696 0.0000 B 0.0316 0.1200 0.0612 0.2069 O 0.6770 0.6900 0.6602 0.5723 合计1.0001.0001.0001.000问题 一个群体与另一群体的接近程度如何?换句话说,就是要一个表示基因的“距离”的合宜的量度。
解 有人提出一种利用向量代数的方法。
首先,我们用单位向量来表示每一个群体。
为此目的,我们取每一种频率的平方根,记ki ki f x =.由于对这四种群体的每一种有141=∑=i kif,所以我们得到∑==4121i ki x .这意味着下列四个向量的每个都是单位向量.记.444342414,343332313,242322212,141312111⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=x x x x a x x x x a x x x x a x x x x a 在四维空间中,这些向量的顶端都位于一个半径为1的球面上.现在用两个向量间的夹角来表示两个对应的群体间的“距离”似乎是合理的.如果我们把a 1和a 2之间的夹角记为θ,那么由于| a 1|=| a 2|=1,再由内只公式,得21cos a a ⋅=θ而.8307.03464.02943.03216.0,8228.01778.00000.05398.021⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=a a 故 9187.0cos 21=⋅=a a θ 得 2.23=θ°. 按同样的方式,我们可以得到表1.2.表1.2基因间的“距离”爱斯基摩人 班图人 英国人 朝鲜人 爱斯基摩人0° 23.2° 16.4° 16.8° 班图人 23.2° 0° 9.8° 20.4° 英国人 16.4° 9.8° 0° 19.6° 朝鲜人16.8°20.4°19.6°0°由表 1.2可见,最小的基因“距离”是班图人和英国人之间的“距离”,而爱斯基摩人和班图人之间的基因“距离”最大.3.9样品间相似程度的刻化问题有甲、乙、丙三名男生,他们的身高、胸围和体重的数据见下表。
MSEA
Author's personal copy
Materials Science and Engineering A 527 (2010) 3245–3252
Contents lists available at ScienceDirect
Materials Science and Engineering A
ห้องสมุดไป่ตู้
scanning electronic microscopy (SEM). The fracture behaviors of the basalt fibers were analyzed from these fractographs. Based on the filament tows model and the statistical theory of fiber strength, a single Weibull statistical model was employed to describe the strength distribution of the basalt filament tows, and the Weibull parameters were obtained by the filament tows testing method. Consistency between the simulated and experimental results indicates that the model and the method are valid and reliable. 2. Experimental 2.1. Basalt fibers The basalt filament tows (as shown in Fig. 1) were manufactured by Hengdian Group Shanghai Russia & Gold Basalt Fiber Co. Ltd. in China. The fineness of the basalt filament tows is 2400tex/21800f (provided by the manufacturer). The diameter of monofilamanet is 7 m. The volume density is 2.6 g/cm3 . The photograph of the bobbin of basalt filament tows is show in Fig. 1. 2.2. Testing The quasi-static tensile tests (with the strain rate of 0.001 s−1 ) and high strain rate tensile tests (impact tensile tests) were performed on a MTS 810.23 materials tester system and a self-designed split Hopkinson tension bar (SHTB) apparatus (as shown in Fig. 2) [12], respectively. The basalt fiber tows were connected with the
第2章 夸克与轻子 (2)
第二章夸克与轻子Quarks and leptons2.1 粒子园The particle zoo学习目标Learning objectives:我们怎样发现新粒子?能否预言新粒子?什么是奇异粒子?大纲参考:3.1.1 ̄太空入侵者宇宙射线是由包括太阳在内的恒星发射而在宇宙空间传播的高能粒子。
如果宇宙射线粒子进入地球大气层,就会产生寿命短暂的新粒子和反粒子以及光子。
所以,就有“太空入侵者”这种戏称。
发现宇宙射线之初,大多数物理学家都认为这种射线不是来自太空,而是来自地球本身的放射性物质。
当时物理学家兼业余气球旅行者维克托·赫斯(Victor Hess)就发现,在5000m高空处宇宙射线的离子效应要比地面显著得多,从而证明这种理论无法成立。
经过进一步研究,表明大多数宇宙射线都是高速运动的质子或较小原子核。
这类粒子与大气中气体原子发生碰撞,产生粒子和反粒子簇射,数量之大在地面都能探测到。
通过云室和其他探测仪,人类发现了寿命短暂的新粒子与其反粒子。
μ介子(muon)或“重电子”(符号μ)。
这是一种带负电的粒子,静止质量是电子的200多倍。
π介子(pion)。
这可以是一种带正电的粒子(π+)、带负电的粒子(π-)或中性不带电粒子(π0),静止质量大于μ介子但小于质子。
K介子(kaon)。
这可以是一种带正电的粒子(K+)、带负电的粒子(K-)或中性不带电粒子(K0),静止质量大于π介子但小于质子。
科学探索How Science Works不同寻常的预言An unusual prediction在发现上述三种粒子之前,日本物理学家汤川秀树(Hideki Yukawa)就预言,核子间的强核力存在交换粒子。
他认为交换粒子的作用范围不超过10-15m,并推断其质量在电子与质子之间。
由于这种离子的质量介于电子与质子之间,所以汤川就将这种粒子称为“介子”(mesons)。
一年后,卡尔·安德森拍摄的云室照片显示一条异常轨迹可能就是这类粒子所产生。
庞加莱猜想前言
庞加莱猜想-前言Wir m\"ussen wissen! Wir werden wissen!(我们必须知道!我们必将知道!)—— David Hilbert两年前科学版举行过一次版聚,我报告了低维拓扑里面的一些问题和进展,其中有一半篇幅是关于Poincar\'e 猜想。
版聚后,flyleaf 要求大家回去后把自己所讲的内容发在版上。
当时我甚至已经开始写了一两段,但后来又搁置了。
主要是因为自己对于低维拓扑还是一个门外汉,写出来的东西难免有疏漏之处,不敢妄下笔。
两年过去,我对低维拓扑这门学科的了解比原先多了,说话的底气也就比原先足了。
另外,由于Clay 研究所的百万巨赏,近年来Poincar\'e 猜想频频在媒体上曝光;而且Perelman 最近的工作使数学家们有理由相信我们已经充分接近于这一猜想的最后解决。
所以大概会有很多人对Poincar\'e 猜想的来龙去脉感兴趣,我也好借机一偿两年来的宿愿。
现代科学的高速发展使各学科之间的鸿沟加大,不同学科之间难以互相理解,所以非数学专业的读者在阅读本文时可能会遇到一些困难。
但限于篇幅和文章的形式,我也不可能对很多东西详细解释。
一些最基本的拓扑概念如“流形”,我将在本文的附录中解释。
还有一些“同调群”、“基本群”之类的名词,读者见到时大可不去理会它们的确切含义。
我将尽量避免使用这一类的专业术语。
作者并非拓扑方面的专家,对下面要说的很多内容都是道听途说,只知其然而不知其所以然;作者更不善于写作,写出来的东东总会枯燥无味,难登大雅之堂。
凡此种种,还请读者诸君海涵。
问题的由来Consid\'erons maintenant une vari\'et\'e [ferm\'ee] $V$ \`a trois dimensions ... Est-il possible que le groupe fondamental de $V$ ser\'eduise \`a la substitution identique, et que pourtant $V$ ne soit pas simplement connexe?—— Henri Poincar\'e在拓扑学家的眼里,篮球、排球和乒乓球并没有什么不同,它们都同胚于三维空间中的球面S^2. (我们把n+1维欧氏空间中到原点距离为1的点的集合记作S^n,称为n维球面(sphere)。
西工大偏微分方程数学物理方程讲义姜礼尚等人(第三版)课后习题解答
x x
ES u x
x
ESu x x
u xx 0
菜没油
3
4.解: 上端固定说明 u 0, t 0 ,下端悬有质量为 P 的重物可得
Eux l , t pg / s ,即有边界条件
u 0, t 0 p ux l , t E
30.边界条件:u 0, t u l , t 0 弦线两端固定
2.解: 由动量定理及已知条件
x2
x1
ut x, t2 ut x, t1 dx
t2 t1
x2
x1
f x, t dxdt T
t2
t1
u x , t u x, t dt
泛定方程: t a x 0 又有初始条件: x, 0 0 x 0 边界条件: t 0, t A 1 sin t t 0
11.解: 设 A a, , B b, ,连接 A 和 B 的短程线方程为 y f x 则 A, B 距离为 d f
问题2 问题3:
由 Gauss 公式得
菜没油
8
uv uv fv dx+ x uv g v ds u = v ds v udx uv fvdx x uv gv ds n
取 x 0 ,即得在点 x 处,相对伸长为 u x x, t . 由胡克定理,张力 T x, t Eu x x, t 此外容易得知圆锥在 x 点处的截面面积存在函数:
hx x S x r x R R 2 1 h h
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
arXiv:cond-mat/0112482v1 [cond-mat.stat-mech] 28 Dec 2001Euler–Poincar´eCharacteristicandPhaseTransitioninthePottsModel
PhilippeBlanchard1,SantoFortunato2andDanielGandolfo1,3,4
Abstract:Recentresultsconcerningthetopologicalpropertiesofrandomgeomet-ricalsetshavebeensuccessfullyappliedtothestudyofthemorphologyofclustersinpercolationtheory.Thisapproachprovidesanalternativewayofinspectingthecriticalbehaviourofrandomsystemsinstatisticalmechanics.
Forthe2dq-statesPottsmodelwithq≤6,intensiveandaccuratenumericsindi-catesthattheaverageoftheEulercharacteristic(takenwithrespecttotheFortuin-Kasteleynrandomclustermeasure)isanorderparameterofthephasetransition.
Keywords:ClusterMorphology,Euler-Poincar´echaracteristic,PhaseTransition.
1IntroductionRecently,newinsightsinthestudyofthecriticalpropertiesofclustersinperco-lationtheoryhaveemergedbasedonideascomingfrommathematicalmorphology[Se]andintegralgeometry[Ha,S,Sch].Thesemathematicaltheoriesprovideasetofgeometricalandtopologicalmeasuresallowingtoquantifythemorphologicalpropertiesofrandomsystems.Inparticularthesetoolshavebeenappliedtothestudyofrandomclusterconfigurationsinpercolationtheoryandstatisticalphysics[MW,O,J,Wa1,M1].
OneofthesemeasuresistheEuler-Poincar´echaracteristicχwhichisawellknowndescriptorofthetopologicalfeaturesofgeometricpatterns.ItbelongstothefinitesetofMinkowskifunctionalswhoseoriginliesinthemathematicalstudyofconvexbodiesandintegralgeometry(see[Ha,S,Sch]).Thesemeasures,aswe2shallexplainbelow,sharethefollowingremarkableproperty:anyhomogeneous,additive,isometry-invariantandconditionallycontinuousfunctionalonacompactsubsetoftheEuclideanspaceRdcanbeexpressedasalinearcombinationoftheMinkowskifunctionals.ThisisthewellknownHadwiger’stheorem[Ha]ofintegralgeometrywhichhasawidescopeofapplicationsinmathematicalphysicsdueitsrathergeneralsettings.Theuseofthesemeasuresinimageanalysis[Gra],problemsofshaperecognition[Se],determinationofthelargescalestructuresoftheuniverse[Wa2],modellingofporousmedia[AKPM],microemulsions[HK]andfractalanalysis[M2]hasbeenatopicofgrowinginterestrecently.
Theapplicationofthesedescriptiontoolsforthestudyofrandomsystemsinstatisticalmechanicshasalreadyprovidedinterestingresults.In[MW,O],thecomputationoftheEuler-Poincar´echaracteristicχforasystemofpenetrabledisksinseveralmodelsofcontinuumpercolationhasledtoconjecturenewboundsforthecriticalvalueofthecontinuumpercolationdensity.In[MW],anexactcalculationofχhasshownthatacloserelationexistsbetweenthezerooftheEuler-Poincar´echaracteristicandthecriticalthresholdforcontinuumpercolationindimensions2and3.
Ofsimilarinterestinthesamedomain,letusrecallthatfortheproblemofbondpercolationonregularlattices,SykesandEssam[SyEs]wereabletoshow,usingstandardplanardualityarguments,thatforthecaseofself-dualmatchinglattices(e.g.Z2),themeanvalueoftheEuler-Poincar´echaracteristicchangessignatthecriticalpoint(thisevenledthemtoannounceaprooffortheexistenceofthecriticalprobabilityofbondpercolationonZ2),seealso[Gri].
Morerecently,Wagner[Wa1]wasabletocomputetheEuler-Poincar´echarac-teristiconthesetofallplaneregularmosaics(the11archimedeanlattices)asafunctionofthesiteoccupancyprobabilityp∈[0,1]]andshowedthataclosecon-nectionexistsbetweenthethresholdforsitepercolationontheselatticesandthepointwheretheEuler-Poincar´echaracteristic(expressedasafunctionofp)changessign.
Theaimofthisarticleistofurtherinvestigatetheroleplayedbythismor-phologicalindicatorinstatisticalphysicsandtopresentnewresultsconcerningitsbehaviourinthecaseofthe2-dimensionalPottsmodel.Namelywepresenthereclearevidence,basedonMonteCarlosimulations,thatforthe2dPottsmodel,theEuler-Poincar´echaracteristicisanorderparameterofthephasetransition.Namelywefindthatforq=2,...,4itchangessigncontinuouslyatthetransitionpointwhile,forq=5,6ithasafirstordertransitionatthecriticalpoint.Asfarasweknow,thisisthefirstexampleofadiscontinuousbehaviourofthisparameterinaphysicalmodel.Thepaperisorganizedasfollows.InSection2weintroduceaminimalback-
