函数的基本性质ppt(1) 下载
合集下载
人教版高中数学必修1(A版) 1.3.1 函数的基本性质-单调性与最值 PPT课件

回到目录
课后思考:函数y=f(x)在区间D上具有 单调性,那么在区间D的子区间(即区 间D的子集)上是否具有相同的单调 性?
回到目录
回到目录
二、自主学习
自学辅导教材50页§1.3.1 时间20分钟 (完成所有探究与练习) 集中全部精力!提升自学能力!
回到目录
三、教师点拨 y
yx
2
f (x1 )
x1
O
x
回到目录
三、教师点拨 y
yx
2
f (x1 )
x1 O
x
回到目录
三、教师点拨 y
yx
2
f (x1 )
x1 O
x
回到目录
yx
2
f (x1 )
O
x1
x
函数f(x)=x2在区间[0,+∞)上,随着x的增大,相应 的f(x)值也随着增大 在区间(-∞,0)上,随着x的增大,相应的f(x) 值反而随着减小.
回到目录
三、教师点拨
如何利用函数解析式y=f(x)描述 “随着x的增大,相应的f(x)随着 减小”,“随着x的增大,相应的f (x)也随着增大”?
标题
§1.3.1函数的基本性质—单调性
§1.3.1函数的基本性质——单调性
一、问题情景 二、自主学习 三、教师点拨 四、课堂小结
本课结束
一、问题情景
大家是否记得这样精彩的瞬间:烟花在绽放 的刹那、高台跳水运动员纵身起跳至入水的 一瞬、陨星划过长空坠落的时刻,上述场景 多么美丽壮观啊!让我们闭上眼睛想一想: 烟花绽放后的轨迹、运动员跳入水中的过程 的身影、陨星坠落的弧线,这些曲线有的上 升、有的下降,这与我们研究的函数的单调 性有关.
自变量的值x x2 , 当x1 x 2时,都有f x1 f x2 1,
课后思考:函数y=f(x)在区间D上具有 单调性,那么在区间D的子区间(即区 间D的子集)上是否具有相同的单调 性?
回到目录
回到目录
二、自主学习
自学辅导教材50页§1.3.1 时间20分钟 (完成所有探究与练习) 集中全部精力!提升自学能力!
回到目录
三、教师点拨 y
yx
2
f (x1 )
x1
O
x
回到目录
三、教师点拨 y
yx
2
f (x1 )
x1 O
x
回到目录
三、教师点拨 y
yx
2
f (x1 )
x1 O
x
回到目录
yx
2
f (x1 )
O
x1
x
函数f(x)=x2在区间[0,+∞)上,随着x的增大,相应 的f(x)值也随着增大 在区间(-∞,0)上,随着x的增大,相应的f(x) 值反而随着减小.
回到目录
三、教师点拨
如何利用函数解析式y=f(x)描述 “随着x的增大,相应的f(x)随着 减小”,“随着x的增大,相应的f (x)也随着增大”?
标题
§1.3.1函数的基本性质—单调性
§1.3.1函数的基本性质——单调性
一、问题情景 二、自主学习 三、教师点拨 四、课堂小结
本课结束
一、问题情景
大家是否记得这样精彩的瞬间:烟花在绽放 的刹那、高台跳水运动员纵身起跳至入水的 一瞬、陨星划过长空坠落的时刻,上述场景 多么美丽壮观啊!让我们闭上眼睛想一想: 烟花绽放后的轨迹、运动员跳入水中的过程 的身影、陨星坠落的弧线,这些曲线有的上 升、有的下降,这与我们研究的函数的单调 性有关.
自变量的值x x2 , 当x1 x 2时,都有f x1 f x2 1,
1.3函数的基本性质——奇偶性1课件人教新课标

(是偶函数)
练习
3. 如图⑴,给出了奇函数y=f (x)的局部
图象,求f (-4).
y
y
2
2
O⑴
4 x – 3 –1 O ⑵ x
4. 如图⑵,给出了偶函数y=f (x)的局部 图象,试比较f (1)与 f (3) 的大小.
《习案》P.168第3题
例1 已知函数f (x)是偶函数,而且 在(0,+∞)上是减函数,判断f (x) 在(-∞,0)上是增函数还是减函数, 并证明你的判断.
例2 (1)设f (x)是偶函数,g (x)是奇函数,
且 f ( x) g( x) 1 ,求函数f (x),g(x) x1
的解析式;
(2)设函数f (x)是定义在(-∞, 0)∪(0,+∞)
上的奇函数,又f (x)在(0, +∞)上是减函 数,且f (x)<0,试判断函数 F ( x) 1
f (x)
在(-∞,0)上的单调性,并给出证明.
课堂小结
1. 奇函数、偶函数的定义; 2. 奇函数、偶函数图象的对称性; 3. 判断函数奇偶性的步骤和方法.
课后作业
1.阅读教材P.33-P.36; 2.《学案》双基训练P.37-P.38.
1.3 函数的基本性质 ——奇偶性
练习 1. 如果f (0)=a≠0,函数f (x)可以是奇函 数吗?可以是偶函数吗?为什么?
2. 如果函数f (x)、g (x)为定义域相同的 偶函数,试问F (x)=f (x)+g (x)是不是 偶函数?是不是奇函数?为什么?
练习 1. 如果f (0)=a≠0,函数f (x)ቤተ መጻሕፍቲ ባይዱ以是奇函 数吗?可以是偶函数吗?为什么?
(不能为奇函数但可以是偶函数)
2. 如果函数f (x)、g (x)为定义域相同的 偶函数,试问F (x)=f (x)+g (x)是不是 偶函数?是不是奇函数?为什么?
练习
3. 如图⑴,给出了奇函数y=f (x)的局部
图象,求f (-4).
y
y
2
2
O⑴
4 x – 3 –1 O ⑵ x
4. 如图⑵,给出了偶函数y=f (x)的局部 图象,试比较f (1)与 f (3) 的大小.
《习案》P.168第3题
例1 已知函数f (x)是偶函数,而且 在(0,+∞)上是减函数,判断f (x) 在(-∞,0)上是增函数还是减函数, 并证明你的判断.
例2 (1)设f (x)是偶函数,g (x)是奇函数,
且 f ( x) g( x) 1 ,求函数f (x),g(x) x1
的解析式;
(2)设函数f (x)是定义在(-∞, 0)∪(0,+∞)
上的奇函数,又f (x)在(0, +∞)上是减函 数,且f (x)<0,试判断函数 F ( x) 1
f (x)
在(-∞,0)上的单调性,并给出证明.
课堂小结
1. 奇函数、偶函数的定义; 2. 奇函数、偶函数图象的对称性; 3. 判断函数奇偶性的步骤和方法.
课后作业
1.阅读教材P.33-P.36; 2.《学案》双基训练P.37-P.38.
1.3 函数的基本性质 ——奇偶性
练习 1. 如果f (0)=a≠0,函数f (x)可以是奇函 数吗?可以是偶函数吗?为什么?
2. 如果函数f (x)、g (x)为定义域相同的 偶函数,试问F (x)=f (x)+g (x)是不是 偶函数?是不是奇函数?为什么?
练习 1. 如果f (0)=a≠0,函数f (x)ቤተ መጻሕፍቲ ባይዱ以是奇函 数吗?可以是偶函数吗?为什么?
(不能为奇函数但可以是偶函数)
2. 如果函数f (x)、g (x)为定义域相同的 偶函数,试问F (x)=f (x)+g (x)是不是 偶函数?是不是奇函数?为什么?
函数的基本性质 复习课件.ppt

优秀课件
29
规律方法总结
(3)①若f(x)是偶函数,则f(x)= f(|x|),反之亦真.
②若f(x)为奇函数,且0在定义域 内,则f(0)=0.
③若f(x)=0且f(x)的定义域关于 原点对称,则f(x)既是奇函数又是偶 函数.
优秀课件
30
(2)作差:即f(x2)-f(x1)(或f(x1)- f(x2)),并通过通分、配方、因式分解 等方法,向有利于判断差的符号的方 向变形.
优秀课件
18
课堂互动讲练
(3)定号:根据给定的区间和x2- x1的符号,确定差f(x2)-f(x1)(或f(x1) -f(x2))的符号.当符号不确定时,可 以进行分类讨论.
优秀课件
27
规律方法总结
2.理解函数的奇偶性应注意的问题 (1)定义域在数轴上关于原点对称是 函数f(x)为奇函数或偶函数的必要但不充 分条件.f(-x)=-f(x)或f(-x)=f(x)是定 义域上的恒等式.
优秀课件
28
规律方法总结
(2)奇偶函数的定义是判断函数奇偶性 的主要依据.为了便于判断函数的奇偶性 有时需要先将函数进行化简,或应用定义 的等价形式:f(-x)=±f(x)⇔f(-x)∓f(x)= 0⇔f(f-(xx) )=±1(f(x)≠0).
13
三基能力强化
3.(教材习题改编)函数f(x)=x2- 2x,x∈[a2+1,4]的最大值为________.
答案:8
优秀课件
14
课堂互动讲练
考点一 函数单调性的判断与证明
函数的单调性用以揭示随着自 变量的增大,函数值的增大与减小 的规律.在定义区间上任取x1、x2, 且x1<x2的条件下,判断或证明 f(x1)<f(x2)或f(x1)>f(x2),这一过程 就是实施不等式的变换过程.
函数的基本性质.ppt

数x总有f(-x)=f(x),且f(x)在区间(-∞,-1]上是增
函数,则( )
A.
f(
3) 2
<f(-1)<f(2)
B.f(-1)< f( 3)<f(2)
2 C.f(2)<f(-1)<
f(
3) 2
D.f(2)< f( 3) <f(-1)
2
2020-11-16
xx
9
【解析】选D.由f(-x)=f(x)可知f(2)=f(-2),而f(x)
2020-11-16
xx
12
类型二:利用奇偶性、单调性求最值 【典例2】(1)设f(x)在[-2,-1]上为减函数,最小值 为3,且f(x)为偶函数,则f(x)在[1,2]上 ( ) A.为减函数,最大值为3 B.为减函数,最小值为-3 C.为增函数,最大值为-3 D.为增函数,最小值为3
2020-11-16
函数的基本性质
2020-11-16
xx
1
学习目标 1.会用函数的单调性、奇偶性求最值; 2.能运用函数的单调性和奇偶性比较大小,解不等式等问题; 重难点 1.能运用函数的单调性、奇偶性求最值; 2.单调性、奇偶性的灵活运用; 学法指导 1.系统总结函数的重要性质,结合例题明确性质间的相互联系及在解决问题中的作用; 2.进一步提升分析问题、解决问题的能力。
2020-11-16
xx
2
类型一:利用奇偶性、单调性比较大小 【典例1】(1)函数f(x)是定义在R上的偶函数,当x≥0 时,f(x)单调递减.则下列各式成立的是 ( ) A.f(1)<f(-3) B.f(3)>f(2) C.f(-2)>f(3) D.f(2)>f(0)
函数的基本性质PPT精品课件

2021/7/31
基础知识梳理
(2)单调区间的定义 具 的减单有函若调(数严函区,格间数则的.f称()x单)函在调数区性f间(,x)D在区上这间是一D增叫区函做间数f上(x或)
2021/7/31
基础知识梳理
1.单调区间与函数定义域有 何关系?
【思考·提示】 单调区间 是定义域的子区间.
2021/7/31
x2
x1 x2
因为x1<x2<0,所以x1x2>0,x2-x1>0,所
以
x2-x1 x1 x2
>0,即f(x2)-f(x1)>0,
所以f(x2)>f(x1).
故f(x)在(-∞,0)上是单调增函数.
2021/7/31
课堂互动讲练
【规律小结】 用定义证明函数 单调性的一般步骤:
(1)取值:即设x1,x2是该区间内 的任意两个值,且x1<x2.
二、减函数
y
f(x1)
f(x2)
0 x1
x2
设函数f(x)的定义域为I:
如果对于属于定义域I内某
个区间上的任意两个自变量
的值x1,x2, 当x1<x2时,都有
x
f(x1)> f(x2),那么就说f(x)在 这个区间上是减函数
三、单调性与单调区间
如果函数y=f(x)在某个区间是增函数或减函数, 那么就说函数y=f(x)在这个区间具有(严格的)单调性, 这一区间叫做y=f(x)的单调区间.
(4)判断:根据定义得出结论.
2021/7/31
课堂互动讲练
练习:证明函数 f (x) = x 1 , x ,1
数
x
是增函
2021/7/31
课堂互动讲练
考点二 函数奇偶性的判定
判断函数的奇偶性,应该首先 分析函数的定义域,在分析时,不 要把函数化简,而要根据原来的结 构去求解定义域,如果定义域不关 于原点对称,则一定是非奇非偶函 数.
基础知识梳理
(2)单调区间的定义 具 的减单有函若调(数严函区,格间数则的.f称()x单)函在调数区性f间(,x)D在区上这间是一D增叫区函做间数f上(x或)
2021/7/31
基础知识梳理
1.单调区间与函数定义域有 何关系?
【思考·提示】 单调区间 是定义域的子区间.
2021/7/31
x2
x1 x2
因为x1<x2<0,所以x1x2>0,x2-x1>0,所
以
x2-x1 x1 x2
>0,即f(x2)-f(x1)>0,
所以f(x2)>f(x1).
故f(x)在(-∞,0)上是单调增函数.
2021/7/31
课堂互动讲练
【规律小结】 用定义证明函数 单调性的一般步骤:
(1)取值:即设x1,x2是该区间内 的任意两个值,且x1<x2.
二、减函数
y
f(x1)
f(x2)
0 x1
x2
设函数f(x)的定义域为I:
如果对于属于定义域I内某
个区间上的任意两个自变量
的值x1,x2, 当x1<x2时,都有
x
f(x1)> f(x2),那么就说f(x)在 这个区间上是减函数
三、单调性与单调区间
如果函数y=f(x)在某个区间是增函数或减函数, 那么就说函数y=f(x)在这个区间具有(严格的)单调性, 这一区间叫做y=f(x)的单调区间.
(4)判断:根据定义得出结论.
2021/7/31
课堂互动讲练
练习:证明函数 f (x) = x 1 , x ,1
数
x
是增函
2021/7/31
课堂互动讲练
考点二 函数奇偶性的判定
判断函数的奇偶性,应该首先 分析函数的定义域,在分析时,不 要把函数化简,而要根据原来的结 构去求解定义域,如果定义域不关 于原点对称,则一定是非奇非偶函 数.
高中数学1.3函数的基本性质知识框架素材新人教必修1.ppt
函数
函数及其表示
函数的基本性质
函数图象的画法
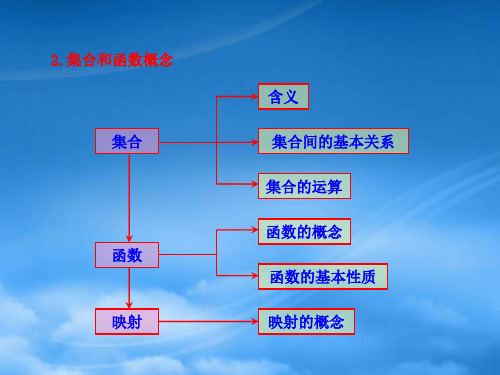
Hale Waihona Puke 2.集合和函数概念 集合
函数 映射
含义 集合间的基本关系 集合的运算 函数的概念 函数的基本性质 映射的概念
3.函数框架图 一次函数
函数 图象与性质
二次函数
定义域
值域
单调性
奇偶性
待定系数法确定解析式
4.函数及其基本性质
函数定义:设A,B是非空的数集,如果按某种确定的 对应关系f,使对于集合A中的任意一个元素x,在集 合B中都有唯一确定的元素f(x)与之对应,那么就 称对应f:A→B为从集合A到集合B的一个函数
函数的基本性质PPT教学课件
2021/9/18
多媒体课件
11
向 日 葵
凡·高《包 扎着耳朵 的自画像》
从照镜子开始
从照镜子开始
镜 子 改 变 了 什 么
1、客厅中的餐桌在小明的什么方向?
2、小明举起的是哪只手?
3、哪些数字在镜子中的像与 原来的数字完全一样?
4、将纸条在桌面上旋转90度,哪些 数字在镜子中的像与原来的数字完全 一样?如果小明举起纸条正对镜面呢?
28
你能根 据镜子 中的像 说出小 华左、 右腿的 前后位 置吗?
你能根 据镜子 中的像 说出小 华左、 右腿的 前后位 置吗?
小明放假去外地看爷爷,他买的 是11点的火车,由于去的早,小明 不小心睡着了,等他醒来的时候, 他从镜子中看到背面墙上的电子钟 上显示 : ,他吓了一身汗,认 为自己错过了火车,同学们,小明 到底能不能赶上11点的火车呢?
例2 (1)设f (x)是偶函数,g (x)是奇函数,
且 f ( x) g( x) 1 ,求函数f (x),g(x) x1
的解析式;
(2)设函数f (x)是定义在(-∞, 0)∪(0,+∞)
上的奇函数,又f (x)在(0, +∞)上是减函 数,且f (x)<0,试判断函数 F ( x) 1
f (x)
(不能为奇函数但可以是偶函数)
2. 如果函数f (x)、g (x)为定义域相同的 偶函数,试问F (x)=f (x)+g (x)是不是 偶函数?是不是奇函数?为什么?
练习 1. 如果f (0)=a≠0,函数f (x)可以是奇函 数吗?可以是偶函数吗?为什么?
(不能为奇函数但可以是偶函数)
2. 如果函数f (x)、g (x)为定义域相同的 偶函数,试问F (x)=f (x)+g (x)是不是 偶函数?是不是奇函数?为什么?
高三第一轮复习《函数的基本性质》市公开课一等奖省赛课获奖PPT课件
返回
第30页
返回
第31页
考点 六
返回
第32页
返回
第33页
返回
第34页
返回
第35页
真题再现
返回
第36页
返回
第37页
返回
第38页
返回
第39页
误区警示
返回
第40页
规律探究
返回
第41页
返回
第42页
返回
第43页
即时巩固
返回
第44页
返回
第45页
返回
第46页
返回
第47页
返回
第48页
返回
第70页
第71页
第10页
返回
第11页
返回
第12页
返回
第13页
考点 二
返回
第14页
返回
第15页
返回
第16页
返回
第17页
返回
第18页
考点 三
返回
第19页
返回
第20页
返回
第21页
返回
第22页
考点 四
返回
第23页
返回
第24页
返回
第25页
考点 五
返回
第26页
返回
第27页
返回
第28页
返回
第29页
学案3 函数性质
第1页
考点 六 考点 五 考点 四 考点 三 考点 二 考点 一
考纲解读 考向预测 课前热身
考点突破
即时巩固 课后拔高
真题再现 误区警示 规律探究
第2页
考纲解读
返回
第3页
考向预测
返回
函数的基本性质PPT精品课件
k p= V 例2:物理学中的玻意耳定律
(k为正常数) 告诉我们,对于一定量的气体,当其体积V减小时, 压强p将增大。试用函数的单调性证明之。 分析:按题意,只要证明函数在区间上是减函数 即可。
点此播放讲课视频
1 探究: y= 画出反比例函数 x 的图象。 (1)这个函数的定义域I是什么? (2)它在定义域I上的单调性是怎样的?证明 你的结论。
例2.将进货单价40元的商品按50元一个售 出时,能卖出500个,若此商品每个涨价1 元,其销售量减少10个,为了赚到最大利 润,售价应定为多少? 解:设利润为 x 元,每个售价为 x 元,则 每个涨( x -50)元,从而销售量减少 10( x 50)个, 共售出500-10(x-50)=100-10x(个) 2 ∴ y=(x-40)(1000-10x) =-10(x-70) 9000 (50 x<100) ∴ x = 70时 ymax = 9000 ∴答:为了赚取最大利润,售价应定为70 元.
考点二 函数奇偶性的判定
判断函数的奇偶性,应该首先 分析函数的定义域,在分析时,不 要把函数化简,而要根据原来的结 构去求解定义域,如果定义域不关 于原点对称,则一定是非奇非偶函 数.
课堂互动讲练
例2 判断下列各函数的奇偶性: 1 2 (1)f(x)=lgx +lg 2; x 1+x (2)f(x)=(x-1) ; 1-x x2+x,x<0 (3)f(x)= 2 - x +x,x>0; lg(1-x2) (4)f(x)= . |x-2|-2
基础知识梳理
3.奇偶函数的定义域有何特点? 【思考·提示】 若函数f(x)具 有奇偶性,则f(x)的定义域关于原点 对称.反之,若函数的定义域不关于 原点对称,则该函数无奇偶性.
人教版高中数学函数的基本性质精品PPT推荐1
在已知函数的单调性,求参数的范围时, 要注意利用数形结合、分类讨论的数学思想.
人教版高中数学函数的基本性质精品P PT推荐 1【PPT 教研课 件】
人教版高中数学函数的基本性质精品P PT推荐 1【PPT 教研课 件】
思考
1.已知函数 f ( x) x2 2(a 1)x 2 在区间 (, 3] 上是为减函数,求 实 数 a的取值范围。
人教版高中数学函数的基本性质精品P PT推荐 1【PPT 教研课 件】
人教版高中数学函数的基本性质精品P PT推荐 1【PPT 教研课 件】
知识回顾:
❖ 1. 【回顾】 函数单调性的定义
增函数
减函数
定义
一般地,设函数f(x)的定义域为I.如果对于定义域I内某个区间
D上的任意两个自变量x1,x2,
当x1<x2时,都有 f(x1)<f(x2), 当x1<x2时,有 f(x1)>f(x2) , 那么就说函数f(x)在区间D上 那么就说函数f(x)在区间D上是
人教版高中数学函数的基本性质精品P PT推荐 1【PPT 教研课 件】
作业:辅导训练100页到102页
1.
讨论f
(x)
ax , x2 1
(a
0)
学习重点、难点
1.会分类讨论含有参数的函数的单调性; 2.学生对函数的单调性和单调区间的正确理解。
人教版高中数学函数的基本性质精品P PT推荐 1【PPT 教研课 件】
人教版高中数学函数的基本性质精品P PT推荐 1【PPT 教研课 件】
引入:
《望庐山瀑布》……飞流直下三千尺,疑是银河落九天。这是出自 于著名唐代诗人李白的一首诗。如果把瀑布的轨迹可以看成一段函 数的图像,诗中的这个“三千尺”是否是函数在单调减区间上的区间 长度?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在[4,14]上任取两个值t1,t2,只要t1<t2 ,就有θ1<θ2,就可以说在区间[4,14]上,θ 随t的增大而增大.
在[4,14]上内任取两个值t1,t2,只要t1<t2 ,就有θ1<θ2,就可以说在区间[4,14]上,θ随t 的增大而增大.
问题:
设函数y=f(x)的定义域为A,区间IA, 在区间I上,y随x的增大而增大,该如何用 数学符号语言来刻画呢?
增。大
3、分别指出图(1)、图(2)中,当x ∈[0,+∞) 和x∈(-∞,0)时,函数图象是上升的还是 下降的? 4、通过前面的讨论,你发现了什么?
结论:若一个函数在某个区间内图象是上升的, 则函数值y随x的增大而增大,反之亦真;
若一个函数在某个区间内图象是下降的, 则函数值y随x的增大而减小,反之亦真。
在[4,14]上,取几个不同的输入值,例如 θ
t1=5,t2=6,t3 =8,t4=10,得到相对应的
输出值θ1,θ2,θ3,θ4.在t1<t2<t3<t4时,有
θ1<θ2<θ3<θ4,所以在[4,14]上,θ随t的增 大而增大.
O
t
取区间内n个输入值t1,t2,t3,…, tn, 得到相对应的输出值θ1,θ2,θ3,…,θn,在 t1<t2<t3<…<tn时,有θ1<θ2<θ3<…<θn ,所以在区间[4,14]上,θ随t的增大而增大 .
解:函数y=f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5], 其中y=f(x)在区间[-5,-2),[1,3)上是减函数, 在区间[-2,1),[3,5]上是增函数.
例2:物理学中的玻意耳定律
p= k V
(k为正常数)
告诉我们,对于一定量的气体,当其体积V减小时,
压强p将增大。试用函数的单调性证明之。
分析:按题意,只要证明函数在区间上是减函数 即可。
如果函数y=f(x)在某个区间是增函数或减函数, 那么就说函数y=f(x)在这个区间具有(严格的)单调性, 这一区间叫做y=f(x)的单调区间.
请问: 在单调区间上增函数的图象是___上__升__的___, 减函数的图象是___下__降__的___. (填“上升的”或“下降的”)
想一想 :如何从一个函数的图象来判断这个 函数在定义域内的某个单调区间上是增函数 还是减函数?
(2)任意性:它的取值是在区间上的任意两个自变量, 决不能理解为很多或无穷多个值。
(3)一致性
增函数: 减函数:
xx11
< <
x2 x2
f( x1 ) < f( x2 ) f( x1) > f( x2 )
例1.下图是定义在 闭区间[-5,5]上的函数y=f(x)的图 象,根据图象说出y=f(x)的单调区间,以及在每个单调 区间上, y=f(x)是增函数还是减函数?
如果这个函数在某个单调区间上的图象 是上升的,那么它在这个单调区间上就是增 函数;如果图象是下降的,那么它在这个单 调区间上就是减函数。
1、增函数、减函数的三个特征:
(1)局部性:也就是说它肯定有一个区间。区间可以 是整个定义域,也可以是其真子集,因此,我们说增函 数、减函数时,必须指明它所在的区间。如y=x+1 (X∈Z)不具有单调性
3.已知函数y=f(x)的定义域为[0,+∞),若 对于任意的x2>0,都有f(x2)<f(0),则函数y=f(x) 在区间[0,+∞)上是单调减函数.
y
x2
O
x
f(x2)
一、增函数
y
f(x1)
0
x1
设函数f(x)的定义域为I:
如果对于属于定义域I内某
个区间上的任意两个自变量
f(x2)
的值x1,x2, 当x1<x2时,都有
当x1<x2时,都有f(x1)>f(x2), 那么就说函数y=f(x)在区间I上是单调减函数,
区间I称为函数y=f(x)的单调减区间.
概念辨析
1.函数y=f(x),x ∈[0,3]的图象如图所示.
y
O 123
x
区间[0,3]是该函数的单调增区间吗?
判断
2.对于二次函数f(x)=x2,因为-1,2∈(-∞, +∞),当-1<2时,f(-1)<f(2),所以函数f(x) =x2在区间(-∞,+∞)上是单调增函数.
函数y=f(x)的定义域为A,区间IA,如果 对于区间I内的任意两个值x1,x2,
当x1<x2时,都有f(x1)<f(x2),
那么就说函数y=f(x)在区间I上是单调增函数, 区间I称为函数y=f(x)的单调增区间.
问题: 如何定义单调减函数和单调减区间呢?
函数y=f(x)的定义域为A,区间I A,如 果对于区间I内的任意两个值x1,x2
1、观察这三个图象,你能说出图象的特征吗? 2、随x的增大,y的值有什么变化?
1.3.1 单调性与最大(小)值
请观察函数y=x2与y=x3图象,回答下列问题:
1、当x∈[0,+∞),x增大时,图(1)中的y
值 增大 ;图(2)中的y值
增。大
2、当x∈(-∞,0),x增大时,图(1)中的y
值 减小 ;图(2)中的y值
教学目的
• (1)通过已学过的函数特别是二次函数, 理解函数的单调性及其几何意义;
• (2)学会运用函数图象理解和研究函数的 பைடு நூலகம்质;
• (3)能够熟练应用定义判断数在某区间上 的的单调性.
• 教学重点:函数的单调性及其几何意义. • 教学难点:利用函数的单调性定义判断、
证明函数的单调性.
观察下列各个函数的图象,并说说它们 分别反映了相应函数的哪些变化规律:
观察某城市一天24小时气温变化图.
θ=f (t),t∈[0,24]
问题:如何描述气温θ随时间t的变化情况?
如图,研究函数θ=f(t),t∈[0,24]的图 象在区间[4,14]上的变化情况.
(t2,θ2)
(t1,θ1) t1 t2
问题: 在区间[4,14]上,如何用数学符号语言来刻
画“θ随t的增大而增大”这一特征?
f(x1)< f(x2),那么就说f(x)在
x2 x 这个区间上是增函数
二、减函数
y
f(x1)
f(x2)
0 x1
x2
设函数f(x)的定义域为I:
如果对于属于定义域I内某
个区间上的任意两个自变量
的值x1,x2, 当x1<x2时,都有
x
f(x1)> f(x2),那么就说f(x)在 这个区间上是减函数
三、单调性与单调区间
在[4,14]上内任取两个值t1,t2,只要t1<t2 ,就有θ1<θ2,就可以说在区间[4,14]上,θ随t 的增大而增大.
问题:
设函数y=f(x)的定义域为A,区间IA, 在区间I上,y随x的增大而增大,该如何用 数学符号语言来刻画呢?
增。大
3、分别指出图(1)、图(2)中,当x ∈[0,+∞) 和x∈(-∞,0)时,函数图象是上升的还是 下降的? 4、通过前面的讨论,你发现了什么?
结论:若一个函数在某个区间内图象是上升的, 则函数值y随x的增大而增大,反之亦真;
若一个函数在某个区间内图象是下降的, 则函数值y随x的增大而减小,反之亦真。
在[4,14]上,取几个不同的输入值,例如 θ
t1=5,t2=6,t3 =8,t4=10,得到相对应的
输出值θ1,θ2,θ3,θ4.在t1<t2<t3<t4时,有
θ1<θ2<θ3<θ4,所以在[4,14]上,θ随t的增 大而增大.
O
t
取区间内n个输入值t1,t2,t3,…, tn, 得到相对应的输出值θ1,θ2,θ3,…,θn,在 t1<t2<t3<…<tn时,有θ1<θ2<θ3<…<θn ,所以在区间[4,14]上,θ随t的增大而增大 .
解:函数y=f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5], 其中y=f(x)在区间[-5,-2),[1,3)上是减函数, 在区间[-2,1),[3,5]上是增函数.
例2:物理学中的玻意耳定律
p= k V
(k为正常数)
告诉我们,对于一定量的气体,当其体积V减小时,
压强p将增大。试用函数的单调性证明之。
分析:按题意,只要证明函数在区间上是减函数 即可。
如果函数y=f(x)在某个区间是增函数或减函数, 那么就说函数y=f(x)在这个区间具有(严格的)单调性, 这一区间叫做y=f(x)的单调区间.
请问: 在单调区间上增函数的图象是___上__升__的___, 减函数的图象是___下__降__的___. (填“上升的”或“下降的”)
想一想 :如何从一个函数的图象来判断这个 函数在定义域内的某个单调区间上是增函数 还是减函数?
(2)任意性:它的取值是在区间上的任意两个自变量, 决不能理解为很多或无穷多个值。
(3)一致性
增函数: 减函数:
xx11
< <
x2 x2
f( x1 ) < f( x2 ) f( x1) > f( x2 )
例1.下图是定义在 闭区间[-5,5]上的函数y=f(x)的图 象,根据图象说出y=f(x)的单调区间,以及在每个单调 区间上, y=f(x)是增函数还是减函数?
如果这个函数在某个单调区间上的图象 是上升的,那么它在这个单调区间上就是增 函数;如果图象是下降的,那么它在这个单 调区间上就是减函数。
1、增函数、减函数的三个特征:
(1)局部性:也就是说它肯定有一个区间。区间可以 是整个定义域,也可以是其真子集,因此,我们说增函 数、减函数时,必须指明它所在的区间。如y=x+1 (X∈Z)不具有单调性
3.已知函数y=f(x)的定义域为[0,+∞),若 对于任意的x2>0,都有f(x2)<f(0),则函数y=f(x) 在区间[0,+∞)上是单调减函数.
y
x2
O
x
f(x2)
一、增函数
y
f(x1)
0
x1
设函数f(x)的定义域为I:
如果对于属于定义域I内某
个区间上的任意两个自变量
f(x2)
的值x1,x2, 当x1<x2时,都有
当x1<x2时,都有f(x1)>f(x2), 那么就说函数y=f(x)在区间I上是单调减函数,
区间I称为函数y=f(x)的单调减区间.
概念辨析
1.函数y=f(x),x ∈[0,3]的图象如图所示.
y
O 123
x
区间[0,3]是该函数的单调增区间吗?
判断
2.对于二次函数f(x)=x2,因为-1,2∈(-∞, +∞),当-1<2时,f(-1)<f(2),所以函数f(x) =x2在区间(-∞,+∞)上是单调增函数.
函数y=f(x)的定义域为A,区间IA,如果 对于区间I内的任意两个值x1,x2,
当x1<x2时,都有f(x1)<f(x2),
那么就说函数y=f(x)在区间I上是单调增函数, 区间I称为函数y=f(x)的单调增区间.
问题: 如何定义单调减函数和单调减区间呢?
函数y=f(x)的定义域为A,区间I A,如 果对于区间I内的任意两个值x1,x2
1、观察这三个图象,你能说出图象的特征吗? 2、随x的增大,y的值有什么变化?
1.3.1 单调性与最大(小)值
请观察函数y=x2与y=x3图象,回答下列问题:
1、当x∈[0,+∞),x增大时,图(1)中的y
值 增大 ;图(2)中的y值
增。大
2、当x∈(-∞,0),x增大时,图(1)中的y
值 减小 ;图(2)中的y值
教学目的
• (1)通过已学过的函数特别是二次函数, 理解函数的单调性及其几何意义;
• (2)学会运用函数图象理解和研究函数的 பைடு நூலகம்质;
• (3)能够熟练应用定义判断数在某区间上 的的单调性.
• 教学重点:函数的单调性及其几何意义. • 教学难点:利用函数的单调性定义判断、
证明函数的单调性.
观察下列各个函数的图象,并说说它们 分别反映了相应函数的哪些变化规律:
观察某城市一天24小时气温变化图.
θ=f (t),t∈[0,24]
问题:如何描述气温θ随时间t的变化情况?
如图,研究函数θ=f(t),t∈[0,24]的图 象在区间[4,14]上的变化情况.
(t2,θ2)
(t1,θ1) t1 t2
问题: 在区间[4,14]上,如何用数学符号语言来刻
画“θ随t的增大而增大”这一特征?
f(x1)< f(x2),那么就说f(x)在
x2 x 这个区间上是增函数
二、减函数
y
f(x1)
f(x2)
0 x1
x2
设函数f(x)的定义域为I:
如果对于属于定义域I内某
个区间上的任意两个自变量
的值x1,x2, 当x1<x2时,都有
x
f(x1)> f(x2),那么就说f(x)在 这个区间上是减函数
三、单调性与单调区间
