试验设计与数据处理(第三版)
试验设计与数据处理第2章试验数据的表图表示

(1)分别做出加药量和剩余浊度、总氮 TN、总磷 TP、CODCr 的变化关系图 (共四张图,要求它们的格式大小一致,并以两张图并列的形式排版到 Word
用Excel做出中下,表注数意据调整带图数形据的点大小的)折;线散点图(1)分别做出加药量和剩余浊度、总 氮总氮TNT、N去总除磷( 率率T2、P、)、C在总OCD一磷OC张r D去T图CP除r中去的率做除变的出率变化加化、关药关C量系系O和图折D浊线C;度r去散(去点除2除图)率率。在的、总一变氮张化T图关N中系去做除折率出线、加散总药点磷量图TP。和去浊除度去除率、
记录表突出原始数据,结果表突出试验结果。
❖ 试验数据不多时,两类表合二为一,不加区别。
将试验数据列成表格,将各变量的数值依照一定的形式和 顺序一一对应起来
(1)试验数据表 ①记录表 试验记录和试验数据初步整理的表格 表中数据可分为三类: ➢ 原始数据 ➢ 中间数据 ➢ 最终计算结果数据
表2-1 离心泵特性曲线测定实验的数据记录表
图14 坐标比例尺对图形形状的影响
解:设2ΔpH=2ΔA=2mm
∵ ΔpH=0.1,ΔA=0.01
∴
横轴的比例尺为 M pH
2mm 2pH
2mm 1(0 mm / 单位pH值) 0.2
纵轴的比例尺为
MA
2mm 2A
2mm 0.01
10(0 mm / 单位吸光度)
2.3 计算机绘图软件在图表绘制中应用
x 0.50 A
E
0.75
xA
1.00
B
0.00
xC
0.25
M
●
0.50
F
0.25
xB
0.75
xA
0.00
《实验设计与数据处理》教学大纲

《实验设计与数据处理》教学大纲(Experiment Design and Data Analysis)一、基本信息课程代码:学分:2总课时:32课程性质:硕士专业基础课适用专业:环境工程先修课程:高等数学、概率论、线性代数二、本课程教学目的和任务本课程是环境工程硕士生的专业课。
数据分析作为一种研究手段,主要是通过从系统设计、参数设计和允许误差设计入手,运用一定的物质手段,在人为控制或模拟自然现象的条件下,使环境过程以纯粹的、典型的形式表现出来,以便进行观察、研究、探索环境本质及其规律,使试验设计建立在统计理论基础之上,试验设计与数据处理相并重。
三、教学方法与手段以课堂教学为主,采用多媒体教学。
四、教学内容及要求第一章环境实验设计与数据处理概论要求掌握(1)环境试验研究的目的与任务;(2)环境试验研究的类型;(3)环境试验研究的程序重点内容:准确理解环境试验研究类型的区分;理解环境试验研究的设计步骤,以及试验设计的基本要求。
难点内容:理解环境试验因子、水平、处理、重复、响应指标等要素,了解准确度、精密度等概念。
第二章环境试验的优化设计要求掌握(1)非均分设计;(2)黄金分割设计;(3)纵横对折设计;(4)平行线设计;(5)环境试验的正交设计;(6)环境试验点均匀设计;熟悉单因子、双因子优选设计的基本方法,熟悉正交表的定义和类型;了解均匀设计与正交设计的区别。
重点内容:正交试验的设计步骤,常见的正交设计运用方法,均匀设计的步骤难点内容:了解分数法设计;旋升设计;逐步提高设计;陡度法设计;单纯形法设计等。
第三章环境数据的展示分析要求掌握(1)频数频率分布表;(2)茎叶图和箱线图;(3)轮廓图和雷达图;(4)概率密度和分布函数。
熟悉常用的概率分布函数;了解正态分布。
重点内容:离散型概率分布和连续型概率分布的条件和数字特征,正态分布的概率密度函数及特点。
难点内容:了解空间序列数据的展示分析,联合概率分布和随机变量的函数。
试验设计与数据处理试验报告

试验设计与数据处理试验报告正交试验设计1.为了通过正交试验寻找从某矿物中提取稀土元素的最优工艺条件,使稀土元素提取率最高,选取的水平如下:需要考虑交互作用有A×B,A×C,B×C,如果将A,B,C分别安排在正交表L8(2)的1,2,4列上,试验结果(提取量/ml)依次是1.01,,1,33,1,13,1.06,,1.03,0.08,,0.76,0.56.试用方差分析法(α=0.05)分析实验结果,确定较优工艺条件解:(1)列出正交表L8(27)和实验结果,进行方差分析。
试验号 A B A×B C A×C B×C 空号提取量(ml)1 1 1 1 1 1 1 1 1.012 1 1 1 2 2 2 2 1.333 1 2 2 1 1 2 2 1.134 1 2 2 2 2 1 1 1.065 2 1 2 1 2 1 2 1.036 2 1 2 2 1 2 1 0.87 2 2 1 1 2 2 1 0.768 2 2 1 2 1 1 2 0.56K1 4.53 4.17 3.66 3.93 3.5 3.66 3.63K2 3.15 3.51 4.02 3.75 4.18 4.02 4.05k1 2.265 2.085 1.83 1.965 1.75 1.83 1.815k2 1.575 1.755 2.01 1.875 2.09 2.01 2.025极差R 1.38 0.66 0.36 0.18 0.68 0.36 0.42因素主次 A A×C B A×B B×C优选方案 A1B1C1SSJ0.23805 0.05445 0.0162 0.00405 0.0578 0.0162 0.02205Q 7.7816总和T 7.68P=T^2/n 7.3728SST0.4088差异源SS df MS F 显著性A 0.23805 1 0.23805 19.5925 9259*B 0.05445 1 0.05445 4.48148 1481A*B 0.0162 1 0.0162 1.33333 3333C 0.00405 1 0.00405 0.33333 3333A*C 0.0578 1 0.0578 4.75720 1646B*C 0.0162 10.01621.333333333误差e0.02205 10.02205 1.814814815误差e2 0.03645 3 0.01215 F 0.05(1,3) 10.12796449F 0.01(1,3) 34.11622156可见A 因素对实验有显著性影响优方案的确立:由上述分析可知,由于提取率越高越好,且交互作用影响不显著,所以优方案为A1B1C1,即酸用量25ml ,水用量20ml ,反应时间为1小时2.为了提高粒混凝土的抗压强度,考察了A ,B ,C ,D ,E ,F 六因素,每个因素都有3个水平,因素水平表如下:表L 27(331)的1,2,5,9,12,13列上,试验结果(抗压强度/kg )依次为100,98,97,95,96,99,,94,99,101,85,82,98,85,90,85,91,89,80,73,90,77,84,80,76,89,78,85,试用方差分析(α=0.05)试验结果,确定较优水平组合。
实验设计与数据处理第八章例题及课后习题答案doc资料
0
428
0 1.162084
492
0 1.162084
512
0
0
509
0
0
Signific ance F
7.93E-05
Lower Upper 下限 上限
95%
95% 95.0% 95.0%
465.4405 471.5595 465.4405 471.5595
5.242078 12.93644 5.242078 12.93644
0.002795085 2.593838854 0.122018
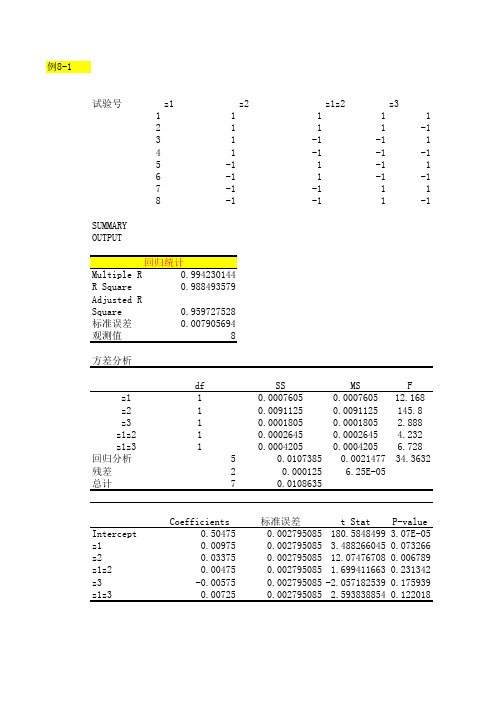
例8-2
回归方程: 由该回归方程 中偏回归系数 绝对值的大 小,可以得到 各因素和交互 作用的主次顺 序为:
y=0.50475+0.00 975z1+0.03375z 2+0.00475z1z20.00575z3+0.00 725z1z3
0 0 -41.73590203
y=468.5+9.09z1 -26.56z2+z3
标准误差
t Stat P-value
1.10193312 425.1619191 1.84E-10
1.385649972 6.55956341 0.002794
1.385649972 -19.17042163 4.36E-05
SS 0.0091125
0.001626 0.0108635
MS
F
0.0091125 33.62546
0.000271
试验号
z1 1 2 3 4 5 6 7 8 9 10 11
z2 1 1 1 1 -1 -1 -1 -1 0 0 0
z3 1 1 -1 -1 1 1 -1 -1 0 0 0
食品试验设计与数据处理教学设计

食品试验设计与数据处理教学设计一、背景介绍现代食品科技越来越受到重视,人们对食品品质和安全性的要求也越来越高。
为此,在大学食品科学相关专业中开设食品试验设计与数据处理课程,可以帮助学生全面掌握食品试验和数据分析的相关技能,提高他们的实验能力和解决问题的能力,满足当前社会对高素质食品科技人才的需求。
二、教学目标本课程的核心目标是帮助学生掌握以下技能:1.掌握食品试验研究的基本流程和方法;2.掌握不同试验设计和实验方案的特点和优缺点;3.掌握常用的数据采集和处理方法;4.学习如何使用统计软件对实验数据进行分析和展示;5.培养学生的实验能力和创新能力。
三、教学内容3.1 食品试验设计•基本试验要素和设计原则•常用试验设计与实验方案的优缺点•食品试验的常用工具和仪器3.2 数据采集和处理方法•常用食品指标和测试方法•数据采集的方法和技巧•常用数据处理和分析方法3.3 统计软件的应用•数据处理软件的基本功能和操作•实验数据统计分析的方法和步骤•实验数据可视化和报告编写四、教学方式和方法本课程采用多种教学方式和方法,包括上课讲授、讨论研究、实验演示、案例分析和作业练习等。
通过讲授理论知识和实际案例,帮助学生理解食品试验设计和数据处理的基本原则和技能,并在实际实验中进行应用和实践。
通过啮合理论与实践,培养学生解决实践问题的能力和创新思维。
五、教学评价和考核方式课程评价与考核分为实验报告、课堂讨论等几个方面,建立适应教学内容和教学目标的考核方式,评价学生在课程中的实际表现,反馈学生的不足和优点,并给予鼓励和指导,提高学生综合素质。
同时,学生表现突出的可以加分。
六、教材参考•《食品试验设计与数据处理》(第3版),罗冬松等编,化学工业出版社•《实验设计与数据处理》(第2版),王景生编,高等教育出版社七、教学成果通过本课程的学习,学生将掌握实验设计、数据采集和处理、统计分析及展示等方面的知识和技能,能够独立设计并实施食品试验研究,并能运用所学知识和技能解决实践问题。
试验设计及数据处理

试验设计及数据处理试验设计是科学研究过程中的一个重要环节,是科学研究的基础。
试验设计的主要目的是为了得到可靠和有效的数据,从而得出科学真相。
试验设计包括实验对象的选择、实验条件的控制、实验步骤的安排、实验数据的记录等。
试验设计的主要内容有两方面:实验因素与实验设计。
实验因素是指影响实验结果的各方面因素,如环境、时间、温度、药物、剂量等;实验设计是指建立实验计划,控制实验因素,使得实验结果能够准确、可靠地反应出实验因素的影响程度。
在试验设计中,常使用的设计方法有一因素试验设计、多因素试验设计、阶段试验设计等。
其中,一因素试验设计是指只控制一个因素进行试验,如控制温度和时间等单一因素;多因素试验设计是指控制多个因素同时进行试验,如控制温度、湿度、压力等多个因素。
阶段试验设计则是指控制因素按一定顺序分阶段进行试验,在每个阶段逐步分析试验结果。
试验设计需要进行数据分析,以得出一些有意义的结论。
数据分析主要分为描述性数据分析和推论性数据分析两类。
描述性数据分析是对试验数据进行描述和总结,如计算平均值、标准差、频率分布等;推论性数据分析则是对试验数据进行推断和判断,如t检验、方差分析、回归分析等。
数据处理是试验设计的最后一个环节,其主要目的是对数据进行清洗、整理和处理,以达到最终的分析和报告目的。
数据处理的过程中需要注意数据的可靠性和有效性。
其具体流程主要包括数据测量、数据收集、数据清洗、数据整理、数据处理和数据分析等。
在实验数据处理中,常用的数据处理方法有数据筛选、异常数据处理、数据标准化、数据归一化、数据转换、数据分组等。
其中,数据筛选是指选择符合要求的数据,剔除不符合要求的数据;异常数据处理则是对数据中的异常值进行处理,如处理缺失值、填充空值等;数据标准化是指对数据进行统一的处理,使其符合某种标准;数据归一化是指将数据转化为0到1之间的数值,使其具有可比性;数据转换是对数据进行变换,使其适应分析要求;数据分组是指将数据分为不同的组别,以便进行分析和研究。
实验设计与数据处理第一章例题及课后习题(附答案)

1、 根据三组数据的绝对误差计算权重:12322211110000,25,400000.010.20.005w w w ====== 因为123::400:1:1600w w w = 所以1.54400 1.71 1.53716001.53840011600pH ⨯+⨯+⨯==++2、 因为量程较大的分度值也较大,用量程大的测量数值较小的物理量会造成很大的系统误差。
3.、含量的相对误差为0.2g ,所以相对误差为:0.20.99790525.3Rx E x ∆===。
4、 相对误差18.20.1%0.0182x mg mg ∆=⨯= 故100g 中维生素C 的质量范围为:18.2±0.0182。
5、1)、压力表的精度为1.5级,量程为0.2,则max 0.2 1.5%0.003330.3758R x MPa KPa x E x ∆=⨯==∆===2)、1的汞柱代表的大气压为0.133,所以max 20.1330.133 1.6625108R x KPax E x -∆=∆===⨯ 3)、1水柱代表的大气压为gh ρ,其中29.8/g m s =则:3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯6、样本测定值算术平均值 3.421666667 3.48 几何平均值 3.421406894 3.37 调和平均值 3.421147559 3.47 标准差s 0.046224092 3.38 标准差 0.04219663 3.4 样本方差 0.002136667 3.43 总体方差0.001780556 算住平均误差 0.038333333极差 0.117、依题意,检测两个分析人员测定铁的精密度是否有显著性差异,用F双侧检验。
根据试验值计算出两个人的方差及F值:221221223.733, 2.3033.7331.621232.303s s s F s ===== 而0.9750.025(9,9)0.248386,(9,9) 4.025994F F ==, 所以0.9750.025(9,9)(9,9)F F F <<两个人的测量值没有显著性差异,即两个人的测量方法的精密度没有显著性差异。
实验设计与数据处理_复习总结

3、多元线性回归分析
(1)多元线性回归方程的建立与求解
(2)多元线性回归方程显著性R检验 (复SS相R关系数,F检验) (3)因素主次的判断 (3种方法) SS T
偏回归系数的标准化
偏回归系数的显著性检验(F检验) 偏回归系数的 t 检验
Pj b j
L jj L yy
tj Fj
4、非线性回归分析 (1)一元非线性回归分析 (2)一元多项式回归 (3)多元非线性回归
第六章 正交试验设计 1、基本概念 (1)正交表 等水平正交表符号 混合水平正交表符号 (2)等水平正交表的正交特性 (3)混合水平正交表的正交特性
2、正交试验设计的基本步骤 (六大步骤) (1)明确试验目的,确定评价指标; (2)挑选因素,确定水平; (3)选正交表,进行表头设计; (4)明确试验方案,进行试验,得到结果; (5)对试验结果进行统计分析; (6)进行验证试验,做进一步分析。
第四章 试验数据的回归分析
线性回归
一元线性回归 多元线性回归
回归分析 非线性回归
一元非线性回归 多元非(2)相关关系 (3)回归分析 2、一元线性回归分析 / 直线拟合 (1)回归方程的建立与求解 (2)一元线性回归效果的检验(相关系数,F检验)
r Lxy Lxx L yy
4、正交试验设计结果的方差分析法 (1)方差分析的基本步骤与格式 若某因素或交互作用的均方≤MSe,则应将它们归入误差列; (2)二水平正交试验的方差分析 二水平正交试验中,正交表中任一列(第j列)对应的离差平方和为:
SSj 1n(K1 K2)2
(3)三水平和四水平正交试验的方差分析
对于3水平和4水平正交试验的方差分析,任一列(第j列)的离差平方和为 :
第八章回归正交设计 1、一次回归正交设计的基本方法 (1)确定因素的变化范围 上水平、下水平、零水平xj0 、变化间距Δj (2) 因素水平的编码
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
试验设计与数据处理(第三版)
引言
试验设计与数据处理是实验科学中至关重要的一部分。
良
好的试验设计可以最大限度地减少误差,提高数据的可靠性和准确性。
数据处理则是对实验数据进行统计分析和解释的过程,通过合理的数据处理方法,我们可以从数据中提取出有用的信息,进一步深入研究问题。
本文档是《试验设计与数据处理》第三版,旨在提供一套
系统的试验设计与数据处理方法和原则,帮助实验者更好地进行实验研究。
一、试验设计
试验设计是指在实验过程中确定实验方案的过程。
良好的
试验设计应该具备以下几个要素:
1.目标明确:明确实验的研究目标和问题,确定实验
需要探究的变量。
2.采样方法:确定合适的采样方法,保证样本的代表
性和可靠性。
3.随机分组:如果实验需要进行随机分组,确保每组
之间的随机性和均衡性。
4.控制变量:控制实验过程中可能引入的干扰变量,
以提高实验结果的可靠性。
5.重复实验:适当重复实验以验证实验结果的可靠性
和稳定性。
6.双盲设计:在可能的情况下,采用双盲设计以减少
主观偏差的影响。
二、数据处理
数据处理是试验结果的统计分析和解释过程,通过数据处
理可以得到结论并回答实验问题。
常见的数据处理方法包括:
1.描述统计:对数据进行总体特征的描述,包括均值、
方差、标准差等。
2.图表绘制:使用统计图表对数据进行可视化展示,
比如直方图、散点图、箱线图等。
3.假设检验:根据样本数据对总体参数进行假设检验,
判断样本结果是否有统计学意义。
4.相关分析:分析变量之间的相关性,使用相关系数
进行量化描述。
5.回归分析:确定变量之间的线性关系,建立线性回
归模型并进行参数估计和显著性检验。
三、实例分析
为了更好地理解试验设计和数据处理的应用,下面以一个实例进行说明。
实例:药物对癌症的治疗效果
我们假设有一种新型药物用于治疗癌症,我们希望通过实验研究来验证其治疗效果。
1.实验设计:
–目标明确:验证新型药物对癌症的治疗效果。
–采样方法:随机抽取癌症患者作为实验样本。
–随机分组:将样本随机分为两组,一组接受新
型药物治疗,另一组接受常规治疗。
–控制变量:控制治疗过程中其他因素的影响,如年龄、性别、病情等。
–重复实验:重复实验多次以验证结果的可靠性。
–双盲设计:医生和患者均不知道患者所属的治疗组别。
2.数据处理:
–描述统计:计算两组患者的治疗效果均值、方差等。
–图表绘制:绘制柱状图对比两组患者的治疗效果。
–假设检验:使用T检验验证两组患者的治疗效果是否有统计学意义。
–相关分析:分析药物剂量和治疗效果之间的关系。
–回归分析:建立线性回归模型,预测药物治疗效果的影响因素。
四、总结
试验设计与数据处理是实验研究中不可或缺的部分,良好
的试验设计和合理的数据处理方法可以最大程度地提高实验结果的可靠性和准确性。
本文介绍了试验设计和数据处理的基本原则和方法,并以实例说明其应用。
希望本文能对实验科学的研究者有所启发,引导他们进行科学、系统、可靠的实验研究工作。
更多详细内容请参考本书《试验设计与数据处理》第三版。
