广西百所示范性中学2015届高三第一次大联考数学试题 扫描版含答案
2015年3月2015届高三第一次全国大联考(江苏版)数学卷(原卷版)
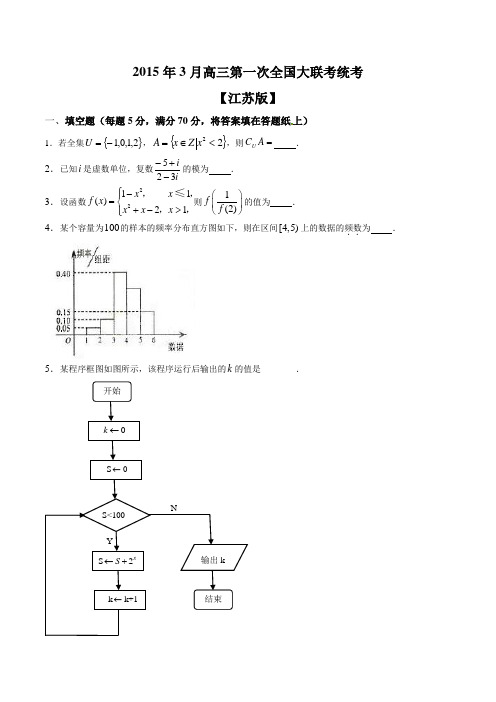
2015年3月高三第一次全国大联考统考【江苏版】一、填空题(每题5分,满分70分,将答案填在答题纸上)1.若全集{}2,1,0,1-=U ,{}22<∈=x Z x A ,则=A C U .2.已知i 是虚数单位,复数ii325-+-的模为 . 3.设函数2211()21x x f x x x x ⎧-⎪=⎨+->⎪⎩,,,, ≤则1(2)f f ⎛⎫⎪⎝⎭的值为 .4.某个容量为100的样本的频率分布直方图如下,则在区间[4,5)上的数据的频数..为 .5.某程序框图如图所示,该程序运行后输出的k 的值是________.开始结束输出kk ←S ←0S<100 k ←k+1 Y NS 2S S ←+6. 已知R ∈ω,则“1=ω”是“函数x x f ωsin )(=的最小正周期为π2”的________条件. 7.已知数列{}n a 为等差数列,,11=a 公差0≠d ,1a 、2a 、5a 成等比,则2014a 的值为 . 8. 已知四边形ABCD 为菱形,边长为1,120BAD ∠=︒,AE AD t AB =+(其中R t ∈且10<<t ),则当AE 最小时,DEEC=. 9.若实数,a b 满足22log (2)log (22)3a b -+-=,则a b +的最小值是 .10.平面直角坐标系xOy 中,点),(y x P 满足⎪⎪⎩⎪⎪⎨⎧≤+≥≥14600y x y x ,当y x ,均为整数时称点),(y x P 为整点,则所有整点中满足y x +为奇数的点),(y x P 的概率为 .11.若函数3()3f x x x t =--([]2,2x ∈-)的最大值为52,则实数t = . 12.已知双曲线22221x y a b -=的左右焦点分别为12,F F ,过左焦点1F 作直线l 与双曲线左右两支分别交于A 、B 两点,若∆2ABF 为正三角形,则双曲线的渐近线方程为 .13.若函数()f x 的导数5()()(),1,2k f x x x k k k Z '=--≥∈,已知x k =是函数()f x 的极大值点,则k = .14.已知()f x 是定义在R 上且以4为周期的奇函数,当(0,2)x ∈时,2()ln()f x x x b =-+,若函数()f x 在区间[2,2]-上的零点个数为5,则实数b 的取值范围是 .二、解答题 (本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15.(本小题满分14分)在平面直角坐标系xOy 中,角α的终边经过点34(,)55P . (1)求tan()4πα+的值;(2)若P 关于y 轴的对称点为Q ,求OP OQ ⋅的值.16.(本小题满分14分)如图四棱锥P-ABCD 中,底面ABCD 是菱形,∠BAD =60°,AD =1,侧面PAD 是正三角形,且与底面垂直,Q 是AD 的中点. (1) 求四棱锥P-ABCD 的体积;(2) M 在线段PC 上,PM =tPC ,线段BC 上是否存在一点R ,使得当t ∈(0,1)时,总有BQ ∥平面MDR ?若存在,确定R 点位置;若不存在,说明理由.17.(本小题满分14分)如图,半径为r 的圆M 与正三角形ABC 的两边AB,AC 相切,且与圆弧BEC 相切.圆M 与OA 相交于E,N 两点.已知圆弧BEC 所在圆半径为R ,圆心为O. (0,].3BOA π∠∈(1)求rR的最大值; (2)若6,R =求DN 的最大值.18.(本小题满分14分)已知P 为椭圆:22221(0)x y a b a b +=>>任一点,12,F F 为椭圆的焦点,12||||4PF PF +=,离心率为22. (1)求椭圆的方程;(2)若直线:(0)l y kx m m =+≠与椭圆的两交点,A B 的中点C 在直线12y x =上,O 为坐标原点,求三角形OAB 面积S 的最大值.CBAD OM RE N19.(本小题满分16分)设等比数列{}n a 的首项为12a =,公比为q (q 为正整数),且满足33a 是18a 与5a 的等差中项;数列{}n b 满足()23202n n n t b n b -++=(,t R n N *∈∈). (1)求数列{}n a 的通项公式;(2)试确定t 的值,使得数列{}n b 为等差数列;(3)当{}n b 为等差数列时,对每个正整数k ,在k a 与k a +1之间插入k b 个2,得到一个新数列{}n c . 设n T 是数列{}n c 的前n 项和,试求满足68n T =的正整数n . 20.(本小题满分16分)已知函数21()ln 1,()2a f x x ax g x x -=-+=,a R ∈; (1)已知2a <,()()()h x f x g x =+,求()h x 的单调区间; (2)已知1a =,若1201x x <<<,211221()()()()f x f x f t x t x x x -'=<<-,求证:122x x t +<.数学Ⅱ 附加题部分【理】21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题.......,并在相应的答题区域内作答.............若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. 【选做题】(在A 、B 、C 、D 四小题中只能选做2题) 21.A .选修4—1几何证明选讲.如图,已知AE 交BC 于点D ,交△ABC 外接圆于点E ,且AB ⋅AC =AD ⋅AE .xylOABC求证:AE 为△ABC 的内角A 的平分线21. B .选修4—2:矩阵与变换已知点P (a ,b ),先对它逆时针旋转060,再作N 2002⎡⎤=⎢⎥⎣⎦对应的变换,得到的点的坐标为 (8,43),求实数a ,b 的值.21. C 选修4—4:坐标系与参数方程 在极坐标系中,设直线l 过点()3 A π6,,()3 B 0,,且直线l 与曲线C :cos (0)a a ρθ=> 有公共点,求实数a 的最小值. 21. D .选修4—5:不等式选讲已知a ,b ,c >0,且a +b +c =1,求证:31313132a b c +++++≤.22. 已知箱中装有2个白球3个黑球,每次任取一球(不放回),取完白球则停止取球. (1)求取2次后仍不能停止的概率;(2)记X 为停止取球后取球的次数,求X 的数学期望()E X . 23. (本小题满分10分)已知数集A ={a 1,a 2,…,a n }(0≤a 1<a 2<…<a n ,n ≥2,n ∈N *)具有性质P :∀i ,j (1≤i ≤j ≤n ), a i +a j 与a j -a i 两数中至少有一个属于A .(1)分别判断数集{1,2,3,4}是否具有性质P ,并说明理由; (2)证明:a 1=0;(3)证明:当n =5时,a 1,a 2,a 3,a 4,a 5成等差数列.ABCD E(第21—A 题)。
安徽省示范高中2015届高三第一次联考文科数学试卷(解析版)

安徽省示范高中2015届高三第一次联考文科数学试卷(解析版)【试卷综析】试卷贴近中学教学实际,在坚持对五个能力、两个意识考查的同时,注重对数学思想与方法的考查,体现了数学的基础性、应用性和工具性的学科特色.以支撑学科知识体系的重点内容为考点挑选合理背景,考查更加科学.试卷从多视角、多维度、多层次地考查数学思维品质,考查考生对数学本质的理解,考查考生的数学素养和学习潜能.第一卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.【题文】 (1)设是虚数单位,z 是Z 的共轭复数,若12ii z+=-,则z 的虚部是 A.15 B. 35 C. 35- D. 35i 【知识点】复数代数形式的乘除运算.L4 【答案解析】C 解析:设,z a bi =+由12i i z +=-可得:12i i a bi +=-+,解得13,55a b ==,所以1355z i =-,则z 的虚部是35-,故选C. 【思路点拨】利用复数代数形式的乘除运算解出z ,再作出判断即可.【题文】 (2)双曲线2212x y -=-的离心率为A.3 B. 2C. D.32【知识点】双曲线及其几何性质.H6【答案解析】C 解析:由2212x y -=-转化成标准形式为2212x y -=,易知1,a b =所以c e 故选C.【思路点拨】先把原式转化为标准形式找出a,b,c,然后求出离心率即可.【题文】 (3)已知,m n 为不同的直线,,αβ为不同的平面,则下列说法正确的是 A. ,////m n m n αα⊂⇒ B. ,m n m n αα⊂⊥⇒⊥ C. ,,////m n m n αβαβ⊂⊂⇒D. ,n n βααβ⊂⊥⇒⊥【知识点】空间中直线与平面之间的位置关系.G4 G5【答案解析】D 解析:A 选项可能有n α⊂,B 选项也可能有n α⊂,C 选项两平面可能相交,故选D.【思路点拨】分别根据线面平行和线面垂直的性质和定义进行判断即可. 题文】(4)执行如图所示的程序框图,输出的k 值为A.2B.3C.4D.5 【知识点】程序框图.L1【答案解析】B 解析:k=0时,5cos cos 02A p ==;k=1时,5cos cos 02A p ==;k=2时,5cos08p <;k=3时,5cos 016p<;故选B. 【思路点拨】本题考查了程序框图中的当型循环结构,当型循环结构是先判断再执行,满足条件进入循环体,不满足条件算法结束.【题文】(5)若x y 、满足202200x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩则z y x =-的最大值为A.2B.-2C.1D.-1【知识点】简单线性规划.E5【答案解析】A 解析:线性可行域如图所示,三个顶点坐标分别为(0,2),(2,0),(-1,0),通过上顶点时Z 值最大。
【全国百强校】广西柳州铁路第一中学2015-2016学年高一上学期段考数学试题解析(解析版)

一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合M ={x |x 2+2x =0,x ∈R },N ={x |x 2-2x =0,x ∈R },则M ∪N =( ) A .{0} B .{0,2} C .{-2,0} D .{-2,0,2} 【答案】D 【解析】试题分析: M ={x|x 2+2x =0,x ∈R }={0,-2},N ={x|x 2-2x =0,x ∈R }={ 0,2},所以M ∪N ={-2,0,2},故选D .考点:1、一元二次方程求根;2、集合并集的运算.2.f (x )是定义在R 上的奇函数,f (-3)=2,则下列各点在函数f (x )图象上的是( ) A .(3,- 2) B .(3, 2) C .(-3,-2) D .(2,-3) 【答案】A考点:1、奇函数满足()()f x f x -=-;2、奇函数图象关于原点对称.【方法点晴】此题考点重在奇函数性质,一定要注意区分偶函数的性质()()f x f x -=,以及二者图象对称性的区别,奇函数关于原点对称,而偶函数则关于y 轴对称.其次要注意,两点关于原点对称,则他们的横坐标,纵坐标均互为相反数.3.下列函数中,值域为(0,+∞)的是( ) A .y =x B .y =x1 C .y =x 1D .y =x 2+1【答案】B 【解析】试题分析: A 选项中,定义域为为[)0,+∞,0≥,即值域应为[)0,+∞;B 选项中,定义域为()0,+∞,0>,则值域应为(0,+∞);C 选项中,定义域为()(),00,-∞⋃+∞,对应的值域也为()(),00,-∞⋃+∞;D 选项中,定义域为R ,其对应的值域则为[)1,+∞,由题中的值域可选B .考点:求函数的定义域以及值域.【易错点晴】求函数的定义域时一定要注意,对于偶次根式,应该使被开方式非负,而对于分式,则应该使分母不等于0,列不等式,进而求出定义域,对于值域则要根据定义域以及函数法则来求;其次判断两区间是否相同,首先两个端点需相同,其次同一端必须要同为开或者同为闭. 4.下列四组函数中,表示同一个函数的是( )A. ()(),f x x g x ==()()21,11x f x g x x x -==-+C.()()2f xg x ==D.1(1)()|1|,()1(1)x x f x x g x x x +≥-⎧=+=⎨--<-⎩【答案】D考点:1、求函数的定义域;2、函数的化简;3、相同函数的特点.【方法点晴】一个函数由他的定义域以及对应的函数法则所决定,所以在判断几个函数是否相同时,只需要看他们的定义域及函数法则是否对应相同;首先求他们的定义域,(一定要注意,此步骤应该在化简函数之前进行)定义域相同,再对每个函数进行化简,或者写为分段函数,然后在定义域的相同区间上,看他们的函数法则是否一致.5.{|02}A x x =≤≤,{|12}B y y =≤≤,下列图形中表示以A 为定义域,B 为值域的函数的是( )【答案】B考点:函数图象与定义域,值域的关系.6.用二分法求方程f(x)=0在(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程 的根在区间( )A .(1.25,1.5)B .(1,1.25)C .(1.5,2)D .不能确定 【答案】A 【解析】试题分析:因为f(1)<0,f(1.5)>0,方程的解应该在1和1.5之间,所以取1和1.5的平均值1.25,又f(1.25)<0 结合f(1.5)>0,可知方程的解应该在1.25和1.5之间,故选A . 考点:二分法求解方程.7.设f (x )=()3,105,10x x f x x +>⎧⎪⎨+≤⎪⎩,则f (5)的值为( )A .16B .18C .21D .24【答案】B 【解析】试题分析: 由分段函数可知(5)(10)(15)f f f ==,因为15>10,所以(5)(15)15318f f ==+=,故选B .考点:1、分段函数;2、函数求值.8.三个数0)3.0(-=a ,23.0=b ,3.02=c 的大小关系为( ) A .c b a << B .b c a << C .c a b <<D .a c b << 【答案】C 【解析】试题分析:020.3(0.3)1,0.31,21a b c =-==<=>,所以有b a c <<,故选C .考点:指数的大小比较.9.函数2y =-的值域是( )A .[2,2]-B .[1,2]C .[0,2]D .[【答案】C考点:1、函数值域的求法;2、二次函数的值域.10.函数2()2(1)2f x x a x =+-+在区间(,4]-∞上递减,则实数a 的取值范围是( ) A .3a ≤- B .3a ≥- C .5a ≤ D .3a ≥ 【答案】A 【解析】试题分析: 抛物线开口向上,对称轴为x=1-a ,在对称轴左侧函数为递减,所以41a ≤-,得3a ≤-,选A .考点:1、二次函数的图象与性质;2、函数的单调性. 11.函数)6(log )(231x x x f --=的单调递增区间是( )A.(),2-∞B.1,22⎡⎫-⎪⎢⎣⎭C.13,2⎛⎤-- ⎥⎝⎦ D.()3,+∞【答案】B 【解析】试题分析:)(x f 为关于x 复合函数,可写为13()log f u u =,2()u x x x =--,对数函函数的定义域为R +,即0u >,也即()0u x >,所以有260x x --+>,解不等式得(3,2)-,此区间为函数)(x f 的定义域,因为13()log f u u =的底数为13,所以()f u 为减函数,由复合函数的单调性可知,()u x 必须为单调减函数方可使)(x f 为增函数,而()u x 在(3,2)-的单调减区间为1(,2)2-,故选B. 考点:1、对数函数的定义域;2、二次函数,对数函数与其复合函数的单调性的关系.【思路点晴】此题主要考查对数函数的定义域,单调性及复合函数的单调性,对数函数的定义域为R +,不可误认为时非负实数,而复合函数的单调性的判断,可由外函数与内函数共同决定,方法是:外函数与内函数单调性一致时,复合函数的单调性为递增,相反,当外函数与内函数单调性相反时,复合函数的单调性为递减.如在区间1(3,)2--上,()u x 为增函数,而()f u 为减函数,则)(x f 也为减函数,而在区间1(,2)2-上,()u x ,()f u 同为减函数,故)(x f 为增函数.12.设错误!未找到引用源。
广西百所示范性中学高三第一次大联考——文综文综

参考答案地理试题部分评分细则一、选择题(本大题共11小题,每小题4分,共计140分。
每小题列出的四个选项中,只有一项符合题意。
)1.A 【解析】D点房价为6 000—7 000元/平方米,N点房价为3 000—4 000元/平方米,D点与N点房价差值为2 000—4 000。
2.C 【解析】M位于河流上游,与盛行风向相垂直的郊外,环境好。
3.A 【解析】公租房、经济适用房需建造在成本较低的地区,城市郊区土地价格较低,适合建设。
4.D【解析】由图可知,1980~2015年少儿人口比重逐渐降低,老年人口比重逐渐升高,说明人口平均年龄在增大;图中劳动年龄人口比重在增加。
5.B【解析】由上题可知,我国少儿人口逐渐下降,老年人口逐渐上升,为此我国应适度调整人口生育政策,适当增加人口出生率,以避免出现劳动力断层。
6.C【解析】根据题干中信息可知,无流区多出现在干旱少雨的地区,故地表景观最可能为沙漠。
7.A【解析】图示的纬度位置为南半球的某国中部,降水较多时期为夏季,A选项符合题意。
8.D【解析】据图中纬度位置可知,该区域分布在澳大利亚,D选项符合题意。
9.C【解析】由图可知,图中L区域分布在靠近北极地区的岛屿与陆地之间,位于海洋上,且此时为1月份,气压低于两侧陆地,同时该地区受暖流影响,故选C。
10.C【解析】据提供信息,可知G为冷高压。
冷高压向南移至北美五大湖地区,导致五大湖地区气温急剧下降。
11.B【解析】该图是以北极为中心的图,此时为1月份,北极圈以内出现极夜现象,根据图中北极圈位置可知,该地区出现黑夜范围接近70%。
36题评分细则(共22分)36.(1)原版答案:地处我国内陆(鄂尔多斯高原),属于中温带干旱与半干旱区,气候干燥、降水量小;(2分)地表植被稀疏,土质疏松,沙土广布;(2分)风力作用强,沉积作用形成沙漠、搬运作用形成流动沙丘(2分)。
答案:地处我国内陆(鄂尔多斯高原),属于中温带干旱与半干旱区,气候干燥、降水量小(2分);评分细则:地处我国内陆;或答:地处鄂尔多斯高原;或答:地处西北地区(1分)。
河南省天一大联考2015届高三阶段测试(一)数学(文)试题(扫描版,有答案)

天一大联考(原豫东、豫北十所名校联考)2014—2015学年高中毕业班阶段性测试(一)数学(文科)·答案一、选择题:本大题共12小题,每小题5分. 题号1 2 3 4 5 6 7 8 9 10 11 12 答案 B C D C C B B A C D C B二、填空题:本大题共4小题,每小题5分.(13)4 (14)29 (15)16π5 (16)1 008三、解答题(17)解:(Ⅰ)因为sin 2sin A C =,由正弦定理得2a c =,…………………………(2分)又因为222b ac c ==,所以2223cos 24a c b B ac +-==.…………………………………(5分) (Ⅱ)由3b =得,32c =,6a =,…………………………………………………(8分) 又因为27sin 1cos 4B B =-=,………………………………………………………(10分) 所以13sin 728ABC S ac B ∆==.…………………………………………………………(12分) (18)解:(Ⅰ)由题意可得3721,,20202010a b c ====,……………………………(2分) 中位数是160,………………………………………………………………………………(4分)平均数__1(7011031404160720032202)15620X =+⨯+⨯+⨯+⨯+⨯=.……(6分) (Ⅱ)由已知可设12Y X B =+,因为当70X =时,460Y =,所以425B =, 所以14252Y X =+,当505Y …时, 160X …,…………………………………………(8分) 所以发电量不低于505万千瓦时包含降雨量160,200和220三类,它们彼此互斥, ………………………………………………………………………………………………(10分)所以发电量不低于505万千瓦时的概率73232020205P =++=.………………………(12分) (19)解:(Ⅰ)取1AB 的中点G ,连接,EG FG ,因为,F G 分别是1,AB AB 的中点,所以111,2FG BB FG BB =∥, 因为E 为侧棱1CC 的中点,所以,FG EC FG EC =∥,…………………………………(3分) 所以四边形FGEC 是平行四边形,则CF EG ∥,因为CF ⊂/平面1AB E ,EG ⊂平面1AB E ,所以CF ∥平面1AB E .…………………(6分)(Ⅱ)因为三棱柱111ABC A B C -的侧棱1AA ⊥底面ABC ,所以1BB ⊥平面ABC , 又AC ⊂平面ABC ,所以1AC BB ⊥,又90ACB ∠=︒,所以AC BC ⊥, 因为1BB BC B ⋂=,所以AC ⊥平面1EB C ,所以1AC B C ⊥, 得111111(11)13326A EB C EB C V S AC -∆==⨯⨯⨯⨯=,………………………………………(10分) 因为112,6AE EB AB ===,所以132AB E S ∆=, 因为11C AB E A EB C V V --=,所以三棱锥1C AB E -在底面1AB E 上的高为11333C AB EAB E V S -∆=.…………………………(12分) (20)解:(Ⅰ)因为()e x f x '=,所以(0)1f '=,又(0)1f =,得()y f x =在0x =处的切线方程为1y x =+,…………………………………………(2分) 又因为()2g x ax b '=+,所以(0)g b '=,又(0)1g =,得()y g x =在0x =处的切线方程为1y bx =+,因为曲线()y f x =与()y g x =在0x =处有相同的切线,所以1b =.…………………(4分) (Ⅱ)由0a =,则()()()e 1x x f x g x bx ϕ=-=--,所以()e x x b ϕ'=-,(i )当0b …时,()>0x ϕ'>,函数()x ϕ在R 上单调递增, 又(0)0ϕ=,所以当(,0)x ∈-∞时,()0x ϕ<,与函数()()f x g x …矛盾,…………(6分)(ii )当0b >时,由()0x ϕ'>,得ln x b >;由()0x ϕ'<,得ln x b <,所以函数()x ϕ在(,ln )b -∞上单调递减,在(ln ,)b +∞上单调递增,…………………(8分)①当01b <<时,ln 0b <,又(0)0ϕ=, (ln )0b ϕ<,与函数()()f x g x …矛盾; ②当1b >时,同理(ln )0b ϕ<,与函数()()f x g x …矛盾; ③当1b =时, ln 0b =,所以函数()x ϕ在(,0)-∞上单调递减,在(0,)+∞上单调递增,()(0)0x ϕϕ=…,故1b =满足题意.综上所述,b 的取值的范围为{1}.…………………………………………………………(12分) (21)解:(Ⅰ)因为点(3,0)F 在圆22:(3)16M x y ++=内,所以圆N 内切于圆M ,因为||NM +||4||NF FM =>,所以点N 的轨迹E 为椭圆,且24,3a c ==,所以1b =,所以轨迹E 的方程为2214x y +=.…………………………………………………………(4分) (Ⅱ)(i )当AB 为长轴(或短轴)时,依题意知,点C 就是椭圆的上下顶点(或左右顶点), 此时1||2ABC S OC ∆=⨯⨯||2AB =.…………………………………………………………(5分) (ii )当直线AB 的斜率存在且不为0时,设其斜率为k ,直线AB 的方程为y kx =,联立方程221,4,x y y kx ⎧+=⎪⎨⎪=⎩得2222244,,1414A A k x y k k ==++ 所以2||OA =2A x2224(1)14Ak y k++=+.…………………………………………………………(7分) 由||||AC CB =知,ABC △为等腰三角形,O 为AB 的中点,OC AB ⊥,所以直线OC 的方程为1y x k =-,由221,41,x y y x k ⎧+=⎪⎪⎨⎪=-⎪⎩解得2224,4C k x k =+2C y =24,4k +2224(1)||4k OC k +=+, …………………………………………………………………………………………………(9分)2||||ABC OAC S S OA OC ∆∆==⨯=22222224(1)4(1)4(1)144(14)(4)k k k k k k k +++⨯=++++, 由于22222(14)(4)5(1)(14)(4)22k k k k k ++++++=…,所以85ABC S ∆…,………(11分)当且仅当22144k k +=+,即1k =±时等号成立,此时ABC △面积的最小值是85,因为825>,所以ABC △面积的最小值为85,此时直线AB 的方程为y x =或y x =-.………………………………………………………………………………………………(12分)(22)证明:(Ⅰ) 因为BC 是圆O 的直径,BE 是圆O 的切线,所以EB BC ⊥,又因为AD BC ⊥,所以AD BE ∥,可知B F C D G C ∽△△, FEC GAC ∽△△,所以BF CF EF CF DG CG AG CG ==,,所以BF EFDG AG=,因为G 是AD 的中点,所以DG AG =,所以F 是BE 的中点,BF EF =. …………………………………………………………………(5分)(Ⅱ)如图,连接AO AB ,,因为BC 是圆O 的直径,所以90BAC ∠=°.在Rt BAE △中,由(Ⅰ)知F 是斜边BE 的中点, 所以AF FB EF ==,所以FBA FAB ∠=∠. 又因为OA OB =,所以ABO BAO ∠=∠. 因为BE 是圆O 的切线,所以90EBO ∠=°.因为90EBO FBA ABO FAB BAO FAO ∠=∠+∠=∠+∠=∠=°,所以PA 是圆O 的切线.……………………………………………………………………(10分) (23)解:(Ⅰ)直线l 的参数方程为4cos ,(2sin x t t y t αα=+⎧⎨=+⎩为参数).………………………(2分)因为4cos ρθ=,所以24cos ρρθ=,所以曲线C 的直角坐标方程为224x y x +=. …………………………………………………………………………………………………(4分) (Ⅱ)将4cos ,2sin x t y t αα=+⎧⎨=+⎩代入22:4C x y x +=中,得24(sin cos )40t t αα+++=,则有2121216(sin cos )160,4(sin cos ),4,t t t t ∆αααα⎧=+->⎪+=-+⎨⎪=⎩………………………………………………………(6分) 所以sin cos 0αα>.又[0,π)α∈,所以π0,2α⎛⎫∈ ⎪⎝⎭, 1212||||||||()t t t PN t PM +=-++==π4(sin cos )42sin 4ααα⎛⎫+=+ ⎪⎝⎭,………(8分)由ππ3π,444α⎛⎫+∈ ⎪⎝⎭得2πsin 124α⎛⎫<+ ⎪⎝⎭…,所以||||(4,42]PM PN +∈.………(10分) (24)解:(Ⅰ)当3x -…时,原不等式化为3224x x --+…, 得3x -…; 当132x -<…时,原不等式化为424x x -+…,得30x -<…; 当12x >时,原不等式化为3224x x ++…,得2x …, 综上,{|0A x x =…或2}x ….………………………………………………………………(5分) (Ⅱ)当2x -…时,|2||3|024x a x x -+++厖成立, 当2x >-时, |2||3||2|324x a x x a x x -++=-+++…,得1x a +…或13a x -…, 所以12a +-…或113a a -+…,得2a -…. 综上,a 的取值范围为(],2-∞-.…………………………………………………………(10分)。
安徽省皖南八校2015届高三第一次联考数学(文)试题 Word版含答案

安徽省皖南八校2015届高三(上)第一次联考数学试卷(文科)一.选择题(每小题5分,共50分)1.设全集U={﹣2,﹣1,0,1,2},集合A={﹣1,1,2},B={﹣1,1},则A∩(∁U B)为()A.{1,2} B.{1} C.{2} D. {﹣1,1}2.函数y=的定义域为()A.(﹣∞,]B.(﹣∞,)C.(0,] D.(﹣∞,0)∪(0,]3.已知复数,则在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限4.若a=20.3,b=sin1,c=log30.2,则()A.b>c>a B.b>a>c C.c>a>b D.a>b>c5.已知f(x)=那么f((1))的值是()A.0 B.﹣2 C.1D.﹣1 6.等于()A.sin2+cos2 B.c os2﹣sin2 C.﹣sin2﹣cos2D.sin2﹣cos27.已知△ABC中,a=,b=,B=60°,那么角A等于()A.45°B.60°C.120°或60°D.135°或45°8.已知向量,满足||=||≠0,且关于x的函数f(x)=x3+||x2+•x+2014在R 上有极值,则与的夹角θ的取值范围为()A.(0,]B.(,π]C.(,π] D.(,)9.把曲线ysinx﹣2y+3=0先沿x轴向左平移个单位长度,再沿y轴向下平移1个单位长度,得到曲线方程是()A.(1﹣y)cosx+2y﹣3=0 B.(1+y)sinx﹣2y+1=0C.(1+y)cosx﹣2y+1=0 D.﹣(1+y)cosx+2y+1=010.已知函数f(x)=ax3﹣3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是()A.(2,+∞)B.(1,+∞)C.(﹣∞,﹣2)D.(﹣∞,﹣1)二.填空题(每小题5分,共25分)11.已知sinα﹣cosα=,则sinαcosα=_________.12.已知向量=(1,﹣2),=(﹣3,2),则=_________.13.设直线y=x+b是曲线y=lnx(x>0)的一条切线,则实数b的值为_________.14.已知函数y=sin(ωx+φ)(ω>0,0<φ≤)的部分图象如示,则φ的值为_________.15.已知函数y=f(x)对任意x∈R有f(x+1)=﹣,且当x∈[﹣1,1]时,f(x)=x2+1,则以下命题正确的是:①函数y=f(x)是周期为2的偶函数;②函数y=f(x)在[2,3]单调递增;③函数y=f(x)+的最大值是4;④若关于x的方程[f(x)]2﹣f(x)﹣m=0有实根,则实数m的范围是[0,2];⑤当x1,x2∈[1,3]时,f()≥.其中真命题的序号是_________.三.解答题(共6小题,共75分)16.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosA=.(1)求sin(B+C)的值;(2)若a=2,S△ABC=,求b,c的值.17.(12分)已知命题p:≤0,命题q:(x﹣m)(x﹣m+2)≤0.m∈R,若p是q的充分不必要条件,求实数m的取值范围.18.(12分)函数f(x)对任意x,y∈(0,+∞)满足f(xy)=f(x)+f(y)且当x>1时,f(x)<0.(1)判断函数f(x)的单调性并证明相关结论;(2)若f(2)=1,试求解关于x的不等式f(x)+f(x﹣3)≥2.19.(13分)已知向量=(mcosθ,﹣),=(1,n+sinθ)且⊥(1)若m=,n=1,求sin(θ﹣)的值;(2)m=且θ∈(0,),求实数n的取值范围.20.(13分)设函数f(x)=x2+bx+c(b,c∈R),已知不论α,β为何实数,恒有f(cosα)≥0,f(2+sinβ)≤0.(1)求证:b+c=﹣1;(2)求实数c的取值范围.21.(13分)设函数f(x)=x3+ax2﹣a2x+m(a>0)(1)若a=1时函数f(x)有三个互不相同的零点,求实数m的取值范围;(2)若对任意的a∈[3,6],x∈[﹣2,2],不等式f(x)≤1恒成立,求实数m的取值范围.皖南八校2015届第一次联考数学(文科)参考答案一.选择题二.填空题11.1225 12.(2,2)- 13.ln 21- 14.3π15.①②④ 三.解答题16.(满分12分)解析:31cos )1(=A 分2322sin =∴AA CB -=+π又分6322sin )sin()sin( ==-=+∴A A C B π2sin 212)2(==∆A bc S ABC 得由分83 =∴bcA bc c b a cos 2222-+=又分10622 =+∴c b由上解得分123 ==c b17.(满分12分)解析:对于命题1:0x p x -≤,得(1)00x x x -≤⎧⎨≠⎩,∴ 01x <≤………3分 对于命题:()(2)0q x m x m --+≤得2m x m -≤≤………………6分又因为p 是q 的充分不必要条件∴p q ⇒∴201m m -≤⎧⎨≥⎩∴12m ≤≤………………………………………………………………12分 18.(满分12分)解析:()f x 在(0,)+∞上单调递减 …………3分分单调递减在即分分则且任取12),0()()()(0)()(90)(0)()()(6)()()()(),0(,,21121221121212112122121 +∞∴><-∴<∴<<=-∴+=⋅=+∞∈<x f x f x f x f x f x x f x x x x f x f x f x xf x f x x x f x f x x x x注:第2小题由于校稿失误,故不评分,提供答案,仅供参考题:若(2)1f =-,试求解关于x 的不等式()(3)2f x f x +-≥-.答案:{}43434)3(0300)()4())3((2)2()2()4(≤<∴≤<⎪⎩⎪⎨⎧≤->->∴∞+≥-∴-=+=x x x x x x x x f f x x f f f f 原不等式解集为解得)上单调递增,在(又原不等式可化为a b ⊥,0a b ∴=cos 2(sin )02m n θθ∴+=即cos 0m n θθ-=………………2分 ⑴2,1m n ==10θθ-=1θθ=1sin()42πθ∴-=-………………6分⑵2m = 0n θθ-=sin )2cos(),(0,)42n ππθθθθ∴=-=+∈………………9分(0,)2πθ∈ 3444πππθ∴<+<cos()242πθ∴-<+<n <13分20.(满分13分)解析:⑴令30,2παβ==得3cos 01,2sin 12π=+= (10(10f f ∴≥≤),) (1=0f ∴)1+0b c ∴+= 即1b c +=-………………6分⑵1b c +=- 1b c ∴=--2()(1)(1)()f x x c x c x x c ∴=-++=--1sin 1β-≤≤ 12sin 3β∴≤+≤又(2sin )0f β+≤ (3)0f ∴≤3c ∴≥………………13分(1)当1a =时32()f x x x x m =+-+,因为()f x 有三个互不相同的零点,所以32()f x x x x m =+-+,即32m x x x =--+有三个互不相同的实数根。
安徽省皖南八校2015届高三上学期第一次联考数学(文)试题 Word版含解析
安徽省皖南八校2015届高三上学期第一次联考数学(文)试题(解析版)【试卷综析】试卷注重对基础知识和基本方法全面考查的同时,又突出了对数学思想、数学核心能力的综合考查, 试卷以考查考生对“双基”的掌握情况为原则,重视基础,紧扣教材,回归课本,整套试卷中有不少题目可以在教材上找到原型.对中学数学教学和复习回归课本,重视对基础知识的掌握起到好的导向作用.一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.【题文】1.设全集{2,1,1,2,3}U =--,集合A={-1,1,2},B={-1,1},则()U A C B =I A.{1} B.{2} C.{1,2} D.{-1,1} 【知识点】集合运算. A1【答案解析】B 解析:因为全集{2,1,1,2,3}U =-- ,B={-1,1},所以{2,2,3}U C B =- 所以()U A C B =I {2},故选B.【思路点拨】根据补集、交集的定义求解.【题文】2A. B. C. D. 【知识点】函数的定义域. B1【答案解析】D故选D.【思路点拨】根据函数解析式写出函数有意义的条件,进而求得函数的定义域.【题文】3 A.第一象限 B.第二象限 C.第三象限 D.第四象限 【知识点】复数的基本概念与运算. L4【答案解析】C 对应的点位于第三象限,故选C.【思路点拨】根据复数除法及共轭复数的定义求得结论.【题文】4.若0.332,sin1,log 0,2a b c ===,则 A.b>c>a B.b>a>c C.c>a>b D.a>b>c 【知识点】数值大小的比较. E1【答案解析】D 解析:0.3321,sin1(0,1),log 0.20,>∈<Q a b c ∴>>,故选D. 【思路点拨】分析各值所在的范围,这些范围两两的交集是空集,从而得a,b,c 的大小关系. 【题文】5.已知()1,13,1x x f x x x +≤⎧=⎨-+>⎩那么((1))f f 的值是A.0B.-2C.1D.-1 【知识点】函数值的意义. B1 【答案解析】C 解析:因为()1,13,1x x f x x x +≤⎧=⎨-+>⎩,所以()12f =,所以((1))f f =()2f =1,故选C. 【思路点拨】根据函数值的意义求解.【题文】A.sin2+cos2B.cos2-sin2C.-sin2-cos2D.sin2-cos2 【知识点】三角函数的求值化简. C7【答案解析】D因为2 D.【思路点拨】根据诱导公式、二倍角公式、同角三角函数关系化简已知的式子得2的终边位置去掉绝对值.【题文】7.已知ABC 中,A 等于( )A .45︒ B. 60︒ C. 60120︒︒或 D. 45135︒︒或 【知识点】解三角形.C8【答案解析】A 解析:由正弦定理可得2a b <∴∠【思路点拨】根据正弦定理即可求出角的大小 .【题文】8.已知向量,a b ,满0a b =≠,且关于x 的函数22014a x a bx +⋅+在R 上有极值,则a 与b 的夹角θ的取值范围为( )A. B. C. D. 【知识点】导数;向量的运算 B11 F2 2a x ab +⋅,函数在实数上有极值,220,0cos a a b a b -⋅>=≠∴【思路点拨】求出导数,再利用函数性质列出条件求解.【题文】9.把曲线sin 230y x y -+=先沿x y 轴向下平移1个单位长度,得到曲线方程是( )A ()1cos 230y x y -+-= B. ()1sin 210y x y +-+= C. ()1cos 210y x y +-+= D. ()1cos 210y x y -+++= 【知识点】函数的平移变换 B8【答案解析】C 解析:把曲线ysinx-2y+3=0先沿xy 轴向下平移1个单位长度,即曲线(1+y )cosx-2y+1=0, 故选:C .【思路点拨】根据题意对函数进行平移变换即可.【题文】10.已知函数()3231f x ax x =-+,若()f x 存在唯一的零点0x ,且00x >,则a的取值范围是( )A. ()2,+∞B. (),2-∞-C. ()1,+∞D. (),1-∞-【知识点】利用导数研究函数的极值;函数零点的判定定理.B9,B11 【答案解析】B 解析:当a=0时,f (x )=﹣3x 2+1=0,解得x=,函数f (x )有两个零点,不符合题意,应舍去;﹣)x=>0,列表如下: ,) (,+∞)f (x )=0,不符合条件:f (x )存在唯一的零点x 0,且x 0>0,应舍去.﹣)x=<0,列表如下: (﹣∞,)(,0f (x 0)=0, ∵f(x )存在唯一的零点x 0,且x 0>0,∴极小值f ()=a ()3﹣3()2+1>0, 化为a 2>4,∵a<0,∴a<﹣2.综上可知:a 的取值范围是(﹣∞,﹣2). 故答案为:(﹣∞,﹣2). 【思路点拨】分类讨论:当a≥0时,容易判断出不符合题意;当a <0时,求出函数的导数,利用导数和极值之间的关系转化为求极小值f ()>0,解出即可.5小题,每小题5分,共25分,请将答案填在题后横线上.11.,则sin cos αα=【思路点拨】根据同角三角函数的基本关系式可直接求解. 【题文】12.已知向量()()1,2,3,2OA OB =-=-,则1AB = 【知识点】向量的加减及坐标运算.F1【答案解析】()2,2- 解析:由题可知()(14,42,AB OB OA AB =-=-∴=-. 【题文】13.是曲线()ln 0y x x =>的一条切线,则实数b= 【知识点】导数的几何意义及其运算.B11【答案解析】ln 21- 解析:设切点坐标为()00,x y ,得:02x =,代入曲线方程()ln 0y x x =>可得:0ln 2y =,又因为()00,x y 在直线上,故ln 21b =-,故答案为:ln 21-。
安徽省皖南八校2015届高三上学期第一次联考数学(理)试
安徽省皖南八校2015届高三上学期第一次联考数学(理)试题(解析版)【试卷综析】试题考查的知识涉及到函数、三角函数、数列、导数等几章知识,重视学科基础知识和基本技能的考察,同时侧重考察了学生的学习方法和思维能力的考察,知识点综合与迁移。
试卷的整体水准应该说比较高,综合知识、创新题目的题考的有点少,试题适合阶段性质考试. 一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.【题文】1.已知复数z 满足(3)10i z i +=(其中i 是虚数单位,满足21i =-),则复数z 的共轭复数是A.13i -+B.13i -C.13i +D.13i -- 【知识点】复数的基本概念与运算. L4【答案解析】BB.【思路点拨】利用复数除法运算求得复数z=1+3i ,再由共轭复数的定义求z 的共轭复数.【题文】2.则下列结论正确的是A.{2,1}A B =--B.()(,0)R A B =-∞ðC.(0,)AB =+∞ D.(){2,1}R A B =--ð【知识点】集合运算. A1【答案解析】D 解析:{|0},{2,1,1,2},A y y B =>=--Q()(){}{1,2},,01,2U A B C A B ∴==-∞I U U ,(){}(){}0,1,2,2,1U A B C A B =+∞--=--U U I ,故选D.【思路点拨】求出集合A ,然后依次求各选项中的集合,得出正确选项.【题文】3.设,a b R ∈,”是“||||ab >”成立的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分又不必要条件【知识点】充分条件;必要条件. A2【答案解析】Aa=-5,b=1时,||||a b >但 . ”是“||||a b >”成立的充分而不必要条件.故选A.【思路点拨】分别判断充分性、必要性是否成立得结论.【题文】4.则与向量AB方向相同的单位向量是【知识点】平面向量的概念;向量的坐标运算. F1 F2【答案解析】C量AB 方向相同的单位向量是 C.【思路点拨】求出向量AB的坐标,提出向量AB的模得与向量AB方向相同的单位向量.【题文】5.已知函数()f x是R上的奇函数,且在区间[0,)+∞上单调递增,若则A.b a c<< B.c b a<< C.b c a<< D.a b c<<【知识点】函数奇偶性、单调性的应用. B3 B4【答案解析】B,而函数()f x是R上的奇函数,且在区间[0,)+∞上单调递增,所以a>0,b<0,c<0,又因为b>c,所以a>b>c,故选B.【思路点拨】利用诱导公式化简各自变量值,根据函数的奇偶性、单调性,把a,b,c分成正b,c大小关系,从而得a,b,c的大小顺序.【题文】6.函数()cos22sinf x x x=+的最大值与最小值的和是A.2-B.0【知识点】与三角函数有关的最值.C7【答案解析】C 所以函数()f x-3,所以最大值与最小值的和是C.【思路点拨】把已知函数化为二次函数形式求得结论.【题文】7.函数1()x x f x xe e +=-的单调递增区间是A.(,)e -∞B.(1,)eC.(,)e +∞D.(1,)e -+∞ 【知识点】导数法求函数的单调区间. B12 【答案解析】D 解析:()1(1)x x x xf x e xe e x e e +'=+-=-+,由()0f x '>得x>e-1,故选D.【思路点拨】求定义域上导函数大于0的x 范围.【题文】8.及y 轴所围成的封闭图形的面积是A.2ln 2B.2ln 21-【知识点】定积分与微积分基本定理. B13【答案解析】A A.【思路点拨】由定积分的几何意义及微积分基本定理求解.【题文】9.在ABC ∆中,角,,A B C 所对的边分别是,,a b c ,若2015120aBC bCA cAB ++=,则ABC ∆的最小角的正弦值等于【知识点】向量;解三角形. F1 C8【答案解析】C 解析:由2015120aBC bCA cAB ++=得()2015120aCB bCA c CB CA -++-=(1512)(2012)b c CA a c CB⇒-=-,因为,CA CB 不共线,所以A 最小,又cosA= C.【思路点拨】根据向量共线的意义得关于a,b,c 的方程组,由此确定三角形的最小内角,再由余弦定理求得此最小内角的余弦值,进而求其正弦值.【题文】10.已知定义在R 上的奇函数()f x 的导函数为'()f x ,当0x <时,()f x 满足2()'()f x xf x x +<,则()f x 在R 上的零点个数为A.1B.3C.5D.1或3 【知识点】函数的奇偶性;函数的零点;导数的应用. B4 B9 B12【答案解析】A 解析:设2()()h x x f x =则[]2()2()()2()()h x xf x x f x x f x xf x '''=+=+,因为0x <时,()f x 满足2()'()f x xf x x +<, 所以0x <时,[]()2()()h x x f x xf x ''=+ 20x >>,所以函数()f x 是(),0-∞上的增函数,又()f x 是定义在R 上的奇函数,所以()f x 是R 上增函数,所以()f x 在R 上的零点个数为1,故选 A.【思路点拨】构造函数,利用导数确定函数在(),0-∞的单调性,再由奇偶性得函数在R 上单调性,从而得到函数的零点个数.二、填空题:本大题共5小题,每小题5分,共25分,请将答案填在题后横线上.【题文】11.命题“对任意2,310x R x x ∈-+>”的否定是 【知识点】含量词的命题的否定. A3【答案解析】存在0x R ∈,使得200310x x -+≤. 解析:命题“对任意2,310x R x x ∈-+>”的否定是“存在0x R ∈,使得200310x x -+≤”【思路点拨】根据含量词的命题的否定方法写出结论.【题文】12.已知向量(3,4),a =向量b 满足||3a b -=,则||b 的取值范围是 【知识点】向量的几何意义. F1【答案解析】[2,8] 解析:||3a b -=表示b 对应的点与a 对应的点距离是35a =所以||b 的最小值5-3=2,最大值5+3=8,即||b 的取值范围是[2,8].【思路点拨】根据向量差的模的几何意义,得b 对应点的轨迹是以(3,4)为圆心3为半径的圆,由此得||b 的取值范围.【题文】13.,递减,则ω=【知识点】函数sin()y A x ωϕ=+的性质. C4,在时,()f x 在调递增,.【思路点拨】时,()f x 在,.【题文】14.设函数266,0()34,0x x x f x x x ⎧-+≥=⎨+<⎩,若互不相等的实数123,,x x x 满足123()()()f x f x f x ==,则123x x x ++的取值范围是【知识点】分段函数. B1解析:设123x x x <<,则 所以123x x x ++的取值范围是【思路点拨】画出函数()f x 的图像,由图像可知若123x x x <<,,由此得123x x x ++的取值范围. 【题文】15.有下列五个命题①不论,a b 为什么值,函数()y f x =的图象关于原点对称; ②若0a b =≠,函数()f x 的极小值是2a ,极大值是2a -;③若0ab ≠,则函数()y f x =的图象上任意一点的切线都不可能经过原点;④当0,0a b >>时,对函数()y f x =图象上任意一点A ,都存在唯一的点B ,使得其中点O 是坐标原点)⑤当0ab ≠时,函数()y f x =图象上任意一点的切线与直线y ax =及y 轴所围成的三角形的面积是定值. 其中正确的命题是 (填上你认为正确的所有命题的序号)【知识点】函数的性质. B12【答案解析】①③⑤ 解析:显然函数()f x 是奇函数,故命题①正确;当a=b<0时函数()f x 的极小值是-2a ,极大值是2a,故命题②不正确;假设存在过原点的切线,切点为b=0,与0ab ≠矛盾,故命题③正确;当a=b=1y=x,y 轴为渐近3,4ππ⎫⎛⎤⎪ ⎥⎭⎝⎦,所以对函数()y f x =图象上任意一点A ,都存在唯一的点B ,xy=ax 联立得交点()002,2x ax ,切线与y 轴交点0,0),所以围成三角形的面积是2ab 是定值,故命题⑤正确.所以正确命题有①③⑤.【思路点拨】①可判断函数()f x 的奇偶性;②当a=b<0时函数()f x 的极小值是-2a ,极大值是2a ,故结论不成立;③反证法,假设存在过原点的切线,切点为()b x a x =-b=0,与0ab ≠矛盾,故命题③正确;④特殊值法,当a=b=1y=x,y 轴为渐近线,3,4ππ⎫⎛⎤⎪ ⎥⎭⎝⎦不成立,故命题④不正确;⑤由③得切线方y=ax 联立得交点()002,2x ax ,切线与y 轴交点0,0),所以围成三角形的面积是2ab 是定值,故命题⑤正确.三、解答题本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤. 【题文】16(本小题满分12分)如图,动点12,A A 与12,B B 分别在射线,OA OB 上,且线段12A A 的长为1,线段12,B B 的长为2,点,M N 分别是线段1122,A B A B 的中点.(Ⅰ)用向量12A A 与12B B 表示向量MN ;(Ⅱ)求向量MN 的模.【知识点】向量在几何中的应用;向量的线性运算;向量的模.F1【答案解析】(Ⅰ)1()2MN A A B B =+.解析:(Ⅰ)1122MN MA A A A N =++,1122MN MB B B B N =++两式相加,并注意到点,M N 分别是线段11A B 、22A B 的中点,得1()MN A A B B =+分(Ⅱ)由已知可得向量12A A 与12B B 的模分别为1与2,夹角为所以12121A AB B =,由1()MN A A B B =+22 211()2MN A A B B A A B B A A B B =+=++∙12分【思路点拨】(Ⅰ)根据向量加法的多边形法则求解;(Ⅱ)根据向量模的平方与向量数量积的关系求解.【题文】17(本小题满分12分)在ABC∆中,角,,A B C所对的边分别是,,a b c,(Ⅰ)求cos C的值;(Ⅱ)若5a=,求ABC∆的面积.【知识点】解三角形. C8【答案解析】解析:3分所以,所以)6分(Ⅱ)由(1在△ABC中,由正弦定理,……………9分……………12分【思路点拨】(Ⅰ)已知等式展开,代入余弦定理得cosA,代入cos cos()C A B=-+得结论;(Ⅱ)由正弦定理求得边c.【题文】18(本小题满分12分)的导函数为'()f x .(Ⅰ)若函数()f x 在2x =处取得极值,求实数a 的值;(Ⅱ)已知不等式2'()f x x x a >+-对任意(0,)a ∈+∞都成立,求实数x 的取值范围. 【知识点】导数的应用. B12【答案解析】(Ⅰ)(Ⅱ) }{|20x x -≤≤.解析:(Ⅰ)'2()f x ax x a =-+,由于函数()f x 在2x =时取得极值,所以 '(2)0f =.即 420,a a -+=解得此时'()f x 在2x =两边异号,()f x 在2x =处取得极值--------6分(Ⅱ) 方法一:由题设知:22ax x a x x a -+>+- 对任意(0,)a ∈+∞都成立即22(2)20a x x x +-->对任意(0,)a ∈+∞都成立……………9分 设22()(2)2()g a a x x x a R =+--∈, 则对任意x R ∈,()g a 为单调递增函数()a R ∈ 所以对任意(0,)a ∈+∞,()0g a >恒成立的充分必要条件是(0)0g ≥即 220x x --≥,20x -≤≤∴, 于是x 的取值范围是}{|20x x -≤≤………12分方法二: 由题设知:22ax x a x x a -+>+-,对任意(0,)a ∈+∞都成立即22(2)20a x x x +-->对任意(0,)a ∈+∞都成立 对任意(0,)a ∈+∞都成立,即9分20x -≤≤∴, 于是x 的取值范围是}{|20x x -≤≤……………12分【思路点拨】(Ⅰ)由可导函数在某点取得极值的条件求a 值;(Ⅱ)法一 即22(2)20a x x x +-->对任意(0,)a ∈+∞都成立,把不等式左边看成关于a 的一次函数,利用一次函数单调性得关于x的不等式求解;法二:分离参数法求x范围. 【题文】19(本小题满分12分)已知函奇函数,且函数()y f x=的图象的两相邻对称轴之间的距离为(Ⅰ);(Ⅱ)将函数()y f x=的图象向右平移,得到函数()y g x=的图象,求函数()g x的单调递增区间.【知识点】函数sin()y A xωϕ=+解析式的确定;图像变换. C4【答案解析】(k∈Z).解析:3分因为()f x为奇函数,所以所以()2sinf x xω=,由题意得π22,所以2ω=.故()2sin2f x x=.因此……………6分(Ⅱ)将()f x的图象向右平移……………9分(k∈Z),(k ∈Z )时,()g x 单调递增,因此()g x 的单调递增区间为(k ∈Z ). ……………12分 【思路点拨】(Ⅰ)由奇偶性求ϕ,由周期性求ω,得解析式,从而求(Ⅱ)根据图像变换规律得函数()y g x =的解析式,再根据正弦函数的单调性求得函数()g x 的单调递增区间.【题文】20(本小题满分13分)其中0a <.(Ⅰ)若函数()f x 在其定义域内单调递减,求实数a 的取值范围;(Ⅱ)且关于x 在[1,4]上恰有两个不相等的实数根,求实数b 的取值范围.【知识点】导数的应用. B12 【答案解析】(Ⅰ)(,1]-∞- ;(Ⅱ).解析:(Ⅰ)()f x 的定义域是(0,)+∞,求导得依题意'()0f x ≤在0x >时恒成立,即2210ax x +-≤在0x >恒成立. ……3分 这个不等式提供2种解法,供参考解法一:因为0a <,所以二次函数开口向下,对称轴问题转化为2240a =+≤所以1a ≤-,所以a 的取值范围是(,1]-∞- ……………6分在0x >恒成立,当1=x 时,取最小值1-,∴a 的取值范围是(,1]-∞- ………6分,()(2)ln 22g x g b ==--极小值,又(4)2ln 22g b =--………10分方程()0g x =在[1,4]上恰有两个不相等的实数根.则(1)0(2)0(4)0g g g ≥⎧⎪<⎨⎪≥⎩, 得………13分【思路点拨】(Ⅰ)利用导数转化为不等式恒成立问题,再由分离参数法等求a 范围;在[1,4]上恰有两个不相等的实数根,利用导数求极值,通过分析极值的取值条件求得b 范围.【题文】21(本小题满分14分)已知函数()ln ()f x x x mx m R =+∈的图象在点(1,(1))f 处的切线的斜率为2. (Ⅰ)求实数m 的值;(Ⅱ)讨论()g x 的单调性;(Ⅲ)已知*,m n N ∈且1m n >>,【知识点】导数的应用;分析法证明不等式. B12 E7【答案解析】(Ⅰ)1;(Ⅱ) ()g x 在区间(0,1)和(1,)+∞都是单调递增的;(Ⅲ)见解析.解析:(Ⅰ)()ln ,f x x x mx =+所以'()1ln f x x m =++ 由题意'(1)1ln12f m =++=,得1m =……3分(Ⅱ当1x >时,,()h x 是增函数,()(1)0h x h >=,,故()g x 在()1,+∞上为增函数; ………6分 当01x <<时,,()h x 是减函数,()(1)0h x h >=,,故()g x 在()0,1上为增函数; 所以()g x 在区间(0,1)和(1,)+∞都是单调递增的。
河南八校2015届高三上学期第一次联考数学(文)试卷(扫描版)
河南八校2014—2015学年上期第一次联考高三数学(文)试题参考答案一选择题:二填空题: 13. [5,1]-- 14. 12n n a -=- 15. [3,0]- 16. ②⑤ 三解答题:17. (本小题满分12分)解:(Ⅰ)由题设3,2,ABC b c S ∆===1sin 2ABC S bc A ∆=得,132sin 2A ⨯⨯=,∴sin A =…………………………4分 ∴60A =或120A =………………….………………6分 (Ⅱ)由已知120A =…………………………………………7分 由余弦定理得,29412cos12019a =+-=,∴a =………10分 设BC 边上的高为h ,由三角形面积相等得,h =⇒=12分题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A B A B B C A C ADCC19. (本小题满分12分) 证明:(Ⅰ)在矩形ABCD 中,取BC 的中点G ,连接FG ,OG 由O 为BD 中点知,OG ∥DC ,OG =12DC ,又EF ∥DC ,EF = 12AB= 12DC ∴OG ∥EF 且OG=EF ,∴OGFE 是平行四边形,……………4分∴EO ∥FG ,又FG ⊂平面BCF ,∴EO ∥平面BC F ……………………6分解:(Ⅱ)连接AC ,AF ,则几何体ABCDEF 的 体积为A EDCF F ABC V V V --=+………………………7分由ED ⊥平面ABCD ,ABCD 为矩形得,AD ⊥平面EDCF, ∴AD 是四棱锥A EDCF -的高,又EF ∥DC ,∴EDCF 是直角梯形,又EF=DE=AD=12AB=2,∴1162433A EDCF EDCF V S AD -=⨯⨯=⨯⨯=………………………9分在三棱锥F ABC -中,高ED=2,∴11842333F ABC ABC V S ED -∆=⨯⨯=⨯⨯=…………………………11分∴几何体ABCDEF 的体积为820433V =+=…………………………12分20. (本小题满分12分)证明:(Ⅰ)设过点(0,2)P 的直线l :2y kx =+,由2214y kx y x =+⎧⎪⎨=⎪⎩得,2480x kx --=令1122(,),(,)A x y B x y ,∴12124,8x x k x x +==-………………4分 ∴2212121212116OA OB x x y y x x x x ⋅=+=+844=-+=-为定值……6分 解:(Ⅱ)由(Ⅰ)知,12||||AB x x =-==,原点到直线l 的距离d =……………10分A BC DOEFG 高三数学(文科)参考答案 第2页(共5页)∴1||2AOB S AB d ∆=⨯⨯=≥当0k =时,三角形AOB面的最小,最小值是………………12分21.(本小题满分12分)解:(Ⅰ)函数()1xe f x x =+的定义域为{|,x x ∈R 且1}x ≠-,………………2分2()(1)xxe f x x '=+.令()0f x '=,得0x =.当x 变化时,()f x 和()f x '的变化情况如下: x (,1)-∞- (1,0)- 0(0,)+∞ ()f x ' - - 0 + ()f x↘ ↘ 极小 ↗ 所以()f x 的单调减区间为(,1)-∞-,(1,0)-;单调增区间(0,)+∞.故当0x =时,函数()f x 有极小值(0)1f =. ……………… 5分(Ⅱ)结论:函数()g x 存在两个零点.证明过程如下:由题意,函数2()11xe g x x x =-++.因为22131()024x x x ++=++>.所以函数()g x 的定义域为R .求导,得22222e (1)e (21)e (1)()(1)(1)x x x x x x x x g x x x x x ++-+-'==++++,…………………… 7分 令()0g x '=,得0x =,1x =,当变化时,()g x 和()g x '的变化情况如下: 故函数()g x 的单调减区间为(0,1);单调增区间为(,0)-∞,(1,)+∞. 当0x =时,函数()g x 有极大值(0)0g =;当1x =时,函数()g x 有极小值e(1)13g =-. ………………………… 10分 因为函数()g x 在(,0)-∞单调递增,且(0)0g =,所以对于任意(,0)x ∈-∞,()0g x ≠. 因为函数()g x 在(0,1)单调递减,且(0)0g =,所以对于任意(0,1)x ∈,()0g x ≠.因为函数()g x 在(1,)+∞单调递增,且e(1)103g =-<,2e (2)107g =->, 所以函数()g x 在(1,)+∞上存在唯一0x ,使得0()0g x =,高三数学(文科)参考答案 第3页(共5页)故函数()g x 存在两个零点(即0和0x ). ……………… 12分 请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分。
2015年全国高中数学联赛广西赛区预赛试题参考答案
2. 答案: 5 解析: 原式= (6 1)
11 11 10 9 ∵ 7 2 7 1 3 (7 1)(7 7 7 1) 3 2 711 2 ,
8(710 79 7) 5 ,∴原式被 8 除余数为 5.
3.答案:
a4 b4 c4 x2 3 3 , 2 2 2 , 2 b c c a a b x3 2
3 . 2
∵ f ( x) f (3)
∴当且仅当 a b c 1 时取到最小值,所求最小值为 12. 证明:连结 OP, OA, OC , EP . ∵ N 是 AB 的中点,∴ O, P, N单 调 递 减 . 同 理 , 当 x 1 时 y f (0) g (0) 2 ,当 x 1 时 y
11
f ( x) g ( x ) 递 增 , 而 当 x 0 时 函 数 值
f (1) g (1) ,而当 x 时 y ,∴ ymin 1 .
取得最小值,当且仅当 10.答案:81
2 a 3 2a 3 a 8 7 5 .解得 a ,b , 3a 4b 12. 1 b 2 3b 3 2b 6 3 4
解析:∵由题设 n 恰有 5 个约数,设 n 的质因数分解是 n p1 1 pk k ,∴n 的约数个
a4 c4 2a 2 c 2 a 2 c2 b2 ac 1 2 2 2 2 ,∴ B [ , ) . b 2 2 a c 2 2 .∵ cos B a c 3 2 2ac 2 a c a c
2
9. 答案: 12
解析: ∵易求得 z1 z2 z3 8 6i , z1 z2 z3 z1 z2 z3 =10, ∴ z1 z2 z3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广西百所示范性中学2015届高三第一次大联考2015届百所示范性中学高三年级第一次大联考理数试题部分评分细则一、选择题1.D 【解析】2i1+i =2i (1-i )(1+i )(1-i )=2i (1-i )2=i(1-i)=1+i.2.C 【解析】解得N ={x |-3<x <0},M ={x |x <-1},由图中阴影部分可知,表示的是∁U M ∩N ={x |-1≤x <0}.3.A 【解析】由x 与y 正相关可排除C ,又回归方程过点(x -,y -),将x -=3,y -=3.5代入方程验算可知A 正确.4.B 【解析】由题可知能输出的函数是偶函数且存在零点,所以只有f ()x =cos x 正确,f (x )=x 2+1是偶函数但不存在零点,所以A 不正确,f ()x =e x 不是偶函数也不存在零点,所以C 不正确,f ()x =1x不是偶函数也不存在零点,所以D 不正确,综合可知只有B 正确.5.C 【解析】l 1∥l 2时,m =32,l 2:3x +4y +8=0,d =|8+2|32+42=105=2,选C.6.C 【解析】由题意得a 1=3,a 2=7,a 3=1,a 4=7,a 5=7,a 6=9,a 7=3,a 8=7,其循环周期为6,则2 015÷6=335…5,所以a 2 015=a 5=7.7.B 【解析】因为a ⊥b ,所以2()x -z +y +z =0,∴z =2x +y ,由可行域可知函数在()1,1点有最大值3.8. A 【解析】y =sin ⎝ ⎛⎭⎪⎫4x -π6――→横坐标伸长到原来的2倍y =sin ⎝ ⎛⎭⎪⎫2x -π6――→向左平移π4个单位y =sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x +π4-π6=sin ⎝ ⎛⎭⎪⎫2x +π3,所以函数y =sin ⎝ ⎛⎭⎪⎫2x +π3的对称轴为2x +π3=π2+k π,k ∈Z ,即x =π12+k π2,k ∈Z ,令k =0,x =π12为函数y =⎝⎛⎭⎪⎫2x +π3的一条对称轴.9.C 【解析】由双曲线C 1:x 2-y 23=1,可得a 1=1,b 1=3,c =2.设椭圆C 2的方程为x 2a 2+y2b2=1,(a >b >0).则||F 1A -||F 2A =2a 1=2,||F 1A +||F 2A =2a ,∴2||F 1A =2a +2,∵||F 1F 2=||F 1A =2c =4,∴2×4=2a +2,a =3.则C 2的离心率=c a =23.10.C 【解析】由三视图可知该几何体的底面形状为60°中心角为的扇形,其高为3,所以侧面积为2×3×2+2π×26×3=12+2π.11.A 【解析】因为e x f (x )>e x +3⇔e x f ()x -e x -3>0,设h ()x =e x f ()x -e x -3,则h ′()x =e xf ()x +e x f ′()x -e x =e x []f ()x +f ′()x -1>0,所以h ()x 为增函数,又因为h ()0=0,所以h ()x >0的解集为x>0.12.D 【解析】设O 是△ABC 的三边中垂线的交点,故O 是三角形外接圆的圆心,如图所示,延长AO 交外接圆于D ,AD 是⊙O 的直径,∴∠ACD =∠ABD =90°,cos ∠CAD =ACAD,cos ∠BAD =AB AD ,∴AO →·BC →=12AD →·()AC →-AB →=12AD →·AC →-12AD →·AB →=12||AC →2-12||AB →2= 12b 2-12c 2=12b 2-12()2b -b 2=b 2-b =⎝⎛⎫b -122-14,∵c 2=2b -b 2>0,∴0<b <2.令f ()b =⎝⎛⎭⎫b -122-14,所以当b =12时,有最小值-14.∵f ()0=0,f ()2=2,所以-14≤f ()b <2,所以BC →·AO →的范围是⎣⎡⎭⎫-14,2. 二、填空题13.3π3【解析】由题意得:l =2,2πr =π×2,r =1,h =l 2-r 2=3,所以圆锥的体积为V=13h πr 2=3π3. 14.6【解析】设第T r +1项为常数项,则T r +1=()-1rC r n x 2n -3r,∴2n -3r =0,∴C r n =15, ∵C 46=C 26=15,∴n =6,r =4. 15.23【解析】因为y =x 2,所以在第一象限有x =y ,则在第一象限的阴影部分的面积为⎠⎛01ydy =⎪⎪23y 3210=23,所以概率为23×42×2=23,故答案为23.16.e 2【解析】设数列{a n }的公比q ,则q >0,因为a 3a 4a 5=a 34=1,所以a 4=1,①当q >1时,则0<a 1<a 2<a 3<a 4=1<a 5<a 6,∴f (a 1)+f (a 2)+…+f (a 6)=ln a 1a 1=2a 1,∵ln a 1<0,所以等式不成立;②当q =1时,则a 1=a 2=…a 6=1,f (a 1)+f (a 2)+…+f (a 6)=0≠2a 1;③当0<q <1时,则a 1>a 2>a 3>a 4=1>a 5>a 6>0,∴f (a 1)+f (a 2)+…+f (a 6)=a 1ln a 1=2a 1,∴a 1=e 2.17题评分细则(共12分)【解析】(1)由sin B sin A =1-cos Bcos A 得sin B cos A =sin A -sin A cos B ,(2分)所以sin ()B +A =sin A ,sin ()π-C =sin A ,C =A ,(4分) 因此△ABC 为正三角形. ∴∠A =π3.(6分)(2)设该三角形的边长为a ,则S OABC =12×1×2sin θ+34a 2(8分)=sin θ+34()12+22-2×2cos θ(10分) =2sin ⎝ ⎛⎭⎪⎫θ-π3+534.(11分)显然当θ=5π6时()S OABC max=8+534.(12分)18题评分细则(共12分)【解析】(1)由直方图得:轻度拥堵的路段个数是()0.1+0.2×1×20=6个,(2分) 中度拥堵的路段个数是()0.25+0.2×1×20=9.(4分) (2) X 的可能取值为0,1,2,3.(5分)P ()X =0=C 311·C 09C 320=1176,P ()X =1=C 211·C 19C 320=3376,P ()X =2=C 111·C 29C 320=3395,P ()X =3=C 011·C 39C 320=795.(9分)(每算对一个给1分) 所以X 的分布列为(10分)E ()X =0×1176+1×3376+2×3395+3×795=513380.(12分)19题评分细则(共12分)【解析】解法一:(1)以C 为原点,分别以CB 、CA 、CC 1为x 轴、y 轴、z 轴建立空间直角坐标系,(1分)则F (1,0,0),E (1,1,0),A (0,2,0),C 1(0,0,2), AC 1→=(0,-2,2).(2分)设G (0,2,h ),则EG →=(-1,1,h ).∵AC 1⊥EG ,∴EG →·AC 1→=0. (4分)∴-1×0+1×(-2)+2h =0.∴h =1,即G 是AA 1的中点.(5分)(2)设m =(x ,y ,z )是平面EFG 的法向量,则m ⊥FE →,m ⊥EG →.(6分)所以⎩⎪⎨⎪⎧0×x +1×y +0×z =0,-x +y +z =0.令x =1,则平面EFG 的一个法向量为m =(1,0,1).(8分)∵sin θ=|m ·AC 1→||m |·|AC 1→|=22×22=12,(10分)∴θ=π6, 即AC 1与平面EFG 所成角θ为π6.(12分)解法二:(1)取AC 的中点D ,连结DE 、DG ,则ED ∥BC ,(1分) ∵BC ⊥AC ,∴ED ⊥AC .又CC 1⊥平面ABC ,而ED ⊂平面ABC ,∴CC 1⊥ED . ∵CC 1∩AC =C ,∴ED ⊥平面A 1ACC 1.(3分) 又∵AC 1⊥EG ,∴AC 1⊥DG .(4分) 连结A 1C ,∵AC 1⊥A 1C ,∴A 1C ∥DG . ∵D 是AC 的中点,∴G 是AA 1的中点. (5分)(2)取CC 1的中点M ,连结GM 、FM ,则EF ∥GM,∴E 、F 、M 、G 共面.作C 1H ⊥FM ,交FM 的延长线于H ,∵AC ⊥平面BB 1C 1C ,C 1H ⊂平面BB 1C 1C ,∴AC ⊥C 1H ,(8分)又AC ∥GM ,∴GM ⊥C 1H . ∵GM ∩FM =M ,∴C 1H ⊥平面EFG ,设AC 1与MG 相交于N 点,所以∠C 1NH 为直线AC 1与平面EFG 所成角θ. (10分)因为C 1H =22,C 1N =2,∴sin θ=222=12,∴θ=π6. (12分)20题评分细则(共12分)【解析】(1)设M ()x ,y ,P ()0,y ′,Q ()x ′,0,∵PM →=-32MQ →,HP →·PM →=0. (1分)∴()x ,y -y ′=-32()x ′-x ,-y ,()3,y ′·()x ,y -y ′=0,(2分)∴x ′=13x ,y ′=-12y ,3x +yy ′-y ′2=0,∴y 2=4x ()x >0,(4分)所以动点M 的轨迹C 是以()0,0为顶点,以()1,0为焦点的抛物线(除去原点). (5分) (2)①当直线l 与x 轴垂直时,根据抛物线的对称性,有∠AED =∠BED ;(6分) ②当l 与x 轴不垂直时,依题意可设直线l 的方程为y =k ()x -m()k≠0,m >0,设A ()x 1,y 1,B ()x 2,y 2,则A 、B 两点的坐标满足方程组⎩⎪⎨⎪⎧y =k ()x -m y 2=4x ()x >0,(7分)消去x 并整理得ky 2-4y -4km =0,∴y 1+y 2=4k ,y 1y 2=-4m . (8分)设直线AE 和BE 的斜率分别为k 1,k 2,则k 1+k 2=y 1x 1+m +y 2x 2+m =14y 1y 22+14y 2y 21+m ()y 1+y 2()x 1+m ()x 2+m=14y 1y 2()y 1+y 2+m ()y 1+y 2()x 1+m ()x 2+m =14()-4m ⎝⎛⎭⎫4k +4m k ()x 1+m ()x 2+m =0,(10分) ∴tan ∠AED +tan ()180°-∠BED =0,∴tan ∠AED =tan ∠BED .∵0<∠AED <π2,0<∠BED <π2,∴∠AED =∠BED . (11分) 综合①②可知∠AED =∠BED .(12分)21题评分细则(共12分)【解析】(1)由题意a >0,f ′(x )=e x -a ,由f ′(x )=e x -a =0得x =ln a . (1分)当x ∈(-∞,ln a )时,f ′(x )<0;当x ∈(ln a ,+∞)时,f ′(x )>0.∴f (x )在(-∞,ln a )单调递减,在(ln a ,+∞)单调递增.(2分)即f (x )在x =ln a 处取得极小值,且为最小值,其最小值为f (ln a )=e ln a -a ln a -1=a -a ln a -1.(3分)f (x )≥0对任意的x ∈R 恒成立,即在x ∈R 上,f (x )min ≥0. (4分)设g (a )=a -a ln a -1,所以g (a )≥0.由g ′(a )=1-ln a -1=-ln a =0得a =1. (5分)易知g (a )在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,∴g (a )在a =1处取得最大值,而g (1)=0.因此g (a )≥0的解为a =1,∴a =1.(6分)(2)由(1)知,对任意实数x 均有e x -x -1≥0,即1+x ≤e x . (7分)令x =-k n (n ∈N *,k =0,1,2,3,…,n -1),则0<1-k n ≤e -k n.(8分) ∴⎝⎛⎭⎫1-k n n ≤⎝⎛⎭⎫e -k n n =e -k . (9分)∴⎝⎛⎭⎫1n n +⎝⎛⎭⎫2n n +…+⎝ ⎛⎪⎫n -1n n +⎝⎛⎭⎫n n n≤e -(n -1)+e -(n -2)+…+e -2+e -1+1=1-e -n1-e -1<11-e -1=e e -1.(12分)选做题:请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号. 22题评分细则(共10分)【解析】(1)由弦切角定理知∠DBE =∠DAB ,(2分)由∠DBC =∠DAC ,∠DAB =∠DAC ,(3分)所以∠DBE =∠DBC ,即BD 平分∠CBE .(4分)(2)由(1)可知BE =BH ,(5分)所以AH ·BH =AH ·BE ,(6分)因为∠DAB =∠DAC ,∠ACB =∠ABE ,所以△AHC ∽△AEB ,(8分)所以AH AE =HC BE,即AH ·BE =AE ·HC ,(9分) 即AH ·BH =AE ·HC .(10分)23题评分细则(共10分)【解析】(1)由ρ=4cos θ得ρ2=4ρcos θ,(1分)结合极坐标与直角坐标的互化公式⎩⎪⎨⎪⎧x =ρcos θy =ρsin θ得x 2+y 2=4x ,(3分) 即(x -2)2+y 2=4.(4分)(2)由直线l 的参数方程⎩⎪⎨⎪⎧x =a +3ty =t (t 为参数)化为普通方程得,x -3y -a =0. (7分) 结合圆C 与直线l 相切,得|2-a |1+3=2,(9分) 解得a =-2或6.(10分)24题评分细则(共10分)②当a =1时,不等式的解集为{x |x =1};(9分) ③当a <1时,不等式的解集为⎣⎢⎡⎦⎥⎤2+a 3,2-a .(10分)。
