4静电场中的导体
电磁学02静电场中的导体与介质

A q -q
-q+q
UA
q'
4 0 R0
q ' 4 0R1
q q '
4 0 R2
0
可得 q ( q) 1(9略)
例4 接地导体球附近有一点电荷,如图所示。
求:导体上感应电荷的电量
R
解: 接地 即 U0
o
感应电荷分布在表面,
l
q
电量设为:Q’(分布不均匀!)
由导体等势,则内部任一点的电势为0
选择特殊点:球心o计算电势,有:
1) Dds
S
1 (
r
1) q0内
l i mq内
V0V
1 (
r
1) limq0内 V0V
1 (
r
1)0
00 0。 40
[例2] 一无限大各向同性均匀介质平板厚度为 d
表明:腔内的场与腔外(包括壳的外表面)
物理 内涵
的电荷及分布无关。
在腔内 E 腔 外表 E 腔 面外 0带
电 量 的电 体 的
二.腔内有带电体时
q
① 带电量: Q腔内 q (用高斯定理易证)
表面
23
② 腔内的电场: 不为零。
由空腔内状况决定,取决于:
*腔内电量q;
*腔内带电体及腔内壁的 几何因素、介质。
平行放置一无限大的不带电导体平板。
0 1 2 求:导体板两表面的面电荷密度。
E2 • E1 解: 设导体电荷密度为 1、 2 ,
E0 电荷守恒: 1 + 2 = 0
(1)
导体内场强为零:E0 +E1‐E2 = 0
0 1 2 0 20 20 20
(1)、(2)解得:
大学物理,静电场中的导体和电介质8-5 静电场的能量

2
R1
r
dr
Q R2 dWe wedV dr 2 8 π εr 2 2 R Q Q 1 1 2 dr We dWe ( ) 2 8 π ε R1 r 8 π ε R1 R2 9
8.5 静电场的能量
2
第8章 静电场中的导体和电介质
第8章 静电场中的导体和电介质
例:同轴电缆由内径为 R1、外径为 R2的两无限长金属圆柱 面构成,单位长度带电量分别为 +、 -,其间充有 r 电介 质。求: 1)两柱面间的场强 E;2)电势差 U;3)单位长 度电容 ;4)单位长度贮存能量。
介质中高斯定理: D dS q 0
5
8.5 静电场的能量
第8章 静电场中的导体和电介质
二、静电场的能量 能量密度 以平行板电容器为例,将电能用电场的量表示。
1 1 1 1 εS 2 2 2 2 ( Ed ) εE Sd εE V We CU 2 2 2 d 2
电场中单位体积的能量 称为电场能量密度:
d
S
εr
We we V
8.5 静电场的能量
第8章 静电场中的导体和电介质
静电场的能量 ( Electrostatic Energy ) 一个带电系统包含许多的电荷。电荷之间 存在着相互作用的电场力。 任何一个带电系统在形成的过程中,外力 必须克服电场力做功,即要消耗外界的能量。 外界对系统所做的功,应该等于系统能量 的增加。 因此,带电系统具有能量。
第8章 静电场中的导体和电介质
1 We QU 2
R1
1 λ R2 λh ln 2 2πε0 εr R1 2 λh R2 ln 4πε0 εr R1
华南师范大学电磁学习题课-静电场中的导体
15
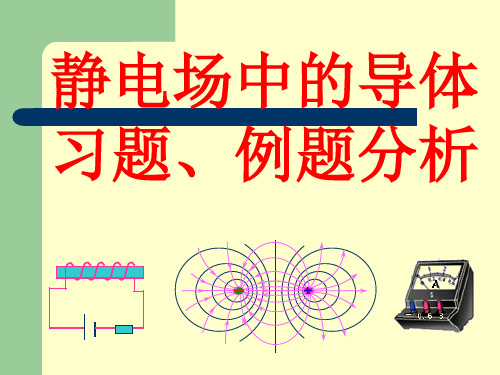
由电荷守恒定律可得 对A、C板: 1 2 5 6 0 (4) 对B 板: 3 4 (5)
A
1 2
B C
3 4
5.0cm
5 6
8.0cm
由于A、C板用导线相连,故它们电势相等,所以有
AB CB 即 E23 d 23 E54 d 54
Qq ; 4 0 r
Qq E 4 0 r 2
3
4.4 一个接地的导体球,半径为R,原来不带电. 今将一 点电荷q放在球外距球心的距离为r的地方,求球上的 感生电荷总量. r
解:因为导体球接地,故其电 势为零,即 0 设导体球上的感应电量为Q 由导体是个等势体知: o点的电势也为0 由电势叠加 原理有关系式:
荷在P1和P2点处产生的场强分别为 E 21和 E 22 由于P1和P2点非常靠近,因此可认为
P2E 22S E12 • P1 • E11 导体内 又设导体上其它地方以及导体外的电 导体外 E 21
E11 2 0
, E12
2 0
ห้องสมุดไป่ตู้E21 E22
Q外
Q内
QA B k k +k 4.5 103 (V ) R3 R3 R3
6
(2) 当球壳B接地时,A球所带电荷的电量 不变,分布也不变.
8 QA=QA 3 10 (C)
Q外 B Q 内 Q A R A 1 R2 R3
由高斯定理可得球壳B内表面上带有的电量为
8 = Q Q内 - 3 10 (C) A
• E 21
2 ˆn f E e 2 0 显然,此力方向与电荷的符号无关,总指向导体外 14 部.
1、静电场中的导体-13
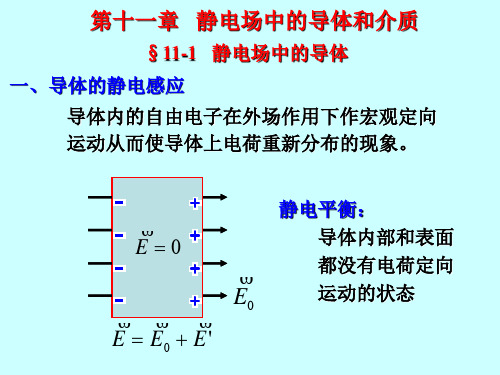
P
3S + 4S = QB
又电荷守恒,所以有: 1S + 2S = QA
Q A QB 联立得: 1 4 2S QB Q A Q A QB 3 2 2S 2S
两板中间的场强为:
1 2 3 4 E 2 0 2 0 2 0 2 0 2 0 B 2 Q A QB U AB E dl Ed d d A 0 2 0 S
U ab
b
a
E dl
0
导体整体是等势体 导体表面是等势面
E0
三、静电平衡时导体上电荷的分布
导体的静电平衡条件; 根据:
1 静电场的高斯定理: E dS S 0
q
S内
i
(1)导体内部无净电荷,电荷分布在导体表面; 在导体内任作一高斯面S ,则:
1 SE dS 0
球A与壳B之间的电势差为:
q3 q2
q1
R3 R1 R2
U AB
R2
R1
q1 1 1 q1 ( ) dr 2 4 π 0 R1 R2 4 π 0 r
q3 q2
q1
R3 R1 R2
q1 q 2 0 q2 - q1
由电荷守恒定律:
q3 q q2 q q1
考虑电荷分布的对称性,由高斯定理得:
E 0 r R1
q1 E 2 4π 0 r
R1 r R2
E 0 R3 r R2 q1 q E r R3 2 4π o r
S内
q
S内
i
=0
S
qi 0 不存在净电荷
(2)导体表面上各处的面电荷密度与该处表面外 附近的场强大小成正比;
第十章静电场中的导体和电介质

第⼗章静电场中的导体和电介质第⼗章静电场中的导体和电介质在上⼀章中,我们讨论了真空中的静电场。
实际上,在静电场中总有导体或电介质存在,⽽且在静电的应⽤中也都要涉及导体和电介质的影响,因此,本章主要讨论静电场中的导体和电介质。
本章所讨论的问题,不仅在理论上有重⼤意义,使我们对静电场的认识更加深⼊,⽽且在应⽤上也有重⼤作⽤。
§10-1 静电场中的导体⼀、静电平衡条件1、导体与电介质的区别:(1)宏观上,它们的电导率数量级相差很⼤(相差10多个数量级,⽽不同导体间电导率数量级最多就相差⼏个数量级)。
(2)微观上导体内部存在⼤量的⾃由电⼦,在外电场下会发⽣定向移动,产⽣宏观上的电流⽽电介质内部的电⼦处于束缚状态,在外场下不会发⽣定向移动(电介质被击穿除外)。
2、导体的静电平衡条件(1)导体内部任何⼀点处的电场强度为零;(2)导体表⾯处的电场强度的⽅向,都与导体表⾯垂直.导体处于静电平衡状态的必要条件:0=i E(当导体处于静电平衡状态时,导体内部不再有⾃由电⼦定向移动,导体内电荷宏观分布不再随时间变化,⾃然其内部电场(指外场与感应电荷产⽣的电场相叠加的总电场)必为0。
⼆、静电平衡时导体上的电荷分布1、导体内部没有净电荷,电荷(包括感应电荷和导体本⾝带的电荷)只分布在导体表⾯。
这个可以由⾼斯定理推得:ii sq E ds ε?=,S 是导体内“紧贴”表⾯的⾼斯⾯,所以0i q =。
2、导体是等势体,导体表⾯是等势⾯。
显然()()0b a b i a V V E dl -=?=?,a,b 为导体内或导体表⾯的任意两点,只需将积分路径取在导体内部即可。
3、导体表⾯以处附近空间的场强为:0E n δε=,δ为邻近场点的导体表⾯⾯元处的电荷密度,?n 为该⾯元的处法向。
简单的证明下:以导体表⾯⾯元为中截⾯作⼀穿过导体的⾼斯柱⾯,柱⾯的处底⾯过场点,下底⾯处于导体内部。
由⾼斯定理可得:12i s s dsE ds E ds δε?+?=,1s ,2s 分别为⾼斯柱⾯的上、下底⾯。
静电场中的导体

电风实验
++ ++
+ +
+ +
32
小结: 静电平衡导体的电荷分布 1、实心导体内部无电荷。
Q 1 4 2S Q 2 3 2S
场强分布:
A 板左侧
A
B
1 Q E 0 2 0 S
2 3 Q E 0 0 2 0 S
1 2 3 4 E E E
两板之间
B 板右侧
4 Q E 0 2 0 S
应用:精密测量上的仪器屏蔽罩、屏蔽室、高压 带电作业人员的屏蔽服(均压服)等。
正误题:
1、导体放入电场中,自由电荷要重新分布。两端感应 出的正负电荷一定相等。此时,导体两端的电势相等, 但符号相反。 E 2、带电导体表面附近的电场强度 方向总是与表面 0 垂直,与外部是否存在其它带电体无关; 3、将带+Q的导体A移近不带电的孤立导体B时,B的电势将 升高;如果B是接地的,则B的电势就保持不变,且UB=0 4、导体静电平衡时,内部场强必为零。
静电场中的导体和电介质
主要内容: 导体静电平衡条件和性质
▲
电场中导体和电介质的电学性质 有电介质时的高斯定理 电容器的性质和计算 静电场的能量
▲ ▲
▲
静电场中的导体
Effects of Conductor in Electrostatic Field
一、静电感应
6 大学物理 第06章 静电场中的导体和电介质
E外
16
物理学
第五版
+ + + + + + + + + +
第六章 静电场中的导体和电介质 加上外电场后
E外
17
物理学
第五版
+ + + + + + + + + +
E外
加上外电场后 第六章 静电场中的导体和电介质
18
物理学
第五版
导体达到静平衡
+ + + + + + + + + +
介质电容率 ε ε0 εr
41
- - - - - - - σ
相对电容率 εr 1
第六章 静电场中的导体和电介质
物理学
第五版
+++++++
- - - - - - - σ
σ E0 ε0
ε0
σ
+++++++
- - - - - - - σ
σ E ε
ε
σ
第六章 静电场中的导体和电介质
②用导线连接A、B,再作计算
连接A、B,
Q q
q
( q )
中和
B
q q
A R1 O
R2
球壳外表面带电 Q q
R3
r R3
R3
E0
Qq uo Edr Edr 4 0 R3 0 R3
第14章-大学物理静电场中的导体
***物质分类***9导体•导体内存在大量的自由电子(在晶格离子的正电背景下)•导体的电中性与带电状态;自由电子的热运动9绝缘体•与导体相对,绝缘体内没有可自由移动的电子半导体•导体、电介质(绝缘体和半导体)与静电场作用的物理机制各不相同半导体内有少量的可自由移动的电荷用的物理机制各不相同。
14静电场中的导体体第14 章静电场中的导1414--1 导体的静电平衡性质1414--2 静电平衡的导体上的电荷分布1414--3 有导体存在时静电场的分析与计算1414--4 静电屏蔽§(实心)导体的静电平衡性质静电感应一、导体的静电平衡状态静电感应:在外电场作用下,导体内自电有宏体表由电子有宏观移动,导体表面出现宏观电荷分布的现象。
+-静电平衡:-F -+++--0'0E E E =+=当导体内部和表面都没有宏观的电荷移动时,导体处于静电此时感应电荷产生的E+-平衡。
此时,感应电荷产生的附加电场与外加电场在导体内部相抵消部相抵消。
二、导体的静电平衡条件(1)导体内部,场强处处为零。
否则,自由电子将继续有宏观移动。
0'E E E =+ 0=(2)导体表面外的场强垂直于导体的表面。
否则,自由电子将继续沿表面宏观移动。
E-F在导体内任意两点间的电势差为三、导体的电势在导体内任意两点间的电势差为:a•∫⋅−=−)()(d b a a b lE V V=b•a bV V = ,0 )1(=E•处于静电平衡时,导体中各点导体内部;电势相等;•导体成为等势体,导体表面为(2) d 0,E l ⋅= 导体表面等势面。
导体表面。
四、导体上电荷的分布1. 电荷只分布在导体表面上,导体内部处处不带电在导体内任取高斯面由高斯定在导体内任取一高斯面S ,由高斯定理:++++++d 0SE S ⋅=∫0=E S+++++0=E 0d ==∫∑V q Vρ内+++++++++内S 内∵高斯面为任意形状0=ρ(导体内部)导体内部没有净电荷,电荷只能分布在导体表面。
静电场中的导体与电介质---常见疑问解答
静电场中的导体与电介质---常见疑问解答1. 无限大均匀带电平面(面电荷密度为σ)两侧场强为)2/(0εσ=E ,而在静电平衡状态下,导体表面(该处表面面电荷密度为σ)附近场强为0/εσ=E ,为什么前者比后者小一半?参考解答:关键是题目中两个式中的σ不是一回事。
下面为了讨论方便,我们把导体表面的面电荷密度改为σ′,其附近的场强则写为./0εσ'=E对于无限大均匀带电平面(面电荷密度为σ),两侧场强为)2/(0εσ=E .这里的 σ 是指带电平面单位面积上所带的电荷。
对于静电平衡状态下的导体,其表面附近的场强为./0εσ'=E这里的 σ′是指带电导体表面某处单位面积上所带的电荷。
如果无限大均匀带电平面是一个静电平衡状态下的无限大均匀带电导体板,则σ是此导体板的单位面积上(包括导体板的两个表面)所带的电荷,而σ′仅是导体板的一个表面单位面积上所带的电荷。
在空间仅有此导体板(即导体板旁没有其他电荷和其他电场)的情形下,导体板的表面上电荷分布均匀,且有两表面上的面电荷密度相等。
在此情况下两个面电荷密度间的关系为σ =2σ′。
这样,题目中两个E 式就统一了。
2. 把一个带电物体移近一个导体壳,带电体单独在导体壳的腔内产生的电场是否为零?静电屏蔽效应是如何发生的?参考解答:把一个带电物体移近一个导体壳时,带电体单独在导体壳的腔内产生的电场不是零,因为带电物体在空间任何一点都可以产生电场。
本题正确的说法是:带电物体上的电荷和导体壳外表面上的感应电荷在导体壳外表面以内空间(包括导体金属部分占据的空间和导体壳的腔内空间)所产生的合电场为零(详细解释仍需用到“惟一性定理”),也可以说是在导体壳外表面以内空间,导体壳外表面上感应电荷的电场把带电物体上电荷所产生的电场给抵消了。
正因有以上结论,一个导体壳可以保护其腔内空间不受导体壳外带电体的影响,这就是静电屏蔽(接地导体壳可保护壳外空间不受腔内带电体的影响也是静电屏蔽)。
第二章-静电场与导体
第二章静电场与导体教学目的要求:1、深入理解并掌握导体的静电平衡条件及静电平衡时导体的基本性质,加深对高斯定理和环路定理的理解,结合应用电场线这一工具,会讨论静电平衡的若干现象,会结合静电平衡条件去理解静电感应、静电屏蔽等现象,并会利用前章的知识求解电场中有导体存在时的场强和电势分布。
2、确理解电容的概念,并能计算几种特殊形式的电容器的电容值。
3、进一步领会静电能的概念、会计算一些特殊带电导体的静电能。
4、深刻理解电场能量的概念,会计算电场能。
教学重点:1、静电场中的导体2、电容和电容器教学难点:1、静电场的唯一定理§2.1 静电场中的导体§2.2 电容和电容器§2.3 静电场的能量§2.1 静电场中的导体1、导体的特征功函数(1)金属导体的特征金属可以看作固定在晶格点阵上的正离子(实际上在作微小振动)和不规则运动的自由电子的集合。
①大量自由电子的运动与理想气体中分子的运动相同,服从经典的统计规律。
②自由电子在电场作用下将作定向运动,从而形成金属中的电流。
③自由电子的平均速率远大与定向运动速率。
(2)功函数金属表面存在一种阻止自由电子从金属逸出的作用,电子欲从金属内部逸出到外部,就要克服阻力作功。
一个电子从金属内部跑到金属外部必须作的最小功称为逸出功,亦称功函数。
2、导体的静电平衡条件(1)什么是静电感应?当某种原因(带电或置于电场中)使导体内部存在电场时,自由电子受到电场力的作用而作定向运动,使导体一侧因电子的聚集而出现负电荷布另一侧因缺少电子而有正电荷分布,这就是静电感应,分布在导体上的电荷便是感应电荷。
(2)静电平衡状态当感应电荷在导体内产生的场与外场完全抵消时,电子的定向运动终止,导体处于静电平衡状态。
(3)静电平衡条件所有场源包括导体上的电荷共同产生的电场的合场强在导体内部处处为零。
静电平衡时:①导体是等势体。
②导体外表面附近的电场强度与导体表面垂直。
