数学人教版八年级下册三角形的中位线练习题
专题14 直角三角形斜边上的中线-2020-2021学年八年级数学下册常考题专练(人教版)(解析版)

专题14直角三角形斜边上的中线★知识归纳●直角三角形斜边上的中线的性质直角三角形斜边上的中线等于斜边的一半.要点梳理:(1)直角三角形斜边上的中线的性质是矩形性质的推论.性质的前提是直角三角形,对一般三角形不可使用.(2)学过的直角三角形主要性质有:①直角三角形两锐角互余;②直角三角形两直角边的平方和等于斜边的平方;③直角三角形中30°所对的直角边等于斜边的一半.(3)性质可以用来解决有关线段倍分的问题.★实操夯实一.选择题(共16小题)1.如图,在三角形ABC中,AB=AC,BC=6,三角形DEF的周长是7,AF⊥BC于F,BE⊥AC于E,且点D是AB的中点,则AF=()A.B.C.D.7【解答】解:∵AF⊥BC,BE⊥AC,D是AB的中点,∴DE=DF=AB,∵AB=AC,AF⊥BC,∴点F是BC的中点,∴BF=FC=3,∵BE⊥AC,∴EF=BC=3,∴△DEF的周长=DE+DF+EF=AB+3=7,∴AB=4,由勾股定理知AF==,故选:B.2.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为()A.3B.3.5C.4D.4.5【解答】解:∵∠ACB=90°,∠ABC=60°,∴∠A=30°,∵BD平分∠ABC,∴∠CBD=∠DBA=30°,∴BD=AD,∵AD=6,∴BD=6,∵P点是BD的中点,∴CP=BD=3.故选:A.3.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离()A.不变B.变小C.变大D.无法判断【解答】解:不变.连接OP,在Rt△AOB中,OP是斜边AB上的中线,那么OP=AB,由于木棍的长度不变,所以不管木棍如何滑动,OP都是一个定值.故选:A.4.如图,∠ABC=∠ADC=Rt∠,E是AC的中点,则()A.∠1>∠2B.∠1=∠2C.∠1<∠2D.∠1与∠2大小关系不能确定【解答】解:∵∠ABC=∠ADC=90°,E是AC的中点,∴DE=AC,BE=AC,∴DE=BE,∴∠1=∠2.故选:B.5.如图,在△ABC中,∠ACB=90°,AC=8,BC=6,点D为斜边AB上的中点,则CD为()A.10B.3C.5D.4【解答】解:在Rt△ABC中,AC=8,BC=6,∴AB===10,∵点D为斜边AB上的中点,∴CD=AB=×10=5,故选:C.6.已知直角三角形斜边上的中线长为3,则斜边长为()A.3B.6C.9D.12【解答】解:∵直角三角形斜边上的中线长为3,∴斜边长是6.故选:B.7.直角三角形的斜边长为6cm,则斜边上的中线长为()A.2cm B.2.5cm C.3cm D.4cm【解答】解:直角三角形的斜边长为6cm,则斜边上的中线长为3cm,故选:C.8.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,CE为AB边上的中线,AD=2,CE=10,则CD=()A.2B.3C.4D.6【解答】解:在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=10,∴AE=CE=10,∵AD=2,∴DE=8,∵CD为AB边上的高,在Rt△CDE中,CD===6,故选:D.9.在Rt△ABC中,∠ACB=90°,AB=6cm,D为AB的中点,则CD等于()A.2cm B.2.5cm C.3cm D.4cm【解答】解:∵∠ACB=90°,D为AB的中点,∴CD=AB=×6=3cm.故选:C.10.如图,在△ABC中,∠BAC=90°,点D在BC延长线上,且AD=BC,若∠D=40°,则∠B=()A.10°B.20°C.30°D.40°【解答】解:取BC的中点E,连接AE,∵∠BAC=90°,点E是BC的中点,∴AE=BC=BE,∴∠B=∠EAB,∵AD=BC,∴AE=AD,∴∠AED=∠D=40°,∴∠B=20°,故选:B.11.如图,△ABC中,AB=AC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则DE的长为()A.10B.6C.8D.5【解答】解:∵AB=AC=10,AD平分∠BAC,∴AD⊥BC,∵E为AC的中点,∴DE=AC=×10=5,故选:D.12.如图在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=3,BC=8,则△EFM的周长是()A.21B.15C.13D.11【解答】解:∵CF⊥AB,BE⊥AC,M为BC的中点,∴EM=FM=BC=×8=4,∴△EFM的周长=8+8+3=11.故选:D.13.如图,边长为2的等边三角形ABC,点A,B分别在y轴和x轴正半轴滑动,则原点O到C的最长距离()A.B.C.D.【解答】解:取AB的中点D,连接OD,CD,在△OCD中,OC<OD+CD,只有当O,D,C三点在一条线上时,OC=OD+CD,此时OC最大,如图所示,OC⊥AB,∵△AOB为等腰直角三角形,AB=2,∴OD=AB=1,在Rt△BCD中,BC=2,BD=1,根据勾股定理得:CD==,∴OC=+1.故选:D.14.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是()A.2.5B.C.D.2【解答】解:如图,连接AC、CF,∵正方形ABCD和正方形CEFG中,BC=1,CE=3,∴AC=,CF=3,∠ACD=∠GCF=45°,∴∠ACF=90°,由勾股定理得,AF===2,∵H是AF的中点,∴CH=AF=×2=.故选:B.15.如图,△ABC中,∠A+∠B=90°,AD=DB,CD=3,则AB的长度为()A.3B.4C.5D.6【解答】解:∵△ABC中,∠A+∠B=90°,∴∠ACB=90°.∵AD=DB,∴CD是该直角三角形斜边AB上的中线,∴AB=2CD=6.故选:D.16.如图,在△ABC中,AB=AC=3,BC=4,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是()A.3B.4C.5D.6【解答】解:∵在△ABC中,AB=AC=3,AE平分∠BAC,∴BE=CE=BC=2,又∵D是AB中点,∴BD=AB=,∴DE是△ABC的中位线,∴DE=AC=,∴△BDE的周长为BD+DE+BE=++2=5.故选:C.二.填空题(共7小题)17.如图,BE、CF分别是△ABC的高,M为BC的中点,EF=4,BC=10,则△EFM的周长是14.【解答】解:∵BE、CF分别是△ABC的高,M为BC的中点,BC=8,∴在Rt△BCE中,EM=BC=5,在Rt△BCF中,FM=BC=5,又∵EF=4,∴△EFM的周长=EM+FM+EF=5+5+4=14.故答案是:14.18.如图,已知△ABC中,AB=AC,AD平分∠BAC,E是AC的中点,若AB=6,则DE的长为3.【解答】解:∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴∠ADC=90°,∵点E为AC的中点,∴DE=AC=3.故答案为:3.19.如图所示,在△ABC中,∠C=2∠B,点D是BC上一点,AD=5,且AD⊥AB,点E是BD上的点,AE=BD,AC=6.5,则AB的长度为12.【解答】解:∵Rt△ABD中,AE=BD,∴AE=BE=DE;∴∠B=∠BAE,即∠AED=2∠B;∵∠C=2∠B,∴∠AEC=∠C,即AE=AC=6.5;∴BD=2AE=13;由勾股定理,得:AB==12.20.如图,△AEF是直角三角形,∠AEF=90°,B为AE上一点,BG⊥AE于点B,GF∥BE,且AD=BD=BF,∠BFG=60°,则∠AFG的度数是20°.【解答】解:∵四边形BEFG是长方形,∴FG∥BE,∴∠FBE=∠BFG=60°,∵AD=BD=BF,∴∠A=∠ABD,∠BDF=∠BFD,∵∠BDF=∠DFB=∠A+∠ABD=2∠A,∴∠EBF=∠A+∠AFB=3∠A=60°,∴∠A=20°,∵FG∥BE,∴∠AFG=∠A=20°,故答案为:20°.21.如图,在△ABC中,∠BAC=90°,点D是BC的中点,点E、F分别是AB、AC上的动点,∠EDF=90°,M、N分别是EF、AC的中点,连接AM、MN,若AC=6,AB=5,则AM﹣MN的最大值为.【解答】解:如图,连接DM,DN,由图可以得到M的轨迹是一条线段(AD的垂直平分线的一部分),M在AN上的时候最大(此时AM最大,MN最小),当M在AN上时,设AM=x,则MN=3﹣x,DM=AM=x,DN=AB=,在直角三角形DMN中,根据勾股定理,得DM2=DN2+MN2,∴x2=(3﹣x)2+2.52,解得x=,∴3﹣x=,此时AM﹣MN=﹣=.∴AM﹣MN的最大值为.故答案为:.22.如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=CD,过点B 作BE∥DC交AF的延长线于点E,则BE的长为6.【解答】解:∵Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,∴CD=AB=4.5.∵CF=CD,∴DF=CD=×4.5=3.∵BE∥DC,∴DF是△ABE的中位线,∴BE=2DF=6.故答案为6.23.如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=50°,则∠ACB′=10°.【解答】解:∵∠ACB=90°,∠B=50°,∴∠A=40°,∵∠ACB=90°,CD是斜边上的中线,∴CD=BD,CD=AD,∴∠BCD=∠B=50°,∠DCA=∠A=40°,由翻折变换的性质可知,∠B′CD=∠BCD=50°,∴∠ACB′=∠B′CD﹣∠DCA=10°,故答案为:10°.三.解答题(共4小题)24.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.(1)求证:CG=EG.(2)已知BC=13,CD=5,连接ED,求△EDC的面积.【解答】(1)证明:连接DE,在Rt△ADB中,点E是AB的中点,∴DE=AB=AE,∵CD=AE,∴DE=DC,又DG⊥CE,∴CG=EG.(2)解:作EF⊥BC于F,∵BC=13,CD=5,∴BD=13﹣5=8,∵DE=BE,EF⊥BC,∴DF=BF=4,∴EF===3,∴△EDC的面积=×CD×EF=×5×3=7.5.25.如图:BE、CF是锐角△ABC的两条高,M、N分别是BC、EF的中点,若EF=6,BC=24.(1)证明∠ABE=∠ACF;(2)判断EF与MN的位置关系,并证明你的结论;(3)求MN的长.【解答】解:(1)∵BE、CF是锐角△ABC的两条高,∴∠ABE+∠A=90°,∠ACF+∠A=90°,∴∠ABE=∠ACF;(2)MN垂直平分EF.证明:如图,连接EM、FM,∵BE、CF是锐角△ABC的两条高,M是BC的中点,∴EM=FM=BC,∵N是EF的中点,∴MN垂直平分EF;(3)∵EF=6,BC=24,∴EM=BC=×24=12,EN=EF=×6=3,由勾股定理得,MN===3.26.拓展:如图四边形ABCD中,∠ABC=∠ADC=90°,E是AC中点,EF平分∠BED交BD于点F.(1)猜想EF与BD具有怎样的关系?(2)试证明你的猜想.【解答】解:(1)EF垂直平分BD,(2)∵∠ABC=∠ADC=90°,E是AC中点,∴BE=AE=EC,ED=AE=EC,∴BE=DE,∵EF平分∠BED交BD于点F,∴EF⊥BD,BF=FD,即EF垂直平分BD.27.如图,在Rt△ABC中,∠ACB=90°,M是斜边AB的中点,AM=AN,∠N+∠CAN=180°.求证:MN=AC.【解答】证明:∵∠ACB=90°,M是斜边AB的中点,∴CM=AM,∴∠MCA=∠MAC,∵AM=AN,∴∠AMN=∠ANM,∵∠N+∠CAN=180°,∴AC∥MN,∴∠AMN=∠MAC,∴∠AMC=∠NAM,∴AN∥MC,又AC∥MN,∴四边形ACMN是平行四边形,∴MN=AC.。
八年级数学三角形中位线培优专题训练

八年级数学三角形中位线培优专题训练一、内容提要1. 三角形中位线平行于第三边,并且等于第三边的一半。
梯形中位线平行于两底,并且等于两底和的一半。
2. 中位线性质定理的结论,兼有位置和大小关系,可以用它判定平行,计算线段的长度,确定线段的和、差、倍关系。
3. 运用中位线性质的关键是从出现的线段中点,找到三角形或梯形,包括作出辅助线。
4. 中位线性质定理,常与它的逆定理结合起来用。
它的逆定理就是平行线截比例线段定理及推论,①一组平行线在一直线上截得相等线段,在其他直线上截得的线段也相等 ②经过三角形一边中点而平行于另一边的直线,必平分第三边 ③经过梯形一腰中点而平行于两底的直线,必平分另一腰 5. 有关线段中点的其他定理还有: ①直角三角形斜边中线等于斜边的一半②等腰三角形底边中线和底上的高,顶角平分线互相重合 ③对角线互相平分的四边形是平行四边形 ④线段中垂线上的点到线段两端的距离相等 因此如何发挥中点作用必须全面考虑。
二、例题例1. 已知:△ABC 中,分别以AB 、AC 为斜边作等腰直角三角形ABM 和CAN ,P 是BC 的中点。
求证:PM =PN证明:作ME ⊥AB ,NF ⊥AC ,垂足E ,F ∵△ABM 、△CAN 是等腰直角三角形∴AE =EB=ME ,AF =FC =NF ,根据三角形中位线性质 PE =21AC =NF ,PF =21AB =MEPE ∥AC ,PF ∥AB∴∠PEB =∠BAC =∠PFC 即∠PEM =∠PFN∴△PEM ≌△PFN ∴PM =PN例2.已知△ABC 中,AB =10,AC =7,AD 是角平分线,CM ⊥AD 于M ,且N 是BC 的中点。
求MN 的长。
分析:N 是BC 的中点,若M 是另一边中点, 则可运用中位线的性质求MN 的长, 根据轴称性质作出△AMC 的全等三角形即可。
辅助线是:延长CM 交AB 于E (证明略 例3.如图已知:△ABC 中,AD 是角平分线,BE =CF ,M 、N 分别是BC 和EF 的中点 求证:MN ∥AD 证明一:连结EC ,取EC 的中点P ,连结PM 、PNP NMP ∥AB ,MP =21AB ,NP ∥AC ,NP =21AC ∵BE =CF ,∴MP =NP∴∠3=∠4=2MPN-180∠∠MPN +∠BAC =180(两边分平行的两个角相等或互补)∴∠1=∠2=2MPN-180∠ , ∠2=∠3∴NP ∥AC ∴MN ∥AD证明二:连结并延长EM 到G ,使MG =ME 连结CG ,FG则MN ∥FG ,△MCG ≌△MBE ∴CG =BE =CF ∠B =∠BCG∴AB ∥CG ,∠BAC +∠FCG =180∠CAD =21(180-∠FCG ) ∠CFG =21(180-∠FCG )=∠CAD ∴ MN ∥AD 例4. 已知:△ABC 中,AB =AC ,AD 是高,CE 是角平分线,EF ⊥BC 于F ,GE ⊥CE交CB 的延长线于G 求证:FD =41CG 证明要点是:延长GE 交AC 于H , 可证E 是GH 的中点过点E 作EM ∥GC 交HC 于M ,则M 是HC 的中点,EM ∥GC ,EM =21GC由矩形EFDO 可得FD =EO =21EM =41GC三、练习1. 如图11,M 、P 分别为△ABC 的AB 、AC 上 的点,且AM=BM ,AP=2CP ,BP 与CM 相交于N ,已知PN=1,则PB 的长为 ( ) A. 2 B. 3 C .4 D. 52. 如图12,△ABC 中,∠B =2∠C ,AD ⊥BC 于D ,M 为BC 的中点,AB=10,则MD 的长为 ( )A. 10B. 8 C .6 D. 53. 如图13,△ABC 是等边三角形,D 、E 、F 分别是AB 、BC 、AC 的中点,P 为不同于B 、E 、C 的BC 上的任意一点,△DPH 为等边三角形.连接FH ,则EP 与FH 的大小关系是 ( ) A. E P>FH B. EP=FH C. EP<FH D.不确定4. 如图14,在△ABC 中,AD 平分∠BAC ,BD ⊥AD ,DE ∥AC ,交AB 于E ,若AB=5,则DE 的长为 .C5. 如图15,△ABC中,AB=4,AC=7,M为BC的中点,AD平分∠BAC,过M作MF∥AD,交AC于F,则FC的长等于.6. 如图25,P为△ABC内一点,∠P AC=∠PBC,PM⊥AC于M,PN⊥BC于N.D是AB的中点.求证:DM=DN7. 如图16,在△ABC中,D、E是AB、AC上的点,且BD=CE,M、N分别是BE、CD的中点,直线MN分别交AB、AC于P、Q.求证:AP=AQ8. 如图17,BE、CF是△ABC的角平分线,AN⊥BE于N,AM⊥CF于M.求证:MN∥BC.9. 如图18,在△ABC中,AD平分∠BAC,AD=AB,CM⊥AD于M.求证:AB+AC=2AM10.如图19,四边形ABCD中,G、H分别是AD、BC的中点,AB=CD.BA、CD的延长线交HG的延长线于E、F.求证:∠BEH=∠CFH.1. 如图20,在△ABC中,∠ABC=2∠C,AD平分∠BAC,过BC的中点M作ME⊥AD,交BA的延长线于E,交AD的延长线于F.求证:12BE BD.2. 如图21,在△ABC中,AB<AC,P为AC上的点,CP=AB,K为AP的中点,M为BC的中点,MK的延长线交BA的长线于N.求证:AN=AK.3. 如图22,分别以△ABC的边AC、BC为腰,A、B为直角顶点,作等腰直角△ACE和等腰直角△BCD,M为ED的中点.求证:AM⊥BM.4. 如图23,点O是四边形ABCD内一点,∠AOB=∠COD=1200,AO=BO,CO=DO,E、F、G分别为AB、CD、BC的中点.求证:△EFG为等边三角形.5. 如图24,△ABC中,M是AB的中点,P是AC的中点,D是MB的中点,N是CD的中点,Q是MN的中点,直线PQ交MB于K.求证:K是DB的中点.6. 如图25,P为△ABC内一点,∠P AC=∠PBC,PM⊥AC于M,PN⊥BC于N.D是AB的中点.求证:DM=DN图21 图22 图23 图24 图257. 如图26,AP是△ABC的角平分线,D、E分别是AB、AC上的点,且BD=CE.又G、H分别为BC、DE的中点.求证:HG∥AP.8. 如图27,已知△ABD和△ACE都是直角三角形,且∠ABD=∠ACE=900,如图(a),连接DE,设M为DE的中点.(1)求证:MB=MC;(2)设∠BAD=∠CAE,固定△ABD,让Rt△ACE绕顶点A在平面内旋转到图(b)的位置,试问MB=MC是否成立?并证明其结论.9. 已知△ABC面积为S,作直线l∥BC,交AB于D,交AC于E,若△BED的积为K.求证:S≥4K.10.如图28,在△ABC中,AB=AC,D是BC边上的一点,E是线段AD上的一点.且∠BED=2∠CED=∠BAC.求证:BD=2CD.图26 图27。
与三角形的中位线有关的问题求解-【微专题】2022-2023学年八年级数学下册常考点微专题提分精练
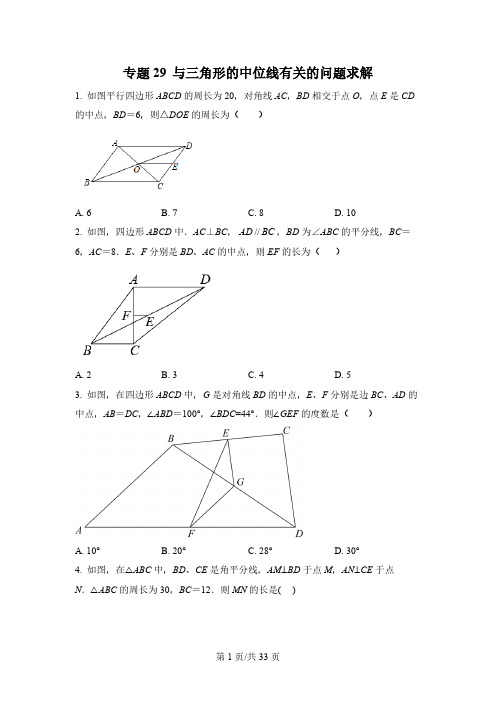
专题29 与三角形的中位线有关的问题求解1. 如图平行四边形ABCD的周长为20,对角线AC,BD相交于点O,点E是CD 的中点,BD=6,则△DOE的周长为()A. 6B. 7C. 8D. 102. 如图,四边形ABCD中.AC⊥BC,AD//BC,BD为∠ABC的平分线,BC=6,AC=8.E、F分别是BD、AC的中点,则EF的长为()A. 2B. 3C. 4D. 53. 如图,在四边形ABCD中,G是对角线BD的中点,E、F分别是边BC、AD的中点,AB=DC,∠ABD=100°,∠BDC=44°.则∠GEF的度数是( )A. 10°B. 20°C. 28°D. 30°4. 如图,在△ABC中,BD、CE是角平分线,AM⊥BD于点M,AN⊥CE于点N.△ABC的周长为30,BC=12.则MN的长是( )A. 15B. 9C. 6D. 35. 如图,在△ABC 中,AB =10,BC =6,点D 为AB 上一点,BC =BD ,BE ⊥CD 于点E ,点F 为AC 的中点,连接EF ,则EF 的长为( )A. 1B. 2C. 3D. 46. 如图,△ABC 以点O 为旋转中心,旋转180°后得到△A ′B ′C ′,ED 是△ABC 的中位线,经旋转后为线段E ′D ′.已知ED =6,则B ′C ′等于( )A. 8B. 10C. 12D. 147. 如图,在平行四边形ABCD 中,点M 为边AD 上一点,2AM MD =,点E ,点F 分别是,BM CM 中点,若6EF =,则AM 的长为__________.8. 如图,▱ABCD 中,∠B =60°,AB =4,AE ⊥BC 于E ,F 为边CD 上一动点,连接AF 、EF ,点G ,H 分别为AF 、EF 的中点,则GH 的长为_____.9. 如图,Rt△ABC中,∠ACB=90°,∠A=30°,AB=6,点P是AC边上的一个动点,将线段BP绕点B顺时针旋转60°得到线段BQ,连接CQ,则在点P运动过程中,线段CQ的最小值为________.10. 如图,在△ABC中,∠BAC=90°,点D是BC的中点,点E、F分别是直线AB、AC上的动点,∠EDF=90°,M、N分别是EF、AC的中点,连接AM、MN,若AC=6,AB=5,则AM-MN的最大值为________.11. 如图,已知在Rt△ABC中,∠ACB=90°,点D是AC延长线上的一点,AD =24,点E是BC上一点,BE=10,连接DE,M、N分别是AB、DE的中点,则MN=____.12. 如图,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点,若AE =3,EM+CM 的最小值为_____.13. 如图,在四边形ABCD 中,90,4ABC AB BC ∠=︒==,E ,F 分别是,AD CD 的中点,连接,,BE BF EF ,若四边形ABCD 的面积为12,则BEF △的面积为________.三、解答题14. 如图1,直线AB 和直线AC 相交于A 点()4,0-,B 、C 分别在y 轴的正半轴和负半轴上,且2OB OC =,C 点坐标为()0,2-.(1)求直线AB 的函数表达式;(2)在线段AC 上找一点P ,使得2ABP ACO S S ∆∆=,求P 点的坐标;(3)如图2,D 点为线段AO 的中点,若点Q 是线段AB (不与点A 、B 重合)上一点,且使得DQA OQB ∠=∠,请求出Q 点坐标.15. 如图1,在四边形ABCD 中,AC 和BD 相交于点O ,,AO CO BCA CAD =∠=∠.(1)求证:四边形ABCD 是平行四边形;(2)如图2,E ,F ,G 分别是,,BO CO AD 的中点,连接,,EF GE GF ,若2,15,16BD AB BC AC ===,求EFG 的周长.16. 如图,在 ABCD 中,∠ABC ,∠BCD 的平分线交于点F ,E 是边BC 的中点,连接EF ,AF ,AF 的延长线交边CD 于点G ,BF 的延长线交CD 的延长线于点H .(1)∠BFC = °;(2)求证:BC =CH ;(3)若EF =5,AB =6,求CG 的长.17. 如图,在平行四边形ABCD 中,对角线AC ,BD 相交于点O ,2BD AB =,点E 为线段OC 的中点.(1)求证:2ABO ODE ∠=∠;(2)若F ,G 分别是OB ,AD 的中点.①判断EFG 的形状并证明你的结论;②当EF EG ⊥,且AB =ABCD 的面积.18. 已知,在ABC 中,点M 是BC 的中点,点D 是线段AM 上一点(不与点A 重合).过点D 作AB 的平行线,过点C 作AM 的平行线,两线交于点E ,连结AE .(1)如图1,当点D 与M 重合时,求证:四边形ABDE 是平行四边形;(2)如图2,当点D 不与M 重合时,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由;(3)图3,延长BD 交AC 于点H ,若BH AC ⊥,且BH AM =,求CAM ∠的度数.19. 如图,在△ABC 中,∠ACB =90°,AC =BC ,D 为BC 边的中点,过点B 作BF ⊥AB 交AD 的延长线于点F ,CE 平分∠ACB 交AD 于点E .(1)判断四边形CEBF 的形状,并证明;(2)若AD =,求BF 及四边形CEBF 的面积.20. 如图1,在△ABC 中,∠A =120°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接BE ,点M ,N ,P 分别为DE ,BE ,BC 的中点,连接NM ,NP .(1)图1中,线段NM ,NP 的数量关系是 ,∠MNP 的度数为 ;(2)把△ADE绕点A顺时针旋转到如图2所示的位置,连接MP.求证:△MNP 是等边三角形;(3)把△ADE绕点A在平面内旋转,若AD=2,AB=5,请直接写出△MNP面积的最大值.专题29 与三角形的中位线有关的问题求解【1题答案】【答案】C【解析】【分析】根据平行四边形的对边相等和对角线互相平分可得,OB=OD,又因为E点是CD的中点,可得OE是△BCD的中位线,可得OE=12BC,所以易求△DOE 的周长.【详解】解:∵▱ABCD的周长为20,∴2(BC+CD)=20,则BC+CD=10.∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=6,∴OD=OB=12BD=3.∵点E是CD的中点,点O是BD的中点,∴OE是△BCD的中位线,DE=12CD,∴OE=12BC,∴△DOE的周长=OD+OE+DE=12BD+12(BC+CD)=5+3=8,故选:C.【点睛】本题考查了三角形中位线定理、平行四边形的性质,解题的关键是掌握平行四边形对角线互相平分、平行四边形的对边相等.【2题答案】【答案】A【解析】【分析】根据勾股定理得到AB=10,根据平行线的性质和角平分线的定义得到∠ABD=∠ADB,求得AB=AD=10,连接BF并延长交AD于G,根据全等三角形的性质得到BF=FG,AG=BC=6,求得DG=10-6=4,根据三角形中位线定理即可得到结论.【详解】解:∵AC⊥BC,∴∠ACB=90°,∵BC=6,AC=8.∴10AB==,∵AD BC∥,∴∠ADB=∠DBC,∵BD为∠ABC的平分线,∴∠ABD=∠CBD,∴∠ABD=∠ADB,∴AB=AD=10,连接BF并延长交AD于G,∵AD BC∥,∴∠GAC=∠BCA,∵F是AC的中点,∴AF=CF,在△AFG和△CFB中,AFG CFBGAC BCA AF CF⎧∠=∠⎪⎪∠=∠⎨⎪=⎪⎩,∴△AFG≌△CFB(AAS),∴BF=FG,AG=BC=6,∴DG=10-6=4,∵E是BD的中点,∴EF= 12DG=2.故选:A.【点睛】此题考查了三角形的中位线定理,全等三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.【3题答案】【答案】C【解析】【分析】根据三角形中位线定理得到EG ∥CD ,12EG CD =,FG ∥AB ,12FG AB =,再求出124EGF ∠=︒,根据等腰三角形的性质和三角形内角和定理,即可得出答案.【详解】∵点E ,G 分别是BC ,BD 的中点,∴EG ∥CD ,12EG CD =,∴44BGE BDC ∠=∠=︒,∵点F ,G 分别是AD ,BD 的中点,∴FG ∥AB ,12FG AB =,∴100ABD FGD ∠=∠=︒,∴18080,BGF ABD ∠=︒-∠=︒∴8044124,EGF ∠=︒+︒=︒∵AB =CD ,∴GE =GF ,∴1(180124)282GEF GFE ∠=∠=⨯︒-︒=︒,故选:C .【点睛】本题考查三角形中位线定理,等腰三角形的判定与性质,三角形内角和定理和平行线的性质,掌握三角形中位线定理,等腰三角形的判定与性质,三角形内角和定理是解题关键.【4题答案】【答案】D【解析】【分析】延长AM、AN分别交BC于点F、G,根据BN为∠ABC的角平分线,AN⊥BN得出∠BAN=∠G,故△ABG为等腰三角形,所以BN也为等腰三角形的中线,即AN=GN.同理AM=MF,根据三角形中位线定理即可得出结论.【详解】∵△ABC的周长为30,BC=12.∴AB+AC=30﹣BC=18.延长AN、AM分别交BC于点F、G.如图所示:∵BN为∠ABC的角平分线,∴∠CBN=∠ABN,∵BN⊥AG,∴∠ABN+∠BAN=90°,∠AGB +∠CBN=90°,∴∠BAN=∠AGB,∴AB=BG,∴AN=GN,同理AC=CF,AM=MF,∴MN为△AFG的中位线,GF=BG+CF﹣BC,∴MN=12(AB+AC﹣BC)=12(18﹣12)=3.故选D.【点睛】本题考查了等腰三角形的判定与性质、三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.【5题答案】【答案】B【解析】【分析】根据等腰三角形的性质求出CE=ED,根据三角形中位线定理解答.【详解】解:BD=BC=6,∴AD=AB﹣BD=4,∵BC=BD,BE⊥CD,∴CE=ED,又CF=FA,∴EF=12AD=2,故选B.【点睛】本题考查的是三角形中位线定理、等腰三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.【6题答案】【答案】C【解析】【分析】先根据旋转的性质可得E'D'=ED=6,再根据三角形的中位线定理求解即可.【详解】解:∵△ABC以点O为旋转中心,旋转180°后得到△A′B′C′,ED是△ABC的中位线,经旋转后为线段E'D'∴E'D'=ED=6,∴B'C'=2E'D'=12.故选:C.【点睛】本题考查旋转的性质、中位线定理,掌握旋转的性质是解题的关键.【7题答案】【答案】8【解析】【分析】先根据三角形中位线定理可得BC的长,再根据平行四边形的性质可得AD的长,然后根据2AM MD=即可得.【详解】 点E,点F分别是,BM CM中点EF∴是BCM的中位线22612BC EF∴==⨯=四边形ABCD是平行四边形12AD BC ∴==又2AM MD= 2212833AM AD ∴==⨯=故答案为:8.【点睛】本题考查了三角形中位线定理、平行四边形的性质等知识点,解题的关键是熟记三角形中位线定理.【8题答案】【解析】【分析】根据含30°的直角三角形的性质得出AE ,进而利用三角形中位线得出GH 即可.【详解】解:∵∠B =60°,AB =4,AE ⊥BC 于E ,∴∠BAE=30°,∴122BE AB ==∴AE ∵点G ,H 分别为AF 、EF 的中点,∴GH 是△AEF 的中位线,∴GH =1AE 2=,【点睛】此题考查平行四边形的性质和三角形中位线定理,关键是根据含30°的直角三角形的性质得出AE 解答.【9题答案】【答案】32【解析】【分析】将Rt △ABC 绕点B 顺时针旋转60°得到Rt △EBD ,则此时E ,C ,B 三点在同一直线上,得出Q 的运动轨迹为线段ED ,当CQ ⊥ED 时,CQ 的长度最小,由直角三角形的性质及三角形中位线定理可得出答案.【详解】解:将Rt △ABC 绕点B 顺时针旋转60°得到Rt △EBD ,则此时E ,C ,B 三点在同一直线上,∵∠ABC =60°,∠PBQ =60°,∴∠ABP =∠EBQ ,随着P 点运动,总有AB =EB ,PB =QB ,∴总有△APB ≌△EQB (SAS ),即E ,Q ,D 三点在同一直线上,∴Q 的运动轨迹为线段ED ,∴当CQ ⊥ED 时,CQ 的长度最小,Rt △ABC 中,∠ACB =90°,∠A =30°,AB =6,∴BC =BD =3,EC =3,即C 为EB 的中点,∵CQ ⊥ED ,∠D =90°,∴CQ ∥BD ,CQ 为△EBD 的中位线,∴CQ =12BD =32,故答案为:32.【点睛】本题考查了旋转的性质,直角三角形的性质,全等三角形的性质,三角形中位线定理,熟练掌握旋转的性质是解题的关键.【10题答案】【答案】52【解析】【分析】由题分析可以得到M 的轨迹是一条直线(AD 的垂直平分线),再通过计算求出DN 的值即可.【详解】解:如图,连接DM ,DN ,∵90EDF BAC ∠=∠=︒,且M 点是EF 的中点,∴MA=MD=12 EF,可以得到M的轨迹是一条直线(AD的垂直平分线),∴AM MN DM MN-=-,∵点D、N分别是BC、AC的中点,∴1522 DN AB==,∵AM MN DM MN DN-=-≤(D、M、N三点共线时取等号),∴52 AM MN-的最大值为.故答案为:52.【点睛】本题考查了三角形中位线定理、线段的垂直平分线的判定、直角三角形的性质和三角形的三边关系,解决本题的关键是掌握相关概念以及正确分析出取最大值时M点的位置.【11题答案】【答案】13【解析】【分析】连接BD,取BD的中点F,连接MF、NF,由中位线定理可得NF、MF 的长度,再根据勾股定理求出MN的长度即可.【详解】连接BD,取BD的中点F,连接MF、NF,如图所示∵M、N、F分别是AB、DE、BD的中点∴NF 、MF 分别是△BDE 、△ABD 的中位线∴11//,//,5,1222NF BE MF AD NF BE MF AD ====∵90ACB ∠=︒∴AD BC⊥∵//MF AD∴MF BC⊥∵//NF BE∴NF MF⊥在Rt MNF △中,由勾股定理得13MN ===故答案为:13.【点睛】本题考查了三角形中位线的问题,掌握中位线定理、勾股定理是解题的关键.【12题答案】【答案】【解析】【详解】试题解析:连接BE ,与AD 交于点M .则BE 就是EM+CM 的最小值.取CE 中点F ,连接DF .∵等边△ABC 的边长为6,AE=2,∴CE=AC-AE=6-2=4,∴CF=EF=AE=2,又∵AD 是BC 边上的中线,∴DF 是△BCE 的中位线,∴BE=2DF ,BE ∥DF ,又∵E 为AF 的中点,∴M 为AD 的中点,∴ME 是△ADF 的中位线,∴DF=2ME ,∴BE=2DF=4ME ,∴BM=BE-ME=4ME-ME=3ME ,∴BE=43BM .在直角△BDM 中,BD=12BC=3,DM=12∴,∴BE=43.∵EM+CM=BE∴EM+CM 的最小值为.考点:1.轴对称-最短路线问题;2.勾股定理.【13题答案】【答案】5【解析】【分析】连接AC ,过B 作EF 的垂线,利用勾股定理可得AC ,易得ABC ∆的面积,可得BG 和ADC ∆的面积,三角形ABC 与三角形ACD 同底,利用面积比可得它们高的比,而GH 又是ACD ∆以AC 为底的高的一半,可得GH ,易得BH ,由中位线的性质可得EF 的长,利用三角形的面积公式可得结果.【详解】解:连接AC ,过B 作EF 的垂线交AC 于点G ,交EF 于点H ,90ABC ∠=︒ ,4AB BC ==,AC ∴===E ,F 分别是AD ,CD 的中点,EF ∴是ADC ∆的中位线,//EF AC ∴,⊥ BH EF ,BH AC ∴⊥,ABC ∆ 为等腰三角形,ABG ∴∆,BCG ∆为等腰直角三角形,AG BG ∴==,1144822ABC S AB BC ∆=⋅⋅=⨯⨯= , 四边形ABCD 的面积为12,1284ADC S ∆∴=-=, 824ABC ACD S S ∆∆==,∴122122AC BG AC GH ⋅⋅=⋅⋅,14GH BG ∴==BH ∴=,又12EF AC ==,11522BEF S EF BH ∆∴=⋅⋅=⨯=.故答案为:5.【点睛】此题主要考查了三角形的中位线定理,勾股定理,三角形面积的运算,作出恰当的辅助线得到三角形的底和高是解答此题的关键.三、解答题【14题答案】【答案】(1)4y x =+(2)44(,)33P -- (3)84(,)33Q-【解析】【分析】(1)根据2OB OC =,C 点坐标为()0,2-,确定2224OB OC ==⨯=,确定点(0,4)B ,设直线AB 的函数表达式为y kx b =+,代入A 、B 两点的坐标计算即可.(2)设直线AC 的函数表达式为y mx n =+,代入A 、C 两点的坐标,确定解析式,设(,)P a ma n +,连接BP ,根据坐标可计算ACO S ∆,结合2ABP ACO S S ∆∆=确定ABP S ∆,再运用分割法得到11||22ABP ABC P x BC BC OA S B P S C S ∆∆∆==-- ,计算即可.(3)在AB 上取一点E ,使得AQ QE =,连接OE ,结合AD DO =得到DQ 是中位线,得到DQ OE ∥,得到DQA OEQ ∠=∠,结合DQA OQB ∠=∠,可证明OEQ OQB ∠=∠,继而得到OQ OE =,过点Q 作QG OA ⊥于点G ,利用等腰直角三角形的性质,运用勾股定理,求算QG AG OG ,,的长,结合点的位置,写出坐标即可.【小问1详解】因为2OB OC =,C 点坐标为()0,2-,所以2224OB OC ==⨯=,所以点(0,4)B ,设直线AB 的函数表达式为y kx b =+,代入A 、B 两点的坐标,得:404k b b -+=⎧⎨=⎩,解得14k b =⎧⎨=⎩,所以直线AB 的函数表达式为4y x =+.【小问2详解】设直线AC 的函数表达式为y mx n =+,代入A 、C 两点的坐标,得:402m n n -+=⎧⎨=-⎩,解得122m n ⎧=-⎪⎨⎪=-⎩,所以直线AC 的函数表达式为122y x =--.设1(,2)2P a a --,连接BP ,因为A 点()4,0-,C 点坐标为()0,2-,点(0,4)B ,所以424(2)6OA OC BC ===--=,,,所以11=42422ACO AO O S C ∆=⨯⨯= ,因为2ABP ACOS S ∆∆=所以=8ABP S ∆,因为ΔΔΔ11··22ABP ABC PBC P S S S BC OA BC x =-=-,所以1164622⨯⨯-⨯⨯(-a)=8,解得43a =-,所以44(,)33P --.【小问3详解】如图,因为4OB OA ==,D 点为线段AO 的中点,所以45DAQ OBQ ∠=∠= ,2DA DB ==,AB ==,在AB 上取一点E ,使得AQ QE =,连接OE ,因为AD DO =,所以DQ 是中位线,所以DQ OE ∥,所以DQA OEQ ∠=∠,2OE DQ =,因为DQA OQB ∠=∠,所以OEQ OQB ∠=∠,所以2OQ OE DQ ==,过点Q 作QG OA ⊥于点G ,则QG AG =,设QG AG x ==,则2,4DG x OG x =-=-,根据勾股定理,得222222(2),(4)DQ x x OQ x x =-+=-+,所以2222(4)4[(2)]x x x x -+=-+,解得43x =,所以48==33QG AG OG OA AG =-=,因为点Q 在第二象限,所以84(,)33Q -.【点睛】本题考查了待定系数法求一次函数的解析式,勾股定理,等腰直角三角形的判定和性质,线段与坐标的关系,三角形中位线定理,勾股定理,三角形面积分割法计算,熟练掌握待定系数法,勾股定理,三角形中位线定理是解题的关键.【15题答案】【答案】(1)证明过程见解析(2)24【解析】【分析】(1)由∠=∠BCA CAD得到BC//AD,再证明△AOD≌△COB得到BC=AD,由此即可证明四边形ABCD为平行四边形;(2)由ABCD为平行四边形得到BD=2BO,结合已知条件BD=2BA得到BO=BA=CD=OD,进而得到△DOF与△BOA均为等腰三角形,结合F为OC中点得到∠DFA=90°,GF为Rt△ADF斜边上的中线求出11522GF AD==;过B点作BH⊥AC于H,求出BH=9,再证明四边形BHGE为平行四边形得到GE=BH=9,最后将GE、GF、EF相加即可求解.【小问1详解】证明:∵∠=∠BCA CAD,∴BC∥AD,在△AOD和△COB中:BCA CAD CO AOCOB AOD ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AOD≌△COB(ASA),∴BC=AD,∴四边形ABCD为平行四边形.【小问2详解】解:∵点E、F分别为BO和CO的中点,∴EF是△OBC的中位线,∴11522 EF BC==;∵ABCD为平行四边形,∴BD=2BO,又已知BD=2BA,∴BO=BA=CD=OD,∴△DOC与△BOA均为等腰三角形,又F为OC的中点,连接DF,∴DF⊥OC,∴∠AFD=90°,又G为AD的中点,由直角三角形斜边上的中线等于斜边的一半可知:1115222 GF AD BC===;过B点作BH⊥AO于H,连接HG,如上图所示:由等腰三角形的“三线合一”可知:AH=HO=12AO=14AC=4,∴HC=HO+OC=4+8=12,在Rt△BHC中,由勾股定理可知9BH===,∵H为AO中点,G为AD中点,∴HG为△AOD的中位线,∴HG∥BD,即HG∥BE,且1122HG OD BO BE===,∴四边形BHGE为平行四边形,∴GE=BH=9,∴151592422EFGC GE GF EF=++=++=.【点睛】本题考查了三角形全等的判定方法、平行四边形的性质、三角形中位线定理、直角三角形斜边上的中线等于斜边的一半等,熟练掌握各图形的性质及定理是解决本题的关键.【16题答案】【答案】(1)90;(2)见解析;(3)CG=4.【解析】【分析】(1)根据题意,平行四边形邻角互补,结合已知条件则,根据∠BFC=12∠ABC +12∠BCD ,即可求解;(2)根据已知条件,直接证明△BCF ≌△HCF 即可;(3)根据已知条件,先证明EF 为B CH 的中位线,求得CH ,再证明△ABF ≌△HGF ,求得H G ,根据CG HC HG =-即可求得【详解】(1)∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD ,∴∠ABC +∠BCD =180°,∵BF 平分∠ABC ,CF 平分∠BCD ,∴∠FBC =12∠ABC ,∠DCF =∠BCF =12∠BCD ,∴∠FBC +∠BCF =90°,∴∠BFC =90°,故答案为90;(2)在△BCF 和△HCF 中,90BCF HCF CF CFBFC HFC ︒∠=∠⎧⎪=⎨⎪∠=∠=⎩,∴△BCF ≌△HCF (ASA ),∴BC =CH ;(3)∵△BCF ≌△HCF ,∴BF =FH ,又∵E 是边BC 的中点,∴CH =2EF =10,∵AB ∥CD ,∴∠H =∠ABF ,在△ABF 和△GHF 中,ABF H BF HFAFB HFG ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABF ≌△HGF (ASA ),∴AB =HG =6,∴CG =CH ﹣GH =4.【点睛】本题考查了平行四边形的性质,角平分线的定义,中位线的性质与判定,三角形全等的性质与判定,熟练掌握以上知识点是解题的关键.【17题答案】【答案】(1)见解析,(2)EFG ①的形状为等腰三角形,理由见解析;②24【解析】【分析】(1)由平行四边形的性质易证CDO ABO ∠=∠,再证CDO 是等腰三角形,由等腰三角形三线合一性质得出12ODE CDE CDO ∠=∠=∠,即可得出结论;(2)①易证DE CO ⊥,由G 为AD 中点,得出12E G A D =,再由E 、F 分别是OC 、OB 的中点,得出12EF BC =,由平行四边形的性质得AD BC =,即可得出EG EF =,则EFG 是等腰三角形;②先证四边形BEFG 是平行四边形,得出EFG GDE ∠=∠,DGE FEG ∠=∠,再证EFG 、DEG △、AED △都是等腰直角三角形,设DG GE x ==,则DE AE ==,13CE AE ==3x =,得出DE =4AC CE ==,最后由122ABCD S AC DE =⨯⋅平行四边形,即可得出答案.【小问1详解】四边形ABCD 是平行四边形,,AB CD ∴∥AB CD =,22BD DO BO ==,CDO ABO ∴∠=∠,2BD AB = ,AB DO CD ∴==,CDO ∴ 是等腰三角形,点E 为线段OC 的中点,1122ODE CDE CDO ABO ∴∠=∠=∠=∠,2ABO ODE ∴∠=∠;【小问2详解】①EFG 的形状为等腰三角形,理由如下:CDO 是等腰三角形,E 是CO 中点,DE CO ∴⊥,90DEA ∴∠=︒,G 为AD 中点,12EG AD ∴=,E 、F 分别是OC 、OB 的中点,12EF BC ∴=, 四边形ABCD 是平行四边形,AD BC ∴=,EG EF ∴=,EFG ∴△是等腰三角形;②解: 四边形ABCD 是平行四边形,OA OC ∴=,AB CD ==,AD BC =,AD BC ∥,E 、F 分别是OC 、OB 的中点,13CE AE ∴=,EF 是OBC △的中位线,EF BC ∴∥,12EF BC =,EF BC DG ∴∥∥,G 是AD 的中点,1122DG AD BC ∴==,EF DG ∴=,∴四边形BEFG 是平行四边形,EFG GDE ∴∠=∠,EF DG ∥,DGE FEG ∴∠=∠,EF EG ⊥ ,90FEG DGE ∴∠=∠=︒,由①得:EG EF =,EFG ∴△是等腰直角三角形,45EFG GDE ∴∠=∠=︒,DEG ∴ 是等腰直角三角形,DG GE ∴=,90DEA ∠=︒ ,AED ∴ 是等腰直角三角形,DE AE ∴=,设DG GE x ==,则DE AE ==,13CE AE ==,在Rt DEC 中,由勾股定理得:222CD DE CE =+,即222)=+,解得:3x =或3(x =-不合题意,舍去),DE ∴=,4443AC CE ∴====,12242ABCD S AC DE ∴=⨯⋅==平行四边形.【点睛】本题主要考查了平行四边形的判定与性质、等腰三角形的判定与性质、等腰直角三角形的判定与性质、中位线定理、平行线的判定与性质、勾股定理、平行四边形面积的计算等知识;熟练掌握平行四边形的判定与性质和等腰直角三角形的判定与性质是解题的关键.【18题答案】【答案】(1)见解析(2)成立,证明见解析(3)30°【解析】【分析】(1)利用平行线的性质可得同位角相等,再利用ASA 证明ABD EDC ∆≅∆,得AB ED =,从而证明结论;(2)过点M 作MG DE ∥交EC 于点G ,则四边形DMGE 为平行四边形,得ED GM =且//ED GM ,由(1)可得AB GM =且AB GM ∥,从而得出结论;(3)取线段HC 的中点I ,连接MI ,由三角形中位线定理得MI BH ∥,12MI BH =,则12MI AM =,MI AC ⊥,即可解决问题.【小问1详解】解:证明:DE AB ∥ ,EDC ABM ∴∠=∠,CE AM ∥,ECD ADB ∴∠=∠,AM 是ABC ∆的中线,且D 与M 重合,BD DC ∴=,()ABD EDC ASA ∴∆≅∆,AB ED ∴=,AB ED ∥,∴四边形ABDE 是平行四边形;【小问2详解】成立,理由如下:过点M 作MG DE ∥交EC 于点G ,CE AM ∥,∴四边形DMGE 为平行四边形,ED GM ∴=且ED GM ∥,由(1)可得AB GM =且AB GM ∥,AB ED ∴=且AB ED ∥,∴四边形ABDE 为平行四边形;【小问3详解】取线段HC 的中点I ,连接MI ,MI ∴是BHC ∆的中位线,MI BH ∴∥,12MI BH =,BH AC ⊥ 且BH AM =,12MI AM ∴=,MI AC ⊥,30CAM ∴∠=︒.【点睛】本题是四边形综合题,主要考查了平行四边形的判定与性质,三角形中位线定理,全等三角形的判定与性质等知识,遇中点取中点构造中位线是解决问题(3)的关键.【19题答案】【答案】(1)四边形CEBF 是平行四边形,证明见解析;(2)BF =CEBF 的面积=12.【解析】【分析】(1)由等腰直角三角形的性质、垂直的定义和角平分线的定义可得∠DCE =∠CBF ,而可根据ASA 证明△CDE ≌△BDF ,于是可得DE =DF ,进一步即可得出结论;(2)设CD =x ,则AC=BC =2x ,然后在Rt △ACD 中,由勾股定理可求出x ,从而可得AC 、AB 的长,由等腰三角形的性质可得CE 垂直平分AB ,进而可得AE=BE ,然后根据等腰三角形的性质和判定以及余角的性质可得AE=EF ,于是可得AD =3DE ,AF =4DE ,而AD 已知,则DE 和AF 可得,于是可在直角△AFB 中根据勾股定理求出BF ,过点C 作CG ⊥DE 于点G ,如图,则由三角形的面积可求出CG 的长,于是可得△CDE 的面积,而所求的四边形CEBF 的面积是△CDE 面积的4倍,问题即得解决.【详解】(1)四边形CEBF 是平行四边形.证明:∵∠ACB =90°,AC =BC ,∴∠ABC =45°,∵FB ⊥AB ,∴∠ABF =90°,∴∠CBF =45°,∵CE 平分∠ACB ,∴∠DCE =45°=∠CBF ,又∵DC =DB ,∠CDE =∠BDF ,∴△CDE ≌△BDF (ASA ),∴DE =DF ,∵DC =DB ,∴四边形CEBF 是平行四边形;(2)解:设CD =x ,则AC=BC =2x ,在Rt △ACD 中,由勾股定理得:()(2222x x +=,解得:x =3,∴CD =3,AC=BC =6,∴AB ==∵AC=BC ,CE 平分∠ACB ,∴CE 垂直平分AB ,∴AE=BE ,∴∠BAE =∠ABE ,∵∠BAE +∠AFB =90°,∠ABE +∠FBE=90°,∴∠AFB =∠FBE ,∴EF=BE ,∴AE=EF ,∵EF =2DE ,∴AD =3DE ,AF =4DE ,∴13DE AD ==,∴AF =,∴BF ===,过点C 作CG ⊥DE 于点G ,如图,则由三角形的面积可得:AC CD AD CG = ,即63CG ⨯=,解得:CG =∴S △CDE =132=,∴四边形CEBF 的面积=4S △CDE =4×3=12.【点睛】本题考查了等腰直角三角形的性质、等腰三角形的判定和性质、线段垂直平分线的性质、勾股定理、全等三角形的判定和性质以及利用三角形的面积求高等知识,属于常考题型,具有一定的综合性,熟练掌握上述知识是解题的关键.【20题答案】【答案】(1)NM =NP ,60°;(2)见解析;(3【解析】【分析】(1)根据点M,N,P分别为DE,BE,BC的中点,得MN=12BD,PN=12CE,MN∥AB,PN∥AC,可知MN=PN,而∠MNP=∠MNE+∠ENP=∠ABE+∠AEB,即可求出∠MNP=60°;(2)先证△ABD≌△ACE(SAS),得BD=CE,∠ABD=∠ACE,然后由(1)同理可得MN=PN,∠MNP=60°;(3)先求出MN的最大值,由(2)知△MNP为等边三角形知,MN最大时,△MNP面积的最大,求出此时的面积即可.【详解】解:(1)∵AB=AC,AD=AE,∴BD=CE,∵点M,N,P分别为DE,BE,BC的中点,∴MN=12BD,PN=12CE,MN∥AB,PN∥AC,∴MN=PN,∠ENM=∠EBA,∠ENP=∠AEB,∴∠MNE+∠ENP=∠ABE+∠AEB,∵∠ABE+∠AEB=180°-∠BAE=60°,∴∠MNP=60°,故答案为:NM=NP,60°;(2)由旋转得:∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴BD=CE,∠ABD=∠ACE,∵点M,N,P分别为DE,BE,BC的中点,∴MN=12BD,PN=12CE,MN∥BD,PN∥CE,∴MN=PN,∠ENM=∠EBD,∠BPN=∠BCE,∴∠ENP=∠NBP+∠NPB=∠NBP+∠ECB,∵∠EBD=∠ABD+∠ABE=∠ACE+∠ABE,∴∠MNP=∠MNE+∠ENP=∠ACE+∠ABE+∠EBC+∠EBC+∠ECB=180°-∠BAC=60°,∴△MNP是等边三角形;(3)由题意知BD≤AB+AD,即BD≤7,∴MN≤72,由(2)知△MNP是等边三角形,∴MN=72时,S△MNP最大,∴S△MNP 77 22⨯【点睛】本题主要考查了旋转的性质、三角形中位线定理、三角形全等的判定与性质等知识,证明出△MNP是等边三角形是解题的关键.。
八下数学每日一练:三角形中位线定理练习题及答案_2020年压轴题版

(2) 己知AB=10,
.
①当四边形ECBH是菱形时,求EG的长.
②连结CH,DH,记△DEH的面积为S1,△CBH的面积为S2.若EG=2FH,求S1+S2的值.
考点: 三角形的面积;三角形中位线定理;菱形的性质;矩形的判定;
答案
2020年 八 下 数 学 : 图 形 的 性 质 _三 角 形 _三 角 形 中 位 线 定 理 练 习 题 答 案
②若
,点 是 的中点,直接写出当点 由点 运动到点 时,点 运动路线的长. 28.
(2) 已知,
中,
,
.如图 ,把
绕点 旋转到
边 与边 的交点,点 在边 上且
,连接 .求点 到直线 的距离.
考点: 全等三角形的判定与性质;角平分线的性质;等边三角形的性质;三角形中位线定理;
的位置,点 是 答案
~~第2题~~ (2019宜兴.八下期中) 在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2 的正方形 AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.连接DG,BE,易得DG=BE且DG⊥BE(不需要说明 理由)
八下数学每日一练:三角形中位线定理练习题及答案_2020年压轴题版
2020年 八 下 数 学 : 图 形 的 性 质 _三 角 形 _三 角 形 中 位 线 定 理 练 习 题
~~第1题~~ (2019兰州.八下期中) (1) 如图 ,已知点
在正三角形
的边 上,以 为边作正三角形
,连接 .
①求证:
;
考点: 勾股定理;三角形中位线定理;正方形的性质;
答案
~~第5题~~
(2019温州.八下期末) 如图,点C在线段AB上,过点C作CD⊥AB,点E,F分别是AD,CD的中点,连结EF并延长EF
人教版初中数学八年级下册期末提分题习题课件第2课时 方法训练 构造三角形中位线的五种常用方法

4.如图,在四边形 ABCD 中,AB 与 CD 不平行,M,N 分别是 AD,BC 的中点.若 AB=10,CD=8,求 MN 长度的取值 范围.
解:如图,取 BD 的中点 P,连接 PM,PN. ∵M 是 AD 的中点,P 是 BD 的中点, ∴PM 是△ABD 的中位线,
∴PM=12AB=5. 同理得 PN=21CD=4. 在△PMN 中,∵PM-PN<MN<PM+PN, ∴1<MN<9.
2. 如图,在△ABC 中,已知 AB=6,AC=10,AD 平分∠BAC, BD⊥AD 于点 D,点 E 为 BC 的中点.求 DE 的长.
解:如图,延长 BD 交 AC 于点 F. ∵AD 平分∠BAC, ∴∠BAD=∠CAD. ∵BD⊥AD, ∴∠ADB=∠ADF.
又 AD=AD,∴△ADB≌△ADF(ASA).ቤተ መጻሕፍቲ ባይዱ∴AF=AB=6,BD=FD. ∵AC=10, ∴CF=AC-AF=10-6=4. ∵E 为 BC 的中点,BD=FD, ∴DE 是△BCF 的中位线. ∴DE=21CF=12×4=2.
∵△ABD 和△BCE 是等边三角形, ∴AB=DB,BE=BC,∠ABD=∠CBE=60°. ∴∠ABE=∠DBC. ∴△ABE≌△DBC. ∴AE=DC. ∴PM=PN.
(2)求∠MPN 的度数. 解:如图,设 PM 交 AE 于 F,PN 交 CD 于 G, AE 交 CD 于 H. 由(1)知△ABE≌△DBC,∴∠BAE=∠BDC. ∴∠AHD=∠ABD=60°,∴∠FHG=120°. 由三角形中位线定理可得 PM∥CD,PN∥AE, ∴四边形 PFHG 为平行四边形.∴∠MPN=∠FHG=120°.
5.如图,在△ABC 中,AB=AC,AD⊥BC 于点 D,点 P 是 AD 的中点,延长 BP 交 AC 于点 N.求证 AN=13AC.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
DCB
A
E
F
三角形的中位线
◆随堂检测
1.如图,D、E、F分别为△ABC三边上的中点.
(1)线段AD叫做△ABC的 ,线段DE叫做△ABC的 ,DE
与AB的位置和数量关系是 _________ ;
(2)图中全等三角形有 _________________ ;
(3)图中平行四边形有 ___________ .
2. 三角形各边长为5、9、12,则连结各边中点
所构成的三角形的周长是 .
3. 如图,在矩形ABCD中,BC=8cm,AC与BD交
于O,M、N分别为OA、OD的中点.
求证:四边形BCNM是等腰梯形.
4. 已知:如图,矩形ABCD中,E、F、G、H分别为AB、BC、CD、AD
的中点
求证:四边形EFGH是菱形
H
G
DCBA
E
F
5、如图,要测出池塘的宽度AB,小强在池塘边上取一个能直接到达
A、B的点C,量的AC=20cm,BC=25cm,又取AC的中点D,BC的中点
E,量得DE=12cm,求池塘宽AB,为多少?
◆典例分析
如图,在梯形ABCD中,AD∥BC,E是DC的
中点,EF∥AB交BC于F,若EF=3,求AB的
长.
解:过D作DG∥AB交BC于G,∵AD∥BC,
AB∥DG,
∴四边形ABGD是平行四边形,∴AB=DG.
∵EF∥AB,∴EF∥DG,∵DE=CE,∴GF=CF.
∴EF是△CDG的中位线,∴EF=21DG.
∴DG=2EF=6,即AB=6.
点拨:此题目在考察三角形中位线的同时考
察了平行四边形的判定问题,解题时注意条件的转化.
◆课下作业
●拓展提高
1、如图,D、E、F分别为△ABC三边上的中点,G为AE的中点,BE
与DF、DG分别交于P、Q两点,则PQ∶BE= .
