轴向拉伸与压缩2
第二章 轴向拉伸和压缩
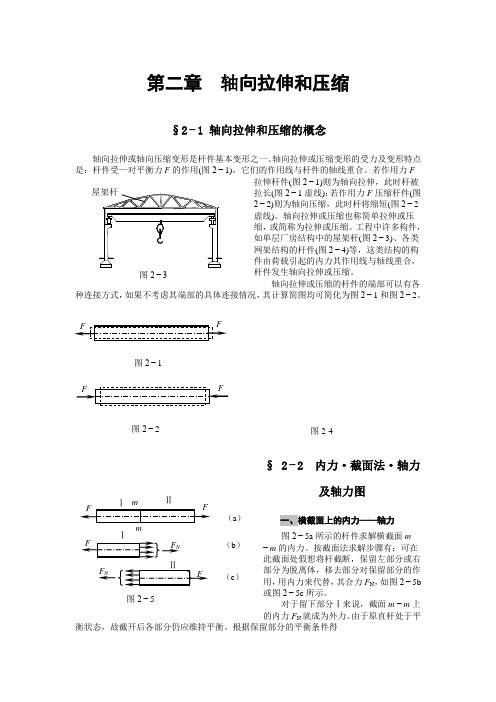
第二章 轴向拉伸和压缩§2−1 轴向拉伸和压缩的概念F(图2−1)则为轴向拉伸,此时杆被2−1虚线);若作用力F 压缩杆件(图(图2−2工程中许多构件,(图2−3)、各类(图2−4)等,这类结构的构2−1和图2−2。
§ 2−2 内力·截面法·轴力及轴力图一、横截面上的内力——轴力图2−5a 所示的杆件求解横截面m−m 的内力。
按截面法求解步骤有:可在此截面处假想将杆截断,保留左部分或右部分为脱离体,移去部分对保留部分的作用,用内力来代替,其合力F N ,如图2−5b 或图2−5c 所示。
对于留下部分Ⅰ来说,截面m −m 上的内力F N 就成为外力。
由于原直杆处于平衡状态,故截开后各部分仍应维持平衡。
根据保留部分的平衡条件得 mF N F N(a )(b ) (c )图2−5Ⅱ图2−1图2−2图2-4F F F F Fx==-=∑N N ,0,0 (2−1)式中,F N 为杆件任一截面m −m 上的内力,其作用线也与杆的轴线重合,即垂直于横截面并通过其形心,故称这种内力为轴力,用符号F N 表示。
若取部分Ⅱ为脱离体,则由作用与反作用原理可知,部分Ⅱ截开面上的轴力与前述部分上的轴力数值相等而方向相反(图2−5b,c)。
同样也可以从脱离体的平衡条件来确定。
二、轴力图当杆受多个轴向外力作用时,如图2−7a ,求轴力时须分段进行,因为AB 段的轴力与BC 段的轴力不相同。
要求AB 段杆内某截面m −m 的轴力,则假想用一平面沿m −m 处将杆截开,设取左段为脱离体(图2−7b),以F N Ⅰ代表该截面上的轴力。
于是,根据平衡条件∑F x =0,有 F F -=ⅠN负号表示的方向与所设的方向相反,即为压力。
要求B C 段杆内某截面n-n 的轴力,则在n −n 处将杆截开,仍取左段为脱离体(图2−7c ),以F N Ⅱ代表该截面上的轴力。
于是,根据平衡条件∑F x =0,有 02N Ⅱ=+-F F F由此得F F =N Ⅱ在多个力作用时,由于各段杆轴力的大小及正负号各异,所以为了形象地表明各截面轴力的变化情况,通常将其绘成“轴力图”(图2−7d)。
材料力学(机械类)第二章 轴向拉伸与压缩

二
章
拉伸压缩与剪切
1
பைடு நூலகம்
§2-1
轴向拉伸与压缩的概念和实例
轴向拉伸——轴力作用下,杆件伸长 (简称拉伸) 轴向压缩——轴力作用下,杆件缩短 (简称压缩)
2
拉、压的特点:
1.两端受力——沿轴线,大小相等,方向相反 2. 变形—— 沿轴线
3
§2-2 轴向拉伸或压缩时横截面上的内力和应力
1 、横截面上的内力
A3
2
l1 l2 y AA3 A3 A4 sin 30 tan 30 2 1.039 3.039mm
A
A A4
AA x2 y2 0.6 2 3.039 2 3.1mm
40
目录
例 2—5 截面积为 76.36mm² 的钢索绕过无摩擦的定滑轮 F=20kN,求刚索的应力和 C点的垂直位移。 (刚索的 E =177GPa,设横梁ABCD为刚梁)
16
§2-4
材料在拉伸时的力学性能
材料的力学性能是指材料在外力的作用下表现出的变 形和破坏等方面的特性。
现在要研究材料的整个力学性能(应力 —— 应变):
从受力很小
破坏
理论上——用简单描述复杂
工程上——为(材料组成的)构件当好医生
17
一、 低碳钢拉伸时的力学性能 (含碳量<0.3%的碳素钢)
力均匀分布于横截面上,σ等于常量。于是有:
N d A d A A
A A
得应力:
N A
F
FN
σ
10
例题2-2
A 1
45°
C
2
§5–1 轴向拉伸与压缩的概念§5–2 轴向拉伸与压缩时横截.

F
F
D
解: 杆件横截面 上的正应力为:
s
4F 4 20103 N = = 2 2 D -d 2 - 0.015m 2 0.020m
= 145106 Pa = 145MPa
材料的许 用应力为:
235106 Pa = = = 156106 Pa = 156MPa ns 1.5
FN=F
FN’
II
F
x
单位:
SFX=0:-FN’+F=0
FN’=F
N(牛顿)或 kN(千牛)
8
3. 轴力的正负规定: FN 与外法线同向,为正轴力(拉力) FN与外法线反向,为负轴力(压力) FN FN FN FN FN>0 FN<0
三、 轴力图—— FN(x) 的图象表示。
意 义 ①反映出轴力与截面位置变化关系,较直观; ②确定出最大轴力的数值 及其所在横截面的位置, 即确定危险截面位置,为 FN F + x
FN ( x) max= max( ) A( x)
4. 公式的应用条件: 直杆、杆的截面无突变、截面到载荷作用点有一定 的距离。 5. Saint-Venant原理: 离开载荷作用处一定距离,应力分布与大小不受外载荷作
用方式的影响。 6. 应力集中:
在截面尺寸突变处,应力急剧变大。
Saint-Venant原理与应力集中示意图 F a b c F
§5–2 轴向拉伸与压缩时横截面上的内力-轴力
一、内力
指由外力作用所引起的、物体内相邻部分之间分布内
力系的合成(附加内力)。
二、截面法 ·轴力 内力的计算是分析构件强度、刚度、稳定性等问题的 基础。求内力的一般方法是截面法。 1. 截面法的基本步骤:
轴向拉伸与压缩的变形概念

轴向拉伸与压缩的变形概念轴向拉伸与压缩是材料在受到外力作用下发生的一种变形形式。
这两种变形形式本质上都是由于材料内部的原子或分子受到外力的影响而改变了其平衡位置从而引起的。
轴向拉伸与压缩的变形概念可以通过弹簧的拉伸与压缩来加以理解。
首先我们来看轴向拉伸的变形。
当作用在弹簧两端的力朝相反方向拉伸时,弹簧会发生轴向拉伸的变形。
这是因为受到拉力的作用,弹簧内部原子或分子之间的间距增大,原本处于平衡位置的原子或分子会发生位移,使得整个弹簧长度增加。
这种拉力作用下的变形被称为轴向拉伸变形。
接下来我们来看轴向压缩的变形。
当作用在弹簧两端的力朝相同方向压缩时,弹簧会发生轴向压缩的变形。
这是因为受到压力的作用,弹簧内部原子或分子之间的间距减小,原本处于平衡位置的原子或分子会发生位移,使得整个弹簧长度减小。
这种压力作用下的变形被称为轴向压缩变形。
轴向拉伸与压缩的变形概念实际上可以通过杨氏模量来更加详细地描述。
杨氏模量是一个材料的机械特性参数,它描述了材料在轴向拉伸和压缩变形时的抵抗能力。
杨氏模量越大,材料的抵抗能力越强,抗拉强度也就越大。
相反地,杨氏模量越小,材料的抗拉强度越低。
在材料实际应用中,轴向拉伸与压缩的变形是非常常见的。
比如在建筑、桥梁、汽车、飞机等工程领域中,钢材往往被用于受力构件中,它能够在受到拉力或压力时保持较好的稳定性。
而在金属加工、塑料成型等制造领域中,轴向拉伸与压缩的变形则常常是一种设计和生产工艺。
例如在金属加工中,通过轴向拉伸可以制造出细丝,而通过轴向压缩则可以制造出坯料。
总结起来,轴向拉伸与压缩是材料在受到外力作用下发生的一种变形形式。
轴向拉伸是指材料的长度增加,原子或分子之间的间距变大;轴向压缩是指材料的长度减小,原子或分子之间的间距变小。
这两种变形形式与杨氏模量密切相关,它描述了材料在受力时的抵抗能力。
在工程和制造领域中,轴向拉伸与压缩的变形是非常常见的,它们对于材料的选择、设计和生产工艺具有重要意义。
建筑力学 第六章 轴向拉伸与压缩

应力正负号规定
• 正应力:离开截面的正应力为正,指向 截面的正应力为负。
• 切应力以其对分离体内一点产生顺时针 转向的力矩时为正值的切应力,反之, 则为负的切应力 。
• 切应力的说法只对平面问题有效。
(3). 应力的特征: 1 应力定义在受力物体的某一截面上的某一点处,因
此,讨论应力必须明确是在哪一个截面上的哪一点处。
5. 要判断杆是否会因强度不足而破坏,还必须知道: ① 度量分布内力大小的分布内力集度-应力。 ② 材料承受荷载的能力。
大多数情形下,工程构件的内力并非均匀分布,内力集度 的定义不仅准确而且重要,因为“破坏”或“失效”往往从内 力集度(应力)最大处开始。
(2)应力的表示: F1 截面
F
△A上的内力平均集度为:
–
C
D
F
轴向拉压杆件横截面上的应力
一. 应力的概念:
F
F
(1)问题提出:
F
F
1. 两杆的轴力都为F. 2. 但是经验告诉我们,细杆更容易被拉断。同样材料,
同等内力条件下,横截面积较大的拉杆能承受的 轴向拉力较大。
3. 内力大小不能衡量构件强度的大小。 4. 根据连续性假设,内力是连续分布于整个横截面上的, 一般而言,截面上不同点处分布的内力大小和方向都不 同。
遇到向右的F , 轴力 F N 增量为负F。
如果左端是约束,需先求出约束反力(约束反力也是外力)
8kN
5kN
3kN
8kN 3kN
5kN +
8kN – 3kN
如果杆件由几段不同截面的等直杆构成,轴力的计算方 法和单一截面的轴力计算方法一样。
O
B
C
4F 3F
D 2F
轴向拉伸和压缩解读

X 0 FN 4 FD 0 FN4= F
FD
FN1 2F, FN2= –3F, FN3= 5F, FN4= F
FN1 2F, FN2= –3F, FN3= 5F, FN4= F
轴力图如下图:
OA
BC
D
FA
FB
FC
FD
FN 2F +
5F
+
F
x
-
3F
总结上面例子得到以下结论: ➢轴力只与外力有关,截面形状变化不会改变轴力大小; ➢集中外力多于两个时,轴力以分段函数表示,以集中力作用 点、分布载荷起止点为界点; ➢轴力等于脱离体上所有轴向外力的代数和; ➢求轴力时外力的符号法则:
第2章 轴向拉伸和压缩
§2.1 轴向拉伸和压缩的概念与实例 §2.2轴力及轴力图 §2.3轴向拉压杆横截面上的应力 §2.4材料的力学性质和基本试验 §2.5拉压杆的强度计算 §2.6拉压杆的变形 §2.7拉压变形的超静定问题 §2.8应力集中的概念
§2.1 轴向拉伸和压缩的概念与实例
一、轴向拉压的工程实例
•变形前为平面的横截面,变形后仍保持为平面——平面假设; •各横截面沿轴向作相对平移,两截面间各纵向线绝对变形相同, 应变ε也相同;
•横向线与纵向线始终保持垂直,切应变γ为零。
4、应力的分布规律—— 沿横截面均匀分布
从平面假设可以判断:
F
(1)各纵向纤维应变相等——各点处正应力
相等,为常量。即正应力在截面上均匀分布;
F 4F 8F 5F FN1 0
FN1 2F
OA
BC
D
FA
FB
FC
FD
求AB 段内力:
X 0
FN2
第5章 轴向拉伸和压缩(已修改)

σ
2
sin 2α
为斜截面上的应 力计算公式
2. 最大应力和最小应力 (1)最大 最小正应力 当 α = 00 时 拉杆 σ max = σ 压杆 σ min = - σ ( 2 ) 最大 最小剪应力 当 α =+45 0 时
τ
max
σ/2
450 -450
τ max α=45 = sin 2α =
0
已知: FP = 3kN FP2 = 2kN 1 求:轴力和轴力图。 解:1. 求轴力 1-1:
FP3 =1kN
1 1
FP1
FP2
2 2
FP3
∑F = 0,
x
FN1 + FP1 = 0 FN1 = FP1 = −3kN
FP1
FP1
FN1
FP2
x
2-2:左: ∑Fx = 0, FN2 + FP1 − FP2 = 0 2-2:右:
FCE 15 ×10 3 = = = 15 A 0.02 × 0.05
MPa
σ DE
FDE = = 50 MPa A
图示直杆在上半部两侧面受有平行于杆轴线的均匀分布载荷,其集度 p = 10k N/m,在自由端D处作用有集中力FP = 20 kN。已知杆的横截面面积 A = 2.0×10-4m2,l = 4m。试求: p 1.A、B、E截面上的正应力; 2.杆内横截面上的最大正应力,并指明其作用位置。 解:由已知,用截面法求得 FNA = 40 kN FNB = 20 kN FNE = 30 kN
FN2
x
FN2 = FP2 − FP1 = −1kN
x
∑F = 0,
FN2
N
FP3 x
x
轴向拉伸和压缩—拉(压)杆的强度计算(建筑力学)

轴向拉伸与压缩
例7-12 图示三角支架,在节点A处受铅直荷载FP作用。已 知AB为圆截面钢杆,直径d=30mm,许用应力[σ]=160MPa, AC为正方形木杆,边长a=100mm,许用压应力[σc]=10MPa试 求许用荷载[ FP ]。
解 (1)计算杆的轴力
由∑Fy=0 -FNACsin30°-FP=0
A FNAB 63 103 mm2 393.8mm2
[ ] 160
轴向拉伸与压缩
当拉杆选用角钢时,每根角型的最小面积应为
A1
A 2
393.8 2
mm 2
196.9mm2
查型钢表,选用两根25×4的2.5号等边角钢。
A1=185.9mm2 故此时拉杆的面积为
A=2×185.9mm2=371.8mm2>370.6mm2 满足强度要求。
材料的安全系数比塑性材料的大。建筑工程中,一般,取nS =1.4~1.7,nb=2.5~3.0。
轴向拉伸与压缩
3. 强度条件 为了保证轴向拉(压)杆在承受外力作用时能安全正常地
使用,不发生破坏,必须使杆内的最大工作应力不超过材料 的许用应力,即
σmax≤[σ]
塑性材料: 脆性材料:
max
FN max A
解(1)先求支座反力。
FAy = FBy= 0.5q l = 0.5×10×8.4 = 42kN
轴向拉伸与压缩
(2)再求拉杆的轴力。
用截面法取左半个屋架为研究对 象,如图示。
由 MC 0
FNAB
h
FAy
l 2
q
l 2
l 4
0
FNAB
42 42 10 4.2 2.1 kN 1.4
63kN
(3)校核拉杆的强度。
