第六章12-弯曲变形
第六章 钻孔弯曲与测量

第三节 钻孔弯曲的原因和规律
二、钻孔弯曲的原因
形成钻孔弯曲的原因大致可分为三类:
钻孔弯曲与测量 Deflection&Logging
地质因素
技术因素
工艺方面的原因
吉林大学建设工程学院
2013-8-23
第三节 钻孔弯曲的原因和规律
二、钻孔弯曲的原因 1. 地质因素
钻孔弯曲与测量 Deflection&Logging
液面水平原理(氢氟酸测斜)
把20~30%浓度的氢氟酸注入长度为100~150mm内径为15~25mm的玻璃 试管中。注入量为试管长度的1/3左右。然后,将盛有氢氟酸的玻璃试管装 在特制的接头内,用橡胶塞加以密封。用钻杆将其下到孔内待测位置,静止 停留15~25min后,提钻取出试管。由于氢氟酸对玻璃的腐蚀作用,在试管 上留有液面痕迹。根据液面的高低,就可算出顶角。
钻孔轨迹的基本要素
钻孔轨迹弯曲强度
吉林大学建设工程学院
2013-8-23
一 钻孔轨迹的基本要素
钻孔弯曲与测量 Deflection&Logging
为了解钻孔轨迹在地下空间的位置,表征其空间形态,就必须了 解和控制钻孔轨迹要素。图中0代表开孔点,X轴代表南北,Y轴代表 东西,Z轴代表地下方向,0ABC是钻孔的空间轨迹。其基本要素包括: 顶角(θA)
钻孔弯曲与测量 Deflection&Logging
吉林大学建设工程学院
2013-8-23
第三节 钻孔弯曲的原因和规律
钻孔弯曲与测量 Deflection&Logging
而从硬岩进入软岩时,则钻具轴线有偏离层面法线方向的 趋势。但由于上方孔壁较硬,限制了钻具偏倒,结果基本保 持着原来的方向。 钻孔通过硬岩进入软岩又从软岩进入硬岩时,最终还是沿 层面法线方向延伸。
第6节(弯曲变形)

Mechanics of Materials
中南大学土木建筑学院力学系
Department of Mechanics of School of Civil Engineering and Architecture of Central South University
第六章 弯曲变形 第一节 概述
Fx Fl
转角方程
EI(x)1Fx2FlxC
2 挠度方程
E Iv(x)1F x31F lx2C xD 62
EI
d2v dx2
Fx Fl
EI(x)1Fx2FlxC
2
E Iv(x)1F x31F lx2C xD 62
⑶ 确定积分常数
EI(0)1F02Fl0C0
2 E Iv(0 )1F 0 31F l0 2 C 0D 0
EI(x)b2F l x2C1
E I(x)b 2 F l x2F 2(xa)2C 2
挠度方程
EIv(x)b6F l x3C1xD1 E Iw (x ) b 6 F lx 3F 6(x a )3 C 2xD 2
⑶ 确定积分常数
v(0)E 1 I(b 6 F l03C 10D 1)0
v (l) E 1 I[ b 6 F ll3 F 6(l a )3 C 2 l D 2 ] 0
max
(0)
Fl2 3EI
(x) 0
x (3 3)l 3
(33)l F l3
F l3
vm a xv(
) 0 .0 6 4 2
3 93E I
E I
例:简支梁AB如图所示(图中a > b),承受集中载荷F作 用,梁的弯曲刚度为EI。求此梁的挠曲轴方程和转角方程, 并确定挠度的最大值。
材料力学课件 第六章弯 曲 内 力(土木专业)

M
A
0
FRA
A
a
F1
C
F2
D
FRB
B
FRB l F1a F2b 0
MB 0
c
E
F
d
FRAl F1 ( l a ) F2 ( l b) 0
FRA F1 ( l a ) F2 ( l b) l
b l
FRB
F1a F2b l
第六章
记 E 截面处的剪力为
FRA
A
弯曲内力
a F1 C F2 D B
FSE 和弯矩 ME ,且假设
FSE 和弯矩ME 的指向和转 向均为正值.取左段为研究
E
c b l
F
d
对象。
Fy 0 , M 0,
E
FRA FS E 0
M E FRA c 0
FRA
A E
FSE
解得 FSE FRA
ME
M E FRA c
第六章
6.1引言
1.弯曲的概念
弯曲内力
工程实例
第六章
工程实例
弯曲内力
第六章
弯曲内力
车刀轴
第六章
弯曲内力
火车轮轴
第六章
弯曲内力
起重机大梁
第六章
弯曲内力
镗刀杆轴
第六章
基本概念
弯曲内力
1.弯曲变形 (1) 受力特征 外力(包括力偶)的作用线垂直于杆轴线. (2) 变形特征 变形前为直线的轴线,变形后成为曲线. 2.梁 以弯曲变形为主的杆件 3.平面弯曲 作用于梁上的所有外力都在纵向对称面内,弯曲变形后的轴 线是一条在该纵向对称面内的平面曲线,这种弯曲称为平面弯曲.
工程力学(第二版)PPT吴玉亮主编-第6章 弯曲

一般情况,在截面m—m上应有一个与截面相切的力Q和一个在外力所在平面内的力 偶M与之平衡,如图6-5(b)所示。
第6章 弯曲
6.2 梁的弯曲内力及弯矩图
6.2.1 剪力与弯矩 Q称为剪力,M称为弯矩,剪力和弯矩统称为弯曲内力,其值可由左段梁的平衡
第6章 弯曲
6.3 梁的弯曲应力和强度条件
6.3.1 梁的纯弯曲 若梁的各个横截面上只有弯矩而无剪力,从而只有正应力而无切应力的情况,称
为纯弯曲。当横截面上同时存在弯矩和剪力,即同时存在正应力和切应力的情况称为 横力弯曲。例如,图6-13(a)所示简支梁,从其剪力图和弯矩图可知,CD段为纯弯 曲,AC和DB段为横力弯曲。
第6章 弯曲
6.3 梁的弯曲应力和强度条件
6.3.5 弯曲正应力的强度条件 一般地,σmax发生在危险截面上离中性轴最远的点处,即截面的上、下边缘处。
而在这些点处的切应力为零,故限定梁内最大正应力不得超过材料的许用应力,便是 细长梁的强度条件。
上式称弯曲强度条件。
第6章 弯曲
6.3 梁的弯曲应力和强度条件
截面。
第6章 弯曲
6.3 梁的弯曲应力和强度条件
6.3.3 惯性矩 同理,圆形截面惯性矩
,如图6-18所示。
第6章 弯曲
6.3 梁的弯曲应力和强度条件
6.3.3 惯性矩 圆环形截面惯性矩
,如图6-19所示。
第6章 弯曲
6.3 梁的弯曲应力和强度条件
6.3.4 弯曲正应力的计算 已知梁的某确定横截面上,最大正应力σmax发生在离中性轴最远处,即横截面的
上下边缘处。设该处到中性轴的距离为ymax,则最大弯矩所在截面(危险截面)的最 大应力为
理论力学 第六章 弯曲应力

Fs 2 q( x2 a L)
qL
图(a) B M2 x2 Fs2
mB (Fi ) 0 , 1 qLx2 M 2 q( x2 a)2 0 2
M2
1 q( x2 a)2 qLx2 2
图(c)
从上面例题的计算过程,可以总结出如下 规律: (1) 横截面上的剪力在数值上等于截面 左侧或右侧梁段上外力的代数和。 左侧梁段上向上的外力或右侧梁段上 向下的外力将引起正值的剪力;反之,则
x
Fab l
Fa l
x
M
a
F
C
l
b * 在 集中力F 作用 处,剪力图有突变, 突变值为集中力的 大小;弯矩图有尖 角转折
A
x Fb l
FS
Fa l
x
Fab l
x
M
a b l / 2时,M max
Fl 为极大值。 4
讨论 由剪力图可见,在梁上 的集中力(包括集中荷载和约
束力)作用处剪力图有突变,
y
F
2.求截面1-1上的内力
FS D
2 FA F 3
2 M D FA a Fa 3
同理,对于C左截面: 2 FSC左 FA F 3 2 l 2 M C左= F Fl 3 3 9 对于C右截面:
F l 2 FSC右 FA F M C右 FA Fl 3 3 9 FSC左 FSC右 , M C左=M C右
M2
FS2
FB
建议:求截面FS和M时,均按规定正向假设,这 样求出的剪力为正号即表明该截面上的剪力为正 的剪力,如为负号则表明为负的剪力。对于弯矩 正负号也作同样判断。
•
§6-3 剪力方程和弯矩方程 剪力图和弯矩图
第六章梁弯曲时的位移
① 2倍
F
② 4倍
A
B
③ 8倍
④ 16倍
分析:
vB
Fl3 3EI
7. 不计自重的圆截面梁,外力作用于自由端, 如只使外力增加一倍,其他不变,则自由端的 挠度为原来的(②)。
① 2倍
F
② 4倍
A
B
③ 8倍
④ 16倍
分析:
vB
Fl3 3EI
8.弯曲刚度为EI梁,正确说法为(④)。
①A、B、C处转角相等 ②B、C处转角不相等
③、q B
3Pl2 2EI
④
、q B
Pl2 EI
11. 一等截面悬臂梁,在均匀自重作用下, 自由 端的挠度与(④)。 ① 梁的长度成正比 ② 梁的长度的平方成正比 ③ 梁的长度的立方成正比
式中C1、C2为积分常数,由梁边界、连续条件确定。 2.支承条件与连续条件: 1) 支承条件:
y
y
y
v0
v0
v 0;v 0
2) 连续条件:挠曲线是光滑、连续、唯一的
F
A
C
B
v |xC v |xC ,q |xC q |xC
3.积分法确定梁弯曲变形的步骤:
①建立坐标系,确定支反力。 ②写出弯矩方程;若弯矩不能用一个函数给出,则要分段写出。 ③写出挠曲线近似微分方程,并积分得到转角、挠度函数。 ④利用边界条件、连续条件确定积分常数。
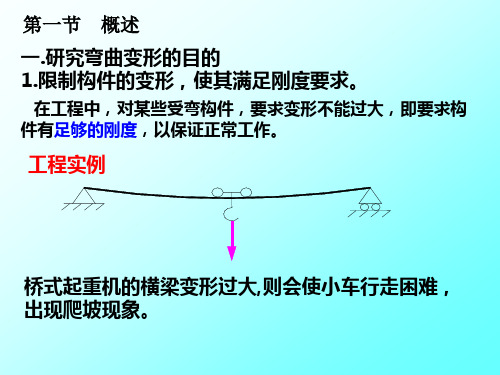
第一节 概述 一.研究弯曲变形的目的 1.限制构件的变形,使其满足刚度要求。
在工程中,对某些受弯构件,要求变形不能过大,即要求构 件有足够的刚度,以保证正常工作。
工程实例
桥式起重机的横梁变形过大,则会使小车行走困难, 出现爬坡现象。
2.利用弯曲变形
6第六章 梁弯曲时的位移讲解
第六章梁弯曲时的位移§6.1 概述§概述研究变形的目的1. 限制弯曲变形,建立刚度条件;限制弯曲变形建立刚度条件2利用弯曲变形以便能够缓冲减振;2. 利用弯曲变形,以便能够缓冲、减振;3. 解静不定问题。
钢板轧机:轧辊压轧钢板汽车轮轴上的叠板弹簧§6.2梁的挠曲线近似微分方程§6.2 梁的挠曲线近似微分方程θCB ′′ABw CC F xC通常用横截面的两个基本位移量来反映梁的变形情况一、挠度和转角通常用横截面的两个基本位移量,来反映梁的变形情况11. 挠度w 2. 转角θ转y挠曲线′θCθCB C ′ABxw CC Fx——1. w 横截面形心在垂直于x 轴方向的线位移挠度小变形,挠度远小于跨长,形心沿x 轴方向的线位移与挠度相比属于高阶微量,可略去不计挠曲线方程w = f (x )挠曲线是一条光滑连续的曲线——横截面对其原来位置的角位移2. 转角θ(弹性曲线)(绕中性轴转过的角度)横截面的转角= 由x 轴转到曲线对应点处切线方向的夹角横截(锐角)x = 0,x = l,,)(当a > b()时最大挠度当a > b 时,最大挠度1==dw 应在AC 段内,令01θdx 得因此,工程计算中,不论受什么荷载作用,只要简支梁的挠曲即使荷载非常靠近右支座这种极端情况下,最大挠度所在位置仍与跨中位置非常靠近,w max 与w 跨中相差≤3%线上没有拐点(即挠曲线向一边弯),都可以用w max ←w 跨中积分法求梁的变形积分常数的确定:边界条件,连续条件优点:可全面表达挠度和转角缺点:方程与坐标选择有关;计算量大。
通常只关心某些特殊截面的挠度和转角:1. 简单荷载作用下,基本形式的静定梁某些特殊截面的挠度和转角的结果列出来用时直接查表2.某些特殊截面的挠度和转角的结果列出来,用时直接查表。
2.复杂情况(例,多个荷载作用或组合梁)可以采用叠加法。
叠加法求梁的位移1. 叠加原理:当所求参数(内力、应力或位移)与梁上荷载为线性关系时,由几项荷载共同作用时所引起的某一参数,就等于每项荷载单独作用时所引起的该参数值的代数和叠加适用条件:所求物理量必须与荷载成线性正比关系前提:线弹性、小变形各荷载的作用互不相干,互不影响2. 方法(1)分解每种情况都是简单模型;——(2)分别计算——查表;(3)叠加。
弯曲变形1
第六章 弯曲变形一、是非判断题6.1 正弯矩产生正转角,负弯矩产生负转角。
( ) 6.2 弯矩最大的截面转角最大,弯矩为零的截面上转角为零。
( ) 6.3 弯矩突变的地方转角也有突变。
( ) 6.4 弯矩为零处,挠曲线曲率必为零。
( ) 6.5 梁的最大挠度必产生于最大弯矩处。
( ) 二、填空题6.1 梁的转角和挠度之间的关系是 。
6.2 梁的挠曲线近似微分方程的应用条件是 。
6.3 画出挠曲线的大致形状的根据是 。
判断挠曲线的凹凸性与拐点位置的根据是 。
6.4 用积分法求梁的变形时,梁的位移边界条件及连续性条件起 作用。
6.5 梁在纯弯时的挠曲线是圆弧曲线,但用积分法求得的挠曲线却是抛物线,其原因是。
6.6 两悬臂梁,其横截面和材料均相同,在梁的自由端作用有大小相等的集中力,但一梁的长度为另一梁的2倍,则长梁自由端的挠度是短梁的 倍,转角又是 短梁的 倍。
6.7 应用叠加原理的条件是 。
6.8 试根据填题6.8图所示载荷及支座情况,写出由积分法求解时,积分常数的数目及确定积分常数的条件。
积分常数 个; 支承条件 。
连续条件是 。
6.9 试根据填题6.9图用积分法求图示挠曲线方程时,需应用的支承条件是;连续条件是 。
填题6.8图 填题6.9图 三、选择题5.1挠曲线近似微分方程形式为( )A.22dx y d = GI x M )(B. 22dx y d = EI x M )(C.22dx y d = GA x M )(D. 22dx y d = EA x M )(5.2用积分法求图示变截面梁自由端的挠度时,挠曲线近似微分方程应分( )段来列。
A. 一段 B.二段 C..三段 D.四段5.3A.0=A θ,0≠A yB. 0≠B θ,0=B y C. 0=B θ,0≠B y D. 0=B θ,三、计算题6.1 用积分法求图示各梁的挠曲线方程及自由端的挠度和转角。
设EI =常量。
材料力学简明教程(景荣春)课后答案第六章
( ) wA
= − q0l 4 30EI
↓
,θB
= q0l3 24EI
(顺)
讨论:请读者按右手坐标系求 wA ,θB 并与以上解答比较。
(c)
(c1)
解 图(c1)
( ) ∑ M B = 0 , FC
= − Me l
↓
CA 段
M
=
−
Me l
x1
⎜⎛ 0 ⎝
≤
x1
<
l 2
⎟⎞ ⎠
AB 段
M
=
−
Me l
l 2
≤
x2
≤
l ⎟⎞ ⎠
Ew1′′
=
3 8
qlx1
−
1 2
qx12
EIw1′
=
3 16
qlx12
−
1 6
qx13
+
C1
EIw1
=
1 16
qlx13
−
1 24
qx14
+
C1 x1
+
D1
EIw′2′
=
3 8
qlx2
−
ql 2
⎜⎛ ⎝
x2
−
l ⎟⎞ 4⎠
EIw′2
=
3 16
qlx22
−
ql 4
⎜⎛ ⎝
x2
24
EIw′(l) = 0 ,− q l 3 + 3Al 2 + 2Bl = 0
6
解式(a),(b)得
A = ql , B = − ql 2
12
24
即挠曲线方程为
EIw = − q x4 + ql x3 − ql 2 x2 24 12 24
工程力学2第六章 弯曲变形
§6-4 用叠加法求弯曲变形
设梁上有n 个载荷同时作用,任意截面上的弯矩 为M(x),转角为 ,挠度为y,则有:
d2y EI 2 EIy'' M ( x ) dx n
由弯矩的叠加原理知: 所以, 即,
§6–3 用积分法求弯曲变形 (Beam deflection by integration )
一、微分方程的积分 (Integrating the differential equation )
M ( x) w EI
若为等截面直梁, 其抗弯刚度EI为一常量上式可改写成
EIw M ( x )
代入求解,得
1 Fb 3 C1 C 2 Fbl 6 6l D1 D2 0
FAy x1
ymax
x2
a
b
目录
§6-3 用积分法求弯曲变形
5)确定转角方程和挠度方程
AC 段: 0 x1 a
Fb 2 Fb 2 EI 1 x1 (l b2 ) 2l 6l
Fb 3 Fb 2 EIy1 x1 ( l b 2 ) x1 6l 6l
转角
4、挠度与转角的关系 ( Relationship between deflection and slope): w
A
tg w ' w '( x )
B
x
C C'
转角
w挠度
挠曲线
B
5、挠度和转角符号的规定
(Sign convention for deflection and slope) 挠度 向上为正,向下为负. 转角 自x 转至切线方向,逆时针转为正,顺时针转为负. w
