第四章达标检测卷
人教版第四章 人体内物质的运输单元达标专项训练检测试卷

人教版第四章人体内物质的运输单元达标专项训练检测试卷一、选择题1.下图为人体某一部位的血液循环示意图,c代表某器官处的毛细血管,请根据图分析下列问题,正确的是()A.a代表的一定是上、下腔静脉B.如果c表示人体肺部的毛细血管,则b代表的血管是肺静脉C.如果c代表大脑处的毛细血管,当血液流经c后氧气和养料增加D.如果流经c后,血液中的营养物质明显增加,则c处的器官是小肠2.如图是显微镜下观察到的小鱼尾鳍内的一部分血管的分支情况,箭头代表血流方向。
对此,下列说法不正确的是()A.图中A代表的是小动脉B.图中的B代表的是小静脉C.图中C代表的是毛细血管D.图中血液在三种血管内的速度依次是A>C>B3.如图是用显微镜观察到的人血涂片视野,下列表述中正确的是A.①个体最小,能穿透血管壁B.②数量最多,能够吞噬病菌C.③的数量最多,具有运输氧的功能D.①②③三种细胞中只有③没有细胞核4.用显微镜观察人血涂片时,具有细胞核的是()A.红细胞B.血红蛋白C.白细胞D.血小板5.如图所示血液分层实验,错误的是()A.①是抗凝剂B.②是血浆C.③是白细胞D.④是红细胞6.下列对血浆主要功能的描述中,正确的是()①运输养料和废物②促进止血和加速凝血③运输氧和部分二氧化碳④运载血细胞A.①③B.②④C.①④D.②③7.小强同学在探究血液的成分时,将等量的新鲜鸡血分别放入A、B、C、D四支试管中。
在A、D两支试管内加入抗凝剂,B、C不做上述处理。
静置较长一段时间后,下列图示中正确的是A.B.C.D.8.如图为人体血液循环示意图,下列有关叙述正确的是()A.体循环是指血液流经“左心室→②→右心房”的过程B.当血液流经①时,血液由动脉血变为静脉血C.右心房是肺循环的起点D.心房与动脉相连,心室与静脉相连9.下列有关观察血液和血管实验的叙述,正确的是()A.图一中判断2为毛细血管的主要依据是只允许红细胞单行通过B.图一中三种血管内的血液流动速度不同,血流速度为 1>2>3C.图二中在低倍显微镜下可观察到三种血细胞的形态和数量D.图二中①白细胞数量较少不易观察,可移动涂片进一步寻找10.图是心脏解剖示意图,下列说法正确的是A.肺循环的终点是aB.②和③分别与c和d相连C.含有动脉血的腔是b和dD.①和④分别是肺静脉和上腔静脉11.如图是血液循环示意图,1、2、3、4表示与心脏直接相连的血管,甲、乙表示不同部位的毛细血管。
九年级物理上册第四章探究电流达标检测卷

九年级物理上册第四章研究电流达标检测卷————————————————————————————————作者:————————————————————————————————日期:第四章达标检测卷(100分,60分钟)题号一二三四总分得分一、选择题( 每题 3 分,共30 分)1.以下用品中,一般状况部下于导体的是()A.钢尺 B .玻璃瓶 C .纸杯 D .橡皮擦2.物理学成就在军事上有宽泛的应用,有一种称为石墨炸弹的武器在战争期间被用来损坏敌方的供电设备,这类炸弹在爆炸时一般不会造成人员的伤亡,而是在空气中分布大批极细的石墨丝,这些石墨丝飘到供电设备上能使供电系统瘫痪。
以下对石墨导电性能的判断()和对供电设备造成损坏的原由,剖析正确的选项是A.石墨是导体,会使供电设备短路B.石墨是导体,会使供电设备断路C.石墨是绝缘体,会使供电设备短路D.石墨是绝缘体,会使供电设备断路3.从图中的长方形金属薄板abdc中剪出一块,以下哪一种剪法获得的金属板条电阻最大()A.剪出abfe B.剪出efdcC.剪出暗影部分的细金属条 D .保存整块金属板( 第3题图)( 第4 题图) 4.如下图滑动变阻器,将其接入电路,当滑片P 向B 端滑动时,使其连入电路的电阻变大,应选择的接线柱是()A.C和 A B .C和 B C.D和 B D.A和B5.如下图的电路,电源电压不变,闭合开关S1、 S2,两灯都发光,当把开关S2断开时,灯泡L1的亮度及电流表示数变化的状况是()A. L1变亮,电流表示数变小 B . L1亮度不变,电流表示数变小C. L1变亮,电流表示数不变 D . L1亮度不变,电流表示数不变(第 5 题图)(第6题图)6.如下图的电路中,将开关 S 闭合,灯 L和灯 L 均发光,则以下说法中正确的选项是() 12A.灯 L1和灯 L2并联B.灯 L1和灯 L2串连C.经过灯 L1和灯 L2的电流必定相等12两头的电压必定不相等D.灯 L和灯 L7.如下图,电源电压为 4.5 V 且恒定不变,当开关S 闭合后,滑动变阻器的滑片P 从 a 端滑向 b 端的过程中,三只理想电压表的示数变化的绝对值分别为ΔU、ΔU 、ΔU ,123以下可能出现的状况是 ()A.ΔU1=0 V ,ΔU2= 2 V ,ΔU3= 1 VB.ΔU1=0 V ,ΔU2= 2 V ,ΔU3= 2 VC.ΔU1=0.5 V ,ΔU2= 1 V,ΔU3= 1.5 VD.ΔU1=0.2 V ,ΔU2= 1 V,ΔU3= 0.8 V(第 7题图)8.为了研究电阻与资料的关系,采纳如下图的电路,此中(第8题图) AB 是锰铜丝, CD是镍铬合金丝,它们应当()A.长度同样,横截面积不一样B .长度同样,横截面积也同样C.长度和横截面积都不一样D .横截面积同样,长度不一样(第 9题图) 9.如下图的电路,以下剖析正确的选项是()A.只闭合 S时, L发光、 L不发光, A测经过 L的电流12122 B.只闭合 S2时, L1发光、 L2不发光, A1测经过 L2的电流C.闭合 S1、 S2时, L1、L2并联, A2测经过 L2的电流D.闭合 S1、 S2时, L1、L2串连, A1、A2示数相等10.如下图的电路,闭合开关,滑动变阻器的滑片向右挪动的过程中( 电源电压不变) ,电流表与电压表示数变化的状况分别是()A.变小、变大 B .变小、不变 C .不变、不变 D .变小、变小(第 10题图)(第 11题图 )( 第12 题图)二、填空题( 每空 2 分,共42 分)11.如下图电阻箱的读数为________Ω。
湘教版数学七年级下册第4章 相交线与平行线 达标测试卷(含答案)

第4章相交线与平行线达标测试卷一、选择题(共6题,每题3分,共18分)1. 下列图形中,能将其中一个三角形平移得到另一个三角形的是()A B C D2. 如图,对于图中标记的各角,下列条件能够推理得到a∥b的是()A.∠1=∠2B.∠2=∠4C.∠3=∠4D.∠1+∠4=180°(第2题)(第3题)(第4题)3. 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C的度数为()A.30°B.60°C.80°D.120°4. 在体育课上某同学立定跳远的情况如图所示,l表示起跳线,在测量该同学的实际立定跳远成绩时,应测量的线段及理由是()A.BP,经过一点有且只有一条直线垂直于已知直线B.CP,垂线段最短C.DP,两点之间,线段最短D.BD,两平行线间的公垂线段相等5. 如图,已知正方形ABCD的面积为4,则三角形EBC的面积为()A.4 B.3 C.2 D.1(第5题)(第6题)(第7题)(第8题)6. 如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=()A.120°B.130°C.140°D.150°二、填空题(共6题,每题4分,共24分)7. 如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE=______°.8. 如图,a∥b,点P在直线a上,点A在直线b上,P A⊥b,P A=2 cm,则点A到直线a的距离为________cm.9. 如图,AB∥CD,EF分别交AB,CD于G,H两点,若∠1=50°,则∠EGB=________.(第9题) (第10题)10. 如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西________.11. 如图,若直线EF⊥MN于F,且∠1=140°,则当∠2=________时,AB∥CD.(第11题) (第12题)12. 如图,直线AB,CD交于点O,∠BOC=70°,现作射线OE⊥CD,则∠AOE的大小为__________.三、解答题(共6题,共58分)13. (8分)如图,要把水渠中的水引到C点,在渠岸AB的什么地方开沟,才能使沟最短?画出图形,并说明理由.14. (8分)如图,直线AB、CD相交于点O, OD垂直于OE,∠BOE=18°.求∠AOC的度数.15. (8分)如图,已知AD∥BC,AC=15 cm,BC=12 cm,BE⊥AC于点E,BE=10 cm,求AD与BC之间的距离.16. (10分)如图,已知∠ABC=180°-∠A,BD⊥CD于点D,EF⊥CD于点F.(1)试说明:AD∥BC.(2)若∠1=36°,求∠2的度数.317. (10分)如图,将周长为18 cm的三角形ABC沿BC方向平移得到三角形DEF.如果四边形ABFD的周长是21 cm,求平移的距离.18. (14分)问题情境:如图①,AB∥CD,∠P AB=130°,∠PCD=120°,求∠APC的度数.小明的解题思路:如图②,过P作PE∥AB,通过平行线的性质,可得∠APC =50°+60°=110°.问题迁移:(1)如图③,AD∥BC,点P在射线OM上运动,当点P在A,B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD,∠α,∠β之间有何数量关系?请说明理由;(2)在(1)的条件下,如果点P在A,B两点外侧运动(点P与A,B,O三点不重合),请你直接写出∠CPD,∠α,∠β之间的数量关系.答案一、1.A 2.D 3.A 4.B 5.C 6.C二、7.258.2【点拨】因为a∥b,P A⊥b,P A=2 cm,所以AP⊥a,所以点A到直线a 的距离=P A=2 cm.9.50°10.48°【点拨】如图,因为AC∥BD,∠1=48°,所以∠2=∠1=48°,根据方向角的概念可知,乙地所修公路的走向是南偏西48°.11.50°【点拨】如图,因为AB∥CD,所以∠3=∠4(两直线平行,同位角相等).又因为∠1+∠3=180°,∠1=140°,所以∠3=∠4=40°.因为EF⊥MN,所以∠2+∠4=90°,所以∠2=50°.12.20°或160°【点拨】因为OE⊥DC,所以∠DOE=90°.因为∠AOD=∠BOC,∠BOC=70°,所以∠AOD=70°.①当OE在DC的左侧时,∠AOE=∠DOE-∠AOD=90°-70°=20°;②当OE在DC的右侧时,∠AOE=∠DOE+∠AOD=90°+70°=160°.综上,∠AOE=20°或160°.5三、13.解:图略.过C作CD⊥AB,垂足为D,在D处开沟,则沟最短.因为直线外一点与直线上各点连线的所有线段中,垂线段最短.14.解:因为OD⊥OE,所以∠BOD+∠EOB=90°.因为∠BOE=18°,所以∠BOD=90°-18°=72°,所以∠AOC=∠BOD=72°.15.解:过点A作BC的垂线,交BC于点P,三角形ABC的面积为12×AC×BE=12×15×10=75(cm2),又因为三角形ABC的面积为12×BC×AP=75(cm2),所以AP=12.5 cm,因此AD与BC之间的距离为12.5 cm.16.解:(1)因为∠ABC=180°-∠A,所以∠ABC+∠A=180°,所以AD∥BC.(2)因为AD∥BC,∠1=36°,所以∠3=∠1=36°.因为BD⊥CD,EF⊥CD,所以∠BDC=∠EFC=90°.所以BD∥EF.所以∠2=∠3=36°.17.解:因为三角形DEF是由三角形ABC沿BC方向平移得到的,所以AD=CF,AC=DF.所以四边形ABFD的周长为AD+AB+BF+DF=AD+AB+BC+AC+CF=2AD+(AB+BC+AC)=21 cm.因为AB+BC+AC=18 cm,所以2AD=3 cm,解得AD=1.5 cm.答:平移的距离为1.5 cm.18.解:(1)∠CPD=∠α+∠β.理由如下:如图①,过P作PE∥AD交CD于E,因为AD∥BC,所以AD∥PE∥BC.所以∠α=∠DPE,∠β=∠CPE.所以∠CPD=∠DPE+∠CPE=∠α+∠β.(2)当点P在线段BA的延长线上时,如图②.∠CPD=∠β-∠α.当点P在线段AB的延长线上时,如图③. ∠CPD=∠α-∠β.7。
苏科版七年级上册数学第4章 达标检测卷

第4章达标检测卷一、选择题(每小题3分,共24分)1.把方程12x =1变形为x =2,其依据是( )A .等式的性质1B .等式的性质2C .分数的基本性质D .以上均不正确2.下列方程中:①2x +4=6,②x -1=1x,③3x 2-2x ,④5x <7,⑤3x -2y =2,⑥x =3,其中是一元一次方程的有( ) A .5个 B .4个 C .3个 D .2个3.已知关于x 的一元一次方程2(x -1)+3a =3的解为x =4,则a 的值是( )A .-1B .1C .-2D .-34.已知(a -2)x|a|-1=-2是关于x 的一元一次方程,则a 的值为( ) A .-2 B .2 C .±2 D.±15.解一元一次方程12(x -1)=2-15x 时,去分母正确的是( )A .2(x -1)=2-5xB .2(x -1)=20-5xC .5(x -1)=2-2xD .5(x -1)=20-2x6.如图,根据图中给出的信息,可得正确的方程是( )A .π×⎝ ⎛⎭⎪⎫822x =π×⎝ ⎛⎭⎪⎫622×(x-5)B .π×⎝ ⎛⎭⎪⎫822x =π×⎝ ⎛⎭⎪⎫622×(x+5)C .π×82x =π×62×(x+5)D .π×82x =π×62×5 7.某种衬衫因换季打折出售,如果按原价的六折出售,那么每件赔本40元;如果按原价的九折出售,那么每件盈利20元,则这种衬衫的原价是( )A .160元B .180元C .200元D .220元8.中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是:有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地.则此人第三天走的路程为( )A.96里 B.48里 C.24里 D.12里二、填空题(每小题3分,共30分)9.关于x的方程3x-8=x的解为x=________.10.若单项式3acx+2与-7ac2x-1是同类项,则可以得到关于x的方程为________________.11.方程3-=2x,处被墨水盖住了,已知该方程的解是x=0,那么处的数是________.12.若代数式1-8x与9x-4的值互为相反数,则x=________.13.如图,小刚从一张正方形纸片上剪去一个宽为5 cm的长条后,再从剩下的长方形纸片上剪去一个宽为6 cm的长条.如果两次剪下的长条面积正好相等,那么每一个长条的面积为________cm2.14.我国古代数学著作《算学启蒙》中有这样一个数学问题,其大意是:跑得快的马每天跑240里,跑得慢的马每天跑150里,慢马先跑12天,快马几天可以追上慢马?设快马x 天可以追上慢马,根据题意,可列方程为____________.15.已知数轴上点A 表示的数为4,点B 表示-2,有一个动点P 从点A出发,沿着数轴以每秒2个单位长度的速度向左运动,有一个动点Q 从点B 出发,沿着数轴以每秒3个单位长度的速度向右运动,若点P ,Q 同时出发,运动时间为t 秒,则当点P 与点Q 的距离为10时,t =________.16.已知2-6的值为________.17.有一列数,按一定的规律排列成13,-1,3,-9,27,-81,….若其中某三个相邻数的和是-567,则这三个数中的第一个数是________. 18.对于有理数a 、b ,规定一种新运算:a*b =ab +b.例如,2*3=2×3+3=9.有下列结论:①(-3)*4=-8;②a*b =b*a ;③方程(x -4)*3=6的解为x =5;④(4*3)*2=32.其中,正确的有________.(填序号) 三、解答题(19题10分,20-24题每题7分,25题9分,26题12分,共66分) 19.解下列方程:(1)3x -2=10-2(x +1); (2)x -x -22=1+2x -13.20.已知方程3x -3=2x 的解为x =a +2,求关于x 的方程3x -2(x -a)=3a 的解.21.已知x =12是方程5m +12x =2x +12的解,求关于(1-2x)的解.22.已知a 、b 、c 、d 都是有理数,现规定一种新的运算:⎪⎪⎪⎪⎪⎪⎪⎪a b c d =ad -bc ,例如:⎪⎪⎪⎪⎪⎪⎪⎪1 23 4=1×4-2×3=-2. (1)计算⎪⎪⎪⎪⎪⎪⎪⎪-2355; (2)若⎪⎪⎪⎪⎪⎪⎪⎪x -31-x 2=6,求x 的值.23.规定:若两个一元一次方程所含未知数相同,并且其中一个方程的解是另一个方程解的2倍,则这个方程叫做另一个方程的倍解方程.如一元一次方程x +7=17的解是x =10,2x =10的解是x =5.10是5的2倍,因此一元一次方程x +7=17是2x =10的倍解方程.已知关于x 的一元一次方程ax -7=5是3(x +1)-4=11-x 的倍解方程,求a 的值.24.某超市有线上和线下两种销售方式.与4月份相比,该超市4月份销售总额增长10%,其中线上销售额增长43%,线下销售额增长4%. (1)设4月份的销售总额为a 元,线上销售额为x 元,请用含a ,x 的代数式表示4月份的线下销售额(直接在表格中填写结果);(2)求4月份线上销售额与当月销售总额的比值.25.若关于x 的一元一次方程ax =b(a≠0)的解恰好为x =a +b ,则称该方程为“友好方程”.例如:方程2x =-4的解为x =-2,而-2=-4+2,则方程2x =-4为“友好方程”.(1)在①-2x =4,②3x =-4.5,③12x =-1这三个方程中,为“友好方程”的是________;(填序号)(2)若关于x的一元一次方程3的值.26.某校举行元旦汇演,七(1)班、七(2)班各需购买贺卡70张,已知贺卡的价格如下表:(1)若七(1)班分两次购买,第一次购买24张,第二次购买46张,七(2)班一次性购买贺卡70张,则七(1)班、七(2)班购买贺卡费用各是多少元?哪个班的费用比较高?高多少元?(2)若七(1)班分两次购买贺卡共70张(第二次多于第一次),共付费150元,则第一次、第二次分别购买贺卡多少张?答案一、1.B 2.D 3.A 4.A 5.D 6.B7.C 【】设这种衬衫的原价是x 元,根据衬衫的成本不变,可得出关于x 的一元一次方程0.6x +40=0.9x -20,解得x =200.8.B 【】设此人第三天走的路程为x 里,则其他五天走的路程分别为4x 里,2x 里,12x 里,14x 里,18x 里,根据六天共走了378里,可得出关于x 的一元一次方程为4x +2x +x +12x +14x +18x =378,解得x =48. 二、9.4 10.x +2=2x -1 11.3 12.3 13.150 14.(240-150)x =150×1215.165【】当运动时间为t 秒时,点P 表示的数为-2t +4,点Q 表示的数为3t -2,依题意,得|(-2t +4)-(3t -2)|=10,即6-5t =10或5t -6=10,解得t =-45(不合题意,舍去)或t =165. 16.1 【】因为2x -3y +1=0,所以2=1.17.-81 【】设这三个数中的第一个数为x ,则另外两个数分别为-3x ,9x ,根据三个数之和为-567,即可得出关于x 的一元一次方程x -3x +9x =-567,解得x =-81.18.①③④ 【】①根据题中的新定义得:(-3)*4=-12+4=-8,正确;②a*b =ab +b ,b*a =ab +a ,不一定相等,错误;③将方程整理,得3(x -4)+3=6,解得x =5,正确;④(4*3)*2=(12+3)*2=15*2=30+2=32,正确.三、19.解:(1)去括号,得3x -2=10-2x -2,移项、合并同类项,得5x =10,系数化为1,得x =2;(2)去分母,得6x -3(x -2)=6+2(2x -1),去括号,得6x -3x +6=6+4x -2,移项,得6x -3x -4x =6-6-2,合并同类项,得-x =-2,系数化为1,得x =2.20.解:因为方程3x -3=2x 的解为x =a +2,所以3(a +2)-3=2(a +2),解得a =1.当a =1时,方程3x -2(x -a)=3a 可变为3x -2(x -1)=3,解得x =1.21.解:把x =12代入方程5m +12x =2x +12,得5m +6=1,解得m=-1.把m=-1代入方程mx+2=m(1-2x),得-x+2=-(1-2x),解得x=1.22.解:(1)由题中的新定义,得原式=-2×5-3×5=-10-15=-25;(2)由题中的新定义,得2x-(-3)×(1-x)=6,去括号,得2x+3-3x=6,移项、合并同类项,得-x=3,系数化为1,得x=-3.23.解:3(x+1)-4=11-x去括号,得3x+3-4=11-x,移项、合并同类项,得4x=12,系数化为1,得x=3.又因为关于x的一元一次方程ax-7=5是3(x+1)-4=11-x的倍解方程,所以ax-7=5的解是x=6,所以6a-7=5,解得a=2.24.解:(1)1.04(a -x) 【】因为与4月份相比,该超市4月份线下销售额增长4%,所以该超市4月份线下销售额为1.04(a -x)元.(2)依题意,得1.1a =1.43x +1.04(a -x),解得x =213a , 所以1.43x 1.1a =1.43·213a 1.1a =0.22a 1.1a=0.2. 答:4月份线上销售额与当月销售总额的比值为0.2.25.解:(1)② 【】-2x =4的解是x =-2,而-2≠-2+4,即方程-2x =4不是“友好方程”.3x =-4.5的解是x =-1.5,且-1.5=3+(-4.5),即方程3x =-4.5是“友好方程”.12x =-1的解是x =-2,而-2≠12+(-1),即方程12x =-1不是“友好方程”.(2)因为关于x 的一元一次方程3x =b 是“友好方程”,所以b 3=3+b , 解得b =-4.5;(3)因为关于+1是“友好方程”,所以2m +1-2=-2+(2m +1),解得m =16. 26.解:(1)七(1)班购买贺卡费用为3×24+2.5×46=187(元), 七(2)班购买贺卡费用为2×70=140(元).187>140,187-140=47(元).答:七(1)班购买贺卡费用为187元,七(2)班购买贺卡费用为140元,七(2)班的费用比较高,高47元.(2)设第一次购买贺卡m 张,则第二次购买贺卡(70-m)张.当0<m <20时,3m +2(70-m)=150,解得m =10,此时70-m =60;当20≤m≤30时,3m +2.5(70-m)=150,解得m =-50(不合题意,舍去);当30<m <35时,2.5m +2.5(70-m)=175≠150.答:第一次购买贺卡10张,第二次购买贺卡60张.。
初中数学人教版七年级上册第4章达标测试卷(含答案)
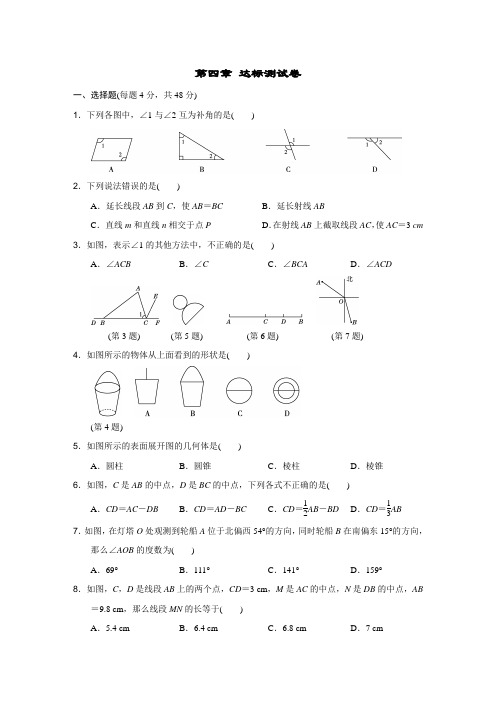
第四章 达标测试卷一、选择题(每题4分,共48分)1.下列各图中,∠1与∠2互为补角的是( )2.下列说法错误的是( )A .延长线段AB 到C ,使AB =BC B .延长射线ABC .直线m 和直线n 相交于点PD .在射线AB 上截取线段AC ,使AC =3 cm3.如图,表示∠1的其他方法中,不正确的是( )A .∠ACBB .∠CC .∠BCAD .∠ACD(第3题) (第5题) (第6题) (第7题)4.如图所示的物体从上面看到的形状是( )(第4题)5.如图所示的表面展开图的几何体是( )A .圆柱B .圆锥C .棱柱D .棱锥6.如图,C 是AB 的中点,D 是BC 的中点,下列各式不正确的是( )A .CD =AC -DBB .CD =AD -BCC .CD =12AB -BD D .CD =13AB7.如图,在灯塔O 处观测到轮船A 位于北偏西54°的方向,同时轮船B 在南偏东15°的方向,那么∠AOB 的度数为( ) A .69°B .111°C .141°D .159°8.如图,C ,D 是线段AB 上的两个点,CD =3 cm ,M 是AC 的中点,N 是DB 的中点,AB=9.8 cm ,那么线段MN 的长等于( ) A .5.4 cmB .6.4 cmC .6.8 cmD .7 cm(第8题) (第11题) (第12题)9.若一个角的余角比它的补角的12少30°,则这个角为( )A .30°B .40°C .60°D .75°10.在直线AB 上任取一点O ,过点O 作射线OC ,OD ,∠COD =90°,当∠AOC =30°时,∠BOD 的度数是( ) A .60°B .120°C .60°或90°D .60°或120°11.如图,点C ,O ,B 在同一条直线上,∠AOB =90°,∠AOE =∠DOB ,下列结论:①∠EOD =90°;②∠COE =∠AOD ;③∠COE =∠DOB ;④∠COE +∠BOD =90°.其中正确的个数是( ) A .1B .2C .3D .412.如图,每个图形都是由同样大小的正方形按照一定的规律组成的,其中第①个图形的面积为6 cm 2,第②个图形的面积为18 cm 2,第③个图形的面积为36 cm 2,…,那么第⑥个图形的面积为( ) A .84 cm 2B .90 cm 2C .126 cm 2D .168 cm 2二、填空题(每题4分,共24分) 13.48°30′36″=________°.14.如图,已知∠BOC =2∠AOB ,OD 平分∠AOC ,∠BOD =14°,则∠AOC 的度数是________.(第14题) (第16题)15.将线段AB 延长至点C ,使BC =13AB ,延长BC 至点D ,使CD =13BC ,延长CD 至点E ,使DE =13CD ,若CE =8 cm ,则AB =________ cm .16.如图,将长方形纸片ABCD 沿AF 折叠,点D 落在点E 处,已知∠AFE =40°,则∠CFE的度数为________.17.如图,已知B 是线段AC 上的一点,M 是线段AB 的中点,N 是线段AC 的中点,P 是线段NA 的中点,Q 是线段AM 的中点,则MN ∶PQ 等于__________.(第17题) (第18题)18.一个几何体是由大小相同的小立方体摆成的,如图是从正面、左面、上面看这个几何体得到的平面图形,组成这个几何体所用的小立方体的个数是________. 三、解答题(每题8分,共16分)19.已知线段AB =6 cm ,点C 在直线AB 上,AC =13AB ,求BC 的长度.20.如图,∠AOB =90°,OD 平分∠BOC ,∠AOC =2∠1,求∠1的度数.(第20题)四、解答题(每题10分,共50分)21.如图,延长线段AB 到C ,使BC =2AB ,若AC =6 cm ,且AD =DB ,BE ∶EF ∶FC =1∶1∶3,求DE ,DF 的长.(第21题)22.如图,∠AOC与∠BOC互余,OD平分∠BOC,∠EOC=2∠AOE.(1)若∠AOD=75°,求∠AOE的度数;(2)若∠DOE=54°,求∠EOC的度数.(第22题)23.如图,OD平分∠BOC,OE平分∠AOC,∠BOC=60°,∠AOC=58°.(1)求∠AOB的度数.(2)①求∠DOC和∠AOE的度数;②判断∠DOE与∠AOB是否互补,并说明理由.(第23题)24.如图,点C在线段AB上,AC=6 cm,MB=10 cm,点M,N分别为AC,BC的中点.(1)求线段BC,MN的长;(2)若C在线段AB的延长线上,且满足AC-BC=a cm,M,N分别是线段AC,BC的中点,请画出图形,并用含a的式子表示MN的长度.(第24题)25.已知∠AOB内部有三条射线,其中OE平分∠BOC,OF平分∠AOC.(1)如图①,若∠AOB=90°,∠AOC=30°,求∠EOF的度数;(2)如图②,若∠AOB=α,求∠EOF的度数(用含α的式子表示);(3)若将题中的“平分”的条件改为“3∠EOB=∠COB,3∠COF=2∠COA”,且∠AOB=α,用含α的式子表示∠EOF的度数为__________.(第25题)五、解答题(共12分)26.如图,已知点C,D,E是线段AB上的点,点D是CB的中点,BE=2DE,AC=m cm,DE=n cm,且m,n满足(m-4)2+|1-n|=0.(1)求线段AB的长度;(2)点P从A点以2.5 cm/秒的速度向点B的方向运动,点Q从B点以1.5 cm/秒的速度向点A的方向运动,几秒后,①BP=3BQ?②PQ=2 cm?(第26题)答案一、1.D 2.B 3.B 4.D 5.B 6.D7.C8.B9.C10.D11.C12.C二、13.48.5114.84°15.5416.100°17.2∶118.8三、19.解:当B、C在点A的同侧时,BC=4 cm,当B、C在点A的异侧时,BC=8 cm.20.解:因为OD平分∠BOC,所以∠BOC=2∠1.因为∠AOC=2∠1,所以∠BOC=∠AOC=12×(360°-∠AOB)=12×(360°-90°)=135°,所以∠1=12∠BOC=67.5°.四、21.解:因为BC=2AB,AC=6 cm.所以AB=2 cm,BC=4 cm.因为AD=BD,所以AD=BD=1 cm.因为BE∶EF∶FC=1∶1∶3,所以BE=EF=15BC=0.8 cm.所以DE=BD+BE=1+0.8=1.8(cm).DF=BD+BE+EF=2.6 cm.22.解:设∠AOE=x°,则∠EOC=2x°,所以∠AOC=3x°,所以∠COB=90°-3x°.因为OD平分∠COB,所以∠COD=∠DOB=12∠COB=45°-32x°.(1)若∠AOD=75°,即∠AOC+∠COD=75°,则3x°+45°-32x°=75°,解得x=20.即∠AOE=20°.(2)因为∠DOE=∠EOC+∠COD=2x°+45°-32x°=45°+12x°,∠DOE=54°,所以45°+12x°=54°,解得x=18.所以∠EOC=36°.23.解:(1)∠AOB =∠BOC +∠AOC =60°+58°=118°.(2)①因为OD 平分∠BOC ,OE 平分∠AOC ,所以∠DOC =∠BOD =12∠BOC =12×60°=30°,∠AOE =∠COE =12∠AOC =12×58°=29°.②∠DOE 与∠AOB 不互补.理由:因为∠DOC =30°,∠COE =29°, 所以∠DOE =∠DOC +∠COE =59°. 所以∠DOE +∠AOB =59°+118°=177°. 故∠DOE 与∠AOB 不互补. 24.解:(1)因为M 是AC 的中点,所以MC =12AC =3 cm , 所以BC =MB -MC =7 cm , 又N 为BC 的中点, 所以CN =12BC =3.5 cm , 所以MN =MC +NC =6.5 cm. (2)如图.(第24题)因为M 是AC 的中点,所以CM =12AC ,因为N 是BC 的中点,所以CN =12BC ,所以MN =CM -CN =12AC -12BC =12(AC -BC )=12a cm. 25.解:(1)因为OF 平分∠AOC ,所以∠COF =12∠AOC =12×30°=15°.因为∠BOC =∠AOB -∠AOC =90°-30°=60°,OE 平分∠BOC , 所以∠EOC =12∠BOC =30°, 所以∠EOF =∠COF +∠EOC =45°. (2)因为OF 平分∠AOC , 所以∠COF =12∠AOC ,同理,∠EOC=12∠BOC,所以∠EOF=∠COF+∠EOC=12∠AOC+12∠BOC=12(∠AOC+∠BOC)=12∠AOB=1 2α.(3)2 3α五、26.解:(1)因为(m-4)2+|1-n|=0,所以m-4=0,1-n=0.所以m=4,n=1.即:AC=4 cm,DE=1 cm.因为BE=2DE,所以BE=2×1=2(cm).所以DB=DE+EB=1+2=3(cm).因为D是BC的中点,所以CB=2DB=2×3=6(cm),所以AB=AC+CB=4+6=10(cm).(2)①设t秒后,BP=3BQ.10-2.5t=3×1.5t,t=10 7.所以107秒后,BP=3BQ.②当P,Q未相遇,且PQ=2 cm时,2.5t+1.5t+2=10,t=2. 当P,Q相遇后,且PQ=2 cm时,2.5t+1.5t-2=10,t=3.综上,2秒或3秒后,PQ=2 cm.。
2020人教版化学九年级上册第四章达标测试卷(附答案)

第四章达标测试卷中15 小题,每小题 1 分,共15 分。
每小题的 4 个选项一、选择题(本大题包括)只有1 个符合题意1.我国西藏靠尼泊尔地区边界曾发生过多起地震,灾区饮用水被严重污染,为确保灾民的生活用水安全,急需对水进行净化处理。
下列措施中,不属于净水方法的是( )A.吸附沉淀B.过滤C.静置沉淀D.加肥皂水2.自来水厂生产流程如图所示,其中分离水中固态杂质的设备是( )(第2 题)A.反应沉淀池B.过滤池C.活性炭吸附池D.清水池3.碘酸钙是一种补碘、补钙的添加剂,其化学式为Ca(IO3)2,碘酸钙中碘元素的化合价是( )A.+5 B.+1C.-1 D.+74.下列化学用语书写正确的是( )+A.三个钾原子:3KB.两个二氧化氮分子:2NO2+2C.镁离子:MgD.地壳中含量最多的金属元素:AL5.每年6 月5 日是世界环境日。
我国2017 年环境日的主题是“绿水青山就是金山银山”。
下列做法不符合这一主题要求的是( )A.生活污水不经过处理直接排放B.推广使用脱硫煤,防止酸雨的产生C.使用清洁能源,积极植树种草D.使用可降解塑料,避免产生“白色污染”6.2015年3 月20 日联合国发布报告:到2030年,全球将有40%的国家和地区任和的责应面临干旱问题。
节约用水和合理开发利用水资源是每个公民尽义务。
下列关于水的认识正确的是( )A.过滤能除去天然水中所有的杂质B.将活性炭放入硬水中可使其软化C.工业废水要经过处理后再排放D.过量使用农药、化肥不会造成水体污染7.下列有关水的说法不正确的是( )A.水是由水分子构成的B.电解水的实验中,得到的氢气与氧气的体积比为 1 2C.过滤、吸附、蒸馏、消毒等都是常用的净水方法D.地球上的水储量是丰富的,但可供利用的淡水资源是有限的8.科学家发现,水在-157 ℃超低温、正常压力或真空条件下呈液态,比蜂蜜还黏稠。
下列关于这种“高密度液态水”的说法正确的是( )A.化学性质与普通水不同B.分子不再运动C.氢、氧两种原子的个数比为2:1D.分子间的间隔比普通水大9.下列各组物质中,前者是化合物,后者是混合物的是( )A.胆矾、洁净的空气B.液氧、碘酒C.冰水共存物、碳酸钠D.稀硫酸、加碘食盐10.水是生命之源。
泸科版七年级数学上册第4章达标检测卷附答案
泸科版七年级数学上册第4章达标检测卷一、选择题(每题3分,共30分)1.下面几种图形是平面图形的是()2.下列现象,能说明“线动成面”的是()A.天空划过一道流星B.汽车雨刷在挡风玻璃上刷出的痕迹C.抛出一块小石子,石子在空中飞行的路线D.旋转一扇门,门在空中运动的痕迹3.下列说法正确的是()A.两点确定一条直线B.两条射线组成的图形叫做角C.两点之间直线最短D.若AB=BC,则点B为AC的中点4.下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的是() 5.将一副三角尺按不同位置摆放,摆放方式中∠α与∠β互余的是()6.已知互为补角的两个角的差为35°,则较大的角是()A.107.5°B.108.5°C.97.5°D.72.5°7.在直线AB上任取一点O,过点O作射线OC,OD,使∠COD=90°,当∠AOC=50°时,∠BOD的度数是()A.40°B.140°C.40°或140°D.40°或90°8.已知点A,B,C共线,如果线段AB=5 cm,BC=4 cm,那么A,C两点间的距离是()A.1 cm B.9 cmC.1 cm或9 cm D.2 cm或10 cm9.如图,已知C是线段AB的中点,D是线段BC的中点,下列各式不正确的是()A.CD=AC-DB B.CD=AD-BCC.CD=12AB-BD D.CD=13AB10.钟表在8:25时,时针与分针的夹角是() A.101.5°B.102.5°C.120°D.125°二、填空题(每题3分,共18分)11.把58°18′化成度的形式,则58°18′=________°.12.一个角的余角是它的补角的14,这个角是________度.13.如图,图中线段有________条,射线有________条.14.如图,点O在直线AB上,射线OC,OD在直线AB的同侧,∠AOD=50°,∠BOC=40°,OM,ON分别平分∠BOC和∠AOD,则∠MON的度数为________.15.如图,将长方形纸片ABCD折叠,使边AB,CB均落在对角线BD上,得折痕BE,BF,则∠EBF=________.16.已知点O在直线AB上,且OA=4 cm,OB=6 cm,点E,F分别是OA,OB的中点,则EF=_________________________.三、解答题(17题6分,21题10分,22题12分,其余每题8分,共52分) 17.如图,已知平面上点A,B,C,D.按下列要求画出图形:(1)作直线AB、射线CB;(2)取线段AB的中点E,连接DE并延长与射线CB交于点O;(3)尺规作图:连接AD并延长至点F,使得DF=AD.18.如图,已知A,B,C三点在同一直线上,AB=24 cm,BC=38AB,点E是AC的中点,点D是AB的中点,求DE的长.19.若第一个角的补角比第二个角的余角的3倍少20°,而第二个角的补角比第一个角的余角的3倍多20°,求这两个角的度数.20.如图,已知直线AB与CD相交于点O,∠COE是直角,OF平分∠AOE,∠COF=34°,求∠BOD的度数.21.如图,OM是∠AOC的平分线,ON是∠BOC的平分线.(1)如图①,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?(2)如图②,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;(3)如图③,当∠AOB=α,∠BOC=β(0°<α+β<180°)时,猜想∠MON与α,β的数量关系,并说明理由.22.定义:若线段上的一个点把这条线段分成1:2的两条线段,则称这个点是这条线段的三等分点.如图①,点C在线段AB上,且AC:CB=1:2,则点C是线段AB的一个三等分点,显然,一条线段的三等分点有两个.(1)如图②,已知DE=15 cm,点P是DE的三等分点,求DP的长.(2)如图③,已知线段AB=15 cm,点P从点A出发以每秒1 cm的速度在射线AB上向点B方向运动,点Q从点B出发,先向点A方向运动,当与点P重合后立马改变方向与点P同向而行且速度始终为每秒2 cm,设运动时间为t s.①若点P、点Q同时出发,当点P与点Q重合时,求t的值;②若点P、点Q同时出发,当点P是线段AQ的三等分点时,求t的值.答案一、1.A 2.B 3.A 4.B 5.C 6.A 7.C 8.C 9.D 10.B二、11.58.3 12.60 13.6;6 14.135° 15.45° 16.1 cm 或5 cm 三、17.解:如图所示.18.解:因为AB =24 cm ,所以BC =38AB =38×24=9(cm). 所以AC =AB +BC =24+9=33(cm). 因为点E 是AC 的中点,所以AE =12AC =12×33=16.5(cm). 因为点D 是AB 的中点, 所以AD =12AB =12×24=12(cm). 所以DE =AE -AD =16.5-12=4.5(cm). 19.解:设第一个、第二个角的度数分别为x ,y .由题意得⎩⎨⎧180°-x =3(90°-y )-20°,180°-y =3(90°-x )+20°,解得⎩⎨⎧x =50°,y =40°.答:这两个角的度数分别为50°和40°. 20.解:因为∠COE 是直角,∠COF =34°,所以∠EOF =56°. 因为OF 平分∠AOE , 所以∠AOF =∠EOF =56°. 因为∠COF =34°,所以∠AOC =∠AOF -∠COF =22°.因为∠BOD +∠BOC =180°,∠AOC +∠BOC =180°, 所以∠BOD =∠AOC =22°.21.解:(1)∠MON =∠MOC -∠NOC =12∠AOC -12∠BOC =12(∠AOC -∠BOC )=12∠AOB =12×90°=45°.(2)∠MON =∠MOC -∠NOC =12∠AOC -12∠BOC =12(∠AOC -∠BOC )=12∠AOB =12α.(3)∠MON =12α.理由:∠MON =∠MOC -∠NOC =12∠AOC -12∠BOC =12(α+β)-12β=12α.22.解:(1)当DP =2PE 时,DP =23DE =15×23=10(cm);当2DP =PE 时,DP =13DE =13×15=5(cm).综上所述,DP 的长为5 cm 或10 cm. (2)①根据题意,得(1+2)t =15, 解得t =5.所以当t =5时,点P 与点Q 重合. ②点P ,Q 重合前:当2AP =PQ 时,有t +2t +2t =15, 解得t =3;当AP =2PQ 时,有t +12t +2t =15,解得t =307. 点P ,Q 重合后:当AP =2PQ 时,有t =2(t -5), 解得t =10;当2AP =PQ 时,有2t =t -5, 解得t =-5(不合题意,舍去).综上所述,当t =3,307或10时,点P 是线段AQ 的三等分点.七年级数学上册期中测试卷一、选择题(每题3分,共30分)1.现实生活中,如果收入1 000元记作+1 000元,那么-800元表示( )A .支出800元B .收入800元C .支出200元D .收入200元 2.据国家统计局公布数据显示:2020年我国粮食总产量为13 390亿斤,比上年增加113亿斤,增长0.9%,我国粮食生产喜获“十七连丰”.将13 390亿用科学记数法表示为( ) A .1.339×1012B .1.339×1011C .0.133 9×1013D .1.339×10143.⎪⎪⎪⎪⎪⎪-16的相反数是( ) A.16 B .-16C .6D .-64.在-6,0,-2,4这四个数中,最小的数是( )A .-2B .0C .-6D .45.a ,b 两数在数轴上对应点的位置如图所示,下列结论中正确的是( )(第5题)A .a <0B .a >1C .b >-1D .b <-16.数轴上与表示-1的点距离10个单位的点表示的数是( )A .10B .±10C .9D .9或-117.已知|a |=-a ,则a -1的绝对值减去a 的绝对值所得的结果是( )A .-1B .1C .2a -3D .3-2a8.计算:(-3)3×⎝ ⎛⎭⎪⎫13-59+427的结果为( ) A.23 B .2 C.103D .109.若代数式x 2+ax +9y -(bx 2-x +9y +3)的值恒为定值,则-a +b 的值为( )A .0B .-1C .-2D .210.如果a +b +c =0,且|a |>|b |>|c |.则下列说法中可能成立的是( )A .b 为正数,c 为负数B .c 为正数,b 为负数C .c 为正数,a 为负数D .c 为负数,a 为负数二、填空题(每题3分,共15分)11.将代数式4a2b+3ab2-2b3+a3按a的升幂排列是________________________.12.被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面总面积相当于35个标准足球场的总面积.已知每个标准足球场的面积为7 140m2,则用科学记数法表示FAST的反射面总面积约为____________m2.(精确到万位)13.若|x+2|+(y-3)4=0,则x y=________.14.如果规定符号“*”的意义是a*b=aba+b,则[2*(-3)]*(-1)的值为________.15.如图①是三阶幻方(从1到9,一共九个数,每行、每列以及两条对角线上的3个数之和均相等).如图②是三阶幻方,已知此幻方中的一些数,则图②中9个格子中的数之和为________.(用含a的式子表示)(第15题)三、解答题(17题16分,22题9分,23题10分,其余每题8分,共75分) 16.将下列各数在如图所示的数轴上表示出来,并把它们用“<”号连接起来.-|-2.5|,414,-(+1),-2,-⎝⎛⎭⎪⎫-12,3.(第16题)17.计算:(1)25.7+(-7.3)+(-13.7)+7.3; (2)⎝ ⎛⎭⎪⎫-12-59+712÷⎝ ⎛⎭⎪⎫-136;(3)(-1)3+⎪⎪⎪⎪⎪⎪-12-⎝ ⎛⎭⎪⎫-32×⎝ ⎛⎭⎪⎫-23; (4)-14-(1-0.5)×13×[1-(-2)2].18.先化简,再求值:2(x 2y +3xy )-3(x 2y -1)-2xy -2,其中x =-2,y =2.19.已知A =2x 2+3xy -2x -1,B =-x 2+xy -1. (1)求3A +6B ;(2)若3A +6B 的值与x 无关,求y 的值.20.小敏对算式:(-24)×⎝ ⎛⎭⎪⎫18-13+4÷⎝ ⎛⎭⎪⎫12-13进行计算时的过程如下: 解:原式=(-24)×18+(-24)×⎝ ⎛⎭⎪⎫-13+4÷⎝ ⎛⎭⎪⎫12-13……第一步 =-3+8+4×(2-3)……第二步 =5-4……第三步 =1.……第四步根据小敏的计算过程,回答下列问题:(1)小敏在进行第一步时,运用了乘法的________律;(2)她在计算时出现了错误,你认为她从第________步开始出错了; (3)请你给出正确的计算过程.21.某服装店以每套82元的价格购进了30套保暖内衣,销售时,针对不同的顾客,这30套保暖内衣的售价不完全相同,若以100元为标准,将超过的钱数记为正,不足的钱数记为负,则记录结果如下表:则该服装店在售完这30套保暖内衣后,共赚了多少钱?22.下面的图形是由边长为1的正方形按照某种规律组成的.(第22题)(1)观察图形,填写下表:图形序号①②③正方形的个数9图形的周长16(2)推测第n个图形中,正方形的个数为____________,周长为____________;(都用含n的代数式表示)(3)写出第2 020个图形的周长.23.如图,一个点从数轴上的原点开始,先向左移动2cm到达A点,再向左移动3cm到达B点,然后向右移动9cm到达C点,数轴上一个单位长度表示1cm.(1)请你在数轴上表示出A,B,C三点的位置.(2)把点C到点A的距离记为CA,则CA=________cm.(3)若点B沿数轴以3cm/s的速度匀速向右运动,经过________s后点B到点C的距离为3cm.(4)若点B沿数轴以2cm/s的速度匀速向左运动,同时点A,C沿数轴分别以1cm/s和4cm/s的速度匀速向右运动.设运动时间为t s,试探索:CA-AB的值是否会随着t的变化而改变?请说明理由.(第23题)答案一、1.A 2.A 3.B 4.C 5.D 6.D 7.B 8.B9.D 【点拨】x 2+ax +9y -(bx 2-x +9y +3)=x 2+ax +9y -bx 2+x -9y -3=(1-b )x 2+(a +1)x -3,因为代数式x 2+ax +9y -(bx 2-x +9y +3)的值恒为定值,所以1-b =0,a +1=0,解得a =-1,b =1,则-a +b =1+1=2. 10.C 【点拨】由题意可知a ,b ,c 三数中只有两正一负或两负一正两种情况,假设a ,b ,c 两负一正,要使a +b +c =0成立,则必有b <0,c <0,a >0,但题中并无此选项,故假设不成立.假设a ,b ,c 两正一负,要使a +b +c =0成立,则必有a <0,b >0,c >0,故只有选项C 符合题意.二、11.-2b 3+3ab 2+4a 2b +a 3 12.2.5×105 13.-814.-65 【点拨】[2*(-3)]*(-1)=2×(-3)2+(-3)*(-1)=6*(-1)=6×(-1)6+(-1)=-65. 15.9a -27三、16.解:在数轴上表示如图所示.(第16题)-|-2.5|<-2<-(+1)<-⎝ ⎛⎭⎪⎫-12<3<414.17.解:(1)原式=[25.7+(-13.7)]+[(-7.3)+7.3]=12+0=12.(2)原式=⎝ ⎛⎭⎪⎫-12-59+712×(-36)=18+20+(-21)=17.(3)原式=-1+12-1=-32.(4)原式=-1-12×13×(-3)=-1+12=-12. 18.解:原式=2x 2y +6xy -3x 2y +3-2xy -2=-x 2y +4xy +1.当x =-2,y =2时,原式=-(-2)2×2+4×(-2)×2+1=-8-16+1=-23.19.解:(1)3A +6B =3(2x 2+3xy -2x -1)+6(-x 2+xy -1)=6x 2+9xy -6x -3-6x 2+6xy -6 =15xy -6x -9.(2)由(1)知3A +6B =15xy -6x -9=(15y -6)x -9, 由题意可知15y -6=0,解得y =25. 20.解:(1)分配 (2)二(3)原式=(-24)×18+(-24)×⎝ ⎛⎭⎪⎫-13+4÷⎝ ⎛⎭⎪⎫36-26 =-3+8+4÷16 =-3+8+4×6 =-3+8+24 =29.21.解:7×(100+5)+6×(100+1)+7×100+8×(100-2)+2×(100-5)=735+606+700+784+190=3 015(元),30×82=2 460(元),3 015-2 460=555(元). 答:共赚了555元.22.解:(1)从上到下、从左往右依次填:14;22;19;28(2)5n +4; 6n +10(3)当n =2 020时,周长为6×2 020+10=12 130. 23.解:(1)如图所示.(第23题) (2)6 (3)2或4(4)CA -AB 的值不会随着t 的变化而改变.理由如下: 根据题意得CA =(4+4t )-(-2+t )=6+3t (cm), AB =(-2+t )-(-5-2t )=3+3t (cm), 所以CA -AB =(6+3t )-(3+3t )=3(cm), 所以CA -AB 的值不会随着t 的变化而改变.。
沪科版七年级上《第4章直线与角》达标检测试卷含答案
第4章达标检测卷(120分,90分钟)题号一二三总分得分一、选择题(每题4分,共40分)1.下列几何图形中为圆柱体的是()2.如图,将长方形绕它的一条边MN所在的直线旋转一周而成的几何体是()(第2题)3.如图所示,能相交的图形有()(第3题) A.1个B.2个C.3个D.4个4.如图所示,C,D是线段AB上的两点,若BC=3 cm,DB=5 c m,且D是AC的中点,则AC的长等于()A.3 cm B.4 cm C.8 cm D.10 cm(第4题)(第6题) 5.下列说法中,正确的有()①如果∠1=∠2,∠3=∠4,那么∠1=∠3;②如果∠1=∠2,∠2=∠3,那么∠1=∠3;③如果∠1是∠2的补角,∠3是∠4的补角,且∠2=∠4,那么∠1=∠3;④如果∠1是∠2的余角,∠3+∠2=90°,那么∠1=∠3.A.1个B.2个C.3个D.4个6.如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是()A.20°B.25°C.30°D.70°7.已知点A,B,C共线,如果线段AB=5 cm,BC=4 cm,那么A,C两点间的距离是()A.1 cm B.9 cm C.1 cm或9 cm D.2 cm或10 cm8.如图,由A测B的方向是()A.南偏东25°B.北偏西25°C.南偏东65°D.北偏西65°(第8题)(第10题) 9.在时刻8:30,时钟上的时针和分针之间的夹角为()A.85°B.75°C.70°D.60°10.如图,C、D在线段BE上,下列说法:①直线CD上以B、C、D、E为端点的线段共有6条;②图中有2对互补的角;③若∠BAE=100°,∠DAC=40°,则以A为顶点的所有小于平角的角的度数和为360°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B、C、D、E的距离之和最大值为15,最小值为11.其中说法正确的有() A.1个B.2个C.3个D.4个二、填空题(每题5分,共20分)11.(中考·济南)如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释这一现象的原因:________________________.12.用度分秒表示:57.32°=________°________′________″.13.如图,从A到B的最短的路线是________.(第11题)(第13题)(第14题)14.如图,∠AOB=∠COD=90°,下列说法:①∠BOC=∠AOC=∠BOD;②∠AOC =∠BOD;③∠BOC与∠AOD互补;④∠BOC的余角只有∠AOC;⑤若∠AOD=2∠BOC,则∠BOC=60°,其中一定正确的序号是________.三、解答题(17、20题每题9分,21题8分,22题10分,其余每题6分,共60分)15.计算:(1)55°25′57″+27°37′24″-16°48′22″;(2)(58°47′25″+12°36′45″)÷5.16.如图,已知∠α和∠β(∠α>∠β),求作∠AOD,使得∠AOD=2∠α-∠β.(第16题)17.若第一个角的补角比第二个角的余角的3倍少20°,而第二个角的补角比第一个角的余角的3倍多20°,求这两个角的度数.18.下面是小马虎解的一道题.题目:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.解:根据题意画出图形,如图所示.∠AOC=∠BOA-∠BOC=70°-15°=55°.若你是老师,会给小马虎满分吗?若会,请说明理由;若不会,请指出小马虎的错误.(第18题)19.如图,线段AD上两点B,C将AD分成2∶3∶4三部分,M是AD的中点,若MC=2,求线段AD的长.(第19题)20.如图,OB,OC是∠AOD内任意两条不同的射线,OM平分∠AOB,ON平分∠COD,若∠MON=45°,∠BOC=20°,求∠AOD的度数.(第20题)21.已知直线AB上有一点C,且AB=10 cm,BC=4 cm,M是AB的中点,N是BC 的中点,求MN的长.22.(1)如图,已知∠AOB是直角,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;(2)若在(1)中,∠AOB=α,其他条件不变,求∠MON的度数;(3)若在(1)中,∠AOB=α,∠BOC=β,其他条件不变,求∠MON的度数;(4)你能从(1)(2)(3)中发现什么规律?(第22题)答案一、1.C 2.C 3.B 4.B 5.C 6.D 7.C 8.C 9.B 10.B 二、11.两点之间,线段最短 12.57;19;12 13.A -F -E -B14.②③⑤ 点拨:因为∠AOB =∠COD =90°,所以根据同角的余角相等,可得∠BOD =∠AOC ,但不能得到∠BOD 或∠AOC 与∠BOC 相等,故①错误,②正确;因为∠BOC +∠AOD =∠AOB +∠COD =180°,所以∠BOC 与∠AOD 互补,故③正确;∠BOC 的余角是∠BOD 或∠AOC ,故④错误;当∠AOD =2∠BOC 时,∠AOD +∠BOC =3∠BOC ,而∠AOD +∠BOC =∠AOB +∠COD =180°,所以3∠BOC =180°,即∠BOC =60°,故⑤正确.因此填②③⑤.三、15.解:(1)原式=(55°+27°-16°)+(25′+37′-48′)+(57″+24″-22″)=66°+14′+59″=66°14′59″.(2)原式=70°83′70″÷5=14°+16′+(180″+70″)÷5=14°+16′+50″=14°16′50″. 16.解:作法:如图.(1)作∠AOB =∠α;(2)以射线OB 为边,在∠AOB 的外部作∠BOC =∠α; (3)以射线OC 为边,在∠AOC 的内部作∠COD =∠β. 则∠AOD 就是所求作的角.(第16题)17.解:设第一个、第二个角的度数分别为x ,y ,则⎩⎪⎨⎪⎧180°-x =3(90°-y )-20°,180°-y =3(90°-x )+20°,解得⎩⎪⎨⎪⎧x =50°,y =40°. 所以这两个角的度数分别为50°和40°.18.解:不会给小马虎满分.小马虎只考虑了OC 落在∠AOB 内部的情况.当OC 落在∠AOB 的外部时,∠AOC =∠BOA +∠BOC =85°.19.解:设AB 的长为2k(k >0),则BC ,CD 的长分别为3k ,4k , 所以AD =2k +3k +4k =9k.因为M 是AD 的中点,所以MD =12AD =4.5k ,所以MC =MD -CD =4.5k -4k =0.5k =2,解得k =4. 所以AD =9k =9×4=36.20.解:因为OM 平分∠AOB ,ON 平分∠COD ,所以∠AOB =2∠BOM ,∠COD =2∠CON ,所以∠AOD =∠AOB +∠COD +∠BOC =2∠BOM +2∠CON +∠BOC =2(∠BOM +∠CON)+∠BOC =2(∠MON -∠BOC)+∠BOC =2×(45°-20°)+20°=70°.21.解:分两种情况:(1)当点C 在AB 的延长线上时,因为AB =10 cm ,M 是AB 的中点,所以BM =5 cm . 因为BC =4 cm ,N 是BC 的中点,所以BN =2 cm ,所以MN =5+2=7(cm ). (2)当点C 在线段AB 上时,因为AB =10 cm ,M 是AB 的中点,所以BM =5 cm . 因为BC =4 cm ,N 是线段BC 的中点,所以BN =2 cm ,所以MN =5-2=3(cm ). 综上所述,MN 的长为7 cm 或3 cm .22.解:(1)因为∠AOB 是直角,∠BOC =30°,所以∠AOC =∠AOB +∠BOC =90°+30°=120°.因为OM 平分∠AOC , 所以∠MOC =60°.因为∠BOC =30°,ON 平分∠BOC ,所以∠NOC =15°. 所以∠MON =∠MOC -∠NOC =60°-15°=45°. (2)因为∠AOB =α,所以∠AOC =∠AOB +∠BOC =α+30°.因为OM 平分∠AOC ,所以∠MOC =α+30°2=α2+15°.因为∠BOC =30°,ON 平分∠BOC ,所以∠NOC =15°. 所以∠MON =∠MOC -∠NOC =⎝⎛⎭⎫α2+15°-15°=α2. (3)因为∠AOB =α,∠BOC =β, 所以∠AOC =∠AOB +∠BOC =α+β. 因为OM 平分∠AOC ,所以∠MOC =α+β2.因为ON 平分∠BOC ,所以∠NOC =β2.所以∠MON =∠M OC -∠NOC =α+β2-β2=α2.(4)从(1)(2)(3)中发现:∠MON 的度数只与∠AOB 的度数有关,和∠BOC 的度数无关,∠MON 的度数等于∠AOB 的度数的一半.。
北师大版七年级数学下册 第四章 三角形 达标检测卷(含详细解答)
北师大版七年级数学下册第四章达标检测卷(考试时间:120分钟满分:120分)班级:________ 姓名:________ 分数:________第Ⅰ卷(选择题共30分)一、选择题(每小题3分,共18分)1.下列图形中与已知图形全等的是( )2.若三角形有两个内角的和是85°,那么这个三角形是 ( )A.钝角三角形 B.直角三角形C.锐角三角形 D.不能确定3.(襄州区期末)如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,如图所示的这种方法,是利用了三角形全等中的( ) A.SSS B.ASA C.AAS D.SAS第3题图4.已知三角形的三边分别为4,a,8,那么该三角形的周长c的取值范围是( ) A.4<c<12 B.12<c<24C.8<c<24 D.16<c<245.根据下列条件,能画出唯一△ABC的是 ( )A.AB=3,BC=4,AC=8B.AB=4,BC=3,∠A=30°C.AB=5,AC=6,∠A=45°D.∠A=30°,∠B=60°,∠C=90°6.(东营中考)如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( )A.50° B.30° C.20° D.15°第6题图7.如图,在△ABC中,BD⊥AC,EF∥AC,交BD于点G,那么下列结论错误的是( ) A.BD是△ABC的高 B.CD是△BCD的高C.EG是△ABD的高 D.BG是△BEF的高第7题图第8题图8.(金华中考)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD9.★如图,在△PAB中,∠A=∠B,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=42°,则∠P的度数为 ( )A.44° B.66° C.96° D.92°第9题图第10题图10.已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论中正确的个数是()①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.A.1 B.2 C.3 D.4第Ⅱ卷(非选择题共90分)二、填空题(每小题3分,共24分)11.如图,照相机的底部用三脚架支撑着,请你说说这样做的依据是.第11题图第12题图12.(朔州月考)如图,CD是△ABC的中线,若AB=8,则AD的长为.13.已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为.第13题图第14题图14.如图所示,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1 km,DC=1 km,村庄A,C和A,D间也有公路相连,且公路AD是南北走向,AC=3 km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2 km,BF=0.7 km,则建造的斜拉桥长至少有 km.15.(河南中考)将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为.16.如图,∠ACB=90°,AC=BC,AD⊥CE于点D,BE⊥CD交CD的延长线于点E,AD=2.4 cm,DE=1.7 cm,则BE的长为 cm.17.如图,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为.第17题图第18题图18.★(锡山区期末)如果三角形的两个内角α与β满足3α+β=90°,那么我们称这样的三角形为“准直角三角形”.如图,B,C为直线l上两点,点A在直线l外,且∠ABC=45°.若P是l上一点,且△ABP是“准直角三角形”,则∠APB 的所有可能的度数为.三、解答题(共66分)19.(6分)如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF,试说明:AB∥DE.20.(8分)如图,已知线段a,b,∠α,求作三角形ABC,使AC=b,BC=2a,∠C=180°-α.(不写作法,保留作图痕迹)21.(8分)如图,AM平分∠CAD,CN平分∠ACB,△ACB≌△CAD,请你判断AM和CN的位置关系,并说明理由.22.(8分)如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C =70°,求∠AEC和∠DAE的度数.23.(10分)如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.(1)试说明:△ABE≌△CBD;(2)试说明:∠1=∠3.24.(12分)(南岗区校级期中)已知AD是△ABC的角平分线(∠ACB>∠B),P是射线AD上一点,过点P作EF⊥AD,交射线AB于点E,交直线BC于点M.(1)如图①,∠ACB=90°,试说明:∠M=∠BAD;(2)如图②,∠ACB为钝角,P在AD延长线上,连接BP,CP,BP平分∠EBC,CP 平分∠BCF,∠BPD=50°,∠CPD=21°,求∠M的度数.25.(14分)如图①,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN.(1)试说明:AM=BN;(2)分别写出点M在如图②和图③所示位置时,线段AB,BM,BN三者之间的数量关系,不需证明.①②③参考答案第Ⅰ卷(选择题共30分)一、选择题(每小题3分,共18分)1.下列图形中与已知图形全等的是( B)2.若三角形有两个内角的和是85°,那么这个三角形是 ( A)A.钝角三角形 B.直角三角形C.锐角三角形 D.不能确定3.(襄州区期末)如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,如图所示的这种方法,是利用了三角形全等中的( D) A.SSS B.ASA C.AAS D.SAS第3题图4.已知三角形的三边分别为4,a,8,那么该三角形的周长c的取值范围是( D) A.4<c<12 B.12<c<24C.8<c<24 D.16<c<245.根据下列条件,能画出唯一△ABC的是 ( C)A.AB=3,BC=4,AC=8B.AB=4,BC=3,∠A=30°C.AB=5,AC=6,∠A=45°D.∠A=30°,∠B=60°,∠C=90°6.(东营中考)如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于( C)A.50° B.30° C.20° D.15°第6题图7.如图,在△ABC中,BD⊥AC,EF∥AC,交BD于点G,那么下列结论错误的是( C) A.BD是△ABC的高B.CD是△BCD的高C.EG是△ABD的高D.BG是△BEF的高第7题图第8题图8.(金华中考)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( A)A.AC=BDB.∠CAB=∠DBAC.∠C=∠DD.BC=AD9.★如图,在△PAB中,∠A=∠B,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=42°,则∠P的度数为 ( C)A.44° B.66° C.96° D.92°第9题图第10题图10.已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论中正确的个数是( D)①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.A.1 B.2 C.3 D.4第Ⅱ卷(非选择题共90分)二、填空题(每小题3分,共24分)11.如图,照相机的底部用三脚架支撑着,请你说说这样做的依据是__三角形的稳定性__.第11题图第12题图12.(朔州月考)如图,CD是△ABC的中线,若AB=8,则AD的长为__4__.13.已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为__10__.第13题图第14题图14.如图所示,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1 km,DC=1 km,村庄A,C和A,D间也有公路相连,且公路AD是南北走向,AC=3 km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2 km,BF=0.7 km,则建造的斜拉桥长至少有__1.1__km.15.(河南中考)将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为__75°__.16.如图,∠ACB=90°,AC=BC,AD⊥CE于点D,BE⊥CD交CD的延长线于点E,AD=2.4 cm,DE=1.7 cm,则BE的长为__0.7___cm.17.如图,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为__60°.第17题图第18题图18.★(锡山区期末)如果三角形的两个内角α与β满足3α+β=90°,那么我们称这样的三角形为“准直角三角形”.如图,B ,C 为直线l 上两点,点A 在直线l 外,且∠ABC =45°.若P 是l 上一点,且△ABP 是“准直角三角形”,则∠APB 的所有可能的度数为__15°或22.5°或120°__.三、解答题(共66分)19.(6分)如图,点B ,E ,C ,F 在同一条直线上,AB =DE ,AC =DF ,BE =CF ,试说明:AB ∥DE.解:∵BE =CF ,∴BC =EF ,在△ABC 与△DEF 中,⎩⎪⎨⎪⎧AB =DE ,AC = DF ,BC=EF ,∴△ABC ≌△DEF(SSS),∴∠ABC =∠DEF ,∴AB ∥DE.20.(8分)如图,已知线段a ,b ,∠α,求作三角形ABC ,使AC =b ,BC =2a ,∠C =180°-α.(不写作法,保留作图痕迹)解:如图,△ABC 即为所求.21.(8分)如图,AM 平分∠CAD ,CN 平分∠ACB ,△ACB ≌△CAD ,请你判断AM 和CN 的位置关系,并说明理由.解:AM ∥CN.理由:∵△ACB ≌△CAD ,∴∠ACB =∠CAD.∵AM 和CN 分别平分∠CAD 和∠ACB ,∴∠ACN =12 ∠ACB ,∠CAM =12 ∠CAD ,∴∠ACN =∠CAM ,∴AM ∥CN.22.(8分)如图,AD 是△ABC 的BC 边上的高,AE 平分∠BAC ,若∠B =42°,∠C=70°,求∠AEC 和∠DAE 的度数.解:∵∠B =42°,∠C =70°,∴∠BAC =180°-∠B -∠C =68°.∵AE 平分∠BAC ,∴∠EAC =12 ∠BAC =34°.∵AD 是高,∠C =70°,∴∠DAC =90°-∠C =20°,∴∠DAE =∠EAC -∠DAC =34°-20°=14°,∴∠AEC =90°-∠DAE =76°.23.(10分)如图,点E 在CD 上,BC 与AE 交于点F ,AB =CB ,BE =BD ,∠1=∠2.(1)试说明:△ABE ≌△CBD ;(2)试说明:∠1=∠3.解:(1)∵∠1=∠2,∴∠1+∠CBE =∠2+∠CBE ,即∠ABE =∠CBD ,在△ABE 和△CBD 中,⎩⎪⎨⎪⎧AB =CB ,∠ABE =∠CBD ,BE =BD ,∴△ABE ≌△CBD(SAS);(2)∵△ABE ≌△CBD ,∴∠A =∠C ,∵∠AFB =∠CFE ,∴∠1=∠3.24.(12分)(南岗区校级期中)已知AD 是△ABC 的角平分线(∠ACB >∠B),P 是射线AD 上一点,过点P 作EF ⊥AD ,交射线AB 于点E ,交直线BC 于点M.(1)如图①,∠ACB =90°,试说明:∠M =∠BAD ;(2)如图②,∠ACB 为钝角,P 在AD 延长线上,连接BP ,CP ,BP 平分∠EBC ,CP 平分∠BCF ,∠BPD =50°,∠CPD =21°,求∠M 的度数.解:(1)∵EF ⊥AD ,∴∠APF =∠MCF =90°.∵∠AFP =∠MFC ,∴∠M =∠PAF.∵∠BAD =∠CAD ,∴∠M=∠BAD.(2)∵∠BPD=50°,∠CPD=21°,∴∠BPC=71°,∴∠PBC+∠PCB=109°.∵∠BCF=2∠PCB,∠EBC=2∠PBC,∴∠EBC+∠BCF=218°,∴∠ABC+∠ACB=360°-218°=142°,∴∠BAC=180°-142°=38°,∴∠DCP=∠FCP=∠CPD+∠CAD=40°,∴∠MDP=∠DPC+∠DCP=61°.∵EF⊥AP,∴∠MPD=90°,∴∠M=90°-61=29°.25.(14分)如图①,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN.(1)试说明:AM=BN;(2)分别写出点M在如图②和图③所示位置时,线段AB,BM,BN三者之间的数量关系,不需证明.①②③解:(1)∵△PAB和△PMN是等边三角形,∴∠BPA =∠MPN =60°, AB =BP =AP ,PM =PN =MN ,∴∠BPA -∠MPB =∠MPN -∠MPB , ∴∠APM =∠BPN.在△APM 和△BPN 中,⎩⎪⎨⎪⎧AP =BP ,∠APM =∠BPN ,PM =PN ,∴△APM ≌△BPN(SAS), ∴AM =BN.(2)图②中,BN =AB +BM ; 图③中,BN =BM -AB.。
人教版第四章 人体内物质的运输单元达标测试题试卷
人教版第四章人体内物质的运输单元达标测试题试卷一、选择题1.下面是有关“人体内物质运输”的结构或生理过程示意图,有关分析中错误的是A.甲图中,血管A可表示医生给病人静脉注射时,针刺入的血管B.图乙中,若b表示大脑,则c所示血管里流的血液一定是静脉血C.丙图中,若曲线代表血液中氧气的变化,则B处表示组织细胞间的毛细血管D.丙图中,若曲线代表血液中二氧化碳的变化,则B表示肺泡周围的毛细血营2.如图甲为“观察小鱼尾鳍内血液流动”的实验中对材料的处理;图乙是用显微镜观察时看到的一个视野。
下列有关该实验的描述错误的是()A.应时常用滴管往图甲中的湿棉絮上滴水,以保证鱼的正常呼吸B.应将图甲中的尾鳍放在低倍显微镜下观察血管内血液的流动情况C.图乙中的a是小静脉,b是毛细血管,c是小动脉D.图乙中的b是毛细血管,判断的依据是其内的红细胞单行通过3.下图是心脏、血管的示意图,“→”表示血流方向,下列表述正确的是()A.图甲流出的血液一定是动脉血B.图乙、图丙和图丁所示的血管都能进行物质交换C.图丙所示血管中血流速度最快D.血液流动的方向是甲→乙→丁→丙4.张某面色苍白,感到头晕、精神不振、肌肉无力。
就医后,做了血常规化验。
请结合化验报告单的部分化验结果(如图)分析,下列叙述错误的是()A.送检物可从张某的毛细血管中采集B.张某应多食用含蛋白质和铁丰富的食物C.张某体内可能有炎症D.张某可通过适量运动促进红细胞分裂,使症状缓解5.下列细胞中能能吞噬病菌的是()A.红细胞B.脂肪细胞C.白细胞D.精细胞6.下表是老师展示的李某血常规化验单的部分内容,同学们就此展开了激烈的讨论,你认为,下列论述错误的是()姓名:李某性别:男年龄:35化验项目结果参考值WBC(白细胞)26×109/L(4~10)×109/LRBC(红细胞) 1.8×1012/L(4.0~5.5)×1012/LHGB(血红蛋68g/L120~160g/L白)PLT(血小板)198×109/L(100~300)×109/LA.镜检李某的血涂片,发现白细胞数量最多B.李某的止血和凝血功能正常C.李某患有炎症,需要消炎处理D.李某要多吃富含蛋白质和铁的食物7.下图中长方形高度表示甲、乙、丙、丁四种组织处,血红蛋白与氧气的结合情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章达标检测卷 (100分,90分钟)
题 号 一 二 三 四 总 分 得 分
一、选择题(每题3分,共36分)
(第1题图) 1.2016年5月9日19时12分左右,“水星凌日”的天象于本世纪第三次出现。如图所示,水星如一颗小黑痣从太阳“脸上”缓慢爬过。它的形成与下列光现象原理相同的是( ) A.小孔成像 B.河水看起来变浅 C.海市蜃楼 D.水中荷花的倒影 2.有经验的渔民都知道,只有瞄准鱼的下方才能把鱼叉到,如图所示。下列四幅光路图,能够正确说明叉到鱼道理的是( )
(第2题图)
3.光射到平面镜上反射后,反射角为30°,则入射角为( ) A.10° B.15° C.30° D.60° 4.“猴子捞月”的寓言故事说,猴子看到水中有个月亮,以为月亮掉水中了,大叫起来“不得了啦,不得了啦,月亮掉水里了!”关于水中的月亮,以下说法正确的是( ) A.水中的月亮比天上的月亮小 B.水中出现月亮是光的折射现象 C.水中出现月亮是光的反射现象 D.水中月亮到水面的距离比天上月亮到水面的距离远 5.如图所示,将平面镜和铅笔竖直放置在水平桌面上,下列说法正确的是( ) A.铅笔水平向右移动时,它的像将变小 B.平面镜竖直向上移动时,铅笔的像也将向上移动 C.若改用一块较小的平面镜,铅笔的像将变小 D.若铅笔按图示箭头方向转过45°,铅笔将与它的像垂直
(第5题图) (第6题图) (第7题图) 6.如图所示,人眼在A点看见河里B点有一条小鱼,若从A点射出一束激光,要使激光能照射到小鱼,该激光应射向( ) A.B点 B.B点上方 C.B点下方 D.B点左方或右方 7.把一块长方体玻璃砖压在有“科学”两字的书上,如图所示。图中“科学”两字是( ) A.变浅的虚像 B.变浅的实像 C.变深的虚像 D.变深的实像 8.在“五岳”之一泰山上,历史上曾多次出现“佛光”奇景。据目击者说:“佛光”是一个巨大的五彩缤纷的光环,与常见的彩虹色彩完全一样。“佛光”形成的主要原因是( ) A.直线传播 B.小孔成像 C.光的反射 D.光的色散 9.电动车的反光镜是用来观察车后情况的平面镜,小明在某次行驶时,发现左侧反光镜中看到是车后的树梢和天空,却看不见路面的情况。为确保行驶安全,左侧反光镜的镜面应该( )
10.王派晚自习下课回家的路上,她发现某行人在路灯下经过时,行人影子的变化情况是( ) A.逐渐变短 B.逐渐变长 C.先变长后变短 D.先变短后变长 11.新修的武昌东湖路上,在传统的交通标志白线上每隔2米安装了一个凸起的纯玻璃元件,这种元件叫“夜精灵”。晚上只要汽车的灯光一照,司机就能看到附近地上的“夜精灵”亮起来(如图所示)。下面几种元件的工作原理与夜精灵完全不同的是( ) A.高速公路反光标志牌 B.十字路口的红绿交通标志灯 C.自行车的尾灯 D.环卫工人身上穿的反光马甲
(第11题图) (第12题图) (第13题图) 12.构建思维导图是整理知识的重要方法,如图是小金复习光学知识时构建的思维导图,图中Ⅰ处可补充的现象( ) A.镜子中的“自己” B.湖水有青山的倒影 C.阳光下绿树的影子 D.岸上的人看到水中的“鱼” 二、填空与作图题(19、20题各3分,其余每空1分,共19分) 13.如图所示,小明想通过A、B两张纸片上的小孔看见烛焰,他应将烛焰、两个小孔和人眼调到上,这样操作的依据是。操作过程中他还在B纸片上看到了一个烛焰的像,这个像是(填“正立”或“倒立”)的。 14.身高1.70 m的李洋同学面向穿衣镜站在镜前1 m处,镜中的像与他相距,若他远离平面镜后退0.5 m,则镜中像高为。 15.站在湖边的小雪看到小鱼在水中游动,同时发现有一只“小鸟”在水中飞翔。小雪看到的鱼是由于光的现象形成的,水中的“小鸟”是由于光的现象形成的。 16.青海湖水清澈见底,平静如镜。站在湖边的游客能清晰地看见自己在水中的倒影,这是光的现象;湟鱼洄游时游客也能欣赏到水中的鱼在游玩,他们看到的是鱼的像(填“虚”或“实”);有时,游客还能看到鱼在白云中穿行的趣景,以白云为参照物,鱼是的。 17.生活中的一些光现象:①阳光下树的影子;②水面波光粼粼;③交警身上穿的警用背心在灯光照射下很亮;④站在岸边能看到水里的鱼。其中能用光的反射知识解释的是(填序号)。 18.如图所示,在“观看水中的硬币”活动中,把一枚硬币固定在空杯的底部,找一个角度使人刚好看不到硬币的最右端A点。保持眼睛和杯子的位置不变,在同学逐渐把水加入到杯中的过程中,硬币上的B点和C点能先后被你看到。 (1)人所看到的水中硬币是一个变的虚像。 (2)图中画出了刚看到C点时光的传播示意图,入射角是αC;如果刚看到B点时的入射角是αB,则ααC。
(第18题图)
(第19题图)(第20题图) 19.如图所示,光源S发出一条光线射向水面,在水面处发生反射和折射,
反射光线经过A点。请画出入射光线、反射光线和折射光线的大致方向。 20.“井底之蛙”这个成语大家都很熟悉。如图所示,在一个干枯的井底正中央P点有一只青蛙,它的视野范围如图a所示。大雨将井全部灌满水,若青蛙仍在P点,请你在图b中画出青蛙视野发生变化后的大致情况。 三、实验与探究题(21题8分,22题6分,23题10分,共24分) 21.如图甲所示是小宇同学探究“光的反射规律”的实验装置。平面镜M平放在水平桌面上,白色硬纸板垂直立在平面镜上。
(第21题图) (1)小宇让一束光贴着纸板沿方向射向镜面,反射光沿方向射出,测出反射角和入射角大小。改变光的入射角度,多次重复上述实验步骤。 ①上述实验探究得到的规律是(填字母)。 A.光沿直线传播 B.反射角等于入射角 C.平面镜成像的特点 ②白色硬纸板在实验中的作用是 (写出一条即可)。 (2)实验过程中若将纸板倾斜,如图乙所示,让光仍贴着纸板沿方向射向镜面,此时反射光(填“在”或“不在”)纸板这一平面内;通过平面镜观察镜中硬纸板的像,则看到的像与图丙中相符的是(填序号)。
(第22题图) 22.某实验小组在探究光的折射规律时,让一束光从空气斜射入玻璃水槽
内的水中,看到如图所示的现象: (1)请在图中分别作出入射角(用字母i表示)和折射角(用字母r表示)。 (2)为了探究光从空气斜射入水中时折射角和入射角的关系,以下方案中正确的是( ) A.只测量图中的入射角和折射角,分析并得出结论 B.保持入射角不变,进行多次实验,测量入射角和每次实验的折射角,分析并得出结论 C.改变入射角,进行多次实验,测量每次实验的入射角和折射角,分析并得出结论
(第23题图) 23.在研究“平面镜成像特点”的实验中,选取完全相同的蜡烛A和B,高为7 。如图所示,在竖直的玻璃板前10 处放一支点燃的蜡烛A,烛焰高2 。 (1)最好选用玻璃板(填“茶色”或“无色透明”)进行实验。 (2)选取A、B两支相同的蜡烛是为了比较 。 (3)在利用蜡烛B确定出蜡烛A成像的位置后,移去蜡烛B,并在其所在位置上放一光屏,光屏上不能得到蜡烛A的像。则平面镜所成的像是像(填“实”或“虚”)。 (4)根据平面镜成像的特点可判断,身高1.7 m的人,站在镜前5 m处,他在镜中所成的像到平面镜的距离是;当他远离平面镜时,像的大小(填“变大”“变小”或“不变”)。 四、综合应用题(24题7分,25题14分,共21分) 24.为了捕捉到一条鱼,猩猩用矛拼命地刺向水里却没有成功,请你说明其中的物理道理。
25.利用激光束测量月球和地球间的距离是目前最为精确的方法,测量工具是一架天文望远镜、一台激光器,和登月行动中留在月球上的角反射列阵。1969年7月,阿波罗11号的宇宙航行员第一次登上了月球,在上边放置了一台重30 的“角反射列阵”,它由100块石英制成的角反射镜组成,排列成10行,每行10块。角反射器刚放好,各国立即向它发射激光。宇航员还没有离开月球,科学家就捕获到了反射光。后来,人们又不断把角反射器送到月球,其中阿波罗15号的角反射器列阵由300块角反射镜组成,测月的误差已经减小到15 。 (1)想一想:我们能利用高能量、方向性好的超声波测量地球和月球之间的距离吗?为什么? (2)角反射器其实就是两个相互垂直的平面镜,如图所示。请在图上准确画出所给入射光线经两平面镜反射的反射光线。 (第25题图) 并说出下面生活中哪些地方用到类似的装置( ) A.自行车尾灯 B.汽车后视镜 C.手电筒反光罩 (3)若从发射激光开始到接收到反射回的激光共用时2.56 s,求月球和地球间的距离约为多少千米? 第四章达标检测卷 一、1 点拨:当水星转到太阳与地球中间且三者在一条直线上时,在地球上看到水星从太阳面上移过,这就是“水星凌日”现象,成因是光的直线传播,在给出的四个选项中“A.小孔成像”属于光的直线传播,“B.河水看起来变浅”属于光的折射,“C.海市蜃楼”属于光的折射,“D.水中荷花的倒影”属于光的反射。 2.C 点拨:水中鱼反射出的光,在水面处发生了折射,折射角大于入射角,人认为光是沿直线传播的,所以逆着折射光线看过去,看到的是变浅的鱼的虚像。所以有经验的渔民应该用鱼叉瞄准看到鱼的下方位置,才能将鱼叉到。由此可知,B、D选项光的传播方向错误,A选项折射角等于入射角,故错误,只有C选项正确。 3.C 点拨:在光的反射现象中,反射角等于入射角。 4.C 5.D 点拨:由平面镜成像的特点可知,铅笔与平面镜的距离改变,铅笔在镜中的像的大小不变,故A错误;平面镜竖直向上移动时,铅笔的像与铅笔还是关于平面镜所在平面对称的,像不动,故B错误;像的大小与物体相等,故若改用一块较小的平面镜,铅笔的像将不变,故C错误;铅笔与平面镜的夹角为45°,根据平面镜成像的特点,此时平面镜将铅笔与像的夹角平分,所以铅笔与它在平面镜中的像互相垂直,故D正确。 6.A 点拨:连接,过折射点作法线,根据光从空气斜射入水中,折射角小于入射角,画出折射光线的位置,虽然人看到的B点是鱼的虚像,鱼的实际位置在B点的正下方,因为激光在进入水的时候也会发生折射,所以照着B点,激光也就刚好落在鱼上了,如图所示。
