高二下册数学期中考三角函数知识点总结
高中数学- 三角函数公式总结

高中数学-三角函数公式总结一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=,正弦:ry =αsin 余弦:rx =αcos 正切:xy=αtan 二、同角三角函数的基本关系式商数关系:αααcos sin tan =,平方关系:1cos sin 22=+αα三、诱导公式(奇变偶不变,符号看象限)⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
⑵απ+2、απ-2、απ+23、απ-23的三角函数值,等于α的异名函数值,前面加上一个把α看成..锐角时原函数值的符号。
公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2k π+α)=sin α(k ∈Z )cos (2k π+α)=cos α(k ∈Z )tan (2k π+α)=tan α(k ∈Z )公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin (π+α)=-sin αcos (π+α)=-cos αtan (π+α)=tan α公式三:任意角α与-α的三角函数值之间的关系:sin (-α)=-sin αcos (-α)=cos αtan (-α)=-tan α公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin (π-α)=sin αcos (π-α)=-cos αtan (π-α)=-tan α公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin (2π-α)=-sin αcos (2π-α)=cos αtan (2π-α)=-tan α微生筑梦公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin (π/2+α)=cos αsin (π/2-α)=cos αcos (π/2+α)=-sin αcos (π/2-α)=sin αtan (π/2+α)=-cot αtan (π/2-α)=cot αsin (3π/2+α)=-cos αsin (3π/2-α)=-cos αcos (3π/2+α)=sin αcos (3π/2-α)=-sin αtan (3π/2+α)=-cot αtan (3π/2-α)=cot α四、和角公式和差角公式βαβαβαsin sin cos cos )cos(⋅+⋅=-βαβαβαsin sin cos cos )cos(⋅-⋅=+βαβαβαsin cos cos sin )sin(⋅+⋅=+βαβαβαsin cos cos sin )sin(⋅-⋅=-βαβαβαtan tan 1tan tan )tan(⋅-+=+βαβαβαtan tan 1tan tan )tan(⋅+-=-五、二倍角公式αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-=ααα2tan 1tan 22tan -=六、辅助角公式)sin(cos sin 22ϕ++=+x b a x b x a 其中:角ϕ的终边所在的象限与点),(b a 所在的象限相同,22sin b a b +=ϕ,22cos b a a +=ϕ,ab=ϕtan 。
(精心整理)高中数学三角函数专题(重要知识点和经典方法大合集)
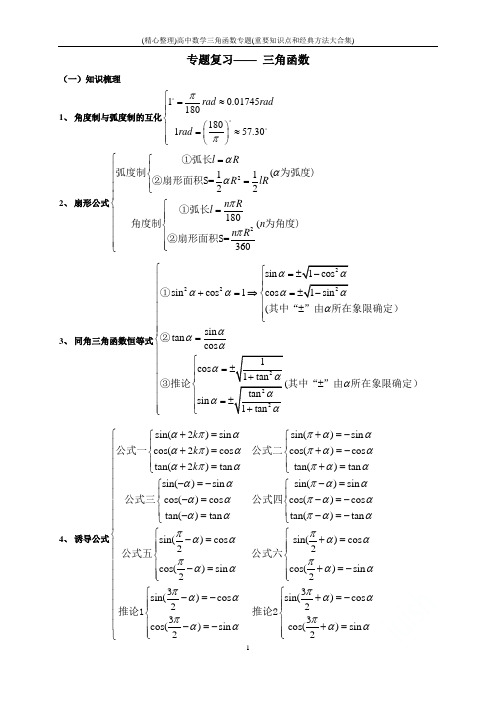
专题复习—— 三角函数(一)知识梳理1、 角度制与弧度制的互化10.01745180180157.30rad rad rad ππ⎧=≈⎪⎪⎨⎛⎫⎪=≈ ⎪⎪⎝⎭⎩2、 扇形公式22(11=22180(=360l R R lR n R l n n R αααππ⎧=⎧⎪⎪⎨⎪=⎪⎪⎩⎪⎨⎧=⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩⎩①弧长弧度制为弧度)②扇形面积S ①弧长角度制为角度)②扇形面积S3、 同角三角函数恒等式22sin sin cos 1cos (sin tan cos cos sin ααααααααααα⎧⎧=⎪⎪⎪⎪+=⇒=⎨⎪⎪⎪±⎪⎩⎪⎪⎪=⎨⎪⎪⎧=⎪⎪⎪⎪±⎨⎪⎪⎪=⎪⎪⎩⎩①其中“”由所在象限确定)②③推论其中“”由所在象限确定)4、 诱导公式sin(2)sin sin()sin cos(2)cos cos()cos tan(2)tan tan()tan sin()sin sin()sin cos()cos cos()cos tan()tan tan()tan s k k k απαπαααπαπαααπαπααααπααααπααααπαα+=+=-⎧⎧⎪⎪+=+=-⎨⎨⎪⎪+=+=⎩⎩-=--=⎧⎧⎪⎪-=-=-⎨⎨⎪⎪-=-=-⎩⎩公式一公式二公式三公式四公式五in()cos sin()cos 22cos()sin cos()sin 2233sin()cos sin()cos 2233cos()sin cos()sin 22ππααααππααααππααααππαααα⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎧⎨-=+=⎪⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪-=+=-⎪⎪⎪⎩⎩⎪⎧⎧⎪-=-+=-⎪⎪⎪⎪⎪⎨⎨⎪⎪⎪⎪-=-+=⎪⎪⎩⎩⎩公式六推论1推论25、差(和)角公式cos()cos cos sin sincos()cos cos sin sinsin()sin cos cos sinsin()sin cos cos sintan tantan()1tan tantan tantan()1tan tanαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβ⎧-=+⎪+=-⎪⎪-=-⎪⎪+=+⎨-⎪-=⎪+⎪+⎪+=⎪-⎩余余正正号相反正余余正号相同6、二倍角公式(倍角公式)22222221sin22sin cos sin cos sin22cos2cos sin1cos2cos212sin sin21cos2 cos22cos1cos22tantan21tanαααααααααααααααααααα⎧⎪=⇒=⎪⎪=-⎪⎪-⎪=-⇒=⎨⎪+⎪=-⇒=⎪⎪⎪=⎪-⎩7、正弦定理及推论2(sin sin sin2sin,2sin,2sinsin,sin,sin222::sin:sin:sinsin sin sin,,sin sin sina b cR R ABCA B Ca R Ab R Bc R Ca b cA B CR R Ra b c A B Ca A a Ab Bb Bc C c C⎧===∆⎪⎪===⎪⎪⎪===⎨⎪⎪=⎪⎪===⎪⎩①为外接圆的半径)②③④⑤8、余弦定理及推论222 222222 222222 2222cos cos22cos cos22cos cos2b c a a b c bc A Abca c bb ac ac B Baca b c c a b ab C Cab⎧+-=+-⇒=⎪⎪+-⎪=+-⇒=⎨⎪⎪+-=+-⇒=⎪⎩9、三角形面积公式1(21()(2111=sin sin sin222S ah aS r a b c r ABCS ab C ac B bc A⎧=⎪⎪⎪=++∆⎨⎪⎪==⎪⎩为底,h为高)为内切圆的半径)10、求最小正周期的公式sin()2= cos()tan()= y A x kTy A x ky A x k Tωϕπωϕωπωϕω⎧=++⎪=++⎪⎨⎪=++⎪⎩最小正周期为的最小正周期为11、正弦函数y=sinx[]maxmin111+2,2,22(2)3+2,2,.222()1;2(3)2() 1.2(4)((5)y sinRk k k Zk k k Zx k k Z yx k k Z yk k Z kxππππππππππππππ-⎧⎡⎤-+∈⎪⎢⎥⎪⎣⎦⎨⎡⎤⎪+∈⎢⎥⎪⎣⎦⎩⎧+∈=⎪⎪⎨⎪+∈=-⎪⎩∈≠=()定义域:,值域:,在单调递增;单调性在单调递减当且仅当=时,最值当且仅当=-时,周期性:周期为2且0),最小正周期为2.奇偶性:,;(6)2.Rx k k Zk k Zπππ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧+∈⎪⎪⎨⎪⎪∈⎪⎩⎩为上的奇函数.①为轴对称图形,对称轴为=对称性②为中心对称图形,对称中心为(,0),12、余弦函数y=cosx[][][]maxmin111+2,2,(2)2,2,.2()1;(3)2() 1.(4)((5)y cos,(6)Rk k k Zk k k Zx k k Z yx k k Z yk k Z kx Rx k kππππππππππππ-⎧-∈⎪⎨+∈⎪⎩∈=⎧⎨+∈=-⎩∈≠=()定义域:,值域:,在单调递增;单调性在单调递减当且仅当=时,最值当且仅当=时,周期性:周期为2且0),最小正周期为2.奇偶性:为上的偶函数.①为轴对称图形,对称轴为=对称性;+.2Zk k Zππ⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪∈⎧⎪⎪⎪⎨∈⎪⎪⎩⎩②为中心对称图形,对称中心为(,0),13、正切函数y=tanx1|,,22-+,),.22(3)(0.(4)y tan(5),0),.2x x k k Z Rk k k Zk k Z kxkk Zπππππππππ⎧⎧⎫≠+∈⎪⎨⎬⎩⎭⎪⎪+∈⎪⎪⎪∈≠⎨⎪=⎪⎪⎧⎪⎪⎨⎪∈⎪⎪⎩⎩()定义域:值域:()单调性:在开区间(单调递增周期性:周期为且),最小正周期为奇偶性:为奇函数.①不是轴对称图形;对称性②是中心对称图形,对称中心为(14、简谐运动sin()y A xωϕ=+[)2=1(0,0,0,)2xA xTπωωωπωϕϕ⎧⎪⎪⎪⎪⎪=>>∈+∞⎨⎪⎪⎪⎪⎪⎩①振幅:A②周期:T③频率:f=其中④相位:x+⑤初相:=0时的相位2222sin cos)(tan)0)sin cos)(tan)ba xb x a b xaa aa xb x a b xbωωωϕϕωωωϕϕ⎧+=++=⎪⎪⎨>⎪+=+-=⎪⎩①其中15、三角恒等变换之辅助角公式(其中②其中辅助角公式的证明如下:证明:asin xω+bcos xω22a b+22a b+sin xω22a b+cos xω),①22a b+=cosϕ22a b+=sinϕ,则asin xω+bcos xω22a b+xωcosϕ+cos xωsinϕ)22a b+xω+ϕ) (其中tanϕ=ba)② 22a a b+=sin ϕ22b a b+ϕ,则asin x ω+bcos x ω22a b +x ωsin ϕ+cos x ωcos ϕ) 22a b +x ω-ϕ),(其中tan ϕ=a b) 注:其中ϕ的大小可以由sin ϕ、cos ϕ的符号确定ϕ的象限,再由tan ϕ的值求出;或由tan ϕ=ba和(a,b)所在的象限来确定. 例:化简32cos 2y x x =+.法一:逆用差(和)角公式3132cos 22(2cos 2)2(sin 2cos cos 2sin )2sin(2)2666y x x x x x x x πππ=+=+=+=+法二:应用辅助角公式32cos 22sin(2)6y x x x π=+=+ (其中3tan 363πϕϕ==⇒=)(二)考点剖析考点一:正、余弦定理,三角形面积公式的应用 例1: 在△ABC 中,C =2B ,AB AC =43. (1)求cos B ;(2)若BC =3,求S △ABC . 解:(1)由C =2B 和正弦定理得sin C =2sin B cos B =2·AC AB sin C ·cos B ∴cos B =AB 2AC =23 (2)设AC =3x ,则AB =4x . 由余弦定理得(3x )2=(4x )2+32-2×4x ×3cos B ,即9x 2=`16x 2+9-16x ∴7x 2-16x +9=0 解得x =1或x =97当x =1时,AC =3,AB =4 ∴S △ABC =12BA ×BC ×sin B =12×4×3×53=2 5.当x =97时,AC =277,AB =367 ∴S △ABC =12BA ×BC ×sin B =12×367×3×53=1875.考点二:利用正、余弦定理判断三角形的形状例2:在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =(2b +c )sin B +(2c +b )sin C . (1)求角A 的大小;(2)若sin B +sin C =1,试判断△ABC 的形状.解:(1) 2a sin A =(2b +c )sin B +(2c +b )sin C由正弦定理得2a 2=(2b +c )b +(2c +b )c ,即a 2=b 2+c 2+bc ① 由余弦定理得a 2=b 2+c 2-2bc cos A12cos cos 2bc A bc A ∴-=⇒=- 又0A π<< 23A π∴=. (2)由①得sin 2A =sin 2B +sin 2C +sin B sin C 又sin B +sin C =1 ∴sin B =sin C =12又0,022B C ππ<<<<∴B =C ∴△ABC 是等腰三角形.考点三:三角恒等变换之辅助角公式:sin cos )(tan )ba xb x x aωωωϕϕ+=+=其中例3:已知函数2()2sin cos 2cos f x x x x =+,x R ∈(1) 求f(x)的最小正周期及最大值; (2) 求函数f(x)的单调递增区间; (3) 若0,2x π⎡⎤∈⎢⎥⎣⎦,求函数f(x)的值域 .解:2()2sin cos 2cos f x x x x =+sin 2cos21x x =++)14x π=++(1) f(x)的最小正周期为22T ππ==,最大值为max ()1f x =. (2) 由222,242k x k k Z πππππ-+≤+≤+∈得3,88k x k k πππππ-+≤≤+∈∴函数f(x)的单调递增区间为3,,88k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦(3)02x π≤≤52444x πππ∴≤+≤sin(2)14x π≤+≤ 0)114x π∴≤++≤即0()1f x ≤≤∴函数f(x)的值域为1⎡⎤⎣⎦即时训练:已知函数22(sin cos )y x x x =++x R ∈(1) 求函数f(x)的最小正周期、最小值及单调递减区间; (2) 当02x π<<时,求函数f(x)的值域.【高考地位】三角函数式的化简和求值是高考考查的重点内容之一. 掌握化简和求值问题的解题规律和一些常用技巧,以优化我们的解题效果,做到事半功倍. 这也是解决三角函数问题的前提和出发点. 在高考中常以选择题、填空题出现,其试题难度考查不大.【方法点评】方法一 切割化弦使用情景:一般三角求值类型解题模板:第一步 利用同角三角函数的基本关系sin tan cos θθθ=,将题设中的切化成弦的形式; 第二步 计算出正弦与余弦之间的关系; 第三步 结合三角恒等变换可得所求结果.例1已知1tan()2πα+=,则sin cos 2sin cos αααα-+=( ) A .41 B .21 C .41- D .21- 【答案】C 【解析】试题分析:21tan =α,将原式上下同时除以αcos ,即411tan 21tan cos sin 2cos sin -=+-=+-αααααα,故选C.考点:同角三角函数基本关系学*科网 【变式演练1】已知2)tan(-=-απ,则=+αα2cos 2cos 1( )A .3 B. 52C.25- D.3- 【答案】C 【解析】考点:诱导公式,同角间的三角函数关系,二倍角公式.方法二 统一配凑使用情景:一类特殊三角求值类型解题模板:第一步 观察已知条件中的角和所求的角之间的联系;第二步 利用合理地拆角,结合两角和(或差)的正弦(或余弦)公式将所求的三角函数值转化为已知条件中的三角函数值;第三步 利用三角恒等变换即可得出所求结果.例2已知,31tan ,71tan ==βα则=+)2tan(βα 【答案】1 【解析】 试题分析:212tan 3tan ,tan 231tan 4ββββ===-,()13tan tan 274tan 21131tan tan 2174αβαβαβ++∴+===--⨯考点:两角和的正切公式.方法三 公式活用例3 下列式子结果为3的是( ) ①tan25tan353tan25tan35︒+︒+︒︒; ②()2sin35cos25cos35cos65︒︒+︒︒; ③1tan151tan15+︒-︒;④2tan61tan6ππ-.A. ①②B. ③C. ①②③D. ②③④ 【答案】C【高考再现】1.(2018年全国卷Ⅲ文)若,则A .B .C .D .【答案】B 【解析】 分析:由公式可得.详解:,故答案为B.点睛:本题主要考查二倍角公式,属于基础题.2. 【2016高考新课标3理数】若3tan 4α= ,则2cos 2sin 2αα+=( ) (A)6425 (B) 4825 (C) 1 (D)1625【答案】A 【解析】试题分析:由3tan 4α=,得34sin ,cos 55αα==或34sin ,cos 55αα=-=-,所以2161264cos 2sin 24252525αα+=+⨯=,故选A .考点:1、同角三角函数间的基本关系;2、倍角公式.【方法点拨】三角函数求值:①“给角求值”将非特殊角向特殊角转化,通过相消或相约消去非特殊角,进而求出三角函数值;②“给值求值”关键是目标明确,建立已知和所求之间的联系.4.【2017山东,文4】已知3cos 4x =,则cos2x = A.14- B.14 C.18- D.18【答案】D 【解析】【考点】二倍角公式【名师点睛】(1)三角函数式的化简与求值要遵循“三看”原则,一看角,二看名,三看式子结构与特征.(2)三角函数式化简与求值要注意观察条件中角之间的联系(和、差、倍、互余、互补等),寻找式子和三角函数公式之间的共同点.6. 【2015高考福建,文6】若5sin13α=-,且α为第四象限角,则tanα的值等于()A.125B.125-C.512D.512-【答案】D【考点定位】同角三角函数基本关系式.【名师点睛】本题考查同角三角函数基本关系式,在sinα、cosα、tanα三个值之间,知其中的一个可以求剩余两个,但是要注意判断角α的象限,从而决定正负符号的取舍,属于基础题.6.(2018年全国卷II文)已知,则__________.【答案】.【解析】分析:利用两角差的正切公式展开,解方程可得.详解:,解方程得.学科*网点睛:本题主要考查学生对于两角和差公式的掌握情况,属于简单题型,解决此类问题的核心是要公式记忆准确,特殊角的三角函数值运算准确.7.【2018年全国普通高等学校招生统一考试数学(江苏卷)】已知为锐角,,.(1)求的值;(2)求的值.【答案】(1);(2)【解析】分析:先根据同角三角函数关系得,再根据二倍角余弦公式得结果;(2)先根据二倍角正切公式得,再利用两角差的正切公式得结果.详解:解:(1)因为,,所以.因为,所以,因此,.点睛:应用三角公式解决问题的三个变换角度(1)变角:目的是沟通题设条件与结论中所涉及的角,其手法通常是“配凑”.(2)变名:通过变换函数名称达到减少函数种类的目的,其手法通常有“切化弦”、“升幂与降幂”等. (3)变式:根据式子的结构特征进行变形,使其更贴近某个公式或某个期待的目标,其手法通常有:“常值代换”、“逆用变用公式”、“通分约分”、“分解与组合”、“配方与平方”等. 学#科网【反馈练习】1.【山东省济南市2018届高三第一次模拟考试数学(文)试题】若72sin 410A π⎛⎫+=⎪⎝⎭, ,4A ππ⎛⎫∈ ⎪⎝⎭,则sin A 的值为( )A .35 B . 45 C . 35或45 D . 34【答案】B 【解析】5,,,4424A A πππππ⎛⎫⎛⎫∈∴+∈⎪ ⎪⎝⎭⎝⎭,所以cos 04A π⎛⎫+< ⎪⎝⎭,且22cos 1sin 4410A A ππ⎛⎫⎛⎫+=--+=- ⎪ ⎪⎝⎭⎝⎭, 所以4sin sin sin cos cos sin 4444445A A A A ππππππ⎡⎤⎛⎫⎛⎫⎛⎫=+-=+-+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,选B. 点睛:本题主要考查同角三角函数基本关系式、两角差的正弦公式等,属于易错题.解答本题的关键是拆角,将sin A 拆成sin 44A ππ⎡⎤⎛⎫+- ⎪⎢⎥⎝⎭⎣⎦.2.【山西省2018年高考考前适应性测试文科数学试题】已知tan 3α=,则sin21cos2αα=+( )A . 3-B . 13-C . 13D . 3 【答案】D 【解析】222sin cos 3122sin tan cos cos αααααα===+故选D3.【江西省上饶市2018届高三下学期第二次高考模拟数学(理)试题】000sin65sin35cos30cos35-=( ) A . 3-B . 12-C . 12D . 3【答案】C 【解析】由题得()00000000sin 3530sin35cos30cos35sin301sin30cos35cos352+-===,故选C. 4.【河南省濮阳市2018届高三第一次模拟考试数学(理)试题】设()0,90α∈︒︒,若()3sin 7525α︒+=-,则()()sin 15sin 75αα︒+⋅︒-= ( )A .110 B . 2 C . 110- D . 2-【答案】B【解析】()()sin 75cos 15αα-=+, 所以原式等于()()()1sin 15cos 15sin 3022ααα++=+ 而()()()()2sin 302sin 75245sin 752cos 7522αααα⎡⎤⎡⎤+=+-=+-+⎣⎦⎣⎦ , ()75275,255α+∈ ,又因为()sin 7520α+<,所以()752180,255α+∈,可求得()4cos 7525α+=- , 那么()()()22342sin 302sin 752cos 7525510ααα⎡⎤⎛⎫⎛⎫⎡⎤+=+-+=---= ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭⎣⎦,那么()12sin 3022α+=,故选B. 5.【安徽省宣城市2018届高三第二次调研测试数学理试题】已知3cos 5α=, 3,22παπ⎛⎫∈⎪⎝⎭,则cos 3πα⎛⎫-= ⎪⎝⎭__________.【答案】34310- 【解析】∵3cos 5α=, 3,22παπ⎛⎫∈⎪⎝⎭∴4sin 5α=- ∴3143343cos cos cos sin sin 333525πππααα-⎛⎫⎛⎫-=+=⨯+-⨯= ⎪⎪⎝⎭⎝⎭ 故答案为343-. 三角函数的图像和性质问题【高考地位】近几年高考降低了对三角变换的考查要求,而加强了对三角函数的图象与性质的考查,因为函数的性质是研究函数的一个重要内容,是学习高等数学和应用技术学科的基础,又是解决生产实际问题的工具,因此三角函数的性质是高考的重点和难点。
三角函数知识点归纳总结

三角函数知识点归纳总结三角函数是数学中研究角度与三角形边长之间关系的函数。
它们在解决几何问题、物理问题以及工程学中有着广泛的应用。
以下是三角函数的一些基本知识点归纳总结:1. 定义:- 正弦函数(sin):在直角三角形中,正弦是锐角的对边与斜边的比值。
- 余弦函数(cos):余弦是锐角的邻边与斜边的比值。
- 正切函数(tan):正切是锐角的对边与邻边的比值。
- 余切函数(cot):余切是锐角的邻边与对边的比值。
- 正割函数(sec):正割是斜边与邻边的比值。
- 余割函数(csc):余割是斜边与对边的比值。
2. 三角函数的值:- 特殊角(如0°, 30°, 45°, 60°, 90°)的三角函数值是基础,需要熟记。
- 正弦和余弦函数的值域是[-1, 1]。
- 正切和余切函数的值域是所有实数,但正切在90°(π/2弧度)处无定义,余切在0°和180°(0和π弧度)处无定义。
3. 单位圆:- 单位圆是一个半径为1的圆,三角函数可以在这个圆上定义。
- 角度可以用弧度制或角度制表示。
π弧度等于180°。
4. 三角恒等式:- 基本恒等式:sin²θ + cos²θ = 1。
- 双角公式:如sin(2θ) = 2sinθcosθ,cos(2θ) = cos²θ -sin²θ。
- 和差公式:如sin(α ± β) = sinαcosβ ± cosαsinβ,cos(α ± β) = cosαcosβ ∓ sinαsinβ。
5. 三角函数的图像:- 正弦函数和余弦函数是周期函数,周期为2π。
- 正切函数和余切函数也是周期函数,但它们在某些点有垂直渐近线。
6. 反三角函数:- 反三角函数是三角函数的逆运算,如arcsin、arccos、arctan 等。
- 反三角函数的值域通常被限制在特定的区间内,以保证其为单值函数。
三角函数知识点归纳总结高中

三角函数知识点归纳总结高中1. 弧度与角度在学习三角函数之前,我们首先要了解弧度和角度的概念。
角度是一个常见的度量角的单位,通常用°来表示,而弧度是另一种度量角的单位,通常用rad来表示。
其中180°对应着π rad,这是一个重要的换算关系。
2. 正弦函数正弦函数是三角函数中的一个重要函数,通常用sin表示。
对于一个角θ,其正弦值可以通过直角三角形中的对边与斜边的比值来定义,即sin(θ) = 对边/斜边。
正弦函数的图像是一个周期性的波形,其周期为2π。
3. 余弦函数余弦函数是另一个重要的三角函数,通常用cos表示。
对于一个角θ,其余弦值可以通过直角三角形中的邻边与斜边的比值来定义,即cos(θ) = 邻边/斜边。
余弦函数的图像也是一个周期性的波形,与正弦函数的图像相似,但相位不同。
4. 正切函数正切函数是三角函数中的第三个主要函数,通常用tan表示。
对于一个角θ,其正切值可以通过正弦值除以余弦值来定义,即tan(θ) = sin(θ) / cos(θ),也可以表示为对边/邻边。
正切函数的图像在某些角度上会出现无穷大的情况,这些点称为其渐近线。
5. 三角函数的性质三角函数具有一些重要的性质,包括周期性、奇偶性、增减性等。
正弦函数和余弦函数都是周期函数,其周期为2π;正弦函数是奇函数,余弦函数是偶函数;正弦函数在0到π/2上是增函数,在π/2到π上是减函数。
这些性质对于理解和分析三角函数的图像至关重要。
6. 三角函数的应用三角函数在实际中有广泛的应用,如在解决三角形相关的问题时常常需要用到正弦定理、余弦定理等;在物理学中,三角函数也被广泛运用在描述波动、振动等现象中;在工程领域,三角函数被用于建模和计算各种工程问题,如声音传播、光学等。
综上所述,三角函数是高中数学中的一个重要内容,通过深入理解和掌握三角函数的性质和应用,可以更好地应用于实际问题的解决中。
学好三角函数对于提高数学素养和解决实际问题都具有重要的意义。
2022年高中数学三角函数知识点总结

高考三角函数1.特殊角旳三角函数值:2.角度制与弧度制旳互化:,2360π= ,1800π=3.弧长及扇形面积公式 弧长公式:r l.α= 扇形面积公式:S=r l .21α----是圆心角且为弧度制。
r-----是扇形半径4.任意角旳三角函数设α是一种任意角,它旳终边上一点p (x,y ), r=22y x + (1)正弦sin α=ry 余弦cos α=r x正切tan α=xy(2)各象限旳符号:xyO — —+ xy O — ++y O— +sin α cos α tan α5.同角三角函数旳基本关系:(1)平方关系:sin 2α+ cos 2α=1。
(2)商数关系:ααcos sin =tan α(z k k ∈+≠,2ππα)6.诱导公式:()()1sin 2sin k παα+=,()cos 2cos k παα+=,()()tan 2tan k k παα+=∈Z . ()()2sin sin παα+=-,()cos cos παα+=-,()tan tan παα+=. ()()3sin sin αα-=-,()cos cos αα-=,()tan tan αα-=-. ()()4sin sin παα-=,()cos cos παα-=-,()tan tan παα-=-.口诀:函数名称不变,符号看象限.()5sin cos 2παα⎛⎫-=⎪⎝⎭,cos sin 2παα⎛⎫-= ⎪⎝⎭. ()6sin cos 2παα⎛⎫+=⎪⎝⎭,cos sin 2παα⎛⎫+=-⎪⎝⎭. 口诀:正弦与余弦互换,符号看象限. 7正弦函数、余弦函数和正切函数旳图象与性质8、三角函数公式:降幂公式: 升幂公式 :两角和与差旳三角函数关系 sin(α±β)=sin α·cos β±cos α·sin β cos(α±β)=cos α·cos β sin α·sin ββαβαβαtan tan 1tan tan )tan(⋅±=±倍角公式 s in2α=2sin α·cos α cos2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2αααα2tan 1tan 22tan -=1+cos α=2cos 22αcos 2α22cos 1α+=1-cos α=2sin22αsin 2α22cos 1α-=9.正弦定理 :2sin sin sin a b cR A B C===.余弦定理:2222cos a b c bc A =+-; 2222cos b c a ca B =+-; 2222cos c a b ab C =+-.三角形面积定理.111sin sin sin 222Sab C bc A ca B ===. 1.直角三角形中各元素间旳关系:如图,在△ABC 中,C =90°,AB =c ,AC =b ,BC =a 。
关于三角函数的知识点总结

关于三角函数的知识点总结三角函数是数学中的一门重要学科,其应用广泛,不仅在初中、高中、大学的数学课程中涉及,而且在物理、工程、计算机等领域中也有广泛的应用。
下面我们就来总结一下有关三角函数的知识点。
一、三角函数的定义和常见关系1. 正弦函数 $\sin \theta$ 的定义:$\sin \theta = \frac{\text{对边}}{\text{斜边}}$,其中 $\theta$ 为角度(弧度制)。
2. 余弦函数 $\cos \theta$ 的定义:$\cos \theta = \frac{\text{邻边}}{\text{斜边}}$,其中 $\theta$ 为角度(弧度制)。
3. 正切函数 $\tan \theta$ 的定义:$\tan \theta = \frac{\text{对边}}{\text{邻边}}$,其中 $\theta$ 为角度(弧度制)。
4. 三角函数的常见关系:- $\sin^2 \theta + \cos^2 \theta = 1$- $\tan \theta = \frac{\sin \theta}{\cos \theta}$二、三角函数的图像1. 正弦函数的图像:周期为 $2\pi$,在 $[0,\pi]$ 上单调递增,在 $[\pi,2\pi]$ 上单调递减,对称轴为 $x=\frac{\pi}{2}$。
2. 余弦函数的图像:周期为 $2\pi$,在 $[0,\pi]$ 上单调递减,在 $[\pi,2\pi]$ 上单调递增,对称轴为 $x=0$。
3. 正切函数的图像:周期为 $\pi$,在 $(-\frac{\pi}{2},\frac{\pi}{2})$ 上单调递增。
三、三角函数的性质1. 周期性:$\sin (\theta + 2k\pi) = \sin \theta, \cos(\theta + 2k\pi) = \cos \theta$,其中 $k$ 为整数。
高中三角函数知识点整理

高中三角函数知识点整理三角函数是数学中重要的概念,存在于高中数学课程中,是几何、代数、微积分等领域的基础知识。
下面整理了高中三角函数的重要知识点,希望对学生们的学习有帮助。
一、三角函数的基本概念1.弧度制:角的度量单位,一个角所对应的弧长等于半径的长度时,这个角的大小为1弧度。
2.角的三要素:顶点,始边,终边,顶点为角的端点,始边为角的起始边,终边为角的结束边。
3.弧度与角度的转换:角度数×π/180=弧度。
4.等角:具有相同角度的两个角是等角。
5. 正弦:给定一个锐角∠A,对于 A 的任何弧 B,就有 sin A = sin B。
二、正弦、余弦和正切函数1. 正弦函数:在数轴上,根据半径 r 的终端点 (x, y),它的正弦函数值定义为 y / r,可以表示为sinθ。
2. 余弦函数:在数轴上,根据半径 r 的终端点 (x, y),它的余弦函数值定义为 x / r,可以表示为cosθ。
3. 正切函数:在数轴上,根据半径 r 的终端点 (x, y),它的正切函数值定义为 y / x,可以表示为tanθ。
4.三角函数的性质:正弦和余弦函数的值在-1到1之间,正切函数的值没有限制。
三、三角函数的基本性质1.三角函数的周期性:正弦和余弦函数周期为2π,正切函数周期为π。
2.函数图像:正弦函数和余弦函数的图像为曲线,正切函数的图像为直线。
3.函数值的变化:正弦函数和余弦函数的值在一个周期内从-1到1变化,正切函数在不同区间内的值无限制变化。
4. 正弦函数和余弦函数的图像对称:sin(-θ) = -sinθ,cos(-θ) = cosθ。
5. 周期性的性质:sin(θ + 2πn) = sinθ,cos(θ + 2πn) =cosθ,n为整数。
6. 三角函数的诱导公式:sin(α + β) = sinαcosβ +cosαsinβ,cos(α + β) = cosαcosβ - sinαsinβ。
高中数学三角函数知识点

高中数学三角函数知识点一、基础概念1. 三角函数三角函数是数学中的一种函数,用来描述一个直角三角形中各边和角度之间的关系。
三角函数包括正弦函数(sin)、余弦函数(cos)、正切函数(tan)、余切函数(cot)、正割函数(sec)和余割函数(csc)。
2. 角度制和弧度制角度制是指用度数来描述角度大小的一种测量方法,以“度”作为单位。
1圆周角等于360度,1度等于60分,1分等于60秒。
弧度制是指用弧长来描述角度大小的一种测量方法,以“弧度”作为单位。
1圆周角等于2π弧度,1弧度等于圆的半径所对应的弧长的长度。
3. 函数的周期与函数值域函数的周期是指函数在一段区间内重复出现的最小长度。
正弦函数和余弦函数的周期都是2π,正切函数和余切函数的周期都是π,正割函数和余割函数的周期都是π。
函数的值域是指函数所有可能的输出值所组成的集合。
正弦函数和余弦函数的值域都是[-1,1],正切函数的值域是(-∞,∞),余切函数的值域也是(-∞,∞),正割函数的值域是[1,∞),余割函数的值域也是[-∞,-1]∪[1,∞)。
4. 常用三角函数的图形正弦函数的图形是一条周期为2π、在x=π/2处取得最大值1,在x=3π/2处取得最小值-1的正弦曲线。
余弦函数的图形是一条周期为2π、在x=0处取得最大值1,在x=π处取得最小值-1的余弦曲线。
正切函数的图形是一条周期为π、在x=π/2+kπ(k∈Z)处有一个无穷大的跳跃,且在x=kπ(k∈Z)处取值为0的正切曲线。
5. 三角函数的基本关系式正弦函数和余弦函数之间满足关系式sin(x)=cos(x-π/2),cos(x)=sin(x+π/2)。
正切函数和余切函数之间满足关系式tan(x)=1/cot(x),cot(x)=1/tan(x)。
二、三角函数的运算1. 三角函数的加减法公式sin(x±y)=sinxcosy±cosxsinycos(x±y)=cosxcosy∓sinxsinytan(x±y)=(tanx±tany)/(1∓tanxtany)cot(x±y)=(cotxcoty∓1)/(cotx±coty)2. 三角函数的积化和差公式sinx+siny=2sin((x+y)/2)cos((x-y)/2)sinx-siny=2cos((x+y)/2)sin((x-y)/2)cosx+cosy=2cos((x+y)/2)cos((x-y)/2)cosx-cosy=-2sin((x+y)/2)sin((x-y)/2)3. 三角函数的倍角公式和半角公式sin2x=2sinxcosxcos2x=cos^2x-sin^2xtan2x=(2tanx)/(1-tan^2x)sin(x/2)=±√[(1-cosx)/2]cos(x/2)=±√[(1+cosx)/2]tan(x/2)=±√[(1-cosx)/(1+cosx)]4. 三角函数的反函数sin(-1)x:[-1,1]→[-π/2,π/2]cos(-1)x:[-1,1]→[0,π]tan(-1)x:(-∞,∞)→(-π/2,π/2)cot(-1)x:(-∞,∞)→(0,π)三、三角函数的应用1. 三角函数在几何中的应用在直角三角形中,正弦函数和余弦函数可以用来计算任意两边和一个角的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二下册数学期中考三角函数知识点总结在中国古代把数学叫算术,又称算学,最后才改为数学。
以下是查字典数学网为大家整理的高二下册数学期中考三角函数知识点,希望可以解决您所遇到的相关问题,加油,查字典数学网一直陪伴您。
01锐角三角函数定义锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。
正弦(sin)等于对边比斜边;sinA=a/c余弦(cos)等于邻边比斜边;cosA=b/c正切(tan)等于对边比邻边;tanA=a/b余切(cot)等于邻边比对边;cotA=b/a正割(sec)等于斜边比邻边;secA=c/b余割(csc)等于斜边比对边。
cscA=c/a02互余角的三角函数间的关系sin(90-)=cos, cos(90-)=sin,tan(90-)=cot, cot(90-)=tan.03平方关系sin^2()+cos^2()=1tan^2()+1=sec^2()cot^2()+1=csc^2()04积的关系sin=tancoscos=cotsintan=sinseccot=coscscsec=tancsccsc=seccot05倒数关系tancot=1sincsc=1cossec=1特殊角三角函数值角度a030456090120190sina01/22/23/213/20cosa13/22/21/20-1/2-1ta na03/313无穷大-30cota/313/30-3/3/06锐角三角函数公式两角和与差的三角函数:sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinB ?cos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)三角和的三角函数:sin(++)=sincoscos+cossincos+coscossin-sinsinsincos(++)=coscoscos-cossinsin-sincossin-sinsincostan(++)=(tan+tan+tan-tantantan)/(1-tantan-tantan-tantan) 辅助角公式:Asin+Bcos=(A^2+B^2)^(1/2)sin(+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsin+Bcos=(A^2+B^2)^(1/2)cos(-t),tant=A/B倍角公式:sin(2)=2sincos=2/(tan+cot)cos(2)=cos^2()-sin^2()=2cos^2()-1=1-2sin^2()tan(2)=2tan/[1-tan^2()]三倍角公式:sin(3)=3sin-4sin^3()cos(3)=4cos^3()-3cos半角公式:sin(/2)=((1-cos)/2)cos(/2)=((1+cos)/2)tan(/2)=((1-cos)/(1+cos))=sin/(1+cos)=(1-cos)/sin 降幂公式sin^2()=(1-cos(2))/2=versin(2)/2cos^2()=(1+cos(2))/2=covers(2)/2tan^2()=(1-cos(2))/(1+cos(2))万能公式:sin=2tan(/2)/[1+tan^2(/2)]cos=[1-tan^2(/2)]/[1+tan^2(/2)]tan=2tan(/2)/[1-tan^2(/2)]积化和差公式:sincos=(1/2)[sin(+)+sin(-)]cossin=(1/2)[sin(+)-sin(-)]coscos=(1/2)[cos(+)+cos(-)]sinsin=-(1/2)[cos(+)-cos(-)]和差化积公式:sin+sin=2sin[(+)/2]cos[(-)/2]sin-sin=2cos[(+)/2]sin[(-)/2]cos+cos=2cos[(+)/2]cos[(-)/2]cos-cos=-2sin[(+)/2]sin[(-)/2]推导公式:tan+cot=2/sin2tan-cot=-2cot21+cos2=2cos^21-cos2=2sin^21+sin=(sin/2+cos/2)^2其他:sin+sin(+2/n)+sin(+2*2/n)+sin(+2*3/n)++sin[+2*(n-1)/n]=0 cos+cos(+2/n)+cos(+2*2/n)+cos(+2*3/n)++cos[+2*(n-1)/n]=0 以及sin^2()+sin^2(-2/3)+sin^2(+2/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0函数名正弦余弦正切余切正割余割在平面直角坐标系xOy中,从点O引出一条射线OP,设旋转角为,设OP=r,P点的坐标为(x,y)有正弦函数sin=y/r余弦函数cos=x/r正切函数tan=y/x余切函数cot=x/y正割函数sec=r/x余割函数csc=r/y正弦(sin):角的对边比上斜边余弦(cos):角的邻边比上斜边正切(tan):角的对边比上邻边余切(cot):角的邻边比上对边正割(sec):角的斜边比上邻边余割(csc):角的斜边比上对边三角函数万能公式万能公式(1)(sin)^2+(cos)^2=1(2)1+(tan)^2=(sec)^2(3)1+(cot)^2=(csc)^2证明下面两式,只需将一式,左右同除(sin)^2,第二个除(cos)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=-Ctan(A+B)=tan(-C)(tanA+tanB)/(1-tanAtanB)=(tan-tanC)/(1+tantanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nZ)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC万能公式为:设tan(A/2)=tsinA=2t/(1+t^2) (A+,kZ)tanA=2t/(1-t^2) (A+,kZ)cosA=(1-t^2)/(1+t^2) (A+,且A+(/2) kZ)就是说sinA.tanA.cosA都可以用tan(A/2)来表示,当要求一串函数式最值的时候,就可以用万能公式,推导成只含有一个变量的函数,最值就很好求了.三角函数关系倒数关系tan cot=1sin csc=1cos sec=1商的关系sin/cos=tan=sec/csccos/sin=cot=csc/sec平方关系sin^2()+cos^2()=11+tan^2()=sec^2()1+cot^2()=csc^2()同角三角函数关系六角形记忆法构造以上弦、中切、下割;左正、右余、中间1的正六边形为模型。
倒数关系对角线上两个函数互为倒数;商数关系六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。
(主要是两条虚线两端的三角函数值的乘积,下面4个也存在这种关系。
)。
由此,可得商数关系式。
平方关系在带有阴影线的三角形中,上面两个顶点上的三角函数值的平方和等于下面顶点上的三角函数值的平方。
两角和差公式sin(+)=sincos+cossinsin(-)=sincos-cossincos(+)=coscos-sinsincos(-)=coscos+sinsintan(+)=(tan+tan )/(1-tan tan)tan(-)=(tan-tan)/(1+tan tan)二倍角的正弦、余弦和正切公式sin2=2sincoscos2=cos^2()-sin^2()=2cos^2()-1=1-2sin^2() tan2=2tan/(1-tan^2())tan(1/2*)=(sin )/(1+cos )=(1-cos )/sin半角的正弦、余弦和正切公式sin^2(/2)=(1-cos)/2cos^2(/2)=(1+cos)/2tan^2(/2)=(1-cos)/(1+cos)tan(/2)=(1cos)/sin=sin/1+cos万能公式sin=2tan(/2)/(1+tan^2(/2))cos=(1-tan^2(/2))/(1+tan^2(/2))tan=(2tan(/2))/(1-tan^2(/2))三倍角的正弦、余弦和正切公式sin3=3sin-4sin^3()cos3=4cos^3()-3costan3=(3tan-tan^3())/(1-3tan^2())诱导公式诱导公式的本质所谓三角函数诱导公式,就是将角n(/2)的三角函数转化为角的三角函数。
常用的诱导公式公式一:设为任意角,终边相同的角的同一三角函数的值相等:sin(2k)=sin kzcos(2k)=cos kztan(2k)=tan kzcot(2k)=cot kz公式二:设为任意角,的三角函数值与的三角函数值之间的关系:sin()=-sincos()=-costan()=tan其实,任何一门学科都离不开死记硬背,关键是记忆有技巧,“死记”之后会“活用”。
不记住那些基础知识,怎么会向高层次进军?尤其是语文学科涉猎的范围很广,要真正提高学生的写作水平,单靠分析文章的写作技巧是远远不够的,必须从基础知识抓起,每天挤一点时间让学生“死记”名篇佳句、名言警句,以及丰富的词语、新颖的材料等。
这样,就会在有限的时间、空间里给学生的脑海里注入无限的内容。
日积月累,积少成多,从而收到水滴石穿,绳锯木断的功效。
cot()=cot我国古代的读书人,从上学之日起,就日诵不辍,一般在几年内就能识记几千个汉字,熟记几百篇文章,写出的诗文也是字斟句酌,琅琅上口,成为满腹经纶的文人。
为什么在现代化教学的今天,我们念了十几年书的高中毕业生甚至大学生,竟提起作文就头疼,写不出像样的文章呢?吕叔湘先生早在1978年就尖锐地提出:“中小学语文教学效果差,中学语文毕业生语文水平低,……十几年上课总时数是9160课时,语文是2749课时,恰好是30%,十年的时间,二千七百多课时,用来学本国语文,却是大多数不过关,岂非咄咄怪事!”寻根究底,其主要原因就是腹中无物。
