(完整版)清华大学_杨虎_应用数理统计课后习题参考答案

习题一
1 设总体X 的样本容量5=n ,写出在下列4种情况下样本的联合概率分布. 1)),1(~p B X ; 2))(~λP X ; 3)],[~b a U X ; 4))1,(~μN X .
解 设总体的样本为12345,,,,X X X X X , 1)对总体~(1,)X B p ,
11223344555
11
1
55(1)
(,,,,)()(1)(1)i i
n
x x i i i i x x P X x X x X x X x X x P X x p p p p -==-========-=-∏∏
其中:5
1
15i
i x x ==∑
2)对总体~()X P λ
11223344555
1
1
555
1
(,,,,)()!
!
i
x
n
i i i i i x
i i P X x X x X x X x X x P X x e x e x λ
λ
λλ-==-==========
∏∏
∏
其中:5
1
15i
i x x ==∑
3)对总体~(,)X U a b
55
1151
1
,,1,...,5 (,,)()0i i i i a x b i f x x f x b a
==?≤≤=?==-???
∏∏
L ,其他
4)对总体~(,1) X N μ
()()
()2
55
55/2
22
1511
1
1 (,,)()=2exp 2i x i i i i i f x x f x x μπμ--
-===??==-- ???
∑∏L
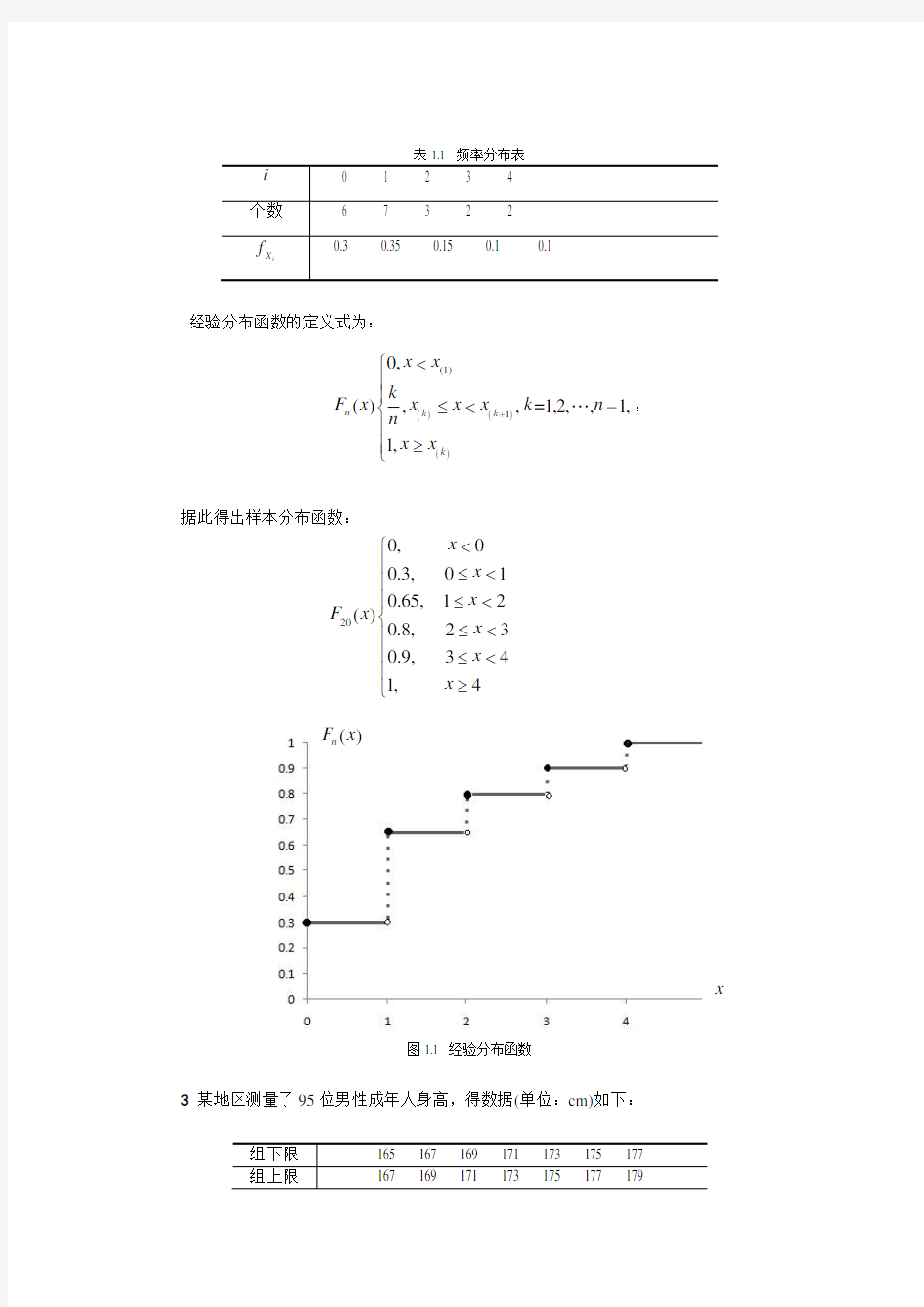
2 为了研究玻璃产品在集装箱托运过程中的损坏情况,现随机抽取20个集装箱检查其产品损坏的件数,记录结果为:1,1,1,1,2,0,0,1,3,1,0,0,2,4,0,3,1,4,0,2,写出样本频率分布、经验分布函数并画出图形.
解 设(=0,1,2,3,4)i i 代表各箱检查中抽到的产品损坏件数,由题意可统计出如下的样本频率分布表1.1:
i 0 1 2 3 4 个数
6 7 3 2 2 i
X f
0.3 0.35 0.15 0.1 0.1
经验分布函数的定义式为:
()()()
(1)10,(),,=1,2,,1,1,n k k k x x k
F x x x x k n n x x +
据此得出样本分布函数:
200,00.3,010.65,12()0.8,
230.9,341,4x x x F x x x x
?≤
≤
≥?
图1.1 经验分布函数
3 某地区测量了95位男性成年人身高,得数据(单位:cm)如下:
组下限
165 167 169 171 173 175 177 组上限
167 169 171 173 175 177 179
x
()
n F x
人 数
3 10 21 23 22 11 5
试画出身高直方图,它是否近似服从某个正态分布密度函数的图形.
解
图1.2 数据直方图
它近似服从均值为172,方差为5.64的正态分布,即(172,5.64)N .
4 设总体X 的方差为4,均值为μ,现抽取容量为100的样本,试确定常数k ,使得满足9.0)(=<-k X P μ.
解 ()
- 54100X P X k P k μμ?
-?<=
()()
555 P k X k μ=-<-<
因k 较大,由中心极限定理(0,1)4100
X N : ()
()()
-55P X k k k μ<≈Φ-Φ-
(5)(1(5))
k k =Φ--Φ
()2510.9k =Φ-=
所以:()50.95
k Φ=
查表得:5 1.65k =,0.33k ∴=.
5 从总体2
~(52,6.3)X N 中抽取容量为36的样本,求样本均值落在50.8到53.8之间的概率.
解 (
)50.853.8 1.1429 1.7143X P X P ??<<=-<
< ???
(0,1)X U N =
Q
()()
50.853.8 1.1429 1.7143(1.7143)( 1.14290.9564(10.8729)0.8293
P X P U ∴<<=-<<=Φ-Φ-=--=)
6 从总体~(20,3)X N 中分别抽取容量为10与15的两个独立的样本,求它们的均值之差的绝对值大于0.3的概率.
解 设两个独立的样本分别为:110,,X X K 与115,,Y Y K ,其对应的样本均值为:X 和Y . 由题意知:X 和Y 相互独立,且: 3~(20,)10X N ,3~(20,)15Y N
(0.3)1(0.3)P X Y P X Y ->=--≤
1P =-
~(0,0.5)~(0,1)(0.3)22(0.4243)0.6744
X Y N X Y
N P X Y -->=-Φ=Q
7 设110,,X X K 是总体~(0,4)X N 的样本,试确定C ,使得10
2
1()0.05i i P X C =>=∑.
解 因~(0,4)i X N ,则
~(0,1)2
i
X N ,且各样本相互独立,则有:
10
12
2~(10)2i i X χ=??
???∑
所以:10
102
2
1
1
(
)()144
i
i
i i C
P X C P X ==>=>
∑
∑
1021
110.0544i i c P X =??
=-≤= ???∑
1021
10.9544i i c P X =??
≤= ???∑
查卡方分位数表:c/4=18.31,则c=73.24.
8 设总体X 具有连续的分布函数()X F x ,1,,n X X K 是来自总体X 的样本,且
i EX μ=,定义随机变量:
1,
,1,2,,0,
i i i X Y i n X μμ
>==≤??
?L
试确定统计量∑=n
i i Y 1的分布.
解 由已知条件得:~(1,)i Y B p ,其中1()X p F μ=-.
因为i X 互相独立,所以i Y 也互相独立,再根据二项分布的可加性,有
1
~(,)n
i
i Y
B n p =∑,1()X p F μ=-.
9 设1,,n X X K 是来自总体X 的样本,试求2,,EX DX ES 。假设总体的分布为: 1)~(,);X B N p 2) ~();X P λ 3) ~[,];X U a b 4) ~(,1);X N μ 解 1) EX EX Np ==
(1)
DX Np p DX n n
-=
=
2(1)ES DX Np p ==-
2) EX EX λ==
DX DX n n
λ=
= 2ES DX λ==
3) 2
a b
EX EX +==
()2
12b a DX DX n n
-== ()2
2
12
b a ES DX -==
4) EX EX μ==
1DX DX n n
=
= 21ES DX ==
10 设1,,n X X K 为总体2~(,)X N μσ的样本,求
21()n i i E X X =??-????∑与21()n i i D X X =??-????
∑。 解
()2
2212
(1)(1)(1)(1)n i i E X X E n S n ES n DX n σ=??-=-=-????????
=-=-∑ ()2224
21(1)(1)n i i n S D X X D n S D σσ=??-????-=-=??????????
∑ 又因为
2
2
2
(1)~(1)n S n χσ--,所以:()24
12(1)n i i D X X n σ=??-=-????
∑
11 设1,,n X X K 来自正态总体(0,1)N ,定义:121
1
||,||n
i
i Y X Y X n
===
∑,计算12,EY EY .
解 由题意知~(0,1/)X N n
,令:Y =,则~(0,1)Y N
()E Y X
2
2
||y y e
dy +∞
-
=
?22
y ye
dy +∞
-
=?
t e dt +∞
-=
(1)=
=
1((||))E Y E X ==
21111(||(||))()n n
i i i i E Y E X E X n n E X ===??=== ???
∑∑
12 设1,,n X X K 是总体~(,4)X N μ的样本,X 为样本均值,试问样本容量n 应分别取多大,才能使以下各式成立:
1)2
||0.1E X μ-≤;2)||0.1E X μ-≤;3)(||1)0.95P X μ-≤=。 解 1)
4~(,4)
~(,)X N X N n μμ∴Q
~(0,1)X U N =
2
E X μ
-2
4X E n =
24X X D E n ??=
+????
()4
100.1n
=
+≤ 所以:40n ≥
2)
~(0,1)X U N =
()E
E U
=22
u u du +∞
-
-∞
=?
22
2u du +∞
-
==
?
所以:0.1E X μ-=
≤ 计算可得:225n ≥
3)
()
()111P X P X μμ-≤=-≤-≤
P ?=≤≤ ??
22??=Φ-Φ- ????
210.95=Φ-≥??
0.975 1.96,15.36u n ≥=≥ ,而n 取整数,16n ∴≥. 13 设1(,,)n X X K 和1(,,)n Y Y K 是两个样本,且有关系式:1()i i Y X a b
=-(,a b 均为常
数,0b ≠),试求两样本均值X 和Y 之间的关系,两样本方差2
X S 和2
Y S 之间的关系.
解 因:()111
n i i Y X a n b
==-∑
111n i i X na b n =??
=- ???
∑ ()1
X a b
=
- 所以:()1
EY EX a b
=
- 即:
()
()()()2
2
21
12
221111111111=
1n
n Y
i i i i n
i X i S Y Y X a X a n n b b X X S n b b
===??=-=---??--??
??-=??-??∑∑∑
14 设15,,X X K 是总体~(0,1)X N 的样本.
1) 试确定常数11,c d ,使得2221121345()()~()c X X d X X X n χ++++,并求出n ; 2) 试确定常数2c ,使得222212345()/()~(,)c X X X X X F m n +++,并求出m 和n . 解 1)因:12~(0,2)X X N +,345~(0,3)X X X N ++
~(0,1)N
~(0,1)N 且两式相互独立
故:2
2
2
~(2)χ+ 可得:112c =
,11
3
d =,2n =. 2) 因:222
1
2
~(2)X X χ+,
()2
3452~(1)3
X X X χ++,
所以:
()()
221
22
3452
~(2,1)3
X
X F X X X +++,
可得:23
,2,12
c m n =
==. 15 设(),(,)p p t n F m n 分别是t 分布和F 分布的p 分位数,求证
21/21[()](1,)p p t n F n --=.
证明 设1(1,)p F n α-=
,
则:()1(1P F p P p α≤=-?≤
≤
=-
((12(2(12
P T P T p P T p p P T ?≤-≤=-?≤=-?≤=
-
12
()p t
n -
=
故:2
112
()(1,)p p t
n F n α--==.
16 设21,X X 是来自总体)1,0(~N X 的一个样本,求常数c ,使:
1.0)()()(2212212
21=???
? ??>-+++c X X X X X X P .
解 易知12~(0,2)X X N
+~(0,1)N ; 同理12~(0,2)X X N
-~(0,1)N 又因:1212(,)0Cov X X X X +-=,所以12X X +与12X X -相互独立.
221212222
121212()(1)()()()()X X c X X P c P c X X X X X X ????+-+>=> ? ?++--????
2122
12()()1X X c P X X c ??+=> ?--??
20.11c P c ???=>=- ? ???
所以:
0.9(1,1=39.91c
F c
=-) 计算得:c = 0.976.
17 设121,,,,n n X X X X +K 为总体2~(,)X N μσ的容量1n +的样本,2
,X S 为样本
1(,,)n X X K 的样本均值和样本方差,求证:
1
)~(1)T t n -;
2)211~(0,)n n X X N n
σ++-;
3)2
11~(0,
)n X X N n
σ--.
解 1)因:1()0n E X X +-=,2
11()n n D X X n
σ++-=
所以:2
11~(0,
)n n X
X N n σ++-
~(0,1)X N 又:222
1
~(1)n S n χσ
--
X 221
n S σ-相互独立
=(1)t n -
2) 由1)可得:2
11~(0,
)n n X X
N n
σ++- 3) 因:1()0E X X -=,2
11()n D X X n
σ--= 所以:2
11~(0,
)n X X N n
σ-- 18 设1,,n X X K 为总体2~(,)X N μσ的样本,X 为样本均值,求n ,使得
(||0.25)0.95P X μσ-≤≥.
解
(
)
~(0,1)
0.25X U N X P X P μσ=
?∴-≤=-≤ ?Q
(210.95=Φ-≥
所以:(0.975Φ≥
查表可得:0.975 1.96u =,即62n ≥. 19 设1,,n X X K 为总体~[,]X U a b 的样本,试求: 1)(1)X 的密度函数; 2)()n X 的密度函数; 解 因:~[,]X U a b , 所以X 的密度函数为:
1
,[,]()0,[,]
x a b f x b a
x a b ?∈?
=-????, 0,(),1,x a x a F x a x b b a x b ≤?
?-?=<≤?-?
>??
由定理:1
(1)()(1())
()n f x n F x f x -=-
11
(
),[,]0,[,]n b x n x a b b a b a
x a b --?∈?=--????
1
()()(())
()n n f x n F x f x -=
11
(
),[,]0,[,]n x a n x a b b a b a
x a b --?∈?=--????
20 设15,,X X K 为总体~(12,4)X N 的样本,试求: 1)(1)(10)P X <; 2)(5)(15)P X < 解
~(12,4)12
~(0,1)2
i X N X N -∴
Q
()()(1)(1)10110P X P X <=-≥
()5
1
110i
i P X
==-
≥∏
()()5
1
1110i i P X ==--≤∏
5
1121112i i X P =?-?
??=--≤- ? ????
?∏
51(1(1))=--Φ- 51(1)0.5785=-Φ=
()()5
(5)11515i i P X P X =<=<∏
5
1
12 1.52i i X P =-??
=< ???∏
55(1.5)0.93320.7077=Φ==
21 设11(,,,,,)m m m n X X X X ++K K 为总体2~(0,)X N σ的一个样本,试确定下列统计量的分布:
1
)1m
i
X Y =
; 2)2
122
1
m
i
i m n
i
i m n X Y m X =+=+=
∑∑;3)2
12
212311??
? ??+???
??=∑∑++==n m m i i m i i X n X m Y σσ 解 1)因为:
21
~(0,)m
i
i X
N m σ=∑
~(0,1)m
i X
N ∑,
2
22
1
~()
m n
i i m X n χσ
+=+∑
m
i X
∑与
2
2
1
m n
i i m X σ
+=+∑相互独立,由抽样定理可得:
1~()m
i
m
i
X
X Y t n =
∑ 2)因为:
22
2
1
1
~()m
i
i X
m χσ
=∑,
222
1
1
~()
m n i i m X n χσ
+=+∑
且
22
1
1
m
i
i X
σ=∑与
221
1
m n
i i m X σ+=+∑
相互独立,
所以:
222
112
22
1
1
1=
~(,)1
m
m
i
i
i i m n
m n i i i m i m n X
X
m
F m n m X X n
σ
σ
==++=+=+∑∑∑∑
3)因为:
2
1
~(0,)m
i
i X
N m σ=∑,
21
~(0,)m n i i m X N n σ+=+∑
所以:
2
21
2
()
~(1)m
i i X m χσ
=∑,
2
212
()~(1)
m n
i i m X n χσ
+=+∑
且
2
1
2
()
m
i i X m σ
=∑与
2
1
2
()m n
i i m X n σ
+=+∑相互独立,
由卡方分布可加性得:2
2
2
22111~(2)m m n i i i i m n X X m n χσσ+==+????+ ? ?????
∑∑. 22 设总体X 服从正态分布),(2
σμN ,样本n X X X ,,,21Λ来自总体X ,2S 是样本
方差,问样本容量n 取多大能满足95.067.32)1(22=???
?
??≤-σS n P ?
解 由抽样分布定理:
222
1
~(1)n S n χσ
--,22
1
(
32.67)0.95n P S σ
-≤=,
查表可得:n 121-=,n 22=.
23 从两个正态总体中分别抽取容量为20和15的两独立的样本,设总体方差相等,
22
21
,S S 分别为两样本方差,求???
?
??>39.22221S S P .
解 设12=20=15n n ,分别为两样本的容量,2σ为总体方差,由题意,
222222
1112222222
(1)19(1)14=~(19)=~(14)n S S n S S χχσσσσ
--, 又因22
2
1,S S 分别为两独立的样本方差:2
12
2
12
22
2
2
1919=~(19,14)1414
S S F S S σσ
所以:221122222.391 2.3910.950.05S S P P S S ????
>=-≤=-= ? ?????
.
24 设总体),(~2
σμN X ,抽取容量为20的样本2021,,,X X X Λ,求概率
1)????
??
??≤-≤
∑=57.37)(85.102
20
1
2
σμi i X P ;
2)????
?
?
?
?≤-≤
∑=58.38)(65.112
20
1
2
σi i X X P .
解 1)因
~(0,1)i X N μ
σ
-,且各样本间相互独立,所以:
()
20
2
2
20
221
2
1~(20)i
i i i X X μμχχσσ==--??== ???
∑∑ 故:()210.8537.570.990.050.94P χ≤≤=-=
2)因:
()
20
2
2
21
2
2
19~(19)i
i X
X S χσ
σ
=-=
∑, 所以:
221911.6538.580.9950.10.895.S P σ??
≤≤=-= ???
25 设总体),80(~2
σN X ,从中抽取一容量为25的样本,试在下列两种情况下
)380(>-X P 的值:
1) 已知20=σ;
2) σ未知,但已知样本标准差2674.7=S . 解 1)
()
22
~(80,)80
~(80,
)~(0,1),~(24)255
80380320/54X N X X X N N t S X P X P σσ-∴??
- ?
->=> ???
Q 314P U ?
?=-≤ ???12(0.75)1=-Φ+
220.77340.4532=-?=
2)()
80803 2.0647.2674/5X P X P ??
- ?->=> ???
()1 2.064120.97510.05P T =-≤=-?+=
26 1,,n X X K 设为总体2~(,)X N μσ的样本,2,X S 为样本均值和样本方差,当20n =时,求:
1)();4.472
P X σμ<+
2)2
22(||);2
P S σ
σ-<
3)确定C ,使()0.90S P C X μ
>=-.
解 1)
2~(,)
~(0,)1 4.4724.472X N N X X P X P μσμμσσ??-?
?<+=< ? ?
????
Q
10.8413X P ??
=<=???
2)2222222
22
2P S P S σσσσσ????-<=-<-< ? ?????
222
322P S σσ??=<< ???
221322S P σ
??
=<< ???
2
2199.528.5S P σ??=<< ?
??
其中2
2
22
19=
~(19)S χχσ,则
()2222
22199.528.529.528.50.950.050.9
S P S P P σσσχ????-<=<< ? ?
????=<<=-= 3)
1
<
S X X
P c P P
X S c
μ
μ
?
??
??-
>==
?
?
-
?????
其中,(19)
X
T t,则
0.9
S
P c P T
Xμ
?
??
>==
?
-
????
所以:
0.9
(19)=1.328
t=,计算得: 3.3676
c=.
27 设总体X的均值μ与方差2σ存在,若n X
X
X,
,
,
2
1
Λ为它的一个样本,X是样本均值,试证明对j
i≠,相关系数
1
1
)
,
(
-
-
=
-
-
n
X
X
X
X
r
j
i
.
证明
cov(,)
(,)
i j
X X X X
r X X X X
--
--=
2
1
()()
i j
n
D X X D X X
n
σ
-
-=-=
2
1
ov(,)()
i j i j i j
C X X X X E X X X X X X X X
n
σ
--=---=-
所以:
1
(,)
1
i j
r X X X X
n
--=-
-
.
28.设总体2
~(,)
X Nμσ,从该总体中抽取简单随机样本)1
(
,
,
,
2
2
1
≥
n
X
X
X
n
Λ,X
是它的样本均值,求统计量∑
=
+
-
+
=
n
i
i
n
i
X
X
X
T
1
2
)
2
(的数学期望.
解因2
~(,)
X Nμσ,)1
(
,
,
,
2
2
1
≥
n
X
X
X
n
Λ为该总体的简单随机样本,令
i i n i
Y X X
+
=+,则有2
~(2,2)
i
Y Nμσ
可得:
1
1
2
n
i
i
Y Y X
n=
==
∑
()2
22
11
(2)(1)
n n
i n i i Y
i i
T X X X Y Y n S
+
==
=+-=-=-
∑∑
22
(1)2(1)
Y
ET n ES nσ
=-=-
习题二
1 设总体的分布密度为:
(1),01
(;)0,
x x f x ααα+<<=???其它
1(,,)n X X L 为其样本,求参数α的矩估计量1?α和极大似然估计量2?α .现测得样本观测值
为:0.1,0.2,0.9,0.8,0.7,0.7,求参数α的估计值 .
解 计算其最大似然估计:
()()
11
1
11
(,)11ln (,)ln(1)ln n
n
n
n i i i i n
n i
i L x x x x L x x n x α
α
αααααα===??=+=+??=++∏∏∑K K
11
21
ln (,)ln 01?10.2112
ln n n i i n i
i d n L x x x d n x ααααα====+=+=--=∑∑K
其矩估计为:
()1 3.40.10.20.90.80.70.766
X =
+++++= 3077
.01
21?,212)
1()1(11
01
21=--==++=++=+=?++X X
X x dx x EX αααααααα
所以:12112??,11ln n
i
i X n X X αα=??
?- ?==-+-
? ??
?
∑, 12??0.3077,0.2112αα≈≈.
2 设总体X 服从区间[0, θ]上的均匀分布,即~[0,]X U θ,1(,,)n X X L 为其样本,
1)求参数θ的矩估计量1?θ和极大似然估计量2
?θ; 2)现测得一组样本观测值:1.3,0.6,1.7,2.2,0.3,1.1,试分别用矩法和极大似然法求总体均值、总体方差的估计值. 解 1)矩估计量:
11
??,2 2.42
EX X X θθ=
=== 最大似然估计量:
11
11
1
(,)ln (,)0
n
n n
i n L x x n
L x x θθ
θθθ
===
=-
=∏
K K
无解 .此时,依定义可得:2
1?max i i n
X θ≤≤=
2)矩法:21
1
??1.2,0.472212EX DX θθ=
==
=
极大似然估计:22
2??1.1,0.4033212EX DX θ
θ====.
3 设1,...,n X X 是来自总体X 的样本,试分别求总体未知参数的矩估计量与极大似然估计量 .已知总体X 的分布密度为:
1),0(;),
00,
x
e
x f x x λλλλ->=>≤??
?未知
2)(;),
0,1,2,,0!
x
f x e x x λ
λ
λλ-=
=>L 未知
3)1,
(;,)0
a x
b f x a b a b b a
≤≤=<-??
???,
其它
未知
4) 2
,0(;)0
x
x f x θθθ-<≤<+∞=??
?,
其它
θ未知
5)()/1,(;,),
00,x e x f x x αβ
ααβββα
--≥=>
6)1
,0(;,),
,00,
x
x f x x αααβαβαββα
-≤≤=>
7
)2
2
2,0
(;),
00,0
x x f x x θ
θθ-
>=>≤??
未知
8)
2
2
(;)(1)(1)
,2,3,,01x f x x x θθθθ
-=--=< 解 1) 矩法估计:1 1 1?,EX X X λλ= == 最大似然估计: 1 111 1 (,),ln (,)ln n i i i n n x x n n n i i i L x x e e L x x n x λ λλλλλλλ=--==∑===-∑∏K K 2 1 1 1 ?ln 0,n i n i i i d n n L x d X x λλλ===-=== ∑∑. 2) ~()X P λ 矩估计: 1 ?,EX X X λλ=== 最大似然估计: 11 (,),ln ln i x nx n n n i i i i L x x e e L n nx x x x λλ λλλλλ--====-+-∑∏ ∏K 2 ?ln 0,d nx L n X d λλλ =-+==. 3) 矩估计:()2 ,212 b a a b EX DX -+== 联立方程: ( )2 *221?2 ?a X b X a b X b a M ?=- ?→+?=???-?=???=+?? 最大似然估计: 11 1 (,)(;)() n n i n i L x x f x b a θθ== = -∏ K ,ln ln()L n b a =-- ln 0d L n da b a ==-,无解,当1?min i i n a X ≤≤=时,使得似然函数最大, 依照定义,1?min i i n a X ≤≤=,同理可得1?max i i n a X ≤≤=. 4) 矩估计: ln EX dx x x θ θ+∞ +∞= =? ,不存在 最大似然估计: 122111 (,),ln ln 2ln n n n n i i i i i L x x L n x x x θ θθθ=====-∑∏∏K ln 0n L αθ ?==?,无解;依照定义,(1) ?X θ=. 5) 矩估计: ()/0 ()(1)(2)x t x EX e dx t e dt αβα αβαββ +∞ +∞ ---= = +=Γ+Γ?? X α β=+= 2222 ()(1)2(2)(3)t EX t e dt αβααββ+∞ -= +=Γ+Γ+Γ? 2222221 22()i M X n ααββαββ=++=++== ∑ 2 2222*2111 ??i M X X X M n X βα β=-= -==-=∑ 即11??X X αβ==== 最大似然估计: ()()/111 1(,,)exp , 1ln ln i n x n n i L x x e nx n n L n nx αβαββαββα βββ ---=??==--???? =--+ ∏K 2ln 0,ln ()0n n n L L x ααββββ ??===-+-=??,无解 依定义有:(1)(1) ??,L L X X X X α βα==-=-. 第三章 假设检验 课后作业参考答案 某电器元件平均电阻值一直保持Ω,今测得采用新工艺生产36个元件的平均电阻值为Ω。假设在正常条件下,电阻值服从正态分布,而且新工艺不改变电阻值的标准偏差。已知改变工艺前的标准差为Ω,问新工艺对产品的电阻值是否有显著影响(01.0=α) 解:(1)提出假设64.2:64.2:10≠=μμH H , (2)构造统计量36 /06.064 .261.2/u 00 -=-= -= n X σμ (3)否定域???? ??>=???? ??>?? ??? ??<=--21212 αααu u u u u u V (4)给定显著性水平01.0=α时,临界值575.2575.22 12 =-=- α αu u , (5) 2 αu u <,落入否定域,故拒绝原假设,认为新工艺对电阻值有显著性影响。 一种元件,要求其使用寿命不低于1000(小时),现在从一批这种元件中随机抽取25件,测 得其寿命平均值为950(小时)。已知这种元件寿命服从标准差100σ=(小时)的正态分布, 试在显著水平下确定这批元件是否合格。 解: {}01001:1000, H :1000 X 950 100 n=25 10002.5 V=u 0.05H x u αμμσμα-≥<====->=提出假设:构造统计量:此问题情形属于u 检验,故用统计量:此题中:代入上式得: 拒绝域: 本题中:0.950.950 u 1.64u 0.0u H =>∴即,拒绝原假设认为在置信水平5下这批元件不合格。 某厂生产的某种钢索的断裂强度服从正态分布( )2 ,σ μN ,其中()2 /40cm kg =σ。现从一 批这种钢索的容量为9的一个子样测得断裂强度平均值为X ,与以往正常生产时的μ相比, X 较μ大20(2/cm kg )。设总体方差不变,问在01.0=α下能否认为这批钢索质量显著提 高 解: (1)提出假设0100::μμμμ>=H H , (2)构造统计量5.13 /4020 /u 00 == -= n X σμ (3)否定域{}α->=1u u V (4)给定显著性水平01.0=α时,临界值33.21=-αu (5) α-<1u u ,在否定域之外,故接受原假设,认为这批钢索质量没有显著提高。 某批矿砂的五个样品中镍含量经测定为(%): 设测定值服从正态分布,问在0.01α=下能否接受假设,这批矿砂的镍含量为 习题五 1 试检验不同日期生产的钢锭的平均重量有无显著差异?(=0.05) 解 根据问题,因素A 表示日期,试验指标为钢锭重量,水平为5. 假设样本观测值(1,2,3,4)ij y j =来源于正态总体2 ~(,),1,2,...,5i i Y N i μσ= . 检验的问题:01251:,:i H H μμμμ===不全相等 . 计算结果: 表5.1 单因素方差分析表 ‘*’ . 查表0.95(4,15) 3.06F =,因为0.953.9496(4,15)F F =>,或p = 0.02199<0.05, 所以拒绝0H ,认为不同日期生产的钢锭的平均重量有显著差异. 2 考察四种不同催化剂对某一化工产品的得率的影响,在四种不同催化剂下分别做试验 试检验在四种不同催化剂下平均得率有无显著差异?(=0.05) 解 根据问题,设因素A 表示催化剂,试验指标为化工产品的得率,水平为4 . 假设样本观测值(1,2,...,)ij i y j n =来源于正态总体2 ~(,),1,2,...,5i i Y N i μσ= .其中 样本容量不等,i n 分别取值为6,5,3,4 . 检验的问题:012341:,:i H H μμμμμ===不全相等 . 计算结果: 表5.2 单因素方差分析表 查表0.95(3,14) 3.34F =,因为0.952.4264(3,14)F F =<,或p = 0.1089 > 0.05, 所以接受0H ,认为在四种不同催化剂下平均得率无显著差异 . 3 试验某种钢的冲击值(kg ×m/cm2),影响该指标的因素有两个,一是含铜量A , 试检验含铜量和试验温度是否会对钢的冲击值产生显著差异?(=0.05) 解 根据问题,这是一个双因素无重复试验的问题,不考虑交互作用. 设因素,A B 分别表示为含铜量和温度,试验指标为钢的冲击力,水平为12. 假设样本观测值(1,2,3,1,2,3,4)ij y i j ==来源于正态总体2 ~(,),1,2,3,ij ij Y N i μσ= 1,2,3,4j = .记i α?为对应于i A 的主效应;记j β?为对应于j B 的主效应; 检验的问题:(1)10:i H α?全部等于零,11 :i H α?不全等于零; (2)20:j H β?全部等于零,21:j H β?不全等于零; 计算结果: 表5.3 双因素无重复试验的方差分析表 查表0.95(2,6) 5.143F =,0.95(3,6) 4.757F =,显然计算值,A B F F 分别大于查表值, 或p = 0.0005,0.0009 均显著小于0.05,所以拒绝1020,H H ,认为含铜量和试验温度都会对钢的冲击值产生显著影响作用. 4 下面记录了三位操作工分别在四台不同的机器上操作三天的日产量: 北航2010《应用数理统计》考试题及参考解答 09B 一、填空题(每小题3分,共15分) 1,设总体X 服从正态分布(0,4)N ,而12 15(,,)X X X 是来自X 的样本,则22 110 22 11152() X X U X X ++=++服从的分布是_______ . 解:(10,5)F . 2,?n θ是总体未知参数θ的相合估计量的一个充分条件是_______ . 解:??lim (), lim Var()0n n n n E θθθ→∞ →∞ ==. 3,分布拟合检验方法有_______ 与____ ___. 解:2 χ检验、柯尔莫哥洛夫检验. 4,方差分析的目的是_______ . 解:推断各因素对试验结果影响是否显著. 5,多元线性回归模型=+Y βX ε中,β的最小二乘估计?β 的协方差矩阵?βCov()=_______ . 解:1?σ-'2Cov(β) =()X X . 二、单项选择题(每小题3分,共15分) 1,设总体~(1,9)X N ,129(,, ,)X X X 是X 的样本,则___B___ . (A ) 1~(0,1)3X N -; (B )1 ~(0,1)1X N -; (C ) 1 ~(0,1) 9X N -; (D ~(0,1)N . 2,若总体2(,)X N μσ,其中2σ已知,当样本容量n 保持不变时,如果置信度1α-减小,则μ的 置信区间____B___ . (A )长度变大; (B )长度变小; (C )长度不变; (D )前述都有可能. 3,在假设检验中,就检验结果而言,以下说法正确的是____B___ . (A )拒绝和接受原假设的理由都是充分的; (B )拒绝原假设的理由是充分的,接受原假设的理由是不充分的; (C )拒绝原假设的理由是不充分的,接受原假设的理由是充分的; (D )拒绝和接受原假设的理由都是不充分的. 4,对于单因素试验方差分析的数学模型,设T S 为总离差平方和,e S 为误差平方和,A S 为效应平方和,则总有___A___ . 习题1 1.1 解:由题意95.01=? ?? ???<--u x p 可得: 95.0=??? ???????????<-σσn n u x p 而 ()1,0~N u x n σ ??? ??-- 这可通过查N(0,1)分布表,975.0)95.01(2195.0=-+=??? ? ??????????<--σσn n u x p 那么 96.1=σ n ∴2296.1σ=n 1.2 解:(1)至800小时,没有一个元件失效,则说明所有元件的寿命>800小时。 {}2.10015.0800 0015.00800 | e 0015.0800--∞ +-=∞ +-==>?e e dx x p x x 那么有6个元件,则所求的概率() 2.76 2 .1--==e e p (2)至300小时,所有元件失效,则说明所有元件的寿命<3000小时 {}5.430000 0015.03000 0015.001|e 0015.03000----=-== 因为~()i X P λ,所以 112233{,,}P X x X x X x ≤≤≤ 112233{}{}{}P X x P X x P X x =≤≤≤1233123!!! x x x e x x x ++-λ λ= 其中,0,1,2, ,1,2,3k x k == (2) 123{(,,)|0;1,2,3}k x x x x k χ=≥= 因为~()i X Exp λ,其概率密度为,0 ()0,0 x e x f x x -λ?λ≥=? ? 所以,1233 1 (,,)() f x x x b a = -,其中;1,2,3k a x b k ≤≤= (4) 123{(,,)|;1,2,3}k x x x x k χ=-∞<<+∞= 因为~(,1)i X N μ, 其概率密度为(2(),()x f x x 2 -μ) -=-∞<<+∞ 所以,3 1 1 (212332 1 (,,)(2)k k x f x x x e π2=- -μ)∑=,其中;1,2,3k x k -∞<<+∞= 解:由题意可得:()?? ???∞ <<=--,其它00,21)(i 2ln i i 2 2 i x e x x f u x σσπ 则∏ == n i x f x x f 1 i n i )(),...(=??? ????=∞<<∏=∑--=,其它0,...1,0,1 n )2()(ln 212n 1 2 i 2 i x x e i n i i u x n i σπσ 习题三 1 正常情况下,某炼铁炉的铁水含碳量2 (4.55,0.108)X N :.现在测试了5炉铁水,其含碳量分别为4.28,4.40,4.42,4.35,4.37. 如果方差没有改变,问总体的均值有无显著变化?如果总体均值没有改变,问总体方差是否有显著变化(0.05α=)? 解 由题意知 2~(4.55,0.108),5,0.05X N n α==,1/20.975 1.96u u α-==,设立统计原假设 0010:,:H H μμμμ=≠ 拒绝域为 {}00K x c μ=->,临界值 1/2 1.960.108/0.0947c u α-==?=, 由于 0 4.364 4.550.186x c μ-=-=>,所以拒绝0H ,总体的均值有显著性变化. 设立统计原假设 2222 0010:,:H H σσσσ=≠ 由于0μμ=,所以当0.05α=时 22220.0250.9751 1()0.03694,(5)0.83,(5)12.83,n i i S X n μχχ==-===∑% 2210.02520.975(5)/50.166,(5)/5 2.567c c χχ==== 拒绝域为 {} 222200201//K s c s c σσ=><%%或 由于22 0/ 3.167 2.567S σ=>%,所以拒绝0H ,总体的方差有显著性变化. 2 一种电子元件,要求其寿命不得低于1000h .现抽测25件,得其均值为x =950h .已知该种元件寿命2(100,)X N σ:,问这批元件是否合格(0.05α=)? 解 由题意知 2(100,)X N σ:,设立统计原假设 0010:,:,100.0.05.H H μμμμσα≥<== 拒绝域为 {}00K x c μ=-> 临界值为 0.050.0532.9c u u =?=?=- 由于 050x c μ-=-<,所以拒绝0H ,元件不合格. 3 某食品厂用自动装罐机装罐头食品,每罐标准重量为500g ,现从某天生产的罐头中随机抽测9罐,其重量分别为510,505,498,503,492,502,497,506,495(g ),假定罐头重量服从正态分布. 问 (1)机器工作是否正常(0.05α=)? 2)能 习题五 1 某钢厂检查一月上旬内的五天中生产的钢锭重量,结果如下:(单位:k g) 日期重旦量 1 5500 5800 5740 5710 2 5440 5680 5240 5600 4 5400 5410 5430 5400 9 5640 5700 5660 5700 10 5610 5700 5610 5400 试检验不同日期生产的钢锭的平均重量有无显著差异? ( =0.05) 解根据问题,因素A表示日期,试验指标为钢锭重量,水平为 5. 2 假设样本观测值y j(j 123,4)来源于正态总体Y~N(i, ),i 1,2,...,5 检验的问题:H。:i 2 L 5, H i : i不全相等. 计算结果: 注释当=0.001表示非常显著,标记为*** '类似地,=0.01,0.05,分别标记为 查表F0.95(4,15) 3.06,因为F 3.9496 F0.95(4,15),或p = 0.02199<0.05 ,所 以拒绝H。,认为不同日期生产的钢锭的平均重量有显著差异 2 考察四种不同催化剂对某一化工产品的得率的影响,在四种不同催化剂下分别做试验 解 根据问题,设因素A表示催化剂,试验指标为化工产品的得率,水平为 4 . 2 假设样本观测值y j(j 1,2,..., nJ来源于正态总体Y~N(i, ), i 1,2,...,5 .其中样本容量不等,n分别取值为6,5,3,4 . 日产量 操作工 查表 F O .95(3,14) 3.34,因为 F 2.4264 F °.95(3,14),或 p = 0.1089 > 0.05, 所以接受H 。,认为在四种不同催化剂下平均得率无显著差异 3 试验某种钢的冲击值(kg Xm/cm2 ),影响该指标的因素有两个,一是含铜量 A ,另 一个是温度 试检验含铜量和试验温度是否会对钢的冲击值产生显著差异? ( =0.05 ) 解 根据问题,这是一个双因素无重复试验的问题,不考虑交互作用 设因素A,B 分别表示为含铜量和温度,试验指标为钢的冲击力,水平为 12. 2 假设样本观测值y j (i 1,2,3, j 1,2,3,4)来源于正态总体 Y j ~N (j , ),i 1,2,3, j 1,2,3,4 .记i 为对应于A 的主效应;记 j 为对应于B j 的主效应; 检验的问题:(1) H i 。: i 全部等于零,H i — i 不全等于零; (2) H 20 : j 全部等于零,H 21: j 不全等于零; 计算结果: 查表F 0.95(2,6) 5.143 ,局.95(3,6) 4.757 ,显然计算值F A , F B 分别大于查表值, 或p = 0.0005 , 0.0009均显著小于0.05,所以拒绝H i°,H 20,认为含铜量和试验温度 都会对钢的冲击值产生显著影响作用 . 4 下面记录了三位操作工分别在四台不同的机器上操作三天的日产量: 检验的问题:H 0: 1 计算结果: H i : i 不全相等 应用数理统计答案 学号: 姓名: 班级: 目录 第一章数理统计的基本概念 (2) 第二章参数估计 (14) 第三章假设检验 (24) 第四章方差分析与正交试验设计 (29) 第五章回归分析 (32) 第六章统计决策与贝叶斯推断 (35) 对应书目:《应用数理统计》施雨著西安交通大学出版社 第一章 数理统计的基本概念 1.1 解:∵ 2 (,)X N μσ ∴ 2 (,)n X N σμ ∴ (0,1)N 分布 ∴(1)0.95P X P μ-<=<= 又∵ 查表可得0.025 1.96u = ∴ 2 2 1.96n σ= 1.2 解:(1) ∵ (0.0015)X Exp ∴ 每个元件至800个小时没有失效的概率为: 800 0.00150 1.2 (800)1(800) 10.0015x P X P X e dx e -->==-<=-=? ∴ 6个元件都没失效的概率为: 1.267.2 ()P e e --== (2) ∵ (0.0015)X Exp ∴ 每个元件至3000个小时失效的概率为: 3000 0.00150 4.5 (3000)0.00151x P X e dx e --<===-? ∴ 6个元件没失效的概率为: 4.56 (1)P e -=- 1.4 解: i n i n x n x e x x x P n i i 1 2 2 )(ln 2121)2(),.....,(1 22 =-- ∏∑ = =πσμσ 1.5证: 2 1 1 2 2)(na a x n x a x n i n i i i +-=-∑∑== ∑∑∑===-+-=+-+-=n i i n i i n i i a x n x x na a x n x x x x 1 2 2 2 2 11) ()(222 a) 证: ) (1111 1+=+++=∑n n i i n x x n x ) (1 1 )(1 1 11n n n n n x x n x x x n n -++=++=++ 第 三 章 作 业 参 考 答 案 2、解:计算矩估计:2 1)1(1 ++= +?= ? αααα dx x x EX , 令 X EX =++= 2 1αα ,解得 1 2-1?1-=X X α ; 计算极大似然估计:α α αα α)()1()1()()(1 1 1 ∏∏∏ ===+=+= = n i i n n i i n i i x x x f L )ln()1ln()(ln 1 ∏=++=?n i i x n L ααα0 )ln(1 )(ln 1 =++= ??? ∏=n i i x n L αα α 解得 ) ) ln(1(?1 2∏=+-=n i i x n α ; 将样本观测值代入,得到估计值分别为0.3077?1=α ,0.2112?2=α。 6、 解:(1)由例3.2.3可知,μ的极大似然估计分别为 X =μ ?, 05.0)(1)(=-Φ-=>μA A X P )645.1(95.0)(Φ==-Φ?μA 645 .1+=?μA ,由46页上极大似然估计的不变性可知645.1??+=μA ; (2)由例3.2.3可知,2 σμ,的极大似然估计分别为 ∑=-= =n i i X X n X 1 2 2 ) (1 ??σ μ,, 05.0)( 1)(=-Φ-=>σ μ A A X P )645.1(95.0)( Φ==-Φ?σ μ A σ μ645.1+=?A ,由46页上极大似然估计的不变性可知σμ?645.1??+=A 。 8、解:计算2 2 2 2222)()()(σσ μC n S CE X E CS X E -+ =-=-,由题意则有 2 2 2 2 μσ σ μ=-+ C n ,解得n C 1= 。 4-45. 自动车床加工中轴,从成品中抽取11根,并测得它们的直径(mm )如下: 10.52,10.41,10.32,10.18,10.64,10.77,10.82,10.67,10.59,10.38,10.49 试用W 检验法检验这批零件的直径是否服从正态分布?(显著性水平05.0=α) (参考数据:) 4-45. 解:数据的顺序统计量为: 10.18,10.32,10.38,10.41,10.49,10.52,10.59,10.64,10.67,10.77,10.82 所以 6131 .0][)()1(5 1 ) (=-= -+=∑k k n k k x x a L , 又 5264.10=x , 得 38197 .0)(11 1 2 =-∑=i i x x 故 984.0) (11 1 2 2 =-= ∑=i i x x L W , 又 当n = 11 时,85.005.0=W 即有 105.0< 研究生 习题2: 2-7. 设 )1,0(~N ξ,),,,,,(654321ξξξξξξ为其一样本,而26542321)()(ξξξξξξη+++++=, 试求常数c ,使得随机变量ηc 服从2 χ分布。 2-7解:设3211ξξξη++=,所以 )3,0(~1N η 6542ξξξη++=,所以 )3,0(~2N η 所以 )1,0(~3 1 N η , )1,0(~3 2 N η )2(~)(3 1332 22212 22 1χηηηη+=??? ??+??? ?? 由于 2 22 1ηηη+= 因此 当 3 1=c 时,)2(~2 χηc 。 2-8. 设 ),,,(1021ξξξΛ为)3.0,0(2 N 的一个样本,求 ? ?? ???>∑=101244.1i i P ξ 。(参考数据:) 2-8解:因为 )3.0,0(~),,,(2 1021N ξξξξΛ=, 所以 )1,0(~3 .0N ξ , 即有)10(~3.0210 12 χξ∑=?? ? ??i i 所以 ??? ???>∑=101244.1i i P ξ??????>=∑=1012223.044.13.0i i P ξ??????>=∑=10122163.0i i P ξ ? ?? ???≤-=∑=10122163.01i i P ξ1.09.01=-= 2-14. 设总体)4,1(~N ξ,求{}20≤≤ξP 与{} 20≤≤ξP ,其中ξ是样本容量为16的样 本均值。(参考数据:) 2-14解: {}20≤≤ξP )0()2(F F -=)210()212( -Φ--Φ=)2 1 ()21(-Φ-Φ= 1)2 1 (2-Φ=3830.016915.02=-?= 由于 )4,1(~N ξ , 所以 )1,0(~21 1 16 21N -=-ξξ {} 20≤≤ξP ????? ?-≤-≤-=21122112110ξP ? ?? ???≤-≤-=22112ξP )2()2(-Φ-Φ=9545.019725.021)2(2=-?=-Φ= 2-17. 在总体)20,80(2 N 中随机抽取一容量为100的样本,问样本平均值与总体均值的差的 绝对值大于3的概率是多少?(参考数据:) 2-17解:因为 )20,80(~2 N ξ, 所以 )1,0(~2 80 100 20 80 N -= -ξξ 所以 {}380>-ξP {} 3801≤--=ξP ?? ? ?????? ?≤--=232801ξP ? ?? ???≤ -≤--=23280 231ξP )]5.1()5.1([1-Φ-Φ-= ]1)5.1(2[1-Φ-=1336.0)93319.01(2)5.1(22=-=Φ-= 2-25. 设总体ξ的密度函数为 ?? ?<<=其它 102)(x x x p 取出容量为4的样本),,,(4321ξξξξ,求: (1) 顺序统计量)3(ξ的密度函数)(3x p ;(2))3(ξ的分布函数)(3x F ;(3)??? ? ??>21)3(ξP 。 2-25解:(1)由 ()()[][])()(1)(! !1! )(1)(x p x F x F k n k n x p k n k k -----= ξ 所以 当 10< 2009(上)《数理统计》考试题(A 卷)及参考解答 一、填空题(每小题3分,共15分) 1,设总体X 和Y 相互独立,且都服从正态分布2(0,3)N ,而129(,,)X X X 和129(,,)Y Y Y 是分别来自X 和Y 的样本,则U = 服从的分布是_______ . 解:(9)t . 2,设1?θ与2?θ都是总体未知参数θ的估计,且1?θ比2?θ有效,则1?θ与2 ?θ的期望与方差满足_______ . 解:1212 ????()(), ()()E E D D θθθθ=<. 3,“两个总体相等性检验”的方法有_______ 与____ ___. 解:秩和检验、游程总数检验. 4,单因素试验方差分析的数学模型含有的三个基本假定是_______ . 解:正态性、方差齐性、独立性. 5,多元线性回归模型=+Y βX ε中,β的最小二乘估计是?β=_______ . 解:1?-''X Y β= ()X X . 二、单项选择题(每小题3分,共15分) 1,设12(,,,)(2)n X X X n ≥ 为来自总体(0,1)N 的一个样本,X 为样本均值,2 S 为样本方差,则 ____D___ . (A )(0,1)nX N ; (B )2 2()nS n χ ; (C ) (1)()n X t n S - ; (D )2 12 2 (1)(1,1)n i i n X F n X =--∑ . 2,若总体2(,)X N μσ ,其中2σ已知,当置信度1α-保持不变时,如果样本容量n 增大,则μ的 置信区间____B___ . (A )长度变大; (B )长度变小; (C )长度不变; (D )前述都有可能. 3,在假设检验中,分别用α,β表示犯第一类错误和第二类错误的概率,则当样本容量n 一定时,下列说法中正确的是____C___ . (A )α减小时β也减小; (B )α增大时β也增大; (C ),αβ其中一个减小,另一个会增大; (D )(A )和(B )同时成立. 4,对于单因素试验方差分析的数学模型,设T S 为总离差平方和,e S 为误差平方和,A S 为效应平方 清华大学应用数理统计课后习题及答案 习题三 1 正常情况下,某炼铁炉的铁水含碳量2 (4.55,0.108)X N :.现在测试了5炉铁水,其含碳量分别为4.28,4.40,4.42,4.35,4.37. 如果方差没有改变,问总体的均值有无显著变化?如果总体均值没有改变,问总体方差是否有显著变化(0.05α=)? 解 由题意知 2 ~(4.55,0.108),5,0.05X N n α==,1/20.975 1.96u u α-==,设立 统计原假设 0010:,:H H μμμμ=≠ 拒 绝 域 为 {} 00K x c μ=->,临界值 1/2 1.960.108/0.0947c u α-==?=, 由于 0 4.364 4.550.186x c μ-=-=>,所以拒绝0H ,总体的均值有显著性 变化. 设立统计原假设 2 2 2 2 0010:,:H H σσσσ=≠ 由于0μμ=,所以当0.05α=时 22220.0250.9751 1()0.03694,(5)0.83,(5)12.83,n i i S X n μχχ==-===∑% 22 10.02520.975(5)/50.166,(5)/5 2.567c c χχ==== 拒绝域为 {} 222200201//K s c s c σσ=><%%或 由于2 2 / 3.167 2.567S σ=>%,所以拒绝0H ,总体的方差有显著性变化. 2 一种电子元件,要求其寿命不得低于1000h .现抽测25件,得其均值为 x =950h .已知该种元件寿命2(100,)X N σ:,问这批元件是否合格 (0.05α=)? 解 由题意知 2 (100,)X N σ:,设立统计原假设 0010:,:,100.0.05.H H μμμμσα≥<== 拒绝域为 {} 00K x c μ=-> 习题一 1 设总体X 的样本容量5=n ,写出在下列4种情况下样本的联合概率分布. 1)),1(~p B X ; 2))(~λP X ; 3)],[~b a U X ; 4))1,(~μN X . 解 设总体的样本为12345,,,,X X X X X , 1)对总体~(1,)X B p , 11223344555 11 1 55(1) (,,,,)()(1)(1)i i n x x i i i i x x P X x X x X x X x X x P X x p p p p -==-========-=-∏∏ 其中:5 1 15i i x x ==∑ 2)对总体~()X P λ 11223344555 1 1 555 1 (,,,,)()! ! i x n i i i i i x i i P X x X x X x X x X x P X x e x e x λ λ λλ-==-========== ∏∏ ∏ 其中:5 1 15i i x x ==∑ 3)对总体~(,)X U a b 55 11511 ,,1,...,5 (,,)()0i i i i a x b i f x x f x b a ==?≤≤=?==-??? ∏∏ L ,其他 4)对总体~(,1) X Nμ () ()() 2 555 5/22 2 15 1 11 1 (,,)()=2exp 2 i x i i i i i f x x f x x μ πμ - -- = == ?? ==-- ? ?? ∑ ∏ L 2 为了研究玻璃产品在集装箱托运过程中的损坏情况,现随机抽取20个集装箱检查其产品损坏的件数,记录结果为:1,1,1,1,2,0,0,1,3,1,0,0,2,4,0,3,1,4,0,2,写出样本频率分布、经验分布函数并画出图形. 解设(=0,1,2,3,4) i i代表各箱检查中抽到的产品损坏件数,由题意可统计出如下的样本频率分布表1.1: 经验分布函数的定义式为: 应用数理统计试题 1.设15,,X X 是独立且服从相同分布的随机变量,且每一个()1,2,,5i X i = 都服从()0,1.N (1)试给出常数c ,使得()22 12c X X +服从2χ公布,并指出它的自由度; (2)试给出常数,d 使得 服从t 分布,并指出它的自由度. 2.设总体X 的密度函数为 ???<<+=其他, 01 0,)1();(x x x f ααα 其中1->α是未知参数, ),,(1n X X 是一样本, 试求: (1) 参数α的矩估计量; (2) 参数α的最大似然估计量. 3.有一种新安眠剂,据说在一定剂量下能比某种旧安眠剂平均增加睡眠时间3小时,为了检验新安眠剂的这种说法是否正确,收集到一组使用新安眠剂的睡眠时间(单位:小时): 26.7, 22.0, 24.1, 21.0, 27.2, 25.0, 23.4. 根据资料用某种旧安眠剂时平均睡眠时间为20.8小时,假设用安眠剂后睡眠时间服从正态分布,试问这组数据能否说明新安眠剂的疗效?()0.05.α= 4.若总体X 服从正态分布() 22.1,1N ,样本n X X X ,,,21 来自总体X ,要使样本均值X 满足不等式{}95.01.19.0≥≤≤X P ,求样本容量n 最少应取多少? 5.在某种产品表明进行腐蚀刻线实验,得到腐蚀深度y 与腐蚀时间x 对应的一 (1)预测腐蚀时间75s 时,腐蚀深度的范围(α-1=95%); (2)若要求腐蚀深度在10~20um 之间,问腐蚀时间应如何控制? 6.简述方差分析,主成分分析的基本思想 附:统计查表数据 0.025(6) 2.447t =,0.025(7) 2.365t =,(1.96)0.975Φ= 参考答案: 1.设15,,X X 是独立且服从相同分布的随机变量,且每一个()1,2,,5i X i = 都服从()0,1.N (1)试给出常数c ,使得() 22 12c X X +服从2χ公布,并指出它的自由度; (2)试给出常数,d 使得服从t 分布,并指出它的自由度. 解 (1)由于()()()22 21212~0,1,~0,1, ~2X N X N X X +χ故 因此1c =,1222 X X +服从自由度为2的2χ分布. (2)由于()()~0,11,2,5i X N i = 且独立,则()12~0,2X X N + ()~0,1N 而 ()22223453X X X ++=χ ()~3,t ()~3t 所以d =自由度为3. 2. 设总体X 的密度函数为 ???<<+=其他, 01 0,)1();(x x x f ααα 其中1->α是未知参数, ),,(1n X X 是一样本, 试求: 习题三 1 正常情况下,某炼铁炉的铁水含碳量2 (4.55,0.108)X N .现在测试了5炉铁水,其含碳量分别为4.28,4.40,4.42,4.35,4.37. 如果方差没有改变,问总体的均值有无显著变化?如果总体均值没有改变,问总体方差是否有显著变化(0.05α=)? 解 由题意知 2 ~(4.55,0.108),5,0.05X N n α==,1/20.975 1.96u u α-==,设立 统计原假设 0010:,:H H μμμμ=≠ 拒 绝 域 为 {} 00K x c μ=->,临界值 1/2 1.960.108/0.0947c u α-==?=, 由于 0 4.364 4.550.186x c μ-=-=>,所以拒绝0H ,总体的均值有显著性 变化. 设立统计原假设 2 2 2 2 0010:,:H H σσσσ=≠ 由于0μμ=,所以当0.05α=时 2 222 0.0250.9751 1()0.03694,(5)0.83,(5)12.83,n i i S X n μχχ==-===∑ 22 10.02520.975(5)/50.166,(5)/5 2.567c c χχ==== 拒绝域为 {} 2222 00201//K s c s c σσ=><或 由于22 0/ 3.167 2.567S σ=>,所以拒绝0H ,总体的方差有显著性变化. 2 一种电子元件,要求其寿命不得低于1000h .现抽测25件,得其均值为 x =950h .已知该种元件寿命2(100,)X N σ,问这批元件是否合格(0.05α=)? 解 由题意知 2 (100,)X N σ,设立统计原假设 0010:,:,100.0.05.H H μμμμσα≥<== 拒绝域为 {} 00K x c μ=-> 临界值为 0.050.0532.9c u u =?=?=- 由于 050x c μ-=-<,所以拒绝0H ,元件不合格. 第五章 方差分析 课后习题参考答案 5.1 下面给出了小白鼠在接种三种不同菌型伤寒杆菌后的存活日数: 设小白鼠存活日数服从方差相等的正态分布,试问三种菌型的平均存活日数有无显著差异?(01.0=α) 解:(1)手工计算解答过程 提出原假设:()3,2,10:0==i H i μ 记 167.20812 11112 =???? ??-=∑∑∑∑====r i n j ij r i n j ij T i i X n X S 467.7011 2 11211=???? ??-???? ??=∑∑∑ ∑====r i n j ij r i n j ij i A i i X n X n S 7.137=-=A T e S S S 当 0H 成立时, ()()()r n r F r n S r S F e A --- -= ,1~/1/ 本题中r=3 经过计算,得方差分析表如下: 查表得 ()()35.327,2,195.01==---F r n r F α且F=6.909>3.35,在95%的置信度下,拒绝原 假设,认为不同菌型伤寒杆菌对小白鼠的存活日数有显著影响。 (2)软件计算解答过程 从上表可以看出,菌种不同这个因素的检验统计量F 的观测值为6.903,对应的检验概率p 值为0.004,小于0.05,拒绝原假设,认为菌种之间的差异对小白鼠存活日数有显著影响。 5.2 现有某种型号的电池三批,他们分别是甲、乙、丙三个工厂生产的,为评论其质量,各随机抽取6只电池进行寿命试验,数据如下表所示: 试在显著水平0.05α=下,检验电池的平均寿命有无显著性差异?并求 121323,μμμμμμ---及的95%置信区间。这里假定第i 种电池的寿命 2i X (,)(1,2,3)i N i μσ=。 解:手工计算过程: 1.计算平方和 其检验假设为:H0:,H1:。 2.假设检验: 所以拒绝原假设,即认为电池寿命和工厂显著相关。 3.对于各组之间的均值进行检验。 6 .615])394.44()3930()396.42[(*4)()(4 .216)3.28108.15(*4*))(1()(832 429.59*14*))(1()(2221 22 1 21 22 222=-+-+-=-=-==++=-==-===-==-=∑∑∑∑∑∑∑∑∑===r i i i i A r i i i r i i i i ij e ij T X X n X X S S n S n X X S s n ns X X S 0684 .170333 .188 .30712/4.2162/6.615)/()1/(===--= r n S r S F e A 89 .3)12,2(),1(95.01==-->-F r n r F F α 第一章 数理统计的基本概念 P26 1.2 设总体X 的分布函数为()F x ,密度函数为()f x ,1X ,2X ,…,n X 为X 的子样,求最大顺序统计量()n X 与最小顺序统计量()1X 的分布函数与密度函数。 解:(){}{}()12n n i n F x P X x P X x X x X x F x =≤=≤≤≤=???? ,,,. ()()()()1n n n f x F x n F x f x -'=??=??????. (){}{}1121i n F x P X x P X x X x X x =≤=->>> ,,,. {}{}{}121n P X x P X x P X x =->>> {}{}{}121111n P X x P X x P X x =-?-≤??-≤??-≤??????? ()11n F x =-?-??? ()()()()1111n f x F x n F x f x -'=??=?-???? ?. 1.3 设总体X 服从正态分布()124N , ,今抽取容量为5的子样1X ,2X ,…,5X ,试问: (i )子样的平均值X 大于13的概率为多少? (ii )子样的极小值(最小顺序统计量)小于10的概率为多少? (iii )子样的极大值(最大顺序统计量)大于15的概率为多少? 解:()~124X N , ,5n =,4 ~125 X N ?? ∴ ?? ?,. (i ) {}{ } ()13113111 1.1210.86860.1314P X P X P φφ???? ???>=-≤=-=-=-=-=. (ii )令{}min 12345min X X X X X X =,,,,,{}max 12345max X X X X X X =,,,,. {}{}{}min min 125101*********P X P X P X X X <=->=->>> ,,, {}{}{}55 5 1 1 11011101110i i i i P X P X P X ===->=-?- 习题三 2.设总体的分布密度为: (1),01 (;)0, x x f x ααα+<<=???其它 1(,,)n X X 为其样本,求参数α的矩估计量1?α 和极大似然估计量2?α .现测得样本观测值为:0.1,0.2,0.9,0.8,0.7,0.7,求参数α的估计值 . 解 计算其最大似然估计: ()() 11 1 1 1 (,)11ln (,)ln(1)ln n n n n i i i i n n i i L x x x x L x x n x α α αααααα===??=+=+??=++∏∏∑ 11 21 ln (,)ln 01?10.2112 ln n n i i n i i d n L x x x d n x ααααα====+=+=--=∑∑ 其矩估计为: ()1 3.40.10.20.90.80.70.766 X = +++++= 3077 .01 21?,212) 1()1(11 01 21=--==++=++=+=?++X X X x dx x EX αααααααα 所以:12112??,11ln n i i X n X X α α=?? ?- ?==-+- ? ?? ? ∑, 12??0.3077,0.2112αα≈≈. 3. 设元件无故障工作时间X 具有指数分布,取1000个元件工作时间的记录数据,经分组后得到它的频数分布为: 如果各组中数据都取为组中值,试用最大似然法求参数的点估计. .解 最大似然估计: 1 1 (,),ln ln i n x n nx n i L x x e e L n nx λλλλλλλ--====-∏ 7 11120000?ln 0,,2010001000 i i i d n L nx X x v d X λλλ==-=====∑ 1 ?0.05X λ ==. 4. 已知某种灯泡寿命服从正态分布,在某星期所生产的该种灯泡中随机抽取10只,测得其寿命(单位:小时)为: 1067,919,1196,785,1126,936,918,1156,920,948 设总体参数都未知,试用极大似然法估计这个星期中生产的灯泡能使用1300小时以上的概率. 解 设灯泡的寿命为x ,2 ~(,)x N μσ,极大似然估计为:2 21 1??,()n i i x x x n μ σ===-∑ 根据样本数据得到:2??997.1,17235.81μ σ== . 经计算得,这个星期生产的灯泡能使用1300小时的概率为0.0075. 5. 为检验某种自来水消毒设备的效果,现从消毒后的水中随机抽取50升,化验每升水中大肠杆 菌的个数(假定一升水中大肠杆菌个数服从Poisson 分布),其化验结果如下: 试问平均每升水中大肠杆菌个数为多少时,才能使上述情况的概率为最大? 解 设x 为每升水中大肠杆菌个数,~ ()x P λ,Ex λ=,由3题(2)问知,λ的 最大似然估计为x ,所以 ().150/1*42*310*220*117*0?=++++==X L λ 所以平均每升氺中大肠杆菌个数为1时,出现上述情况的概率最大 . 7. 设1234,,,X X X X 是总体X 的样本,设有下述三个统计量: 123411 1 6 3 ?()()X X X X a ++=+应用数理统计吴翊李永乐第三章假设检验课后作业参考答案
应用数理统计课后习题参考答案
北航应用数理统计考试题及参考解答
应用数理统计,施雨,课后答案,
清华大学-杨虎-应用数理统计课后习题参考答案2
应用数理统计课后习题参考答案
应用数理统计习题答案 西安交大 施雨
应用数理统计课后习题 清华大学出版社 杨虎 钟波第三章作业参考答案
研究生《应用数理统计基础》庄楚强 四五章部分课后答案
最新研究生《应用数理统计基础》庄楚强-何春雄编制---课后答案
2009(上)《数理统计》考试题(A卷)及参考解答
清华大学应用数理统计课后习题及答案
清华大学-杨虎-应用数理统计课后习题参考答案
概率数理统计试题及答案
清华大学杨虎应用数理统计课后习题参考答案
《应用数理统计》吴翊李永乐第五章方差分析课后作业参考答案详解
应用数理统计作业题及参考答案(第一章 )
应用数理统计 杨虎 第三章习题及答案
