投影与视图2
投影与视图知识点总结

投影与视图知识点总结投影与视图是工程图学中的重要内容,是工程师进行设计与制造的基础。
下面是投影与视图的知识点总结。
一、投影的定义与种类1. 投影是将三维实体在二维画面上的投影。
2. 投影分为平行投影和透视投影两种。
平行投影是物体在无穷远处时的投影,保持物体形状和大小不变,适用于工程制图中的多视图投影。
透视投影是通过模拟人眼的透视原理,使物体在近处大远处小,用于绘制逼真的效果图。
二、主视图与副视图1. 主视图是从物体六个主要方向观察并绘制的视图。
2. 副视图是从物体其它非主要方向观察并绘制的视图。
3. 任何物体至少需要主视图和一个副视图来完整表示。
三、视图的投影规律1. 视图的投影规律是指根据物体的几何特性,确定其视图的位置、大小及间隔等规律。
2. 正投影规律:物体的投影与视图同侧,上投下,前投后,左投右。
3. 在主视图、俯视图和立体图中,物体的主要特征线分别为前、上、左三个面上的轮廓线。
四、视图的基本要求1. 视图的大小适中,方便观察和绘制。
2. 视图之间的间距要均匀,以突出主要的特征和轮廓线。
3. 视图应尽量减少折角,直线尽量不折断。
五、视图的选择原则1. 选择平易近人的主视图。
2. 主视图要选主要面直接对称的视图。
3. 选择于构造、加工、检验方便的视图。
4. 尽量选择存在完整轮廓线的视图。
六、常见视图1. 正投主视图:从正前方观察物体并绘制的视图。
2. 俯视图:从物体的上方直接向下观察并绘制的视图。
3. 阜视图:从物体的左前方斜向观察并绘制的视图。
4. 左视图:从物体的左侧观察并绘制的视图。
5. 右视图:从物体的右侧观察并绘制的视图。
七、主视图与副视图的绘制方法1. 主视图绘制方法:a. 确定主视图的位置,主视图应水平或竖直地绘制在图纸上。
b. 根据主视图的投影规律,绘制主视图的轮廓线。
c. 绘制主视图上的特征线、尺寸和字体。
2. 副视图绘制方法:a. 根据几何原理,确定副视图的位置和大小。
人教版九年级数学下册第29章投影与视图 2三视图习题2
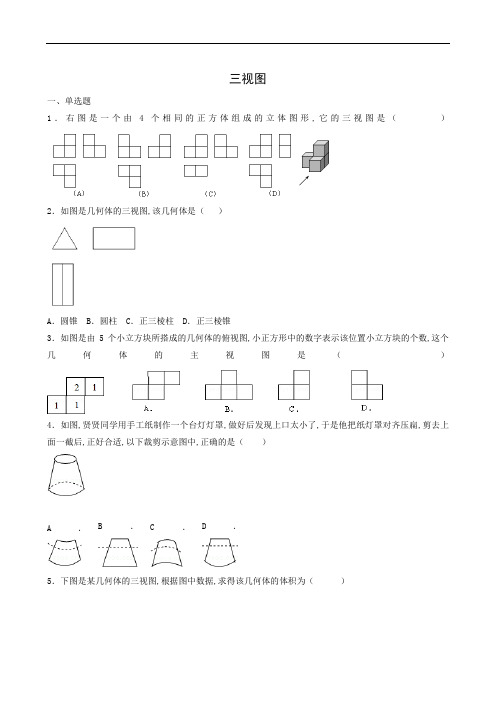
三视图一、单选题1.右图是一个由4个相同的正方体组成的立体图形,它的三视图是()2.如图是几何体的三视图,该几何体是()A.圆锥B.圆柱C.正三棱柱D.正三棱锥3.如图是由5个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,这个几何体的主视图是()4.如图,贤贤同学用手工纸制作一个台灯灯罩,做好后发现上口太小了,于是他把纸灯罩对齐压扁,剪去上面一截后,正好合适,以下裁剪示意图中,正确的是()A.B.C.D.5.下图是某几何体的三视图,根据图中数据,求得该几何体的体积为()A.60πB.70πC.90πD.160π6.用6个完全相同的小正方体组合成如图所示的立方体图形,它的主视图为D.A .B.C .7.如图是由六个棱长为1的正方体组成的几何体,其俯视图的面积是A.3 B.4 C.5 D.68.如图是一个几何体的三视图,已知正视图和左视图都是边长为2的等边三角形,则这个几何体的全面积为A. B. C. D.二、填空题9.若干桶方便面摆放在桌子上,如图是它的三视图,则这一堆方便面共有 _____ 桶.10.桌上放着一个长方体和一个圆柱体,说出下面三幅图分别是从哪个方向看到的? 11.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是.12.下图是由几个相同的小立方块组成的几何体的三视图,小立方块的个数是.13.如图是一个正方体纸盒的展开图,其中的四个正方形内标有数字1,2,3和-3.要在其余正方形内分别填上一个数,使得折成正方形后,相对面上的两数均为互为相反数,则A处应填.14.如图是一个包装盒的三视图,则这个包装盒的体积是15.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是.三、解答题16.如图,是由若干个完全相同的小正方体组成的一个几何体.(1)请画出这个几何体的主视图、左视图和俯视图;(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加几个小正方体?17.某一空间图形的三视图如右图所示,其中主视图:半径为1的半圆以及高为1的矩形;左视图:半径为1的14圆以及高为1的矩形;俯视图:半径为1的圆.求此图形的体积.18.如图,是由5个正方体组成的图案,请在方格纸中分别画出它的主视图、左视图、俯视图.19.如图是一些小正方块所搭几何体的俯视图,小正方块中的数字表示该位置的小方块的个数,请画出这个几何体的主视图和左视图:20.一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的形状,并根据图中所给的数据求出它的侧面积21.已知一个几何体的三视图为一个直角三角形,和两个长方形,有关的尺寸如图所示,描述该几何体的形状,并根据图中数据计算它的表面积.22.在平整的地面上,有若干个完全相同的棱长为10cm的小正方体堆成一个几何体,如图所示。
投影与视图2

知识点一、投影:(一)投影:一般地,用光线照射物体,在某个平面上得到的影子叫做物体的投影。
其中,照射光叫做线,投影所在的平面叫做面。
(二)平行投影:由光线形成的投影是平行投影,如物体在太阳光的照射下的影子。
(三)中心投影:由(点光源)发出的光线形成的投影叫做中心投影,如灯泡发出的光照射下的影子。
(四)正投影:投影线于投影面产生的投影,叫做正投影;性质:当线段平行于投影面时,它的正投影长短,当线段倾斜于投影面时,它的正投影线段,当线段垂直于投影面时,它的正投影。
知识点二、视图(一)视图:当我们从某一角度观察一个物体时,所看到的图像叫做物体的一个视图。
视图也可以看作物体在某一个角度的光线下的投影。
(二)三视图:(1)主视图:在正面内得到的观察物体的视图叫做主视图。
(2)俯视图:在水平面内得到的观察物体的视图,叫做俯视图。
(3)左视图:在侧面得到的观察物体的视图,叫做左视图。
(三)三视图的位置确定:主视图要在左上边,它下方是俯视图,左视图放在右边。
如下图主视图与俯视图长对,主视图与左视图高,左视图与俯视图宽。
(四)三视图的画法:(1)确定主视图的位置,画出主视图;(2)在主视图正下方画出俯视图,注意与主视图“长对正”;(3)在主视图正右方画出左视图,注意与主视图“高平齐”与俯视图“宽相等”。
(五)由三视图想象立体图形:要先分别想象立体图形的前面、上面和左侧面,然后再综合起来考虑整个图形。
(六)求立体图形表面积:一般先将立体图形,再按平面图形计算。
考点一、投影例1.在平行投影中,两人的高度和他们的影子。
考点:平行投影思路点拨:根据平行投影及三角形相似。
答案:例2.小军晚上到广场去玩,他发现有两人的影子一个向东,一个主视图左视图俯视图经典例题——自主学习认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三。
若有其它补充可填在右栏空白处。
更多精彩请参看网校资源ID:#jdlt0#251283向西,于是他肯定地说:“广场上的大灯泡一定位于两人”。
2012年中考数学解析汇编投影与视图2

2012年中考数学解析汇编*投影与视图2
14、(2012浙江省义乌市,2,3分)下列四个立体图形中,主视图为圆的是( )
15、(2012安徽)下面的几何体中,主(正)视图为三角形的是(
)
A. B. C. D.
16、(2012四川省南充市) 下列几何体中,俯视图相同的是(
)
A .①②
B .①③
C .②③
D .②④
17、(2012广州市)一个几何体的三视图如图1所示,则这个几何体是( ) 主视图左视图
俯视图
A. 四棱锥
B.四棱柱
C.三棱锥
D.三棱柱
18、(2012山东省荷泽市)如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下面右图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是 ( )
19、(2012浙江省衢州)长方体的主视图、俯视图如图所示,则其左视图面积为(
) A B C D A . B . C . D .
A.3
B.4
C.12
D.16
20、(2012山东省临沂市)如图是一个几何体的三视图,则这个几何体的侧面积是()
A.18cm2
B. 20cm2
C. (18+3
2)cm2 D. (18+3
4)cm2
21.(2012山东省滨州)某几何体的三视图如图所示,则这个几何体是()
A.圆柱B.正方体C.球D.圆锥
22.(2012贵州六盘水)图1是教师每天在黑板上书写用的粉笔,它的主视图是()
23.(2012贵州省毕节市)王老师有一个装文具用的盒子,它的三视图如图所示,这个盒子类似于()
A.圆锥
B.圆柱
C.长方体
D.三棱柱。
第二讲-投影体系和基本视图

Z
a'
b' Z
b'
a''(b'')
A
B
W a''(b'')
x
X
0
o
YW
a
a
b
Y
b
YH
• 与直线垂直旳投影面上旳投影积聚成一点。 • 在另外两个投影面上旳投影平行于相应旳投影轴反应真长。
例题2-6:鉴定直线AB、CD旳名称。
a’ X
c’ b’
OX
a
b
c
d’ O
d
2.3.2.4 两直线旳相对位置
(1)平行两直线 (2)相交两直线 (3)交叉两直线 (4)交叉两直线重影点旳可见性鉴别
S
平面P称为投影面,S称为投射中心,
需作出点ABC在平面P上旳图象。
将S与A连成直线,作出SA与平面 P旳交点a ,即为点A旳图象。直线SA 称为投射线,点a称为点A旳投影,这 种产生图象旳措施称为投影法。
A
C
B
a
c
b 投影面 P
投影法分为两类:中心投影法和平行投影法。
(1)中心投影法
前例即是中心投影法,即投射线都从投射中心出发旳,所 得旳投影称为中心投影。
C
Ac
B D
o
a
k
b
d
鉴别措施:
交点是两直线 旳共有点
d’ b’
k’
a’
x c’
o
c b
k a
d
若空间两直线相交,则其同名投影必相交,且交点旳
投影必符合空间一点旳投影规律。
例2-9:过C点作水平线CD与AB相交。
湘教版九年级下册数学精品教学课件 第3章 投影与视图 小结与复习 (2)

例8 由一些大小相同的小正方体组成的几何体 三视图如图所示,那么,组成这个几何体的小正方体 的个数是( )
A.7
B.6
C.5
D.4
【解析】C 由主视图和俯视图可知,俯视图右边 两个方格的位置上各放置了一个正方体,所以在这两 个方格里分别填入数字 1 (如图);
由主视图和俯视图又知,俯视图左边一列上两个方
MO OP
即 MA 1.6 , 解得 MA = 5. 20+MA 8
同理,由 △NBD ∽ △NOP,
可得 NB = 1.5.
所以小明的身影变短了 5-1.5 = 3.5 (米).
考点三 圆锥的相关计算 例3 圆锥的侧面积为 6π cm2,底面圆的半径为 2 cm, 则这个圆锥的母线长为___3____cm.
1. 如图,小明与同学合作利用太阳光测量旗杆的高度, 身高 1.6 m 的小明落在地面上的影长为 BC = 2.4 m.
(1) 请你在图中画出旗杆在同一时刻阳光照射下落在地 面上的影子 EG;
(2) 若小明测得此刻旗杆
落在地面的影长 EG = 16 m,
请求出旗杆 DE 的高度.
解: (1) 影子 EG 如图所示. (2) ∵ DG∥AC, ∴∠G =∠C. ∴ Rt△ABC ∽ △Rt△DGE. ∴ AB BC ,即 1.6 2.4, DE EG DE 16
发出的,像这样的光线所形成的投影称为中心投影.
4. 平行投影与中心投影的区别与联系:
平行投影 中心投影
区别
投影线互相平行, 形成平行投影
投影线发自一点, 形成中心投影
联系
都是物体在光线的 照射下,在某个平 面内形成的影子. (即都是投影)
正投影
(1) 概念:投影线垂直于投影面产生的投影叫做正投影. (2) 性质:当物体的某个面平行于投影面时,这个面的
投影与视图2(2)

△ABD经过旋转后到达△ACE的位置 。
(1)旋转中心是哪一点? A点
A
(2)旋转了多少度? 60度
(3)如果M是AB上中点,
M
那么经过上述的旋转后,
E
点M到了什么位置?
BD
C
M点到了AC的中点上
思考题一:
如图, △ABD 、△AEC都是等边三角形, BE与DC有什么关系? 你能用旋转的性质说明上述关系成立的理由吗?
人教版数学九年级上册《图形的旋转》
图形的旋转
高明镇高明学校: 黄志峰
你熟悉下列物体变换的方式吗?
轴对称变换
平移
观 察
继续观察并思考:
请你描述出下列物体运动的共同点?
问题:上面情景中的转动现 象,有什么共同的特征?
顺时针
A
B
旋转角
o
旋转中心
A点的对应点是B点 ∠AOB是旋转角
把一个平面图形绕着平面内某一点O转动一个角度的 图形变换叫做图形的旋转。其中点O叫做旋转中心, 转动的角叫做旋转角。
旋转中心: O点
旋转方向: 逆时针
旋转角: ∠AOA’、 ∠BOB’ 、 ∠COC’
问题:钟表的指针、秋千在 转动过程中,其形状、大小、 位置是否发生变化呢?
如 图 , 将 △ ABC 绕 点 O 按 顺 时 针 方 向 旋 转 到 △A'B'C'的位置 . 动手操作:度量∠AOA'、∠BOB'、∠COC'的度 数;
AO与A'O、BO与AB'O、CO与C'O的长度. 你发现了什么?
B
C B'
A'
O
C画' 板
第29章 投影与视图全章教案

第二十九章投影与视图29.1投影(1)学习目标1、经历实践探索,了解投影、投影面、平行投影和中心投影的概念;2、了角平行投影和中心投影的区别。
3、使学生学会关注生活中有关投影的数学问题,提高数学的应用意识。
学习重点理解平行投影和中心投影的特征;学习难点在投影面上画出平面图形的平行投影或中心投影。
教学互动设计备注(一)创设情境你看过皮影戏吗?皮影戏又名“灯影子”,是我国民间一种古老而奇特的戏曲艺术,在关中地区很为流行。
皮影戏演出简便,表演领域广阔,演技细腻,活跃于广大农村,深受农民的欢迎。
(二)你知道吗北京故宫中的日晷闻名世界,是我国光辉出灿烂文化的瑰宝.它是我国古代利用日影测定时刻的仪器,它由“晷面”与“晷针”组成,当太阳光照在日晷中轴上产生投影,晷针的影子就会投向晷面,随着时间的推移,晷针的影的长度发生变化,晷针的影子在晷面上慢慢移动,聪明的古人以此来显示时刻.问题:那什么是投影呢?出示投影让学生感受在日常生活中的一些投影现象。
一般地.用光线照射物体.在某个平面(地面、墙壁等)上得到的影子叫做物体的投影.照射光线叫做投影线,投影所在的平面叫做投影面.有时光线是一组互相平行的射线.例如太阳光或探照灯光的一束光中的光线(如图).由平行光线形成的投影是平行投影.例如.物体在太阳光的照射下形成的影子(简称日影)就是平行投影.由同一点(点光源)发出的光线形成的投影叫做中心投影.例如.物体在灯泡发出的光照射下形成影子就是中心投影.(三)问题探究(在课前布置,以数学学习小组为单位)探究平行投影和中心投影和性质和区别1、以数学习小组为单位,观察在太阳光线下,木杆和三角形纸板在地面的投影。
2、不断改变木杆和三角形纸板的位置,什么时候木杆的影子成为一点,三角形纸板的影子是一条线段?当木杆的影子与木杆长度相等时,你发现木杆在什么位置?三角形纸板在什么位置时,它的影子恰好与三角形纸板成为全等图形?还有其他情况吗?(四)应用新知:(1)地面上直立一根标杆AB如图,杆长为2cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
延大附中九年级数学科导学案时间____________
编写人董新峰审核人冯海燕教务处审核__________ 课题29.2三视图(第一课时)
学习目标知识目标1.会从投影角度理解视图的概念。
2.会画简单几何体的三视图。
学习重点 1.从投影的角度加深对三视图概念的理解。
2.会画简单几何体的三视图。
学习难点 1.对三视图概念理解的升华。
2、正确画出三棱柱的三视图和小零件的三视图
教学过程
一、自主探究
学生观察思考:(1)三个视图位置上的关系。
(2)三个视图除了位置上的关系,在大小尺寸上,彼此之间
又存在什么关系?
小结:
1.三视图位置有规定,主视图要在,俯视图
应在,
左视图要在。
2.三视图中各视图的大小也有关系。
主视图与俯视图表示同一物体的,主视图与左视图表示同一物体的,左视图与俯视图表示同一物体的。
因此三视图的大小是互相联系的。
画三视图时,三个视图要放在正确的位置,并且使主视图与俯视图的,主视图与左视图的,左视图与俯视图的。
二、合作探究
例1、画出下图2所示的一些基本几何体的三视图.
题后小结:
画这些基本几何体的三视图时,要注意从个方面观察它们.具体画法为:
1.确定视图的位置,画出视图;
2.在视图正下方画出视图,注意与主视图“”。
3.在视图正右方画出视图.注意与主视图“”,与俯视图“”.
三、课堂检测
1.画出图中的几何体的三视图。
课后作业
一、画基本几何体的三视图时,要注意从个方面观察它们.具体画法为:
1.确定视图的位置,画出视图;
2.在视图正下方画出视图,注意与主视图“”。
3.在视图正右方画出视图.注意与主视图“”,与俯视图“”.
4.看得见的轮廓线通常画成_______,看不见的部分通常画成_______。
二、画出下图中几何体的三视图。
