2018年高考文数解析几何圆锥曲线精选试题及知识点分析
2018年高考真题汇编——理科数学(解析版)10:圆锥曲线

2018高考真题分类汇编:圆锥曲线一、选择题1.【2018高考真题浙江理8】如图,F 1,F 2分别是双曲线C :22221x y a b-=(a,b >0)的左、右焦点,B 是虚轴的端点,直线F 1B 与C 的两条渐近线分别交于P ,Q 两点,线段PQ 的垂直平分线与x 轴交与点M ,若|MF 2|=|F 1F 2|,则C 的离心率是A.23 B 62 D. 3【答案】B【解析】由题意知直线B F 1的方程为:b x c b y +=,联立方程组⎪⎪⎩⎪⎪⎨⎧=-+=0,b y a x b x cb y 得点Q ),(a c bc a c ac --,联立方程组⎪⎪⎩⎪⎪⎨⎧=++=0,b y a x b x cb y 得点P ),(ac bc a c ac ++-,所以PQ 的中点坐标为),(222b c b c a ,所以PQ 的垂直平分线方程为:)(222bca xbc b c y --=-,令0=y ,得)1(22b a c x +=,所以c ba c 3)1(22=+,所以2222222a cb a -==,即2223c a =,所以26=e 。
故选B2.【2018高考真题新课标理8】等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B 两点,43AB =;则C 的实轴长为( )()A 2 ()B 22 ()C 4 ()D 8【答案】C【解析】设等轴双曲线方程为)0(22>=-m m y x ,抛物线的准线为4-=x ,由34=AB ,则32=A y ,把坐标)32,4(-代入双曲线方程得4121622=-=-=y x m ,所以双曲线方程为422=-y x ,即14422=-y x ,所以2,42==a a ,所以实轴长42=a ,选C. 3.【2018高考真题新课标理4】设12F F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,P 为直线32ax =上一点,12PF F ∆是底角为30o 的等腰三角形,则E 的离心率为( )()A 12 ()B 23 ()C 34 ()D 45【答案】C【解析】因为12PF F ∆是底角为30o 的等腰三角形,则有PF F F 212=,,因为2130=∠F PF ,所以0260=∠D PF ,0230=∠DPF ,所以21222121F F PF D F ==,即c c c a =⨯=-22123,所以c a 223=,即43=a c ,所以椭圆的离心率为43=e ,选C.4.【2018高考真题四川理8】已知抛物线关于x 轴对称,它的顶点在坐标原点O ,并且经过点0(2,)M y 。
2018年高考数学圆锥曲线的综合问题

y y2 x x 2x 1 =-9· 1 2 =-9· M =(-9)· ,kl· kOM=-9(常数). 2 yM x1 x2 y1 y2 kOM
所以直线OM的斜率与l的斜率的乘积为定值. 解法二:设A(x1,y1),B(x2,y2),中点M(x0,y0),
(去伪存真).
2.(2015课标Ⅱ,20,12分,0.145)已知椭圆C:9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴,l与
C有两个交点A,B,线段AB的中点为M.
(1)证明:直线OM的斜率与l的斜率的乘积为定值; (2)若l过点 , m ,延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜 率;若不能,说明理由.
因为直线l过点 , m ,所以l不过原点且与C有两个交点的充要条件是k>0,k≠3.
由(1)得OM的方程为y=- x. 设点P的横坐标为xP.
9 km k 2 m2 y x, 2 x 由 得 = ,即xP= 2 . k P 2 9 k 81 2 2 2 3 k 9 9 x y m m(3 k ) m 的坐标代入l的方程得b= 将点 , ,m 3 3 k ( k 3)m . 因此xM= 3(k 2 9)
m 3
解析 (1)解法一:设直线l:y=kx+b(k≠0,b≠0),A(x1,y1),B(x2,y2),M(xM,yM). 将y=kx+b代入9x2+y2=m2得(k2+9)x2+2kbx+b2-m2=0,故
x x2 kb 9b = ,yM=kxM+b= . 2 2 k 9 k 9 2 yM 9 于是直线OM的斜率kOM= =- ,即kOM· k=-9. xM k
高考圆锥曲线中的定点与定值问题(题型总结超全)

专题08 解锁圆锥曲线中的定点与定值问题一、解答题1.【陕西省榆林市第二中学2018届高三上学期期中】已知椭圆的左右焦点分别为,离心率为;圆过椭圆的三个顶点.过点且斜率不为0的直线与椭圆交于两点.(Ⅰ)求椭圆的标准方程;(Ⅱ)证明:在轴上存在定点,使得为定值;并求出该定点的坐标.【答案】(1)(2)【解析】试题分析:(Ⅰ)设圆过椭圆的上、下、右三个顶点,可求得,再根据椭圆的离心率求得,可得椭圆的方程;(Ⅱ)设直线的方程为,将方程与椭圆方程联立求得两点的坐标,计算得。
设x轴上的定点为,可得,由定值可得需满足,解得可得定点坐标。
解得。
∴椭圆的标准方程为.(Ⅱ)证明:由题意设直线的方程为,由消去y整理得,设,,要使其为定值,需满足,解得.故定点的坐标为.点睛:解析几何中定点问题的常见解法(1)假设定点坐标,根据题意选择参数,建立一个直线系或曲线系方程,而该方程与参数无关,故得到一个关于定点坐标的方程组,以这个方程组的解为坐标的点即所求定点; (2)从特殊位置入手,找出定点,再证明该点符合题意.2.【四川省成都市第七中学2017-2018学年高二上学期半期考】已知斜率为k 的直线l 经过点()1,0-与抛物线2:2C y px =(0,p p >为常数)交于不同的两点,M N ,当12k =时,弦MN的长为. (1)求抛物线C 的标准方程;(2)过点M 的直线交抛物线于另一点Q ,且直线MQ 经过点()1,1B -,判断直线NQ 是否过定点?若过定点,求出该点坐标;若不过定点,请说明理由. 【答案】(1)24y x =;(2)直线NQ 过定点()1,4- 【解析】试题分析:(1)根据弦长公式即可求出答案;(2)由(1)可设()()()2221122,2,,2,,2M t t N t t Q t t ,则12MN k t t =+, 则()11:220MN x t t y tt -++=; 同理: ()22:220MQ x t t y tt -++=()1212:220NQ x t t y t t -++=.由()1,0-在直线MN 上11t t ⇒=(1);由()1,1-在直线MQ 上22220t t tt ⇒+++=将(1)代入()121221t t t t ⇒=-+- (2) 将(2)代入NQ 方程()()12122420x t t y t t ⇒-+-+-=,即可得出直线NQ 过定点.(2)设()()()2221122,2,,2,,2M t t N t t Q t t ,则12211222=MN t t k t t t t -=-+, 则()212:2MN y t x t t t -=-+即()11220x t t y tt -++=; 同理: ()22:220MQ x t t y tt -++=;()1212:220NQ x t t y t t -++=.由()1,0-在直线MN 上11tt ⇒=,即11t t =(1); 由()1,1-在直线MQ 上22220t t tt ⇒+++=将(1)代入()121221t t t t ⇒=-+- (2) 将(2)代入NQ 方程()()12122420x t t y t t ⇒-+-+-=,易得直线NQ 过定点()1,4-3.【四川省成都市第七中学2017-2018学年高二上学期半期考】已知抛物线()2:0C y mx m =>过点()1,2-, P 是C 上一点,斜率为1-的直线l 交C 于不同两点,A B (l 不过P 点),且PAB ∆的重心的纵坐标为23-. (1)求抛物线C 的方程,并求其焦点坐标;(2)记直线,PA PB 的斜率分别为12,k k ,求12k k +的值. 【答案】(1)方程为24y x =;其焦点坐标为()1,0(2)120k k +=【解析】试题分析;(1)将()1,2-代入2y mx =,得4m =,可得抛物线C 的方程及其焦点坐标;(2)设直线l 的方程为y x b =-+,将它代入24y x =得22220x b x b -++=(),利用韦达定理,结合斜率公式以及PAB ∆的重心的纵坐标23-,化简可12k k + 的值;因为PAB ∆的重心的纵坐标为23-, 所以122p y y y ++=-,所以2p y =,所以1p x =,所以()()()()()()1221121212122121221111y x y x y y k k x x x x ------+=+=----, 又()()()()12212121y x y x --+--()()()()12212121x b x x b x ⎡⎤⎡⎤=-+--+-+--⎣⎦⎣⎦()()()12122122x x b x x b =-+-+-- ()()()22212220b b b b =-+-+--=.所以120k k +=.4.已知椭圆2222:1(0)x y C a b a b+=>>的短轴端点到右焦点()10F ,的距离为2.(Ⅰ)求椭圆C 的方程;(Ⅱ)过点F 的直线交椭圆C 于A B ,两点,交直线4l x =:于点P ,若1PA AF λ=,2PB BF λ=,求证: 12λλ-为定值.【答案】(1) 22143x y +=;(2)详见解析. 【解析】试题分析:(Ⅰ)利用椭圆的几何要素间的关系进行求解;(Ⅱ)联立直线和椭圆的方程,得到关于x 或y 的一元二次方程,利用根与系数的关系和平面向量的线性运算进行证明.(Ⅱ)由题意直线AB 过点()1,0F ,且斜率存在,设方程为()1y k x =-, 将4x =代人得P 点坐标为()4,3k ,由()221{ 143y k x x y =-+=,消元得()22223484120k xk x k +-+-=,设()11,A x y , ()22,B x y ,则0∆>且21222122834{ 41234k x x kk x x k +=+-⋅=+, 方法一:因为1PA AF λ=,所以11141PA x AF x λ-==-. 同理22241PB x BFx λ-==-,且1141x x --与2241x x --异号,所以12121212443321111x x x x x x λλ⎛⎫---=+=--+ ⎪----⎝⎭()()1212123221x x x x x x +-=-+-++()2222238682412834k k k k k --=-+--++0=. 所以, 12λλ-为定值0.当121x x <<时,同理可得120λλ-=. 所以, 12λλ-为定值0.同理2223PB my BFmy λ-==,且113my my -与223my my -异号,所以()12121212123332y y my my my my my y λλ+---=+=-()()36209m m ⨯-=-=⨯-.又当直线AB 与x 轴重合时, 120λλ-=, 所以, 12λλ-为定值0.【点睛】本题考查直线和椭圆的位置关系,其主要思路是联立直线和椭圆的方程,整理成关于x 或y 的一元二次方程,利用根与系数的关系进行求解,因为直线AB 过点()1,0F ,在设方程时,往往设为1x my =+()0m ≠,可减少讨论该直线是否存在斜率.5.【四川省绵阳南山中学2017-2018学年高二上学期期中考】设抛物线C : 24y x =, F 为C 的焦点,过F 的直线l 与C 相交于,A B 两点. (1)设l 的斜率为1,求AB ; (2)求证: OA OB ⋅是一个定值. 【答案】(1) 8AB =(2)见解析【解析】试题分析:(1)把直线的方程与抛物线的方程联立,利用根与系数的关系及抛物线的定义、弦长公式即可得出;(2)把直线的方程与抛物线的方程联立,利用根与系数的关系、向量的数量积即可得出;(2)证明:设直线l 的方程为1x ky =+,由21{4x ky y x=+-得2440y ky --= ∴124y y k +=, 124y y =-()()1122,,,OA x y OB x y ==,∵()()1212121211OA OB x x y y kx ky y y ⋅=+=+++,()212121222144143k y y k y y y y k k =++++=-++-=-,∴OA OB ⋅是一个定值.点睛:熟练掌握直线与抛物线的相交问题的解题模式、根与系数的关系及抛物线的定义、过焦点的弦长公式、向量的数量积是解题的关键,考查计算能力,直线方程设成1x ky =+也给解题带来了方便.6.【内蒙古包头市第三十三中2016-2017学年高一下学期期末】已知椭圆C : 22221(0,0)x y a b a b+=>>的,右焦点为求椭圆C 的方程; (2)若过原点作两条互相垂直的射线,与椭圆交于A ,B 两点,求证:点O 到直线AB 的距离为定值.【答案】(1) 2213x y += ,(2) O 到直线AB 的距离为定值2. 【解析】试题分析:(1)根据焦点和离心率列方程解出a ,b ,c ;(2)对于AB 有无斜率进行讨论,设出A ,B 坐标和直线方程,利用根与系数的关系和距离公式计算;有OA⊥OB知x1x2+y1y2=x1x2+(k x1+m) (k x2+m)=(1+k2) x1x2+k m(x1+x2)=0 代入,得4 m2=3 k2+3原点到直线AB的距离d==,当AB的斜率不存在时, 11x y= ,可得,1x d==依然成立.所以点O 到直线点睛:本题考查了椭圆的性质,直线与圆锥曲线的位置关系,分类讨论思想,对于这类题目要掌握解题方法.设而不求,套用公式解决.7.【四川省成都市石室中学2017-2018学年高二10月月考】已知双曲线()222210x yb aa b-=>>渐近线方程为y=,O为坐标原点,点(M在双曲线上.(Ⅰ)求双曲线的方程;(Ⅱ)已知,P Q为双曲线上不同两点,点O在以PQ为直径的圆上,求2211OP OQ+的值.【答案】(Ⅰ)22126x y-=;(Ⅱ)221113OP OQ+=.【解析】试题分析:(1)根据渐近线方程得到设出双曲线的标准方程,代入点M的坐标求得参数即可;(2)由条件可得OP OQ⊥,可设出直线,OP OQ的方程,代入双曲线方程求得点,P Q的坐标可求得221113OP OQ+=。
2018届浙江省高考试题逐类透析――圆锥曲线

七、平面解析几何(二)圆锥曲线一、高考考什么?[考试说明]5.掌握椭圆、抛物线的定义、标准方程、几何图形及简单几何性质。
6.会解决直线与圆、椭圆、抛物线的位置关系的问题,会判断圆与圆的位置关系。
7.了解双曲线的定义、标准方程、几何图形及简单几何性质,了解直线与双曲线的位置关系。
8. 了解方程与曲线的对应关系,会求简单的曲线的方程。
[知识梳理]弦长公式:若直线与圆锥曲线相交于两点A()、B(),则:==通径:椭圆、双曲线,抛物线定义及基本量:椭圆双曲线抛物线定义基本量离心率抛物线:若的焦点弦为AB,,则:①②;③[全面解读]圆锥曲线是高中数学教学的核心内容之一,在高考数学中占有十分重要的地位,是高考的重点、热点和难点。
综观历年高考,试题中几乎考查了解析几何教学中的所有内容,重点考查了定义、位置关系、弦长、离心率、渐近线等问题,有较高的思维度和灵活性,通过一定量的计算,分析研究圆锥曲线的性质特点,充分考查解析几何的本质。
[难度系数] ★★★★☆二、高考怎么考?[原题解析][2004年](4)曲线y2=4x关于直线x=2对称的曲线方程是( )A.y2=8-4x B.y2=4x-8 C.y2=16-4x D.y2=4x-16(9)若椭圆(a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx 的焦点分成5∶3的两段,则此椭圆的离心率为 ( )A. B. C. D.[2005年](13)过双曲线(a>0,b>0)的左焦点且垂直于轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于_________.[2008年](12)已知为椭圆的两个焦点,过的直线交椭圆于A、B两点若,则=___________。
[2009年](9)过双曲线()的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C.若=,则双曲线的离心率是()A. B. C. D.[2010年](8)设、分别为双曲线的左、右焦点.若在双曲线右支上存在点,满足,且到直线的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )A. B.C. D.(13)设抛物线的焦点为,点.若线段的中点在抛物线上,则到该抛物线准线的距离为________。
2018年高考数学试题分类汇编之圆锥曲线解析版

2018年高考数学试题分类汇编之圆锥曲线(解析版)一、选择题1.(浙江卷)(2)双曲线221 3=x y -的焦点坐标是A .(0),0)B .(−2,0),(2,0)C .(0,,(0D .(0,−2),(0,2)解:∵双曲线方程可得双曲线的焦点在x 轴上,且a 2=3,b 2=1, 由此可得222=+=b a c ∴该双曲线的焦点坐标为(±2,0)故选:B2.(天津文)(7)已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于,A B 两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126,d d += 则双曲线的方程为(A )22139x y -= (B )22193x y -= (C )221412x y -=(D )221124x y -= 解:由题意可得,CD 是双曲线的一条渐近线x aby =,即0=-ay bx ,)0,(c F故选:A3.(天津理)(7)已知双曲线22221(0,0)x y a b a b-=>>的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点. 设A ,B 到双曲线同一条渐近线的距离分别为1d 和2d ,且126d d +=,则双曲线的方程为A221412x y -= B221124x y -= C 22139x y -= D 22193x y -=解:由题意可得,CD 是双曲线的一条渐近线x aby =,即0=-ay bx ,)0,(c F故选:C4.(全国卷一文)(4)已知椭圆C :22214x y a +=的一个焦点为(20),,则C 的离心率为A .13B .12C D 解:椭圆的一个焦点为(2,0),可得a 2-4=4,解得22=a ,故选:C5.(全国卷一理)(8)设抛物线C :y 2=4x 的焦点为F ,过点(–2,0)且斜率为23的直线与C 交于M ,N 两点,则FM FN ⋅= A .5B .6C .7D .8解:抛物线C :y 2=4x 的焦点为F (1,0),过点(-2,0联立直线与抛物线C :y 2=4x ,消去x 可得:y 2-6y+8=0, 解得y 1=2,y 2=4,不妨M (1,2),N (4,4),FM =(0,2), FN =(3,4).则 FM ∙FN =(0,2)•(3,4)=8. 故选:D6.(全国卷一理)(11)已知双曲线C :2213x y -=,O 为坐标原点,F 为C 的右焦点,过F 的直线与C 的两条渐近线的交点分别为M 、N .若△OMN 为直角三角形,则|MN |= A .32B .3 C. D .4故选:B7.(全国卷二文)(6)双曲线22221(0,0)x y a b a b-=>>A.y =B.y =C.y = D .y = 解:∵双曲线的离心率为==ace则2222±=-=aa c ab 故选:A.8.(全国卷二文)(11)已知1F ,2F 是椭圆C 的两个焦点,P 是C上的一点,若12PF PF ⊥,且2160PFF ∠=︒,则C 的离心率为 A.1 B.2C D 1-解:F 1,F 2是椭圆C 的两个焦点,P 是C 上的一点,若PF 1⊥PF 2,且∠PF 2F 1=60°, 可得椭圆的焦点坐标F 2(c ,0),所以P(c 23,21故选:D9.(全国卷二理)(5)双曲线22221(0,0)x y a b a b-=>>A .y =B .y =C .y x =D .y =解:∵双曲线的离心率为==ace则2222±=-=aa c ab 故选:A .10.(全国卷二理)(12)已知1F ,2F 是椭圆22221(0)x y C a b a b+=>>:的左,右焦点,A 是C 的左顶点,点P在过A 12PF F △为等腰三角形,12120F F P ∠=︒,则C 的离心率为 A .23B .12C .13D .14解:由题意可知:A (-a ,0),F 1(-c ,0),F 2(c ,0),直线AP 的方程为:)(a x y +=63,故选:D11.(全国卷三文)(10)已知双曲线22221(00)x y C a b a b-=>>:,(4,0)到C 的渐近线的距离为AB .2CD .故选:D12.(全国卷三理)(11)设12F F ,是双曲线22221x y C a b-=:(00a b >>,)的左、右焦点,O 是坐标原点.过2F 作C 的一条渐近线的垂线,垂足为P .若1PF ,则C 的离心率为A B .2 C D在三角形F 1PF 2中,由余弦定理可得|PF 1|2=|PF 2|2+|F 1F 2|2-2|PF 2|•|F 1F 2|COS ∠PF 2O ,故选:C二、填空题1.(北京文)(10)已知直线l 过点(1,0)且垂直于 轴,若l 被抛物线24y ax =截得的线段长为4,则抛物线的焦点坐标为_________.解:∵直线l 过点(1,0)且垂直于x 轴,∴x=1,代入到y 2=4ax ,可得y 2=4a ,显然a >0,∴y=±∴抛物线的焦点坐标为(1,0), 故答案为:(1,0)2.(北京文)(12)若双曲线2221(0)4x y a a -=>的离心率为2,则a =_________.解:双曲线的离心率为245422=+a a ,解得a=4. 故答案为:43.(北京理)(14)已知椭圆22221(0)x y M a b a b +=>>:,双曲线22221x y N m n -=:.若双曲线N 的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点,则椭圆M 的离心率为__________;双曲线N 的离心率为__________.解:若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点,4.(江苏卷)(8)在平面直角坐标系xOy中,若双曲线22221(0,0)x ya ba b-=>>的右焦点(,0)F c到一条渐近,则其离心率的值是.,故答案为:25.(浙江卷)(17)已知点P(0,1),椭圆24x+y2=m(m>1)上两点A,B满足AP=2PB,则当m=_______时,点B横坐标的绝对值最大.解:设A(x1,y1),B(x2,y2),由P(0,1),AP=2PB,可得-x 1=2x2,1-y1=2(y2-1),即有x1=-2x2,y1+2y2=3,又x12+4y12=4m,即为x22+y12=m,①x22+4y22=4m,②①-②得(y1-2y2)(y1+2y2)=-3m,可得y1-2y2=-m,即有m=5时,x22有最大值4,即点B横坐标的绝对值最大.故答案为:5.6.(全国卷三理)(16)已知点()11M -,和抛物线24C y x =:,过C 的焦点且斜率为k 的直线与C 交于A ,B 两点.若90AMB =︒∠,则k =________.解:∵抛物线C :y 2=4x 的焦点F (1,0),∴过A ,B 两点的直线方程为y=k (x-1),联立⎩⎨⎧-==)1(42x k y xy 可得,k 2x 2-2(2+k 2)x+k 2=0,设A (x 1,y 1),B (x 2,y 2),y 1y 2=k 2(x 1-1)(x 2-1)=k 2[x 1x 2-(x 1+x 2)+1]=-4,∵M (-1,1),∴ MA =(x 1+1,y 1-1), MB =(x 2+1,y 2-1), ∵∠AMB=90°=0,∴MA *MB =0∴(x 1+1)(x 2+1)+(y 1-1)(y 2-1)=0,整理可得,x 1x 2+(x 1+x 2)+y 1y 2-(y 1+y 2)+2=0,∴即k 2-4k+4=0, ∴k=2. 故答案为:2三、解答题1.(北京文)(20)(本小题14分)已知椭圆2222:1(0)x y M a b a b +=>>焦距为斜率为k 的直线l 与椭圆M 有两个不同的交点A ,B .(Ⅰ)求椭圆M 的方程;(Ⅱ)若1k =,求||AB 的最大值;(Ⅲ)设(2,0)P -,直线P A 与椭圆M 的另一个交点为C ,直线PB 与椭圆M 的另一个交点为D .若C ,D和点71(,)42Q -共线,求k .解析(Ⅰ)由题意得2c =,所以c =3c e a ==,所以a =2221b a c =-=, 所以椭圆M 的标准方程为2213x y +=.(Ⅱ)设直线AB 的方程为y x m =+,由2213y x m x y =+⎧⎪⎨+=⎪⎩消去y 可得2246330x mx m ++-=, 则2223644(33)48120m m m ∆=-⨯-=->,即24m <,设11(,)A x y ,22(,)B x y ,则1232m x x +=-,212334m x x -=,则12|||AB x x =-=,易得当20m =时,max ||AB =||AB(Ⅲ)设11(,)A x y ,22(,)B x y ,33(,)C x y ,44(,)D x y , 则221133x y += ①,222233x y += ②, 又(2,0)P -,所以可设1112PA y k k x ==+,直线PA 的方程为1(2)y k x =+, 由122(2)13y k x x y =+⎧⎪⎨+=⎪⎩消去y 可得2222111(13)121230k x k x k +++-=, 则2113211213k x x k +=-+,即2131211213k x x k =--+, 又1112y k x =+,代入①式可得13171247x x x --=+,所以13147y y x =+, 所以1111712(,)4747x y C x x --++,同理可得2222712(,)4747x y D x x --++.故3371(,)44QC x y =+-,4471(,)44QD x y =+-, 因为,,Q C D 三点共线,所以34437171()()()()04444x y x y +--+-=,将点,C D 的坐标代入化简可得12121y y x x -=-,即1k =.2.(北京理)(19)(本小题14分)已知抛物线C :2y =2px 经过点P (1,2).过点Q (0,1)的直线l 与抛物线C 有两个不同的交点A ,B ,且直线P A 交y 轴于M ,直线PB 交y 轴于N . (Ⅰ)求直线l 的斜率的取值范围;(Ⅱ)设O 为原点,μλ==,,求证:μλ11+为定值.解析:(Ⅰ)因为抛物线y 2=2px 经过点P (1,2), 所以4=2p ,解得p =2,所以抛物线的方程为y 2=4x . 由题意可知直线l 的斜率存在且不为0, 设直线l 的方程为y =kx +1(k ≠0). 由241y x y kx ⎧=⎨=+⎩得22(24)10k x k x +-+=. 依题意22(24)410k k ∆=--⨯⨯>,解得k<0或0<k<1. 又P A ,PB 与y 轴相交,故直线l 不过点(1,-2).从而k ≠-3. 所以直线l 斜率的取值范围是(-∞,-3)∪(-3,0)∪(0,1). (Ⅱ)设A (x 1,y 1),B (x 2,y 2). 由(I )知12224k x x k -+=-,1221x x k =. 直线P A 的方程为y –2=1122(1)1y y x x --=--. 令x =0,得点M 的纵坐标为1111212211M y kx y x x -+-+=+=+--. 同理得点N 的纵坐标为22121N kx y x -+=+-. 由μλ==,得=1M y λ-,1N y μ=-.所以2212121212122224112()111111=211(1)(1)11M N k x x x x x x k k y y k x k x k x x k k λμ-+---++=+=+=⋅=⋅------. 所以11λμ+为定值.3.(江苏卷)(18)(本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆C过点1)2,焦点12(F F ,圆O 的直径为12F F .(1)求椭圆C 及圆O 的方程;(2)设直线l 与圆O 相切于第一象限内的点P .①若直线l 与椭圆C 有且只有一个公共点,求点P 的坐标; ②直线l 与椭圆C 交于,A B 两点.若OAB △,求直线l 的方程.解析:(1)因为椭圆C的焦点为12(),F F -,可设椭圆C 的方程为22221(0)x y a b a b +=>>.又点1)2在椭圆C 上,所以2222311,43,a b a b ⎧+=⎪⎨⎪-=⎩,解得224,1,a b ⎧=⎪⎨=⎪⎩因此,椭圆C 的方程为2214x y +=.因为圆O 的直径为12F F ,所以其方程为223x y +=.(2)①设直线l 与圆O 相切于0000(),,(00)P x y x y >>,则22003x y +=, 所以直线l 的方程为0000()x y x x y y =--+,即0003x y x y y =-+. 由220001,43,x y x y x y y ⎧+=⎪⎪⎨⎪=-+⎪⎩,消去y ,得222200004243640()x y x x x y +-+-=.(*)因为直线l 与椭圆C 有且只有一个公共点,所以222222000000()()(24)(44364820)4x x y y y x ∆=--+-=-=. 因为00,0x y >,所以001x y =. 因此,点P的坐标为. ②因为三角形OAB,所以1 2AB OP ⋅=,从而AB =.设1122,,()(),A x y B x y ,由(*)得001,2x =,所以2222121()()x B y y x A =-+-222000222200048(2)(1)(4)x y x y x y -=+⋅+. 因为22003x y +=, 所以22022016(2)32(1)49x AB x -==+,即42002451000x x -+=, 解得22005(202x x ==舍去),则2012y =,因此P的坐标为. 综上,直线l的方程为y =+4.(天津文)(19)(本小题满分14分) 设椭圆22221(0)x y a b a b +=>> 的右顶点为A ,上顶点为B .||AB =(I )求椭圆的方程;(II )设直线:(0)l y kx k =<与椭圆交于,P Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若BPM △的面积是BPQ △面积的2倍,求k 的值.解析:(I )设椭圆的焦距为2c ,由已知得2259c a =,又由222a b c =+,可得23.a b =由||AB ==从而3,2a b ==. 所以,椭圆的方程为22194x y +=. (II )解:设点P 的坐标为11(,)x y ,点M 的坐标为22(,)x y ,由题意,210x x >>,点Q 的坐标为11(,).x y -- 由BPM △的面积是BPQ △面积的2倍,可得||=2||PM PQ ,从而21112[()]x x x x -=--,即215x x =.易知直线AB 的方程为236x y +=,由方程组236,,x y y kx +=⎧⎨=⎩ 消去y ,可得2632x k =+.由方程组221,94,x y y kx ⎧+⎪=⎨⎪=⎩消去y,可得1x =由215x x =5(32)k =+,两边平方,整理得2182580k k ++=,解得89k =-,或12k =-. 当89k =-时,290x =-<,不合题意,舍去;当12k =-时,212x =,1125x =,符合题意. 所以,k 的值为12-. 5.(天津理)(19)(本小题满分14分) 设椭圆22221x x a b +=(a >b >0)的左焦点为F ,上顶点为B .,点A 的坐标为(,0)b ,且FB AB ⋅=.(I )求椭圆的方程;(II )设直线l :(0)y kx k =>与椭圆在第一象限的交点为P ,且l 与直线AB 交于点Q .若AQAOQ PQ =∠(O 为原点) ,求k 的值. 解析(Ⅰ):设椭圆的焦距为2c ,由已知知2259c a =,又由a 2=b 2+c 2,可得2a =3b .由已知可得,FB a =,AB,由FB AB ⋅=ab =6,从而a =3,b =2. 所以,椭圆的方程为22194x y +=. (Ⅱ)解:设点P 的坐标为(x 1,y 1),点Q 的坐标为(x 2,y 2).由已知有y 1>y 2>0,故12sin PQ AOQ y y ∠=-.又因为2sin y AQ OAB =∠,而∠OAB =π4,故2AQ.由AQ AOQ PQ =∠,可得5y 1=9y 2. 由方程组22194y kx x y =⎧⎪⎨+=⎪⎩,,消去x,可得1y =.易知直线AB 的方程为x +y –2=0,由方程组20y kx x y =⎧⎨+-=⎩,,消去x ,可得221k y k =+.由5y 1=9y 2,可得5(k +1)=,两边平方,整理得25650110k k -+=,解得12k =,或1128k =.所以,k 的值为111228或. 6.(浙江卷)(21)(本题满分15分)如图,已知点P 是y 轴左侧(不含y 轴)一点,抛物线C :y 2=4x 上存在不同的两点A ,B 满足P A ,PB 的中点均在C 上.(Ⅰ)设AB 中点为M ,证明:PM 垂直于y 轴;(Ⅱ)若P 是半椭圆x 2+24y =1(x <0)上的动点,求△P AB 面积的取值范围.解析(Ⅰ)设00(,)P x y ,2111(,)4A y y ,2221(,)4B y y . 因为PA ,PB 的中点在抛物线上,所以1y ,2y 为方程202014()422y x y y ++=⋅即22000280y y y x y -+-=的两个不同的实数根. 所以1202y y y +=.因此,PM 垂直于y 轴.(Ⅱ)由(Ⅰ)可知120212002,8,y y y y y x y +=⎧⎪⎨=-⎪⎩ 所以2221200013||()384PM y y x y x =+-=-,12||y y -= 因此,PAB △的面积32212001||||4)24PABS PM y y y x =⋅-=-△. 因为220001(0)4y x x +=<,所以2200004444[4,5]y x x x -=--+∈. 因此,PAB △面积的取值范围是7.(全国一卷文)(20)(12分)设抛物线22C y x =:,点()20A ,,()20B -,,过点A 的直线l 与C 交于M ,N 两点. (1)当l 与x 轴垂直时,求直线BM 的方程;(2)证明:ABM ABN =∠∠.解:(1)当l 与x 轴垂直时,l 的方程为x =2,可得M 的坐标为(2,2)或(2,–2).所以直线BM 的方程为y =112x +或112y x =--. (2)当l 与x 轴垂直时,AB 为MN 的垂直平分线,所以∠ABM =∠ABN .当l 与x 轴不垂直时,设l 的方程为(2)(0)y k x k =-≠,M (x 1,y 1),N (x 2,y 2),则x 1>0,x 2>0. 由2(2)2y k x y x=-⎧⎨=⎩,得ky 2–2y –4k =0,可知y 1+y 2=2k ,y 1y 2=–4. 直线BM ,BN 的斜率之和为1221121212122()22(2)(2)BM BN y y x y x y y y k k x x x x ++++=+=++++.① 将112y x k =+,222y x k=+及y 1+y 2,y 1y 2的表达式代入①式分子,可得 121221121224()882()0y y k y y x y x y y y k k ++-++++===. 所以k BM +k BN =0,可知BM ,BN 的倾斜角互补,所以∠ABM +∠ABN .综上,∠ABM =∠ABN .8.(全国一卷理)(19)(12分) 设椭圆22:12x C y +=的右焦点为F ,过F 的直线l 与C 交于,A B 两点,点M 的坐标为(2,0). (1)当l 与x 轴垂直时,求直线AM 的方程;(2)设O 为坐标原点,证明:OMA OMB ∠=∠.解:(1)由已知得(1,0)F ,l 的方程为x =1.由已知可得,点A的坐标为或(1,. 所以AM的方程为y x =+y x =. (2)当l 与x 轴重合时,0OMA OMB ∠=∠=︒.当l 与x 轴垂直时,OM 为AB 的垂直平分线,所以OMA OMB ∠=∠.当l 与x 轴不重合也不垂直时,设l 的方程为(1)(0)y k x k =-≠,1221(,),(,)A y x y x B ,则12x x <<,直线MA ,MB 的斜率之和为212122MA MB x x y y k k +=+--. 由1122,y k k x y k x k =-=-得 121212(23()42)(2)MA MB x x x x k k x x k k k -+++=--. 将(1)y k x =-代入2212x y +=得 2222(21)4220k x k x k +-+-=. 所以,21221222422,2121x x x k k k x k -+==++. 则3131322244128423()4021k k k k k k k k k x x x x --++-++==+. 从而0MA MB k k +=,故MA ,MB 的倾斜角互补,所以OMA OMB ∠=∠.综上,OMA OMB ∠=∠.9.(全国二卷文)(20)(12分)设抛物线24C y x =:的焦点为F ,过F 且斜率为(0)k k >的直线l 与C 交于A ,B 两点,||8AB =.(1)求l 的方程; (2)求过点A ,B 且与C 的准线相切的圆的方程.解:(1)由题意得F (1,0),l 的方程为y =k (x –1)(k >0).设A (x 1,y 1),B (x 2,y 2).由2(1)4y k x y x =-⎧⎨=⎩得2222(24)0k x k x k -++=.216160k ∆=+=,故212224k x x k ++=. 所以212244(1)(1)k AB AF BF x x k +=+=+++=. 由题设知22448k k +=,解得k =–1(舍去),k =1.因此l 的方程为y =x –1. (2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为2(3)y x -=--,即5y x =-+.设所求圆的圆心坐标为(x 0,y 0),则00220005(1)(1)16.2y x y x x =-+⎧⎪⎨-++=+⎪⎩,解得0032x y =⎧⎨=⎩,或00116.x y =⎧⎨=-⎩, 因此所求圆的方程为22(3)(2)16x y -+-=或22(11)(6)144x y -++=.10.(全国卷二理)(19)(12分)设抛物线24C y x =:的焦点为F ,过F 且斜率为(0)k k >的直线l 与C 交于A ,B 两点,||8AB =. (1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程.解:(1)由题意得(1,0)F ,l 的方程为(1)(0)y k x k =->.设1221(,),(,)A y x y x B ,由2(1),4y k x y x=-⎧⎨=⎩得2222(24)0k x k x k -++=. 216160k ∆=+>,故122224k x k x ++=. 所以122244||||||(1)(1)x k AB AF BF kx +=+=+++=. 由题设知22448k k +=,解得1k =-(舍去),1k =.因此l 的方程为1y x =-. (2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为2(3)y x -=--,即5y x =-+. 设所求圆的圆心坐标为00(,)x y ,则00220005,(1)(1)16.2y x y x x =-+⎧⎪⎨-++=+⎪⎩解得003,2x y =⎧⎨=⎩或0011,6.x y =⎧⎨=-⎩ 因此所求圆的方程为22(3)(2)16x y -+-=或22(11)(6)144x y -++=.11.(全国卷三文)(20)(12分) 已知斜率为k 的直线l 与椭圆22143x y C +=:交于A ,B 两点.线段AB 的中点为(1,)(0)M m m >. (1)证明:12k <-; (2)设F 为C 的右焦点,P 为C 上一点,且FP FA FB ++=0.证明:2||||||FP FA FB =+.解:(1)设11()A x y ,,22()B x y ,,则2211143x y +=,2222143x y +=. 两式相减,并由1212=y y k x x --得1212043x x y y k +++⋅=.由题设知1212x x +=,122y y m +=,于是34k m=-. 由题设得302m <<,故12k <-. (2)由题意得F (1,0).设33()P x y ,,则331122(1)(1)(1)(00)x y x y x y -+-+-=,,,,. 由(1)及题设得3123()1x x x =-+=,312()20y y y m =-+=-<.又点P 在C 上,所以34m =,从而3(1)2P -,,3||=2FP uu r .于是1||22x FA =-uu r .同理2||=22x FB -uu r . 所以1214()32FA FB x x +=-+=u u r u u r .故2||=||+||FP FA FB u u r u u r u u r . 12.(全国卷三理)(20)(12分)已知斜率为k 的直线l 与椭圆22143x y C +=:交于A ,B 两点,线段AB 的中点为()()10M m m >,. (1)证明:12k <-; (2)设F 为C 的右焦点,P 为C 上一点,且FP FA FB ++=0.证明:FA ,FP ,FB 成等差数列,并求该数列的公差.解:(1)设1221(,),(,)A y x y x B ,则222212121,14343y x y x +=+=. 两式相减,并由1221y x y k x -=-得 1122043y x y k x +++⋅=. 由题设知12121,22x y x y m ++==,于是 34k m=-.① 由题设得302m <<,故12k <-. (2)由题意得(1,0)F ,设33(,)P x y ,则 331122(1,)(1,)(1,)(0,0)y x x y x y -+-+-=. 由(1)及题设得3321213()1,()20y y x x y x m =-+==-+=-<.又点P 在C 上,所以34m =,从而3(1,)2P -,3||2FP =.于是 1||(22x FA x ==-. 同理2||22x FB =-. 所以121||||4()32FA FB x x +=-+=. 故2||||||FP FA FB =+,即||,||,||FA FP FB 成等差数列.设该数列的公差为d ,则 1212||||||||||2FB FA x x d =-=-=②将34m =代入①得1k =-. 所以l 的方程为74y x =-+,代入C 的方程,并整理得2171404x x -+=.故121212,28x x x x +==,代入②解得||d =.或。
2018年高考圆锥曲线部分大题解析
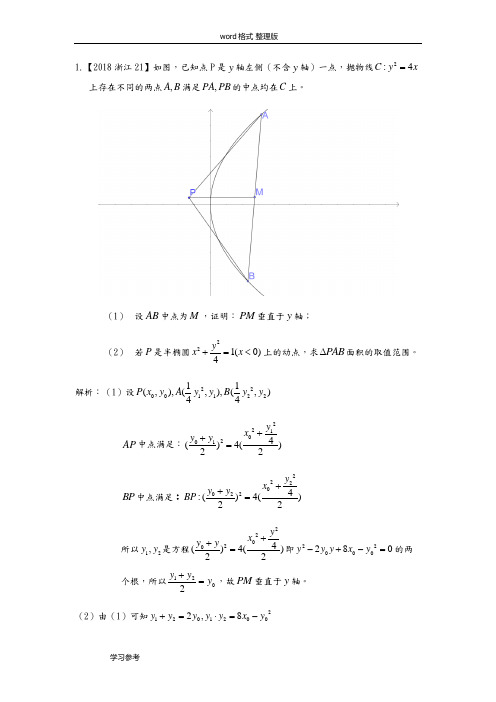
1.【2018浙江21】如图,已知点P 是y 轴左侧(不含y 轴)一点,抛物线2:4C y x =上存在不同的两点,A B 满足,PA PB 的中点均在C 上。
(1) 设AB 中点为M ,证明:PM 垂直于y 轴;(2) 若P 是半椭圆221(0)4y x x +=<上的动点,求PAB ∆面积的取值范围。
解析:(1)设2200112211(,),(,),(,)44P x y A y y B y yAP 中点满足:22102014()4()22y x y y ++= BP 中点满足:22202024:()4()22y x y y BP ++= 所以12,y y 是方程220204()4()22y x y y ++=即22000280y y y x y -+-=的两个根,所以1202y y y +=,故PM 垂直于y 轴。
(2)由(1)可知212012002,8y y y y y x y +=⋅=-所以2221200013||()384PM y y x y x =+-=-,12||y y -=因此,32212001||||4)24PABS PM y y y x ∆=⋅-=- 因为220001(0)4y x x +=<,所以2200004444[4,5]y x x x -=--+∈因此,PAB ∆面积的取值范围是 1. 距离型问题2.【2018全国3 理20】已知斜率为k 的直线l 与椭圆22:143x y C +=交于,A B 两点,线段AB 的中点为(1,)(0)M m m >(1)证明:12k <-; (2)设F 为C 的右焦点,P 为C 上一点且0FP FA FB ++=,证明:,,FP FA FB 为等差数列,并求出该数列的公差。
解析:(1)由中点弦公式22OMb k k a⋅=-,解得34k m =-又因为点M 在椭圆内,故302m <<,故12k <- (2)由题意知2,2FA FB FM FP FM +==-,故(1,2)P m -因为点P 在椭圆上,代入可得3,14m k ==-,即3||2FP = 根据第二定义可知,1211||2,||222FA x FB x =-=- 121||||4()2FA FB x x +=-+联立22212121114371402,42874x y x x x x x x y x ⎧+=⎪⎪⇒-+=⇒+==⎨⎪=-+⎪⎩即121||||4()32FA FB x x +=-+= 故满足2||||||FP FA FB =+,所以,,FP FA FB 为等差数列 设其公差为d ,因为,A B 的位置不确定,则有1212||||||||2d FA FB x x =±-=±-=代入得21428d d =±=±3.【2018全国3 文20】已知斜率为k 的直线l 与椭圆22:143x y C +=交于,A B 两点,线段AB 的中点为(1,)(0)M m m >(1)证明:12k <-; (2)设F 为C 的右焦点,P 为C 上一点且0FP FA FB ++=,证明2||||||FP FA FB =+。
专题10圆锥曲线(热点难点突破)2018年高考数学(文)考纲解读与热点难点突破版含解析数学

1.点A 是抛物线C :x 2=2py (p >0)上一点 ,O 为坐标原点 ,假设以点M (0,8)为圆心 ,|OA |的长为半径的圆交抛物线C 于A ,B 两点 ,且△ABO 为等边三角形 ,那么p 的值是( ) A.38 B .2 C .6 D.23【答案】D 【解析】由题意知|MA |=|OA | ,所以点A 的纵坐标为4 ,又△ABO 为等边三角形 ,所以点A 的横坐标为433 ,又点A 是抛物线C 上一点 ,所以163=2p ×4 ,解得p =23.2.焦点在x 轴上的椭圆方程为x 24a +y 2a 2+1=1 ,随着a 的增大该椭圆的形状( )A .越接近于圆B .越扁C .先接近于圆后越扁D .先越扁后接近于圆【答案】D 【解析】由题意知4a >a 2+1且a >0 ,解得2-3<a <2+ 3 ,又e 2=1-b 2a 2=1-a 2+14a =1-14⎝ ⎛⎭⎪⎫a +1a .因此当a ∈(2- 3 ,1)时 ,e 越来越大 ,当a ∈ (1,2+3)时 ,e 越来越小 ,应选D.3.F 1 ,F 2分别是双曲线x 2a 2-y 2b2=1(a >0 ,b >0)的左、右焦点 ,对于左支上任意一点P 都有|PF 2|2=8a |PF 1|(a为实半轴) ,那么此双曲线的离心率e 的取值范围是( ) A .(1 ,+∞) B .(2,3] C .(1,3]D .(1,2]4.抛物线y 2=2px (p >0)的焦点为F ,点A ,B 为抛物线上的两个动点 ,且满足∠AFB =120°.过弦AB 的中点M 作抛物线准线的垂线MN ,垂足为N ,那么|MN ||AB |的最||大值为( )A.33B .1 C.233D .2【答案】A 【解析】设AF =a ,BF =b ,由余弦定理得|AB |2=a 2+b 2-2ab cos 120°=a 2+b 2+ab =(a +b )2-ab ≥(a +b )2-⎝⎛⎭⎪⎫a +b 22=34(a +b )2.∵a +b =AF +BF =2MN ,∴|AB |2≥34|2MN |2 ,∴|MN ||AB |≤33.5.过点A (0,1)作直线 ,与双曲线x 2-y 29=1有且只有一个公共点 ,那么符合条件的直线的条数为( )A .0B .2C .4D .无数【答案】C 【解析】过点A (0,1)和双曲线的渐近线平行的直线和双曲线只有一个公共点 ,这样的直线有两条 ,过点A (0,1)和双曲线相切的直线只有一个公共点 ,这样的直线也有两条 ,故共四条直线与双曲线有且只有一个公共点.6.椭圆y 2+x 2m2=1(0<m <1)上存在点P 使得PF 1⊥PF 2 ,那么m 的取值范围是( )A.⎣⎢⎢⎡⎭⎪⎪⎫22 1 B .⎝ ⎛⎦⎥⎥⎤0 22 C.⎣⎢⎢⎡⎭⎪⎪⎫12 1 D.⎝ ⎛⎦⎥⎥⎤0 12 【答案】B 【解析】当点P 是短轴的顶点时∠F 1PF 2最||大 ,因此假设椭圆上存在点P 使得PF 1⊥PF 2 ,那么∠F 1PF 2≥90° ,所以∠F 2PO ≥45°(O 是原点) ,从而c a≥22 ,即1-m 2≥12 ,又0<m <1 ,所以0<m ≤22. 7.设点P 是椭圆x 2a 2+y 2b2=1(a >b >0)上一点 ,F 1 ,F 2分别是椭圆的左 ,右焦点 ,I 为△PF 1F 2的内心 ,假设S△IPF 1+S △IPF 2=2S △IF 1F 2 ,那么该椭圆的离心率为( ) A.12 B .22 C.32D.3-128.椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为32.双曲线x 2-y 2=1的渐近线与椭圆C 有四个交点 ,以这四个交点为顶点的四边形的面积为16 ,那么椭圆C 的方程为( ) A.x 28+y 22=1B .x 212+y 26=1 C.x 216+y 24=1 D.x 220+y 25=1 【答案】D 【解析】椭圆的离心率e =c a =a 2-b 2a =32,所以a =2b .所以椭圆方程为x 2+4y 2=4b 2.因为双曲线x 2-y 2=1的渐近线方程为x ±y =0 ,所以渐近线x ±y =0与椭圆x 2+4y 2=4b 2在第|一象限的交点为⎝ ⎛⎭⎪⎪⎫255b 255b ,所以由圆锥曲线的对称性得四边形在第|一象限局部的面积为255b ×255b =4 ,所以b 2=5 ,所以a 2=4b 2=20. 所以椭圆C 的方程为x 220+y 25=1.应选D.9.双曲线M :x 2-y 2b2=1的左、右焦点分别为F 1 ,F 2 ,记|F 1F 2|=2c ,以坐标原点O 为圆心 ,c 为半径的圆与双曲线M 在第|一象限的交点为P ,假设|PF 1|=c +2 ,那么P 点的横坐标为________. 【答案】3+12【解析】根据双曲线的定义知|PF 1|-|PF 2|=2 ,又|PF 1|=c +2 ,所以|PF 2|=c ,由勾股定理得(c +2)2+c 2=4c 2,即c 2-2c -2=0 ,解得c =3+1 ,根据△OPF 2是等边三角形得P 点的横坐标为3+12. 10.F 1 ,F 2为x 2a 2+y 216=1的左、右焦点 ,M 为椭圆上一点 ,那么△MF 1F 2内切圆的周长等于3π ,假设满足条件的点M 恰好有2个 ,那么a 2=________.11.如图141 ,F 1 ,F 2是双曲线x2a2-y 2b2=1(a >0 ,b >0)的左、右焦点 ,过F 1的直线l 与双曲线的左、右两支分别交于点B ,A .假设△ABF 2为等边三角形 ,那么双曲线的离心率为________. 图141 【答案】7【解析】因为△ABF 2为等边三角形 ,由点A 是双曲线上的一点知 ,|F 1A |-|F 2A |=|F 1A |-|AB |=|F 1B |=2a ,由点B 是双曲线上一点知 ,|BF 2|-|BF 1|=2a ,从而|BF 2|=4a ,由∠ABF 2=60°得∠F 1BF 2=120° ,在△F 1BF 2中应用余弦定理得4c 2=4a 2+16a 2-2·2a ·4a ·cos 120° ,整理得c 2=7a 2,那么e 2=7 ,从而e =7.12.设F 1 ,F 2是椭圆x 2+y 2b2=1(0<b <1)的左、右焦点 ,过F 1的直线l 交椭圆于A ,B 两点 ,假设|AF 1|=3|F 1B | ,且AF 2⊥x 轴 ,那么b 2=________.【答案】2313.过抛物线y 2=4x 焦点F 的直线交其于A ,B 两点 ,O 为坐标原点.假设|AF |=3 ,那么△AOB 的面积为________. 【答案】322【解析】设直线AB 的倾斜角为θ(0<θ<π)及|BF |=m , ∵|AF |=3 ,∴点A 到准线l :x =-1的距离为3 , ∴2+3cos θ=3 ,即cos θ=13 ,那么sin θ=223.∵m =2+m cos(π-θ) ,∴m =21+cos θ=32 ,∴△AOB 的面积为S =12×|OF |×|AB |×sin θ=12×1×⎝⎛⎭⎪⎫3+32×223=322. 14.如图142 ,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的右焦点为F ,右顶点、上顶点分别为点A ,B ,且|AB |=52|BF |.图142(1)求椭圆C 的离心率;(2)假设点M⎝ ⎛⎭⎪⎪⎫-1617 217在椭圆C 内部 ,过点M 的直线l 交椭圆C 于P ,Q 两点 ,M 为线段PQ 的中点 ,且OP ⊥OQ .求直线l 的方程及椭圆C 的方程.[解] (1)由|AB |=52|BF | ,即a 2+b 2=52a ,2分 4a 2+4b 2=5a 2,4a 2+4(a 2-c 2)=5a 2, ∴e =ca =32.4分 (2)由(1)知a 2=4b 2,∴椭圆C :x 24b 2+y 2b 2P (x 1 ,y 1) ,Q (x 2 ,y 2) ,由x 214b 2+y 21b 2=1 ,x 224b 2+y 22b2=1 ,可得x 21-x 224b 2+y 21-y 22b 2=0 , 即x 1+x 2x 1-x 24b2+y 1+y 2y 1-y 2b2=0 ,即-3217x 1-x 24+417(y 1-y 2)=0 ,从而k PQ =y 1-y 2x 1-x 2=2 ,6分 ∴直线l 的方程为y -217=2⎣⎢⎡⎦⎥⎤x -⎝ ⎛⎭⎪⎫-1617 ,即2x -y 由⎩⎪⎨⎪⎧2x -y +2=0 x 24b 2+y 2b2=1⇒x 2+4(2x +2)2-4b 2=0 ,即17x 2+32x +16-4b 2=0 ,9分Δ=322+16×17(b 2-4)>0⇔b >21717 ,x 1+x 2=-3217 ,x 1x 2=16-4b 217.∵OP ⊥OQ ,∴OP →·OQ →=0 ,即x 1x 2+y 1y 2=0 ,x 1x 2+(2x 1+2)(2x 2+2)=0,5x 1x 2+4(x 1+x 2)+4=0 ,11分从而516-4b 217-12817+4=0 ,解得b =1 ,椭圆C 的方程为x 24+y 2 15.在△ABC 中 ,A (-1,0) ,B (1,0) ,假设△ABC 的重心G 和垂心H 满足GH 平行于x 轴(G ,H 不重合). (1)求动点C 的轨迹方程;(2)O 为坐标原点 ,假设直线AC 与以O 为圆心 ,以|OH |为半径的圆相切 ,求此时直线AC 的方程. 依题意可得k 21+k 2=9-2k 2+k49+6k 2+k4 ,10分即7k 4+2k 2-9=0 ,解得k 2=1 ,即k =1或-1 , 故所求直线AC 的方程为y =x +1或y =-x16.椭圆E :x 2a 2+y 2b 2=1(a >b >0)的离心率为22,右焦点为F (1 ,0).(1)求椭圆E 的标准方程;(2)设点O 为坐标原点 ,过点F 作直线l 与椭圆E 交于M ,N 两点 ,假设OM ⊥ON ,求直线l 的方程.17.椭圆E :x 2a 2+y 2b 2=1(a >b >0)的离心率为32,点P ⎝ ⎛⎭⎪⎪⎫1 32在椭圆E 上.(1)求椭圆E 的方程;(2)过点P 且斜率为k 的直线l 交椭圆E 于点Q (x Q ,y Q )(点Q 异于点P ) ,假设0<x Q <1 ,求直线l 斜率k 的取值范围.18.抛物线C :x 2=2py (p >0)的焦点为F ,直线2x -y +2=0交抛物线C 于A , B 两点 ,P 是线段AB 的中点 ,过P 作x 轴的垂线交抛物线C 于点Q .(1)D 是抛物线C 上的动点 ,点E (-1 ,3) ,假设直线AB 过焦点F ,求|DF |+|DE |的最||小值; (2)是否存在实数p ,使|2QA →+QB →|=|2QA →-QB →| ?假设存在 ,求出p 的值;假设不存在 ,说明理由. 解:(1)因为直线2x -y +2=0与y 轴的交点为(0 ,2) , 所以F (0 ,2) ,那么抛物线C 的方程为x 2=8y ,准线l :y =-2. 设过D 作DG ⊥l 于G ,那么|DF |+|DE |=|DG |+|DE | , 当E , D ,G 三点共线时 ,|DF |+|DE |取最||小值为2+3=5. (2)假设存在实数p ,满足条件等式成立. 联立x 2=2py 与2x -y +2=0 , 消去y ,得x 2-4px -4p =0.设A (x 1 ,y 1) ,B (x 2 ,y 2) ,那么x 1+x 2=4p ,x 1x 2=-4p ,所以Q (2p ,2p ). 因为|2QA →+QB →|=|2QA →-QB →| , 所以QA ⊥QB ,那么QA →·QB →=0.因此(x 1-2p )(x 2-2p )+(y 1-2p )(y 2-2p )=0. (x 1-2p )(x 2-2p )+(2x 1+2-2p )·(2x 2+2-2p )=0 , 5x 1x 2+(4-6p )(x 1+x 2)+8p 2-8p +4=0 ,把x 1+x 2=4p ,x 1x 2=-4p 代入得4p 2+3p -1=0 ,解得p =14或p =-1(舍去).因此存在实数p =14,使得|2QA →+QB →|=|2QA →-QB →|成立.19.椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为22,点Q ⎝ ⎛⎭⎪⎪⎫b a b 在椭圆上 ,O 为坐标原点.(1)求椭圆C 的方程;(2)点P ,M ,N 为椭圆C 上的三点 ,假设四边形OPMN 为平行四边形 ,证明四边形OPMN 的面积S 为定值 ,并求该定值.。
2018年高考数学—圆锥曲线(解答+答案)

2018年高考数学——圆锥曲线解答1.(18北京理(19)(本小题14分))已知抛物线C :2y =2px 经过点P (1,2).过点Q (0,1)的直线l 与抛物线C 有两个不同的交点A ,B ,且直线PA 交y 轴于M ,直线PB 交y 轴于N . (Ⅰ)求直线l 的斜率的取值范围;(Ⅱ)设O 为原点,QM QO λ=u u u u r u u u r ,QN QO μ=u u u r u u u r ,求证:11λμ+为定值.2.(18江苏18.(本小题满分16分))如图,在平面直角坐标系xOy 中,椭圆C 过点1(3,)2,焦点12(3,0),(3,0)F F ,圆O 的直径为12F F .(1)求椭圆C 及圆O 的方程;(2)设直线l 与圆O 相切于第一象限内的点P .①若直线l 与椭圆C 有且只有一个公共点,求点P 的坐标; ②直线l 与椭圆C 交于,A B 两点.若OAB △26,求直线l 的方程.3.(18全国二理19.(12分))设抛物线24C y x =:的焦点为F ,过F 且斜率为(0)k k >的直线l 与C 交于A ,B 两点,||8AB =.(1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程.4.(18全国三理20.(12分))已知斜率为k 的直线l 与椭圆22143x y C +=:交于A ,B 两点,线段AB 的中点为()()10M m m >,. (1)证明:12k <-;(2)设F 为C 的右焦点,P 为C 上一点,且FP FA FB ++=0u u u r u u u r u u u r.证明:FA u u u r ,FP u u u r ,FB u u u r 成等差数列,并求该数列的公差.5.18全国一理19.(12分)设椭圆22:12x C y +=的右焦点为F ,过F 的直线l 与C 交于,A B 两点,点M 的坐标为(2,0).(1)当l 与x 轴垂直时,求直线AM 的方程; (2)设O 为坐标原点,证明:OMA OMB ∠=∠.6.(18天津理(19)(本小题满分14分))设椭圆22221x x a b+=(a >b >0)的左焦点为F ,上顶点为B .A的坐标为(,0)b,且FB AB ⋅=(I )求椭圆的方程;(II )设直线l :(0)y kx k =>与椭圆在第一象限的交点为P ,且l 与直线AB 交于点Q .若4AQ AOQ PQ=∠(O 为原点) ,求k 的值.7.(18浙江21.(本题满分15分))如图,已知点P 是y 轴左侧(不含y 轴)一点,抛物线C :y 2=4x 上存在不同的两点A ,B 满足PA ,PB 的中点均在C 上.(Ⅰ)设AB 中点为M ,证明:PM 垂直于y 轴;(Ⅱ)若P 是半椭圆x 2+24y =1(x <0)上的动点,求△P AB 面积的取值范围.8.(18北京文(20)(本小题14分))已知椭圆2222:1(0)x y M a b a b +=>>的离心率为63,焦距为22.斜率为k 的直线l与椭圆M 有两个不同的交点A ,B . (Ⅰ)求椭圆M 的方程;(Ⅱ)若1k =,求||AB 的最大值;(Ⅲ)设(2,0)P -,直线PA 与椭圆M 的另一个交点为C ,直线PB 与椭圆M 的另一个交点为D .若C ,D 和点71(,)42Q - 共线,求k .9.(18全国三文20.(12分))已知斜率为k 的直线l 与椭圆22143x y C +=:交于A ,B 两点.线段AB 的中点为(1,)(0)M m m >.(1)证明:12k <-; (2)设F 为C 的右焦点,P 为C 上一点,且FP FA FB ++=0u u u r u u u r u u u r.证明:2||||||FP FA FB =+u u u r u u u r u u u r .10.(18全国一文20.(12分))设抛物线22C y x =:,点()20A ,,()20B -,,过点A 的直线l 与C 交于M ,N 两点. (1)当l 与x 轴垂直时,求直线BM 的方程; (2)证明:ABM ABN =∠∠.参考答案:1.解:(Ⅰ)因为抛物线y 2=2px 经过点P (1,2), 所以4=2p ,解得p =2,所以抛物线的方程为y 2=4x . 由题意可知直线l 的斜率存在且不为0, 设直线l 的方程为y =kx +1(k ≠0). 由241y xy kx ⎧=⎨=+⎩得22(24)10k x k x +-+=. 依题意22(24)410k k ∆=--⨯⨯>,解得k<0或0<k<1. 又PA ,PB 与y 轴相交,故直线l 不过点(1,-2).从而k ≠-3.所以直线l 斜率的取值范围是(-∞,-3)∪(-3,0)∪(0,1). (Ⅱ)设A (x 1,y 1),B (x 2,y 2).由(I )知12224k x x k -+=-,1221x x k =. 直线PA 的方程为y –2=1122(1)1y y x x --=--.令x =0,得点M 的纵坐标为1111212211M y kx y x x -+-+=+=+--. 同理得点N 的纵坐标为22121N kx y x -+=+-. 由=QM QO λuuu r uuu r ,=QN QO μuuu r uuu r得=1M y λ-,1N y μ=-.所以2212121212122224112()111111=2111(1)(1)11M N k x x x x x x k k y y k x k x k x x k k λμ-+---++=+=+=⋅=⋅------. 所以11λμ+为定值.2.解:(1)因为椭圆C的焦点为12(),F F -,可设椭圆C 的方程为22221(0)x y a b a b +=>>.又点1)2在椭圆C 上,所以2222311,43,a ba b ⎧+=⎪⎨⎪-=⎩,解得224,1,a b ⎧=⎪⎨=⎪⎩ 因此,椭圆C 的方程为2214x y +=.因为圆O 的直径为12F F ,所以其方程为223x y +=.(2)①设直线l 与圆O 相切于0000(),,(00)P x y x y >>,则22003x y +=, 所以直线l 的方程为0000()x y x x y y =--+,即0003x y x y y =-+. 由220001,43,x y x y x y y ⎧+=⎪⎪⎨⎪=-+⎪⎩,消去y ,得222200004243640()x y x x x y +-+-=.(*) 因为直线l 与椭圆C 有且只有一个公共点,所以222222000000()()(24)(44364820)4x x y y y x ∆=--+-=-=. 因为00,0x y >,所以002,1x y ==. 因此,点P 的坐标为(2,1). ②因为三角形OAB 的面积为26,所以21 26AB OP ⋅=,从而427AB =. 设1122,,()(),A x y B x y ,由(*)得22000001,22448(2)x y x x ±-=,所以2222121()()x B y y x A =-+- 222000222200048(2)(1)(4)x y x y x y -=+⋅+.因为22003x y +=,所以22022016(2)32(1)49x AB x -==+,即42002451000x x -+=, 解得22005(202x x ==舍去),则2012y =,因此P 的坐标为102(,).综上,直线l 的方程为532y x =-+.学*科网3.解:(1)由题意得(1,0)F ,l 的方程为(1)(0)y k x k =->.设1221(,),(,)A y x y x B , 由2(1),4y k x y x=-⎧⎨=⎩得2222(24)0k x k x k -++=.216160k ∆=+>,故122224k x k x ++=. 所以122244||||||(1)(1)x k AB AF BF k x +=+=+++=.由题设知22448k k+=,解得1k =-(舍去),1k =. 因此l 的方程为1y x =-.(2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为2(3)y x -=--,即5y x =-+.设所求圆的圆心坐标为00(,)x y ,则00220005,(1)(1)16.2y x y x x =-+⎧⎪⎨-++=+⎪⎩解得003,2x y =⎧⎨=⎩或0011,6.x y =⎧⎨=-⎩ 因此所求圆的方程为22(3)(2)16x y -+-=或22(11)(6)144x y -++=.4.解:(1)设1221(,),(,)A y x y x B ,则222212121,14343y x y x +=+=. 两式相减,并由1221y x y k x -=-得1122043y x y k x +++⋅=. 由题设知12121,22x y x ym ++==,于是 34k m=-.① 由题设得302m <<,故12k <-. (2)由题意得(1,0)F ,设33(,)P x y ,则331122(1,)(1,)(1,)(0,0)y x x y x y -+-+-=.由(1)及题设得3321213()1,()20y y x x y x m =-+==-+=-<.又点P 在C 上,所以34m =,从而3(1,)2P -,3||2FP =u u u r .于是1||22x FA ===-u u u r .同理2||22xFB =-u u u r .所以121||||4()32FA FB x x +=-+=u u u r u u u r .故2||||||FP FA FB =+u u u r u u u r u u u r ,即||,||,||FA FP FB u u u r u u u r u u u r成等差数列.设该数列的公差为d ,则1212||||||||||2FB FA x x d =-=-=u u u r u u u r .②将34m =代入①得1k =-. 所以l 的方程为74y x =-+,代入C 的方程,并整理得2171404x x -+=.故121212,28x x x x +==,代入②解得||28d =.所以该数列的公差为28或28-.5解:(1)由已知得(1,0)F ,l 的方程为x =1.由已知可得,点A 的坐标为(1,2或(1,2-.所以AM 的方程为y x =+y x =.(2)当l 与x 轴重合时,0OMA OMB ∠=∠=︒.当l 与x 轴垂直时,OM 为AB 的垂直平分线,所以OMA OMB ∠=∠.当l 与x 轴不重合也不垂直时,设l 的方程为(1)(0)y k x k =-≠,1221(,),(,)A y x y x B ,则12x x <<MA ,MB 的斜率之和为212122MA MB x x y yk k +=+--. 由1122,y k k x y k x k =-=-得121212(23()42)(2)MA MB x x x x k k x x kk k -+++=--.将(1)y k x =-代入2212x y +=得 2222(21)4220k x k x k +-+-=.所以,21221222422,2121x x x k k k x k -+==++. 则3131322244128423()4021k k k k kk k k k x x x x --++-++==+. 从而0MA MB k k +=,故MA ,MB 的倾斜角互补,所以OMA OMB ∠=∠. 综上,OMA OMB ∠=∠.6.(Ⅰ)解:设椭圆的焦距为2c ,由已知知2259c a =,又由a 2=b 2+c 2,可得2a =3b .由已知可得,FB a =,AB =,由FB AB ⋅=,可得ab =6,从而a =3,b =2.所以,椭圆的方程为22194x y +=. (Ⅱ)解:设点P 的坐标为(x 1,y 1),点Q 的坐标为(x 2,y 2).由已知有y 1>y 2>0,故12sin PQ AOQ y y ∠=-.又因为2sin y AQ OAB =∠,而∠OAB =π4,故2AQ =.由AQ AOQ PQ=∠,可得5y 1=9y 2. 由方程组22194y kx x y =⎧⎪⎨+=⎪⎩,,消去x,可得1y =AB 的方程为x +y –2=0,由方程组20y kx x y =⎧⎨+-=⎩,,消去x ,可得221ky k =+.由5y 1=9y 2,可得5(k +1)=,两边平方,整理得25650110k k -+=,解得12k =,或1128k =. 所以,k 的值为111228或.7.(Ⅰ)设00(,)P x y ,2111(,)4A y y ,2221(,)4B y y . 因为PA ,PB 的中点在抛物线上,所以1y ,2y 为方程202014()422y x y y ++=⋅即22000280y y y x y -+-=的两个不同的实数根. 所以1202y y y +=. 因此,PM 垂直于y 轴.(Ⅱ)由(Ⅰ)可知120212002,8,y y y y y x y +=⎧⎪⎨=-⎪⎩ 所以2221200013||()384PM y y x y x =+-=-,12||y y -= 因此,PAB △的面积32212001||||4)24PABS PM y y y x =⋅-=-△. 因为220001(0)4y x x +=<,所以2200004444[4,5]y x x x -=--+∈.因此,PAB △面积的取值范围是.8.【解析】(Ⅰ)由题意得2c =,所以c =又3c e a ==,所以a =2221b a c =-=, 所以椭圆M 的标准方程为2213x y +=.(Ⅱ)设直线AB 的方程为y x m =+,由2213y x m x y =+⎧⎪⎨+=⎪⎩消去y 可得2246330x mx m ++-=, 则2223644(33)48120m m m ∆=-⨯-=->,即24m <,设11(,)A x y ,22(,)B x y ,则1232m x x +=-,212334m x x -=,则12|||2AB x x =-==,易得当20m =时,max ||AB ,故||AB. (Ⅲ)设11(,)A x y ,22(,)B x y ,33(,)C x y ,44(,)D x y ,则221133x y += ①,222233x y += ②,又(2,0)P -,所以可设1112PA y k k x ==+,直线PA 的方程为1(2)y k x =+, 由122(2)13y k x x y =+⎧⎪⎨+=⎪⎩消去y 可得2222111(13)121230k x k x k +++-=, 则2113211213k x x k +=-+,即2131211213k x x k =--+, 又1112y k x =+,代入①式可得13171247x x x --=+,所以13147y y x =+,所以1111712(,)4747x y C x x --++,同理可得2222712(,)4747x y D x x --++.故3371(,)44QC x y =+-u u u r ,4471(,)44QD x y =+-u u u r ,因为,,Q C D 三点共线,所以34437171()()()()04444x y x y +--+-=,将点,C D 的坐标代入化简可得12121y y x x -=-,即1k =. 9..解:(1)设11()A x y ,,22()B x y ,,则2211143x y +=,2222143x y +=.两式相减,并由1212=y y k x x --得1212043x x y y k +++⋅=. 由题设知1212x x +=,122y y m +=,于是34k m=-. 由题设得302m <<,故12k <-. (2)由题意得F (1,0).设33()P x y ,,则 331122(1)(1)(1)(00)x y x y x y -+-+-=,,,,.由(1)及题设得3123()1x x x =-+=,312()20y y y m =-+=-<. 又点P 在C 上,所以34m =,从而3(1)2P -,,3||=2FP uu r .于是1||22x FA ==-uu r .同理2||=22xFB -uu r .所以1214()32FA FB x x +=-+=uu r uu r .故2||=||+||FP FA FB uu r uu r uu r .10.解:(1)当l 与x 轴垂直时,l 的方程为x =2,可得M 的坐标为(2,2)或(2,–2).所以直线BM 的方程为y =112x +或112y x =--.(2)当l 与x 轴垂直时,AB 为MN 的垂直平分线,所以∠ABM =∠ABN .当l 与x 轴不垂直时,设l 的方程为(2)(0)y k x k =-≠,M (x 1,y 1),N (x 2,y 2),则x 1>0,x 2>0.由2(2)2y k x y x=-⎧⎨=⎩,得ky 2–2y –4k =0,可知y 1+y 2=2k ,y 1y 2=–4.直线BM ,BN 的斜率之和为 1221121212122()22(2)(2)BM BN y y x y x y y y k k x x x x ++++=+=++++.① 将112y x k =+,222yx k=+及y 1+y 2,y 1y 2的表达式代入①式分子,可得 121221121224()882()0y y k y y x y x y y y k k++-++++===.所以k BM +k BN =0,可知BM ,BN 的倾斜角互补,所以∠ABM +∠ABN .综上,∠ABM=∠ABN.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
文数解析几何1.已知椭圆L:x2a2+y2b2=1(a>b>0)的一个焦点于抛物线y2=8x的焦点重合,点(2,2)在L上.(Ⅰ)求L的方程;(Ⅱ)直线l不过原点O且不平行于坐标轴,l与L有两个交点A,B,线段AB的中点为M,证明:OM的斜率与直线l的斜率的乘积为定值.【答案】解:(Ⅰ)抛物线y2=8x的焦点为(2,0),由题意可得c=2,即a2−b2=4,又点(2,在L上,可得4a+2b=1,解得a=22,b=2,即有椭圆L:x28+y24=1;(Ⅱ)证明:设直线l的方程为y=kx+b(k,b≠0),A(x1,y1),B(x2,y2),将直线y=kx+b代入椭圆方程x28+y24=1,可得(1+2k2)x2+4kbx+2b2−8=0,x1+x2=−4kb1+2k2,即有AB的中点M的横坐标为−2kb1+2k,纵坐标为−k⋅2kb1+2k+b=b1+2k,直线OM的斜率为k OM=y M xM=−12⋅1k,即有k OM⋅k=−12.则OM的斜率与直线l的斜率的乘积为定值.【解析】(Ⅰ)求得抛物线的焦点,可得c=2,再由点满足椭圆方程,结合a,b,c的关系,解方程可得椭圆的方程;(Ⅱ)设直线l的方程为y=kx+b(k,b≠0),A(x1,y1),B(x2,y2),代入椭圆方程,运用韦达定理和中点坐标公式可得M的坐标,可得直线OM的斜率,进而得到证明.本题考查椭圆的方程的求法,注意运用点满足椭圆方程和a,b,c的关系,考查直线和椭圆方程联立,运用韦达定理和中点坐标公式,以及直线的斜率公式,考查化简整理的运算能力,属于中档题.2.设椭圆C:x2a+y2b=1(a>b>0),过点Q(2,1),右焦点F(2,0),(Ⅰ)求椭圆C的方程;(Ⅱ)设直线l:y=k(x−1)(k>0)分别交x轴,y轴于C,D两点,且与椭圆C交于M,N两点,若CN=MD,求k值,并求出弦长|MN|.【答案】解:(Ⅰ)椭圆过点Q(1),可得2a+1b=1,由题意可得c=2,即a2−b2=2,解得a=2,b=2,即有椭圆C的方程为x24+y22=1;(Ⅱ)直线l:y=k(x−1)与x轴交点C(1,0),y轴交点D(0,−k),联立y=k(x−1)x2+2y2=4,消y得,(1+2k2)x2−4k2x+2k2−4=0,①设M(x1,y1),N(x2,y2),则x1+x2=4k21+2k2,CN=(x2−1,y2),MD=(−x1,−k−y1),由CN=MD,得:x1+x2=4k21+2k2=1,解得k=±22.由k>0得k=22代入①得2x2−2x−3=0,x1+x2=1,x1x2=−32,可得|MN|=2⋅(x1+x2)2−4x1x2=32⋅1+6=422.【解析】(Ⅰ)将Q的坐标代入椭圆方程,以及a,b,c的关系,解方程可得a,b,进而得到椭圆方程;(Ⅱ)求出直线l与x,y轴的交点,代入椭圆方程,运用韦达定理,以及向量共线的坐标表示,可得k的值,运用弦长公式可得弦长|MN|.本题考查椭圆方程的求法,注意运用点满足椭圆方程,考查直线方程和椭圆方程联立,运用韦达定理和向量相等的条件,同时考查弦长公式的运用,以及运算能力,属于中档题.3.在平面直角坐标系xOy中,已知椭圆x2a +y2b=1(a>b>0)的焦距为2,离心率为22,椭圆的右顶点为A.(1)求该椭圆的方程:(2)过点D(2,−2)作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的斜率之和为定值.【答案】解:(1)由题意可知:椭圆x2a +y2b=1(a>b>0),焦点在x轴上,2c=2,c=1,椭圆的离心率e=ca =22,则a=,b2=a2−c2=1,则椭圆的标准方程:x22+y2=1;(2)证明:设P(x1,y1),Q(x2,y2),A(2,0),当直线PQ不存在时,不符合题意。
当直线PQ存在时,设直线PQ的方程:y=k(x−2)−2,则y=k(x−2)−2x22+y2=1,整理得:(2k2+1)x2−(42k2+42k)x+4k2+8k+2=0,则=−4(8k+2)>0,k<−14由韦达定理可知:x1+x2=42k2+42k2k+1,x1x2=4k2+8k+22k+1,则y1+y2=k(x1+x2)−22k−22=−22−22k2k+1,则k AP+k AQ=1x−22x−2=12212(12x x−2(x+x)+2,由y1x2+y2x1=[k(x1−2)−2]x2+[k(x2−2)−2]x1=2kx1x2−(2k+2)(x1+x2)=−4k2k2+1,k AP+k AQ=12212(12x x−2(x+x)+2=−4k2k2+1−2×−22−22k2k2+14k2+8k+22−2×42k2+42k2+2=1,∴直线AP,AQ的斜率之和为定值1.【解析】(1)由题意可知2c=2,c=1,离心率e=ca,求得a=2,则b2=a2−c2=1,即可求得椭圆的方程:(2)则直线PQ的方程:y=k(x−2)−2,代入椭圆方程,由韦达定理及直线的斜率公式,分别求得直线AP,AQ的斜率,即可证明直线AP,AQ的率之和为定值.本题考查椭圆的简单几何性质,直线与椭圆位置关系,韦达定理及直线的斜率公式,考查计算能力,属于中档题.4.已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为32,右顶点A(2,0).(1)求椭圆C的方程;(2)过点M(32,0)的直线l交椭圆于B、D两点,设直线AB斜率为k1,直线AD斜率为k2.求证:k1k2为定值,并求此定值.【答案】解:(Ⅰ)∵椭圆C:x2a+y2b=1(a>b>0)的离心率为32,右顶点A(2,0),∴由题意得a2=b2+c2ca=32a=2,解得a=2.b=1c= 3.∴椭圆C的方程为x24+y2=1.…(4分)证明:(Ⅱ)由题意知直线l斜率不为0,可设直线l方程为x=my+32,与x24+y2=1联立,得(m2+4)y2+3my−74=0,△=9m2+7(m2+4)>0,设B(x1,y1),D(x2,y2),则y1+y2=−3mm+4,y1y2=−74m+4…(8分)k1k2=y1y2(x1−2)(x2−2)=y1y2(my1−12)(my2−12)=y1y2m2y1y2−12m(y1+y2)+14=−74−74m2+32m2+14(m2+4)=−74.∴k1k2为定值,定值为−74…(12分)【解析】(Ⅰ)由椭圆离心率为32,右顶点A(2,0),列出方程组求出a,b,由此能求出椭圆C的方程.(Ⅱ)由题意知直线l斜率不为0,可设直线l方程为x=my+32,与椭圆联立,得(m2+4)y2+3my−74=0,由此利用根的判别式、韦达定理,结合已知条件能证明k1k2为定值,并能求出此定值.本题考查椭圆方程的求法,是中档题,解题时要认真审题,注意椭圆性质、根的判别式、韦达定理的合理运用.5.已知椭圆E:x2a2+y2b2=1(a>b>0)经过点(1,32),且离心率e=12(Ⅰ)求椭圆E的方程;(Ⅱ)设椭圆E的右顶点为A,若直线l:y=kx+m与椭圆E相交于M、N两点(异于A点),且满足MA⊥NA,试证明直线l经过定点,并求出该定点的坐标.【答案】解:(Ⅰ)由椭圆离心率e=ca =12,则a=2c,b2=a2−c2=3c2,将(1,−32)代入椭圆方程:x24c2+y23c2=1,解得:c=1,则a2=4,b2=3,椭圆方程为x24+y23=1…(3分)(Ⅱ)证明:设M(x1,y1),N(x2,y2),由y=kx+mx24+y23=1,整理得(3+4k2)x2+8mkx+4(m2−3)=0,则x1+x2=−8mk3+4k2,x1⋅x2=4(m2−3)3+4k2,且△=64m2k2−16(3+4k2)(m2−3)>0,即3+4k2−m2>0,∵以MN为直径的圆过椭圆的右顶点A∴AM⊥AN,即AM⋅AN=0,则(x1−2,y1)(x2−2,y2)=0,即y1y2+x1x2−2(x1+x2)+4=0,又y1y2=(kx1+m)⋅(kx2+m)=k2x1x2+mk(x1+x2)+m2=3(m2−4k2)3+4k,∴4(m2−3)3+4k2+3(m2−4k2)3+4k2+2×8mk3+4k2+4=0,化简得,7m2+4k2+16mk=0解得m=−2k或m=−2k7且均满足3+4k2−m2>0当m=−2k时,L:y=k(x−2),直线过定点(2,0)与已知矛盾;当m=−2k7时,L;y=k(x−27),直线过定点(27,0),综上,直线l过定点,定点坐标为(27,0).【解析】(Ⅰ)由题意的离心率公式e=ca,求得a=2c,b2=3c2,将点代入椭圆方程,即可求得a和b的值,即可求得椭圆C的标准方程;(Ⅱ)将直线方程代入椭圆方程,由题意可知AM⋅AN=0,由向量数量积的坐标运算及韦达定理,即可求得m和k的关系,代入即可求得直线恒过定点.本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,考查韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.6.已知椭圆x25+y24=1,过右焦点F2的直线l交椭圆于M,N两点.(1)若OM⋅ON=−3,求直线l的方程;(2)若直线l的斜率存在,在线段OF2上是否存在点P(a,0),使得|PM|=|PN|,若存在,求出a的范围,若不存在,请说明理由.【答案】解:(1)当直线l的斜率不存在时,M(1,455),N(1,−455),不符合题意;当直线l的斜率存在时,设M(x1,y1),N(x2,y2),直线l的方程为y=k(x−1),①又椭圆的方程为x25+y24=1,②由①②可得(5k2+4)x2−10k2x+5k2−20=0,(∗)∴x1+x2=10k25k2+4,x1+x2=5k2−205k2+4,∴y1y2=k2[x1x2−(x1+x2)+1]=−16k25k+4,∴OM⋅ON=x1x2+y1y2=−11k2−205k+4=−3,解得k2=2,∴k=±2,即直线l的方程为y=2(x−1)或y=−2(x−1).(2)由(1)可知y1+y2=k(x1+x2)−2k=−8k5k2+4,设MN的中点为Q(x1+x22,y1+y22),即Q(5k25k2+4,−4k5k2+4),假设存在点P(a,0),使得|PM|=|PN|,则k PQ⋅k MN=−1,解得a=k25k2+4=15+42,当k=0时,M,N为椭圆长轴的两个端点,则点P与原点重合,当k≠0时,a∈(0,15),综上所述,存在点P且a∈[0,15).【解析】(1)当直线l的斜率不存在时,不合题意;当直线l的斜率存在时,设直线l的方程为y=k(x−1),代入椭圆的方程为x25+y24=1,得(5k2+4)x2−10k2x+5k2−20=0,由此能求出直线l的方程.(2)求出MN的中点Q(5k25k2+4,−4k5k2+4),假设存在点P(a,0),使得|PM|=|PN|,则k PQ⋅k MN=−1,由此能求出存在点P且a∈[0,15).本题考查直线方程的求法,考查满足条件的点是否存在的判断与求法,是中档题,解题时要认真审题,注意椭圆、直线方程、向量等知识点的合理运用.7.已知椭圆E过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=12,∠F1AF2的平分线所在直线为l.(Ⅰ)求椭圆E的方程;(Ⅱ)设l与x轴的交点为Q,求点Q的坐标及直线l的方程;(Ⅲ)在椭圆E上是否存在关于直线l对称的相异两点?若存在,请找出;若不存在,说明理由.【答案】解:(Ⅰ)设椭圆方程为x2a2+y2b2=1(a>b>0)∵椭圆E经过点A(2,3),离心率e=12,∴ca=124a2+9b2=1a2=b2+c2解a2=16,b2=12.∴椭圆方程E为:x216+y212=1.(Ⅱ)F1(−2,0),F2(2,0),∵A(2,3),∴AF1方程为:3x−4y+6=0,AF2方程为:x=2设角平分线上任意一点为P(x,y),|3x−4y+6|&;&;5=|;得2x−y−1=0或x+2y−8=0∵斜率为正,∴直线方程为2x−y−1=0;l与x轴的交点为Q,点Q的坐标(12,0).(Ⅲ)假设存在B(x1,y1)C(x2,y2)两点关于直线l对称,∴kBC=−12,∴直线BC方程为y=−12x+m代入椭圆方程x216+y212=1.,得x2−mx+m2−12=0,∴BC中点为(m2,3m 4)代入直线2x−y−1=0上,得m=4.∴BC中点为(2,3)与A重合,不成立,所以不存在满足题设条件的相异的两点.【解析】(Ⅰ)设出椭圆方程,根据椭圆E经过点A(2,3),离心率,建立方程组,求得几何量,即可得到椭圆E的方程;(Ⅱ)求得AF1方程、AF2方程,利用角平分线性质,即可求得∠F1AF2的平分线所在直线l的方程;(Ⅲ)假设存在B(x1,y1)C(x2,y2)两点关于直线l对称,设出直线BC方程代入椭圆E的方程,求得BC中点代入直线2x−y−1=0上,即可得到结论.本题考查椭圆的标准方程,考查直线方程,考查对称性,考查学生分析解决问题的能力,属于中档题.8.已知F1(−1,0)和F2(1,0)是椭圆x2a2+y2b2=1(a>b>0)的两个焦点,且点P(1 , 32)在椭圆C上.(Ⅰ)求椭圆C的方程;(Ⅱ)直线l:y=kx+m(m>0)与椭圆C有且仅有一个公共点,且与x轴和y轴分别交于点M,N,当△OMN面积取最小值时,求此时直线l的方程.【答案】(共13分)解:(Ⅰ)∵F1(−1,0)和F2(1,0)是椭圆:x2a +y2b=1(a>b>0)的两个焦点,且点P(1 , 32)在椭圆C上,∴依题意,c=1,又2a=(1+1)2+(32−0)2+32=82=4,故a=2.所以b2=3.故所求椭圆C的方程为x24+y23=1.…(4分)(Ⅱ)由x24+y23=1y=kx+m,消y得(4k2+3)x2+8kmx+4m2−12=0,由直线l与椭圆C仅有一个公共点知,△=64k2m2−4(4k2+3)(4m2−12)=0,整理得m2=4k2+3.…(6分)由条件可得k≠0,M(−mk , 0),N(0,m).所以S△OMN=12|OM|⋅|ON|=12|m|⋅|mk|=m22|k|.①将m2=4k2+3代入①,得S△OMN=12⋅4k2+3|k|=12(4|k|+3|k|).因为|k|>0,所以S△OMN=12(4|k|+3|k|)≥23,当且仅当|k|=32,即k=±32时等号成立,S△OMN有最小值23.因为m2=4k2+3,所以m2=6,又m>0,解得m= 6.…(11分)故所求直线方程为y=32x+6或y=−32x+ 6.…(13分)【解析】(Ⅰ)由F1(−1,0)和F2(1,0)是椭圆的两个焦点,且点P(1 , 32)在椭圆C上,求出a,b,由此能求出椭圆C的方程.(Ⅱ)由x24+y23=1y=kx+m,得(4k2+3)x2+8kmx+4m2−12=0,由此利用根的判别式、韦达定理、弦长公式、基本不等式、椭圆性质,结合已知条件能求出直线方程.本题考查椭圆方程的求法,考查直线方程的求法,是中档难度的解答题,解题时要认真审题,注意根的判别式、韦达定理、弦长公式、基本不等式、椭圆性质的合理运用.9.已知中心在原点,对称轴为坐标轴的椭圆C的一个焦点F在抛物线y2=4x的准线上,且椭圆C过点P(1,32),直线与椭圆C交于A,B两个不同点.(1)求椭圆C的方程;(2)若直线的斜率为12,且不过点P,设直线PA,PB的斜率分别为k1,k2,求证:k1+k2为定值.【答案】解:(1)抛物线y2=4x的准线方程为x=−1,由题意知F(−1,0).故设椭圆C的方程为x2a+y2b=1(a>b>0).则由题意可得a2−b2=112a2+(32)2b2=1,解得b2=3a2=4.故椭圆C 的方程为x 24+y 23=1.(2)证明:∵直线的斜率为12,且不过P (1,32)点,∴可设直线l :y =12x +m (m ≠1). 联立方程组 x 24+y 23=1y =12x +m ,消y 得x 2+mx +m 2−3=0.又设A (x 1,y 1),B (x 2,y 2), 故有 △=m 2−4(m 2−3)>0x 1+x 2=−m x 1x 2=m 2−3,所以k 1+k 2=y 1−32x 1−1+y 2−32x 2−1=(y 1−32)(x 2−1)+(y 2−32)(x 1−1)(x 1−1)(x 2−1)=(12x 1+m −32)(x 2−1)+(12x 2+m −32)(x 1−1)(x 1−1)(x 2−1)=x 1x 2+(m −2)(x 1+x 2)−2m +31212=m 2−3+(m−2)(−m )−2m +3m 2−3−(−m )+1=0,所以k 1+k 2为定值0.【解析】(1)求出抛物线y 2=4x 的准线方程为x =−1,推出c =1,故设椭圆C 的方程为x 2a2+y 2b 2=1(a >b >0).点在椭圆上,列出方程组求解可得椭圆C 的方程.(2)直线的斜率为12,且不过P (1,32)点,设直线l :y =12x +m (m ≠1).联立方程组 x 24+y 23=1y =12x +m ,消y ,设A (x 1,y 1),B (x 2,y 2),利用判别式以及韦达定理,表示k 1+k 2,推出定值.本题考查抛物线以及椭圆的位置关系的综合应用,直线与椭圆的位置关系的应用,定值问题的处理方法,考查计算能力.10. 已知双曲线C :x 24−y 2=1的左右两个顶点是A 1,A 2,曲线C 上的动点P ,Q 关于x 轴对称,直线A 1P 与A 2Q 交于点M ,(1)求动点M 的轨迹D 的方程;(2)点E (0,2),轨迹D 上的点A ,B 满足EA =λEB ,求实数λ的取值范围. 【答案】解:(1)由已知A 1(−2,0),A 2(2,0),设P (t , t 2−42).Q (t ,−t 2−42)则直线A 1P :y = t 2−42(t +2)(x +2),直线A 2Q :y =− t 2−42(t−2)(x −2),两式相乘得y 2=−14(x 2−4),化简得x 24+y 2=1,即动点M 的轨迹D 的方程为x 24+y 2=1;(2)过E (0,2)的直线若斜率不存在则λ=13或3,设直线斜率k 存在,A (x 1,y 1),B (x 2,y 2),x 2+4y 2−4=0y =kx +2⇒(1+4k 2)x 2+16kx +12=0, 则△≥0(1)x 1+x 2=−16k 1+4k (2)x 1x 2=121+4k (3)x 1=λx 2(4)由(2)(4)解得x 1,x 2代入(3)式得λ(1+λ)2⋅(−16k 1+4k 2)2=121+4k 2,化简得λ(1+λ)=364(1k +4),由(1)△≥0解得k 2≥34代入上式右端得,316<λ(1+λ)≤14, 解得13<λ<3,综上实数的取值范围是[13,3].【解析】(1)分别求得A 1P 与A 2Q 的方程,两式相乘,化简整理即可求得动点M 的轨迹D 的方程;(2)当直线斜率存在时,设直线方程,代入椭圆方程,利用韦达定理及向量数量积的坐标运算,即可求得实数λ的取值范围.本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,向量数量积的坐标,考查计算能力,属于中档题.11. 已知椭圆C :x 2a +y 2b =1(a >b >0)的离心率为32,且过点A (2,1). (Ⅰ) 求椭圆C 的方程;(Ⅱ) 若P ,Q 是椭圆C 上的两个动点,且使∠PAQ 的角平分线总垂直于x 轴,试判断直线PQ 的斜率是否为定值?若是,求出该值;若不是,说明理由.【答案】解:(Ⅰ) 因为椭圆C 的离心率为 32,且过点A (2,1),所以4a +1b =1,c a = 32.…(2分)因为a 2=b 2+c 2,解得a 2=8,b 2=2,…(3分) 所以椭圆C 的方程为x 28+y 22=1.…(4分)(Ⅱ)解法一:因为∠PAQ 的角平分线总垂直于x 轴,所以PA 与AQ 所在直线关于直线x =2对称. 设直线PA 的斜率为k ,则直线AQ 的斜率为−k .…(5分)所以直线PA 的方程为y −1=k (x −2),直线AQ 的方程为y −1=−k (x −2). 设点P (x P ,y P ),Q (x Q ,y Q ),由 y −1=k (x −2)x 28+y 22=1,消去y ,得(1+4k 2)x 2−(16k 2−8k )x +16k 2−16k −4=0.①因为点A (2,1)在椭圆C 上,所以x =2是方程①的一个根,则2x P =16k 2−16k−41+4k 2,…(6分)所以x P=8k2−8k−21+4k2.…(7分)同理x Q=8k2+8k−21+4k2.…(8分)所以x P−x Q=−16k1+4k.…(9分)又y P−y Q=k(x P+x Q−4)=−8k1+4k.…(10分)所以直线PQ的斜率为k PQ=y P−y Qx P−x Q=12.…(11分)所以直线PQ的斜率为定值,该值为12.…(12分)解法二:设点P(x1,y1),Q(x2,y2),则直线PA的斜率k PA=y1−1x1−2,直线QA的斜率k QA=y2−1x2−2.因为∠PAQ的角平分线总垂直于x轴,所以PA与AQ所在直线关于直线x=2对称.所以k PA=−k QA,即y1−1x1−2+y2−1x2−2=0,①…(5分)因为点P(x1,y1),Q(x2,y2)在椭圆C上,所以x128+y122=1,②x228+y222=1.③由②得(x12−4)+4(y12−1)=0,得y1−1x1−2=−x1+24(y1+1),④…(6分)同理由③得y2−1x2−2=−x2+24(y2+1),⑤…(7分)由①④⑤得x1+24(y1+1)+x2+24(y2+1)=0,化简得x1y2+x2y1+(x1+x2)+2(y1+y2)+4=0,⑥…(8分)由①得x1y2+x2y1−(x1+x2)−2(y1+y2)+4=0,⑦…(9分)⑥−⑦得x1+x2=−2(y1+y2).…(10分)②−③得x12−x228+y12−y222=0,得y1−y2x1−x2=−x1+x24(y1+y2)=12.…(11分)所以直线PQ的斜率为k PQ=y1−y2x1−x2=12为定值.…(12分)解法三:设直线PQ的方程为y=kx+b,点P(x1,y1),Q(x2,y2),则y1=kx1+b,y2=kx2+b,直线PA的斜率k PA=y1−1x1−2,直线QA的斜率k QA=y2−1x2−2.…(5分)因为∠PAQ的角平分线总垂直于x轴,所以PA与AQ所在直线关于直线x=2对称.所以k PA=−k QA,即y1−1x1−2=−y2−1x2−2,…(6分)化简得x1y2+x2y1−(x1+x2)−2(y1+y2)+4=0.把y1=kx1+b,y2=kx2+b代入上式,并化简得2kx1x2+(b−1−2k)(x1+x2)−4b+4=0.(∗)…(7分)由y=kx+bx28+y22=1,消去y得(4k2+1)x2+8kbx+4b2−8=0,(∗∗)则x1+x2=−8kb4k+1,x1x2=4b2−84k+1,…(8分)代入(∗)得2k(4b2−8)4k2+1−8kb(b−1−2k)4k2+1−4b+4=0,…(9分)整理得(2k−1)(b+2k−1)=0,所以k=12或b=1−2k.…(10分)若b=1−2k,可得方程(∗∗)的一个根为2,不合题意.…(11分)若k=12时,合题意.所以直线PQ的斜率为定值,该值为12.…(12分)【解析】(Ⅰ)由椭圆C的离心率为32,且过点A(2,1),列出方程组,求出a,b,由此能求出椭圆C的方程.(Ⅱ)法一:由∠PAQ的角平分线总垂直于x轴,知PA与AQ所在直线关于直线x=2对称.设直线PA的方程为y−1=k(x−2),直线AQ的方程为y−1=−k(x−2).由y−1=k(x−2)x28+y22=1,得(1+4k2)x2−(16k2−8k)x+16k2−16k−4=0.由点A(2,1)在椭圆C上,求出x P=8k2−8k−21+4k2.同理x Q=8k2+8k−21+4k2,由此能求出直线PQ的斜率为定值12.法二:设点P(x1,y1),Q(x2,y2),则直线PA的斜率k PA=y1−1x1−2,直线QA的斜率k QA=y2−1x2−2.由∠PAQ的角平分线总垂直于x轴,知y1−1x1−2+y2−1x2−2=0,再由点P(x1,y1),Q(x2,y2)在椭圆C上,能求出直线PQ的斜率为定值12.法三:设直线PQ的方程为y=kx+b,点P(x1,y1),Q(x2,y2),则y1=kx1+b,y2=kx2+b,直线PA的斜率k PA=y1−1x1−2,直线QA的斜率k QA=y2−1x2−2.由∠PAQ的角平分线总垂直于x轴,知y1−1x1−2=−y2−1x2−2,由y=kx+bx28+y22=1,得(4k2+1)x2+8kbx+4b2−8=0,由此利用韦达定理能求出直线PQ的斜率为定值12.本题考查椭圆方程的求法,考查直线的斜率是否为定值的判断与求法,是中档题,解题时要认真审题,注意椭圆性质、直线与椭圆位置关系的合理运用.12.已知抛物线C;y2=2px过点A(1,1).(1)求抛物线C的方程;(2)过点P(3,−1)的直线与抛物线C交于M,N两个不同的点(均与点A不重合),设直线AM,AN的斜率分别为k1,k2,求证:k1⋅k2为定值.【答案】解:(1)由题意抛物线y2=2px过点A(1,1),所以p=12,所以得抛物线的方程为y2=x;(2)证明:设过点P(3,−1)的直线l的方程为x−3=m(y+1),即x=my+m+3,代入y2=x得y2−my−m−3=0,设M(x1,y1),N(x2,y2),则y1+y2=m,y1y2=−m−3,所以k1⋅k2=y1−1x1−1⋅y2−1x2−1=y1y2−(y1+y2)+1m2y1y2+m(m+2)y1y2+(m+2)2=−12【解析】(1)利用待定系数法,可求抛物线的标准方程;(2)设过点P(3,−1)的直线l的方程为x−3=m(y+1),即x=my+m+3,代入y2=x利用韦达定理,结合斜率公式,化简,即可求k1⋅k2的值.本题考查抛物线方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.13.如图,抛物线C:y2=2px的焦点为F,抛物线上一定点Q(1,2).(1)求抛物线C的方程及准线l的方程;(2)过焦点F的直线(不经过Q点)与抛物线交于A,B两点,与准线l交于点M,记QA,QB,QM的斜率分别为k1,k2,k3,问是否存在常数λ,使得k1+k2=λk3成立?若存在λ,求出λ的值;若不存在,说明理由.【答案】解:(1)把Q(1,2)代入y2=2px,得2p=4,所以抛物线方程为y2=4x,准线l的方程为x=−1.(2)由条件可设直线AB的方程为y=k(x−1),k≠0.由抛物线准线l:x=−1,可知M(−1,−2k),又Q(1,2),所以k3=2+2k1+1=k+1,把直线AB的方程y=k(x−1),代入抛物线方程y2=4x,并整理,可得k2x2−2(k2+2)x+k2=0,设A(x1,y1),B(x2,y2),则x1+x2=2k2+4k,x1x2=1,又Q(1,2),故k1=2−y11−x1,k2=2−y21−x2.因为A,F,B三点共线,所以k AF=k BF=k,即y1x1−1=y2x2−1=k,所以k1+k2=2−y11−x1+2−y21−x2=2kx1x2−(2k+2)(x1+x2)+2k+4x1x2−(x1+x2)+1=2(k+1),即存在常数λ=2,使得k1+k2=2k3成立.【解析】(1)把Q(1,2)代入y2=2px,得2p=4,即可求抛物线C的方程及准线l的方程;(2)把直线AB的方程y=k(x−1),代入抛物线方程y2=4x,并整理,求出k1+k2,k3,即可得出结论.本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.14.如图,在平面直角坐标系xOy中,已知椭圆x2a2+y2b2=1(a>b>0)的焦距为2,过右焦点F的直线l交椭圆于A、B两点,当l与x轴垂直时,AB长为433.(1)求椭圆的标准方程;(2)若椭圆上存在一点P,使得OP=OA+OB,求直线l的斜率.【答案】解:(1)由题意可知2c=2,c=1,当l与x轴垂直时,丨AB丨=2b2a=433,…(2分)由a2=b2+c2,则a=3,b=,故椭圆的标准方程是:x23+y22=1;…(4分)(2)设直线l的斜率为k,则直线l的方程:y=k(x−1),设点A(x1,y1),B(x2,y2),P(x3,y3),由y=k(x−1)x23+y22=1可得(3k2+2)x2−6k2x+3k2−6=0,…(6分)则x1+x2=6k23k2+2,x1x2=3k2−63k2+2.(∗)因OP=OA+OB,则y3=y1+y2x3=x1+x2,代入椭圆方程(x1+x2)23+(y1+y2)22=1,又x123+y122=1,x223+y222=1,化简得2x1x2+3y1y2+3=0,即(3k2+2)x1x2−3k2(x1+x2)+3k2+3=0,…(10分)将(∗)代入得3k2−6−3k2×6k23k+2+3k2+3=0,k2=2,即k=±2,故直线l的斜率为±…(14分)【解析】(1)由c=1,丨AB丨=2b2a=433,a2=b2+c2,即可求得a和b的值,即可求得椭圆方程;(2)将直线方程代入椭圆方程,由韦达定理,及向量数量积的坐标运算,即可求得直线l的斜率.本题考查椭圆的标准方程与几何性质、直线的方程、直线与椭圆等基础知识,考查分析问题及运算求解能力,属于中档题.15.已知椭圆C:x2a+y2b=1(a>b>0),C的右焦点F(1,0),长轴的左、右端点分别为A1,A2,且FA1.⋅FA2=−1.(Ⅰ)求椭圆C的方程;(Ⅱ)过焦点F 斜率为k (k ≠0)的直线l 交椭圆C 于A ,B 两点,弦AB 的垂直平分线与x 轴相交于点D .试问椭圆C 上是否存在点E 使得四边形ADBE 为菱形?若存在,试求点E 到y 轴的距离;若不存在,请说明理由.【答案】解:(Ⅰ)依题设A 1(−a ,0),A 2(a ,0),则FA 1 =(−a −1,0),FA 2 =(a −1,0). 由FA 1 ⋅FA 2 =−1,得:(−a −1)(a −1)=−1,解得a 2=2,又c =1,所以b 2=1. 所以椭圆C 的方程为x 22+y 2=1.(Ⅱ)椭圆C 上是否存在点E 使得四边形ADBE 为菱形. 事实上,依题直线l 的方程为y =k (x −1).联立 y =k (x −1)x 22+y 2=1,得:(2k 2+1)x 2−4k 2x +2k 2−2=0. 设A (x 1,y 1),B (x 2,y 2),弦AB 的中点为M (x 0,y 0), 则x 1+x 2=4k 22k +1,x 1x 2=2(k 2−1)2k +1,所以x 0=x 1+x 22=2k 22k +1,y 0=k (x 0−1)=k (2k 22k +1−1)=−k 2k +1,所以M (2k 22k 2+1,−k2k 2+1). 则直线MD 的方程为y +k 2k 2+1=−1k (x −2k 22k 2+1), 令y =0,得x D =k 22k +1,则D (k 22k +1,0).若四边形ADBE 为菱形,则x E +x D =2x 0,所以x E =2x 0−x D =4k 22k +1−k 22k +1=3k 22k +1.y E +y D =2y 0,所以y E =2y 0−y D =−2k2k +1. 所以E (3k 22k 2+1,−2k 2k 2+1).若点E 在椭圆C 上,则(3k 22k 2+1)2+2(−2k2k 2+1)2=2.即9k 4+8k 2=2(2k 2+1)2 整理得k 4=2,解得k 2= 2.所以椭圆C 上存在点E 使得四边形ADBE 为菱形. 此时点E 到y 轴的距离为22 2+1=3 2(2 2−1)7=12−3 27.【解析】(Ⅰ)题目给出了椭圆的右焦点坐标,则知道了c 的值,再由FA 1.⋅FA 2 =−1,列式求出a 2的值,结合隐含条件b 2=a 2−c 2求出b 2的值,则椭圆方程可求;(Ⅱ)由点斜式写出直线l 的方程,和椭圆方程联立后利用根与系数的关系求出A ,B 中点的坐标,然后写出MD 所在的直线方程,求出D 点的坐标,根据四边形ADBE 是菱形,列式求出E 点的坐标,把E 点的坐标代入椭圆方程求出k 2的值,则E 点到y 轴的距离可求.本题考查了椭圆的标准方程,考查了直线和椭圆的位置关系,训练了设而不求的解题方法,此法的依据是二次方程中根与系数的关系,训练了学生的计算能力,属有一定难度题目.。
