最新初三数学易错题集锦
初三数学错题集及解析
初三数学错题集及解析1、若一个三角形的三边长分别为10，24，26，则这个三角形的面积是（）。
解释：题目中给出的三边长并不能构成一个三角形，因为它们不满足三角形的两边之和大于第三边的条件。
因此，无法计算这个三角形的面积。
2、如果实数a、b满足a^2 + 4a + 4 + b - 1 = 0，则a、b的值分别为（）。
解释：通过配方，我们可以得到(a+2)2+b−1=0。
从这个方程可以解出a=-2，b=1。
3、在一元二次方程中，如果方程有两个相等的实数根，那么它的判别式（）0。
解释：一元二次方程有两个相等的实数根意味着它的判别式等于0。
4、在一个等腰三角形中，如果底边长为8cm，底边上的高为3cm，则它的面积为（）cm²。
解释：等腰三角形的面积可以通过底边长和高来计算，公式为面积= 底边长×高/ 2。
在这个例子中，底边长为8cm，高为3cm，所以面积为12cm²。
5、在一个直角三角形中，如果两条直角边的长分别为3和4，则斜边长为（）。
解释：根据勾股定理，斜边的平方等于两条直角边的平方和。
在这个例子中，斜边的平方= 3²+ 4²= 25，所以斜边长为5。
6、如果两个相似三角形的相似比为2:3，那么它们的面积比为（）。
解释：相似三角形的面积比等于相似比的平方。
在这个例子中，相似比为2:3，所以面积比为4:9。
7、在一个平行四边形中，如果一组对边相等且相互平行，那么它是一个（）。
解释：根据平行四边形的定义，如果一组对边相等且相互平行，那么它是一个平行四边形。
8、如果一个正方形的周长为8cm，那么它的边长为（）。
解释：正方形的周长是边长的4倍，所以如果周长为8cm，边长为2cm。
9、在一个等腰梯形中，如果上底和下底相等且平行，那么它是一个（）。
解释：等腰梯形是上底和下底相等且平行的四边形。
10、如果两个角相等，那么它们的余角也相等（）。
解释：两个角相等，它们的余角也相等。
九年级上册数学易错题目汇总,初三数学易错题集锦及答案解析
九年级上册数学易错题汇总1. 关于X 的方程¥+21-7〃 = 0有两个相等的实数根，则，〃的值是（）A.m = 1 = - 1 = 2 D.〃，=-2【考点】根的判别式.【解答】由题意可知：△=4+4m = 0,in = - 1,故选：B.2. 下列关于X 的方程是一元二次方程的是（）A./+1 =0B.x+1 = 1X （x+l ） （x-l ） *七€+1故本选项符合题意;C. ”+Z ）x+f = O D.【考点】一元二次方程的定义.【解答】刀、是一元二次方程，不是一元二次方程，故本选项不符合题意；。
、不是一元二次方程，故本选项不符合题意；D 、 不是一元二次方程，故本选项不符合题意；故选：A.3.一个容器盛满纯药液63千克，第一次倒出一部分药液后加满水，第二次 又倒出同样多的药液，再加满水，此时容器内的纯药液剩下28千克，那么每次倒出的药液是（）A.20千克 B.21千克 C.22千克 D.175千克【考点】一元二次方程的应用.【解答】设每次倒出药液x升，63-x依题意，得：士寻二1-咎63 63整理，得：一i26r+2205=0,解得：XI二21,.K2二105（不合题意，舍去）.故选:B.4.已知关于x的一元二次方程（4 1）r—2x+2=0有两个不相等的实数根,则次的取值范围值是（）A.k＜旦B.k＜2CA〈岂且《兴1DAW岂且上尹L2222［考点】一元二次方程的定义；的判别式.【解答】根据题意得：△二〃-4w=4・8（*1）=12.8左＞0,且X-1产0,:上且左乂1./'JT得故选：C.5.—元二次方程寸一6x一1=0配方后可变形为（）A.(X-3)2=8B.(x-3)2=10 c.(x+3)J8 D.(x+3)2 =10【考点】解一元二次方程•配方法.【解答】・.・*2-6*-1=0,•*-x2-6x=1,.•-（x-3）2=10,故选：8.6.某商品原售价为60元，4月份下降了20%,从5月份起售价开始增长，6月份售价为75元，设5、6月份每个月的平均增长率为.「则的值为（）A.15% B.25% C.20% D.30%【考点】一元二次方程的应用.【解答】设5、6月份每个月的平均增长率为X,由题意，得60（1-20%）（1+x）2=755得X=0.25二25%（舍去负值）牧选：B.7.一元二次方程X2-5.X+1=。
九年级上册数学期末精选试卷易错题(Word版 含答案)
九年级上册数学期末精选试卷易错题（Word 版 含答案）一、初三数学 一元二次方程易错题压轴题（难）1．如图，在平面直角坐标系中，()4,0A -，()0,4B ，四边形ABCO 为平行四边形，4,03D ⎛⎫- ⎪⎝⎭在x 轴上一定点，P 为x 轴上一动点，且点P 从原点O 出发，沿着x 轴正半轴方向以每秒43个单位长度运动，已知P 点运动时间为t ． (1)点C 坐标为________，P 点坐标为________；(直接写出结果，可用t 表示) (2)当t 为何值时，BDP ∆为等腰三角形；(3)P 点在运动过程中，是否存在t ，使得ABD OBP ∠=∠，若存在，请求出t 的值，若不存在，请说明理由！【答案】（1）（4，4），（43t ，0）；（2）1101-，4； （3）存在，3109t【解析】 【分析】（1）利用平行四边形的性质和根据P 点的运动速度，利用路程公式求解即可； （2）分三种情况：①当BD BP 时，②当BD DP =时，③当BP DP =时，分别讨论求解，即可得出结果； （3）过D 点作DF BP 交BP 于点F ，设OP x =，则可得224BPx ，43DPx ，453DF,利用1122BDPS DP BO BP DF ，即可求出OP 的长，利用路程公式可求得t 的值。
【详解】解：（1）∵()4,0-A ，()0,4B ，四边形ABCO 为平行四边形， ∴点C 坐标为（4，4），又∵P 为x 轴上一动点，点P 从原点O 出发，沿着x 轴正半轴方向以每秒43个单位长度运动，P 点运动时间为t ，∴P 点坐标为（43t ，0）， （2）∵B ，D 的坐标分别为：()0,4B ，4,03D ⎛⎫- ⎪⎝⎭， ∴4OB =,43OD =, 由勾股定理有：22224441033DB OBOD, 当BDP ∆为等腰三角形时， ①如图所示，当BDBP 时，OD OP =,∴P 点坐标为（43，0）, ∴1t =②如图所示，当BD DP =时，∵4103DB ，OP DP OD∴44410101333OP ,∴101t③如图所示，当BP DP =时，设P 点坐标为：（x ，0） 则有：2224BP x，2243DPx， ∴222443xx，解之得：163x = ∴P 点坐标为（163，0）, ∴4t =综上所述，当t 为1，101-，4时，BDP ∆为等腰三角形；（3）答：存在t ，使得ABD OBP ∠=∠。
九年级数学上册易错题精选练习汇总(解析版)
九年级数学上册易错题精选练习汇总一、选择题1.如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则的正切值是A. 2B.C.D.2.如图，在中，，，垂足为D，AF平分，交CD于点E，交CB于点若，，则CE的长为A. B. C. D.3.如图，菱形OABC的一边OA在x轴的正半轴上，O是坐标原点，，反比例函数的图象经过点C，与AB交于点D，则的面积为A. 12B. 20C. 24D. 404.如图，在中，D、E分别是AB、BC上的点，且，若：：4，则：A. 1：16B. 1：18C. 1：20D. 1：245.已知关于x的一元二次方程有两个实数根，m为正整数，且该方程的根都是整数，则符合条件的所有正整数m的和为A. 6B. 5C. 4D. 36.已知抛物线与x轴交于A，B两点，将这条抛物线的顶点记为C，连接AC，BC，则的值为A. B. C. D. 27.如图，的半径为3，四边形ABCD内接于，连接OB、OD，若，则的长为A.B.C.D.8.如图，AB是的直径，BT是的切线，若，，则阴影部分的面积是A. 2B.C. 1D.9.如图，在边长为6的菱形ABCD中，，以点D为圆心，菱形的高DF为半径画弧，交AD于点E，交CD于点G，则图中阴影部分的面积是A. B. C. D.10.若关于x的一元二次方程有两个相等的实数根，则实数a的值为A. B. 1 C. 或2 D. 或111.如图，某小区有一块长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为60米，两块绿地之间及周边留有宽度相等的人行通道．若设人行道的宽度为x米，则可以列出关于x的方程是A. B.C. D.12.如图，在x轴的上方，直角∠绕原点O按顺时针方向旋转，若∠的两边分别与函数-，的图象交于B、A两点，则∠的值的变化趋势为：A. 逐渐变小B. 逐渐变大C. 时大时小D. 保持不变二、填空题13.如图，在边长为4的正方形ABCD中，以点B为圆心，以AB为半径画弧，交对角线BD于点E，则图中阴影部分的面积是____结果保留．14.如图，在中，，，，点F在边AC上，并且，点E为边BC上的动点，将沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是______．15.已知方程的两根恰好是的两条边的长，则的第三边长为______ ．16.如图，半径为5的半圆的初始状态是直径平行于桌面上的直线b，然后把半圆沿直线b进行无滑动滚动，使半圆的直径与直线b重合为止，则圆心O运动路径的长度等于______．17.如图，一名滑雪运动员沿着倾斜角为的斜坡，从A滑行至B，已知米，则这名滑雪运动员的高度下降了______米．参考数据：，，18.在中，，，点D在边AB上，且，点E在边AC上，当______时，以A、D、E为顶点的三角形与相似．19.在中，，，，则______．20.已知关于x的方程的两根为和，则___，___．三、解答题21.用配方法解方程：．22.如图，在中，，以AB为直径的与边BC、AC分别交于D、E两点，过点D作，垂足为点F．求证：DF是的切线；若，，求DF的长．23.“为了安全，请勿超速”如图，一条公路建成通车，在某直线路段MN限速60千米小时，为了检测车辆是否超速，在公路MN旁设立了观测点C，从观测点C测得一小车从点A到达点B行驶了5秒钟，已知，，米，此车超速了吗？请说明理由．参考数据：，24.如图，已知AB是圆O的直径，弦，垂足为H，与AC平行的圆O的一条切线交CD的延长线于点M，交AB的延长线于点E，切点为F，连接AF交CD于点N．求证：；连接DF，若，，求圆O的直径的长度．25.如图，AE与BD交于点C，，且DM交AC于F，ME交BC于G求证：∽．26.如图，要设计一本画册的封面，封面长40cm，宽30cm，正中央是一个与整个封面长宽比例相同的矩形画．如果要使四周的边衬所占面积是封面面积的，上、下边衬等宽，左、右边衬等宽，应如何设计四周边衬的宽度结果保留小数点后一位，参考数据：．27.如图，游客在点A处坐缆车出发，沿的路线可至山顶D处，假设AB和BD都是直线段，且，，，求DE的长．参考数据：，，28.如果关于x的一元二次方程有两个实数根，且其中一个根为另一个根的2倍，那么称这样的方程为“倍根方程”例如，一元二次方程的两个根是2和4，则方程就是“倍根方程”．若一元二次方程是“倍根方程”，则______；若是“倍根方程”，求代数式的值；若关于x的一元二次方程是“倍根方程”，求a，b，c之间的关系．29.如图，四边形ABCD中，，AC平分，点P是AC延长线上一点，且．证明：；若AC与BD相交于点E，，CE：：3，求AE的长．30.列方程解应用题：某玩具厂生产一种玩具，按照控制固定成本降价促销的原则，使生产的玩具能够及时售出，据市场调查：每个玩具按480元销售时，每天可销售160个；若销售单价每降低1元，每天可多售出2个．已知每个玩具的固定成本为360元，问这种玩具的销售单价为多少元时，厂家每天可获利润20000元？31.如图，和均为等腰直角三角形，且，，点P为线段BE延长线上一点，连接CP以CP为直角边向下作等腰直角，线段BE与CD相交于点F求证：；连接BD，请你判断AC与BD有什么位置关系？并说明理由；设，的面积为S，求S与x之间的函数关系式．答案和解析1.【答案】D【解析】【分析】本题考查了锐角三角函数的定义，先求出AC、AB的长，再求正切函数．连接AC，根据勾股定理，可得AC、AB、BC的长，由勾股定理逆定理可得是直角三角形，根据正切函数的定义，可得答案．【解答】解：如图：，由勾股定理，得，，，为直角三角形，，故选D．2.【答案】A【解析】解：过点F作于点G，，，，，，平分，，，，平分，，，，，∽，，，，，，，，，解得：，即CE的长为．故选：A．根据三角形的内角和定理得出，，根据角平分线和对顶角相等得出，即可得出，再利用相似三角形的判定与性质得出答案．本题考查了直角三角形性质、等腰三角形的性质和判定，三角形的内角和定理以及相似三角形的判定与性质等知识，关键是推出．3.【答案】B【解析】【分析】本题考查了菱形的性质，反比例函数的性质，三角函数的定义，考查了菱形面积的计算，本题中求得菱形是解题的关键．易证菱形，再根据的值即可求得菱形的边长，即可求得点C的坐标，可得菱形的面积和结论．【解答】解：作，，，设，，，，，，由勾股定理得：，，菱形四边形OABC为菱形，，，，，同理，菱形，，菱形；故选B．4.【答案】C【解析】解：：：4，设的面积为a，则的面积为4a，和的点D到BC的距离相等，，，，∽，：：25，，：：：20．故选：C．设的面积为a，表示出的面积为4a，根据等高的三角形的面积的比等于底边的比求出，然后求出和相似，根据相似三角形面积的比等于相似比的平方求出的面积，然后表示出的面积，再求出比值即可．本题考查了相似三角形的判定与性质，等高的三角形的面积的比等于底边的比，熟记相似三角形面积的比等于相似比的平方，用的面积表示出的面积是解题的关键．5.【答案】B【解析】解：，，，关于x的一元二次方程有实数根，．为正整数，且该方程的根都是整数，或3．．故选：B．根据方程的系数结合根的判别式，即可得出，由m为正整数结合该方程的根都是整数，即可求出m的值，将其相加即可得出结论．本题考查了根的判别式以及一元二次方程的整数解，牢记“当时，方程有实数根”是解题的关键．6.【答案】D【解析】解：令，则，解得或1，不妨设，，，顶点，如图所示，作于D．在中，，故选：D．先求出A、B、C坐标，作于D，根据即可计算．本题考查二次函数与x轴交点坐标，锐角三角函数的定义，解题的关键是熟练掌握求抛物线与x轴交点坐标的方法，记住锐角三角函数的定义，属于中考常考题型．7.【答案】C【解析】解：四边形ABCD内接于，，，，，解得：，，的长；故选：C．由圆内接四边形的性质和圆周角定理求出，得出，再由弧长公式即可得出答案．本题考查了弧长公式、圆内接四边形的性质、圆周角定理；熟练掌握圆内接四边形的性质和圆周角定理，求出是解决问题的关键．8.【答案】C【解析】【分析】本题考查了切线的性质，等腰直角三角形的性质，解决本题的关键是利用等腰直角三角形的性质把阴影部分的面积转化为三角形的面积．设AT交于D，连结BD，先根据圆周角定理得到，则可判断、都是等腰直角三角形，所以，然后利用弓形AD的面积等于弓形BD的面积得到阴影部分的面积．【解答】解：是的切线．设AT交于D，连结BD，是的直径，，而，、都是等腰直角三角形，，弓形AD的面积等于弓形BD的面积，阴影部分的面积．故选C．9.【答案】A【解析】解：四边形ABCD是菱形，，，，是菱形的高，，，图中阴影部分的面积菱形ABCD的面积扇形DEFG的面积．故选：A．由菱形的性质得出，，由三角函数求出菱形的高DF，图中阴影部分的面积菱形ABCD的面积扇形DEFG的面积，根据面积公式计算即可．本题考查了菱形的性质、三角函数、菱形和扇形面积的计算；由三角函数求出菱形的高是解决问题的关键．10.【答案】A【解析】解：原方程可变形为．该方程有两个相等的实数根，，解得：．故选：A．将原方程变形为一般式，根据根的判别式即可得出关于a的一元二次方程，解之即可得出结论．本题考查了根的判别式，牢记“当时，方程有两个相等的实数根”是解题的关键．11.【答案】C【解析】【分析】本题考查了由实际问题抽象出一元二次方程，利用两块相同的矩形绿地面积之和为60米得出等式是解题关键设人行道的宽度为x米，根据矩形绿地的面积之和为60米，列出一元二次方程．【解答】解：设人行道的宽度为x米，根据题意得，，化简整理得，．故选C．12.【答案】D【解析】【分析】本题主要考查了反比例函数图象上点的坐标特征、相似三角形的判定等知识点及其应用问题；解题的方法是作辅助线，将分散的条件集中；解题的关键是灵活运用相似三角形的判定等知识点来分析、判断、推理或解答．作辅助线；首先证明∽，得到；设，，得到，，，，进而得到，，此为解决问题的关键性结论；运用三角函数的定义证明知为定值，即可解决问题．【解答】解：如图，分别过点A、B作轴、轴；，，，，∽，；设，，则，，，，，；，；∽，，由知为定值，的大小不变．故选：D．13.【答案】【解析】【分析】本题考查扇形的面积的计算，正方形的性质等知识，解题的关键是学会用分割法求阴影部分面积．根据阴扇形计算即可；【解答】解：，阴扇形故答案为．14.【答案】【解析】【分析】本题考查翻折变换、最短问题、相似三角形的判定和性质、勾股定理．垂线段最短等知识，解题的关键是正确找到点P位置，属于中考常考题型．延长FP交AB于M，当时，点P到AB的距离最小，利用∽，得到求出FM即可解决问题．【解答】解：如图，延长FP交AB于M，当时，点P到AB的距离最小．点P 在以F为圆心CF为半径的圆上，当时，点P到AB的距离最小，，∽，，，，，，，，，，点P到边AB距离的最小值是．故答案为．15.【答案】5或【解析】【分析】解方程可以求出两根，即直角三角形的两边，利用勾股定理就可以求出第三边．知道直角三角形的两边，要分第三边是斜边和直角边两种情况讨论．【解答】解：方程的两个根是3和也就是的两条边的长是3和4．当3和4都是直角边时，第三边．当4为斜边时，第三边故第三边长是5或．故答案为5或．16.【答案】【解析】解：由图形可知，圆心先向前走的长度，从O到的运动轨迹是一条直线，长度为圆的周长，然后沿着弧旋转圆的周长，则圆心O运动路径的长度为：，故答案为：．根据题意得出半圆在无滑动旋转中通过的路程为圆弧，根据弧长公式求出弧长即可．本题考查的是弧长的计算和旋转的知识，解题关键是确定半圆作无滑动翻转所经过的路线并求出长度．17.【答案】280【解析】解：如图在中，，这名滑雪运动员的高度下降了280m．故答案为280如图在中，，可知这名滑雪运动员的高度下降了280m．本题考查解直角三角形、坡度坡角问题、锐角三角函数等知识，解题的关键是熟练掌握锐角三角函数的定义，属于中考常考题型．18.【答案】或【解析】解：当时，，∽，此时；当时，，∽，此时；故答案为：或．若A，D，E为顶点的三角形与相似时，则或，分情况进行讨论后即可求出AE的长度．本题考查了相似三角形的判定，熟练掌握相似三角形的判定方法，解题的关键是分两种情况进行讨论．19.【答案】【解析】解：，，．故答案为：．根据的正弦求出，再根据的正弦值求解即可．本题考查了特殊角的三角函数值，熟记、、角的三角函数值是解题的关键．20.【答案】4；3【解析】【分析】本题考查了根与系数的关系，根据根与系数的关系找出、是解题的关键．由根与系数的关系可得出关于p或q的一元一次方程，解之即可得出结论．【解答】解：关于x的方程的两根为和，，，，．故答案为4；3．21.【答案】解：方程变形得：，配方得：，即，开方得：，解得：，．【解析】方程整理后，利用完全平方公式变形，开方即可求出解．此题考查了解一元二次方程配方法，熟练掌握完全平方公式是解本题的关键．22.【答案】证明：如图，连接OD，作于点G，，，，又，，，，，，是的切线．解：，，，，，四边形OGFD为矩形，．【解析】证明：如图，连接OD，作于点G，推出；然后根据，，推出，即可推出DF是的切线．首先判断出：，然后判断出四边形OGFD为矩形，即可求出DF的值是多少．此题主要考查了切线的性质和应用，等腰三角形的性质和应用，以及解直角三角形的应用，要熟练掌握．23.【答案】解：此车没有超速．理由：过C作，，米，米，米，，米，，千米小时，，此车没有超速．【解析】根据题意结合锐角三角函数关系得出BH，CH，AB的长进而求出汽车的速度，进而得出答案．此题主要考查了勾股定理以及锐角三角函数关系的应用，得出AB的长是解题关键．24.【答案】证明：连接OF，则，如图所示．与相切，．，．，，．，．，，，，，．连接OC，如图2所示．，，．设，则，，，，，，，．设圆的半径为r，则，在中，，，，，，解得：，圆O的直径的长度为．【解析】连接OF，根据切线的性质结合四边形内角和为，即可得出，由三角形外角结合平行线的性质即可得出，再通过互余利用角的计算即可得出，由此即可证出；连接OC，由圆周角定理结合、，即可求出CH、AH 的长度，设圆的半径为r，则，根据勾股定理即可得出关于r的一元一次方程，解之即可得出r，再乘以2即可求出圆O直径的长度．本题考查了切线的性质、勾股定理、解直角三角形、圆周角定理以及解一元一次方程，解题的关键是：通过角的计算找出；利用解直角三角形求出CH、AH的长度．25.【答案】解：是的外角，，且∽【解析】由于是的外角，所以，又因为，所以，从而可证明∽本题考查相似三角形的判定，解题的关键是找出两对对应角相等，本题属于中等题型．26.【答案】解一：设上、下边衬宽均为4xcm，左、右边衬宽均为3xcm，则．整理，得，解之得，，舍去，答：上、下边衬宽均为，左、右边衬宽均为．解二：设中央矩形的长为4xcm，宽为3xcm，则，解得，舍去，上、下边衬宽为，左、右边衬宽均为，答：上、下边衬宽均为，左、右边衬宽均为．【解析】设上、下边衬宽均为4xcm，左、右边衬宽均为3xcm，根据封面的面积关系建立方程求出其解即可．本题考查了一元二次方程解实际问题的运用，一元二次方程的解法的运用，解答时根据矩形的面积公式建立方程是关键．27.【答案】解：在中，，，，在中，，，四边形BCEF是矩形，，．答：DE的长为579m．【解析】本题考查解直角三角形的应用，锐角三角函数、矩形的性质等知识，解题的关键是学会利用直角三角形解决问题，属于中考常考题型．在中，求出BC，在中，求出DF，由四边形BCEF是矩形，可得，由此即可解决问题．28.【答案】；解方程得，，．方程两根是2倍关系，或4，当时，，即，代入代数式，当时，，即，代入代数式．综上所述，；根据“倍根方程”的概念设一元二次方程的两个根为t 和2t．原方程可以改写为，，．解得．，b，c之间的关系是．【解析】【分析】本题考查了根与系数的关系：若，是一元二次方程的两根时，，也考查了一元二次方程的解和解一元二次方程．由一元二次方程是“倍根方程”，得到，，即可得到结论；解方程得，，由方程两根是2倍关系，得到或43，代入解方程即可得到结论；根据“倍根方程”的概念得到原方程可以改写为，解方程即可得到结论．【解答】解：一元二次方程是“倍根方程”，，，即，，，故答案为2；见答案；见答案．29.【答案】证明：，AC平分，，，，，，，，；解：过点C作于点M，，，，，∽，，设，：：3，，，，解得：，故AE．【解析】直接利用等腰三角形的性质结合互余的定义得出；首先过点C作于点M，进而得出∽，求出EC的长即可得出答案．此题主要考查了相似三角形的判定与性质以及等腰三角形的性质等知识，正确得出∽是解题关键．30.【答案】解：设销售单价为x元，由题意，得：，整理，得：，解得：，答：这种玩具的销售单价为460元时，厂家每天可获利润20000元．【解析】根据单件利润销售量总利润，列方程求解即可．本题主要考查一元二次方程的应用、一元二次方程的解法，理解题意找到题目蕴含的相等关系列出方程是解题的关键．31.【答案】证明：和均为等腰直角三角形，，，∽，；解：，理由：，，又，∽，，，，；解：如图所示：作于M，，和均为等腰直角三角形，，∽，，即，，，，，的面积．【解析】此题主要考查了相似形综合、平行线的判定方法以及相似三角形的判定与性质等知识直接利用相似三角形的判定方法得出∽，进而得出答案；首先得出∽，进而求出，即可得出AC与BD的位置关系；首先利用相似三角形的性质表示出BD，PM的长，进而表示出的面积．。
九年级数学上册 _ 月考易错题型专练：二次函数【存在性问题】
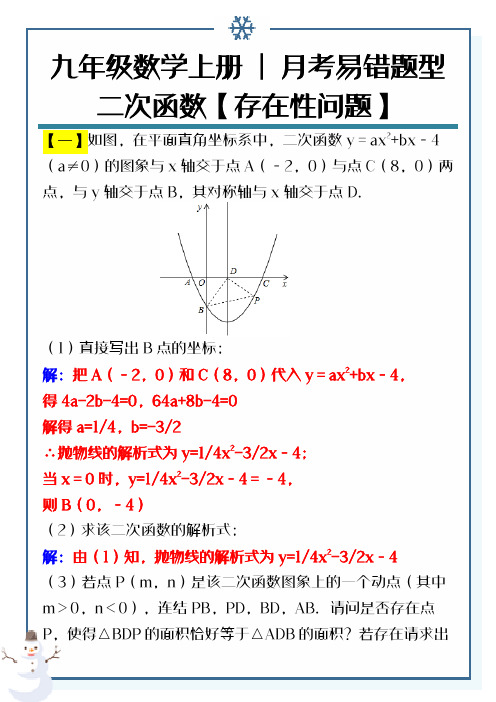
九年级数学上册| 月考易错题型二次函数【存在性问题】【一】如图，在平面直角坐标系中，二次函数y＝ax2+bx﹣4（a≠0）的图象与x轴交于点A（﹣2，0）与点C（8，0）两点，与y轴交于点B，其对称轴与x轴交于点D．（1）直接写出B点的坐标；解：把A（﹣2，0）和C（8，0）代入y＝ax2+bx﹣4，得4a-2b-4=0，64a+8b-4=0解得a=1/4，b=-3/2∴抛物线的解析式为y=1/4x2-3/2x﹣4；当x＝0时，y=1/4x2-3/2x﹣4＝﹣4，则B（0，﹣4）（2）求该二次函数的解析式；解：由（1）知，抛物线的解析式为y=1/4x2-3/2x﹣4（3）若点P（m，n）是该二次函数图象上的一个动点（其中m＞0，n＜0），连结PB，PD，BD，AB．请问是否存在点P，使得△BDP的面积恰好等于△ADB的面积？若存在请求出此时点P的坐标，若不存在说明理由．解：存在．∵y=1/4x2-3/2x﹣4=1/4（x﹣3）2﹣25/4，∴抛物线的对称轴为直线x＝3，∴D（3，0）．由（1）知，B（0，﹣4）．连接OP，如图，设P（m，1/4m2-3/2m﹣4）（0＜m＜8），∵S△PBD＝S△POD+S△POB﹣S△BOD，S△ABD=1/2×5×4＝10，而△BDP的面积恰好等于△ADB的面积，∴1/2×3×（-1/4m2+3/2m+4）+1/2×4×m-1/2×3×4＝10，整理得3m2﹣34m+80＝0，解得m1＝10/3，m2＝8（舍去），∴P点坐标为（10/3，-56/9）．【二】如图，抛物线过A（1，0）、B（﹣3，0），C（0，﹣3）三点，直线AD交抛物线于点D，点D的横坐标为﹣2，点P （m，n）是线段AD上的动点，过点P的直线垂直于x轴，交抛物线于点Q．（1）求直线AD及抛物线的解析式；解：设抛物线的解析式为y＝ax2+bx+c，将A（1，0），B（﹣3，0）C（0，﹣3）代入y＝ax2+bx+c得：a+b+c=0；9a-3b+c=0；c=-3解得：a=1；b=2；c=-3；∴抛物线的解析式为：y＝x2+2x﹣3，当x＝﹣2时，y＝（﹣2）2﹣4﹣3＝﹣3，∴D（﹣2，﹣3），设直线AD的解析式为y＝kx+b，将A（1，0），D（﹣2，﹣3）代入得：k+b=0，-2k+b=-3 解得：k=1，b=-1∴直线AD的解析式为y＝x﹣1；因此直线AD的解析式为y＝x﹣1，抛物线的解析式为：y＝x2+2x﹣3．（2）求线段PQ的长度l与m的关系式，m为何值时，PQ最长？解：∵点P在直线AD上，Q抛物线上，P（m，n），∴n＝m﹣1 Q（m，m2+2m﹣3）∴PQ的长l＝（m﹣1）﹣（m2+2m﹣3）＝﹣m2﹣m+2 （﹣2≤m≤1）∴当m=-（-1/-1×2）=1/2时，PQ的长l最大＝﹣（-1/2）2﹣（-1/2）+2=9/4．∴线段PQ的长度l与m的关系式为：l＝﹣m2﹣m+2 （﹣2≤m≤1）当m=-1/2时，PQ最长，最大值为9/4．（3）在平面内是否存在整点（横、纵坐标都为整数）R，使得P、Q、D、R为顶点的四边形是平行四边形？若存在，求出点R的坐标；若不存在，说明理由．解：①若PQ为平行四边形的一边，则R一定在直线x＝﹣2上，如图：∵PQ的长为0＜PQ≤9/4的整数，∴PQ＝1或PQ＝2，当PQ＝1时，则DR＝1，此时，在点D上方有R1（﹣2，﹣2），在点D下方有R2（﹣2，﹣4）；当PQ＝2时，则DR＝2，此时，在点D上方有R3（﹣2，﹣1），在点D下方有R4（﹣2，﹣5）；②若PQ为平行四边形的一条对角线，则PQ与DR互相平分，当PQ＝1时，即：x﹣1﹣（x2+2x﹣3）＝1，此时x不是整数，当PQ＝2时，即x﹣1﹣（x2+2x﹣3）＝2，此时x1＝﹣1，x2＝0；当x1＝﹣1，R与点C重合，即R5（0，﹣3），当x2＝0；此时R6（2，﹣1）综上所述，符合条件的点R有：R1（﹣2，﹣2），R2（﹣2，﹣4），R3（﹣2，﹣1），R4（﹣2，﹣5），R5（0，﹣3），R6（2，﹣1）．答：符合条件的点R共有6个，【三】如图，抛物线y＝ax2+bx+c（a≠0）的顶点坐标为（2，﹣1），图象与y轴交于点C（0，3），与x轴交于A、B 两点．（1）求抛物线的解析式；解：∵抛物线的顶点坐标为（2，﹣1），∴可设抛物线解析式为y＝a（x﹣2）2﹣1（a≠0），把C（0，3）代入可得a（0﹣2）2﹣1＝3，解得a＝1，∴抛物线解析式为y＝（x﹣2）2﹣1＝x2﹣4x+3；（2）设抛物线对称轴与直线BC交于点D，连接AC、AD，点E为直线BC上的任意一点，过点E作x轴的垂线与抛物线交于点F，问是否存在点E使△DEF为直角三角形？若存在，求出点E坐标，若不存在，请说明理由．解：在y＝x2﹣4x+3中，令y＝0可得x2﹣4x+3＝0，解得x＝1或x＝3，∴A（1，0），B（3，0），设直线BC解析式为y＝kx+3，把B（3，0）代入得：3k+3＝0，解得k＝﹣1，∴直线BC解析式为y＝﹣x+3，由（1）可知抛物线的对称轴为x＝2，此时y＝﹣2+3＝1，∴D（2，1），∴AD2＝2，AC2＝10，CD2＝8，∵AD2+CD2＝AC2，∴∠ADC＝90°，由题意知EF∥y轴，则∠FED＝∠OCB≠90°，∴△DEF为直角三角形，分∠DFE＝90°和∠EDF＝90°两种情况，①当∠DFE＝90°时，即DF∥x轴，则D、F的纵坐标相同，∴F点纵坐标为1，∵点F在抛物线上，∴x2﹣4x+3＝1，解得x＝2±√2，即点E的横坐标为2±√2，∵点E在直线BC上，∴当x＝2+√2时，y＝﹣x+3＝1-√2，当x＝2-√2时，y＝﹣x+3＝1，∴E点坐标为（2+√2，1-√2）或（2-√2，1+√2）；②当∠EDF＝90°时，且∠ADC＝90°，∴点F在直线AD 上，∵A（1，0），D（2，1），∴直线AD解析式为y＝x﹣1，∴直线AD与抛物线的交点即为F点，联立直线AD与抛物线解析式有x2﹣4x+3＝x﹣1，解得x＝1或x＝4，当x＝1时，y＝﹣x+3＝2，当x＝4时，y＝﹣x+3＝﹣1，∴E点坐标为（1，2）或（4，﹣1），综上可知存在满足条件的点E，其坐标为（2+√2，1-√2）或（2-√2，1+√2）或（1，2）或（4，﹣1）．。
数学九年级上册易错题
数学九年级上册易错题一、选择题（1 - 10题）1. 一元二次方程x^2-2x - 3 = 0的根的情况是（）- A. 有两个相等的实数根。
- B. 有两个不相等的实数根。
- C. 没有实数根。
- D. 无法确定。
- 解析：对于一元二次方程ax^2+bx + c = 0(a≠0)，其判别式Δ=b^2-4ac。
在方程x^2-2x - 3 = 0中，a = 1，b=-2，c=-3，则Δ=(-2)^2-4×1×(-3)=4 + 12=16>0。
当Δ>0时，方程有两个不相等的实数根，所以答案是B。
2. 若关于x的一元二次方程(m - 1)x^2+5x+m^2-3m + 2 = 0的常数项为0，则m的值等于（）- A. 1.- B. 2.- C. 1或2。
- D. 0.- 解析：因为方程的常数项为0，所以m^2-3m + 2 = 0，即(m - 1)(m - 2)=0，解得m = 1或m = 2。
又因为方程是一元二次方程，二次项系数m - 1≠0，即m≠1，所以m = 2，答案是B。
3. 二次函数y = x^2-2x + 3的顶点坐标是（）- A. (1,2)- B. (-1,2)- C. (1, - 2)- D. (-1,-2)- 解析：对于二次函数y=ax^2+bx + c(a≠0)，其顶点坐标的横坐标x =-(b)/(2a)，纵坐标y=frac{4ac - b^2}{4a}。
在y = x^2-2x + 3中，a = 1，b=-2，c = 3，x =-(-2)/(2×1)=1，y=frac{4×1×3-(-2)^2}{4×1}=(12 - 4)/(4)=2，所以顶点坐标是(1,2)，答案是A。
4. 已知二次函数y = ax^2+bx + c(a≠0)的图象如图所示，则下列结论中正确的是（）- A. a>0- B. c<0- C. 3是方程ax^2+bx + c = 0的一个根。
人教版九年级数学易错题收集整理+常见数学易错题精选
人教版九年级数学易错题收集整理+常见数学易错题精选人教版九年级数学易错题成长系列1、二次函数2y ax bx c =++图像如图所示，则下列结论正确的是（ ）A.20,0,0,40a b c b ac <<>-> B.20,0,0,40a b c b ac ><>-< C.20,0,0,40a b c b ac <><-> D.20,0,0,40a b c b ac <>>-> 如图，二次函数2y ax bx c =++的图像过（-1,1），（2，-1）两点，下列关于这个二次函数的叙述正确的是（ ）A. 当0x =时，y 的值大于1B. 当3x =时，y 的值小于0C. 当1x =时，y 的值大于1D. y 的最大值小于02、二次函数2y ax bx =+的图像如图，若一元二次方程20ax bx m ++=有实数根，则m 的最大值为（ ）A. -3B. 3C. -5D. 94、设二次函数2y x bx c =++，当1x ≤时，总有0y ≥，当13x ≤≤时，总有0y ≤，那么c 的取值范围是 。
5、已知抛物线212y x bx =+经过点A （4，0）。
设点C （1，-3），请在抛物线的对称轴上确定一点D ，使得|AD-CD|的值最大，则D 的坐标为 。
6、已知：关于x 的方程2(13a)210ax x a --+-=（1）当a 取何值时，二次函数2(13a)21y ax x a =--+-的对称轴是x=-2？ （2）求证：a 取任何实数时，方程2(13a)210ax x a --+-=总有根。
7、如图，抛物线254y ax x a =-+与x 轴相交于A 、B ，且过点C （5, 4）。
（1）求a 的值和该抛物线的顶点P 的坐标（2）请你设计一种平移方法，使平移之后抛物线的顶点落在第二象限，并写出平移后抛物线的解析式。
中考数学易错100题(必考)及答案
中考数学易错100题（必考）1、在实数123.0,330tan ,60cos ,722,2121121112.0,,14.3,64,3,80032----Λπ中，无理数有（ ）A 、3个B 、4个C 、5个D 、6个2、下列运算正确的是（ ）A 、x 2 x 3 =x 6B 、x 2＋x 2=2x 4C 、(-2x)2=4x 2 D 、(-2x)2 (-3x )3=6x 53、算式可化为（ ）A 、B 、C 、D 、4、“世界银行全球扶贫大会”于2004年5月26日在上海开幕.从会上获知，我国国民生产总值达到11.69万亿元，人民生活总体上达到小康水平，其中11.69万亿用科学记数法表示应为（ ）A 、11.69×1410B 、1410169.1⨯C 、1310169.1⨯ D 、14101169.0⨯ 5、不等式2)2(2-≤-x x 的非负整数解的个数为（ ）A 、1B 、2C 、3D 、46、不等式组⎩⎨⎧-≤-->x x x 28132的最小整数解是（ ）A 、－1B 、0C 、2D 、37、为适应国民经济持续协调的发展，自2004年4月18日起，全国铁路第五次提速，提速后，火车由天津到上海的时22222222+++422882162间缩短了7.42小时，若天津到上海的路程为1326千米，提速前火车的平均速度为x 千米/小时，提速后火车的平均速度为y 千米/时，则x 、y 应满足的关系式是（ ）A 、x – y =42.71326 B 、 y – x = 42.71326 C 、y x 13261326-= 7.42 D 、x y 13261326-= 7.428、一个自然数的算术平方根为a ，则与它相邻的下一个自然数的算术平方根为（ ）A 、1+aB 、 1+aC 、12+aD 、1+a9、设B A ,都是关于x 的5次多项式，则下列说法正确的是（ ）A 、B A +是关于x 的5次多项式 B 、B A -是关于x 的4次多项式C 、 AB 是关于x 的10次多项式D 、B A 是与x 无关的常数10、实数a,b 在数轴对应的点A 、B 表示如图，化简a a a b 244-++-||的结果为（ ）A 、22a b --B 、22+-b aC 、2-bD 、2+b11、某商品降价20%后出售，一段时间后恢复原价，则应在售价的基础上提高的百分数是 （ ）A 、20%B 、25%C 、30% A BD 、35%12、某种出租车的收费标准是：起步价7元（即行驶距离不超过3km 都需付7元车费），超过3km 以后，每增加，加收2.4元（不足1km 按1km 计），某人乘这种车从甲地到乙地共支付车费19元，那么，他行程的最大值是（ ）A 、11 kmB 、8 kmC 、7 kmD 、5km13、在高速公路上，一辆长4米，速度为110千米/小时的轿车准备超越一辆长12米，速度为100千米/小时的卡车，则轿车从开始追及到超越卡车，需要花费的时间约是（ ）A 、1.6秒B 、4.32秒C 、5.76秒D 、345.6秒14、如果关于x 的一元二次方程0962=+-x kx 有两个不相等的实数根，那么k 的取值范围是（ ）A 、1<kB 、0≠kC 、1<k 且0≠kD 、1>k15、若a 2+ma +18在整数范围内可分解为两个一次因式的乘积，则整数m 不可能是（ ）A 、 ±9B 、±11C 、±12D 、±1916、在实数范围内把8422--x x 分解因式为（ ）A 、)1)(3(2+-x xB 、)51)(51(--+-x xC 、)51)(51(2--+-x xD 、)51)(51(2++-+x x 17、用换元法解方程x x x x +=++2221时，若设x 2+x=y, 则原方程可化为（ ） A 、y 2+y+2=0 B 、y 2－y －2=0 C 、y 2－y+2=0D 、y 2+y －2=018、某商品经过两次降价，由每件100元降至81元，则平均每次降价的百分率为（ ）A 、8.5%B 、9%C 、9.5%D 、10%19、一列火车因事在途中耽误了5分钟，恢复行驶后速度增加5千米/时，这样行了30千米就将耽误的时间补了回来，若设原来的速度为x 千米/时，则所列方程为（ ）A 、30305560x x --= B 、30530560x x +-= C 、30305560x x -+= D 、303055x x -+= 20、已知关于x 的方程02=+-m mx x 的两根的平方和是3，则m的值是（ ）A 、1-B 、1C 、3D 、1-或321、如果关于x 的一元二次方程0)1(222=+--m x m x 的两个实数根为βα,，则βα+的取值范围是（ ）A 、1≥+βαB 、1≤+βαC 、21≥+βα D 、21≤+βα22、已知数轴上的点A 到原点的距离为2，那么在数轴上到A点的距离是3的点所表示的数有（ ）A 、1个B 、 2个C 、 3个D 、4个23、已知)0(1,≥+==a a y a x ，则y 和x 的关系是（ ） A 、x y = B 、1+=x y C 、2x y = D 、)0(12≥+=x x y24、点A (2 ，－1)关于y 轴的对称点B 在（ ）A 、一象限B 、二象限C 、三象限D 、第四象限25、点P(x+1，x －1)不可能在（ ）A 、第一象限B 、第二象限C 、第三象限D 、第四象限26、已知函数式32+-=x y ，当自变量增加1时，函数值（ ）A 、增加 1B 、减少 1C 、增加 2D 、减少227、在平面直角坐标系内，Ａ、Ｂ、Ｃ三点的坐标为(0,0) 、(4,0)、(3,2),以Ａ、Ｂ、Ｃ三点为顶点画平行四边形，则第四个顶点不可能在（ ）Ａ、第一象限 Ｂ、第二象限 Ｃ、第三象限 Ｄ、第四象限28、已知一元二次方程02=++c bx ax 有两个异号根，且负根的绝对值较大，则),(bc ab M 在（ ）A 、第一象限B 、第二象限C 、第三象限 D 、第四象限29、“龟兔赛跑”讲述了这样的故事：领先的兔子看着缓缓爬行的乌龟，骄傲起来，睡了一觉。
最全最完整初三数学易错题集(全)
最全最完整初三数学易错题集(全)
本文将为初三数学的学生提供一份最全最完整的易错题集，以帮助他们更好地复数学知识。
本文共包括以下几个部分：
一、概率统计
这一部分为初三数学中概率统计部分常见的易错题集，主要包括计数原理、概率公式等知识点。
这些题目均为根据历年试题整理而成。
二、平面几何
这一部分为初三数学中平面几何部分常见的易错题集，主要包括角度、三角形、圆等知识点。
这些题目均为根据历年试题整理而成。
三、立体几何
这一部分为初三数学中立体几何部分常见的易错题集，主要包括空间几何体积、表面积、棱锥、棱柱、圆柱、圆锥等知识点。
这些题目均为根据历年试题整理而成。
四、代数式与方程式
这一部分为初三数学中代数式与方程式部分常见的易错题集，主要包括多项式基本操作、一次方程式、二次方程式等知识点。
这些题目均为根据历年试题整理而成。
五、欧氏几何
这一部分为初三数学中欧氏几何部分常见的易错题集，主要包括向量、坐标系、函数基本知识等。
这些题目均为根据历年试题整理而成。
本文所提供的易错题集是初三数学复习过程中的重要资料，希望各位同学认真复习，并取得好成绩！。
初三经典错题集数学
初三经典错题集数学
1.某地每年的平均温度为16°C，其中1月份的平均温度为5°C，7月份的平均温度为23°C，则该地其余月份的平均温度为多少°C？
2. 在平面直角坐标系中，点A(3,-1)、B(-4,5)、C(-3,-4)，则△ABC的面积是多少？
3. 若a+b=4，a-b=2，则a-b=？
4. 甲、乙两条路线交点为P点，甲路线上距离P点30 km的地方有一村庄，乙路线上距离P点20 km的地方有一村庄。
若两村庄之间的距离为50 km，则甲、乙两路线的长度分别是多少？
5. 有一条直线通过点(1,3)和点(2,4)，则该直线的斜率是多少？
6. 若x+2y=5，则2x+4y=？
7. 若a:b=3:5，且a+b=40，则a的值是多少？
8. 在直角三角形ABC中，∠A=90°，AC=8 cm，BC=10 cm，则AB的长度是多少？
9. 若5a+3b=13，2a+4b=10，则a的值是多少？
10. 某商店打折，原价为x元的商品现在售价为(x-20)元，现在售价为80元，则原价为多少元？
- 1 -。
中考数学重难点易错题汇总含答案解析
精品基础教育教学资料，仅供参考，需要可下载使用！最新初三九年级中考数学易错题集锦汇总学校：__________ 姓名：__________ 班级：__________ 考号：__________ 题号 一 总分 得分注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上评卷人得分 一、选择题1．如图，能判定 AB ∥CD 的条件是（ ）A ．∠1=∠2B ．∠1+∠2= 180°C ．∠3=∠4D ．∠3+∠1=180°2．下列各式中从左到右的变形，是因式分解的是（ ）A ．（a+3）（a-3）=a 2-9；B ．x 2+x-5=（x-2）（x+3）+1；C ．a 2b+ab 2=ab （a+b ）D ．x 2+1=x （x+x1） 3．用科学记数方法表示0000907.0，得（ ）A ．41007.9-⨯B ．51007.9-⨯C ．6107.90-⨯D ．7107.90-⨯ 4．小马虎在下面的计算中只做对了一道题，则他做对的题目是 （ ）A ．222)(b a b a -=-B ．6234)2(a a =-C ．5232a a a =+D ．1)1(--=--a a5．方程x 3＝22-x 的解的情况是（ ） A ．2=x B ．6=xC ．6-=xD ．无解 6．已知235x x ++的值为 3，则代数式2391x x +-的值为（ ）A ．-9B ．-7C ．0D ．37．下列事件中，届于不确定事件的是（ ）A ．2008年奥运会在北京举行B ．太阳从西边升起C ．在1，2，3，4中任取一个教比 5大D ．打开数学书就翻到第10页8．下列长度的三条线段能组成三角形的是（ ）A ．5cm,3cm,1cmB ．6cm,4cm,2cmC ． 8cm, 5cm, 3cmD ． 9cm,6cm,4cm9．在下面四个图形中，既包含图形的旋转，又有图形的轴对称设计的是（ ）A ．B ．C ．D ．10．下列说法中，正确的是（ ）A ．一颗质地均匀的骰子已连续抛掷了 2000次，其中抛掷出 5点的次数最少，则第2001次一定抛掷出 5点B ．某种彩票中奖的概率是1%，因此买100张该种彩票一定会中奖C ．天气预报说明天下雨的概率是50%，所以明天将有一半时间在下雨D ．抛掷一枚图钉，钉尖触地和钉尖朝上的概率不相等11．某地区10户家庭的年消费情况如下：年消费l0万元的有2户，年消费5万元的有l 户，年消费1．5万元的有6户，年消费7千元的有1户．可估计该地区每户年消费金额的一般水平为（）A.1．5万元 B．5万元 C．10万元 D．3.47万元12．三角形的一个外角小于与它相邻的内角，这个三角形是（）A．直角三角形B．锐角三角形C．钝角三角形D．属于哪一类不能确定13．下列图形中，由已知图形通过平移变换得到的是（）14．在同一平面内垂直于同一条直线的两条直线必然（）A．互相平行B．互相垂直C．互相重合D．关系不能确定15．△ABC和△DEF都是等边三角形，若△ABC的周长为24 cm ，△DEF的边长比△ABC 的边长长3 cm，则△DEF的周长为（）A．27 cm B．30 cm C．33 cm D．无法确定16．下列命题不正确的是（）A．在同一三角形中，等边对等角B．在同一三角形中，等角对等边C．在等腰三角形中与顶角相邻的外角等于底角的2倍D．等腰三角形是等边三角形17．在△ABC中，∠A：∠B：∠C=2：3：5，则△ABC是（）A．锐角三角形B．钝角三角形C．直角三角形D．无法确定18．等腰三角形的“三线合一”是指（）A．中线、高、角平分线互相重合B．腰上的中线、腰上的高、底角的平分线互相重合C．顶角的平分线、中线、高线三线互相重合D ． 顶角的平分线、底边上的高及底边上的中线三线互相重合19．在△ABC 中，已知AC AB = ，DE 垂直平分AC ，50=∠A °，则DCB ∠的度数是（ ）A ． 15°B ．30°C ． 50°D ． 65°20．将如图1所示的Rt △ABC 绕直角边BC 旋转一周，所得几何体的左视图是（ ）21．画一个物体的三视图时，一般的顺序是（ ）A ．主视图、左视图、俯视图B ．主视图、俯视图、左视图C ．俯视图、主视图、左视图D ．左视图、俯视图、主视图22．要了解一批电视机的使用寿命，从中任意抽取30台电视机进行试验，在这个问题中，30是（ ）A ．个体B ．总体C ．样本容量D ．总体的一个样本23．济南市某储运部紧急调拨一批物资，调进物资共用４小时，调进物资2小时后开始调出物资（调进物资与调出物资的速度均保持不变）．储运部库存物资S （吨）与时间t （小时）之间的函数关系如图所示，这批物资从开始调进到全部调出需要的时间是（ ）A ．4小时B ．4.4小时C ．4.8小时D ．5小时 24．若分式3242x x +-有意义，则字母x 的取值范围是（ ） A ．12x = B ．23x =- C ．12x ≠ 23x ≠-25．把图中的角表示成下列形式：①∠AP0；②∠P；③∠0PC；④∠0；⑤∠CP0；⑥∠AOP．其中正确的有（）A．6个B．5个C．4个D．3个26．盒子中有白色乒乓球8个和黄色乒乓球若干个，为求得盒中黄色乒乓球的个数，某同学进行了如下实验：每次摸出一个乒乓球记下它的颜色，如此重复360次，摸出白色乒乓球90次，则黄色乒乓球的个数估计为（）A．90个B．24个C．70个D．32个27．如图所示的 6 个数是按一定规律排列的，根据这个规律，括号内的数应是（）A．27 B．56 C．43 D．3028．现有两个有理数 a、b，它们的绝对值相等，则这两个有理数（）A．相等 B．相等或互为相反数 C．都是零 D．互为相反数29．某天股票A 开盘价 19 元，上午 11：30 跌1. 5 元，下午收盘时又涨了 0. 5 元，则投票A 这天收盘价为（）A．0.3 元B．l6.2 元C．16.8 元D．18 元30．蜗牛在井里距井口 lm 处，它每天白天向上爬行 30 cm，每天夜晚又下滑 20 cm，则蜗牛爬出井口需要的天数是（）A．11 天B．10 天C．9 天D．8 天31．小红妈妈的 2 万元存款到期了，按规定她可以得到 2 的利息，但同时必须向国家缴 纳 20% 的利息所得税，则小红妈妈缴税的金额是（ ）A ．80 元B ．60 元C ．40 元D ．20 元32．求0.0529的正确按键顺序为（ ）A ．B ．C ．D ．33．下列方程中，是一元一次方程的为（ ）A ．x+y=1B ．2210x x -+=C ．21x =D ．x=034．有下列计算 ：①0-（-5）=-5；②（-3）+（-9）=-12；③293()342⨯-=-；④(36)(9)4-÷-=-.其中正确的有（ ）A ． 1个B ． 2个C ．3个D ．4个35．一个五次多项式，它的任何一项的次数（ ）A ．都小于5B ．都等于5C ．都不大于5D ．都不小于536．⎩⎨⎧==21y x 是方程3=-y ax 的解，则a 的值是（ ） A ．5 B ．5- C ．2 D ．137．下列说法中正确的是 （ ）A ．直线大于射线B ．连结两点的线段叫做两点的距离C ．若AB=BC ，则B 是线段AC 的中点D ．两点之间线段最短38． 在△ABC 中，∠A ＝30°，∠B ＝50°，则∠C 的外角＝（ ）A ．60°B ．80°C ．100°D ．120°39．如图，∠AOC=∠BOD=90°，下列结论中正确的个数是（ ）①∠AOB=∠COD ；②∠AOD=3∠B0C ；③∠AOD+∠BOC=∠AOC+∠BODA ．0个B ．l 个C ．2个D ．3个40．若两个角互为补角，则这两个角（ ）A ．都是锐角B ．都是钝角C ．一个是锐角，另一个是钝角D ．以上结论都不全对41．下列说法中，错误的是（ ）A ．经过一点可以画无数条直线B ．经过两点可以画一条直线C ．两点之间线段最短D ．三点确定一条直线42．12-的绝对值是（ ） A ．2- B ．12- C ．2 D ．1243．下列说法中正确的是（ ）A ．从三角形一个顶点向它对边所在直线画垂线，此垂线就是三角形的高B ．三角形的角平分线是一条射线C．直角三角形只有一条高D．钝角三角形的三条高所在的直线的交点在此三角形的外部44．如图所示，是轴对称图形的个数有（）A．4个B．3个C．2个D．1个45．将如图所示的图形按照顺时针方向旋转90°后所得的图形是（）46．如图，已知 6.75r=，则图中阴影部分的面积为（结果保留π）（）R=， 3.25A．35π⋅B．12.25πC．27πD．35π47．如图，由△ABC平移而得的三角形有（）A． 8个B． 9个C． 10个D． 16个48．下列各式中不是不等式的为（）A．25x=D．610x+≤C．58-<B．92y+> 49．关于单项式322-的系数、次数，下列说法中，正确的是（）2x y zA．系数为-2，次数为 8B．系数为-8，次数为 5C．系数为-23，次数为 4D ．系数为-2，次数为 750．直角三角形在正方形网格纸中的位置如图所示，则cos α的值是（ ）A ． 43B ． 34C ． 53D ． 5451．下列说法中，正确的个数是（ ）①样本的方差越小，波动性越小，说明样本稳定性越好；②一组数据的方差一定是正数；③一组数据的方差的单位与原数据的单位是一致的；④一组数据的标准差越大，则这组数据的方差一定越大．A ．1个B ．2个C ．3个D ．4个52．如图，在两半径不同的圆心角中，∠AOB=∠A ′O ′B ′=60°，则（ ）A ．AB=A ′B ′ B ．AB<A ′B ′C ．AB 的度数=A ′B ′的度数D ．AB 的长度=A ′B ′的长度53．△ABC 中，A = 47°，AB = 1.5 cm ，AC=2 cm ，△DEF 中，E = 47°，ED =2.8 cm ，EF=2. 1 cnn ，这两个三角形（ ）A ． 相似B ．不相似C ． 全等D ． 以上都不对54．在△ABC 中，AB=AC ，∠A=36°．以点A 为位似中心，把△ABC 放大2倍后得△A ′B ′C ′,则∠B 等于（ ）A ．36°B ．54°C ．72°D ．144°55．如图，∠APD ＝90°，AP ＝PB ＝BC ＝CD ，则下列结论成立的是（ ）A ．ΔPAB ∽ΔPCA B ．ΔPAB ∽ΔPDAC ．ΔABC ∽ΔDBAD ．ΔABC ∽ΔDCA56．如图，已知21∠=∠，那么添加下列一个条件后，仍无法．．判定ABC ∆∽ADE ∆的是（ ）A ．AE AC AD AB = B ．DE BC AD AB = C ．D B ∠=∠ D ．AED C ∠=∠57．若正比例函数2y x =-与反比例函数k y x=的图象交于点A ，且A 点的横坐标是1-，则此反比例函数的解析式为（ ）A ．12y x =B ．12y x =-C ．2y x =D ．2y x=- 58．如图，梯形ABCD 中，AB ∥DC ，AB ⊥BC ，AB ＝2cm ，CD ＝4cm ．以BC 上一点O 为圆心的圆经过A 、D 两点，且∠AOD ＝90°，则圆心O 到弦AD 的距离是（ ）A ．6cmB ．10cmC ．32cmD ．52cm59．等腰三角形的腰长为32，底边长为6，那么底角等于（ ）A ． 30°B ． 45°C ． 60°D ．120°60．下列事件，是必然事件的是（ ）A ．掷一枚均匀的普通正方形骰子，骰子停止后朝上的点数是1B ．掷一枚均匀的普通正方形骰子，骰子停止后朝上的点数是偶数C ．打开电视，正在播广告D ．抛掷一枚硬币，掷得的结果不是正面就是反面61．如图，扇形 OAB 的圆心角为 90°，分别以 OA 、OB 为直径在扇形内作半圆，P 和Q 分别表示两个阴影部分的面积，那么 P 和Q 的大小关系是（ ）A ．P=QB ．P>QC ．P<QD ． 无法确定62．某飞机于空中 A 处探测到平面目标 B ，此时从飞机上看目标B 的俯角α=30°，飞行高度AC= 1200 m，那么飞机到目标B 的距离AB为（）A．2400m B．1200m C．4003 m D．12003 m 63．已知二次函数22(21)1y x a x a=+++-的最小值为 0，则a的值为（）A．34B．34-C．54D．54-64．一箱灯泡有 24 个,灯泡的合格率是87.5%，则从中任意拿出一个是次品的概率是（）A．0 B．124C．78D．1865．设有 10 个型号相同的杯子，其中一等品 7个、二等品 2个、三等品 1 个，从中任取一个杯子是一等品的概率等于（）A．310B．70lC．37D．1766．书架的第一层放有 2 本文艺书、3 本科技书，书架的第二层放有 4 本文艺书、1 本科技书，从两层各取 1 本书，恰好都是科技书的概率是（）A．325B．49C．1720D．2567．在一个有 10 万人的小镇，随机调查了 2000人，其中有 250 人看中央电视台的早新闻，在该镇随机问一个人，他看早新闻的概率大约是（）A．0.75 B． 0.5 C． 0.25 D． 0.12568．有左、中、右三个抽屉,左边的抽屉里放有 2个白球，中间和右边的抽屉里各放一个红球和一个白球，从三个抽屉里任选一个球是红球的概率是（）A．14B．13C．16D．2569．在今年的中考中，市区学生体育测试分成了三类，耐力类，速度类和力量类。
中考数学易错题集锦及答案 [整理版]
![中考数学易错题集锦及答案 [整理版]](https://img.taocdn.com/s3/m/d3e28fb1daef5ef7ba0d3c36.png)
初中数学选择、填空、简答题易错题集锦及答案一、选择题1、A 、B 是数轴上原点两旁的点，则它们表示的两个有理数是（ ）A 、互为相反数B 、绝对值相等C 、是符号不同的数D 、都是负数 2、有理数a 、b 在数轴上的位置如图所示，则化简|a-b|-|a+b|的结果是（ ） A 、2a B 、2b C 、2a-2b D 、2a+b3、轮船顺流航行时m 千米/小时，逆流航行时(m-6)千米/小时，则水流速度（ ）A 、2千米/小时B 、3千米/小时C 、6千米/小时D 、不能确定 4、方程2x+3y=20的正整数解有（ ） A 、1个 B 、3个 C 、4个 D 、无数个 5、下列说法错误的是（ ）A 、两点确定一条直线B 、线段是直线的一部分C 、一条直线是一个平角D 、把线段向两边延长即是直线 6、函数y=(m 2-1)x 2-(3m-1)x+2的图象与x 轴的交点情况是 ( ) A 、当m ≠3时，有一个交点 B 、1±≠m 时，有两个交 C 、当1±=m 时，有一个交点 D 、不论m 为何值，均无交点7、如果两圆的半径分别为R 和r （R>r ），圆心距为d ，且(d-r)2=R 2，则两圆的位置关系是（ ） A 、内切 B 、外切 C 、内切或外切 D 、不能确定8、在数轴上表示有理数a 、b 、c 的小点分别是A 、B 、C 且b<a<c ，则下列图形正确的是（ ）A B C D 9、有理数中，绝对值最小的数是（ ） A 、-1 B 、1 C 、0 D 、不存在10、21的倒数的相反数是（ ）A 、-2B 、2C 、-21D 、2111、若|x|=x ，则-x 一定是（ ）A 、正数B 、非负数C 、负数D 、非正数12、两个有理数的和除以这两个有理数的积，其商为0，则这两个有理数为（ ） A 、互为相反数 B 、互为倒数 C 、互为相反数且不为0 D 、有一个为013、长方形的周长为x ，宽为2，则这个长方形的面积为（ ） A 、2x B 、2(x-2) C 、x-4 D 、2·(x-2)/2 14、“比x 的相反数大3的数”可表示为（ ） A 、-x-3 B 、-(x+3) C 、3-xD 、x+315、如果0<a<1，那么下列说法正确的是（ ） A 、a 2比a 大B 、a 2比a 小C 、a 2与a 相等D 、a 2与a 的大小不能确定16、数轴上，A 点表示-1，现在A 开始移动，先向左移动3个单位，再向右移动9个单位，又向左移动5个单位，这时，A 点表示的数是（ ）A 、-1B 、0C 、1D 、817、线段AB=4cm ，延长AB 到C ，使BC=AB 再延长BA 到D ，使AD=AB ，则线段CD 的长为（ ）A 、12cmB 、10cmC 、8cmD 、4cm18、21-的相反数是（ ）A 、21+B 、12-C 、21--D 、12+-19、方程x(x-1)(x-2)=x 的根是（ ）A 、x 1=1, x 2=2B 、x 1=0, x 2=1, x 3=2C 、x 1=253+, x 2=253- D 、x 1=0，x 2=353+, x 3=253- 20、解方程04)1(5)1(322=-+++xx x x 时，若设y x x =+1，则原方程可化为（ ）A 、3y 2+5y-4=0 B 、3y 2+5y-10=0 C 、3y 2+5y-2=0 D 、3y 2+5y+2=0 21、方程x 2+1=2|x|有（ ）A 、两个相等的实数根；B 、两个不相等的实数根；C 、三个不相等的实数根；D 、没有实数根 22、一次函数y=2(x-4)在y 轴上的截距为（ ）A 、-4B 、4C 、-8D 、823、解关于x 的不等式⎩⎨⎧-<>ax ax ，正确的结论是（ ）A 、无解B 、解为全体实数C 、当a>0时无解D 、当a<0时无解 24、反比例函数xy 2=，当x ≤3时，y 的取值范围是（ ） A 、y ≤32 B 、y ≥32C 、y ≥32或y<0D 、0<y ≤3225、0.4的算术平方根是（ ） A 、0.2 B 、±0.2 C 、510D 、±510 26、李明骑车上学，一开始以某一速度行驶，途中车子发生故障，只好停车修理，车修好后，因怕耽误时间，于时就加快了车速，在下列给出的四个函数示意图象，符合以上情况的是（ ） A B C D27、若一数组x 1, x 2, x 3, …, x n 的平均数为x ，方差为s 2，则另一数组kx 1, kx 2, kx 3, …, kx n 的平均数与方差分别是（ ） A 、k x , k 2s2B 、x , s2C 、k x , ks2D 、k 2x , ks 228、若关于x 的方程21=+-ax x 有解，则a 的取值范围是（ ）A 、a ≠1B 、a ≠-1C 、a ≠2D 、a ≠±129、下列图形中既是中心对称图形，又是轴对称图形的是（ ）A 、线段B 、正三角形C 、平行四边形D 、等腰梯形 30、已知dcb a =，下列各式中不成立的是（ ）A 、d c b a d c b a ++=-- B 、d b c a d c 33++= C 、bd ac b a 23++= D 、ad=bc 31、一个三角形的三个内角不相等，则它的最小角不大于（ ） A 、30B 、45C 、550D 、60032、已知三角形内的一个点到它的三边距离相等，那么这个点是（ ）A 、三角形的外心B 、三角形的重心C 、三角形的内心D 、三角形的垂心33、下列三角形中是直角三角形的个数有（ ）①三边长分别为3:1:2的三角形 ②三边长之比为1:2:3的三角形 ③三个内角的度数之比为3:4:5的三角形 ④一边上的中线等于该边一半的三角形 A 、1个 B 、2个 C 、3个 D 、4个34、如图，设AB=1，S △OAB =43cm 2，则弧AB 长为（ ）A 、3πcm B 、32πcm C 、6πcm D 、2πcm 35、平行四边形的一边长为5cm ，则它的两条对角线长可以是（ ） A 、4cm, 6cm B 、4cm, 3cm C 、2cm, 12cm D 、4cm, 8cm 36、如图，△ABC 与△BDE 都是正三角形，且AB<BD ，若△ABC 不动，将△BDE 绕B 点旋转，则在旋转过程中，AE 与CD 的大小关系是（ ） A 、AE=CD B 、AE>CD C 、AE>CD D 、无法确定37、顺次连结四边形各边中点得到一个菱形，则原四边形必是（ ） A 、矩形 B 、梯形 C 、两条对角线互相垂直的四边形 D 、两条对角线相等的四边形38、在圆O 中，弧AB=2CD ，那么弦AB 和弦CD 的关系是（ ）A 、AB=2CDB 、AB>2CDC 、AB<2CD D 、AB 与CD 不可能相等 39、在等边三角形ABC 外有一点D ，满足AD=AC ，则∠BDC 的度数为（ ）A 、30B 、60C 、150D 、300或150040、△ABC 的三边a 、b 、c 满足a ≤b ≤c ，△ABC 的周长为18，则（ ）A 、a ≤6B 、b<6C 、c>6D 、a 、b 、c 中有一个等于641、如图，在△ABC 中，∠ACB=Rt ∠，AC=1，BC=2，则下列说法正确的是（ ）A 、∠B=30B 、斜边上的中线长为1C 、斜边上的高线长为552 D 、该三角形外接圆的半径为142、如图，把直角三角形纸片沿过顶点B 的直线BE （BE 交CA 于E ）折叠，直角顶点C 落在斜边AB 上，如果折叠后得到等腰三角形EBA ，那么下列结论中（1）∠A=300（2）点C 与AB 的中点重合 （3）点E 到AB 的距离等于CE 的长，正确的个数是（ ） A 、0 B 、1 C 、2 D 、3 43、不等式6322+>+x x 的解是（ ）A 、x>2B 、x>-2C 、x<2D 、x<-244、已知一元二次方程(m-1)x 2-4mx+4m-2=0有实数根，则m 的取值范围是（ ）A 、m ≤1B 、m ≥31且m ≠1C 、m ≥1D 、-1<m ≤1 45、函数y=kx+b(b>0)和y=xk-(k ≠0)，在同一坐标系中的图象可能是（ ）ABA B C D46、在一次函数y=2x-1的图象上，到两坐标轴距离相等的点有（ ）A 、1个B 、2个C 、3个D 、无数个47、若点（-2，y 1）、（-1，y 2）、（1，y 3）在反比例函数xy 1=的图像上， 则下列结论中正确的是（ ）A 、y 1>y 2>y 3B 、y 1<y 2<y 3C 、y 2>y 1>y 3D 、y 3>y 1>y 2 48、下列根式是最简二次根式的是（ ） A 、a 8 B 、22b a + C 、x 1.0 D 、5a49、下列计算哪个是正确的（ ）A 、523=+B 、5252=+C 、b a b a +=+22D 、212221221+=-50、把aa 1--（a 不限定为正数）化简，结果为（ ） A 、a B 、a - C 、-a D 、-a -51、若a+|a|=0，则22)2(a a +-等于（ ） A 、2-2a B 、2a-2 C 、-2 D 、252、已知02112=-+-x x ，则122+-x x 的值（ ）A 、1B 、±21 C 、21 D 、-2153、设a 、b 是方程x 2-12x+9=0的两个根，则b a +等于（ ）A 、18B 、6C 、23D 、±23 54、下列命题中，正确的个数是（ B ）①等边三角形都相似 ②直角三角形都相似 ③等腰三角形都相似④锐角三角形都相似 ⑤等腰三角形都全等 ⑥有一个角相等的等腰三角形相似⑦有一个钝角相等的两个等腰三角形相似 ⑧全等三角形相似 A 、2个 B 、3个 C 、4个 D 、5个 二、填空题1、如果一个数的绝对值等于它的相反数，那么这个数一定是_________。
九年级数学易错题
九年级数学易错题一、一元二次方程部分1. 若关于公式的一元二次方程公式的常数项为公式，求公式的值。
解析：对于一元二次方程公式，在方程公式中，常数项公式。
因为常数项为公式，所以公式。
对公式进行因式分解得公式。
解得公式或公式。
又因为方程是一元二次方程，二次项系数公式，即公式。
所以公式。
2. 解方程公式。
解析：对于一元二次方程公式（这里公式，公式，公式），我们可以使用求根公式公式。
首先计算判别式公式。
然后将公式，公式，公式代入求根公式得：公式。
二、二次函数部分1. 已知二次函数公式的图象经过公式、公式，公式三点，求这个二次函数的表达式。
解析：因为二次函数公式的图象经过公式、公式，公式三点。
把公式代入公式得公式。
把公式代入公式得公式。
把公式代入公式得公式。
将公式代入公式和公式，得到方程组公式。
由公式可得公式。
将公式代入公式得：公式，公式，公式，解得公式。
把公式代入公式得公式。
所以二次函数的表达式为公式。
2. 二次函数公式的图象向左平移公式个单位，再向上平移公式个单位，得到二次函数公式的图象，求公式、公式的值。
解析：先将公式进行逆变换。
把公式向下平移公式个单位得到公式。
再将公式向右平移公式个单位，根据“左加右减”原则，得到公式。
展开公式。
所以公式，公式。
三、旋转部分1. 在平面直角坐标系中，将点公式绕原点公式逆时针旋转公式后得到点公式，求公式的坐标。
解析：设公式绕原点公式逆时针旋转公式后的点公式。
根据旋转的性质，旋转前后的点到原点的距离不变，且旋转公式后坐标的变换规律为公式变为公式。
所以公式。
2. 如图，在公式中，公式，公式，公式，将公式绕点公式逆时针旋转公式得到公式，求公式的长。
解析：因为公式，公式，公式，根据勾股定理可得公式。
由于公式绕点公式逆时针旋转公式得到公式，则公式，公式，公式。
过公式作公式交公式延长线于公式。
因为公式，公式，所以公式。
在公式和公式中，公式，公式，公式，所以公式。
则公式，公式。
公式。
完整word版-初三上学期数学错题集(一二)及答案
初三上学期数学错题集（一元二次方程）（一） 2012.09.09已打印1、若方程（m-2）x㎡-2+mx2=7是关于x的一元二次方程，则m的值为。
2、根据题意，列出方程：（不必求解，写出一般形式）学校图书馆去年年底有图书5万册，预计到明年年底增加到7.2万册，求这两年的平均增长率。
3、方程x2=0的实数根有（）A．0个B．1个C．2个D．1个或2个4、下列二次三项式中，是完全平方式的是（填序号）。
①9x2-12xy+4y2；②4y2-4y-1；③x2-25x+5；④2x2-4x+1；5、写出一个一元二次方程，使它的两根：一根是正数，另一根在-2与-1之间。
6、方程（x-2）(x+3)=6的解是（）A．x1=-4,x2=3 B．x1=2,x2=3C．x1=2,x2=-3 D．x1=4,x2=-37、用因式分解法解方程5（x+3)-2x（x+3)=0，可把它化为两个一元一次方程、求解。
初三上学期数学错题集（一元二次方程）（二）2012.09.15已打印1、解方程：（1）3y(y-1)2=2-2y （2）7 x2=21x （3）（x2+1）2-3(x2+1)-28=02、若△ABC的边长都是方程x2-10x+21=0的根，求△ABC的周长。
3、若△ABC 的边长都是方程x 2-7x+12=0的根，求△ABC 的周长。
4、已知P=157m-1,Q= m 2-158m(m 为任意实数)，则P 、Q 的大小关系为 （ ） A ．P<Q B. P=Q C. P>Q D.不能确定 5、关于x 的方程（k+1）x 2+2(k+1) x+k=0无实数根，则k 的取值范围是 。
6、已知a 是整数，满足⎩⎨⎧>->+023013a a 试解关于x 的一元二次方程x 2-4=x(ax-3).7、k 为何值时，关于x 的方程（k-1）x 2-(2k+1) x+k+1 = 0（1）有一解？（2）有两个不相等的实数根？8、已知△ABC 的两边AB 、AC 的长是关于x 的一元二次方程x 2-(2k+1) x+k(k+1) = 0的两个实数根，第三边BC 的长为5.（1）k 为何值时，△ABC 是以BC 为斜边的直角三角形？（2）k 为何值时，△ABC 是等腰三角形？并求△ABC 的边长。
(完整)初三数学易错题集锦及答案
初中数学选择、填空、简答题易错题集锦及答案一、选择题1、A 、B 是数轴上原点两旁的点，则它们表示的两个有理数是（ C ）A 、互为相反数B 、绝对值相等C 、是符号不同的数D 、都是负数 2、有理数a 、b 在数轴上的位置如图所示，则化简|a-b|-|a+b|的结果是（ A ） A 、2a B 、2b C 、2a-2b D 、2a+b3、轮船顺流航行时m 千米/小时，逆流航行时(m-6)千米/小时，则水流速度（ B ） A 、2千米/小时 B 、3千米/小时 C 、6千米/小时 D 、不能确定4、方程2x+3y=20的正整数解有（ B ）A 、1个B 、3个C 、4个D 、无数个 5、下列说法错误的是（ C ）A 、两点确定一条直线B 、线段是直线的一部分C 、一条直线是一个平角D 、把线段向两边延长即是直线6、函数y=(m 2-1)x 2-(3m-1)x+2的图象与x 轴的交点情况是 ( C ) A 、当m ≠3时，有一个交点 B 、1±≠m 时，有两个交 C 、当1±=m 时，有一个交点 D 、不论m 为何值，均无交点7、如果两圆的半径分别为R 和r （R>r ），圆心距为d ，且(d-r)2=R 2，则两圆的位置关系是（ B ） A 、内切 B 、外切 C 、内切或外切 D 、不能确定8、在数轴上表示有理数a 、b 、c 的小点分别是A 、B 、C 且b<a<c ，则下列图形正确的是（ D ）A B C D 9、有理数中，绝对值最小的数是（ C ） A 、-1 B 、1 C 、0 D 、不存在 10、21的倒数的相反数是（ A ）A 、-2B 、2C 、-21 D 、2111、若|x|=x ，则-x 一定是（ B ）A 、正数B 、非负数C 、负数D 、非正数12、两个有理数的和除以这两个有理数的积，其商为0，则这两个有理数为（ C ） A 、互为相反数 B 、互为倒数 C 、互为相反数且不为0 D 、有一个为0 13、长方形的周长为x ，宽为2，则这个长方形的面积为（ C ） A 、2x B 、2(x-2) C 、x-4 D 、2·(x-2)/2 14、“比x 的相反数大3的数”可表示为（ C ） A 、-x-3 B 、-(x+3) C 、3-x D 、x+3 15、如果0<a<1，那么下列说法正确的是（ B ） A 、a 2比a 大 B 、a 2比a 小C 、a 2与a 相等D 、a 2与a 的大小不能确定16、数轴上，A 点表示-1，现在A 开始移动，先向左移动3个单位，再向右移动9个单位，又向左移动5个单位，这时，A 点表示的数是（ B ）A 、-1B 、0C 、1D 、817、线段AB=4cm ，延长AB 到C ，使BC=AB 再延长BA 到D ，使AD=AB ，则线段CD 的长为（ A ）A 、12cmB 、10cmC 、8cmD 、4cm 18、21-的相反数是（ B ） A 、21+B 、12- C 、21-- D 、12+-19、方程x(x-1)(x-2)=x 的根是（ D ）A 、x 1=1, x 2=2B 、x 1=0, x 2=1, x 3=2C 、x 1=253+, x 2=253-D 、x 1=0，x 2=353+, x 3=253-20、解方程04)1(5)1(322=-+++xx x x 时，若设yx x =+1，则原方程可化为（ B ）A 、3y 2+5y-4=0 B 、3y 2+5y-10=0 C 、3y 2+5y-2=0 D 、3y 2+5y+2=021、方程x 2+1=2|x|有（ B ）A 、两个相等的实数根；B 、两个不相等的实数根；C 、三个不相等的实数根；D 、没有实数根 22、一次函数y=2(x-4)在y 轴上的截距为（ C ） A 、-4 B 、4 C 、-8 D 、823、解关于x 的不等式⎩⎨⎧-<>a x ax ，正确的结论是（ C ）A 、无解B 、解为全体实数C 、当a>0时无解D 、当a<0时无解 24、反比例函数xy 2=，当x ≤3时，y 的取值范围是（ C ） A 、y ≤32 B 、y ≥32C 、y ≥32或y<0D 、0<y ≤3225、0.4的算术平方根是（ C ） A 、0.2 B 、±0.2 C 、510D 、±51026、李明骑车上学，一开始以某一速度行驶，途中车子发生故障，只好停车修理，车修好后，因怕耽误时间，于时就加快了车速，在下列给出的四个函数示意图象，符合以上情况的是（ D ）A B C D27、若一数组x 1, x 2, x 3, …, x n 的平均数为x ，方差为s 2，则另一数组kx 1, kx 2, kx 3, …, kx n的平均数与方差分别是（ A ）A 、k x , k 2s 2B 、x , s 2C 、k x , ks 2D 、k 2x , ks 228、若关于x 的方程21=+-ax x 有解，则a 的取值范围是（ B ） A 、a ≠1 B 、a ≠-1 C 、a ≠2 D 、a ≠±129、下列图形中既是中心对称图形，又是轴对称图形的是（ A ）A 、线段B 、正三角形C 、平行四边形D 、等腰梯形30、已知dcb a =，下列各式中不成立的是（ C ） A 、d c b a d c b a ++=-- B 、d b c a d c 33++= C 、bd ac b a 23++= D 、ad=bc 31、一个三角形的三个内角不相等，则它的最小角不大于（ D ） A 、300 B 、450 C 、550 D 、60032、已知三角形内的一个点到它的三边距离相等，那么这个点是（ C ）A 、三角形的外心B 、三角形的重心C 、三角形的内心D 、三角形的垂心 33、下列三角形中是直角三角形的个数有（ B ）①三边长分别为3:1:2的三角形 ②三边长之比为1:2:3的三角形 ③三个内角的度数之比为3:4:5的三角形 ④一边上的中线等于该边一半的三角形 A 、1个 B 、2个 C 、3个 D 、4个 34、如图，设AB=1，S △OAB =43cm 2，则弧AB 长为（ A ）A 、3πcm B 、32πcm C 、6πcm D 、2πcm 35、平行四边形的一边长为5cm ，则它的两条对角线长可以是（ D ）A 、4cm, 6cmB 、4cm, 3cmC 、2cm, 12cmD 、4cm, 8cm36、如图，△ABC 与△BDE 都是正三角形，且AB<BD ，若△ABC 不动，将△BDE 绕B 点旋转，则在旋转过程中，AE 与CD 的大小关系是（ A ）A 、AE=CDB 、AE>CDC 、AE>CD D 、无法确定37、顺次连结四边形各边中点得到一个菱形，则原四边形必是（ A ） A 、矩形 B 、梯形 C、两条对角线互相垂直的四边形 D 、两条对角线相等的四边形 38、在圆O 中，弧AB=2CD ，那么弦AB 和弦CD 的关系是（C ）A 、AB=2CDB 、AB>2CDC 、AB<2CD D 、AB 与CD 39、在等边三角形ABC 外有一点D ，满足AD=AC ，则∠BDC 的度数为（ D ） A 、300 B 、600 C 、1500 D 、300或150040、△ABC 的三边a 、b 、c 满足a ≤b ≤c ，△ABC 的周长为18，则（ C ）A 、a ≤6B 、b<6C 、c>6D 、a 、b 、c 中有一个等于641、如图，在△ABC 中，∠ACB=Rt ∠，AC=1，BC=2，则下列说法正确的是（ C ）A 、∠B=300B 、斜边上的中线长为1C 、斜边上的高线长为552D 、该三角形外接圆的半径为142、如图，把直角三角形纸片沿过顶点B 的直线BE （BE 交CA 于E 直角顶点C 落在斜边AB 上，如果折叠后得到等腰三角形EBA ，那么下列结论中（1）∠A=300（2）点C 与AB 的中点重合 （3）点E 到AB 的距离等于CE 的长，正确的个数是（ D ） A 、0 B 、1 C 、2 D 、343、不等式6322+>+x x 的解是（ C ）A 、x>2B 、x>-2C 、x<2D 、x<-244、已知一元二次方程(m-1)x 2-4mx+4m-2=0有实数根，则m 的取值范围是（ B ） A 、m ≤1 B 、m ≥31且m ≠1 C 、m ≥1 D 、-1<m ≤1 AB45、函数y=kx+b(b>0)和y=xk-(k ≠0)，在同一坐标系中的图象可能是（ B ） A B C D46、在一次函数y=2x-1的图象上，到两坐标轴距离相等的点有（ B ）A 、1个B 、2个C 、3个D 、无数个 47、若点（-2，y 1）、（-1，y 2）、（1，y 3）在反比例函数xy 1=的图像上， 则下列结论中正确的是（ D ）A 、y 1>y 2>y 3B 、y 1<y 2<y 3C 、y 2>y 1>y 3D 、y 3>y 1>y 2 48、下列根式是最简二次根式的是（ B ） A 、a 8 B 、22b a + C 、x 1.0 D 、5a49、下列计算哪个是正确的（ D ）A 、523=+B 、5252=+C 、b a b a +=+22D 、212221221+=-50、把aa 1--（a 不限定为正数）化简，结果为（ B ）A 、aB 、a- C 、-aD 、-a-51、若a+|a|=0，则22)2(a a +-等于（ A ） A 、2-2a B 、2a-2 C 、-2 D 、252、已知02112=-+-x x ，则122+-x x 的值（ C ） A 、1 B 、±21 C 、21D 、-2153、设a 、b 是方程x 2-12x+9=0的两个根，则b a +等于（ C ）A 、18B 、6C 、23D 、±2354、下列命题中，正确的个数是（ B ）①等边三角形都相似 ②直角三角形都相似 ③等腰三角形都相似④锐角三角形都相似 ⑤等腰三角形都全等 ⑥有一个角相等的等腰三角形相似⑦有一个钝角相等的两个等腰三角形相似 ⑧全等三角形相似A 、2个B 、3个C 、4个D 、5个 二、填空题1、如果一个数的绝对值等于它的相反数，那么这个数一定是_____非正数____。
初三数学易错题集锦
初三数学易错题代数第一章∶一元二次方程1、解方程1112-=+-x m x x 的过程中若会产生增根，则m=＿＿＿＿2.关于x 的方程m 2x 2＋（2m ＋1）x ＋1=0有两个不相等的根，求m 的取值范围＿＿3，若关于x 的方程ax 2－2x ＋1=0有实根，那a 范围＿＿＿＿4，已知方程3x 2－4x －2=0,则x 1－x 2=＿＿＿,大根减小根为＿＿＿＿5，以251+-和251--的一元二次方程是＿＿＿＿6,若关于x 的方程（a+3）x 2－（a 2－a －6）x ＋a=0的两根互为相反数，则a=＿＿＿7，已知a,b 为不相等的实数，且a 2－3a ＋1=0,b 2-3b+1=0则a b ＋ba =＿＿＿ 8，方程ax 2＋c=0（a ≠0）a,c 异号，则方程根为＿＿＿＿＿9,若方程3x 2＋1=mx 的二次项为3x 2,则一次项系数为＿＿＿＿＿23,分解因式4x 2＋8x ＋1=＿＿＿＿＿24,若方程2x 2＋3x －5=0的两根为x 1 ,x 2 则x 12＋x 22=＿＿＿＿＿25,方程组有两组相同的实数解，则k=＿＿＿方程组的解为＿＿＿43，若x 是锐角，cosA 是方程2x 2－5x ＋2=0的一个根，则∠A=＿＿＿1、已知：Rt △ABC 中,∠C=900,斜边c 长为 5 ,两条直角边a,b 的长分别是x 2-(2m-1)x+4(m-1)=0的两根,则m 的值等于 ( )A. –1B. 4C.-4或1D. –1或4.2、已知关于x 的方程012)32(2=+--x m x m 有两个不相等的实数根，则m 的范围是：( )A ．m<3 B. 233≠<m m 且 C. 0,233≠≠<m m m 且 D. 2330≠<≤m m 且3、已知方程①01222=+-x x ，②041x =+-,③1122=++++x x x x ,④0x 12x =---，⑤01)12(2=-+++k x k x 其中一定有．．．实数解的方程有 A 、1个 B 、2个 C 、3个 D 、4个5、已知 ,012=-+m m 那么代数式2001223-+m m 的值是 ( )(A)2000 (B)-2000 (C)2001 (D)-20016,下面解答正确的是( )A ， 分式的值是零，x=-2或x=1B, 实数范围内分解因式2x 2＋x －2=)4171)(4171(+-----x x C, x=-1是无理方程22-2x +7x =-x 的根D, 代数式x 2＋2x －1通过配方法知x=-1时，它有最小值是－27，关于x 的方程x 2－mx ＋n=0有一正一负的两实根，且负根绝对值较大，则（ ）A ， n ＞0, m ＜0 B,n>0, m ＞0, C, n<0 m>0 D,n ＜0 m<08,若 x =-b+b 2+4ac2a 则有（ ）A ，ax 2+bx+c=0 B,ax 2+bx-c=0 C,ax 2-bx+c=0 D, ax 2-bx-c=09、在Rt △ABC 中，∠C=900，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，a 、b 是关于x 的方程0772=++-c x x 的两根，那么AB 边上的中线长是（ ）（A ） 23 （B ）25 （C ） 5 （D ）2 20，已知关于x 的方程x 2＋px ＋q=0的两根为x 1=－3 x 2=4,则二次三项式x 2－px ＋q=（ ）A.（x ＋3）（x －4） B, （x －3）（x ＋4） C,（x ＋3）（x ＋4）D,（x －3）（x －4）三, 解答题1,甲乙二人合作一项工程，4天可完成，若先有甲单独做3天，剩下的由乙独做，则以所用的时间等于甲单独完成这项工程的时间，求甲乙二人单独完成此项工程各需几天？2，解方程mnx 2－（m 2＋n 2）x ＋mn=0 （mn ≠0）3，在⊿ABC 中，∠A ∠B ∠C 的对边分别为a,b,c 且a,b 是关于x 的方程∶x 2－（c ＋4）x＋4c ＋8=0的两根，若25asinA=9c,求⊿ABC 的面积第二章∶函数第一节∶平面直角坐标系22，平面直角坐标系中，点A （1－2a,a-2）位于第三象限且a 为整数，则点A 的坐标是＿＿＿＿＿10、已知点()2,1+-a a M 在第二象限，则a 的取值范围是（ ）（A ）2->a （B ）12<<-a （C ）2-<a （D ）1>a14、若点M （x －1,1－y ）在第一象限，则点N （1－x ，y －1）关于x 轴的对称点在（ ）A 、第一象限B 、第二象限C 、第三象限D 、第四象限第二节∶函数 11、函数321+=x y 中，自变量x 的取值范围是＿＿＿＿12、函数x x y -+=0的自变量的取值范围是＿＿＿＿＿1，锐角三角形ABC 内接于⊙O ，∠B=2∠C ，∠C 所对圆弧的度数为n ，则n 的取值范围是 （ ）A, 0°＜n ＜45° B, 0°＜n ＜90° C, 30°＜n ＜45° D,60°＜n ＜90°第三节∶一次函数15，当＿＿＿时，函数y=（m ＋3）x 2m ＋3＋4x －5（x ≠0）是一个一次函数。
初三数学易错题整理汇编及规范标准答案
天。
9、因式分解：-4x2+y2= (2x y)(2x y) ， x2-x-6= (x 3)(x 2)
10、计算：a6÷a2=__ a4 ____，(-2)-4=__ 1 ____，-22=__-4____
16
11、如果某商品降价 x%后的售价为 a 元，那么该商品的原价为 a 1 0.01x
A、三角形的外心 B、三角形的重心
C、三角形的内心
D、三角形的垂心
33、下列三角形中是直角三角形的个数有（ B ）
①三边长分别为 3 :1:2 的三角形 ②三边长之比为 1:2:3 的三角形 ③三个内角的度数之比
为 3:4:5 的三角形 ④一边上的中线等于该边一半的三角形
A、1 个 B、2 个 C、3 个 D、4 个
15、P 点表示有理数 2，那么在数轴上到 P 点的距离等于 3 个单位长度的点所表示的数是_5 或 1_。
16、a、b 为实数，且满足 ab+a+b-1=0，a2b+ab2+6=0，则 a2-b2=___ 6 17 _____。 17、已知一次函数 y=(m2-4)x+1-m 的图象在 y 轴上的截距与一次函数 y=(m2-2)x+m2-3 的图象
A、两点确定一条直线
B、线段是直线的一部分
C、一条直线是一个平角
D、把线段向两边延长即是直线
6、函数 y=(m2-1)x2-(3m-1)x+2 的图象与 x 轴的交点情况是 ( C )
A、当 m≠3 时，有一个交点
B、 m 1时，有两个交
C、当 m 1时，有一个交点
D、不论 m 为何值，均无交点
34、如图，设 AB=1，S△OAB= 3 cm2源自则弧 AB 长为（ A ）4
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初三数学易错题代数第一章∶一元二次方程1、解方程1112-=+-x m x x 的过程中若会产生增根，则m=＿＿＿＿2.关于x 的方程m 2x 2＋（2m ＋1）x ＋1=0有两个不相等的根，求m 的取值范围＿＿ 3，若关于x 的方程ax 2－2x ＋1=0有实根，那a 范围＿＿＿＿4，已知方程3x 2－4x －2=0,则x 1－x 2=＿＿＿,大根减小根为＿＿＿＿ 5，以251+-和251--的一元二次方程是＿＿＿＿6,若关于x 的方程（a+3）x 2－（a 2－a －6）x ＋a=0的两根互为相反数，则a=＿＿＿7，已知a,b 为不相等的实数，且a 2－3a ＋1=0,b 2-3b+1=0则a b ＋ba=＿＿＿8，方程ax 2＋c=0（a ≠0）a,c 异号，则方程根为＿＿＿＿＿ 9,若方程3x 2＋1=mx 的二次项为3x 2,则一次项系数为＿＿＿＿＿ 23,分解因式4x 2＋8x ＋1=＿＿＿＿＿24,若方程2x 2＋3x －5=0的两根为x 1 ,x 2 则x 12＋x 22=＿＿＿＿＿ 25,方程组有两组相同的实数解，则k=＿＿＿方程组的解为＿＿＿43，若x 是锐角，cosA 是方程2x 2－5x ＋2=0的一个根，则∠A=＿＿＿1、已知：Rt △ABC 中,∠C=900,斜边c 长为 5 ,两条直角边a,b 的长分别是x 2-(2m-1)x+4(m-1)=0的两根,则m 的值等于 ( ) A. –1 B. 4 C.-4或1 D. –1或4. 2、已知关于x 的方程012)32(2=+--x m x m 有两个不相等的实数根，则m 的范围是：( ) A ．m<3 B. 233≠<m m 且 C. 0,233≠≠<m m m 且 D. 2330≠<≤m m 且 3、已知方程①01222=+-x x ，②041x =+-,③1122=++++x x x x ,④0x 12x =---，⑤01)12(2=-+++k x k x 其中一定有．．．实数解的方程有 A 、1个 B 、2个 C 、3个 D 、4个5、已知 ,012=-+m m 那么代数式2001223-+m m 的值是 ( ) (A)2000 (B)-2000 (C)2001 (D)-2001 6,下面解答正确的是( )A ， 分式的值是零，x=-2或x=1B, 实数范围内分解因式2x 2＋x －2=)4171)(4171(+-----x x C, x=-1是无理方程22-2x +7x =-x的根D, 代数式x 2＋2x －1通过配方法知x=-1时，它有最小值是－27，关于x 的方程x 2－mx ＋n=0有一正一负的两实根，且负根绝对值较大，则（ ） A ， n ＞0, m ＜0 B,n>0, m ＞0, C, n<0 m>0 D,n ＜0 m<0 8,若x =-b+b 2+4ac 2a则有（ ）A ，ax 2+bx+c=0 B,ax 2+bx-c=0 C,ax 2-bx+c=0 D, ax 2-bx-c=09、在Rt △ABC 中，∠C=900，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，a 、b 是关于x 的方程0772=++-c x x 的两根，那么AB 边上的中线长是（ ）（A ） 23 （B ）25（C ） 5 （D ）220，已知关于x 的方程x 2＋px ＋q=0的两根为x 1=－3 x 2=4,则二次三项式x 2－px ＋q=（ ） A.（x ＋3）（x －4） B, （x －3）（x ＋4） C,（x ＋3）（x ＋4）D,（x －3）（x －4）三, 解答题1,甲乙二人合作一项工程，4天可完成，若先有甲单独做3天，剩下的由乙独做，则以所用的时间等于甲单独完成这项工程的时间，求甲乙二人单独完成此项工程各需几天？2，解方程mnx 2－（m 2＋n 2）x ＋mn=0 （mn ≠0）3，在⊿ABC 中，∠A ∠B ∠C 的对边分别为a,b,c 且a,b 是关于x 的方程∶x 2－（c ＋4）x＋4c ＋8=0的两根，若25asinA=9c,求⊿ABC 的面积第二章∶函数第一节∶平面直角坐标系22，平面直角坐标系中，点A （1－2a,a-2）位于第三象限且a 为整数，则点A 的坐标是＿＿＿＿＿10、已知点()2,1+-a a M 在第二象限，则a 的取值范围是（ ）（A ）2->a （B ）12<<-a （C ）2-<a （D ）1>a14、若点M （x －1,1－y ）在第一象限，则点N （1－x ，y －1）关于x 轴的对称点在（ ） A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限第二节∶函数 11、函数321+=x y 中，自变量x 的取值范围是＿＿＿＿12、函数x x y -+=0的自变量的取值范围是＿＿＿＿＿1，锐角三角形ABC 内接于⊙O ，∠B=2∠C ，∠C 所对圆弧的度数为n ，则n 的取值范围是 （ ）A, 0°＜n ＜45° B, 0°＜n ＜90° C, 30°＜n ＜45° D,60°＜n ＜90° 第三节∶一次函数15，当＿＿＿时，函数y=（m ＋3）x2m ＋3＋4x －5（x ≠0）是一个一次函数。
16，若直线y=kx+b 经过第一，三，四象限，则直线y=bx+k 过＿＿＿＿象限 17.已知函数y=3x+1,当自变量x 增加h 时，函数值增加＿＿＿＿19,下列图形中，表示一次函数y=mx+n 与正比例函数y=mnx.(m,n 是常数且mn ≠0)图像的是（ ）18，已知直线l 与直线y=2x+1的交点的横坐标是2,与直线y=-x+2的交点的纵坐标为1，求直线l 解析式为＿＿＿＿19.已知y 与x 成正比例，若y 随x 增大而减小，且其图像过（3，－a ）和（a,-1）两点则此解析式为＿＿＿＿＿20，直线y=ax-3与y=bx+4交于x 轴上同一点，则a ∶b=＿＿＿＿21,若一次函数y 1=（m 2－4）x ＋1－m 与一次函数y 2=（m 2－2）x ＋m 2－3的图像与y 轴交点的纵坐标互为相反数，则m=＿＿＿＿11．不论m 何实数，直线m x y 2+=与4+-=x y 的交点不可能在（ ）（A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限 17，对于不同的k 值，函数y=kx+4(k ≠0）时不同直线，则这些直线一定（ ）A, 互相平行 B, 相交于一点 C, 有无数个交点 D, k ＞0交于一点，k<0交于另一点11，一次函数y=kx+b 的图像经过点（m,-1）（1,m ）,其中m ＜－1，则k,b 满足的条件（ ）A,k ＜0,b ＜0 B,k ＞0,b ＞0 C,k ＜0,b ＞0 D,k ＞0,b ＜0 第四节∶二次函数1,二次函数的一般形式是＿＿＿＿＿，它的解为＿＿＿＿＿13、抛物线c bx x y ++=2与y 轴交于点A ，与x 轴的正半轴交于B 、C 点，且BC=2，3=∆ABC S ，则b=＿＿＿＿＿14、若抛物线22)1(2++--=k kx x k y 与x 轴有交点，则k 的取值范围是＿＿＿。
16，已知等腰三角形ABC 周长为20，则底边y 与腰长x 的函数关系式是＿＿＿＿＿＿自变量的取值范围是＿＿＿＿＿11,抛物线y=x 2+（m-4）x －4m ，若顶点在y 轴上，则m=＿＿＿若顶点在x 轴上，则m=＿＿＿11,若二次函数y=mx 2－（m －2）x －1的图像与x 轴交于点A （a,0）B （b,0）且a+b=ab 则m =＿＿＿＿12,用30厘米的铁丝围成的矩形最大面积可以达到＿＿＿＿厘米12，如图，用12米长的木方，作一个有一条横档的矩形窗子，为使透 进的光线最多，应选窗子的长宽各为＿＿＿米11，抛物线y=x 2+11x －2m 于x 轴交于（x 1,0）（x 2,0），已知x 1x 2=x 1＋x 2－15,要是次抛物线经过原点，应将它向＿＿平移＿＿＿个单位。
12，函数y=-2（x ＋3）2＋2的对称轴是＿＿＿，于x 轴的交点为＿＿＿，于y 轴的交点为＿＿＿11，已知函数y=-21x ＋2,当－1＜x ≤1时，y 的取值范围（ ）2523,2523,2523,2325,≤<<≤-<≤≤<-y D y C y B y A13，已知抛物线y=ax 2＋bx,当a ＞0,b ＜0时，它的图像过（ ）A,一，二，三，象限 B,一，二，四象限 C,一，三，四象限 D ，一，二，三，四象限 13，不论x 为何值，函数y=ax 2＋b x ＋c （a ≠0）的值小于0的条件是 （ ）A,a ＜0 ⊿＜0 B,a ＞0 ⊿＜0 C,a ＜0 ⊿＞0 D,a ＞0 ⊿＜0 16、下列四个函数：①2y x =；②2y x=-；③32y x =-；④22(0)y x x x =+≥；⑤)0(1<-=x xy ；⑥)0(2<=x x y 。
其中，在自变量的允许值范围内，y 随x 的减小而减小的函数个数为（ ）A 、1B 、2C 、3D 、4 18、下列四个函数中，y 的值随着x 值的增大而减小的是（ ） （A ）x y 2=（B ）()01>=x xy （C ）1+=x y （D ）()02>=x x y第五节∶反比例函数1，已知反比例函数的图像经过点（a,b ）,则它的图像一定经过（ ） A,（－a,b ） B,(a,-b) C,(-a,b) D,(0,0) 2,下列函数中，反比例函数是（ ）A,x(y-1)=1 B,11+=x y C,y=1/x 2 D,y=1/3x3，若y 与－3x 成反比例，x 与z4成正比例，则y 是z 的（ ）A,正比例函数 B,反比例函数 C,一次函数 D,不确定第三章∶统计初步2，已知一组数据x 1,x 2,x 3,x 4的平均数是2，方差是1，则另一组数据3x 1-2,3x 2-2,3x 3-2,3x 4-2,3x 5-2的平均数和方差分别是＿＿＿＿2，对60名学生的测量身高，落在167.5～170.5cm 之间的频率是0.3，未落在这个区间的学生人数是＿＿＿＿人。
21,下列语句正确的是( )A,四个班的平均成绩分别是a,b,c,d,则这四个班的总体评剧成绩为4dc b a +++B, 方差都为正数 C,标准差都为正数 D,众数，中位数，平均数有可能一样几何第一章∶三角函数1、在Rt △ABC 中，∠C=90°，tanA+2cotA=3，AC=23，则AB=＿＿＿＿ 2，sinA=23,求cos 2A =＿＿＿6,sin 221°39′＋sin 2α=1，α=＿＿＿7，（1＋sin45°－cos30°）（1－sin45°－cos30°）=＿＿＿ 29,cos 231°－2sin59°＋1=__________30，若A 是锐角，且sinA=53则tanA=＿＿＿＿＿31,比较大小∶ sin α＿＿＿＿tan α （α为锐角） 32,在⊿ABC 中，a=2b=332c,则tanC=＿＿＿＿33,利用正切和余切的倒数关系消去公式1／cot38°21′中的分母为＿＿＿ 36，计算 cos 21°＋cos 22°＋cos 23°＋- - -＋cos 288°＋cos 289°=＿＿＿＿ 37，在等腰Rt ⊿ABC 中，∠C=90°，AD 是中线，则∠DAC 的余弦值是＿＿＿＿ 38，tan 230°＋2sin60°＋tan45°×sin90°－tan60°＋cos 230°=＿＿＿＿39，等腰⊿ABC 的腰长为2cm,面积为1cm 2,其顶角度数为＿＿＿＿＿ 41，tanA=2,AA A A c os si n c os si n -+=＿＿＿＿＿＿42，已知sin α＋cos α=3／2,则sin α×cos α=＿＿＿＿1，一直角三角形的两边长为3，4，则较小角的正切值时（ ） A ，3／4 B,4／3 C,3／4 或37 D ，以上答案都不对2、在△ABC 中，∠C ＝90°，△ABC 面积为5cm 2 ,斜边长为4cm ,则tanA +cotB 的值为( )(A)58 (B)516 (C)85 (D)1653，若α为锐角，sin α＞cos30°，则α的取值范围（ ）A,0＜α＜30° B,30°＜α＜60° C,α＞60° D,60°＜α＜90°第二章∶解直角三角形3.在高2m ，坡角为30°的楼梯表面铺地毯，地毯长度至少需＿＿＿m4.在Rt ⊿ABC 中，∠ACB=90°，CD 为斜边上的高，BD ＝3，AD ＝16／3则sinA ＝＿5.以坡面长为42米，水平宽为26米，则这个坡面的坡角为＿＿＿第三章∶圆第一节∶圆的有关性质8、如图，锐角△ABC 中，以BC 为直径的半圆O 分别交AB ，AC 于D 、E 两点，且2:1:=∆DBCE ADE S S 四边形,则cosA=＿＿＿＿＿ 11,一弦分圆周为5∶7，此弦所对的圆周角为＿＿＿＿12，在半径为5cm 的圆内有长为53cm 的弦，则此弦所对的圆周角为＿＿＿＿＿15，⊙O 的半径为5cm 弦AB ∥CD ，AB=6cm,CD=8cm ，则两弦之间的距离为＿＿＿＿16，已知，如图，∠P=40°, ==CD BCAB 则∠ACD=＿＿＿＿ 27，已知A,B,C 三点在⊙0上，且∠A0B=1000，则∠C=＿＿＿＿28，已知⊙0的半径为5cm,A 为线段OP 中点，当OP=6cm 时，点A 与⊙0的位置关系是＿＿＿＿＿＿＿＿40，一直顶角A ＝50°的等腰⊿ABC 内接⊙0，D 为圆周上一点，则∠ADB 度数为＿＿＿ 18，在⊿ABC 中，AB=AC=13cm ，BC=10cm,求⊿ABC 的外接圆半径R=＿＿＿＿第二节∶直线与圆13，正⊿ABC 的边长为a,则它的高为＿＿＿内切圆半径为＿＿＿外接圆直径为＿＿＿14,已知⊿ABC 中，∠C ＝90°，AC ＝9cm,BC ＝12cm ，以C 为圆心，AC 为半径作圆交BA 于D ，则AD 长为＿＿＿＿17，圆中最大弦长为12，若直线与圆相交，设直线与圆心的距离为d ，则d 的取值范围＿＿＿＿ 18，如图⊙O 是⊿ABC 的内切圆⊙0的切线DE 交AB 于D ，交AC 于E①若DE=6，BC=8，则四边形DBCE 的周长为＿＿＿＿②若⊙O 的半径为6，OA=10，则⊿ADE 的周长为＿＿＿＿19、已知P 是△ABC 的内心，O 是△ABC 的外心，若∠BPC=125°则∠BOC ＿＿20、如图，点P 是半径为5的⊙O 内一点，且OP=3，在过点P 的所有⊙O 的弦中，弦长为整数的弦的条数为＿＿＿＿＿21，AB 是⊙O 的弦，P 是AB 上的一点，AB=10cm ，PA=4cm ，OP=5cm 则⊙O 的半径为＿＿＿＿＿＿＿22，已知顶角A 等于50°的等腰三角形ABC 内接⊙O,D 为圆周上一点,则∠ADB 的度数为＿＿＿＿＿23，已知⊙0直径AB ＝22cm,AD=6cm,那麽弧CD 的度数为＿＿＿24，已知⊙O 的半径为2cm ，弦AB 的长为23cm ，求这弦中点到这条弦所对的弧中点的距离为＿＿＿＿2513．如图：△ABC 中∠C=90°，AC=3，BC=4，D 在边AB 上，以AD 为直径的半圆切BC 于E ， 交AC 于F ，则BD = ______________.B CD B26，⊙O 中弦AB,CD 互相垂直，垂足为E ，AE=2,EB=6,ED=3,则⊙0半径为＿＿＿ 34，PAB 为⊙O 的割线，PO 交⊙O 于C ，若⊙O 的半径为R ，PO=d ，则PA ×PB=( )A,2R －2d B,2R+2d C, d 2—R 2 D, R 2－d 2 35，如图，已知正方形ABCD ，以D 为圆心，以DA 为半径的圆与以AB 为直径的圆交于P,AP 的延长线交BC 于Q ，则CQ 与QB 的关系是（ ） A, CQ=QB B, CQ ＞QB C, CQ ＜QB D, 无法确定4、如图，圆外切等腰梯形ABCD 的中位线EF= 15 cm ，那么等腰梯形ABCD 的周长等于 （ ）（A ）15 cm （B ）20 cm （C ）30 cm （D ）60 cm 5.如图，在R t△A B C 中，∠C =90°，A C =4，BC =3，以BC 上一点O 为圆心作⊙O 与AC 、AB 都相切，又⊙O 与BC 的另一个交点为D ，则线段B D 的长为（ ）（A ）1 （B ） （C ） （D ）6、如图，已知⊙O 的直径AB 与弦CD 交于点F ，∠AFD ＝450，AB ＝2，则FC 2＋FD 2＝_______. A ． 2 B.21 C. 1 D.不确定7.⊙O 的直径AB ＝5，弦BC ＝4，∠ABC 的平分线交半圆于点D ，延长AD 、BC 交于E ，则DCE ABCD S S :四的值为（ ）A 、9 B 、8 C 、7 D 、68、相交两圆的公共弦长为24cm,两圆的半径长分别为15cm 和20cm,则这两个圆的圆心距等于 （ ）A ．16cm B. 9cm 或16cm C. 25cm D.7cm 和25cm9.如果两圆心都在X 轴上,⊙O 1的圆心坐标为(7,0),半径为1;⊙O 2的圆心坐标为(X,0),半径为2,当2<X<4时,两圆的位置关系是( ) A.相交 B.相切 C.外离 D.内含10.在直角三角型ABC 中，∠C=60°，以AB 为直径的半圆交斜边BC 于D ，则△ACD 与△ABD 的面积之比为 ( ) A.1:2 B.1:3 C.2:3 D.3:411、使用直角钢尺检查某一工件是否恰好是半圆形的凹面，成半圆形的为合格，如图所示的四种情况中合格的是 （ ）15.在⊙O 中，弦AB=2CD ，则（ ） A ，>2CDABB,<2AB CDC,=2ABCDD,不能确定FAOCDB16、四边形ABCD 内接于圆，∠A 、∠B 、∠C 、∠D 的度数比依次可以是（ ） （A ）1：2：3：4 （B ）6：7：8：9 （C ）4：1：3：2 （D ）4 ：3：1：2 19，已知点P 到⊙0最大距离为a,最小距离为b(a>b)则此圆的半径为（ ） 2,ba A + 2ab D, 2b -a 2b a C, 2b -a B ,或+21,如图，AB 为⊙0的一直径，它把⊙0分成上下两个半圆，自上半圆上一点C 作弦CD ⊥AB ，∠OCP 的平分线交⊙0于点P ，当C 在上半圆（不包括A,B 两点）上移动时，则点P （ ）A, 到CD 的距离保持不变 B,位置不变 C ，等分弧DB D,随C 移动而移动1.已知，如图直径AB ⊥CD ，弦AE ，CD 延长线交于F ，求证：AC ×EF=CE ×DF1,如图，BC 为直径，G 为半圆上任意点，A 为弧BG 中点，AP ⊥BC 于P ，求证AE=BE=EF2，如图，⊿ABC 中，AB=AC,BD 平分∠B 交AC 于D ，⊿ABD 的外接圆交AC 于E ，求证AD ＝EC4，如图等边三角形ABC 内接于圆，P 为BC 上任一点，AP 交BC 于D,求证∶PB 和PC 是方程x 2－PA ×x ＋PA ×PD=0的两根5，如图，从圆外一点P 作圆的一条切线PA ，A 为切点，过点PD OE F C B A PDC OBAODCB A作一直线与圆交于B ，C 两点，弦CD ∥AP ，PD 与圆交于E ，连结EB 并延长交AP 于M ，求证：AM=PM 6，已知PBD 是⊙0的割线，PA ，PC 是⊙0的切线，求证：①PA ×PB ＝PB ×AD ②AD 2／AB 2 =PD ／PB7，P 是⊙0直径CB 延长线上一点，PA 切⊙0于A ，AD ⊥BC 于D ，若PA=10，PB=5，求sin ∠BAP 的值8，如图，BC 为⊙O 的直径，PA 切⊙0与A ，AB ＝15，∠P 的正弦值为3／5，求PC 的长9，已知，如图，⊿ABC 内接于⊙0，∠BAC 的平分线交BC 于D ，交⊙0于E ，⊙0的切线BF 交AE 延长线于F ，过E 作EH ⊥BF ，垂足为H ，求证：①BE 平分∠CBF ②BC ＝2BH ；③AD ×EF=CD ×BF10,已知，如图PA,PB 切⊙0于A,B 求证 ∠OPC=∠OCM11，已知Rt ⊿ABC ，以o 为圆心，OB 为半径的圆交AB 于E ，且AC 于D ，延长ED ，BC 交于F ，求证：BC=CF第三节∶圆与圆9、直径分别为12和4的两个圆的圆心距是8，则这两个圆共有＿＿条公切线。