第三章 气体分子动理论
分子动理论气体分子平均动能
32 103 26 m 5 . 31 10 kg 23 N A 6.02 10 (3)
3 3 k kT 1.38 10 23 ( 27 273) 6.21 10 21 J 2 2
3 – 3 理想气体分子的平均平动动能与温度的关系
第三章气体动理论
子数相等。
分子数 密度
k=R/NA=1.38×10-23J· K-1
称为玻耳斯曼常量
3 – 3 理想气体分子的平均平动动能与温度的关系
第三章气体动理论
二、理想气体分子的平均平动动能与温度的关系
阿伏加德罗定律:
p nkT
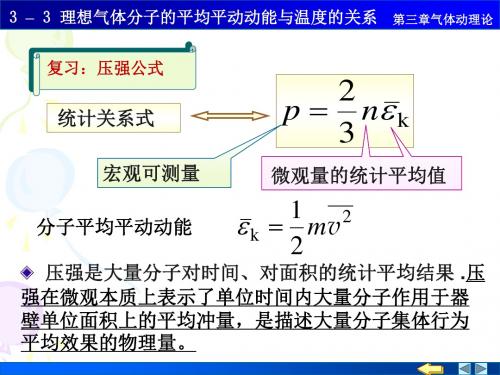
2 1 2 理想气体压强公式 p n mv 3 2 1 3 2 k m v kT 分子平均平动动能 2 2
容器内不同气体的温度相同分子的平均平动动能也相同即kknkk?????????????????21而分子数密度满足????inn故压强为??????????????????????????????????????????????ikiikikikpnnnnp????????32323232即容器中混合气体的压强等于在同样温度体积条件下组成混合气体的各成分单独存在时的分压强之和
例 利用理想气体的温度公式说明Dalton 分压定律。
解:容器内不同气体的温度相同,分子的平均平动动能也 相同,即
k1 k 2 kn k
而分子数密度满足
n ni
故压强为 2 2 2 2 P n k ni k ni k ni ki Pi 3 3 3 3 即容器中混合气体的压强等于在同样温度、体积条件下组成 混合气体的各成分单独存在时的分压强之和。这就是Dalton 分压定律。
理想气体的分子动理论气体分子的运动与理想气体定律

理想气体的分子动理论气体分子的运动与理想气体定律理想气体的分子动理论与气体分子的运动气体是一种物质的形态,也是我们生活中经常接触到的物质。
了解气体分子的运动和理论,能够帮助我们更好地理解气体的性质和行为。
本文将介绍理想气体的分子动理论,并探讨气体分子在空间中的运动方式以及与理想气体定律的关系。
一、理想气体的分子动理论理想气体的分子动理论是描述气体分子运动行为的理论模型。
根据分子动理论,气体分子是以高速无规则的方式在空间中运动的。
以下是气体分子的运动特征:1. 气体分子运动无规则性:气体分子在空间中以高速运动,并且没有固定的运动轨迹。
分子之间相互碰撞,这种碰撞是弹性碰撞,没有能量的损失。
2. 气体分子间的相互作用力可忽略不计:气体分子之间的相互作用力非常微弱,可以忽略不计。
这个假设的前提是气体分子之间的距离相对较远,而且气体分子体积相对较小。
3. 气体分子的速度服从麦克斯韦速度分布定律:根据麦克斯韦速度分布定律,气体分子的速度符合高斯分布(也称为正态分布),其中大多数分子具有平均速度,速度分布呈现钟形曲线。
二、气体分子的运动方式理想气体分子的运动方式可以通过分子运动学理论进行研究。
以下是气体分子的运动方式:1. 直线运动:气体分子在空间中以直线的方式运动。
当碰撞到容器壁或其他分子时,会发生反弹,继续直线运动。
2. 碰撞运动:由于气体分子之间的无规则运动,分子之间会发生碰撞现象。
这种碰撞是弹性碰撞,即碰撞后没有能量损失。
3. 自由平均路径:气体分子在碰撞之间的平均路径称为自由平均路径。
自由平均路径受气体分子的浓度和温度的影响。
三、气体分子的运动与理想气体定律的关系理想气体定律是描述理想气体状态的数学表达式,包括波义耳定律、查理定律和盖-吕萨克定律。
这些定律可以通过气体分子的运动来解释。
1. 波义耳定律:波义耳定律描述了气体压强与温度之间的关系。
根据理论分析,当气体分子碰撞容器壁时会产生压力,而压强与温度成正比。
分子动理论气体分子的运动和理想气体的性质

分子动理论气体分子的运动和理想气体的性质分子动理论: 气体分子的运动和理想气体的性质气体是物质存在的三种基本状态之一,其分子动理论是解释气体性质和行为的重要理论基础。
本文将探讨分子动理论对气体分子的运动和理想气体的性质的解释。
一、分子动理论的基本假设分子动理论基于以下几个基本假设:1. 气体由大量微观粒子组成,这些粒子被称为分子。
2. 分子之间相互独立,它们之间的相互作用力可以忽略不计。
3. 分子具有质量,具有热运动,它们的运动是无规则的,遵循统计规律。
4. 分子之间碰撞时,它们之间的碰撞是弹性碰撞,能量和动量得以守恒。
5. 气体体积与分子体积相比可以忽略。
基于这些假设,分子动理论提供了解释气体性质的理论框架。
二、气体分子的运动根据分子动理论,气体分子的运动是无规则的,并且具有以下几个特点:1. 分子的热运动速度分布是高斯分布,也称作麦克斯韦分布。
即大多数分子的速度接近平均速度,而极端高速和低速分子的数量相对较少。
2. 分子之间碰撞时,它们的碰撞是弹性碰撞。
在碰撞过程中,动能和动量得到守恒,但碰撞后的运动方向和速度可能发生改变。
3. 分子间的相互作用力可以忽略不计。
这是因为气体的分子间距相对较大,在气体的条件下,分子间的吸引或斥力相对较弱。
4. 分子的运动决定了气体的压力。
分子撞击容器壁产生的压力对应于分子的平均动能,而与分子的质量和速度分布有关。
三、理想气体的性质在分子动理论的基础上,我们可以推导出理想气体的性质。
理想气体是指完全符合分子动理论假设的气体,在实际中不存在。
1. 状态方程:理想气体的状态方程可以用理想气体定律描述,即PV = nRT。
其中,P表示气体的压力,V表示气体的体积,n表示气体的物质量,R表示理想气体常数,T表示气体的温度。
2. 温度和压力的关系:根据理想气体定律,温度和压力成正比。
当气体的温度升高时,其压力也会增加。
3. 等温过程和绝热过程:理想气体的等温过程和绝热过程可以用分子动理论解释。
气体分子动理论

气体分子动理论气体分子动理论是描述气体分子运动行为的一种物理理论。
这个理论指出了分子在气体状态下的运动行为,包括分子的速率、轨道和碰撞等。
这个理论解释了许多与气体相关的现象,例如热力学原理、功率引擎行为、热导率等等。
本文将详细介绍气体分子动理论的概念、假设和实验验证,并探讨其在化学、工程和自然科学等领域中的应用。
概念气体分子动理论的概念可以从其名称中得知。
分子是气体的基本单位,而动力学则指出了这些气体分子在气体状态下的运动行为。
按照这个理论,气体分子是在三维空间中随机移动的,其运动速度和方向都是随机的,还会经常碰撞。
分子的速度和能量也很高,而且分子之间的压力和温度通常也非常高。
假设气体分子动理论是建立在一些基本假设的基础上,这些假设可以让我们从分子层面上研究气体状态。
以下是气体分子动理论的基本假设:1.分子运动规律是基于牛顿定律的:分子沿着匀速直线前进,如果有力作用于分子上,分子会产生加速度。
2.分子间的运动足够快、足够随机:分子的平均速度相比于分子间的相互作用力,可以看作是随机热运动。
3.分子之间的互相碰撞是弹性碰撞:分子之间的作用力很小,因此任何碰撞都是弹性碰撞。
4.分子间的空间相对大,可以看做是不存在相互作用的:引力、排斥力等作用力很小,因此新增分子不会对气体的性质产生影响。
这些假设允许我们通过原子和分子的运动来解释理论分析和实验结果,有效推导气体的性质和状态。
实验验证气体分子动理论建立在基础物理尺度上,如角动量守恒定律、速度分布和碰撞等。
因此,文章介绍了几种实验验证气体分子动理论的方法:1.光扩散实验:将悬浮于气体之中的微小颗粒照射红外线。
微小颗粒受到红外线的反射和散射,通过测量其在气体中的扩散行为,可以推断出气体分子的平均速度和碰撞频率。
2.均匀气体分子分布实验:将气体充入小孔振荡单元中,通过与空气的微小污染物有序混合,检测气体分子的运动行为和浓度。
3.气体热传导实验:通过传导热流并测定体系温度梯度,分析气体分子在高温区域的热传导和碰撞频率。
气体分子动理论

气体分子动理论气体分子动理论是物理学中研究气体行为的理论框架。
它基于原子和分子在气体中的微观运动,试图解释和预测气体的宏观性质。
本文将介绍气体分子动理论的基本原理和相关概念。
分子运动和气体行为气体由大量分子组成,这些分子在气体容器中不断运动,并与容器和其他分子发生碰撞。
气体的宏观性质,如温度、压力和体积,可以从分子的运动状态推导出来。
气体分子动理论通过研究分子之间的相互作用和运动规律,解释了气体的行为。
分子运动规律根据气体分子动理论,分子具有以下运动规律:1.分子无规则运动:分子在气体容器中呈现无规则、自由的运动状态。
它们在容器内沿不同方向高速运动,并不断改变运动方向和速度。
2.分子之间的弹性碰撞:分子之间发生弹性碰撞,碰撞后能量和动量守恒,但在碰撞中的分子可能会发生运动速度和方向的改变。
3.平均运动速度:分子的速度服从Maxwell-Boltzmann分布,即分子的速度呈现连续分布,平均速度与温度相关。
4.分子间距和碰撞:分子之间的距离很大,相对于分子的体积而言,分子之间的相互作用可以忽略不计。
然而,当分子靠近时,它们之间的碰撞会对气体的性质产生影响。
气体宏观性质的解释气体分子动理论通过分子的运动规律,解释了气体的一些宏观性质:1.压力:气体分子运动产生的碰撞力对容器壁施加压力,压力与分子速度和碰撞频率有关。
2.温度:气体分子的平均动能与其速度平方成正比,因此温度可以视为分子的平均运动速度的度量。
3.体积:气体分子之间的距离较大,在碰撞时每个分子所占的体积可以忽略不计,因此气体没有固定的形状和体积,可以完全填满容器。
气体状态方程气体状态方程描述了气体的状态和性质。
根据气体分子动理论,可以推导出理想气体状态方程:PV = nRT其中,P是气体的压力,V是气体的体积,n是气体的摩尔数,R是气体常数,T是气体的温度。
这个方程表明,在一定温度下,气体的压力和体积成正比,与摩尔数成正比。
该方程也可以用来推导气体的其他性质。
气体分子动理论

气体分子动理论气体是物质存在的其中一种形态,它的分子运动对于我们理解气体的性质至关重要。
气体分子动理论是一种描述气体性质的科学理论,它通过解释气体分子的运动行为和碰撞规律,为我们提供了对气体行为的深入认识。
1. 分子运动的基本规律气体分子的运动有其基本规律,其中最重要的是玻尔兹曼分布规律。
根据玻尔兹曼分布规律,气体分子的速度分布服从高斯分布,即呈现一个钟形曲线。
这意味着气体分子的速度有一定的平均值,同时也存在一定的速度分散。
这种分布规律的存在,决定了气体的宏观性质,如压强、温度等。
2. 碰撞与压强气体分子之间的碰撞是气体压强产生的主要原因。
当气体分子运动速度较慢,分子之间碰撞不频繁时,气体的压强较低。
相反,当气体分子运动速度较快,分子之间碰撞频繁时,气体的压强较高。
根据气体分子动理论,气体压强与温度呈正相关,其数学关系为压强和温度的乘积与分子间平均速度的平方成正比。
3. 温度与分子速度气体分子运动的速度与气体的温度有着密切的关系。
根据气体分子动理论,气体温度与分子平均动能成正比。
换句话说,温度越高,气体分子的平均动能越大,分子的平均速度也会增加。
这也解释了为什么在相同温度下,不同气体的分子速度可能不同的原因。
例如,氢气分子较轻,根据等温分子速度公式,它的速度较大;而氮气分子较重,其速度相对较低。
4. 分子扩散与扩散速率分子扩散是气体分子运动的另一个重要现象。
根据气体分子动理论,气体分子会自发地从高浓度区域向低浓度区域扩散。
扩散速率受到多种因素的影响,如温度、分子间相互作用力以及分子质量等。
高温下的气体分子动能较大,扩散速率较快;而分子间的相互作用力越大,扩散速率越慢。
5. 分子间相互作用力气体分子间存在一定的相互作用力,这种作用力对气体性质有着重要影响。
分子间相互作用力可以分为吸引力和斥力。
对于吸引力较大的气体分子,它们的运动速度相对较慢,而分子间距离较小。
这种相互作用力称为范德华力。
相反,当气体分子间的斥力较大时,其运动速度较快,分子间距离较大,这种相互作用力被称为排斥力。
《医用物理学》习题解:第三章 分子动理论

第三章 分子动理论通过复习后,应该:1.掌握理想气体物态方程、压强公式、能量公式、混合气体的分压强、表面张力、弯曲液面的附加压强、毛细管中液面的变化;2.理解分子力、理想气体的微观模型、玻尔兹曼分布定律、气体的溶解、毛细现象、接触角;3.了解麦克斯韦速率分布定律、气体栓塞、肺泡的吸气和稳定。
3-1 一容器用隔板分成相等的两部分,一边装CO 2 ,另一边装H 2 ,两边气体的质量相同,温度相同。
如果隔板与容器壁间无摩擦,隔板是否会移动?为什么?答: 根据理想气体状态方程RTμpV M =,可得RTμVp M =。
因容器两部分气体的质量M 、体积V 、温度T 相同,R 是常数,只有摩尔质量μ不同,所以容器两部分的压强不同,隔板会移动。
由于H 2 的摩尔质量小于CO 2 的摩尔质量,故H 2 一侧的压强大于CO 2 ,隔板会向CO 2 一侧移动。
3-2 两瓶不同种类的气体,设分子平均平动动能相同,但气体的分子数密度不同,问它们的温度是否相同?压强是否相同?答: 根据分子平均平动动能公式kT 23=ε,当分子平均平动动能ε相同时,两瓶气体的温度相同。
根据压强公式εn p 32=,当分子平均平动动能ε相同而分子数密度n 不同时,压强不相同。
3-3 在容积为40L 的贮气筒内有112g 氮气,当贮气筒的温度为27℃时,筒内氮气的压强为多少个大气压?分子数密度又是多少?解: 已知V =40L=4×10-2m 3,T =(27+273)K=300K ,μ=2.8×10-2kg·mol -1,M =112g=0.112kg ,R =8.31J·mol -1·k -1 ,根据气态方程RT μpV M=可得筒内氮气的压强为RT μVp M==522105.2104108.230031.8112.0⨯=⨯⨯⨯⨯⨯-- 2.47atm Pa = 其分子数密度为252223100.6104108.210022.6112.01⨯=⨯⨯⨯⨯⨯=⋅==--V N M V N n A μ-3m3-4 某氧气瓶的容积是35L ,瓶内氧气的压强为1.5×107Pa ,给病人输一段时间氧气后,氧气的压强降为1.2×107Pa ,设温度为20℃,求这段时间内用去氧气的质量。
第三章 气体分子动理论

3-4能量按自由度均分定理
一、自由度 i (Degree of freedom)
确定一个物体的空间位置 所需要的独立坐标数目. 1. 质点的自由度
在空间自由运动的质点:
i =3
在曲面上运动的质点:
i =2 i =1
沿直线或曲线运动:
1、单原子分子
(1)分子平均平动动能
1 1 1 2 2 2 kt mvx mv y mvz 2 2 2
压强公式的讨论
压强的物理实质-----压强的微观解释 宏观量
2 p n kt 3
微观量
1.压强方程建立了宏观量和微观量的关系。
2.说明了压强的微观本质。
3-3 温度的微观本质
一.理想气体的能量方程
1 3 2 kt m kT 2 1 2 2 2 p n m 3 2
度和温度有关
扩散运动: 在教室中吃早餐: 3、分子间存在相互作用力(分子力) 满教室味道.
分子力
引力 斥力
f
d r0
r ro r ro r ro
f 0 平衡位置 10 r0 ~ 10 m f 0 f 0
o
R
r
斥力起主要作用
引力起主要作用
rR
f 0
R—分子力有效作用半径
R ~ 109 m
3-1、气体分子动理论的基本概念
一、物质的微观结构
布朗运动: 1、宏观物质是由大量不连续的微观粒子---分子 英国植物学家,他从显微镜中观察 到悬浮在静止液体中的花粉在作 (或原子)组成的多粒子体系。 无规则的杂乱无章的运动,这其中 的机理足足使科学界研究了50年, 分子之间有空隙:水在4000个 例如:标况下,1cm3空气 最后由科学家德尔索给予了正确 大气压下体积减为原来的1/3; 中含有2.7×1019个空气分 解释。 子,排成一行约2.7×109m, 2、分子都在作永不停息的无规则热运动,其剧烈程 可沿赤道绕地球一周。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)由 p nkT 可得单位体积内的分子数为
p 1.013 105 n 2.45 1025 m3 kT 1.38 1023 300
M p 32 103 1.013 105 (2) 1.30kg m 3 V RT 8.31 300
M的统计平均值
M M iWi
归一化条件
Ni Wi N 1
M的平方统计平均值
2
M M i Wi
2
4、涨落现象
当宏观系统处于平衡状态时,任一给定时刻或 者局部范围内观测到的宏观量的实际值不一定等 于统计平均值,这种现象称为涨落。 牛顿力学的决定性和统计力学的概率性的统一 处在平衡态的系统的宏观量,如压强p,不随 时间改变, 但不能保证任何时刻大量分子撞击器 壁的情况完全一样, 分子数越多,涨落就越小。
非刚性双原子分子平均能量
kt kr v
分子的自由度 i
分子能量中独立的速度和坐标的二次方项数目叫做分子能量 自由度的数目
单原子分子
i3
双原子分子
平动自由度t=3 转动自由度r=0 振动自由度v=0 刚性双原子分子
平动自由度t=3 转动自由度r=2
振动自由度v=0 i5 平动自由度t=3 非刚性双原子分子 转动自由度r=2
kt kr
非刚性双原子分子 非刚性双原子分子
分子平均平动动能
y
m2
* C
1 2 1 2 1 2 kt mcx mcy mcz 2 2 2
分子平均转动动能
m1
x
kr
z
分子平均振动能量
1 1 2 J y J z2 2 2
1 1 2 2 v 折合 vCx kx 2 2
何一个方向的运动并不比其他方向更占优
势,因此间的碰撞,因为分子之间的碰撞不 影响分子向各个方向运动的的几率和速度在各个 方向分量的平均值。
统计假设举例 a)沿各方向运动的分子数相等
1 N x N x N y N y N z N z N 6
i
3-4能量按自由度均分定理
一、自由度 i (Degree of freedom)
确定一个物体的空间位置 所需要的独立坐标数目. 1. 质点的自由度
在空间自由运动的质点:
i =3
在曲面上运动的质点:
i =2 i =1
沿直线或曲线运动:
1、单原子分子
(1)分子平均平动动能
1 1 1 2 2 2 kt mvx mv y mvz 2 2 2
二、气体动理论的统计规律性
1、统计规律性定义(Statistical regularity) 大量偶然性从整体上所体现出来的规律性。
2、统计规律性的特点
例如:伽尔顿实验、 扔硬币;成绩分布; (1)只对大量偶然的事件才有意义. 身高分布;人的寿 命;……. (2)它是不同于个体规律的整体规律
3、统计规律性的内容: (1)研究一些量的分布规律 ----某个量对大量偶然事件的分布规律 (2)研究一些量的统计平均值
(2)单原子分子的平均总能量
z
x
o
kt
y
2、刚性双原子分子 (1)分子的平均平动动能
1 1 1 2 2 2 kt mvCx mvCy mvCz 2 2 2
(2)分子的平均转动动能
kr
1 1 2 2 J y J z 2 2
(3)刚性双原子分子的平均总能量
N 2
F 1
e) 压强
m N F 2 2 Nx mx p V S l1l2l3
1 2 2 1 2 2 1 2 nm x nm n( m ) n( m ) 3 2 3 3 2
2
1 2 kt m 2
气体分子平均平动动能
2 p n kt 3
压强公式
M 1 N1 M 2 N 2 M n N n M N
N Ni 算术平均值
i
N
M N
i
i
N
统计平均值
N
M lim ( M i N i ) N M i lim ( N i N )
出现测量值Mi的几率(概率) Wi
lim ( Ni N )
N
M i dE RdT 2 M dE CV dT
i CV R 2
i2 CV i Cp
i2 Cp R 2
例、一容器内储有氧气,其压强为一个标准大气压,其温 度为27℃,求: (1)单位体积内的分子数 (2) 氧气的密度 (3)氧分子的质量 (4)分子的平均平动动能 (5)分子的平均总动能 解: 氧气为双原子分子,自由度i=5
同种类气体分子性质相同,质量相同 质点假设 理 想 分子所受 气 作用假设 体 模 型 ----气体分子的大小和气体分子间 的平均距离相比可以忽略不计 ----分子间的平均距离相当大,因 此除了碰撞以外,分子间的相互作 用力可以忽略不计。同时由于分子 的平均动能远大于分子的重力势能, 所以忽略重力的影响。 -----分子间以及分子与器壁间 的碰撞是完全弹性碰撞
布朗运动是可观测的涨落现象之一。
平衡态
平衡态(equilibrium state):在无外界影响下,
系统的宏观性质将趋于处处均匀且不随时间改变。
指 是一种动态平衡(热、力学、化学平衡) 出
粒子数是宏观量
箱子假想分成两相同体积的部分, 达到平衡时,两侧粒子有的穿越 界线,但两侧粒子数相同。
阿伏加德罗定律
EK(T)
EP(r) 分子间的相互作用力—保守力 理想气体内能 E=EK(T)
理想气体的内能只与温度有关
每个分子的平均总动能(平动、转动、振动动能)
i kT 2
1mol理想气体的内能
i i E N A N A kT RT 2 2
M/µ 摩尔理想气体的内能
M i E RT 2
第三章
气体分子动理论
物质是由大量做永不停息无规则热运动的微观粒 子—原子和分子构成的。
热运动---大量微观粒子永恒的杂乱无章的运动
两种描述方法: 1. 宏观量 :
大量分子的集体表现。从整体上描述系统的状态量,
一般可以直接测量。如 压强P、体积V、温度 T 等。 2. 微观量 描述系统内微观粒子的物理量。 如分子的质 量、 直径、速度、动量、能量 等。微观量实验 上不可测量,为表征单个分子的物理量。 微观量与宏观量有一定的内在联系: -----宏观量是微观量的统计平均值。
1.能量方程从分子运动论的 角度给温度以定义
p nkT
温度是气体分子平 均平动动能大小的 量度
2、温度是大量分子热运动的集体表现--微观本质 3、零点能量
例:(1)在一个具有活塞的容器中盛有一定的气体。如果 压缩气体并对它加热,使它的温度从270C升到1770C,这时 气体分子的平均平动动能变化多少?
3-1、气体分子动理论的基本概念
一、物质的微观结构
布朗运动: 1、宏观物质是由大量不连续的微观粒子---分子 英国植物学家,他从显微镜中观察 到悬浮在静止液体中的花粉在作 (或原子)组成的多粒子体系。 无规则的杂乱无章的运动,这其中 的机理足足使科学界研究了50年, 分子之间有空隙:水在4000个 例如:标况下,1cm3空气 最后由科学家德尔索给予了正确 大气压下体积减为原来的1/3; 中含有2.7×1019个空气分 解释。 子,排成一行约2.7×109m, 2、分子都在作永不停息的无规则热运动,其剧烈程 可沿赤道绕地球一周。
完全弹性 碰撞假设 运动规律
---分子运动遵守经典力学规律
从气体动理论的观点,理想气体可看成是由
大量的不断作无规则运动的、本身可略去不计
的、彼此间相互作用不予考虑的弹性小球所
组成。这是一个理想的模型,只是真实气体
在压强较小时的近似模型。
统计性假设 ---气体在平衡态时,对大量气体分子来说,
分子沿各个方向运动的机会是均等的,任
设气体分子的质量为m,分子的摩尔质量为μ,M 质量气体所含的分子数为N μ =NAm M=Nm
N R p T V NA
N n V
N pV RT RT NA
M
p nkT
n-分子数密度
R k 1.38 1023 J K -1 NA
k--玻尔兹曼常量
3-2理想气体的压强
理想气体压强公式的推导
1. 压强的产生
F p S
y
器壁单位面积上所受的正压力 压力由分子碰撞器壁产生 2、 压强公式的推导
l3
z l1
x
设容器内有N个分子,考虑任意一个分子i的质量为m,
速度为
i (ix、iy、iz )
S= A1 =l2 l3
a) 分子i与容器器壁A1碰撞,是完全弹性碰撞,在Y、
压强公式的讨论
压强的物理实质-----压强的微观解释 宏观量
2 p n kt 3
微观量
1.压强方程建立了宏观量和微观量的关系。
2.说明了压强的微观本质。
3-3 温度的微观本质
一.理想气体的能量方程
1 3 2 kt m kT 2 1 2 2 2 p n m 3 2
度和温度有关
扩散运动: 在教室中吃早餐: 3、分子间存在相互作用力(分子力) 满教室味道.
分子力
引力 斥力
f
d r0
r ro r ro r ro
f 0 平衡位置 10 r0 ~ 10 m f 0 f 0
o
R
r
斥力起主要作用
引力起主要作用
rR
f 0
R—分子力有效作用半径
R ~ 109 m
伽尔顿实验
