8.5因式分解2---公式法
九年级一元二次方程解法--公式法、因式分解法
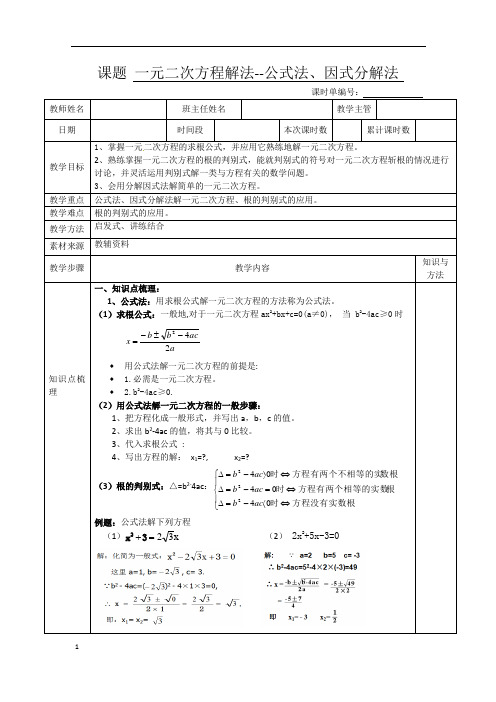
课题一元二次方程解法--公式法、因式分解法课时单编号:教师姓名班主任姓名教学主管日期时间段本次课时数累计课时数教学目标1、掌握一元二次方程的求根公式,并应用它熟练地解一元二次方程。
2、熟练掌握一元二次方程的根的判别式,能就判别式的符号对一元二次方程斩根的情况进行讨论,并灵活运用判别式解一类与方程有关的数学问题。
3、会用分解因式法解简单的一元二次方程。
教学重点公式法、因式分解法解一元二次方程、根的判别式的应用。
教学难点根的判别式的应用。
教学方法启发式、讲练结合素材来源教辅资料教学步骤教学内容知识与方法知识点梳理一、知识点梳理:1、公式法:用求根公式解一元二次方程的方法称为公式法。
(1)求根公式:一般地,对于一元二次方程ax2+bx+c=0(a≠0),当 b2-4ac≥0时aacbbx242-±-=♦用公式法解一元二次方程的前提是:♦ 1.必需是一元二次方程。
♦ 2.b2-4ac≥0.(2)用公式法解一元二次方程的一般步骤:1、把方程化成一般形式,并写出a,b,c的值。
2、求出b2-4ac的值,将其与0比较。
3、代入求根公式:4、写出方程的解:x1=?, x2=?(3)根的判别式:△=b2-4ac:⎪⎩⎪⎨⎧⇔〈-=∆⇔=-=∆⇔〉-=∆方程没有实数根时根方程有两个相等的实数时数根方程有两个不相等的实时444222acbacbacb例题:公式法解下列方程(1)(2) 2x2+5x-3=0x32=+3x22、因式分解法:用因式分解的方法求一元二次方程的根的方法叫做因式分解法. 因式分解法的一般步骤: ①将方程右边化为0;②将方程左边分解为两个一次因式的乘积:()()021=--x x x x 21,x x x x ==⇒或 ③令每个因式等于0,得到两个一元一次方程,解这两个一元一次方程,它们的解就是原一元二次方程的解.(1)提公因式法 例题:解下列方程(1)3x (x+2)=5(x+2) (2)x (3x+2)-6(3x+2)=0 、、注意:方程两边绝不能随便约去含有未知数的代数式。
初中中考数学因式分解的九种方法解析

初中中考数学因式分解的九种方法解析初中中考数学因式分解的九种方法解析把一个多项式在一个范围(如实数范围内分解,即所有项均为实数)化为几个整式的积的形式,这种式子变形叫做这个多项式的因式分解,也叫作把这个多项式分解因式。
xx小编整理了初中中考数学因式分解的九种方法,希望能帮助到您。
一、运用公式法我们知道整式乘法与因式分解互为逆变形。
如果把乘法公式反过来就是把多项式分解因式。
于是有:a^2-b^2=(a+b)(a-b)a^2+2ab+b^2=(a+b)^2a^2-2ab+b^2=(a-b)^2如果把乘法公式反过来,就可以用来把某些多项式分解因式。
这种分解因式的方法叫做运用公式法。
二、平方差公式1、式子:a^2-b^2=(a+b)(a-b)2、语言:两个数的平方差,等于这两个数的和与这两个数的差的积。
这个公式就是平方差公式。
三、因式分解1.因式分解时,各项如果有公因式应先提公因式,再进一步分解。
2.因式分解,必须进行到每一个多项式因式不能再分解为止。
四、完全平方公式1、把乘法公式(a+b)^2=a^2+2ab+b^2 和(a-b)^2=a^2-2ab+b^2反过来,就可以得到:a^2+2ab+b^2=(a+b)^2 和 a^2-2ab+b^2=(a-b)^2,这两个公式叫完全平方公式。
这就是说,两个数的平方和,加上(或者减去)这两个数的积的2倍,等于这两个数的和(或者差)的平方。
把a^2+2ab+b^2和a^2-2ab+b^2这样的式子叫完全平方式。
2、完全平方式的形式和特点:①项数:三项;②有两项是两个数的的平方和,这两项的符号相同;③有一项是这两个数的积的两倍。
3、当多项式中有公因式时,应该先提出公因式,再用公式分解。
4、完全平方公式中的a、b可表示单项式,也可以表示多项式。
这里只要将多项式看成一个整体就可以了。
5、分解因式,必须分解到每一个多项式因式都不能再分解为止。
五、分组分解法我们看多项式am+an+bm+bn,这四项中没有公因式,所以不能用提取公因式法,再看它又不能用公式法分解因式。
因式分解2

因 式 分 解(2) 利用公式法一、利用公式分解因式:1、利用平方差公式因式分解:()()b a b a b a -+=-22 注意:①条件:两个二次幂的差的形式;②平方差公式中的a 、b 可以表示一个数、一个单项式或一个多项式;③在用公式前,应将要分解的多项式表示成22b a -的形式,并弄清a 、b 分别表示什么。
例如:分解因式:(1)291x -; (2)221694b a -; (3)22)(4)(n m n m --+2、利用完全平方公式因式分解:()2222b a b ab a ±=+± 注意:①是关于某个字母(或式子)的二次三项式;②其首尾两项是两个符号相同的平方形式;③中间项恰是这两数乘积的2倍(或乘积2倍的相反数);④使用前应根据题目结构特点,按“先两头,后中间”的步骤,把二次三项式整理成 222)(2b a b ab a ±=+±公式原型,弄清a 、b 分别表示的量。
例如:分解因式:(1)2961x x +-; ⑵ 36)(12)(2+---n m n m 1682++x x 典型例题:1、直接用公式:当所给的多项式是平方差或完全平方式时,可以直接利用公式法分解因式。
例1、 分解因式:(1)x 2-9; (2)9x 2-6x+1。
2、提公因式后用公式:当所给的多项式中有公因式时,一般要先提公因式,然后再看是否能利用公式法。
例2、 分解因式:(1)x 5y 3-x 3y 5; (2)4x 3y+4x 2y 2+xy 3。
3、系数变换后用公式:当所给的多项式不能直接利用公式法分解因式,往往需要调整系数,转换为符合公式的形式,然后再利用公式法分解.例3、 分解因式:(1)4x 2-25y 2; (2)4x 2-12xy 2+9y 4.4、指数变换后用公式:通过指数的变换将多项式转换为平方差或完全平方式的形式,然后利公式法分解因式,应注意分解到每个因式都不能再分解为止.例4、 分解因式:(1)x 4-81y 4; (2)16x 4-72x 2y 2+81y 4.5、重新排列后用公式:当所给的多项式不能直接看出是否可用公式法分解时,可以将所给多项式交换位置,重新排列,然后再利用公式。
8.5.2因式分解公式法

2 2
a 2 b2 (a b)(a b)
(4)
36a 25b (6a) (5b) (6a 5b)(6a 5b)
2 2
随堂练习: 1、填空(把下列各式写成完全平方的形式)
(4) 1 36n2 (1 6n)(1 6n)
(5) 9n2 64m2 48mn (3n 8m) 2
(6) 16 a 2 b2 (ab 4)(ab 4)
例2、把下列各式分解因式
(1) (m n) 6(m n) 9
2
(m n) 3
2a b 5 代入
解:
1 2 1 2 1 2 1 2 x xy y (x 2 xy y ) ( x y ) 2 2 2 2 2 把x y 1代入
1 1 原式= 1= 2 2
小结: 1、内容归纳: (1)因式分解的方法:公式法 (2)因式分解的3个公式 2、方法归纳 在运用公式分解因式时,要通过观察、分 析、判断所给多项式是否符合公式的特征,弄 清所给多项式中,相当于公式的a,b分别是什 么,正确地运用公式。
2
(m n) 2(m n) 3 3
2
2
2
m n 3 (2) 9(a b)2 (a b)2 2 3(a b) (a b) 2
4a 2b 2a 4b
3(a b) (a b)3(a b) (a b)
(3) 1 6 y 9 y 2 (6) 16 a 2 b 2
2
(4) 1 36n 2
人教版八年级上册数学《公式法》整式的乘法与因式分解PPT课件(第2课时)

因此x=-5是原分式方程的解.
随堂练习
1.下列方程是分式方程的是( B )
A.
一元一次方程
B.
C. x2-1=0
D. 2x+1=3x 一元二次方程
一元一次方程
2.(2020·海南中考)分式方程 的解是(
A. x=-1
B. x=1 C. x=5
x-2=3
D. x=2
x=5
) C
解分式方程时,不要忘记检验哦.
用平方差公式分解因式 由于整式的乘法与因式分解是方向相反的变形,把整 式乘法的平方差公式(a+b)(a-b)=a2-b2的等号两边互换位 置,就得到了 a2-b2=(a+b)(a-b)
语言叙述:两个数的平方差,等于这两个数的和与这 两个数的差的积.
用完全平方公式分解因式 把整式乘法的完全平方公式 (a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2 的等号两边互换位置,就可以得到 a2+2ab+b2=(a+b)2,a2-2ab+b2=(a-b)2. 语言叙述:两个数的平方和加上(或减去)这两个数 的积的2倍,等于这两个数的和(或差)的平方.
分析:将b2看成一个整体a,则原式变形为(b2)2-b2-12,
可以看作a2-b-12.
1 -4
b4-b2-12 =(b2-4)(b2+3) =(b+2)(b-2)(b2+3).
13 1×3+1×(-4)=-1
2.(2020·乐山)已知y≠0,且x2-3xy-4y2=0,则 的值是
__4_或__-_1__.
分析:因为x2-3xy-4y2=0, 即(x-4y)(x+y)=0, 可得x=4y或x=-y, 所以 =4或 =−1.
沪科版七年级下册数学精品教学课件-第8章-整式乘法与因式分解-公式法(2024版)

步骤
一提:公因式;
二套:公式;
三查:多项式的因式分解有没有 分解到不能再分解为止.
1. 下列多项式中能用平方差公式分解因式的是( D )
A.a2 + ( - b)2
B.5m2 - 20mn
C.- x2 - y2
D. - x2 + 9
2. 分解因式 ( 2x + 3 )2 - x2 的结果是( D )
A.3(x2 + 4x + 3)
B.3(x2 + 2x + 3)
C.(3x + 3)(x + 3)
x+y = 1①,
所以 x - y = -2②.
联立①②组成二元一次方程组,
解得
x y
3 2
1 2
.
,
方法总结:在与 x2-y2,x±y 有关的求代数式 或未知数的值的问题中,通常需先因式分解, 然后整体代入或联立方程组求值.
例3 计算下列各题: (1) 1012 - 992; (2) 53.52×4 46解.52:×(41.) 原式=(101+99)(101-99)=400.
因式吗? 是 a,b 两数的平方差的形式
平方差公式: 整式乘法
( a + b )( a - b ) = a2 - b2 a2 - b2 = ( a + b )( a - b )
因式分解
两个数的平方 差,等于这两 个数的和与这 两个数的差的 乘积.
辨一辨:下列多项式能否用平方差公式来分解因式,
为什么? (1)x2 + y2 (2)x2 - y2
解析:∵ 16 = (±4)2,∴ - m = 2×(±4),即 m = ±8.
方法总结:本题要熟练掌握完全平方公式的结构 特征,根据参数所在位置,结合公式,找出参数 与已知项之间的数量关系,从而求出参数的值. 计算过程中,要注意积的 2 倍的符号,避免漏解.
公式法因式分解

2 a2 6a 9 原式 x 32
3 4a2 4a 1 原式 2a 12
4 9m2 6mn n2 原式 3m n2
5 x2 1 x
4
原式
x
1 2
2
6 4a2 12ab 9b2 原式 2a 3b2
1. 因式分解 (1)9-a2-4ab-4b2 (2) 1+a2b2-a2-b2 (3) x2-4xy+4y2-5x+10y
(3)-3a+6a2-3a3 (4)4(a-b)3-9(a-b)
2.计算 (1)13×9.98+5.6×99.8+310×0.998
(2)9992-9982 (3)172+26×17+132
2.计算:542 462 2 54 46
3.已知 x y 2, xy ,2 求
x2 y2 6xy 的值。
(2)25m2 80m 64
(3)a2 1 a
(4) 24xy x2 y2
(5)(a b)2 18(a b) 81
[例3]分解因式: (1)(x+4)2+2x(x+4)+x2
(2)a4-2a2b2+b4
(3)(x2+3x)2-(x-1)2 (4)-2an+1+2an- 1 an-1
2
练习. 2.分解因式:
(1)x2 y 4 y
(2) 3x3 12x2 y 12xy2 (3)3ax2 6axy 3ay2 (4)a4 8a2 16
(5)x3 4x2 4x
3、计算:8002-1600×798+7982
应用提高、拓展创新
1.把下列多项式分解因式,从中你能发现 因式分解的一般步骤吗?
《公式法》因式分解PPT课件(第2课时)

B. + −
C. − +
D. − + +
D
)
课堂检测
基础巩固题
3.如果x2-6x+N是一个完全平方式,那么N是(
A . 11
B. 9
C. -11
)
B
D. -9
4.如果x2-mx+16是一个完全平方式,那么m的值为________.
±8
课堂检测
∴++=(+) =112=121.
连接中考
(2020•眉山)已知 + = − − ,则 −
. 4
的值为
解析:由 +
得
+
= − − ,
− + + = ,
即 − + + + + = ,
∵ − = , = ,
∴原式=2.
巩固练习
变式训练
已知-+-+=,求++的值.
解:∵x2-4x+y2-10y+29=0,
∴(-)+(-)=.
∵(-) ≥ ,(-) ≥ ,
∴-=,-=,∴=,=,
是.
巩固练习
变式训练
将前面例题的(2)(3)(4)变为完全平方式?
(2) + ²;
+ ² + ;
(3) + − ;
+ + ;
(4) + + .
+ + .
探究新知
知识点 2
用完全平方公式因式分解
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二课时 公式法
一、学前准备
1、回忆公式
(1)完全平方公式:
(2)平方差公式:
2、把下列整式写成另一个整式的平方
(1)16= (2)16x 2 = (3)0.04m 2=
(4)2291b a = (5)36(m-n)2= (6)2)2(49
25y x +=
3、把下列各式因式分解
(1)a 2-a = (2)5ab -15ac =
(3)4a 2b -8ab 2= (4)()()x y y y x x ---=
二、探究活动
〖一〗探究一:利用平方差公式分解因式
【议一议】
1.下列多项式可以用平方差公式分解吗?
(1)x 2-y 2 (2)x 2+y 2 (3)-x 2-y 2 (4)-x 2+y 2 (5)64x 2-9y 2
2.总结平方差公式的特点:
1.左边特征是: .
2.右边特征是: .
【例题分析】
例1.把下列多项式分解因式:
(1) 36-25x 2 (2) 16a 2-9b 2 (3)49m 2-0.01n 2
例2.观察公式a 2-b 2 =(a +b )(a -b ),你能抓住它的特征吗?公式中的字母a 、b 不仅可以表示数,而且都可以表示代数式.尝试把下列各式分解因式
(1)(x +p )2-(x +q )2 (2)16(m -n )2-9(m +n )2
(3)9x 2-(x -2y ) 2 (4)-4(x +2y )2+9(2x -y )2
【练一练】
1.填空
(1)x 2-16 = ( )( )
(2)9-4y 2=( )( )
(3)1-19
a 2 =( )( ) 2.把下列各式分解因式:
(1)4a 2-(b +c )2 (2)(3m +2n )2-(m -n )2
(3)(4x -3y )2-16y 2 (4)-(x +2y )2+25(x -2y )2
〖二〗探究二:利用完全平方公式分解因式
【议一议】
1.下列多项式可以用完全平方公式分解吗?
(1) a 2+2ab+b 2 (2) a 2-2ab+b 2 (3) a 2-ab+b 2 (4) a 2-2ab+4b 2
2.完全平方式的特点:
左边:①项数必须是_________项; 右边:____________________ ②其中有两项是___________________;
③另一项是__________________ ___.
口诀: .
【例题分析】
例1. 议一议:判断下列各式是完全平方式吗?
(1)a 2-4a +4 (2)x 2+4x +4y 2 (3)4a 2+2ab +14b 2
(4)a 2-ab +b 2 (5)x 2-6x -9 (6)a 2+a +0.25 例2. 把下列多项式分解因式:
(1) x 2+10x +25 (2) 4a 2+36ab +81b 2 (3)-4xy -4x 2-y 2
例3.把下列各式分解因式
(1)(x +y )2-18(x +y )+81 (2)4-12(x -y )+ 9(x -y )2
【练一练】
1.请补上项,使下列多项式成为完全平方式:
(1)4m 2+ +n 2=(2m + )2;
(2)x 2- +16y 2=( )2;
(3)4a 2+9b 2+ =( )2;
(4) +2pq +1=( )2.
2.分解下列因式:
(1)9m 2-6mn +n 2 (2)49x 2+y 2-43xy
(3)a 2-12ab +36b 2 (4)a 2b 2-2ab +1
三、自我测试
1. 下列各式中,能用平方差公式分解因式的是( )
A .22b a +-
B .22b a --
C .22b a +
D .33b a -
2. (x +1)2-y 2分解因式应是( )
A . (x +1-y )(x +1+y )
B . (x +1+y )(x -1+y )
C . (x +1-y )(x -1-y )
D . (x +1+y )(x -1-y )
3.下列各式中能用完全平方公式分解的是 ( )
①442+-x x ②1362++x x ③1442+-x x ④2224y xy x ++ ⑤2216209y xy x +-
A .①③
B .①②
C .②③
D .①⑤
4.若x 2-2mx +1是一个完全平方式,则m 的值为 ;
5.把下列各式分解因式:
(1)216
1211m m +- (2)16-24(a -b )+ 9(a -b )2
(3) 2249x y - (4)()2
24y x z +-
四、应用与拓展
1.已知y x ,互为相反数,且的值求y x y x ,,4)2()2(22=+-+.。
