新人教版初中数学导学案: 平行线分线段成比例定理
数学教案-平行线分线段成比例定理

数学教案-平行线分线段成比例定理一、教学目标通过本课的学习,学生应能够: 1. 了解平行线的性质和判断方法; 2. 掌握平行线分线段成比例定理的概念; 3. 能够运用平行线分线段成比例定理解决实际问题。
二、教学重点平行线分线段成比例定理的理解和应用。
三、教学内容1.平行线的概念和特点;2.平行线分线段成比例定理的表述和证明;3.平行线分线段成比例定理的应用。
四、教学过程1. 导入和复习(5分钟)教师通过提问和回顾上节课的内容,对平行线的定义和性质进行复习。
2. 引入新知(10分钟)教师通过示意图引入平行线分线段成比例定理的问题情境,并提出问题,引发学生思考。
例如:在平行线AB和CD上,点E、F、G分别是线段AC、BD的中点,这时能否得到AB和CD的比例关系?学生可以用自己的方式来解决这个问题。
3. 学习新知(25分钟)教师给出平行线分线段成比例定理的定义和表述,并通过示意图进行说明。
让学生观察图形,理解其中的关系。
然后,教师引导学生进行推理和证明,理解定理的实质和原因。
4. 练习(30分钟)让学生在课堂上进行练习,巩固对平行线分线段成比例定理的理解和应用。
教师可以出几道练习题,让学生自主解答,然后让学生互相交流答案和解题思路。
在解答过程中,教师应及时给予指导和反馈。
5. 拓展应用(15分钟)教师设计几个拓展问题,让学生运用平行线分线段成比例定理解决实际问题,并进行讨论。
例如:已知AB//CD,AD=5,AC=8,求BD的长度。
学生可以自由选择解题方法,然后与同学讨论和比较不同的解法。
6. 总结归纳(5分钟)教师对本课学习的重点进行总结归纳,并强调平行线分线段成比例定理的重要性和应用范围。
五、课堂小结通过本堂课的学习,我们了解了平行线的性质和判断方法,并掌握了平行线分线段成比例定理的概念和应用方法。
这些知识在解决几何问题时非常有用。
六、课后作业1.完成课堂练习中的习题;2.思考并总结平行线分线段成比例定理的应用场景,写一篇小短文。
新人教版初中数学导学案: 平行线分线段成比例定理

课题:27.2.1 平行线分线段成比例定理主编:审核:课型:新授课验收负责人:学习目标:1. 经历平行线分线段成比例定理的探索过程;掌握平行线分线段成比例定理.2. 掌握平行线分线段成比例定理的推论.学习重点:平行线分线段成比例定理及其推论.学习难点:平行线分线段成比例定理的探索过程以及定理的灵活应用.一、预习导学简记如图,△ABC与△DEF相似,求未知边x,y及未知角的度数和相似比.二、学习研讨1.相似三角形定义在△ABC和△A’B’C’中,如果;即,我们就说△ABC 与△A ’B ’C ’相似,记作: , 把 叫做相似比;若△ABC ∽△A ’B ’C ’,则△ABC 与△A ’B ’C ’的相似比为 , △A ’B ’C ’与△ABC 的相似比为 . 2. 平行线分线段成比例定理 探究:如图,任意画两条直线12,l l ,再画三条与12,l l 相交的平行线345,,l l l . 分别测量345,,l l l 在1l 上截得的两条线段得AB= ,BC= , 在2l 上截得的两条线段得DE= ,EF= , 计算得AB BC = ,DE EF = ,发现:AB BC DEEF任意平移5l ,再度量AB,BC,DE,EF 的长度,上述结论还成立吗? 简记 事实上,当3l ∥4l ∥5l 时,都可以得到AB BC DEEF,还可以得到平行线分线段成比例定理 符号语言:.(如图)符号语言:L 54L 545L 35L 3例 在△ABC 中,点D 是AB 的中点,DE//BC ,DE 交AC 于点E. 求证:△ADE ∽△ABC (换课本练习1)三、巩固提高已知,如图,DE//BC ,AE=4cm,(1)若 ,求 EC (2)若 ,求 AC四、教(学)后反思A B C D E BCD E ABCD E 23AD AB =25AD BD =。
初中数学 导学案:平行线分线段成比例

平行线分线段成比例学习目标1.理解平行线分线段成比例定理.2.灵活运用定理解答题目.学习重点:平行线等分线段成比例定理及其应用.学习难点:平行线等分线段成比例的推导.学习过程:一、问题引入1.比例的基本性质是什么?还有其它什么性质?2.什么叫成比例线段?二、问题探究探究一:如图是一架梯子的示意图,由生活常识可以知道:AA1,BB1,CC1,DD1,互相平行,且若AB=BC,则A1B1=B1C1,由此可以猜测:若两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等吗?交流展示:探究点拨:设直线a∥b∥c,直线l1,l2被直线a,b,c截得的线段分别为AB,BC和A1B1,B1C1,且AB=BC.过点B作直线l3∥l2,分别交直线a,c于点A2,C2,由于a∥b∥c,l3∥l2,因此由“夹在两平行线之间的平行线段相等”可知A2B=A1B1,BC2=B1C1,再证明△BAA2≌△BCC2,从而得到A1B1=B1C1.归纳总结:平行线等分线段定理:两条直线被一组平行线所截,如果在其中一条直线上截得的线段相还等,那么在另一条直线上截得的线段也相等.探究二:任意画两条直线l1,l2,再画三条与l1,l2相交的平行直线a,b,c,分别度量l1,l2被直线a,b,c截得的线段AB,BC,A1B1,B1C1的长度,相等吗?任意平移直线 c ,再度量AB,BC,A1B1,B1C1的长度,与还相等吗?交流展示:探究点拨:平行线分线段成比例定理:两条直线被一组平行线所截,所得对应线段成比例.探究三:如图,在△ABC中,已知DE∥BC,则和成立吗?为什么?交流展示:探究点拨:过点A作直线MN,使MN∥DE,利用平行线截线段成比例可得出结论.结论:平行于三角形一边的直线截其它两边,所得的对应线段成比例.三、实践交流例1.如图,已知AA1∥BB1∥CC1,AB=2,BC=3,A1B1=,求B1C1的长.学生解答:交流汇报:教师点拨规范解答:思路点拨:由平行线分线段成比例可知:=,再将已知线段的值代入就可求出B1C1的长.例2.如图,AD平分∠BAC交BC于点D,求证:学生解答:交流汇报:教师点拨规范解答:思路点拨:过C点作CE∥AD,交BA的延长线于点E,易得,再证明AE=AC.四、课堂小结1.本节课你有什么收获?2.平行线等分线段定理的内容是什么?3.平行线分线段成比例定理的内容是什么?4.平行于三角形一边的直线截其它两边,所得的对应线段有什么关系?五、达标检测必做题1.在ABCD中,AE交BC的延长线于点E,交DC于点F,若BC:CE=3:2,则CF:FD= .2.如图,已知DE∥BC,DF∥AC,下列比例式正确的是()3.如图,EF∥BC,AB∥DC,AE=9,BE=12,FD=10,则BF= .4.如图,在△ABC中,DE∥AC,DF∥AE,BD:DA=3:2,BF=6cm,则EF= ,EC= .5.在ABCD中,E是AB延长线上一点,且13BEAE,若BC=6,求BF的长度.选做题如图,在△ABC中,D为BC边的中点,延长AD至E,延长AB交CE的延长线于点P,若AD=2DE,求证:AP=3AB.。
平行线分线段成比例定理数学教案

平行线分线段成比例定理数学教案
标题:平行线分线段成比例定理
一、教学目标:
1. 学生能理解并掌握平行线分线段成比例定理。
2. 学生能运用该定理解决实际问题。
3. 提高学生的空间想象能力和逻辑思维能力。
二、教学内容:
平行线分线段成比例定理:如果一条直线截两条平行线,所得的对应线段成比例。
三、教学步骤:
1. 导入新课
通过复习以前学过的关于平行线的知识,引导学生进入新课的学习。
2. 讲解新课
(1) 介绍平行线分线段成比例定理,并解释其含义。
(2) 利用教具或多媒体进行演示,帮助学生理解这个定理。
(3) 引导学生自己画图,尝试证明这个定理。
3. 巩固练习
设计一些习题让学生做,以此来检验他们是否真正理解了这个定理。
4. 拓展应用
引导学生将这个定理应用到实际生活中,或者解决其他数学问题。
四、教学反思:
在教学过程中,教师应关注学生的学习状态,适时调整教学策略,以达到最佳的教学效果。
同时,教师也应鼓励学生积极思考,培养他们的创新精神和实践能力。
五、作业布置:
设计一些与本节课内容相关的习题作为家庭作业,以便学生巩固所学知识。
六、教学评估:
通过课堂观察、作业批改以及测试等方式,对学生的学习情况进行评估,及时反馈学习效果,为下一步的教学提供参考。
平行线分线段成比例定理导学案(用)
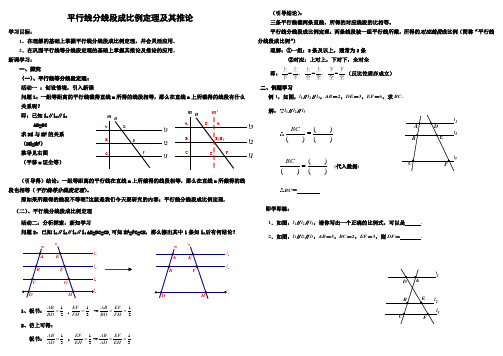
l1l2l3m nFEDCBA 平行线分线段成比例定理及其推论学习目标:1.在理解的基础上掌握平行线分线段成比例定理,并会灵活应用. 2.在巩固平行线等分线段定理的基础上掌握其推论及推论的应用. 新课学习:一、探究(一)、平行线等分线段定理: 活动一 :创设情境,引入新课问题1:一组等距离的平行线截得直线m 所得的线段相等,那么在直线n 上所截得的线段有什么关系呢?即:已知l 1∥l 2∥l 3AB=BC求DE 与EF 的关系 (DE=EF ) 推导见右图 (平移m 证全等)(引导得)结论:一组等距离的平行线在直线m 上所截得的线段相等,那么在直线n 所截得的线段也相等(平行线等分线段定理)。
那如果所截得的线段不等呢?这就是我们今天要研究的内容;平行线分线段成比例定理. (二)、平行线分线段成比例定理 活动二:分析探索,新知学习问题2:已知l 1∥l 2∥l 3∥l 4 AB=BC=CD,可知EF=FG=GH ,那么擦出其中1条如l 3后有何结论?43211、板书:12AB BD = ,12EF FH = →12AB EF BD FH == 2、仿上可得:板书:13AB AD = ,13EF EH =→13AB EF AD EH == (引导结论):三条平行线截两条直线,所得的对应线段的比相等。
平行线分线段成比例定理:两条线段被一组平行线所截,所得的对应线段成比例(简称“平行线分线段成比例”)理解:①一组:3条及以上,通常为3条 ②对应:上对上,下对下,全对全即:===上上上上下下,,下下全全全全(反比性质亦成立) 二、例题学习例1,如图,l 1∥l 2∥l 3,AB =2,DE =3,EF =6,求BC . 解:∵l 1∥l 2∥l 3∴)()() (=BC)()() (=BC (代入数据)∴BC =即学即练:1.如图,l 1∥l 2∥l 3,请你写出一个正确的比例式,可以是 . 2.如图,l 1∥l 2∥l 3,AB =5,BC =2,EF =3,则DF =.l1l2l3m nm'C'(B')A'FE DCBA21FDCBA 三、推论1.观察下图变形后填空:在图3和图4中,都有=BCAB( ),……; 2.总结:几何语言:∵BE ∥CF (或AD ∥CF )∴EFAEBC AB =……四、例题学习例2,已知:如图,DE ∥BC ,AB =15,AC =9,BD =4,求:AE .解:∵DE ∥BC∴)()(AC =CE )()() (=CE (代入数据) ∴CE =∴AE =+=五、课堂练习 A 组:1.如图,已知l 1//l 2//l 3,下列比例式中错误的是( )A 、DF BDCE AC = B 、BFBDAE AC = C 、BF DFAE CE =D 、ACBD BF AE = 2.如图,已知l 1//l 2//l 3,下列比例式中成立的是( )A 、BC CEDF AD = B 、AF BCBE AD = C 、BCADDF CE =D 、CEBEDF AF = B 组:1.已知:如图,AD ∥CF ,AB =3,BC =5,DB =4.5,求BF .令A 、D 两点重合令B 、E 两点重合 将有关线擦掉将有关线擦掉BE ∥CF ,BE 截、AF 两边) (AD ∥CF ,AD 截CB 、FB 两边的延长线)图3图4。
数学教案-平行线分线段成比例定理 (第二课时)

数学教案-平行线分线段成比例定理(第二课时)教学目标•了解平行线分线段成比例定理的概念和原理;•掌握平行线分线段成比例定理的应用方法;•能够解决一些简单的平行线分线段成比例的问题。
教学准备•教学课件;•教学工具:直尺、量角器、黑板、粉笔。
教学过程1. 复习•复习上节课所学的平行线的性质。
2. 引入•引导学生回想一下平行线的性质中是否有关于比例的概念。
3. 学习平行线分线段成比例定理•介绍平行线分线段成比例定理的概念:在两条平行线上,同侧的两个线段成比例,那么这两条线段被一条横截线所截得的线段也成比例。
4. 举例说明•在黑板上画出一条横截线和两条平行线,并标出相关线段。
引导学生观察并总结规律。
5. 确立结论•引导学生通过观察和分析,总结、确定平行线分线段成比例定理。
6. 实例讲解•进行一些简单的实例讲解,让学生理解如何应用平行线分线段成比例定理来解决问题。
7. 合作探究•分成小组,每组给出一些具体的问题,让学生合作探究应用平行线分线段成比例定理解决问题的方法。
8. 提出问题•提出一些让学生思考和讨论的问题,引导学生探索更深层次的问题。
9. 总结归纳•结合学生的讨论和思考,总结归纳平行线分线段成比例定理的相关要点。
10. 小结•对本节课所学内容进行总结,强调平行线分线段成比例定理的重要性和应用价值。
课后练习1.请根据平行线分线段成比例定理,求出下列问题中所问线段的长度:–已知$$\\frac{AC}{CB} = \\frac{2}{3}$$–,求DE–的长度。
–已知$$\\frac{EF}{FG} = \\frac{3}{5}$$–,求CD–的长度。
2.解决下列问题,应用平行线分线段成比例定理:–若$$AB \\parallel CD$$–,$$\\frac{EF}{FG} = \\frac{1}{3}$$–,求证$$AD \\parallel BC$$–。
–在平行四边形ABCD–中,$$\\frac{AB}{BC} = \\frac{1}{2}$$–,$$\\frac{AD}{DC}=\\frac{3}{4}$$–,求证$$AC \\parallel BD$$–。
平行线分线段成比例(优秀教案)
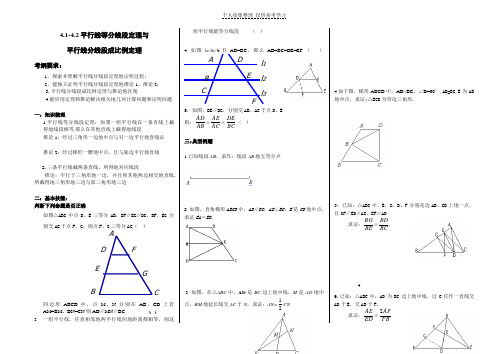
D BE F4.1-4.2平行线等分线段定理与 平行线分线段成比例定理考纲要求:1.探索并理解平行线分线段定理地证明过程;2.能独立证明平行线分线段定理地推论1、推论2; 3.平行线分线段成比例定理与推论地区别4.能应用定理和推论解决相关地几何计算问题和证明问题一:知识梳理1.平行线等分线段定理:如果一组平行线在一条直线上截得地线段相等,那么在其他直线上截得地线段推论1:经过三角形一边地中点与另一边平行地直线必推论2:经过梯形一腰地中点,且与底边平行地直线2.三条平行线截两条直线,所得地对应线段推论:平行于三角形地一边,并且和其他两边相交地直线.所截得地三角形地三边与原三角形地三边二:基本技能:判断下列命题是否正确如图△ABC 中点D 、E 三等分AB ,DF ∥EG ∥BC ,DF 、EG 分别交AC 于点F 、G ,则点F 、G 三等分AC ( )四边形ABCD 中,点M 、N 分别在AB 、CD 上若AM=BM 、DN=CN 则AD ∥MN ∥BC ( )3. 一组平行线,任意相邻地两平行线间地距离都相等,则这组平行线能等分线段. ( )4. 如图l 1//l 2//l 3且AB=BC ,那么AB=BC=DE=EF ( )5.如图,DE ∥BC ,分别交AB 、AC 于点D 、E 则:BCDEAC AE AB AD ==( )三:典型例题1 已知线段AB ,求作:线段AB 地五等分点.2 如图,直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,E 是CD 地中点.求证EA =EB .4 3. 如图,在△ABC 中,AD 是BC 边上地中线,M 是AD 地中点,BM 地延长线交AC 于N ,求证:AN=21CN .4.如下图,梯形ABCD 中,AD//BC ,∠B=60°,AB=BC,E 为AB 地中点,求证:△ECD 为等边三角形.5:已知:△ABC 中,E 、G 、D 、F 分别是边AB 、CB 上地一点,且GF ∥ED ∥AC ,EF ∥AD求证:.BC BDBE BG =6.已知:△ABC 中,AD 为BC 边上地中线,过C 任作一直线交AD 于E ,交AB 于F.求证:FB AFED AE 2=A CGCB E D Fl 3l 2 l 1 A7:如图,已知:D 为BC 地中点,AG ∥BC ,求证:FCAFED EG =DCAG8.已知:△ABC 中,AD 平分∠BAC , 求证:DCBDAC AB =(提示:过C 作CE ∥AD 交BA 地延长线于E )9:△ABC 中,AD 平分∠BAC ,CM ⊥AD 交AD 于E ,交AB 于M ,求证:AMABDC BD =四:能力提升1.如图1所示,F 为AB 地中点,FG ∥BC ,EG ∥CD ,则AG =,AE =.2.如图2,直线l 过梯形ABCD 一腰AB 地中点E ,且平行于BC ,l 与BD ,AC 、CD 分别交于F 、G 、H ,那么,BF =,CG =,DH =.3.如图3,已知CE 是△ABC 地中线,CD=21AD,EF ∥BD ,EG ∥AC ,若EF=10cm ,则BG =cm ,若CD=5cm ,则AF=cm.4.已知:如图,B 在AC 上,D 在BE 上,且AB:BC=2:1,ED:DB=2:1求AD:DF5.△ABC 中,DE ∥BC ,F 是BC 上一点.AF 交DE 于点G ,AD:BD=2:1,BC=8.4cm 求(1)DE 地长(2)AFAG(3)ADE ABC S S ∆∆。
平行线分线段成比例导学案
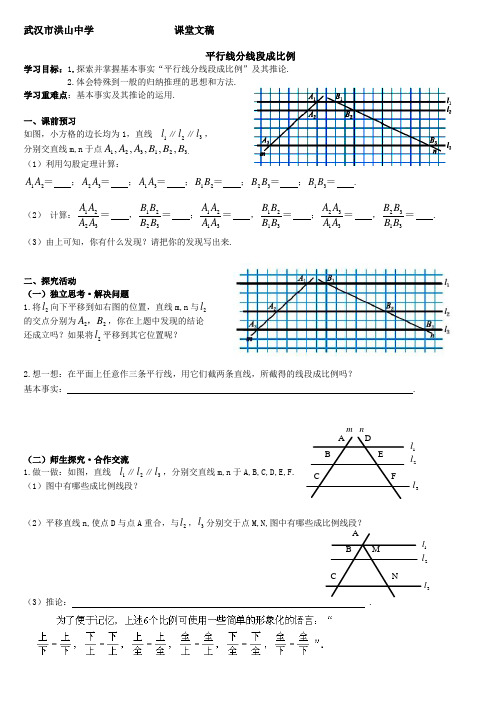
武汉市洪山中学 课堂文稿平行线分线段成比例学习目标:1.探索并掌握基本事实“平行线分线段成比例”及其推论.2.体会特殊到一般的归纳推理的思想和方法.学习重难点:基本事实及其推论的运用.一、课前预习如图,小方格的边长均为1,直线1l ∥2l ∥3l , 分别交直线m,n 于点.321321,,,,,B B B A A A (1)利用勾股定理计算:=21A A ;=32A A ;=31A A ;=21B B ;=32B B ;=31B B .(2) 计算:=3221A A A A ,=3221B B B B ;=3121A A A A ,=3121B B BB ;=3132A A A A ,=3132B B B B . (3)由上可知,你有什么发现?请把你的发现写出来.二、探究活动(一)独立思考·解决问题1.将2l 向下平移到如右图的位置,直线m,n 与2l 的交点分别为22B A ,,你在上题中发现的结论还成立吗?如果将2l 平移到其它位置呢?2.想一想:在平面上任意作三条平行线,用它们截两条直线,所截得的线段成比例吗?基本事实: .(二)师生探究·合作交流1.做一做:如图,直线1l ∥2l ∥3l ,分别交直线m,n 于A,B,C,D,E,F. (1)图中有哪些成比例线段?(2)平移直线n,使点D 与点A 重合,与2l ,3l 分别交于点M,N,图中有哪些成比例线段?(3)推论: .DEF1l 3l 2l m nB A CM 1l 3l 2l B A C ND E A B C 2.如图,在△ABC 中,E, F 分别是AB 和AC 上的点,且 EF ∥BC. (1)如果AE = 7, EB=5,FC = 4,那么AF 的长是多少? (2)如果AB = 10, AE=6,AF = 5,那么FC 的长是多少?三、达标测试1.已知两条直线被三条平行线所截,截得线段的长度如图所示,则x= .2.如图,在△ABC 中,点D ,E 分别在边AB ,AC 上,DE ∥BC ,若AD ∶AB =3∶4,AE=6,则AC 等于( ) A. 3 B. 4 C. 6 D.83.如图所示,直线1l ∥2l ∥3l ,下列比例式中错误的是( ) A.CE BC DF =AD B.AD DF CE BC = C. BE BC AF AD = D. DFAFCE BE =(第1题) (第2 题) (第3题)4. 如图,已知 DE ∥BC, AB = 5, AC = 7,AD= 2,求AE 的长.5.5. 如图,已知直线1l ∥2l ∥3l ,DE = 6, EF = 7,AB=5,求AC 的长.四、拓展延伸如图,在△ABC 中,D ,E ,F 分别是AB ,AC ,BC 上的点,且D E ∥BC ,EF ∥AB ,AD:DB=2:3,BC=20cm ,求BF 的长.A B C D E F 3l 2l 1l a b c。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NO.7 课题:27.2.1 平行线分线段成比例定理
主编:审核:课型:新授课验收负责人:
学习目标:1. 经历平行线分线段成比例定理的探索过程;掌握平行线分线段成比例定理.
2. 掌握平行线分线段成比例定理的推论.
学习重点:平行线分线段成比例定理及其推论.
学习难点:平行线分线段成比例定理的探索过程以及定理的灵活应用.
一、预习导学简记
如图,△ABC与△DEF相似,求未知边x,y
及未知角的度数和相似比.
二、学习研讨
1.相似三角形定义
在△ABC和△A’B’C’中,如果;
即 , 我们就说△ABC 与△A ’B ’C ’相似,记作: , 把 叫做相似比;若△ABC ∽△A ’B ’C ’,则
△ABC 与△A ’B ’C ’的相似比为 , △A ’B ’C ’与△ABC 的相似比为 . 2. 平行线分线段成比例定理 探究:
如图,任意画两条直线12,l l ,再画三条与12,l l 相交的平行线345,,l l l . 分别测量345,,l l l 在1l 上截得的两条线段得AB= ,BC= , 在2l 上截得的两条线段得DE= ,EF= , 计算得
AB BC = ,DE EF = ,发现:AB BC DE
EF
任意平移5l ,再度量AB,BC,DE,EF 的长度,上述结论还成立吗? 简记 事实上,当3l ∥4l ∥5l 时,都可以得到
AB BC DE
EF
,还可以得到
平行线分线段成比例定理 符号语言:
.(如图)
L 54L 54
5L 3
5
L 3
符号语言: 例 在△ABC 中,点D 是AB 的中点,DE//BC ,DE 交AC 于点E. 求证:△ADE ∽△ABC (换课本练习1)
三、巩固提高
已知,如图,DE//BC ,AE=4cm,(1)若 ,求 EC (2)若 ,求 AC
四、教(学)后反思
A B C D E B
C
D E A
B
C
D E 23
AD AB =25
AD BD =。
