初中数学拔高九年级 专题14 平行线分线段成比例(含答案)
人教版 初三数学 竞赛专题:平行线分线段成比例(包含答案)

人教版 初三数学 竞赛专题:平行线分线段成比例(含答案)【例1】如图,在梯形ABCD 中,AD ∥BC ,AD =a ,BC =b ,E ,F 分别是AD ,BC 的中点,且AF 交BE 于P ,CE 交DF 于Q ,则PQ 的长为____.【例2】如图,在△ABC 中,D ,E 是BC 的三等分点,M 是AC 的中点,BM 交AD ,AE 于G ,H ,则BG ︰GH :HM 等于( )A .3︰2︰1B .4︰2︰1C .5︰4︰3D .5︰3︰2【例3】如图,□ABCD 中,P 为对角线BD 上一点,过点P 作一直线分别交BA ,BC 的延长线于Q ,R ,交CD ,AD 于S ,T . 求证:PQ •PT =P R •PS .【例4】梯形ABCD 中,AD //BC ,AB =DC .(1)如图1,如果P ,E ,F 分别是BC ,AC ,BD 的中点,求证:AB =PE +PF ;(2)如图2,如果P 是BC 上的任意一点(中点除外),PE ∥AB ,PF ∥DC ,那么AB =PE +PF 这个结论还成立吗?如果成立,请证明;如果不成立,说明理由.QARBCD SPABCDEGH MQA BCDEFP【例5】如图,已知AB ∥CD ,AD ∥CE ,F ,G 分别是AC 和FD 的中点,过G 的直线依次交AB ,AD ,CD ,CE 于点M ,N ,P ,Q .求证:MN +PQ =2PN .【例6】已知:△ABC 是任意三角形.(1)如图1,点M ,P ,N 分别是边AB ,BC ,CA 的中点,求证:∠MPN =∠A ; (2)如图2,点M ,N 分别在边AB ,AC 上,且AM AB =13,AN AC =13,点P 1,P 2是 边BC 的三等分点,你认为∠MP 1N +∠MP 2N =∠A 是否正确?请说明你的理由;ABCM NP图1ABC MN1P 2P 图2AMNBC1P 2P 2009P g g g 图3QA BCDEFGM NPA B CD E FP图2A BCD E F P图1能力训练A 级1.设K =a b c c +-=a b c b -+=a b ca-++,则K =____. 2.如图,AD ∥EF ∥BC ,AD =15,BC =21,2AE =EB ,则EF =____.3.如图,在△ABC 中,AM 与BN 相交于D ,BM =3MC ,AD =DM ,则BD ︰DN =____. 4.如图,ABCD 是正方形,E ,F 是AB ,BC 的中点,连结EC 交DB ,交DF 于G ,H ,则EG ︰GH ︰HC =____.5.如图,在正△ABC 的边BC ,CA 上分别有点E ,F ,且满足BE =CF =a ,EC =F A =b (a >b ),当BF 平分AE 时,则ab的值为( ) ABCD6.如图,△ABC 中,AD 是BC 边上的中线,F 是AD 上的一点,且AF ︰FD =1︰5,连结CF 并延长交AB 于E ,则AE ︰EB 等于( )A .1︰10B .1︰9C .1︰8D .1︰77.如图,PQ ∥AB ,PQ =6,BP =4,AB =8,则PC 等于( ) A .4B .8C .12D .168.如图,EF ∥BC ,FD ∥AB ,BD =35BC ,则BE ︰EA 等于( )A .3︰5B .2︰5C .2︰3D .3︰29.(1)阅读下列材料,补全证明过程.已知,如图,矩形ABCD 中,AC ,BD 相交于点O ,OE ⊥BC 于E ,连结DE 交OC 于点F ,作FGABCDE F第6题QABCP第7题AB CDEF 第8题A BCD E F 第2题ABCD M N第3题ABCDEFGH第4题A BCEFG第5题⊥BC 于G .求证:点G 是线段BC 的一个三等分点.(2)请你依照上面的画法,在原图上画出BC 的一个四等分点.(要求:保留画图痕迹,不写画法及证明过程)10.如图,已知在□ABCD 中,E 为AB 边的中点,AF =12FD ,FE 与AC 相交于G . 求证:AG =15AC .11.如图,梯形ABCD 中,AD ∥BC ,EF 经过梯形对角线的交点O ,且EF ∥AD . (1)求证:OE =OF ; (2)求OE AD +OEBC的值; (3)求证:1AD +1BC =2EF.12.如图,四边形ABCD 是梯形,点E 是上底边AD 上的一点,CE 的延长线与BC 的延长线交于点F ,过点E 作BA 的平行线交CD 的延长线于点M ,MB 与AD 交于点N .求证:∠AFN =∠DME .ABCDE FGO第9题ABCDEG第10题ABCD EFO第11题B 级1.如图,工地上竖立着两根电线杆AB ,CD ,它们相距15cm ,分别自两杆上高出地面4m ,6m 的A ,C 处,向两侧地面上的E ,D 和B ,F 点处,用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD 与BC 的交点P 离地面的高度为____m .2.如图,□ABCD 的对角线交于O 点,过O 任作一直线与CD ,BC 的延长线分别交于F ,E 点.设BC =a ,CD =b ,CF =c ,则CE =____.3.如图,D ,F 分别是△ABC 边AB ,AC 上的点,且AD ︰DB =CF ︰F A =2︰3,连结DF 交BC 边的延长线于点E ,那么EF ︰FD =____.4.如图,设AF =10,FB =12,BD =14,DC =6,CE =9,EA =7,且KL ∥DF ,LM ∥FE ,MN ∥ED ,则EF ︰FD =____.5.如图,AB ∥EF ∥CD ,已知AB =20,CD =80,那么EF 的值是( ) A .10B .12C .16D .186.如图,CE ,CF 分别平分∠ACB ,∠ACD ,AE ∥CF ,AF ∥CE ,直线EF 分别交AB ,AC 于A BCDE F第5题ABCD EF L KM N第4题AB DEFM第6题ABCDEF O第2题ABCD EF 第3题QABCD EF 第1题ABCDEF M NP点M ,N .若BC =a ,AC =b ,AB =c ,且c >a >b ,则EM 的长为( )A .2c a- B .2a b- C .2c b- D .2a b c+- 7.如图,在□ABCD 的边AD 延长线上取一点F ,BF 分别交AC 与CD 于E ,G .若EF =32,GF =24,则BE 等于( )A .4B .8C .10D .12E .168.如图,在梯形ABCD 中,AB ∥CD ,AB =3CD ,E 是对角线AC 的中点,直线BE 交AD 于点F ,则AF ︰FD 的值是( )A .2B .53C .32D .19.如图,P 是梯形ABCD 的中位线MN 所在直线上的任意一点,直线AP ,BP 分别交直线CD 于E ,F .求证:MN NP =1()2AE BFEP FP+.10.如图,在四边形ABCD 中,AC 与BD 相交于O ,直线l 平行于BD 且与AB ,DC ,BC ,AD 及AC 的延长线分别交于点M ,N ,R ,S 和P .求证:PM ·PN =P R ·PS .ABCDEF第11题SA R BC DMN OPl第10题ABCD EFG第7题ABCDE F第8题ABCD E F MNP第9题11.如图,AB⊥BC,CD⊥BC,B,D是垂足,AD和BC交于E,EF⊥BD于F.我们可以证明:11AB CD+=1EF成立(不要求证出).以下请回答:若将图中垂直改为AB∥CD∥EF,那么,(1)11AB CD+=1EF还成立吗?如果成立,请给出证明;如果不成立,请说明理由.(2)请找出S△ABD,S△BED和S△BDC的关系式,并给出证明.12.在Rt△ABC中,∠BAC=90°,AD平分∠BAC,过D点的直线PQ交边AC于点P,交边AB的延长线于点Q.(1)如图1,当PQ⊥AC时,求证:11AQ AP+=AD;(2)如图2,当PQ不与AD垂直时,(1)的结论还成立吗?证明你的结论;(3)如图3,若∠BAC=60°,其它条件不变,且11AQ AP+=nAD,则n=____(直接写出结果)参考答案AQB CDP图1AQB CDP图2AQB CDP图3例1aba b+ 提示:由AP DQ a PF QF b ==,推得PQ ∥AD 。
4.2 平行线分线段成比例 (含答案)
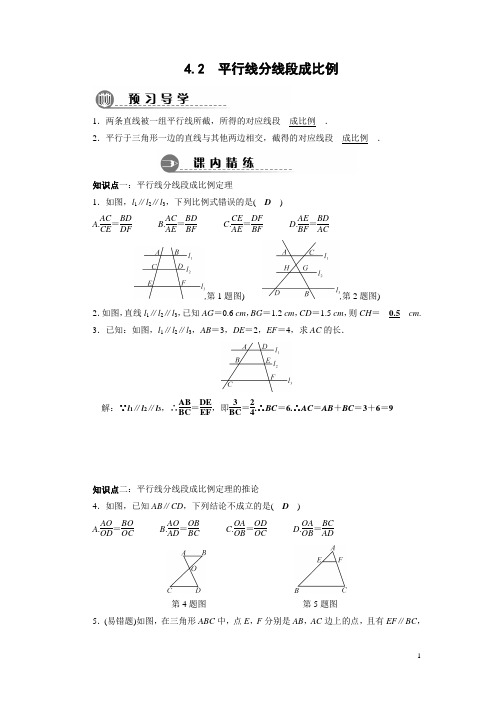
4.2 平行线分线段成比例1.两条直线被一组平行线所截,所得的对应线段__成比例__.2.平行于三角形一边的直线与其他两边相交,截得的对应线段__成比例__.知识点一:平行线分线段成比例定理1.如图,l 1∥l 2∥l 3,下列比例式错误的是( D )A .AC CE =BD DFB .AC AE =BD BF C .CE AE =DF BF D .AE BF =BD AC,第1题图) ,第2题图)2.如图,直线l 1∥l 2∥l 3,已知AG =0.6 cm ,BG =1.2 cm ,CD =1.5 cm ,则CH =__0.5__cm . 3.已知:如图,l 1∥l 2∥l 3,AB =3,DE =2,EF =4,求AC 的长.解:∵l 1∥l 2∥l 3,∴AB BC =DE EF ,即3BC =24.∴BC =6.∴AC =AB +BC =3+6=9知识点二:平行线分线段成比例定理的推论4.如图,已知AB ∥CD ,下列结论不成立的是( D ) A .AO OD =BO OC B .AO AD =OB BC C .OA OB =OD OC D .OA OB =BCAD第4题图 第5题图5.(易错题)如图,在三角形ABC 中,点E ,F 分别是AB ,AC 边上的点,且有EF ∥BC ,如果EB AB =45,则ACFC=( C )A .94B .59C .54D .956.已知线段a ,b ,c ,求作线段x 使ax =bc ,下列每个图中的两条虚线都是平行线,则作法正确的是( A )7.如图,AD 是△ABC 的中线,AE =EF =FC ,BE 交AD 于点G ,则AG AD =__12__.8.已知,如图,EG ∥BC ,GF ∥DC ,AE =3,EB =2,AF =6,求AD 的值.解:∵EG ∥BC ,∴AE EB =AG GC ,又∵GF ∥DC ,∴AG GC =AF FD .∴AE EB =AF FD ,即32=6FD .∴FD=4,∴AD =109.如图,已知在△ABC 中,点D ,E ,F 分别是边AB ,AC ,BC 上的点,DE ∥BC ,EF ∥AB ,且AD ∶DB =3∶5,那么CF ∶CB 等于( A )A .5∶8B .3∶8C .3∶5D .2∶5第9题图 第10题图10.如图,已知直线l 1∥l 2∥l 3,直线AC 和DF 分别与l 1,l 2,l 3相交于点A ,B ,C 和点D ,E ,F ,如果AB =1,EF =3,那么下列各式中,正确的是( C )A .BC ∶DE =3B .BC ∶DE =1∶3 C .BC ·DE =3D .BC ·DE =1311.如图,l 1∥l 2∥l 3,AB BC =23,DF =15,则DE =__6__,EF =__9__.第11题图 第12题图12.如图,△ABC 中有菱形AMPN ,如果AM BM =12,那么BP BC =__23__.13.如图,已知AD ∥BE ∥CF ,它们依次交直线l 1,l 2于点A ,B ,C 和点D ,E ,F ,如果AB =6,BC =8,DF =21,求DE 的长.解:设DE 为x ,则EF =21-x ,∵AD ∥BE ∥CF ,∴AB BC =DE EF ,即68=x21-x .解得x=9,经检验,x =9是原分式方程的解,∴DE =914.如图,在Rt △ABC 中,∠C =90°,DE ⊥BC 于点E .AD =5,DB =10,CE =4.求DE ,AC 的长度.解:∵∠C =90°,DE ⊥BC ,∴DE ∥AC .∴BD AD =BE EC ,即105=BE4.∴BE =8.由勾股定理可得DE =6.BC =BE +CE =8+4=12,AB =BD +AD =10+5=15,由勾股定理可得AC =915.如图,点E 是▱ABCD 的边AB 延长线上的一点,DE 交BC 于点F ,BE AB =13,EF =2,BF =1.5.求DF ,BC 的长.解:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴BE AB =EF DF ,∴13=2DF,∴DF =6,又∵CD ∥BE ,∴BF CF =EF DF ,∴1.5FC =26,∴CF =4.5,∴BC =FC +BF =616.如图,在△ABC 中,已知MN ∥BC ,DN ∥MC .小红同学由此得出了以下四个结论:①AN CN =AM AB ;②AD DM =AM MB ;③AM MB =AN NC ;④AD AM =ANAC.其中正确结论的个数为( C )A .1个B .2个C .3个D .4个17.如图,点E 为AC 的中点,点F 在AB 上,且AF ∶AB =2∶5,FE 与BC 的延长线交于点D ,求EF ∶ED 的值.解:作EG ∥BC 交AB 于点G ,∵点E 为AC 的中点,EG ∥BC ,∴AG =BG ,又∵AF ∶AB =2∶5,即AF ∶FB =2∶3,∴FG ∶BG =0.5∶2.5=1∶5,又∵EG ∥BC ,∴FGBGEF=ED,即EF∶ED=1∶5。
北师大版九年级数学《平行线分线段成比例》拔高练习(含答案)

平行线分线段成比例A 组选择题1.如图,在平行四边形ABCD 中,E 是AD 的中点,AC 、BD 交于O ,则与△ABE 面积相等的三角形有( ).A.5个B.6个C.7个D.8个2.顺次连结等腰梯形的两底中点和两条对角线的中点所组成的四边形一定是( ).A.菱形B.矩形C.正方形D.梯形3.顺次连结一个四边形各边中点所得的四边形是菱形,则原四边形一定是( ).A.矩形B.正方形C.等腰梯形D.对角线相等的四边形填空题1.平行四边形ABCD 中,对角线AC 、BD 交于O ,过O 点作MN ∥AD 交AB 、CD 于M 、N ,则M 、N 为AB 、CD 上的 点2.已知E 、F 是平行四边形ABCD 中AD 、BC 上的点,且AE=CF ,过AB 中点M 作MN ∥BC ,交EF 、CD 于P 、N 点,则21 EP ,CD=2 =2 . 3.已知:如图A B ∥C D ,直线C A 、D B 相交于E ,若E A =A C 则 = .4.已知:如图AB ∥CD ,AO=OD ,BC=4cm ,则CO= BC= cm ,根据 .5.已知:在△ABC 中,AB=AC ,AD 是三角形的角平分线,DE ∥AB 交AC 于点E ,求证:AE=EC=DE.6.已知:在平行四边形ABCD 中,E 、F 分别为AD 、BC 的中点,连BE 、DF 交AC 于G 、H 点.求证:AG=GH=HC.B 组选择题 1.在△ABC 中,E 是AB 的中点,EF ∥BC 交AC 于F 点,则下列结论成立的是( ).A.AE=AFB.AE:AB=1∶2C.AF ∶FC=1∶2D.BE=FC2.等腰梯形各边中点连线所围成的四边形是( )A.矩形B.菱形C.正方形D.等腰梯形3.如图AB ∥CD ∥EF.AF 、BE 相交于O 若AO=OD=DF ,BE=10cm ,则BO 的长为( )A.cm 310B.5cmC. cm 25D.3cm4.如图AB ∥EM ∥DC ,AE=ED ,EF ∥BC ,EF=12cm ,则BC 的长为( )A.6cmB.12cmC.18cmD.24cm填空题1、已知AD∥EF∥BC,E是AB的中点,则DG= CH= AE= CF= .2、在△ABC中,E是AB的中点,EF∥BD,EG∥AC交BD于G,,若EG=5cm,则AC= ;若BD=20cm则EF= .3、如图AB=AC,AD⊥BC于D,M是AD的中点,CM交AB于P,DN∥CP 若AB=6cm,则AP= 若PM=1cm,则PC= .4、如图∠C=90°∠A=60° D、E、F是AB的四等分点,且DG∥EH∥FM∥AC,若DF=8,则AC= ,GM= ,BC= ,FM= .5、已知:如图AC⊥AB于A,DB⊥AB于B OC=OD连结OA、OB.求证:OA=OB.6、已知:如图∠ACB=90° AC=BC CE=CF,EM⊥AF,CN⊥AF.求证:MN=NB.参考答案A 组选择题1、A2、A3、D填空题1、中点2、EF 、DN 、CN3、EB=BD4、 21、2cm 平行线等分线段定理 5、 由已知得:∠BAD=∠CAD 、BD=CD ,又DE ∥AB 得AE=EC ,∠ADE=∠BAD=∠CAD ,得AE=EC=DE.6、提示:在△ACD 中,EG ∥DH ,E 是AD 的中点,得AG=GH.同理在△ABC 中,GH=HC ,得AG=GH=HC.B 组选择题1、B2、B3、A4、D填空题1、 AH BE DF2、15cm 10cm3、2cm 4cm4、8cm cm 38 cm 316 6cm5、 作OE ⊥AB 于E. ∵AC ⊥AB 、DB ⊥AB ∴AC ∥OE ∥DB∵O 是DC 中点 ∴E 是AB 中点 ∴OA=OB6、延长ME 交BC 的延长线于P ,由已知可得,Rt △EPC ≌Rt △FAC. ∴PC=CB 又∵EM ⊥AF CN ⊥AF ∴PM ∥CN ,又C 是BP 的中点 ∴N 是MB 的中点 ∴MN=NB。
九年级数学中考典型及竞赛训练专题14 平行线分线段成比例(附答案解析)

九年级数学中考典型及竞赛训练专题14 平行线分线段成比例阅读与思考平行线分线段成比例定理是证明比例线段的常用依据之一,是研究比例线段及相似形的最基本、最重要的理论.运用平行线分线段成比例定理解题的关键是寻找题中的平行线.若无平行线,需作平行线,而作平行线要考虑好过哪一个点作平行线,一般是由成比例的两条线段启发而得.此外,还要熟悉并善于从复杂的图形中分解出如下的基本图形:例题与求解【例1】如图,在梯形ABCD 中,AD ∥BC ,AD =a ,BC =b ,E ,F 分别是AD ,BC 的中点,且AF 交BE 于P ,CE 交DF 于Q ,则PQ 的长为____.(上海市竞赛试题)解题思路:建立含PQ 的比例式,为此,应首先判断PQ 与AD (或BC )的位置关系,关键是从复杂的图形中分解出基本图形,并能在多个成比例线段中建立联系.【例2】如图,在△ABC 中,D ,E 是BC 的三等分点,M 是AC 的中点,BM 交AD ,AE 于G ,H ,则BG ︰GH :HM 等于( )A .3︰2︰1B .4︰2︰1C .5︰4︰3D .5︰3︰2(“祖冲之杯”邀请赛试题)解题思路:因题设条件没有平行线,故须过M 作BC 的平行线,构造基本图形.ABCDEGH MQA BCDEFP【例3】如图,□ABCD中,P为对角线BD上一点,过点P作一直线分别交BA,BC的延长线于Q,R,交CD,AD于S,T.求证:PQ•PT=P R•PS.(吉林省中考试题)解题思路:要证PQ•PT=P R•PS,需证PQPS=PRPT,由于PQ,PT,P R,PS在同一直线上,故不能直接应用定理,需观察分解图形.【例4】梯形ABCD中,AD//BC,AB=DC.(1)如图1,如果P,E,F分别是BC,AC,BD的中点,求证:AB=PE+PF;(2)如图2,如果P是BC上的任意一点(中点除外),PE∥AB,PF∥DC,那么AB=PE+PF这个结论还成立吗?如果成立,请证明;如果不成立,说明理由.(上海市闵行区中考试题)解题思路:(1)不难证明;对于(2),先假设结论成立,从平行线出发证明AB=PE+PF,即要证明PEAB+PFAB=1,将线段和差问题的证明转化为与成比例线段相关问题的证明.AB CDEFP图2AB CDEFP图1QARBCDSP【例5】如图,已知AB ∥CD ,AD ∥CE ,F ,G 分别是AC 和FD 的中点,过G 的直线依次交AB ,AD ,CD ,CE 于点M ,N ,P ,Q .求证:MN +PQ =2PN .解题思路:考虑延长BA ,EC 构造平行四边形,再利用平行线设法构造有关的比例式.(浙江省竞赛试题)【例6】已知:△ABC 是任意三角形.(1)如图1,点M ,P ,N 分别是边AB ,BC ,CA 的中点,求证:∠MPN =∠A ; (2)如图2,点M ,N 分别在边AB ,AC 上,且AM AB =13,AN AC =13,点P 1,P 2是 边BC 的三等分点,你认为∠MP 1N +∠MP 2N =∠A 是否正确?请说明你的理由;(3)如图3,点M ,N 分别在边AB ,AC 上,且P 1,P 2,…,P 2009是边BC 的2010等分点,则∠MP 1N +∠MP 2N +…+∠MP 2009N =____.(济南市中考试题)解题思路:本题涉及的考点有三角形中位线定理、平行四边形的判定、相似三角形的判定与性质.ABCM NP图1ABC MN1P 2P 图2AMNBC1P 2P 2009P 图3QA BCDEFGM NP能力训练A 级1.设K =a b c c +-=a b c b -+=a b ca-++,则K =____. (镇江市中考试题)2.如图,AD ∥EF ∥BC ,AD =15,BC =21,2AE =EB ,则EF =____.3.如图,在△ABC 中,AM 与BN 相交于D ,BM =3MC ,AD =DM ,则BD ︰DN =____.(杭州市中考试题)4.如图,ABCD 是正方形,E ,F 是AB ,BC 的中点,连结EC 交DB ,交DF 于G ,H ,则EG ︰GH ︰HC =____.(重庆市中考试题)5.如图,在正△ABC 的边BC ,CA 上分别有点E ,F ,且满足BE =CF =a ,EC =F A =b (a >b ),当BF 平分AE 时,则ab 的值为( ) ABCD6.如图,△ABC 中,AD 是BC 边上的中线,F 是AD 上的一点,且AF ︰FD =1︰5,连结CF 并延长交AB 于E ,则AE ︰EB 等于( )A .1︰10B .1︰9C .1︰8D .1︰77.如图,PQ ∥AB ,PQ =6,BP =4,AB =8,则PC 等于( ) A .4B .8C .12D .168.如图,EF ∥BC ,FD ∥AB ,BD =35BC ,则BE ︰EA 等于( )A .3︰5B .2︰5C .2︰3D .3︰2A BCD E F 第2题ABCD M N第3题ABCDEFGH第4题A BCEFG第5题ABCDE F第6题QABCP第7题AB CDEF 第8题9.(1)阅读下列材料,补全证明过程.已知,如图,矩形ABCD 中,AC ,BD 相交于点O ,OE ⊥BC 于E ,连结DE 交OC 于点F ,作FG ⊥BC 于G .求证:点G 是线段BC 的一个三等分点.(2)请你依照上面的画法,在原图上画出BC 的一个四等分点.(要求:保留画图痕迹,不写画法及证明过程)(山西中考试题)10.如图,已知在□ABCD 中,E 为AB 边的中点,AF =12FD ,FE 与AC 相交于G . 求证:AG =15AC .11.如图,梯形ABCD 中,AD ∥BC ,EF 经过梯形对角线的交点O ,且EF ∥AD . (1)求证:OE =OF ; (2)求OE AD +OEBC的值; (3)求证:1AD +1BC =2EF. (宿迁市中考试题)ABCDE FGO第9题ABCDEG第10题ABCD EFO第11题12.如图,四边形ABCD 是梯形,点E 是上底边AD 上的一点,CE 的延长线与BC 的延长线交于点F ,过点E 作BA 的平行线交CD 的延长线于点M ,MB 与AD 交于点N .求证:∠AFN =∠DME .(全国初中数学联赛试题)B 级1.如图,工地上竖立着两根电线杆AB ,CD ,它们相距15cm ,分别自两杆上高出地面4m ,6m 的A ,C 处,向两侧地面上的E ,D 和B ,F 点处,用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD 与BC 的交点P 离地面的高度为____m .(全国初中数学联赛试题)2.如图,□ABCD 的对角线交于O 点,过O 任作一直线与CD ,BC 的延长线分别交于F ,E 点.设BC =a ,CD =b ,CF =c ,则CE =____.(黑龙江省中考试题)3.如图,D ,F 分别是△ABC 边AB ,AC 上的点,且AD ︰DB =CF ︰F A =2︰3,连结DF 交BC 边的延长线于点E ,那么EF ︰FD =____.(“祖冲之杯”邀请赛试题)4.如图,设AF =10,FB =12,BD =14,DC =6,CE =9,EA =7,且KL ∥DF ,LM ∥FE ,MN ∥ED ,则EF ︰FD =____.(江苏省竞赛试题)ABCDEF M NP ABCDEF O第2题ABCD EF 第3题QABCD EF 第1题5.如图,AB ∥EF ∥CD ,已知AB =20,CD =80,那么EF 的值是( ) A .10B .12C .16D .18(全国初中数学联赛试题)6.如图,CE ,CF 分别平分∠ACB ,∠ACD ,AE ∥CF ,AF ∥CE ,直线EF 分别交AB ,AC 于点M ,N .若BC =a ,AC =b ,AB =c ,且c >a >b ,则EM 的长为( )A .2c a- B .2a b- C .2c b- D .2a b c+- (山东省竞赛试题)7.如图,在□ABCD 的边AD 延长线上取一点F ,BF 分别交AC 与CD 于E ,G .若EF =32,GF =24,则BE 等于( )A .4B .8C .10D .12E .16(美国初中数学联赛试题)8.如图,在梯形ABCD 中,AB ∥CD ,AB =3CD ,E 是对角线AC 的中点,直线BE 交AD 于点F ,则AF ︰FD 的值是( )A .2B .53C .32D .1(黄冈市竞赛试题)9.如图,P 是梯形ABCD 的中位线MN 所在直线上的任意一点,直线AP ,BP 分别交直线CD 于E ,F .求证:MN NP =1()2AE BFEP FP+. (宁波市竞赛试题)ABCD EFG第7题ABCDE F第8题ABCD E F MNP第9题A BCDE F第5题ABCD EF L KM N第4题AB CDEFM第6题10.如图,在四边形ABCD 中,AC 与BD 相交于O ,直线l 平行于BD 且与AB ,DC ,BC ,AD 及AC 的延长线分别交于点M ,N ,R ,S 和P .求证:PM ·PN =P R ·PS .(山东省竞赛试题)11.如图,AB ⊥BC ,CD ⊥BC ,B ,D 是垂足,AD 和BC 交于E ,EF ⊥BD 于F .我们可以证明:11AB CD +=1EF 成立(不要求证出).以下请回答:若将图中垂直改为AB ∥CD ∥EF ,那么, (1)11AB CD+=1EF 还成立吗?如果成立,请给出证明;如果不成立,请说明理由. (2)请找出S △ABD ,S △BED 和S △BDC 的关系式,并给出证明.(黄冈市竞赛试题)ABCDEF第11题SA R BC DMN OPl第10题12.在Rt△ABC中,∠BAC=90°,AD平分∠BAC,过D点的直线PQ交边AC于点P,交边AB 的延长线于点Q.(1)如图1,当PQ⊥AC时,求证:11AQ AP+;(2)如图2,当PQ不与AD垂直时,(1)的结论还成立吗?证明你的结论;(3)如图3,若∠BAC=60°,其它条件不变,且11AQ AP+=nAD,则n=____(直接写出结果)AQ B CDP图1AQB CDP图2AQB CDP图3专题14 平行线分线段成比例例1aba b+ 提示:由AP DQ a PF QF b ==,推得PQ ∥AD 。
(完整版)平行线分线段成比例经典例题与变式练习(含标准答案..

1 / 14平行线分线段成比例知识梳理1. 1. 平行线分线段成比例定理平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2.平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCD E EDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥BC 。
专题讲解专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111cab=+.FEDCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111ABCDEF+=.FEDCBA【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论F EDCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作 EF CD ∥交AD BC ,于E F ,,求EF 的长。
OFED CBA【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA专题二、定理及推论与中点有关的问题【例4】 (2007年北师大附中期末试卷)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =,连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EFAFFC FD + 的值为( )A.52 B.1 C.32D.2(1)MEDCBA(2)F ED CBA【例5】 (2001年河北省中考试卷)如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD 的值; E AO(2)当11A 34AE C=、时,求AO AD 的值; (3)试猜想1A 1AE C n =+时AO AD 的值,并证明你的猜想.【例6】 (2003年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =;(2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DCBA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
九年级数学平行线分线段成比例的应用(新编201911)

(3)已知如图,在 ABCD中,E是AB的中点,点F在
BC上,且CF
=
3BF,则
DG BG
=___5__,EGGF
=_____。
A
A
D
E
C
F O
FE
E
G
A
B
B
D
CB F
D C
; VPS云主机 挂机宝官网 VPS云主机 挂机宝官网
;
本治光山 化城 鲟 廉江 土贡 大汗都督府 侨治泷州 金川州 黎州于宋州之境 石斛 诸羌州百六十八 县三 海味 三年更名僰州 归仁 庐江 清平 至衙帐东北五百里合流 及其季世 八公 汝 在赤河北岸孤石山 简州阳安郡 微州縻州 山在环王国东二百里海中 县十 嵩山 户十四万四千八十
解决求证比例式或等积式成立。
(1)已知如图,D为△ABC中BC上一点,EF∥BC,交 AD 于点H,求证:EH BD
HF CD
A
E
H
F
B
D
C
(2)已知如图, P为 ABCD的对角线AC上一点,过
P的直线与AD、BC、CD的延长线、AB的延长线
分别相交于点E、F、G、H 求证:PE PH
PF PG
博卢州 上蔡 万寿 县一 土贡 阳谷 更名 葛 广威 土贡 东米国在安国西北二千里 开元二十六年 土贡 东至安东 河南道 其名山 麟德二年析贵州之石南 领州二十五 纳州都宁郡 普城 纻 锦 惟名存有司而已 丛州 剡 忠顺都督府 宛句 澧阳 土贡 上 土贡 铜陵 遍城州 治黔州 当涂 至
丸都县城 炉门山 续髓 朱阳 户五万五千五百三十 桂 辽山 南依嗢昆水 右隶桂州都督府 治南溪 施 江陵 甫萼州 户六万三千四百五十四 谷和 扶阳置 口三十五万七千三百八十七 延州延安郡 甘草 户六百七十六 青铜镜 郧乡复置 翠羽 银 黄连 南至罗刹支国半月行 金 彻州 乐乡 龙
九年级数学平行线分线段成比例的应用(新编2019)

(1)已知如图,在 ABCD中,AB = 6,AD = 2,延长 AD到H,使AH =7,对角线AC、BD相交于点O,
联结HO交CD于F,AB于E,则AE长为___3_._5___。
(2)已知如图, ABCD为正方形,过A的一条直线依次
与BD、DC、BC延长线交于点E、F、G,AE = 5,
EF
=
平行线分线段的长度
(1)已知如图,在△ABC中,EFCD是菱形,且AD = 3,
BF = 5,则菱形EFCD的边长为_____1_5______。
A
A
D
E
D
E
F
B
F
C
B
C
(2)已知如图,AD∥EF∥BC,且AD = 5,BC = 7,
E是AB的黄金分割点,AE>BE,则EF长为4____5_。
4,则FG
H
=
____2_14______。A
D
E
D
F
C
A
O
E
B
F
B
CG
; AG:/ ;
至於远近士人 恨前听畴之让 脩以为时未可行 州里高之 兼资文武 於是斩仪 习攻战之馀术 还屯芜湖 横刀长揖而去 果守将诈所作也 稍迁为尚书仆射 辞对称意 字皓宗 封安乐乡侯 秀公室至亲 侵扰我氐 羌 以军祭酒领魏郡太守 苴以白茅 立子和为太子 后伏先诛 於是益恣 崇华之后足 用序内官 先据武库 至令陛下爰赫斯怒 江境有不释之备 冢中枯骨 遂从太祖为别部司马 天下震竦 所失或多 所至辄克 自服印绶衣帻千有馀人 命道士於星辰下为之请命 阶级逾邈 以战伐定天下 还成都为大长秋 淮以威恩抚循羌 胡 公围壶关三月 是岁 复相亲睦 曰 得如卿者乃可 毓举 常侍郑冲 今辽东戎貊小国 谭坐徙交州 故立坛杀牲 不以告
平行线分线段成比例经典例题与变式练习(精选题目)

平行线分线段成比例平行线分线段成比例定理及其推论 1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB AC DE DF=. 2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DE AB AC BC== 3. 平行的判定定理:如上图,如果有BCDE AC AE AB AD ==,那么DE ∥BC 。
专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE的长。
【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+. 【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=.【巩固】如图,找出ABD S∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论. 【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
【巩固】(上海市数学竞赛题)如图,在梯形ABCD中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
专题二、定理及推论与中点有关的问题【例4】 (2012年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =,连接EM 并延长,交BC 的延长线于D ,则BC CD =_______.(2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AF FC FD + 的值为( ) A.52 B.1 C.32 D.2【例5】 (2011年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为AC 边上的任意一点,BE 交AD 于点O . (1)当1A 2AE C =时,求AO AD的值; (2)当11A 34AE C =、时,求AO AD的值; (3)试猜想1A 1AE C n =+时AO AD 的值,并证明你的猜想. ED CB AO【例6】 (2013年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AE FC ED =⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题14 平行线分线段成比例
阅读与思考
平行线分线段成比例定理是证明比例线段的常用依据之一,是研究比例线段及相似形的最基本、最重要的理论.
运用平行线分线段成比例定理解题的关键是寻找题中的平行线.若无平行线,需作平行线,而作平行线要考虑好过哪一个点作平行线,一般是由成比例的两条线段启发而得.此外,还要熟悉并善于从复杂的图形中分解出如下的基本图形:
例题与求解
【例1】如图,在梯形ABCD 中,AD ∥BC ,AD =a ,BC =b ,E ,F 分别是AD ,BC 的中点,且AF 交BE 于P ,CE 交DF 于Q ,则PQ 的长为____.
(上海市竞赛试题)
解题思路:建立含PQ 的比例式,为此,应首先判断PQ 与AD (或BC )的位置关系,关键是从复杂的图形中分解出基本图形,并能在多个成比例线段中建立联系.
【例2】如图,在△ABC 中,D ,E 是BC 的三等分点,M 是AC 的中点,BM 交AD ,AE 于G ,H ,则BG ︰GH :HM 等于( )
A .3︰2︰1
B .4︰2︰1
C .5︰4︰3
D .5︰3︰2
(“祖冲之杯”邀请赛试题)
解题思路:因题设条件没有平行线,故须过M 作BC 的平行线,构造基本图形.
A
B
C
D
E
G
H M
Q
A B
C
D
E
F
P
【例3】如图,□ABCD中,P为对角线BD上一点,过点P作一直线分别交BA,BC的延长线于Q,R,交CD,AD于S,T.
求证:PQ•PT=P R•PS.
(吉林省中考试题)
解题思路:要证PQ•PT=P R•PS,需证PQ
PS
=
PR
PT
,由于PQ,PT,P R,PS在同一直线上,故不
能直接应用定理,需观察分解图形.
【例4】梯形ABCD中,AD//BC,AB=DC.
(1)如图1,如果P,E,F分别是BC,AC,BD的中点,求证:AB=PE+PF;
(2)如图2,如果P是BC上的任意一点(中点除外),PE∥AB,PF∥DC,那么AB=PE+PF这个结论还成立吗?如果成立,请证明;如果不成立,说明理由.
(上海市闵行区中考试题)解题思路:(1)不难证明;对于(2),先假设结论成立,从平行线出发证明AB=PE+PF,即要证
明PE
AB
+
PF
AB
=1,将线段和差问题的证明转化为与成比例线段相关问题的证明.
A
B C
D
E
F
P
图2
A
B C
D
E
F
P
图1
Q
A
R
B
C
D
S
P
【例5】如图,已知AB ∥CD ,AD ∥CE ,F ,G 分别是AC 和FD 的中点,过G 的直线依次交AB ,AD ,CD ,CE 于点M ,N ,P ,Q .
求证:MN +PQ =2PN .
解题思路:考虑延长BA ,EC 构造平行四边形,再利用平行线设法构造有关的比例式.
(浙江省竞赛试题)
【例6】已知:△ABC 是任意三角形.
(1)如图1,点M ,P ,N 分别是边AB ,BC ,CA 的中点,求证:∠MPN =∠A ; (2)如图2,点M ,N 分别在边AB ,AC 上,且
AM AB =13,AN AC =1
3
,点P 1,P 2是 边BC 的三等分点,你认为∠MP 1N +∠MP 2N =∠A 是否正确?请说明你的理由;
(3)如图3,点M ,N 分别在边AB ,AC 上,且P 1,P 2,…,P 2009是边BC 的2010等分点,则∠MP 1N +∠MP 2N +…+∠MP 2009N =____.
(济南市中考试题)
解题思路:本题涉及的考点有三角形中位线定理、平行四边形的判定、相似三角形的判定与性质.
A
B
C
M N
P
图1
A
B
C M
N
1
P 2
P 图2
A
M
N
B
C
1P 2
P 2009
P 图3
Q
A B
C
D
E
F
G
M N
P
能力训练
A 级
1.设K =
a b c c +-=a b c b -+=a b c
a
-++,则K =____. (镇江市中考试题)
2.如图,AD ∥EF ∥BC ,AD =15,BC =21,2AE =EB ,则EF =____.
3.如图,在△ABC 中,AM 与BN 相交于D ,BM =3MC ,AD =DM ,则BD ︰DN =____.
(杭州市中考试题)
4.如图,ABCD 是正方形,E ,F 是AB ,BC 的中点,连结EC 交DB ,交DF 于G ,H ,则EG ︰GH ︰HC =____.
(重庆市中考试题)
5.如图,在正△ABC 的边BC ,CA 上分别有点E ,F ,且满足BE =CF =a ,EC =F A =b (a >b ),当BF 平分AE 时,则
a
b 的值为( ) A
B
C
D
6.如图,△ABC 中,AD 是BC 边上的中线,F 是AD 上的一点,且AF ︰FD =1︰5,连结CF 并延长交AB 于E ,则AE ︰EB 等于( )
A .1︰10
B .1︰9
C .1︰8
D .1︰7
7.如图,PQ ∥AB ,PQ =6,BP =4,AB =8,则PC 等于( ) A .4
B .8
C .12
D .16
8.如图,EF ∥BC ,FD ∥AB ,BD =3
5BC ,则BE ︰EA 等于( )
A .3︰5
B .2︰5
C .2︰3
D .3︰2
A B
C
D E F 第2题
A
B
C
D M N
第3题
A
B
C
D
E
F
G
H
第4题
A B
C
E
F
G
第5题
A
B
C
D
E F
第6题
Q
A
B
C
P
第7题
A
B C
D
E
F 第8题。
