02热力学第一定律
热力学第一定律和第二定律

热力学第一定律和第二定律随着科学技术的不断进步,人们开始逐渐认识到自然界的一些规律,其中热力学定律就是其中之一。
热力学定律是描述物体热力学性质以及能量转化的规律。
热力学定律分为第一定律和第二定律。
本文将分别对这两个定律进行详细的说明。
一、热力学第一定律热力学第一定律,也叫做能量守恒定律。
它指出能量在自然界中不存在创生和消失,只是在不同形式之间相互转化。
即,能量的总量是不变的。
这一定律在热力学中的具体应用就是热量的转化。
通过这一定律,我们可以很好地理解物体的温度变化和热量传递。
热力学第一定律的表达式为:ΔU = Q - W。
其中,ΔU 表示系统内能的变化,Q 表示系统从外界吸收的热量,W 表示系统对外界做功。
这个公式告诉我们,一个系统的内能变化等于从外界吸收的热量减去系统对外做的功。
这就是热力学第一定律。
热力学第一定律的应用非常广泛。
比如说,我们可以通过这个定律来分析热机的效率。
热机是指能够将热能转化为机械能的设备,如蒸汽机、内燃机、汽车发动机等。
热机的效率表示为η =W/Qh,其中 W 表示机器输出的功,Qh 表示机器吸收的热能。
热力学第一定律告诉我们,热量和功是能量的两种形式,它们之间的转换只是数量上的变化,而能量本身并没有发生改变。
因此,热机能够将热能转化为机械能的效率受到热力学第一定律的限制,也就是说,热机的效率永远不可能达到 100%。
这个定律的应用不仅局限于工业和生产方面,在其他领域,如生物学、环境保护等方面,也有不同的应用。
二、热力学第二定律热力学第二定律,也叫做热力学中的熵增定律。
它指出,在任何热力学过程中,系统的总熵永远不会减少,而只会不断增加或保持不变。
熵是一个物理量,用来描述系统的无序程度,通俗地讲,就是一个系统的混乱程度。
熵增加意味着系统的混乱程度增加,熵减少意味着系统的有序程度增加。
热力学第二定律的表达式为:ΔS≥Q/T。
其中,ΔS 表示系统的总熵变化,Q 表示从高温热源吸收的热量,T 表示系统的绝对温度。
第二章 热力学第一定律

第二章 热力学第一定律
2
第二章 热力学第一定律
2.1 热、功和内能
2.2 热力学第一定律
2.3 热力学第一定律在某些特殊过程中的应用
2.4 可逆过程 2.5 焓 2.6 热容 2.7 热力学第一定律对理想气体的应用 2.8 热力学第一定律对实际气体的应用 2.9 热力学第一定律在化学反应及相变过程中
(后面有例题进行相关的计算)
6
2.1.1 热
温度反映了物体冷热程度,是分子平均平动动 能的标志,是状态量。
3.热量的计算
Q mc(T2 T1)
c 是比热:1kg物质升高1 ºC吸收的热量; mc是热容:mkg物质升高1 ºC吸收的热量; 此式适用于无相变的过程。
7
2.1.2 功
2.1.2 功
16
2.1.3 内能
•分子运动的动能(平动能、转动能和振动能); 它与温度有关 。 •分子间相互作用的位能 ;它与分子间的作用力有 关,即与体积相关 。 •原子、电子的运动能以及原子核内能量等 ;这些 能量在热力学研究中不会发生变化,可以不考虑这 些能量 。
注:内能是体系的一种热力学性质,处于一个确定状态的
Wb P环(V2 V1) 0Pa (4.54 2.27) 102 m3 0J
该例题能不能按下面的方法计算做功?
W V2 pdV V2 nRT dV nRT ln V2
V1
V1 V
V1
13
2.1.2 功
结果表明:两种膨胀方式尽管系统的初、末态 相同,但因途径不同功也不同,这再一次有力地说 明了功不是状态函数,它的数值不仅与系统的状态 变化有关,而且与变化的途径有关。
活塞与汽缸无摩擦,当气体作 准静态压缩或膨胀时,外界的压强
热力学第一定律与第二定律

热力学第一定律与第二定律热力学是研究能量与热的转化和传递规律的科学,它是自然科学中重要的分支之一。
在热力学中,第一定律和第二定律是两个基本的定律,它们定义了能量守恒和能量转化的方向,对于理解热力学系统的行为和实际应用具有重要意义。
1. 热力学第一定律热力学第一定律,也称为能量守恒定律,表明能量在系统与环境之间的传递和转化后总量保持不变。
它可以通过下式表达:ΔU = Q - W其中,ΔU表示系统内能的变化,Q表示系统吸收的热量,W表示系统对外界做的功。
根据热力学第一定律,一个封闭系统的能量是守恒的,能量既不能被创造也不能被销毁,只能从一种形式转化为另一种形式。
热力学第一定律还可以用来推导出热机效率的表达式。
在一个热机中,根据热力学第一定律,系统吸收的热量等于系统对外界做的功加上系统内能的变化。
根据这个原理,我们可以得到热机效率的公式:η = 1 - Qc/Qh其中,η表示热机的效率,Qc表示热机向冷源放出的热量,Qh表示热机从热源吸收的热量。
这个公式表明,在一个热机中,不能把吸收的热量完全转化为功,一部分热量必须放出到冷源中,效率小于1。
2. 热力学第二定律热力学第二定律是热力学中最重要的定律之一,它表明热量不能自发地从低温物体传递到高温物体,而是自发地从高温物体传递到低温物体。
热力学第二定律有多种等效的表述方式,其中最常见的是克劳修斯表述和开尔文表述。
克劳修斯表述中,热量不会自发地从冷热源传递到热热源,即不存在一个热机,它只从一个热源吸热,然后完全转化为功,再把一部分热量放到冷热源上,不对环境产生任何影响。
这相当于说,在一个封闭系统中,不存在一个循环过程,使得系统对外界做的功等于输入的热量。
这个等效表述被称为克劳修斯表述。
开尔文表述中,不可能制造一个只从一个热源吸热,然后完全转化为功的热机,而不对环境产生任何影响。
这相当于说,在一个封闭系统中,不存在一个循环过程,使得系统吸收的热量完全转化为功,不放出热量到冷热源。
02章热力学第一定律1
而自由膨胀就是对真空膨胀,外压为零,故 W=0 即自由膨胀过程中,系统对环境不做功。
(2).等外压膨胀(pe保持不变)
在外压保持不变的情况下,系统的体积从V1膨 胀到V2, W=-PedV , 积分,有: W=-Pe(V2-V1)
(3)多次等外压膨胀
(a)克服外压pe‘从体积为V1膨胀到V‘,作功: W1= - Pe‘ (V‘ - V1) (b)克服外压Pe“从V‘膨胀到V“,作功: W2= -Pe“(V“ - V‘) (c)克服外压P2从V“膨胀到V2,作功: W3= -P2(V2 - V“) 在这个过程中系统作的总功是所作的功 等于3次作功的加和。 W=W1+W2+W3
状态函数的基本性质:
* 状态函数的特性可描述为:异途同归, 值变相等;周而复始,数值还原。 **状态函数在数学上具有全微分的性质。 即二阶偏微分的值与微分的先后顺序 无关。
(3)状态方程
系统状态函数之间的定量关系式称为状态方 程(state equation )。
对于一定量的单组分均匀系统,状态函数 T,p,V 之间有一定量的联系。经验证明,只有两 个是独立的,它们的函数关系可表示为:
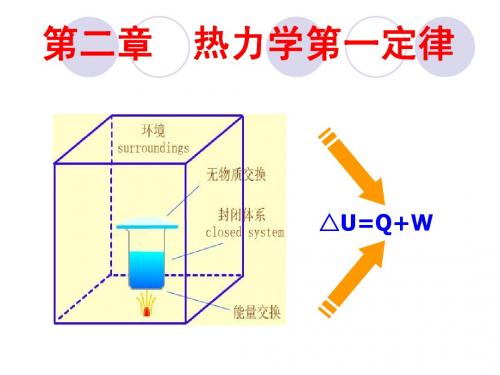
环境(surroundings)
与系统密切相关、有相互作用或影响所能及的 部分。
系统分类
根据系统与环境之间 的关系,把系统分为 三类:
(1)敞开系统(open
system) 系统与环境之间既 有物质交换,又有能 量交换。
(2)封闭系统(closed system)
系统与环境之间无物质交换,但有能量交换。
焦耳(Joule)和迈耶(Mayer)自1840年起, 历经20多年,用各种实验求证热和功的转 换关系,得到的结果是一致的。
02章 热力学第一定律

We' ,2 = − ∫ p e dV = − p1 (V1 − V2 )
V1 V2
We' ,3 = − p" (V " −V2 ) − p' (V ' −V " ) − p1 (V1 − V ' ) We' ,4 = − ∫ ( p i + dp )dV ≈ − ∫ p i dp = − nRT ln
V2 V2 V1 V1
V1 = −We ,4 V2
We ,4 = We' ,4
ΔU = Q + W
(W = We, Wf = 0)
一、等容过程(isochoric process) ΔV = 0
适用条件:封闭体系平衡态,不做非体积功的等容过程。 二、等压过程(isobaric process) p1 = p2 = pe
热力学概论
程
Su
n
2.3
热力学的一些基本概念 P67
一.系统(体系 System)与环境(surroundings) (1)定义: (2)体系的分类:① 敞开体系(open system)② 封闭体系(closed system) ③ 孤立体系(isolated system) 二.体系的性质(状态性质、热力学性质、热力学变量) 分类 广度性质(extensive properties) : 其数值与体系的物质的量成正比, 具加和性, 是 n 的一次齐函数。 如体积、 又称为容量性质, 质量、熵等。 强度性质(intensive properties) : 其数值取决于体系自身的特点,不具加和性,是 n 的零次齐函数。如温度、压力等。
热力学第一定律和第二定律

热力学第一定律和第二定律热力学第一定律1. 内容:一般情况下,如果物体跟外界同时发生做功和热传递的过程,那么外界对物体做的功W,与物体从外界吸收的热量Q之和,等于物体的内能的增加量2. 数学表达式:W+Q=ΔU(1)Q取决于温度变化:温度升高,Q>0;温度降低,Q<0.(2)W取决于体积变化:V增大时,气体对外做功,W<0;V减小时,外界对气体做功,W>0.(3)特例:如果气体向真空扩散,那么W=0.(4)绝热过程Q=0,关键词是“绝热材料”或“变化迅速”。
3. 热力学第1定律的理解(1)做功改变物体的内能:外界对物体做功,物体内能增加;物体对外做功,物体内能减少。
在绝热过程,物体做多少功,改变多少内能。
(2)热传递改变物体的内能:外界向物体传递热量,即物体吸热,物体的内能增加;物体向外界传递热量,即物体放热,物体的内能减少。
传递多少热量,内能就改变多少。
(3)做功和热传递的实质,做功改变内能是能量的变化,用功的数值来度量;热传递改变内能是能量的转移,用热量来度量。
热力学第二定律1.热传导的方向性:热传导的过程可以自发地由高温物体向低温物体进行,但相反方向却不能自发地进行,即热传导具有方向性,是一个不可逆过程。
2.补充说明:(1)“自发地”过程就是不受外界干扰的条件下进行的自然过程;(2)热量可以自发地从高温物体向低温物体传递,却不能自发的从低温物体传向高温物体;(2)热力学第二定律的能量守恒表达式:ds≥δQ/T(3)热量可以从低温物体传向高温物体,必须有“外界的影响或帮助”,就是要由外界对其做功才能完成。
3.热力学第二定律的两种表述(1)克劳修斯表述:热量不能自发地从低温物体传向高温物体。
(2)开尔文表述:不可能从单一热源吸收热量,使之完全变为有用功,而不引起其他变化。
02第二章 热一律2-1热力学第一定律的实质及表达式

吸热膨胀作功(参看图2-3c) 吸热膨胀作功 外界供给热量 –Q 膨胀功 –W 热力学能 –U2
排气过程中(参看图2-3d) 排气过程中 外界消耗排气功 外界获得推动功 排气后(参看图2-3a) 排气后 质量 m = 0 总能量 E2 = 0
开口系在一个工作周期中的能量进出情况
Q=Q ∆E = 0
1 2 2 w = ( p2 v2 − p1v1 ) + (c2 − c1 ) + g ( z 2 − z1 ) + wsh 2
(2-16)
总功(Wtot )、膨胀功(W )、技术功( W t )和轴功 (W sh )之间的区别和内在联系 膨胀功、技术功、轴功孰大孰小取决于 ( p 2 v2 − p1v1 ) 1 2 2 (c2 − c1 ) 、 g ( z 2 − z1 ) 的大小和正负。
二、热力学第一定律表达式
1、一般热力系能量方程
- 热力学第一定律基本表达式
热力系总能量(total stored energy of system)为E(图2-1a)。它是 热力学能(U)、宏观动能(EK)和重力位能(EP)的总和: 热力学能,内部储存能 热力学能,
E =U+Ek +Ep
宏观动能 总能 宏ቤተ መጻሕፍቲ ባይዱ位能 外部储存能
e =u+ek +ep
根据质量守恒定律可知:热力系质量的变化等于流进和流出 质量的差:
dm = δm1 − δm2
根据热力学第一定律可知:
热力系输出的能量的总和= 加入热力系的能量的总和 - 热力系输出的能量的总和=热力系总能量的增量
(δQ + e1δm1) (δW总 + e2δm2 ) = ( E + dE ) − E −
02 热力学第一定律

2–5 开口系统能量方程式
1 2 q h c f g z wi 2
1 2 微元 q dh dc f gdz wi 2
适用条件:任何流动工质、任何稳定流动过程 令 技术功
1 2 wt c g z wi 2
z1
CV
2
Wi
z2
能量守恒原则(热一律):
进入系统的能量 - 离开系统的能量 = 系统储存能量的增加
2–5 开口系统能量方程式
1 c f 1 , p1 , u1 , v1
Ein Eout ECV
进入: 离开:
Q
1
c f 2 , p2 , u2 , v2 2
dE1 p1dV1 Q dE2 p2dV2 Wi
第二章
实质
热力学第一定律
2-1 热力学第一定律的实质
能量守恒与转换定律在热力学中的应用。
两种表述
1 热是能的一种,机械能变热能,或热能变机械能的时候, 他们之间的比值是一定的。 2 热可以变为功,功也可以变为热;一定量的热消失时必 定产生相应量的功;消耗一定量的功时,必出现与之相应
量的热。
2-2 热力学能和总能
q 0, wt 0 h 0, h1 h2
绝热节流过程,前后 h 不变, 但 h 不是处处相等。 h1 h1
热力学解题思路总结
1、仔细审题,掌握已知条件,根据题意画出物理模型; 2、取好热力系统; 3、区分工质,根据工质性质的不同确定描述工质参数的方
法;
4、画热力学图,结合题意在热力学图上画出相应的状态点、
对推进功的说明
(1)与宏观流动有关,流动停止,推进功不存在;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
压缩机工作时,速率很快,来不及进行热交换
Q0
W U 2731J
3. 摩尔恒压热容与摩尔恒容热容的关系
C p ,m CV ,m
H m T U m T
T2 T1
U QV n CV ,mdT
2.4.2
应用——计算单纯pVT 过程的U 恒容过程:
U QV n CV ,mdT
T2 T1
非恒容过程: U QV n
T2
T1
CV ,mdT
(理想气体)
nCV ,m (T2 T1 )
2. 摩尔定压热容
C p ,m
•自由膨胀过程
∵pamb=0 • 恒容过程 dV=0 W=0 ∴W=0
热力学能U:系统内部储存的能量,是广度量的状态函数。
分子平动能 动能 分子转动能 系统总能量 势能 分子振动能 热力学能 分子间作用能 电子运动能 核运动能
符号规定: 若热力学能增加+,若热力学能减小U 的绝对值无法求,但U可求
T,p 2HCl(aq)+Zn(s) ZnCl 2 (aq)+H2 (g)
这是什么体系?界面在什么位置?
如果上述反应是在恒容、绝热,不透光、不导 电的容器中进行,它又是什么体系?
作业:以电解水为例确定界面使系统分别为隔离系统、 封闭系统、敞开系统
2. 状态与状态函数 (1)状态与状态函数 系统的性质:决定系统状态的物理量(如p,V,T,Cp,m)
系统的状态:热力学用系统所有的性质来描述它所处 的状态,当系统所有性质都有确定值时,则系统处于一 定的状态
状态函数:系统处于平衡态时的热力学性质(如U、H、 p、V、T 等)是系统状态的单质函数,故称为状态函数。 对单组分封闭体系,系统具有两个独立变量。
pV nRT F f ( x, y) U U ( p, T )
系统与环境 的相互作用 物质交换
传热
能量交换 作功 体积功 非体积功
三类系统: 隔离系统(isolated system): 封闭系统(closed system): 敞开系统(open system):
界面 真实或虚拟;界面确定对解决问题影响巨大 绝大部分是封闭系统
例题:容器中进行如下化学反应:
C p ,m CV ,m
( R / p)T (0 p) R T p R 2.4.9 C p CV nR
见第九章 近似计算 精确计算
理气单原子:C v,m 3 2 R 理气双原子:C v,m 5 2 R
对凝聚态物质
0
C p ,m CV ,m
Q C T2 T1
温度区间 温度点
真热容
Q C dT
热容的大小显然与系统所含物质的量和升温的条件 有关,所以有各种不同的热容。
1. 摩尔定容热容 CV ,m
C
单位:J mol 1 K 1
CV ,m
Q dT QV ,m QV 1 dU dT n d T n dT V
根据过程进行的特定条件
1) 恒温过程: 变化过程中T(系) = T(环) = 定值(dT=0) (T(始) = T(终),为等温过程)(ΔT=0) 2) 恒压过程: 变化过程中p(系) = p(环) = 定值(dp=0) (p(始)=p(终),为等压过程 )(Δp=0) 3) 恒容过程:体积功W = 0 4) 绝热过程: Q =0
功W :功也是途径函数 。
除热以外,系统和环境之间传递的一切能量。 符号规定:若系统从环境得功+,若系统对环境作功体积功 W
功 电 功 表面功 非体积功 W ' 电化学一章讨论 表面化学一章讨论
体积功的定义式:
W F dl pamb Adl pambdV
•恒(外)压过程 恒外压过程:W=-pamb(V2-V1) 恒压过程(pamb=p):W=-p(V2-V1)
(3)平衡态 当系统的诸性质不随时间而改变,则系统就处于热 力学平衡态,它包括下列几个平衡: 1) 热平衡 heat equilibrium:系统各部分T 相同; 2) 力平衡 force equilibrium:系统各部分p 相同; 3) 相平衡 phase equilibrium:物质在各相分布不随时间 变化; 4) 化学平衡chemical equilibrium:系统组成不随时间变 化.
解: 恒容过程 W=0
U (Ar,g)
373.15 273.15 373.15 273.15
n(CV ,m (Ar)dT n(C p ,m (Ar) R )dT
[4 (20.786 8.3145) (373.15 273.15)]J 4988.6J U (Cu,s)
H 3
CO(g),1/2O2(g)
CO2(g)
H 2
C(g),O2(g)
H1
H1 H 2 H 3 Q1 Q2 Q3
§2.4 摩尔热容
热容定义: 对于不发生相变和化学变化的均相封闭系统,不做 非膨胀功,热容的定义是:使系统升高单位温度所需的 热。根据温度变化范围分为平均热容和真热容。 平均热容
第二章
热力学第一定律
热力学是自然科学中建立最早的学科之一 1. 第一定律:能量守恒,解决过程的能量衡算问题 (功、热、热力学能等) 2. 第二定律:过程进行的方向判据 3. 第三定律:解决物质熵的计算
经典热力学 1 . 研究含有大量质点的宏观系统 2. 只考虑平衡问题
§2.1
基本概念和术语
1. 系统与环境 系统:作为研究对象的那部分物质 环境:系统以外与之相联系的那部分物质(与系统密切 相关、有相互作用或影响所能及的部分)
§2.3 恒容热、恒压热及焓
1. 恒容热(QV):
U Q W , 对于封闭系统,W = 0 的恒容过程
QV U QV dU 2.3.1a 2.3.1b
恒容热与过程的热力学能变在量值上相等
2. 恒压热(Qp)及焓:
U Q W , 对于封闭系统,W = 0 的恒压过程
单位:J dT Q p ,m Q p 1 dH dT ndT n dT p
T2 T1
H Q p n C p ,mdT
应用——计算单纯pVT 过程H 恒压过程:
T2
2.4.5
H Q p n C p ,mdT
373.15 273.15 373.15 273.15
nCV ,m (Cu)dT nC p ,m (Cu)dT
[2 24.435 (373.15 273.15)]J 4887.0J U U (Ar,g) U (Cu,s) 4988.6J+4887J=9875.6J=9.876kJ Q U W U 9.876kJ
H H (Ar,g) H (Cu,s)
T1
非恒压过程: H Q p n
T2
凝聚态物质
nC p,m (T2 T1 )
T1
C p ,mdT
(理想气体)
p48例2.4.1解:空气看成理气
U nCV ,m (T2 T1 ) nCV ,m T (2 25.29 54)J 2731J H nC p ,m T (2 33.60 54)J 3629J
V
C p ,m C v ,m
U m Vm
T
Vm p T
2.4.8
p
C p ,m CV ,m
对理想气体
U m Vm p T p V T
p
p
U m U m (T ,Vm )
dU m
U m T U m T
U m T p U m T p
U m (U m pVm ) U m T V T T p U m Vm p T V T p U m U m dT dVm T Vm Vm T U m Vm Vm T T p Vm U m Vm Vm T T p Vm
U 2 U1 Q p p(V2 V1 ) Q p U 2 pV2 (U1 pV1 )
定义焓:H U pV 2.3.4
焓为广延量的状态函数,单位 J
Q p H Q p H 2.3.5a 2.3.5b
恒压热与过程的焓能变在量值上相等
理想气体,单纯 pVT 变化,恒温时: U=0
3. 过程(process)与途径(path)
当系统和环境间发生物质或能量交换时,系统的性质 随之发生变化,此时完成一个过程。完成该过程具体步骤 称为途径。 按照系统变化前后的状态差异分类 单纯pVT 变化
相变过程,如气化,凝固,晶型转变…… 化学变化过程 g
状态函数是状态的单值函数
dZ 0
途径1
B
途径2
A
Z
途径1
dZ
途径2
dZ Z B Z A
状态函数数学上叫全微分函数
V f (T , p)
V dT V dp dV p T p T
(2)状态函数的分类 状态函数 广度量:具有加和性(如V、m、U…) 强度量:没有加和性(如p、T、 … )
U f (T ,V ) U U dU dT V dV T V T
