江南大学高等数学第一章测试题(答案)
高等数学课后习题答案--第一章
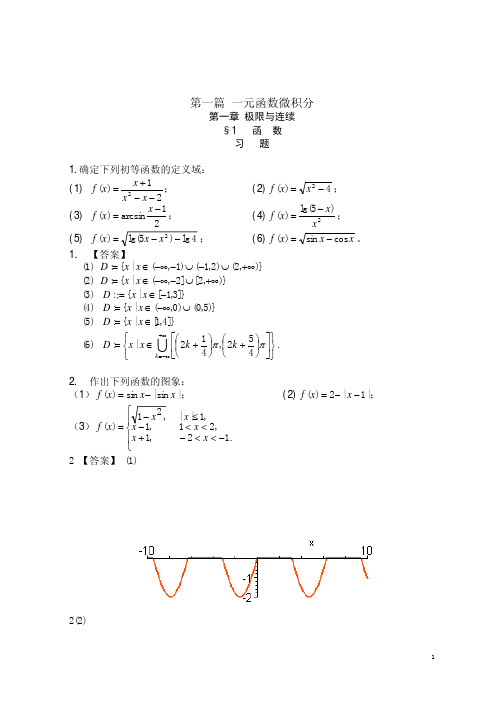
《高等数学》习题参考资料第一篇 一元函数微积分第一章 极限与连续§1 函 数习 题1.确定下列初等函数的定义域：(1) 21)(2−−+=x x x x f ；(2)4)(2−=x x f ；(3) 21arcsin )(−=x x f ；(4)2)5lg()(x x x f −=；(5) 4lg )5lg()(2−−=x x x f ；(6)x x x f cos sin )(−=。
1． 【答案】(1) )},2()2,1()1,(|{:+∞∪−∪−−∞∈=x x D (2) )},2[]2,(|{:+∞∪−−∞∈=x x D (3) ]}3,1[|{:;−∈=x x D (4) )}5,0()0,(|{:∪−∞∈=x x D (5) ]}4,1[|{:∈=x x D (6)+ +∈=+∞−∞=U k k k x x D ππ452,412|:.2. 作出下列函数的图象：（1）|sin |sin )(x x x f −=；(2)|1|2)(−−=x x f ；（3）+−−=,1,1,21)(x x x x f .12,21,1||−<<−<<≤x x x 2 【答案】 (1)2(2)2 (3)3.判断下列函数的奇偶性：（1）x x x f ++−=11)(；（2）xxx f x x +−+−=11lg110110)(；（3）x x a a x f x x sin )(++=−；（4）)1lg()(2x x x f ++=。
3. 【答案】 (1) 偶函数; (2) 偶函数; (3) 偶函数; (4) 奇函数 .4.证明:两个奇函数的乘积是偶函数;一个奇函数与一个偶函数的乘积是奇函数。
4． 【答案】 设)(x f ,)(x h 是奇函数, )(x g 是偶函数,)()()(x h x f x f =,)()()(x g x f x G =, 于是)()()(x h x f x F −−=−))())(((x h x f −−=)()()(x F x h x f ==, 因此)(x F 是偶函数.)()()(x g x f x G −−=−)()(x g x f −=)(x G −=, 因此)(x G 是奇函数.5．设函数f 满足：D （f ）关于原点对称，且()xc x bf x af =+1)(，其中a ,b ,c 都是常数，||||b a ≠,试证明f 是奇函数。
高等数学第一章总习题及答案
7. 已知 lim
x →0
f ( x) ) sin x = 3 , 求 lim f ( x) . x →0 x 2 2x − 1
解
因为 lim(2 − 1) = 0 , lim
x →0
x
ln(1 +
x →0
f ( x) ) sin x = 3 , 故必有 lim ln(1 + f ( x) ) = 0 , x →0 sin x 2x − 1
2
2
x
1 1 . = ( )2 = 2 2
1
(4) (5) (6)
lim
x →0
1 x sin x 1 = lim 2 2 = . x →0 2 x
1
x
lim(1 + 3tan 2 x)cot
x →0
= [lim(1 + 3tan 2 x) 3tan x ]3 = e3 .
2
x →0
设 k 为任一个大于 2c 的自然数, 则当 n > k 时,
0 < x ≤ e, 在 x = e 处, lim+ f ( x) = ln e = 1 , lim− f ( x) = 1 , x →e x →e x > e,
故 f ( x) 在 x = e 处连续, 故函数连续区间为 (0, + ∞) .
9.
⎧ cos x , x ≥ 0, ⎪ ⎪x + 2 设 f ( x) = ⎨ 要使 f ( x) 在 (−∞, + ∞) 内连续, 应如何选择 ⎪ a − a − x , x < 0, ⎪ x ⎩
n →∞ n →∞
(B) 无界数列必定发散; (D) 单调数列必有极限.
yn . xn
高等数学一考试题及答案
高等数学一考试题及答案一、单项选择题（每题2分，共10题）1. 极限的定义中，当x趋近于a时，函数f(x)的极限为L，意味着：A. 对于任意的正数ε，存在正数δ，使得当0<|x-a|<δ时，|f(x)-L|<εB. 对于任意的正数ε，存在正数δ，使得当|x-a|<δ时，|f(x)-L|<εC. 对于任意的正数ε，存在正数δ，使得当x≠a时，|f(x)-L|<εD. 对于任意的正数ε，存在正数δ，使得当x>a时，|f(x)-L|<ε答案：B2. 以下哪个函数是偶函数？A. f(x) = x^2 + xB. f(x) = x^3 - xC. f(x) = cos(x)D. f(x) = sin(x)答案：C3. 积分∫(0 to 1) x^2 dx的值是：A. 1/3B. 1/2C. 2/3D. 3/2答案：A4. 微分方程dy/dx = 2x的通解是：A. y = x^2 + CB. y = 2x^2 + CC. y = x + CD. y = 2x + C答案：A5. 以下哪个级数是收敛的？A. 1 + 1/2 + 1/4 + 1/8 + ...B. 1 - 1/2 + 1/3 - 1/4 + ...C. 1 + 2 + 3 + 4 + ...D. 1/2 + 1/4 + 1/8 + 1/16 + ... 答案：D6. 函数f(x) = e^x的导数是：A. e^xB. e^(-x)C. -e^xD. -e^(-x)答案：A7. 以下哪个函数在x=0处有极值？A. f(x) = x^3B. f(x) = x^2C. f(x) = sin(x)D. f(x) = e^x答案：B8. 以下哪个选项是二阶导数？A. f'(x)B. f''(x)C. f'''(x)D. f(x)答案：B9. 以下哪个函数是周期函数？A. f(x) = x^2B. f(x) = e^xC. f(x) = sin(x)D. f(x) = ln(x)答案：C10. 以下哪个函数是单调递增的？A. f(x) = -x^2B. f(x) = x^3C. f(x) = e^(-x)D. f(x) = ln(x)答案：B二、填空题（每题3分，共5题）1. 函数f(x) = x^3在x=1处的导数是______。
高等数学大一教材答案
高等数学大一教材答案1. 第一章：函数与极限1.1 函数的概念及性质1.2 极限的概念1.3 极限的运算法则2. 第二章：导数与微分2.1 导数的定义2.2 导数的几何意义2.3 微分的概念及运算法则3. 第三章：微分中值定理与导数的应用3.1 微分中值定理3.2 最值问题3.3 凹凸性与拐点4. 第四章：不定积分4.1 不定积分的概念4.2 基本积分表与积分法4.3 特殊曲线的面积5. 第五章：定积分5.1 定积分的定义5.2 区间上的连续函数的积分5.3 定积分的性质与计算方法6. 第六章：定积分的应用6.1 近似计算积分6.2 弧长与曲线面积的计算6.3 牛顿—莱布尼茨公式7. 第七章：多元函数的极限与连续7.1 二元函数的连续与偏导数7.2 多元函数的极限与连续7.3 多重积分8. 第八章：多元函数的微分法与隐函数的求导法8.1 多元函数的全微分8.2 隐函数的求导法8.3 多元函数的泰勒公式9. 第九章：向量代数与空间解析几何9.1 向量的概念与运算9.2 空间中的曲线与曲面9.3 平面与直线的方程10. 第十章：多元函数的导数与微分10.1 偏导数的概念10.2 高阶偏导数和混合偏导数10.3 多元函数的隐函数及其导数11. 第十一章：多元函数的极值与条件极值11.1 多元函数的极值11.2 多元函数的条件极值11.3 二重积分的计算12. 第十二章：曲线积分与曲面积分12.1 曲线积分12.2 曲面积分与高斯积分定理12.3 斯托克斯定理文章结束。
高等数学I本科类第阶段测试题
江南大学现代远程教育 第一阶段测试卷 考试科目:《高等数学》专升本 第一章至第三章（总分100分） 时间：90分钟__________学习中心（教学点） 批次： 层次： 专业： 学号： 身份证号： 姓名： 得分：一、选择题 (每题4分，共20分)1. 函数y = 的定义域是 ( A ). (a) (2,6)- (b) (2,6] (c)[2,6) (d)[2,6]- 2. 10lim(13)xx x →+ ( C) (a) e (b) 1 (c) 3e (d) ∞ 3.要使函数()f x x=在0x =处连续, 应给(0)f 补充定义的数值是( D ). (a) 1 (b)2(c)(d) 5 4. 设 sin 3x y -=, 则 y ' 等于 ( B ). (a)sin 3(ln 3)cos x x - (b) sin 3(ln 3)cos x x -- (c) sin 3cos x x -- (d) sin 3(ln 3)sin x x --5. 设函数 ()f x 在点 0x 处可导, 则 000(3)()lim h f x h f x h→+-等于 ( B ). (a) 03()f x '- (b) 03()f x ' (c) 02()f x '- (d) 02()f x '二.填空题(每题4分，共28分)6. 设 2(1)3f x x x -=++, 则 ()f x =__ x 2+3x+5 __.7. 2sin(2)lim 2x x x →-++=__1__. 8. 设 1,0,()5,0,1,0x x f x x x x -<⎧⎪==⎨⎪+>⎩, 则 0lim ()x f x +→=___1__.9. 设 ,0(),2,0x e x f x a x x -⎧≤=⎨+>⎩ 在点 0x = 处连续, 则常数 a =__0.5__ 10. 曲线 54y x -= 在点 (1,1) 处的法线方程为___y=（4/5）x+1/5__ 11. 由方程 2250xyx y e -+=确定隐函数 ()y y x =, 则 y '=__2xy 22e y +2y -2xy x （）___ 12. 设函数 2()ln(2)f x x x =, 则 (1)f ''=__3+2ln 2___三. 解答题(满分52分)13. 求 45lim()46x x x x →∞--. 答：14. 求01lim sin 3x x→. 答：15. 确定A 的值, 使函数 62cos ,0(),tan ,0sin 2x e x x f x Ax x x -⎧-≤⎪=⎨>⎪⎩在点 0x = 处连续。
大学高等数学试题一答案
《数学试题一》参考答案 一、填空题1、-32、z=(x ²+y ²)3、1ln y y yx dx x xdy -+4、21zye -5、x+y=06、2πR ²7、28、22π二、选择题1、D2、C3、B4、B5、C三、1、解：sin 1lim 1x xx y xy →∞→∞⎛⎫+ ⎪⎝⎭=1..sin 1lim 1xy x xxyx y xy →∞→∞⎛⎫+ ⎪⎝⎭=sin lim xyx y e→∞→∞=0e =12、解：令u=x+y ,D=xy //12..zf u f v f yf xu xv xδδδδδδδδδδ=+=+2//12///122().z f yf x y yf f f y yyδδδδδδδδ=+∂=++其中 /////11112f fx fyδδ=+ /////22122f f x f yδδ=+所以 2///////////////1112221221112222()()zf xf f y f xf f x y f xyf f x yδδ=++++=++++∂四、 解：所求直线的方向向量10443152i j S i j k k⎛⎫ ⎪=-=--- ⎪ ⎪ ⎪-⎝⎭即方向向量(4,3,1)S =---所求直线方程为325431x y z +--==---五、1、解：令2222222x 1x y x y y +=--+=得 ①即在XOY 面上的投影为22x 1y +=由题知P=X Q= -Y R=Z 由高斯公式得xdydz ydzdx zdxdy-+∑⎰⎰22215(111)6dv dv d d dz ρπρπθρρ-ΩΩ=-+===⎰⎰⎰⎰⎰⎰⎰⎰⎰曲面积分为56π。
2、解：连接OA 补全图形，由题知：sin 2xP e y x y=--c o s xQ e y x=-则cos 1xQe y x∂=-∂ c o s 2xPe y y∂=-∂ 由格林公式得(s i n2)(c o s )()2xxLDDQP e y x y dx e y x dy dxdy dxdy x yπ∂∂--+-=-==∂∂⎰⎰⎰⎰⎰ 对AO 段202(sin 2)(cos )(2)222x xLLxdx xdx e y x y dx e y x dy ππ-=-=---+-=--=+⎰⎰⎰所以六、1、解：由111lim1,R=1n n n n nxn∞-→∞=+=±∑得收敛半径R=1,当时幂级数均发散因此：11S x S x 0x n n nx∞-=→∑收敛域为I=(-1,1),设和函数为（）即（）=两边从积分x1221111()(1.............)x (1,1)1............1-xxn nxnnnn n n s x dx nxdx xxx x x x x x x ∞∞∞-=-=====+++++∈-=+++++∑∑∑⎰⎰当时()x21()11x s x dx x xx =--⎰所以两边对求导数得s(x)=所以和函数()21()1s x x =-(1,1)x ∈-122111111111122248489114nn n n n n n n n -∞∞∞+===⎛⎫⎛⎫===⨯=⎪ ⎪⎝⎭⎝⎭⎛⎫- ⎪⎝⎭∑∑∑2、解：2()ln(32)ln(1)ln(2)ln(1)ln(1)ln 22x f x x x x x x =++=+++=++++得(]1(1)ln(1),1,11nn n x xx n ∞+=-+=∈-+∑[]11(1)1ln(1)ln(1),2,22122n nn n x x x x n +∞+=-⎛⎫+==+∈- ⎪+⎝⎭∑(]11111(1)11(1)()ln(1)ln 2(1)ln 2,1,11221nnn n n n n n f x xx xx n n ∞∞++++==--=+++=++∈-++∑∑七、解：作拉格朗日函数 M λ、为参数 2L(,,)(1)()x y z x y z z M x y λ=+++-++则22120,120,10,x ,1,1x y z L ux L uy L y x y λλ=+==+==+===-+=得又，111,,m in 122222x y ==±=-所以由题知，最值一定存在，且在极值点取得，则max=1+八、证明：12n 1111,lim ,(......)n n n n n n n n n n n u u s s s s u u u u s u ∞∞∞∞→∞====∴=∴+++=∑∑∑∑ 绝对收敛收敛，设部分和为则是个常数收敛。
高等数学Ⅱ(专科类)第1阶段江南大学练习题答案 共三个阶段,这是其中一个阶段,答案在最后。
解析过程：
二 填空题 (共7题 ，总分值28分 )
6. 答案：
解析过程：
7. 答案：
解析过程：
8. 答案：
解析过程：
9. 答案：
解析过程：
10. 答案： ,
解析过程：
11. 答案：1,1
解析过程：
12. 答案：1
解析过程：
三 简答题 (共7题 ，总分值57分 )
13. 答案：
解析过程：
1. （3 分）
A.低阶无穷小量
B.等价无穷小量
C.高阶无穷小量
D.同阶但不等价无穷小量
2. （3 分）
A.
B.
C.
D.
3. =（ ） （3 分）
A.
B. 1
C.
D.
4. （3 分）
A.
B.
C. 1
D.
5. （3 分）
A.Biblioteka B.C.D.二 填空题 (共7题 ，总分值28分 )
6. _________ （4 分）
14. （8 分）
15. （8 分）
16. （9 分）
17. （8 分）
18. （8 分）
19. （8 分）
一 单选题 (共5题 ，总分值15分 ，下列选项中有且仅有一个选项符合题目要求，请在答题卡上正确填涂。)
1. 答案：C
解析过程：
2. 答案：A
解析过程：
3. 答案：C
解析过程：
4. 答案：A
解析过程：
14. 答案：
解析过程：
15. 答案：
解析过程：
16. 答案：
解析过程：
17. 答案：
解析过程：
18. 答案：
高等数学1试题(附答案解析)
高等数学1试题(附答案解析)work Information Technology Company.2020YEAR一、填空题（共6小题，每小题3分，共18分）1． 由曲线2cos r θ=所围成的图形的面积是π。
2． 设由方程22x y =所确定的隐函数为)(x y y =，则2y dy dx x=-。
3． 函数2sin y x =的带佩亚诺余项的四阶麦克劳林公式为2441()3x x o x -+。
4．11dx =⎰。
5． 函数x x y cos 2+=在区间⎥⎦⎤⎢⎣⎡20π，上的最大值为6π+。
6． 222222lim 12n nn n n n n n →∞⎛⎫+++⎪+++⎝⎭=4π。
二、选择题（共7小题，每小题3分，共21分）1. 设21cos sin ,0()1,0x x x f x x x x ⎧+<⎪=⎨⎪+≥⎩，则0x =是()f x 的 D 。
A ．可去间断点 B ．跳跃间断点 C ．振荡间断点 D ．连续点2. 设()232x x f x =+-，则当0x →时，下列结论正确的是 B 。
A ．是等价无穷小与x x f )(B ．同阶但非等价无穷小与x x f )(C ．高阶的无穷小是比x x f )(D ．低阶的无穷小是比x x f )( 3.+∞ C 。
A ．不存在B ．0C ．2πD ．π4. 设()f x 具有二阶连续导数，且(0)0f '=，0lim ()1x f x →''=-，则下列叙述正确的是 A 。
A ．(0)f 是()f x 的极大值B ．(0)f 是()f x 的极小值C ．(0)f 不是()f x 的极值D ．(0)f 是()f x 的最小值5.曲线2xy d t π-=⎰的全长为 D 。
A ．1B ．2C ．3D ．46. 当,a b 为何值时，点( 1, 3 )为曲线32y ax bx =+的拐点 A 。
A ．32a =-，92b = B. 32a =，92b =- C ．32a =-，92b =- D. 32a =，92b = 7. 曲线2xy x -=⋅的凸区间为 D 。
《高等数学(一)》练习题参考答案
《高等数学（一）》练习题一参考答案一、是非题1——5对 错 对 错 错 2——6对 对 对 对 错 11——15错 对 对 错 对 16——20 错 对 错 错 错 21——25错 对 错 对 错 26——30 对 对 对 错 错二、选择题1——5 A B B B D 6——10 C A B A B 11——15 B D D D A 16——20 B B A B B 21——25 D B D B B 三、填空题1、2x； 2、充分； 3、1； 4、0； 5、2y x =-622x e --； 7、必要； 8、12-； 9、)1(21+=x y ； 10、0,1,2y x ==-11、1； 12、21dx x+； 13、2； 14、32y x =-； 15、充分性条件.16、22xxe； 17、dx ； 18、x = 19、1(1)2y x =-； 20、216x x+.21、6e -； 22、1y =； 23、11e --； 24、23； 25、cos 2x dx .三、解答题1、00021limlimlim.4x x x x→→→===2、因为函数()f x 在点0x =连续，故其左右极限都应存在且相等，即由20lim ()lim (1)2xx x f x e--→→=+=，sin 22sin 22lim ()lim lim 2x x x x x f x ax axa+++→→→===，推得 221a a=⇒=. 3、 /////2312()1,()(1)2f x f x f xx=+=-⇒=-.4、因为(2)3f '=，而由定义可知2()(2)(2)lim2x f x f f x →-'=-，故所求极限2()(2)lim32x f x f x →-=-。
5、由243lim ()21x x ax b x →+∞+++=-，而2224343()(1)lim ()lim11(4)()3lim21x x x x x ax b x ax b x x a x b a x b x →+∞→+∞→+∞++++-++=--++--+==-存在，于是必有40,2a b a +=-=，可解得常数,a b 的值分别为-4，-2。
高数测试卷一及答案(第一章)
高数第一章测试一、选择题（每题5分）1、当x →0时，下列函数哪一个是其他三个的高阶无穷小（ ）A ．x 2 B. 1-cos x C. x - tan x D. ln(1+x 2)答案：C;211cos ~2x x -，22ln(1)~x x +， 222222000011tan cos 11sin 1cos lim lim lim lim 022cos 2cos x x x x x x x x x x x x x x x→→→→---===-=， ∴该选（C ）2、设当x →0时，(1-cos x )ln(1+x 2)是比x sin x n 高阶的无穷小，而x sin x n 是比（2x e ）高阶的无穷小，则正整数n 为（）A.1B.2C.3D.4答案：B ；因为当0x →时，224121(1cos )ln(1)sin ,(1)2n n x x x x x x x e x +-+-，，所以214n <+<满足题设条件的2n =。
故选B 。
3、设232)(-+=x x x f ,则当x →0时（） A. )(x f 与x 是等价无穷小量 B. )(x f 与x 是同阶但非等价无穷小量C. )(x f 与比x 较高阶的无穷小量D. )(x f 与比x 较低阶的无穷小量 答案：B ；【解法1】ln 22ln32121ln 2(ln 2)2!131ln 3(ln 3)2!()232(ln 2ln 3)()x x x x x x e x x e x x f x x x ο==+++ ==+++∴=+-=++ 故0x →时()f x 与x 是同阶但非等价无穷小量。
【解法2】 000()2322ln 23ln 3lim lim lim ln 2ln 31x x x x x x x f x x x →→→+-+===+ ∴0x →时()f x 与x 是同阶但非等价无穷小量。
4、下列极限存在的是（） A.x x x x 1arctan sin lim 0→ B. x x x x 1arctan sin lim 0→ C. x x x x 1arctan sin lim 0→ D. x x x x 1arctan sin lim 0→答案：A;因为00sin sin 11lim arctan (1)()lim arctan 12222x x x x x x x x ππππ-→→=--==⨯=＋，。
高等数学第一章参考答案（精华）
第一章参考答案习题1.11.（1）证：对0，（要使得33110nn ，考虑到311n n，只要1n，即1n）取1=[]+1N ，则当n N 时，有310n，故31lim0nn。
（2）证：2121131393n n n n，对0，（要使得212313n n ，只要1n 即可，即1n）取1=[]+1N ，则当nN 时，有212313n n ，故212lim313nn n 。
（3）证：0，（要使得22sin 10n nn，由于211nn ，只要1n，即1n）取1=[]+1N ，则当nN 时，有2sin 0n n ，则2sin lim0nn n。
（4）证：1111n nn n n故对0，（要使1n n，只要1n ，即21n）取21=[]+1N ，则当n N 时，有10n n，则lim 10nn n （）。
2.证明:对实数a 、b ，0,ab a b证“”ab ，则0a b，故0a b，即a b再证“”假设a b ，不妨令a b ，取0=2a b ，由条件可知=2a ba b，即112，矛盾。
3. 证明:“”，{}n a 收敛于a ，0，N ，当nN 时，na a，即naa a，nN 时，(,)n a U a ，故(,)U a之外最多只含数列n a 的前N 项。
“”，若对0，(,)U a 之外只含数列n a 的有限项，不妨设为120,,...,m k k k a a a ，取|精. |品. |可. |编. |辑. |学. |习. |资. |料. * | * | * | * | |欢. |迎. |下. |载.12max{,,...,}m Nk k k ，则当nN 时，na (,)U a ，即na a{}n a 收敛于a 。
4.证：lim nna a ，则对0,故N ，当nN 时，n a a（由于a ba b ），故此时nna aa alim nna a 。
该命题的逆命题不成立，例如数列{(1)}n，令(1)nna ，则有lim 1nn a ，而lim n n a 不存在。
高数(一)试题(1)参考答案
高等数学（一）（第一章和第二章练习题）参考答案 一、单项选择题（本大题共5小题，每小题2分，共10分） 1.设f （1-cos x ）=sin 2x, 则f （x ）=（ A ） A.x 2+2x B.x 2-2x C.-x 2+2x D.-x 2-2x解：设：1cos x t -= c o s1x t ∴=+ ()()()21c o s 1c o s 1c o s 1c o s f x x x x -=-=+- ()()2112ft t t t t ∴=++=+ ()22f x x x =+ 2.设x 22)x (,x )x (f =ϕ=，则=ϕ)]x ([f （ D ） A.2x 2B.x2xC.x 2xD.22x解：()2f t t = ()()22[()]222xx xf x f ϕ===3．函数y=31x1ln -的定义域是（ D ） A ．),0()0,(+∞⋃-∞ B ．),1()0,(+∞⋃-∞ C ．(0,1] D ．(0,1)解：110x -> 10x x-> 01x ∴<< ()0,1x ∴∈ 4．设f(x)=⎩⎨⎧>≤0x ,x 0x ,x ，则f(x)在点x=0处（ D ）A ．无定义B ．无极限C ．不连续D ．连续解：()00f = ()0lim lim 0x x f x x --→→== ()0lim lim 0x x f x ++→→==()0l i m 0x f x →∴= ()()0l i m 0x fx f →= 0x ∴=处连续5.函数2x x y -=的定义域是（ D ） A.[)+∞,1B.(]0,∞-C.(][)+∞∞-,10,D.[0，1]解：20x x -≥ ()10x x ∴-≥ []0,1x ∴∈ 6.∑∞==1n n)23ln (（ ） A.23ln 3ln - B. 3ln 23ln - C. 3ln 21-D. 3ln 2)3(ln n-解：此为等比级数，1ln 32a =ln 32q =11l n 3l n 3l n 32()212ln 312n n a q ∞====---∑ 7.设函数=-=)x 2(f 1x x)x 1(f ，则（ A ）A.x211- B.x 12- C.x2)1x (2- D.x)1x (2- 解：设1t x= 1x t ∴= ()11111t f t t t∴==-- ()1212f x x ∴=-8.已知f(x)=ax+b,且f(-1)=2,f(1)=-2,则f(x)=（ ） A.x+3 B.x-3 C.2xD.-2x解：()()12;12f a b f a b -=-+==+=- 2;0a b ∴=-= ()2f x x∴=- 9.lim()1xx x x →∞=+（ B ） A.eB.e -1C.∞D.1解：111lim()lim 111xxx x x e x e x -→∞→∞⎛⎫ ⎪=== ⎪+ ⎪+⎝⎭ 10.函数)1x )(2x (3x y -+-=的连续区间是（ D ）A.),1()2,(+∞---∞B.),1()1,(+∞---∞C.),1()1,2()2,(+∞-----∞D.[)+∞,3解：()()30210x x x -≥⎧⎪⎨+-≠⎪⎩3x ∴≥ [)3,x ∴∈+∞11.设函数⎩⎨⎧-=-≠++=1x a 1x )1x ln()1x ()x (f 2 ， ， 在x=-1连续,则a=（ D ）A.1B.-1C.2D.0解：1x =- 处连续， ()()11lim x f f x →-∴-=()()()()()211112122ln 11lim 1ln 1limlim2lim 101111x x x x x x a x x x x x →-→-→-→-⋅++∴=++===-+=-++12.设f(x+1)=x 2-3x+2，则f(x)=（ B ） A.x 2-6x+5 B.x 2-5x+6 C.x 2-5x+2 D.x 2-x 解：设1x t += 1x t =- ()()()22131256f t t t t t =---+=-+ ()256f x x x =-+13．已知f(x)的定义域是[0,3a]，则f(x+a)+f(x-a)的定义域是（ ） A ．[a,3a] B ．[a,2a] C ．[-a,4a]D ．[0,2a]解：0303x a a x a a ≤+≤⎧⎨≤-≤⎩ 324a x aa x a-≤≤⎧∴⎨≤≤⎩ 2a x a ≤≤ [],2x a a ∴∈14．=→xsin x 1sinx lim20x （ D ）A ．1B ．∞C ．不存在D ．0解：0,sin x x x →∴ 原式= 2001sin1limlim sin 0x x x x x x x→→==15．函数y=ln(22x 1x 1--+)的定义域是（ C ） A ．|x|≤1 B ．|x|<1 C ．0<|x|≤1D ．0<|x|<1解：2010x >-≥⎪⎩ 011x x ≠⎧∴⎨-≤≤⎩ 01x ∴<≤16．0x lim →x 2sin2x1=（ A ）A ．0B ．1C ．-1D ．不存在解：0x lim →x 2sin 2x 1=017.函数y=1-cosx 的值域是（ C ） A.[-1,1] B.[0,1] C.[0,2]D.(-∞,+∞)解：cos 1,110x y ==-=；()cos 1,112x y =-=--= 02y ≤≤ []0,2y ∴∈ 18.设2a 0π<<，则=→x x sin lim a x （ D ）A.0B.1C.不存在D.aasin 解：=→x x sin lima x sin aa19.下列各式中，正确的是（ D ）A.e )x 11(lim x 0x =++→B.e )x 1(lim x 10x =-→ C.e )x11(lim x x -=-∞→D.1x x e )x11(lim -∞→=-解：()1111lim(1)lim 1x x x x e x x -⋅--→∞→∞⎛⎫-=-= ⎪⎝⎭20．设函数f(x-1)=x 2-x,则f(x)=（ B ） A ．x(x-1) B ．x(x+1) C ．(x-1)2-(x-1) D ．(x+1)(x-2)解：设1x t -= 1x t =+ ()()()()22111f t t t tt t t ∴=+-+=+=+()()1fx x x =+21．设f(x)=ln4,则0x lim →∆=∆-∆+x)x (f )x x (f （ C ）A ．4B ．41C ．0D ．∞解：0x lim→∆=∆-∆+x )x (f )x x (f 0ln 4ln 4lim0x x∆→-=∆ 22.设函数f (x )的定义域为[0，4]，则函数f (x 2)的定义域为（ D ） A.[0，2] B.[0，16] C.[-16，16]D.[-2，2]解：204x ≤≤ 24x ≤ 22x -≤≤ []2,2x ∴∈-23.xx x 1lim→=（ C ）A.0B.1C.-1D.不存在解：11limlim 1x x x xx x→→== 24.设f(t)=t 2+1，则f(t 2+1)=（ D ） A.t 2+1 B.t 4+2 C.t 4+t 2+1 D. t 4+2t 2+2解：()21f x x =+ ()()2224211122ft t t t ∴+=++=++25.数列0，31，42，53，64，…的极限是（ ） A.0 B.n2n - C.1 D.不存在解：11n n x n -=+ 111l i m l i m l i m1111n n n n n n x n n→∞→∞→∞--∴===++ 26．设1)1(3-=-x x f ，则f (x )=（ B ）A ．x x x 2223++B ．x x x 3323++C ．12223+++x x xD ．13323+++x x x解；设1x t -= 1x t =+ ()()3321133f x t t t t ∴=+-=++()3233f x x x x ∴=++ 27．下列极限存在的是（ D ） A ．11lim-→xx eB ．xx e 1lim → C ．x x sin lim ∞→D ．221limx x x -∞→解：2221limlim 1111x x x x x →∞→∞==--- 28.下列区间中,函数f (x)= ln (5x+1)为有界的区间是（ C ）A.(-1，51)B.(-51,5)C.(0,51)D.(51,+∞)解：()0,ln1x f x ==；()1,ln 25x f x ==； ()ln1ln 2f x ≤≤ 29.设函数g (x)在x = a 连续而f (x) = (x-a)g(x),则'f (a) =（ D ） A.０ B.g '(a) C.f (a)D.g (a)解：()()()()()()()()f x x a g x x a g x g x x a g x ''''=-+-=+- ()()()()()f ag a a a g a g a''=+-= 30．设⎪⎩⎪⎨⎧=≠-+=0,00,11)(x x xx x f ,则x =0是f (x )的（ A ） A ．可去间断点 B ．跳跃间断点 C ．无穷间断点 D ．连续点解：()00f =()000111lim 2x x x x f x →→→→====()()0l i m 0x fx f →≠ 但极限存在，此为可去间断点31.函数f(x)=arcsin(2x-1)的定义域是（ D ） A.(-1,1) B.[-1,1] C.[-1,0] D.[0,1]解：1211x -≤-≤ 022x ∴≤≤ 01x ≤≤ []0,1x ∴∈ 32.设函数y =f (x )的定义域为(1，2)，则f (ax )(a <0)的定义域是( B )A.(a a 2,1)B.（a a 1,2) C.(a ，2a)D.(a a,2]解：12ax << 0a < 12x a a ∴>> 21,x a a ⎛⎫∴∈ ⎪⎝⎭33．函数f (x )=2211⎪⎭⎫⎝⎛--x 的定义域为（ B ）A ．[]1,1-B ．[]3,1-C ．(-1,1)D ．(-1,3)解：21102x -⎛⎫-≥ ⎪⎝⎭ 2112x -⎛⎫∴≤ ⎪⎝⎭1112x --≤≤ 212x -≤-≤ 13x -≤≤ []1,3x ∴∈-34．设函数f (x )=⎪⎩⎪⎨⎧≥+-<02302sin 2 x k x x x x x在x =0点连续，则k =（ C ）A ．0B ．1C ．2D ．3解：()0f k = ()00sin 2lim lim2x x xf x x→→== 0x = 处连续()()00lim x f f x →∴= 2k ∴=35.函数f (x )=21sin 2x x++是（ C ）A.奇函数B.偶函数C.有界函数D.周期函数解：1sin 1x -≤≤ 12s i n 3x ∴≤+≤ 22212s i n 303111x x x x +∴≤≤≤≤+++ 36．函数f (x )=ln x - ln(x -1)的定义域是（ C ） A ．(-1,+∞) B ．(0,+∞) C ．(1,+∞) D ．(0,1)解：010x x >⎧⎨->⎩ 1x ∴> ()1,x ∈+∞37．极限=→xxx 62tan lim0（ B ）A ．0B ．31C ．21D ．3解：0,tan 22x x x → 00tan 221limlim 663x x x x x x →→==二、填空题（本大题共10小题，每小题3分，共30分） 1．已知f (x +1)=x 2，则f (x )=________.解；设1x t += 1x t =- ()()21f t t ∴=- ()()21f x x ∴=-2．无穷级数 +++++n 31313112的和等于________.解：此为等比级数，111,3a q ==1211113113331213n a q +++++===-- 3.设函数f(x)的定义域是[-2，2]，则函数f(x+1)+f(x-1)的定义域是___________. 解：212212x x -≤-≤⎧⎨-≤+≤⎩ 1331x x -≤≤⎧∴⎨-≤≤⎩11x -≤≤ []1,1x ∴∈-4.=-++∞→]x ln )2x [ln(x lim x ___________.解：22lim [ln(2)ln ]lim ln lim ln 1x x x x x x x x x x x →+∞→+∞→+∞+⎛⎫⎛⎫+-==+⎪ ⎪⎝⎭⎝⎭22222lim ln 1lim ln 1ln 2xxx x e x x ⋅→+∞→+∞⎛⎫⎛⎫=+=+== ⎪ ⎪⎝⎭⎝⎭5．函数y=x ln ln 的定义域是 . 解：0ln 0x x >⎧⎨>⎩1x x >⎧⎨>⎩ 1x ∴> ()1,x ∴∈+∞ 6．nn 999.0lim ⋅⋅⋅∞→= . 解：1lim0.999lim 1110n n n n→∞→∞⎛⎫⋅⋅⋅=-= ⎪⎝⎭7．=∞→x21sinx 3lim x . 解：1110,0,sin 222x x x x →∴→∴ 113l i m 3s i n l i m 3222x x xx x x →∞→∞=⋅= 8.设⎩⎨⎧<-≥+=0x ,1x 0x ,1x )x (f ，则f (-1)= ___________.解：()1112f -=--=-9.=-+∞→)n 1n (n lim n ___________.解：n n =1l i l2n n n→∞====10.2x2xlim2x--→= ___________.解：()()()2222lim2x x xx xx→→→--==-2l i22x→=11.设函数1x2y+=，其反函数的定义域是________________.解：反函数的定义域是原函数的值域；而原函数的值域为0y≥其反函数的定义域是()0,+∞12.=--+∞→)nnn3n(limn________________.解：nn→∞=4l i l211 n n nn n+-=====+13.在一个极限过程中，变量u的极限为A的充分必要条件是u=A+α，其中α是极限过程中的________________.解：无穷小14．若f(x+1)=x+cosx则f(1)=__________.解：设11x+=0x=()10c o s01f=+=15．.__________1n5n)n1(lim233x=++-∞→解：()()33333323233331111(1)lim lim lim151515111n n nnn nnn nn nn nn n n→∞→∞→∞⎛⎫--⎪--⎝⎭====-++++++16．函数y=1+ln(x+2)的反函数是______.解：()1ln 2y x -=+ 12y x e -+= 12y x e-∴=- 反函数是12x y e -=-17. =∞→xxarctan limn _______.解：arctan 1limlim arctan 0x x x x xx →∞→∞=⋅=18.函数y=arcsin(x-3)的定义域为___________。
高等数学(专升本)第1阶段测试题
江南大学现代远程教育2011年上半年第一阶段测试卷 考试科目:《高等数学》专升本 第一章至第三章（总分100分） 时间：90分钟一、选择题 (每题4分)1. 函数y = 的定义域是 ( ). (a) (2,6)- (b) (2,6] (c)[2,6) (d)[2,6]- 2. 10lim(13)xx x →+ (a) e (b) 1 (c) 3e (d) ∞3.要使函数()f x =在0x =处连续, 应给(0)f 补充定义的数值是( ). (a) 1 (b) 2(c)(d) 4. 设 sin 3x y -=, 则 y ' 等于 ( ). (a)sin 3(ln3)cos x x - (b) sin 3(ln3)cos x x -- (c) sin 3cos x x -- (d) sin 3(ln3)sin x x -- 5. 设函数 ()f x 在点 0x 处可导, 则 000(3)()lim h f x h f x h→+-等于 ( ). (a) 03()f x '- (b) 03()f x ' (c) 02()f x '- (d) 02()f x '二.填空题(每题4分)6. 设 2(1)3f x x x -=++, 则 ()f x =___________.7. 2sin(2)lim 2x x x →-++=_____. 8. 设 1,0,()5,0,1,0x x f x x x x -<⎧⎪==⎨⎪+>⎩, 则 0lim ()x f x +→=_______. 9. 设 ,0(),2,0x e x f x a x x -⎧≤=⎨+>⎩ 在点 0x = 处连续, 则常数 a =______10. 曲线 54y x -= 在点 (1,1) 处的法线方程为_______________11. 由方程 2250xy x y e -+=确定隐函数 ()y y x =, 则 y '=________12. 设函数 2()ln(2)f x x x =, 则 (1)f ''=________三. 解答题(满分52分)13. 求 45lim()46x x x x →∞--. 14. 求01sin 3x x→. 15. 确定A 的值, 使函数 62cos ,0(),tan ,0sin 2x e x x f x Ax x x-⎧-≤⎪=⎨>⎪⎩ 在点 0x = 处连续。
大学高等数学各章节练习题
第一章 极限与连续一、填空1、设11()01x f x x ⎧≤⎪=⎨>⎪⎩，则[]()___________.f f x =2、若数列{}n x 收敛，则数列{}n x 一定 。
3、若0lim ()x x f x A →=,而0lim ()x x g x →不存在,则0lim(()())x x f x g x →+ .4、当0→x 时，1132-+ax 与1cos -x 为等价无穷小,则_______=a5、设函数()f x 在点0x x =处连续，则()f x 在点0x x =处是否连续.6、设21))((,sin )(x x f x x f -==ϕ,则)(x ϕ的定义域为_________7、如果⎪⎩⎪⎨⎧=≠-+=0,00,12sin )(2x x xe x xf ax 在),(+∞-∞内连续，则__=a8、 曲线22x e x y -=的渐近方程为__________________二、选择9、如果)(),(x g x f 都在0x 点处间断，那么( ） （A))()(x g x f +在0x 点处间断 (B ）)()(x g x f -在0x 点处间断 （C))()(x g x f +在0x 点处连续 （D ）)()(x g x f +在0x 点处可能连续. 10、设数列n x 与n y 满足lim 0n n n x y →∞=,则下列断言正确的是( )（A ）若n x 发散，则n y 必发散. (B)若n x 无界，则n y 必有界 （C)若n x 有界，则n y 必为无穷小（D ）若1nx 为无穷小，则n y 必为无穷小。
11、已知0()lim0x f x x→=，且(0)1f =，那么（ ）（A)()f x 在0x =处不连续。
(B ）()f x 在0x =处连续。
（C ）0lim ()x f x →不存在。
（D ）0lim ()1x f x →=12、设2()43x x f x x x+=- ，则0lim ()x f x →为（ ）（A ）12 (B ）13 (C) 14 （D)不存在 13、设2(1)sin ()(1)x xf x x x-=-，那么0x =是函数的（ ） （A ）无穷间断点.（B ）第二类间断点。
大学高等数学第一册考试试题+答案
一、选择题（本大题共5小题，每题3分，共15分）1.设-∞=→)(lim 0x f x x ，-∞=→)(lim 0x g x x ，Ax h x x =→)(lim 0，则下列命题不正确的是( B )A. -∞=+→)]()([lim 0x g x f x x ; B. ∞=→)]()([lim 0x h x f x x ;C.-∞=+→)]()([lim 0x h x f x x ; D.+∞=→)]()([lim 0x g x f xx . 2. 若∞→n lim 2)51(++n n=( A )A.5e ; B. 4e ; C. 3e ; D. 2e . 3. 设0lim →x xf x f cos 1)0()(--=3,则在点x=0处 ( C )A. f(x)的导数存在,且)0('f ≠0;B. f(x)的导数不存在;C. f(x)取极小值;D. f(x)取极大值.4设xe 2-是f(x)的一个原函数,则⎰dx x xf )(= ( A )A.x e 2-(x+21)+c; B; x e 2- (1－x)+c; C. x e 2- (x －1)+c; D. －x e 2- (x+1)+c.5.⎰xadt t f )3('= ( D )A. 3[f(x)－f(a)] ;B. f(3x)－f(3a);C. 3[f(3x)－f(3a)] ;D. 31[f(3x)－f(3a)].二、填空题（本大题共7小题，每题3分，共21分）1. 若+∞→x lim (11223-+x x +αx+β)=1,则 α= －2 , β= 1 . .2. 设f(x)在x=a 处可导,则0lim →h hh a f h a f )3()(--+= 4)('a f .3. 设y=522)ln(e x a x +++,则dy. 4. 不定积分dx e xx⎰2=c e xx ++2ln 12 .5. 广义积分⎰-311dx x x = 2310. . 6. ⎰-++1121sin dx x xx x = 0 .7. 用定积分的定义计算：∞→n lim∑=+n i nin 1sin 31π=π2.三、计算题（本大题共7小题，每题7分，共49分）1. 设函数f(x)= ⎩⎨⎧>+≤+0012x b ax x e x 在点x=0可导，求a 与b 的值 .1. 解:f(x)在x=0可导⇒ f(x)在x=0连续⇒-→0lim x f(x)=f(0)= +→0lim x f(x)=b ⇒b=2,又)0('=f =-→0lim x xf x f )0()(-=-→0lim x x e x 12-=2)0('+f =+→0lim x x f x f )0()(-=+→0lim x x ax 22-+=a(因b=2),由已知有)0('=f =)0('+f ，故a=2,b=2 .2.求)1ln(x y +=的n 阶导数 .2.解：nn n x n y)1()!1()1(1)(+--=-3. 求由参数方程2ln(1)arctan x t y t t⎧=+⎨=-⎩ 所确定的隐函数y=y(x)的一阶,二阶导数dx dy ,22dx yd . 3.解： dx dy =2t, 22dx y d =214t t +4. 求0lim →x )sin 1ln(cos sin 1x x xx x +-+ .4.解：原式=0lim→x )cos sin 1(sin cos sin 12x x x x x xx x ++-+=210lim →x x xx sin +=1 5. 求⎰+dx x x )ln 31(1.5.解：原式=⎰++)ln 31()ln 31131x d x =…=c x ++ln 31ln 316. 求⎰-dx xa x 222（a>0）. 6.解：令t a x sin =原式=……=c x a ax a x a +--)(arcsin 222227. 求I=⎰21arcsin xdx .7.解：I=210]arcsin [x x ⎰--+21021)2(21dx xx =……….=12312-+π 四、应用题（5分） 摆线的一拱:)20(,)cos 1(2)sin (2π≤≤⎩⎨⎧-=-=t t y t t x 与直线y=0围成一平面图形, (1)求此平面图形的面积;(2)求此平面图形绕x 轴旋转而成的旋转体的体积.解：(1) S=⎰⋅220πydx =⎰--π20')]sin (2)[cos 1(2dt t t t =… =12π,(2) V x =π⎰⋅2202πdx y =⎰--π20'22)]sin ([)cos 1(dt t t a t a = (240)五、证明题（本大题共2小题，每题5分，共10分） (1) 利用函数图形的凹凸性证明不等式：),0,0(2ln)(ln ln y x y x yx y x y y x x ≠>>++>+. (1)证：令,0)(",ln )(>=t f t t x f 图形凹，由定义得证.(2) 设函数f(x)在[a,b]上连续,在(a,b)上可导,0<a<b,证明:必有二点ξ,η∈(a,b),使得ab )('ξf =)('2ηηf 成立 .(2) 证：结论变为 ab)('ξf =2'1)(ηηf , 设g(x)=x1, f(x),g(x)在[a,b]上满足柯西定理的条件,必存在一点η∈(a,b), 使得a b a f b f 11)()(--=2'1)(ηηf ,即ab a f b f --)()(ab=2η)(;ηf .又f(x)在[a,b]上满足拉氏定理的条件,必存在一点ξ∈(a,b), 使得 ab a f b f --)()(=)('ξf ,即ab )('ξf =2η)(;ηf ,得证.。
高等数学1~3阶段(专升本带答案)
江南大学现代远程教育2009年下半年第一阶段测试卷考试科目:《高等数学》专升本 第一章至第三章（总分100分） 时间：90分钟__________学习中心（教学点） 批次： 层次：专业： 学号： 身份证号： 姓名： 得分：一、选择题 (每题4分) 1. 函数y =的定义域是 ( a ).(a) (2,6)- (b) (2,6] (c)[2,6) (d)[2,6]-2. 1lim (13)x x x →+ ( c )(a) e (b) 1 (c) 3e (d) ∞3.要使函数()f x x=在0x =处连续, 应给(0)f 补充定义的数值是( d ).(a) 1 (b) 2(c) (d)54. 设 sin 3x y -=, 则 y ' 等于 ( b ). (a)sin 3(ln 3)cos xx - (b) sin 3(ln 3)cos xx -- (c) sin 3cos xx -- (d) sin 3(ln 3)sin xx --5. 设函数 ()f x 在点 0x 处可导, 则 000(3)()limh f x h f x h→+-等于 ( b ).(a) 03()f x '- (b) 03()f x ' (c) 02()f x '- (d) 02()f x ' 二.填空题(每题4分)6. 设 2(1)3f x x x -=++, 则 ()f x = 235x x ++ 7. 2sin(2)lim2x x x →-++=__1___.8. 设 1,0,()5,0,1,0x x f x x x x -<⎧⎪==⎨⎪+>⎩, 则 0lim ()x f x +→=___1___.9. 设 ,0(),2,x e x f x a x x -⎧≤=⎨+>⎩ 在点 0x = 处连续, 则常数 a =___1/2___10. 曲线 54y x-= 在点 (1,1) 处的法线方程为11. 由方程 2250xy x y e -+=确定隐函数 ()y y x =, 则 y '=222222xy xyey xyx xye--12. 设函数 2()ln(2)f x x x =, 则 (1)f ''=___2ln2+3_____三. 解答题(满分52分) 13. 求 45lim ()46xx x x →∞--.解：1(4x -6+6)xxx411111444x-664444x-54x-6+111lim ()=lim ()=lim (1+)=lim (1+)4x-64x-64x-64x-611 =lim (1+)+lim (1+)=e .1=e 4x-64x-6x x x x x x →∞→∞→∞→∞→∞→∞⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦14. 求1limsin 3x x→.解：利用等价无穷小2x =x 2S i n 3x 3x则1x 1lim=lim=sin 33x3x x x→→-15. 确定A 的值, 使函数 62cos ,0(),tan ,0sin 2x e x x f x A xx x -⎧-≤⎪=⎨>⎪⎩在点 0x = 处连续。