激光原理z
2024年度激光原理及应用PPT课件

激光的相干性比普通光 强很多,可用于精密测 量和全息照相等领域。
激光器组成及工作原理
激光器组成
激光器一般由工作物质、激励源和光学谐振腔三部分组成。
2024/3/24
工作原理
在激励源的作用下,工作物质中的电子被激发到高能级,形 成粒子数反转分布。当这些电子从高能级跃迁到低能级时, 会辐射出与激励源频率相同的光子,并在光学谐振腔内得到 放大和反馈,最终形成稳定的激光输出。
激光雷达
测距、成像、识别等多元化应 用
激光显示
高清晰度、大色域、节能环保
激光制造
高精度、高效率、无接触加工
2024/3/24
10
激光器类型及其特
03
点分析
2024/3/24
11
固体激光器
01
02
03
工作原理
通过激励固体增益介质( 如晶体、玻璃等)中的粒 子,实现粒子数反转并产 生激光。
2024/3/24
根据实际需要,还可选择佩戴耳塞、手套 等个人防护装备,以降低激光对其他部位 的危害。
2024/3/24
24
未来发展趋势预测
06
与挑战分析
2024/3/24
25
新型激光器研发方向探讨
2024/3/24
新型材料激光器
探索新型增益介质,如量子点、二维材料等,提高激光器的性能 。
微型化与集成化
发展微型激光器,实现与其他光电器件的集成,推动光电子集成技 术的发展。
1960年,美国物理学家 梅曼制造出第一台红宝 石激光器
现代激光技术突破与创新
光纤激光器
高功率、高效率、光束质量好
量子级联激光器
覆盖中红外到太赫兹波段
2024/3/24
激光原理-(9)-高斯光束

−
1 F
0
1
R2
=
AR1 CR1
+ +
B D
(遵循ABCD变换法则) NJUPT
高斯光束q参数的变换规律——ABCD公式
在自由空间的传播
束腰处:
=z 0,q(0=) if=
1 Z
自由空间变换矩阵: TL = 0
1
i πω02 λ
由ABCD法则: q(z=) if + z
11
iλ
z − if
高斯光束的聚焦
F 一定时,ω0′与 l′ 随 l 的变化情况
l
′
F 2(l − F ) = F + (F − l )2 + f 2 ,
ω ′2 0
F 2ω 2
= (F − l )2 0+ f 2
(1) l < F
ω0′随 l 的减小而减小
当 l = 0 时:ω0′(min) =
ω0 =l′
1 + ( f )2 F
i
πω
2 2
=( 1 R1
λ − i πω12 ) −
1 F
=
1 q1
−
1 F
结论:高斯光束q参数经薄透镜的变换规律满足ABCD法则
用q参数分析高斯光束经单透镜的传输过程
ω0
ω0′ ωc
A B l′
C
l
lC
q0
qA qB
qC
求:ωC、RC
方法一: z=0 处:q0 = i πω02 λ
A处: q=A q0 + l
ω ( z )
ω0,z
⇒
R(
z)
θ0
2. 任一 坐标 z处的光斑半径 ω (z)及等相面曲率半径 R(z)
激光原理_名词解释

激光原理_名词解释⼀名词解释1. 损耗系数及振荡条件:0)(m ≥-=ααS o I g I ,即α≥o g 。
α为包括放⼤器损耗和谐振腔损耗在内的平均损耗系数。
2. 线型函数:引⼊谱线的线型函数pv p v v )(),(g 0~=,线型函数的单位是S ,括号中的0v 表⽰线型函数的中⼼频率,且有+∞∞-=1),(g 0~v v ,并在0v 加减2v ?时下降⾄最⼤值的⼀半。
按上式定义的v ?称为谱线宽度。
3. 多普勒加宽:多普勒加宽是由于做热运动的发光原⼦所发出的辐射的多普勒频移所引起的加宽。
4. 纵模竞争效应:在均匀加宽激光器中,⼏个满⾜阈值条件的纵模在震荡过程中互相竞争,结果总是靠近中⼼频率0v 的⼀个纵模得胜,形成稳定振荡,其他纵模都被抑制⽽熄灭的现象。
5. 谐振腔的Q 值:⽆论是LC 振荡回路,还是光频谐振腔,都采⽤品质因数Q 值来标识腔的特性。
定义p v P w Q ξπξ2==。
ξ为储存在腔内的总能量,p 为单位时间内损耗的总能量。
v 为腔内电磁场的振荡频率。
6. 兰姆凹陷:单模输出功率P 与单模频率q v 的关系曲线,在单模频率等于0的时候有⼀凹陷,称作兰姆凹陷。
7. 锁模:⼀般⾮均匀加宽激光器如果不采取特殊的选模措施,总是得到多纵模输出,并且由于空间烧孔效应,均匀加宽激光器的输出也往往具有多个纵模,但如果使各个振荡的纵模模式的频率间隔保持⼀定,并具有确定的相位关系,则激光器输出的是⼀列时间间隔⼀定的超短脉冲。
这种使激光器获得更窄得脉冲技术称为锁模。
8. 光波模:在⾃由空间具有任意波⽮K 的单⾊平⾯波都可以存在,但在⼀个有边界条件限制的空间V 内,只能存在⼀系列独⽴的具有特定波⽮k 的平⾯单⾊驻波;这种能够存在腔内的驻波成为光波模。
9. 注⼊锁定:⽤⼀束弱的性能优良的激光注⼊⼀⾃由运转的激光器中,控制⼀个强激光器输出光束的光谱特性及空间特性的锁定现象。
(分为连续激光器的注⼊锁定和脉冲激光器的注⼊锁定)。
激光原理第二章习题解答

《激光原理》习题解答 第二章习题解答1 试利用往返矩阵证明共焦腔为稳定腔,即任意傍轴光线在其中可以往返无限次,而且两次往返即自行闭合.证明如下:(共焦腔的定义——两个反射镜的焦点重合的共轴球面腔为共焦腔。
共焦腔分为实共焦腔和虚共焦腔。
公共焦点在腔内的共焦腔是实共焦腔,反之是虚共焦腔。
两个反射镜曲率相等的共焦腔称为对称共焦腔,可以证明,对称共焦腔是实双凹腔。
) 根据以上一系列定义,我们取具对称共焦腔为例来证明。
设两个凹镜的曲率半径分别是1R 和2R ,腔长为L ,根据对称共焦腔特点可知:L R R R ===21因此,一次往返转换矩阵为⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+-⎪⎪⎭⎫⎝⎛--=⎥⎦⎤⎢⎣⎡=211121222121221221221R L R L R L R L R R R L L R L D C B A T 把条件L R R R ===21带入到转换矩阵T ,得到:⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=1001D C B A T 共轴球面腔的稳定判别式子()1211<+<-D A 如果()121-=+D A 或者()121=+D A ,则谐振腔是临界腔,是否是稳定腔要根据情况来定。
本题中 ,因此可以断定是介稳腔(临界腔),下面证明对称共焦腔在近轴光线条件下属于稳定腔。
经过两个往返的转换矩阵式2T ,⎥⎦⎤⎢⎣⎡=10012T 坐标转换公式为:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡1111112221001θθθθr r r T r 其中等式左边的坐标和角度为经过两次往返后的坐标,通过上边的式子可以看出,光线经过两次往返后回到光线的出发点,即形成了封闭,因此得到近轴光线经过两次往返形成闭合,对称共焦腔是稳定腔。
2 试求平凹、双凹、凹凸共轴球面腔的稳定条件。
解答如下:共轴球面腔的()21221222121R R L R L R L D A +--≡+,如果满足()1211<+<-D A ,则腔是稳定腔,反之为非稳腔,两者之间存在临界腔,临界腔是否是稳定腔,要具体分析。
激光原理第二章 激光器的工作原理
可以证明,在对称共焦腔内,任意傍轴光线可往返多次
而不横向逸出,而且经两次往返后即可自行闭合。
整个稳定球面腔的模式理论都可以建立在共焦腔振荡理 论的基础上,因此,对称共焦腔是最重要和最具有代表性的 一种稳定腔。
3.平行平面腔——由两个平面反射镜组成的共轴谐振腔
R1=R2=∞,g1=g2=1, g1 g2=1
图(2-2) 共轴球面腔的稳定图
➢凹凸稳定腔,由一个凹面镜和一个凸面镜组成,对应图中5区和6区。
➢ (g1>1,g2<1; g2>1,g1<1)
➢共焦腔,R1=R2=L,因而,g1=0,g2=0,对应图中的坐标原点。(特殊的稳定腔) ➢半共焦腔,由一个平面镜和一个R=2L的凹面镜组成的腔,对应图中E和F点g1=1,g2=1/2
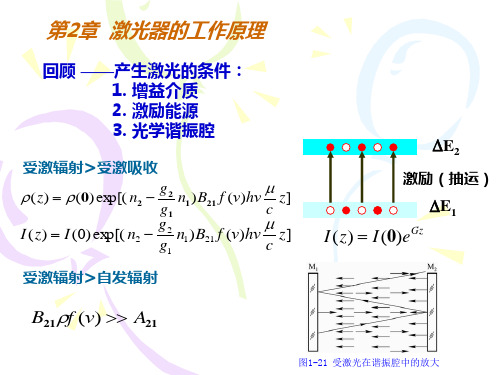
1. 工作物质 2. 激励能源
受激辐射>受激吸收
3. 光学谐振腔
受激辐射>自发辐射
是否只要具备激励能源和工作物质就一定可以实 现粒子数反转? 粒子数反转和什么因素有关?
速率方程方法: 量子理论的一种简化形式
——速率方程理论:把光频电磁场看成量子化的光子,把 物质体系描述成具有量子化能级的粒子体系。
(三)临界腔: g1 g2 = 0 , g1 g2= 1
临界腔属于一种极限情况,其稳定性视不同的腔而不同. 在谐振理论研究和实际应用中,临界腔具有非常重要的意义.
1.对称共焦腔——腔中心是两镜公共焦 点且:
R1=L
R2=L
R1= R2= R = L=2F F——二镜焦距
F
L
∵ g1 = g2 = 0 ∴ g1 g2 = 0
简化前提: 忽略量子化辐射场的位相特性及光子数的起伏特 性
优点: 形式特别简单, 且可给出激光的强度特性,并粗略描 述烧孔、兰姆凹陷、多模竞争等效应
第一章 激光的基本原理及其特性

1913年波尔提出了原子中电子运动状态量子化假设。
1917年爱因斯坦从光量子概念出发,重新推导了黑体
辐射的普朗克公式,在推导中提出了两个极为重要地概
念:受激辐射和自发辐射。
(第一章)
物理与电子工程学院
《激光原理与技术》
原子的能级
• 基态
激发态
电子只能处于分立的能级,电磁辐射与物质的相互作用将 导致物质中电子能级的变化,当吸收或辐射能量时,可在 特 定的能级间跃迁;该能量为这两个能级的能量差,并且 该能量差唯一地决定了电磁辐射的频率: ∆Ed t 0
受激跃迁几 率
(第一章)
物理与电子工程学院
《激光原理与技术》
受激吸收的特点
原子的受激吸收几率与外界辐射场的频率有关 原子的受激吸收几率与受激爱因斯坦系数有关 原子的受激吸收几率与外来光辐射能量密度有关
(第一章)
物理与电子工程学院
《激光原理与技术》
光的受激辐射
入射光
h E 2 E 1
(t ) N u 0 e 1 Au 1 1
N u 0e
t
u
u u
Au i
物理与电子工程学院
《激光原理与技术》
自发辐射的特点
原子的自发辐射与原子的本身性质有关,与外界 辐射场无关 自发辐射的随机性,自发辐射光的相位、偏振态 和传播方向杂乱无章
光源发出的光的单色性、定向性很差。没有确定 的偏振状态。
原子数按能级分布
热平衡时,单位体积内处于各个能级上的原子数分布
玻尔兹曼分布律:
N2 N1
e
( E 2 E1 ) kT
高 能 级 低 能 级
物理与电子工程学院
激光原理总结

激光原理总结⼀共四章§Chapter 1爱因斯坦系数/激光产⽣条件/激光结构/激光优点1. ⾃发辐射: 上能级粒⼦,⾃发地从E2能级跃迁到E1能级,并辐射出光⼦2. 受激辐射: 上能级粒⼦,遇到能量等于能级差的光⼦,在光⼦激励下,粒⼦从E2能级跃迁到E1能级,并辐射出⼀个与⼊射光⼦完全相同的光⼦3. 受激吸收: 下能级粒⼦,遇到能量等于能级差的光⼦,在光⼦激励下,粒⼦从E1能级跃迁到E2能级,并吸收⼀个⼊射光⼦三个爱因斯坦系数:dn21=A21n2dt(⾃发辐射)dn′21=B21n2ρv dt(受激辐射)dn12=B12n1ρv dt(受激吸收)三个爱因斯坦系数的关系:A21 B21=8πhν3 c3B12g1=B21g2粒⼦数反转分布状态:dn′21 dn12=g1n2g2n1>1受激辐射⼤于受激吸收,打破波尔兹曼分布。
此时可称“得到增益”。
⽽普通情况下,受激辐射/⾃发辐射较⼩(计算参看讲义)。
总结:产⽣激光的基本条件是“粒⼦数反转分布和增⼤⼀⽅向上的光能密度”激光器的基本结构:1. ⼯作物质:增益介质/粒⼦数反转/上能级为亚稳态2. 激励装置:能源/光/电3. 谐振腔:反馈/光强/模式三能级系统:亚稳态寿命长,阈值⾼,转换效率低。
如红宝⽯激光器四能级系统:阈值低,连续运转,⼤功率。
如He-Ne激光器的优点:1. 相⼲性好:受激辐射的光具有相⼲性,相⼲长度L c=λ2Δλ,相⼲时间τ=L cc2. ⽅向性好:谐振腔3. 单⾊性好4. 亮度⾼:受激辐射的光强⼤§Chapter 2稳定性/模式分析/⾼斯光束腔的分类参考Ch2-P1光腔的稳定性条件:傍轴模在腔内往返⽆限多次不逸出腔外,数学形式如下g 1=1−L R 1,g 2=1−L R 20≤g 1g 2≤1按照稳定性得到三种腔♥0<g 1g 2<1稳定腔♥g 1g 2=0org 1g 2=1临界腔♥g 1g 2<0org 1g 2>1⾮稳腔 ♥ ♥ ♥ ♥♥ ♥ bbx ♥ nnx 图解法判断腔的稳定条件Ch2-P2⽤上述条件判断各种腔的稳定性,注意曲率R 的⽅向"凹⾯向着腔内时(凹⾯镜),R >0;凸⾯向着腔内时(凸⾯镜),R <0"。
激光 原理

激光原理激光原理激光是一种具有高度单色性、高亮度和直线传播特性的电磁波。
它的产生是通过激发原子或分子中的电子,使其跃迁到高能级,然后从高能级回到低能级时放出光子。
这些光子具有相同的频率、相同的相位和相同的方向,形成了一束高度集中、方向性强的光束。
1. 激发原理激发原理是指将物质中的电子从低能级激发到高能级,使其处于激发态。
当电子从高能级回到低能级时,会放出一个光子。
这个过程称为自发辐射。
2. 反转粒子数密度反转粒子数密度是指在一个物质中,处于激发态的粒子数比处于基态的粒子数多。
只有在反转粒子数密度大于临界值时才能产生激光。
3. 共振腔共振腔是指由两个反射镜组成的空间,在其中放置了具有反转粒子数密度大于临界值的物质。
当一个光学泵浦器向物质注入能量时,会激发物质中的电子,使其处于激发态。
当这些电子从高能级回到低能级时,会放出光子,这些光子被反射镜反射回共振腔内部。
4. 激光输出当光子在共振腔内来回多次反射时,它们会与处于激发态的粒子相互作用,促使更多的粒子从高能级回到低能级。
这个过程称为受激辐射。
随着时间的推移,越来越多的粒子从高能级回到低能级,放出越来越多的光子。
最终,在一个反射镜上形成了一束高度集中、方向性强的光束。
5. 激光特性激光具有单色性、方向性和相干性等特性。
单色性是指激光只有一种频率;方向性是指激光具有非常好的直线传播特性;相干性是指激光具有非常好的波前相干性和时间相干性。
6. 应用领域激光广泛应用于科学研究、医疗、通信、制造业等领域。
例如,激光可以用于制造高精度的零件、切割材料、焊接金属等。
同时,激光还可以用于医疗领域,例如激光手术、激光治疗癌症等。
此外,激光还被广泛应用于通信领域,例如激光通信和光纤通信等。
总结通过对激发原理、反转粒子数密度、共振腔和激光输出等方面的介绍,可以了解到激光的产生和特性。
同时,我们也能够了解到激光在科学研究、医疗、通信和制造业等领域中的广泛应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘要
对拉盖尔-高斯光束通过圆形光阑的透过力进行了计算,并对拉盖尔-高斯光束的透过与未透过进行了简单研究,并对透过与为透过光阑光能的百分比和高斯光束的径向与轴向的光强分布进行了计算。
关键词:拉盖尔-高斯光束;透过百分比;径向与轴向分布。
目录
摘要 (1)
一、引言 (3)
二、原理与方法 (4)
2.1、高斯光束的特性 (4)
2.2、高斯光束的传播 (4)
2.3、计算该拉盖尔高斯光束透过光阑光能百分比涉及的主要公式为: (5)
三、结果(用mathcad制图软件) (6)
四、讨论 (8)
4.1通过的光强分布 (8)
4.2未通过的光强分布 (8)
4.3径向光强分布 (8)
4.4轴向光强分布 (8)
五、参考文献 (9)
一、引言
由于星地之间的光通信具有独特的优点,其一直是人们所追求的目标。
然而其中光束传输是以大气为信道的,光束势必受到由热传递引起的湍流大气的影响。
因而如何选择合适的光束和减弱湍流大气对传输光束的影响程度是大气光通信的研究重点。
拉盖尔高斯光束作为一种携带有轨道角动量的特殊光束,在各个领域的应用越来越广。
特别是其轨道角动量携带的信息在理论上是无限的,可以为实现任意N-位数据传输提供载体。
对拉盖尔一高斯(L-G)光束的传输特性已经做了许多研究讨论了L-G光束(l=0)光阑孔径为无限大时的焦移。
本文从Coillns性,包括光阑孔径为无限大时聚焦后的腰斑半径及位置,l=0时的相对焦移和相对光强增量;光阑孔径有限时的相对焦移及轴上最大光强等,并对数值计算的结果做了分析和讨论。
公式出发详细研究了LG光束的聚焦特因此,研究湍流大气对拉盖尔高斯光束的影响将对大气光通信具有重要意义。
本文的主要研究内容如下: 以拉盖尔高斯光束为光源的湍流空间光传输模型的建立。
首先,利用归一化拉盖尔高斯光束的正交性并采用模式分析理论和李托夫近似研究了大气湍流对拉盖尔高斯光束光子态的影响和湍流引起的光束扩展等问题。
二、原理与方法
2.1、高斯光束的特性
研究普通光学系统的成像时,我们都假定点光源发出的球面波在各个方向上的光强度是相同的,即光束波面上各点的振幅是相等的。
而激光作为一种光源,其光束截面内的光强分布是不均匀的,即光束波面上各点的振幅是不相等的,其振幅A与光束截面半径r的函数关系为
其中A0为光束截面中心的振幅,w为一个与光束截面半径有关的参数,r为光束截面半径。
光束波面的振幅A呈高斯(Guass)型函数分布所以激光光束又称为高斯光束。
高斯光束的光斑延伸到无限远,其光束截面的中心处振幅最大,随着r 的增大,振幅越来越小,因此我们常以r=w时的光束截面半径作为激光束的名义截面半径,并以w来表示,即当r=w时
说明高斯光束的名义截面半径w是当振幅A下降到中心振幅A0的1/e时所对应的光束截面半径。
2.2、高斯光束的传播
由激光谐振腔衍射理论可知,在均匀的透明介质中,高斯光束沿Z轴方向传播的光场分布为
式中, C 为常数因子,,为波数,、和分别为高斯 光束的截面半径、波面曲率半径和位相因子,它们是高斯光束传播中的三个重要参数.
2.3、计算该拉盖尔高斯光束透过光阑光能百分比涉及的主要公式为:
在本题中角向节线0,径向节线2的拉盖尔高斯光束通过圆形光阑
m=0,n=2 带入进行积分运算可得
拉盖尔高斯光束透过光阑光能百分比为:
Lagu m n , x , ()0
n
k n m +()!x -()
k
⋅m k +()!k !⋅n k -()!
⋅∑
=:=
T l p , r0, ()02π
⋅φ0r0
r 2r ω⋅⎛ ⎝⎫⎪
⎭2l
⋅Lagu l p , 2r 2⋅ω2, ⎛ ⎝⎫⎪⎪⎭⎛ ⎝⎫⎪⎪⎭2
⋅exp 2-r 2⋅ω2⎛ ⎝⎫⎪⎪⎭
⋅cos l φ⋅()2⋅⎛⎜⎜⎜⎜⎠d ⎛
⎜⎜⎜⎜⎠
d 02π
⋅φ0
∞
r 2r ω⋅⎛ ⎝⎫⎪⎭2l
⋅Lagu l p , 2r 2⋅ω2, ⎛ ⎝⎫⎪⎪⎭⎛ ⎝⎫⎪⎪⎭2
⋅exp 2-r 2⋅ω2⎛ ⎝⎫⎪⎪⎭
⋅cos l φ⋅()2⋅⎛⎜⎜⎜⎜⎠
d ⎛
⎜⎜⎜⎜⎠
d :=
拉盖尔高斯光束未透过光阑光能百分比为:
L l p , r0, ()1T l p , r0, ()-:=
盖尔高斯光束径向光强分布为:
I l p , r , φ, ()2r ω⋅⎛ ⎝⎫⎪⎭2l
⋅Lagu l p , 2r 2⋅ω2, ⎛ ⎝⎫⎪⎪⎭⎛ ⎝⎫⎪⎪⎭2
⋅exp 2-r 2⋅ω2⎛
⎝⎫⎪⎪⎭⋅cos l φ⋅()2⋅:=
三、结果(用mathcad 制图软件)
1.未通过光阑的百分比分布图如下:
2.通过光阑的百分比分布图如下:
3.ϕ等于0时,径向r光强分布图如下:
4.R等于0时,光强分布图如下:
四、讨论
4.1通过的光强分布
对于光阑半径0~1,光能分布的整体趋势是逐渐下降的,但在0~0.5范围是一个减速下降的过程
在0.5~1范围变成了一个加速下降的过程
4.2未通过的光强分布
对于光阑半径0~1,光能分布的整体趋势是逐渐上升的,但在0~0.5范围是一个加速上升的过程
在0.5~1范围变成了一个减速上升的过程
4.3径向光强分布
径向光强分布是一个关于直线r=0对称的光滑曲线。
在-2~-1,-1~0,0,0~1,1~2之间分别存在一共5个峰值
且越靠近中心峰值越大。
4.4轴向光强分布
输出图像是一条平滑的双曲线,存在一个波峰。
五、参考文献
【1】激光原理(第六版)周炳琨,高以智等编著北京:国防工业出版社,2011.7 【2】激光技术2005年第06期作者:郑振,刘永欣,吕百达。
