13..4理想气体的等温过程和绝热过程
热力学理想气体的等温过程
热力学理想气体的等温过程热力学理想气体的等温过程是指在恒定温度下进行的过程。
在这个过程中，气体的温度保持不变，但压力和体积却有所变化。
热力学理想气体等温过程是理解气体性质和热力学定律的重要基础。
本文将介绍热力学理想气体的等温过程的基本原理和特点。
一、基本原理根据热力学定律，热力学理想气体的等温过程遵循以下基本原理：1. 温度不变：在等温过程中，气体的温度保持恒定。
这是因为外界对气体做功或从气体中吸收的热量正好能够抵消系统放出的热量，使得气体的温度保持不变。
2. 理想气体状态方程：根据理想气体状态方程PV = nRT（其中P为气体的压力，V为气体的体积，n为物质的摩尔数，R为气体常数，T为温度），在等温过程中，气体的压力和体积成反比。
当气体的体积增大时，压力减小；反之，当气体的体积减小时，压力增大。
3. 绝热过程：在等温过程中，外界对气体所做的功可看做绝热过程。
绝热过程是指在无热量交换的情况下，仅通过气体本身内部的压缩或膨胀来做功。
在绝热过程中，气体的温度和压力同时发生变化。
二、特点和实例热力学理想气体的等温过程具有以下特点：1. 压强随体积变化：根据理想气体状态方程，在等温过程中，气体的压强与体积成反比。
当气体体积增大时，气体的压强减小；反之，当气体体积减小时，气体的压强增大。
2. 外界对气体做的功：在等温过程中，外界对气体所做的功等于负的热力学定量。
即外界所做的功正好能够和气体放出的热量相互抵消，使气体的温度保持恒定。
3. 等量热量交换：在等温过程中，系统和外界之间存在等量的热量交换。
当气体的体积发生变化时，外界对气体做的功与系统放出的热量大小相等，从而使得气体内部的能量保持不变。
以下是一个等温过程的实例来说明热力学理想气体的等温过程：考虑一个容器中的理想气体，在恒定温度下进行等温过程。
一开始，气体的压力为P1，体积为V1，温度为T。
外界对气体进行压缩，使得气体体积减小为V2。
根据理想气体状态方程PV = nRT，当体积减小时，气体的压力会增大。
理想气体的等温与绝热过程
理想气体的等温与绝热过程理想气体是物理学中一个重要的理想化模型，它假设气体的分子之间没有相互作用，体积可以忽略不计。
在实际的等温与绝热过程中，理想气体表现出了不同的特性和行为。
本文将深入探讨理想气体在等温与绝热过程中的特点和数学表达方式。
等温过程是指气体在恒定温度条件下发生的过程。
在等温过程中，理想气体的温度保持不变，因此根据理想气体状态方程PV=nRT，压强和体积成反比。
也就是说，当体积增大时，压强会相应减小，反之亦然。
这种关系可以用数学表达式PV=常数来表示，其中常数等于nRT。
绝热过程是指气体在没有热量交换的情况下发生的过程。
在绝热过程中，理想气体的内部能量保持不变，因此根据理想气体状态方程PV=nRT，压强和体积的乘积保持不变。
也就是说，当体积减小时，压强会相应增大，反之亦然。
这种关系可以用数学表达式P₁V₁^γ=P₂V₂^γ来表示，其中γ是气体的绝热指数，对于大多数单原子气体而言，γ≈5/3。
在等温过程中，理想气体的温度保持恒定，因此内能的增加和对外做功相互抵消。
根据气体内能的公式（因为内能只与温度有关），ΔU=nCvΔT，其中ΔU表示内能的变化，n表示物质的摩尔数，Cv表示摩尔定容热容，ΔT表示温度变化。
由于等温过程中温度不变，因此ΔT=0，所以ΔU=0。
这意味着在等温过程中，理想气体的内能保持不变。
在绝热过程中，理想气体没有热量交换，因此热量的增加全都被用于对外做功。
根据绝热过程中的热力学第一定律，Q-W=ΔU，其中Q 表示吸收的热量，W表示对外做的功，ΔU表示内能的变化。
由于绝热过程中没有热量交换，因此Q=0，所以W=ΔU。
这意味着在绝热过程中，理想气体的内能变化全部用于对外做功。
绝热过程和等温过程的比较可以看出，等温过程中理想气体对外做的功为零，内能的变化为零；而绝热过程中理想气体对外做的功不为零，内能的变化全部用于对外做功。
这两个过程都是理想气体在不同条件下的特性，对于理论研究和实际应用都有着重要的意义。
大学物理第 13 章 第 2 次课 -- 理想气体的等温过程和绝热过程..
p1
2'
T C
V2 V2' V1 10
T1 1
V1 V
负号表示外界对气体做功. 2）绝热过程做的功
o
氢气为双原子气体, 表查13-1得 =1.41, CV,m= 20.44 J· mol-1· K-1 . 由绝热过程方程 由此可得,
TV
1
常数c'
得
T1V1
1
T2V2
1
上海师范大学
3 /12
§13.4
理想气体的等温过程和绝热过程
二、绝热过程
绝热过程: 理想气体状态发生变化的过程中, 气体与外界没有热量传递. 绝热过程是一种理想过程, 实际的过程不可能是真正的绝热过程. 但在状态的变化过程中, 如果系统与外界的热传递很小, 以致可以忽略, 则这
种过程可以近似地视为绝热过程. 如汽车发动机气缸中气体的膨胀就可以近 p ( p1 ,V1 , T1 ) 似地看成是绝热过程.
6 /12
上海师范大学
将
Cp,m R CV ,m , C p,m / CV ,m 代入上式, 简得
C p ,m dV dp CV, m V p
§13.4 理想气体的等温过程和绝热过程 (CV ,m R) dV dp CV, m V p
dV dp 0 V p
上海师范大学
(14)
5 /12
§13.4 2. 绝热过程的物态方程 理想气体的物态方程:
理想气体的等温过程和绝热过程
pV RT
V R 常数 等压过程: T p
p R 常数 等体过程: T V 等温过程: pV 常数
绝热过程中, 状态参量p,V,T都发生变化, 能否写出两个量之间的变化关系? 对理想气体的物态方程
理想气体中的等温过程与绝热过程
理想气体中的等温过程与绝热过程在研究理想气体的性质和行为时，等温过程和绝热过程是两个重要的概念。
它们描述了气体在外界条件改变下的变化规律，是热力学和物理学中的基础概念之一。
本文将详细介绍等温过程和绝热过程的定义、特点和数学表达，以及它们在实际应用中的意义和重要性。
一、等温过程等温过程是指在气体与外界保持恒定温度的条件下，体积和压力发生变化的过程。
根据理想气体状态方程PV=nRT，当温度保持不变时，压力和体积成反比关系。
也就是说，当压力增加时，体积减小；压力减小时，体积增加，以保持气体的温度不变。
以一定量的理想气体为例，假设其体积从V₁变化到V₂，对应的压力由P₁变化到P₂。
根据等温过程的特点，我们可以得到以下数学表达式：P₁V₁ = P₂V₂这个表达式被称为爱德华·博伯定律，也是描述等温过程中气体性质的重要公式之一。
从公式中可以看出，当气体的温度不变时，压力和体积之间存在一个不变的乘积关系。
等温过程在实际应用中有着重要的意义。
在工程领域中，等温过程常常用于设计和优化热机、制冷设备等。
在化学实验中，等温过程也是调整反应条件和控制反应速率的基础。
二、绝热过程绝热过程是指在理想气体与外界没有热量交换的条件下，体积和温度发生变化的过程。
在绝热过程中，气体与外界之间没有能量的转移，因此其内能保持不变。
根据内能守恒定律，绝热过程中气体的温度变化与体积变化呈反比关系。
同样以一定量的理想气体为例，假设其体积从V₁变化到V₂，对应的温度由T₁变化到T₂。
根据绝热过程的特点，我们可以得到以下数学表达式：T₁V₁^(γ－1) = T₂V₂^(γ－1)其中，γ为气体的绝热指数，表示气体热容比。
对于单原子分子气体，γ约等于5/3；对于双原子分子气体，γ约等于7/5。
从上述公式中可以看出，当气体的体积增加时，温度会降低，反之亦然。
绝热过程的应用也非常广泛。
例如，在内燃机中，汽缸中的气体在燃烧过程中发生绝热膨胀，从而驱动活塞运动，产生功。
热学练习题理想气体的等温过程与绝热过程的比较
热学练习题理想气体的等温过程与绝热过程的比较在热学中，理想气体的等温过程和绝热过程是两个重要的概念。
虽然它们都涉及气体的热力学性质，但是两者之间存在着明显的区别。
本文将就理想气体的等温过程和绝热过程展开比较和分析。
一、理想气体的等温过程理想气体的等温过程是指在恒温条件下进行的过程。
在这个过程中，系统的温度保持不变，而气体的压力和体积会相应地发生变化。
根据理想气体的状态方程PV=nRT（式中P为气体的压力，V为体积，n为物质的量，R为气体常数，T为温度），我们可以得到等温过程的数学表达式为PV=常数。
在等温过程中，当气体的体积减小时，压力会增加，反之亦然。
这符合气体的玻意耳定律，即在恒温条件下，气体的压力和体积成反比。
在理想气体的等温过程中，工作与热量的转化也是平衡的，即所吸收的热量等于所做的功。
二、理想气体的绝热过程理想气体的绝热过程是指在没有热量交换的情况下进行的过程。
在这个过程中，气体的内能发生改变，但是温度保持不变。
根据绝热条件下的理想气体状态方程，我们可以得到绝热过程的数学表达式为PV^γ=常数。
在绝热过程中，当气体的体积减小时，压力会增加，但是由于没有热量交换，所以气体的温度也不会发生变化。
这符合绝热条件下的理想气体的关系，即压力和体积不再成反比，而是与体积的幂指数γ有关。
这个指数γ被称为绝热指数，对于单原子理想气体，γ=5/3；对于双原子理想气体，γ=7/5。
在绝热过程中，工作与热量的转化是不平衡的，即所吸收的热量不等于所做的功。
三、等温过程与绝热过程的比较1. 温度变化：等温过程中，气体的温度保持不变；绝热过程中，气体的温度也保持不变。
2. 压力变化：等温过程中，气体的压力和体积成反比；绝热过程中，气体的压力和体积不再成反比，而与体积的幂指数γ有关。
3. 热量交换：等温过程中，热量和功的转化是平衡的；绝热过程中，热量和功的转化是不平衡的。
4. 内能变化：等温过程中，气体的内能不变；绝热过程中，气体的内能发生改变。
气体主要热力过程的基本公式
气体主要热力过程的基本公式1.等容过程（isochoric process）在等容过程中，气体体积保持不变。
根据理想气体状态方程PV=nRT，结合理想气体的内能U=C_vT（其中C_v表示摩尔定容热容量），可以得到气体的内能和温度的关系为U2-U1=C_v(T2-T1)2.等压过程（isobaric process）在等压过程中，气体的压强保持不变。
根据理想气体状态方程PV=nRT，结合理想气体的焓H=U+PV（其中H表示焓），可以得到气体的焓和温度的关系为H2-H1=C_p(T2-T1)其中C_p表示摩尔定压热容量。
3. 绝热过程（adiabatic process）在绝热过程中，气体在没有与外界交换热量的情况下发生压缩、膨胀等过程。
根据绝热条件PV^γ=常数，可以得到气体压强和体积的关系为P2V2^γ=P1V1^γ其中γ=C_p/C_v表示绝热指数。
4.等温过程（isothermal process）在等温过程中，气体的温度保持不变。
根据理想气体状态方程PV=nRT，可以得到气体的压强和体积的关系为P1V1=P2V2综合以上各种过程，可以得到气体的理想热力方程为C_p(T2 - T1) - R(ln(V2/V1)) = 0其中 R 表示气体常数，对于摩尔气体，R = 8.314 J/(mol·K)。
另外，对于理想气体的内能和焓，还可以利用摩尔定热容量和摩尔焓的定义进行计算：U=nC_vTH=nC_pT其中C_v和C_p分别为摩尔定容热容量和摩尔定压热容量，n表示气体的物质量。
需要注意的是，以上公式都是在理想气体的情况下推导得到的，在实际情况下可能需要考虑相对论效应、分子间相互作用等因素。
此外，还有其他一些非常特殊的热力过程，如绝热绝热过程、多孔气体的热力过程等，其公式推导及应用较为复杂，对于一般的热力学应用来说已经足够。
13-4理想气体的等温过程和绝热过程
13
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
后为P 例1,一定量的理想气体 1,V1,T1,后为 2,V2, ,一定量的理想气体P T2, 已知 V2>V1, T2=T1 以下说法哪种正确? 以下说法哪种正确? (A)不论经历什么过程,气体对外净作功一定为正值 )不论经历什么过程, (B)不论经历什么过程,气体对外界净吸热一定为正值 )不论经历什么过程, (C)若是等温过程,气体吸的热量最少 )若是等温过程, (D)若不知什么过程,则A,Q的正负无法判断 )若不知什么过程, , 的正负无法判断 [D]
第十三章 热力学基础
14
物理学
第五版
1313-4 理想气体的等温过程和绝热过程 态到b态 例2,一定量的理想气体从 态到 态,这个过程 ,一定量的理想气体从a态到 是什么过程? 是什么过程?
P
b
a
T
(A)绝热压缩(B)等容吸热 )绝热压缩( ) (C)吸热压缩(D)吸热膨胀 )吸热压缩( )
第十三章 热力学基础
γ
E
0
p1V1 p 2V2 γ 1
νcV T
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
P
T
D
A
B
C
T
图中曲线为等 温线.问A, B,C,D状态 时系统的温度 关系.
V
T
PV = νRT
等压过程中,体积越大温度越高;等体过程 中,压强越大温度越大. 在PV图中,等温线上方温度较高,等温线 下方温度较低.
第十三章 热力学基础
8
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
理想气体的等温过程与绝热过程
理想气体的等温过程与绝热过程理想气体是指在一定温度下，气体分子之间完全没有相互作用的气体模型。
在理想气体的热力学过程中，等温过程和绝热过程是两个重要的概念。
本文将分别介绍理想气体的等温过程和绝热过程，并探讨它们的特点和应用。
一、理想气体的等温过程等温过程是指在气体发生变化的过程中，温度保持不变。
对于理想气体而言，等温过程可以用以下方程来描述：PV = 常数（1）式中，P表示气体的压强，V表示气体的体积。
根据理想气体状态方程，PV = nRT，式中，n表示气体的物质的量，R是气体常数，T是气体的绝对温度。
结合方程（1）和PV = nRT，我们可以得到：nRT = 常数（2）由方程（2）可知，在等温过程中，气体的物质的量n和体积V是成反比的关系。
也就是说，在体积增大的同时，物质的量会减少，反之亦然。
这说明了在等温过程中，气体分子会随着体积的改变而发生数量的变化。
等温过程还有一个重要的特点是气体对外做功。
根据热力学的能量守恒定律，气体所做的功等于外界对气体做的功。
在等温过程中，气体扩大或收缩的功可以通过以下公式计算：W = - nRT * ln(V2/V1) （3）式中，W表示气体所做的功，V1和V2分别表示气体的初始体积和最终体积。
二、理想气体的绝热过程绝热过程是指在气体发生变化的过程中，没有热量的交换。
绝热过程的特点是温度和压强同时变化。
对于理想气体而言，绝热过程可以用以下方程来描述：PV^γ = 常数（4）式中，γ表示气体的绝热指数，对于大多数单原子理想气体而言，γ约等于5/3。
根据理想气体状态方程，PV = nRT，我们可以推导出绝热过程中，温度和压强的关系：T = (Pv^(γ-1))/(nR) （5）式中，Tv表示绝热过程中气体的温度。
由方程（5）可知，在绝热过程中，随着气体体积的减小，气体的温度也会随之降低。
反之，体积的增大会导致温度的升高。
这与等温过程中温度保持不变的特点形成了鲜明的对比。
热力学理想气体的绝热过程
热力学理想气体的绝热过程热力学是研究能量转化和传递规律的学科，而理想气体则是热力学中的重要概念。
理想气体在绝热过程中的行为是热力学中的一个经典问题。
本文将介绍热力学理想气体的绝热过程，并且分析绝热过程对气体性质的影响。
1. 绝热过程的定义绝热过程是指气体在与外界无换热的情况下进行的过程。
在绝热过程中，气体系统不与外界交换热量，但压强和体积可能发生变化。
绝热过程中气体能量的转化只通过气体内部的分子间相互作用来实现。
2. 理想气体的特性理想气体是指在宏观情况下，气体分子之间不具有吸引力和排斥力，分子之间的碰撞是完全弹性的，体积可以忽略不计。
理想气体的状态方程为PV=nRT，其中P为压强，V为体积，n为物质的物质的摩尔数，R为气体常量，T为温度。
3. 理想气体绝热过程的基本方程绝热过程中，理想气体的内能U和体积V的关系可以通过以下公式描述：P1V1^γ = P2V2^γ其中，P1和P2分别为绝热过程前后的压强，V1和V2分别为绝热过程前后的体积，γ为气体的绝热指数。
4. 绝热指数的计算绝热指数γ可以通过以下公式计算：γ = C p/Cv其中，Cp为气体在定压过程中的摩尔定压热容，Cv为气体在定容过程中的摩尔定容热容。
5. 绝热过程对气体性质的影响在绝热过程中，气体的温度、压强和体积之间存在着确定的关系。
当气体发生绝热膨胀（体积增大）时，气体的温度降低，压强下降；当气体发生绝热压缩（体积减小）时，气体的温度升高，压强增加。
6. 绝热过程中的熵变由于绝热过程中没有热量交换，因此熵的变化也受到限制。
绝热膨胀过程中，熵的变化为ΔS = 0，即熵保持不变；而绝热压缩过程中，熵的变化为ΔS = 0，即熵同样保持不变。
7. 绝热过程的实际应用绝热过程在实际中有许多应用，比如内燃机的工作过程和空气压缩机的工作过程等。
绝热过程的特性使得气体在压力和体积的变化下能够进行能量的转化，从而实现机械功的输出。
总结：热力学理想气体的绝热过程是热力学中的一个重要问题。
理想气体的等温过程与绝热过程
理想气体的等温过程与绝热过程理想气体在不同的过程中表现出不同的特性，其中等温过程和绝热过程是两种常见的气体过程。
本文将对理想气体的等温过程和绝热过程进行详细介绍。
一、理想气体的等温过程等温过程是指气体在温度恒定的情况下发生的过程。
在等温过程中，气体内部的分子运动速度仍在改变，但总体来说，分子碰撞所产生的压强和分子间的引力相互抵消，使得气体保持恒定的温度。
这是因为等温过程中热量的加入与放出相等，保持热平衡。
在等温过程中，根据理想气体的状态方程PV=nRT（其中P为气体的压强，V为气体的体积，n为气体的物质量，R为气体常数，T为气体的温度），可以得到以下关系式：P1V1=P2V2其中P1和V1表示初始状态下的压强和体积，P2和V2表示最终状态下的压强和体积。
从上式可以看出，在等温过程中，气体的压强和体积呈反比关系。
等温过程的特点是气体对外界做功。
由于气体的体积发生改变，气体向外界提供了一定的功。
在等温过程中，由于气体分子的运动速度和分子间的引力相互抵消，气体没有温度差，故不会产生热量的传递。
二、理想气体的绝热过程绝热过程是指气体与外界没有热量交换的过程。
在绝热过程中，气体受到的外界影响只有气体的压强和体积的改变，而没有温度的改变。
绝热过程中气体内部的分子速度会发生改变，但总体来说，分子的动能和势能保持恒定。
绝热过程中，根据理想气体的状态方程PV^γ=常数（其中γ为气体的绝热指数，在单原子分子中为5/3，在双原子分子中为7/5，例如空气中的氮氧化合物），可以推导出以下关系式：P1V1^γ=P2V2^γ其中P1和V1表示初始状态下的压强和体积，P2和V2表示最终状态下的压强和体积。
从上式可以看出，在绝热过程中，气体的压强和体积的幂函数关系。
绝热过程的特点是气体做功和温度变化。
由于没有热量传递，气体对外界做功时从内部获取能量，导致气体的温度下降。
绝热过程的常见应用是气体膨胀和压缩的过程。
综上所述，理想气体的等温过程和绝热过程在气体状态变化和能量交换方面具有不同的特点。
热学理想气体的等温过程与绝热过程
热学理想气体的等温过程与绝热过程热学中，理想气体是一个非常重要的研究对象。
理想气体在各种过程中的性质以及其与热力学参数的关系一直是科学家们探索和分析的对象。
本文将着重讨论理想气体的等温过程和绝热过程，探究这两种过程在理想气体中的特点以及相互之间的区别。
等温过程是指气体在温度不变的情况下进行的过程。
在等温过程中，气体的温度保持不变，从而使得气体内能的变化与做功的变化相抵消，维持气体的总能量保持不变。
根据理想气体的状态方程，可以得出等温过程中气体压强和体积之间的关系为P1V1=P2V2，即等温过程是一个双曲线，曲线的形状取决于气体的特性。
绝热过程是指气体在没有与外界交换热量的情况下进行的过程。
在绝热过程中，气体的内能发生改变，但是热量的交换量为零，因此气体的温度会发生变化。
根据理想气体的状态方程，可以得出绝热过程中气体压强和体积之间的关系为P1V1^γ=P2V2^γ，其中γ为绝热指数，也是一个气体的特性常数。
绝热过程的压强-体积关系曲线是一个双曲线，且比等温过程更陡峭。
在实际情况中，等温过程和绝热过程往往同时存在。
例如，当理想气体在容器中进行等温膨胀时，同时做功以及与外界交换热量，这个过程既有等温的特点又有绝热的特点。
绝热和等温过程的结合，使得气体的性质更加丰富和复杂。
通过对理想气体等温过程和绝热过程的分析，我们可以得到一些重要的结论。
首先，等温过程中气体的内能保持不变，而绝热过程中气体的内能发生改变；其次，等温过程中气体的压强和体积成反比，绝热过程中气体的压强和体积有一定的幂指数关系；最后，等温过程和绝热过程往往同时存在于实际情况中，使得气体的过程更加复杂多变。
综上所述，热学中的理想气体等温过程和绝热过程是两个重要的研究对象，它们揭示了气体在不同条件下的行为特性。
等温过程中气体保持温度不变，绝热过程中气体没有与外界交换热量。
通过对这两种过程的研究，可以更好地理解和分析理想气体的性质和行为。
对于热学研究的深入和应用，进一步探究和理解理想气体的等温过程和绝热过程具有重要的意义。
13-4 等温、绝热过程,多方过程
CV dT pdV 0 （ 1 ）
由 pV RT 两边取微分,得
pdV Vdp RdT （2）
由 (1)，(2) 两式，得
CV pdV CVVdp RpdV
(CV R) pdV CVVdp
由 得到
R Cp CV ; Cp / CV
3. 过程曲线 在P - V 图上，每一个绝热过程对应一条 双曲线，称为绝热线。 4. 热量 dQ = 0
5. 内能变化 dE CV dT 6. 绝热功 p2
P p1
Q
（1） 由温度变化引起的
O
V1
pdV V2
V
dA dE CV dT
A CV T
（2） 用功的定义计算
V1 1.41 992K T2 T1 V 320 (16.9) 2
1
终了时的压强为
V1 P2 P 1 V 2
1.013 10 (16.9)
5
1.4
45.110 pa
5
例2 一热机用5.8×10-3Kg的空气作为工质，从 初态1（p1=1.013×105pa , T1=300K）等体加热 到状态2（T2=900K），再经绝热膨胀到状态3 （p3=p1），最后经等压过程又回到1，如图。 假定空气可视为理想气体，且γ=1.4， CV=20.8J/(mol· K)， p 2 Cp=29.09J/(mol· K)摩尔质量 p2 M=29×10-3Kg· mol。试求各 3 过程中气体所做的功及从外 p1 1 O 界吸收的热量。 V1 V3 V
V1
V2
V2
V1
dV V
T V1 pdV V2 V
理想气体等温过程和绝热过程的能量变化
理想气体等温过程和绝热过程的能量变化在热力学中，理想气体是一个重要的研究对象。
理想气体的性质简单，易于理解和计算，因此被广泛应用于工程和科学领域。
在理想气体的研究中，等温过程和绝热过程是两个基本概念，它们对气体的能量变化有着重要的影响。
首先，让我们来了解等温过程。
等温过程是指在恒定的温度下进行的过程。
在等温过程中，气体的温度保持不变，因此气体分子的平均动能也不会改变。
当气体在等温过程中发生体积变化时，根据理想气体状态方程PV=nRT，气体的压强和体积成反比。
当气体膨胀时，体积增大，压强减小；当气体压缩时，体积减小，压强增大。
这种压强和体积的变化会导致气体分子之间的碰撞频率发生改变，但总的能量保持不变。
在等温过程中，气体的能量变化主要体现在热量的传递上。
根据热力学第一定律，能量守恒，热量传递是通过气体与外界进行热交换实现的。
当气体膨胀时，从外界吸收热量，当气体压缩时，向外界释放热量。
这种热量的传递使得气体的内能发生变化，但总的能量保持不变。
在等温过程中，热量的传递是通过热机或热泵等装置实现的，这些装置可以将热量从高温源传递到低温源，实现功的输出。
接下来，我们来探讨绝热过程。
绝热过程是指在没有热量交换的情况下进行的过程。
在绝热过程中，气体与外界没有热量的交换，因此气体的内能保持不变。
根据理想气体状态方程PV=nRT，当气体发生绝热膨胀时，体积增大，压强减小；当气体发生绝热压缩时，体积减小，压强增大。
这种体积和压强的变化会导致气体分子之间的碰撞频率发生改变，但总的能量保持不变。
在绝热过程中，气体的能量变化主要体现在功的转化上。
根据热力学第一定律，能量守恒，绝热过程中没有热量的传递，因此能量的变化完全体现在功的转化上。
当气体膨胀时，外界对气体做功，当气体压缩时，气体对外界做功。
这种功的转化使得气体的内能发生变化，但总的能量保持不变。
在绝热过程中，功的转化是通过压力-体积图或者其他形式的图表来描述的，通过计算图表下的面积可以得到功的大小。
例举出理想气体的四个基本热力过程及其过程方程式。
例举出理想气体的四个基本热力过程及其过程方程式。
理想气体是指在恒定温度下，所有气体分子间不存在相互作用力的气体体系。
对于理想气体，四个基本热力过程依次是等温过程、绝热过程、等压过程和等体过程，下面我们来一一介绍这四个过程。
一、等温过程等温过程是指理想气体在恒定温度下发生的过程，此时系统内的温度不变。
在等温过程中，理想气体的压强与体积成反比例关系，即PV = 常数，其中P为气体的压强，V为气体的体积。
二、绝热过程绝热过程是指理想气体在没有任何能量交换的情况下发生的过程。
在绝热过程中，由于没有热量的交换，温度会发生变化。
绝热过程中理想气体的状态方程为PV^{γ} = 常数，其中γ为理想气体的绝热指数。
三、等压过程等压过程是指理想气体在恒定压强下发生的过程。
在等压过程中，理想气体的体积与温度成正比例关系，即V/T = 常数。
等压过程的状态方程为V/T = 常数，其中V为气体的体积，T为气体的绝对温度。
四、等体过程等体过程是指理想气体在恒定体积下发生的过程。
在等体过程中，理想气体的压强与温度成正比例关系，即P/T = 常数。
等体过程的状态方程为P/T = 常数，其中P为气体的压强，T为气体的绝对温度。
通过以上介绍，我们可以看出四个基本热力过程对应的状态方程式分别是：等温过程 PV = nRT、绝热过程PV^{γ} = 常数、等压过程 V/T = 常数、等体过程 P/T = 常数。
在实际应用中，这四个基本热力过程是非常重要的。
通过对这些过程的掌握，我们可以更好地理解理想气体的物理变化规律，为一些实际问题的解决提供指导意义。
理想气体的等温过程和绝热过程
§6－5 理想气体的等温过程和绝热过程一、等温过程（Isothermal Process ）1．特点：理想气体的温度保持不变，T =const 。
2．过程曲线：在PV 图上是一条双曲线，叫等温线。
3．过程方程：P 1V 1= P 2V 24．内能、功和热量的变化系统经过等温过程，从状态()T V P ，，11变成()T V P ，，22内能 012=-=∆E E E功 ⎰=21V V T PdV W由气体状态方程 RT M m PV ＝得 VRT M m P 1＝ 12ln 121V V RT M m dV V RT M m W V V T ==⎰——用体积表示。
用压强表示为21ln P P RT M m W T = 热量：由热力学第一定律得 1221ln ln V V RT M m P P RT M m Q T ==5．特征：在等压过程中，系统从外界吸收的热量，全部用来对外作功。
注意：对于等温过程，不能定义摩尔热容；如果要定义，则∞=C 。
二、绝热过程（Adiabatic Process ）1．特点：系统与外界没有热量交换的过程，Q =0。
2．内能、功和热量的变化系统经过绝热过程，从状态()11T V P ，，变成()22T V P ，，内能 ()12,12T T C Mm E E E m V -=-=∆ 热量 Q =0由热力学第一定律 0=+∆=W E Q ，得功 ()12,T T C Mm W m V -=－ 用状态参量P ,V 表示，根据状态方程R PV T M m ＝，可知()1 22112211,－＝－γV P V P V P V P R C W mV --= 证明：由定义可知，m V m V m V m V mP C R C R C C C ,,,,,1+=+==γ 因而1,-=γm V C R 故 11,-=γR C m V 因而 12211－γV P V P W -= 3．特征：在绝热过程中，系统对外界所作的功是由于系统内能的减少来完成的。
热力学理想气体的绝热过程与等温过程的应用题
热力学理想气体的绝热过程与等温过程的应用题热力学是一门研究能量转化和传递的领域，其中绝热过程和等温过程是热力学中的两个重要概念。
本文将通过应用题的形式，详细讨论热力学理想气体在绝热过程和等温过程中的相关应用。
一、理想气体的绝热过程绝热过程是指在没有任何能量交换和热交换的情况下，气体系统发生的过程。
在绝热过程中，理想气体的压强、体积和温度之间依照绝热方程式有如下关系：$P_1V_1^γ=P_2V_2^γ$，其中P表示压强，V 表示体积，γ表示绝热指数。
假设有一定质量m的理想气体，初始状态下的压强、体积和温度分别为$P_1, V_1, T_1$，终态下的压强、体积和温度分别为$P_2, V_2,T_2$。
根据绝热方程式可得：$P_1V_1^γ=P_2V_2^γ$。
应用题1：某理想气体初始时处于状态A($P_1, V_1, T_1$)，终态为状态B($P_2, V_2, T_2$)。
已知气体的绝热指数为γ，求气体绝热过程中的温度变化。
解析：根据绝热方程式$P_1V_1^γ = P_2V_2^γ$，可得$T_1V_1^{γ-1}=T_2V_2^{γ-1}$。
由此可以得到温度变化的关系式：$T_2=T_1\left(\frac{V_1}{V_2}\right)^{γ-1}$以上就是理想气体在绝热过程中温度变化的应用题。
二、理想气体的等温过程等温过程是指在温度不变的条件下，气体系统发生的过程。
在等温过程中，理想气体的压强和体积之间满足以下关系：$P_1V_1 =P_2V_2$。
假设有一定质量m的理想气体，初始状态下的压强、体积和温度分别为$P_1, V_1, T_1$，终态下的压强、体积和温度分别为$P_2, V_2,T_2$。
根据等温方程式可得：$P_1V_1 = P_2V_2$。
应用题2：某理想气体初始时处于状态C($P_1, V_1, T_1$)，终态为状态D($P_2, V_2, T_2$)。
已知温度不变，求气体等温过程中的压强变化。
10 13-3 理想气体的等体过程和等压过程 摩尔热容
PV RT PV RT
C p,m CV ,m R
理想气体的定压摩尔热容比定体摩尔热容大一个恒量R •在等体过程中，气体吸收的热量全部用来增加系统的内能 •等压过程中，气体吸收的热量，一部分用来增加系统的内能， 还有一部分用于气体膨胀时对外界作功 气体升高相同的温度，在等压过程吸收的热量要比在等温过 程中吸收的热量多。
3
水蒸气
m
蒸气 0.598kg m
3
水
100 C 热源
W pdV pV pm(
1
蒸气
1
1
水
1
)
E Q W m L pm(
蒸气
水
)
E 1 1 L p( ) 2.09106 J kg1 m 蒸气 水
四、多方过程
2、比热容：
单位质量的热容称为比热容。
C 1 dQ c m m dT
13－4 理想气体的等温过程和绝热过程
一、等温过程
•特点：
理想气体的温度保持不变， T=const
•过程曲线：
在PV图上是一条双曲线， 叫等温线。
恒 温 热 源 T
•过程方程：
p1V1 p2V2
p p1
p2
1 ( p1 ,V1 , T )
p
T 常量
Q0
papT
13-(2) 理想气体的等温过程和绝热过程
等体放热，内能减少.
o
等温膨胀过程 V E = 0 ；Q = W > 0
Q Δ E W 等温吸热，对外做功.
依 据
Δ
E
i 2
R
ΔT
等压压缩过程 W < 0 ； E < 0 ；Qp < 0
PV RT
外界做功，内能减少且放出热量.
绝热膨胀过程
Q = 0 ；W > 0；E < 0 绝热对外做功，内能减少.
解：把氮气视为理想气体, 其液化过程为绝热过程。
p1 501.013105 pa，p2 1.013105 pa，T1 300K
i5
γ C p,m
CV,m
i
i
2
1.40
p 1T 常量
p T p T 1 11
1 22
T2
T1 (
p2 p1
1
)
300 (
1
1.401
) 1.40
等温膨胀
p
p1 1 ( p1,V1,T )
p2
o V1
( p2 ,V2 ,T ) 2
W
V2 V
等温压缩
p
p1 1 ( p1,V1,T )
p2
o V1
( p2 ,V2 ,T ) 2
W
V2 V
QT E W
QT E
W
上 页 下 页 返回 5
物理学 §13-4 理想气体的等温过程和绝热过程
例1 将 500J 的热量传给标准状态下 2mol 的氢气。 (1) 若体积不变，这热量变为什么？氢气温度变为多少？ (2) 若温度不变，这热量变为什么？氢气的体积和压强各 变为多少？ (3) 若压强不变，这热量变为什么？氢气的温度和体积各 变为多少？
课件：理想气体的等温过程和绝热过程 多方过程
p
p2
2 T2
Q0
p2' T2' T1
p1
2'
T1
T 常量 1
o V2 V2' V1 10 V1 V
3）对等温过程
T2 753K
W12 CV ,m (T2 T1)
CV ,m 20.44J mol1 K1
W12 4.70104 J
p'2
p1
(V1 V2
)
1.013106 Pa
对绝热过程, 有 p2 p1(VV12 ) 2.55106 Pa
绝热膨胀
p
p1
1( p1,V1,T1)
p2
( p2,V2,T2)
W2
o V1
V2 V
绝热压缩
p
p2
2( p2,V2,T2)
p1
o V2
( p1,V1,T1)
W1
V1 V
§13-4 理想气体的等温过程和绝热过程 多方过程
三 绝热线和等温C
B
o V A V V B V
§13-4 理想气体的等温过程和绝热过程 多方过程
四 多方过程
pVn=C
（1）当n= ( =Cp,m/C V,m)时，为理想气体的绝热方程
pV=C1
（2）当n=1时，为理想气体的等温方程 pV=C2
（3）当n=0时， p=C3为理想气体的等压方程 （4）当n=时， V=C4为理想气体的等体方程
理想气体在多方过程中的W、E、Q
特征 dQ O
p
p1
1( p1,V1,T1)
热一律 dW dE 0
dW dE
p2
( p2,V2,T2)
2
dE CV ,mdT
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
8
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
摩尔定体热容 摩尔定体热容: 1mol 理想气体在等体 定体热容 过程中吸收热量 dQV ，使温度升高 dT , 其 摩尔定体热容为 定体热容为: 摩尔定体热容为
CV ,m
d QV = dT
−1 −1
dQV = CV ,mdT
单位 J ⋅ mol ⋅ K
pV = νRT
RT ν dV = −νCV ,m dT V
p2
o
第十三章 热力学基础
22
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
CV ,m dT dV =− 分离变量得 V R T
dV 1 dT ∫ V = −∫ γ − 1 T
绝
V
γ −1
T=
量
−1 热 V γ −1T = 方 pV γ = 程 γ −1 −γ
第十三章 热力学基础
4
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
Q = E2 − E1 + W = ∆E + W
第一定律的符号规定
Q
∆E
内能增加 内能减少
W
系统对外界做功 外界对系统做功
+
系统吸热 系统放热
第十三章 热力学基础
5
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
计算各等值过程的热量、 计算各等值过程的热量、功和内能的 理论基础. 理论基础 （1） ）
dE = 0
由热力学第一定律
o
dV
V2 V
dQT = dW = pdV
第十三章 热力学基础
16
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
QT = W =
∫V
V2
1
pdV
RT p =ν V
RT V2 QT = W = ∫ ν dV = ν RT ln V1 V V1
V2
p1 = νRT ln p2
第十三章 热力学基础
30
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
氮气可视为理想气体， 解 氮气可视为理想气体， 其液化过 程为绝热过程. 程为绝热过程
p1 = 50 × 1.01×10 Pa
5
T1 = 300K
p2 = 1.01×10 Pa
5
氮气为双原子气体由表查得 γ = 1.40 p2 (γ −1) / γ T2 = T1 ( ) = 98.0K p1
W
p1V1 − p 2V2 = γ −1
第十三章 热力学基础
21
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
绝热过程方程的推导
∵ dQ = 0 , ∴ dW = − dE
pdV = −ν CV , m dT
p
p1
1( p1 , V1 , T1 )
Q=0
( p2 ,V2 ,T2 ) 2
V1 V2 V
系统从外界吸收的热 系统从外界吸收的热 量，一部分使系统的内能 增加， 增加，另一部分使系统对 外界做功 .
o
V1
V2 V
Q = E2 − E1 + W = ∆E + W
第十三章 热力学基础
3
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
准静态过程
Q = ∆E +
微变过程
∫V
V2
1
pdV
dQ = dE + d W = dE + pdV
四 比热容
dQ 热容 C = d T
比热容
dQ C c= = m′dT m′
第十三章 热力学基础
15
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
一 等温过程
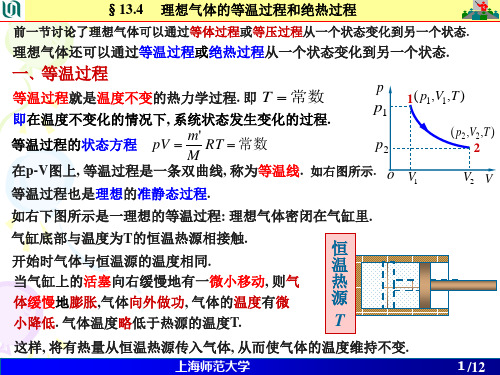
T = 常量 过程方程 pV = 常量
特征
p p1
1 ( p1 ,V1 , T )
( p2,V2,T )
p2
恒 温 热 源 T
2
V1
QT
E
W
QT
E
W
第十三章 热力学基础
18
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
二
绝热过程
dQ = 0
p
p1
1( p1 ,V1 , T1 )
( p2,V2,T2 )
与外界无热量交换的过程 特征 由热力学 dW + dE = 0 第一定律 dW = −dE
p2
2
V2 V
o V1 dV
dE = νCV ,m dT
pV = νRT （理想气体的共性） 理想气体的共性） 共性
d Q = d E + pd V
解决过程中能
（2） ）
Q = ∆E + ∫ pdV 量转换的问题
V1
第十三章 热力学基础
V2
6
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
理想气体的状态函数） （3） E = E (T )（理想气体的状态函数） ） （4） 各等值过程的特性 . ）
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
三个量： 三个量：
W = p (V2 − V1 ) = ν R (T2 − T1 )
Q p = νC p,m (T2 − T1 )
E2 − E1 =νCV ,m (T2 − T1)
第十三章 热力学基础
14
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
1313-4 理想气体的等温过程和绝热过程
等温过程曲线的斜率 等温过程曲线的斜率
p
T =常量
Q=0
∆pa∆pT
A C B
pV = 常量
pdV + Vdp = 0
dp pA ( )T = − dV VA
pA
o
V A ∆V V B
V
绝热线的斜率大于等温线的斜率. 绝热线的斜率大于等温线的斜率
第十三章 热力学基础
第十三章 热力学基础
31
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
一汽缸内有一定的水， 例3 一汽缸内有一定的水，缸壁由良导 热材料制成. 热材料制成 作用于活塞上的压强1.013 × 10 5 Pa 摩擦不计. 开始时，活塞与水面接触. 摩擦不计 开始时，活塞与水面接触 若环境 (热源 温度非常缓慢地升高到100 C . 求把单 热源) 热源 位质量的水汽化为水蒸气，内能改变多少? 位质量的水汽化为水蒸气，内能改变多少 已知 汽化热 密度
W12 = −4.70 × 10 4 J
CV ,m = 20.44 J ⋅ mol−1 ⋅ K −1
（3）对等温过程 ）
V1 p ′ = p1 ( ) 2 V2 = 1 . 01 × 10
6
p
p2
' p2
Pa
2T 2
2'
对绝热过程， 对绝热过程， 有
V1 γ p2 = p1 ( ) V2 = 2.55 × 10 Pa
d Q p = C p ,m dT = dE + pd V
d E = CV ,m d T
p d V = R dT
可得摩尔定压热容和摩尔定体热容的关系 可得摩尔定压热容和摩尔定体热容的关系 定压热容和摩尔定体
C p,m = CV ,m + R
摩尔热容比
γ = Cp,m CV ,m
第十三章 热力学基础
13
V1 γ −1 T2 = T1 ( ) = 753 K V2
' p2
2T 2
2'
T2' = T1 Q=0
p1
T1
o V =V ' =V 10 V V 2 2 1 1
28
T = 常量
1
第十三章 热力学基础
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
W12 = −νCV ,m (T2 − T1 )
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
状态量） 一 内能 （状态量）
实验证明系统从状态A 变化到状态B， 实验证明系统从状态 变化到状态 ， 可以采用做功和传热的方法， 可以采用做功和传热的方法，不管经过 什么过程，只要始末状态确定， 什么过程，只要始末状态确定，做功和 传热之和保持不变. 传热之和保持不变
26
物理学
第五版
1313-4 理想气体的等温过程和绝热过程
的氢气， 例1 设有 5 mol 的氢气，最初温度 20 C ， 压强 1.013×105 Pa ，求下列过程中把氢气压缩 需作的功: 为原体积的 1/10 需作的功 （1）等温过程 ） （2）绝热过程 （3）经这两过程后，气体的 ） ）经这两过程后， p 2 压强各为多少？ 压强各为多少？ T T' =T
第十三章 热力学基础
17
物理学
第五版
1313-4 理想气体的等温过程和绝热过程 等温膨胀 等温膨胀 等温压缩 等温压缩
p p1
1 ( p1 , V1 , T )
p p1
2
1 ( p1 , V1 , T )
p2
( p2 ,V2 ,T )
W
V1
p2
( p2 ,V2 ,T )
W
V1
2
o
V2 V
o
V2 V
第十三章 热力学基础
7
物理学
第五版