1趋中回归现象
回归分析中的案例分析解读

回归分析是统计学中一种重要的分析方法,它用于探讨自变量和因变量之间的关系。
在实际应用中,回归分析可以帮助我们理解变量之间的相互影响,预测未来的趋势,以及解释一些现象背后的原因。
本文将通过几个实际案例,来解读回归分析在现实生活中的应用。
首先,我们来看一个销售数据的案例。
某公司想要了解广告投入对产品销量的影响,于是收集了一段时间内的广告投入和产品销量数据。
通过回归分析,他们得出了一个线性方程,表明广告投入对产品销量有显著的正向影响。
这个结论使得公司更加确定了增加广告投入的决策,并且在后续的实施中也取得了预期的销售增长。
接下来,我们来看一个医疗数据的案例。
一家医院想要探讨患者的年龄、性别、体重指数等因素对疾病治疗效果的影响。
通过回归分析,他们发现年龄和体重指数与治疗效果呈显著的负相关,而性别对治疗效果影响不显著。
这个研究结果为医院提供了重要的临床指导,使得医生们在治疗过程中更加关注患者的年龄和体重指数,以提高治疗效果。
除此之外,回归分析还可以应用在金融领域。
一家投资机构想要了解各种因素对股票价格的影响,于是收集了大量的股票市场数据。
通过回归分析,他们发现了一些关键的影响因素,比如市场指数、行业风险等,这些因素对股票价格都有一定的影响。
这些结论为投资机构提供了重要的决策参考,使得他们在投资过程中能够更加准确地评估风险和收益。
此外,回归分析还可以用于市场调研。
一家公司想要了解产品价格对销量的影响,于是进行了一次调研。
通过回归分析,他们发现产品价格与销量呈负相关关系,即产品价格越高,销量越低。
这个结论使得公司意识到自己的产品定价策略可能存在问题,于是他们调整了产品价格,并且在后续销售中取得了更好的效果。
总的来说,回归分析在实际生活中有着广泛的应用。
通过对一些案例的解读,我们可以看到回归分析在不同领域中的作用,比如市场营销、医疗、金融等。
通过回归分析,我们可以更加深入地了解变量之间的关系,从而为决策提供科学的依据。
回归分析

1 回归分析内涵及相关原理你知道日常生活中的天气预报是如何实现的吗?气象学家根据既往的温度、湿度以及降雨等资料,就可以预报未来一段时间某地的天气变化情况。
这要求对这些变量之间的关系有精确的掌握。
前面的学习中,我们知道相关分析可用来帮助我们分析变量之间关系的强度;而倘若要确定变量之间数量关系的可能形式也即数量模型,则通常可采用回归分析法。
回归分析的应用十分广泛,它不但适用于实验数据,还可以分析未作实验控制的观测数据或历史资料。
有人可能会好奇,为什么叫“回归”这个名称,它有什么具体含义?实际上,回归这种现象最早由英国生物统计学家高尔顿在研究父母亲和子女的遗传特性时所发现的一种有趣的现象:身高这种遗传特性表现出“高个子父母,其子代身高也高于平均身高;但不见得比其父母更高,到一定程度后会往平均身高方向发生‘回归’”。
这种效应被称为“趋中回归”。
现在的回归分析则多半指源于高尔顿工作的那样一整套建立变量间数量关系模型的方法和程序。
1.1 回归分析的概念回归分析是关于研究一个叫做因变量的变量对另一个或多个叫解释变量的变量的依赖关系,其用意在于通过后者(在重复抽样中)的已知或设定值,去估计和(或)预测前者的(总体)均值。
回归分析运用十分广泛,回归分析按照涉及的自变量的多少,可分为一元回归分析和多元回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。
如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
1.2 回归分析的基本原理两变量间的相关关系可以用散点图来反映,图中的每个点都代表一个变量配对样本点,它是自变量与因变量间关系的一个具体代表。
在相关分析中,我们详细地分析过相关关系的几何意义和数量特点。
显然,若这些散点都落在一条直线上(完全相关),则该条直线当然能够代表变量间的数量关系——一次函数关系。
第3章 动物行为学中的一些基本概念和基本行为型

十一、行为的释放机制和关键刺激
1、行为的释放机制(刺激过滤机制) 指与过滤刺激有关的各部分中枢神经系统的总和 (包括感觉器官),即生物体内参与一个特定行为 释放的各种结构成分之总和。该机制能够确保动物 的某一特定行为型只能被某种适当的刺激所释放。 如眼蝶的取食和求偶行为是由不同释放机制释放的。 2、关键刺激 关键刺激是指释放动物某一反应所必需的刺激, 往往是指物种间的信息传递,只同接受信息的一方 有利害关系。
十、刺激过滤
1、外周过滤 (1)不感知不必要信息。 (2)通过侧抑制少传递刺激到中枢神经系统。 侧抑制:某感觉细胞受到刺激发生兴奋,在传递这种兴 奋时能够减弱,甚至防止相邻感觉细胞发生兴奋。 (3)对信息能够作出反应,但不传递到中枢神经系统。 (4)外周过滤的局限性 ①生物信息的性质太复杂,感觉器官往往难以完全适应。 ②一种感受器必须对各种属于不同功能系统的信息发生反 应,感受器的简单过滤方法难以满足多功能的需要。 2、中枢过滤 研究的最好方法是利用模型做实验,就可以确定刺激中的 哪些成分是必要的,哪些成分是多余的,更好地研究动物行 为的机制。
第三章 动物行为学中的 一些基本概念和基本行为型
一、反射 二、动性 三、趋性 四、横定向 五、释放行为的刺激阈值和空放行为 六、行为反应的疲劳现象 七、欲求行为和完成行为 八、动物行为的动机 九、动机的测定 十、刺激过滤 十一、行为的释放机制和关键刺激 十二、释放者 十三、信号刺激 十四、刺激的累积 十五、超常刺激 十六、固定行为型 十七、本能与学习 十八、利他行为
十二、释放者
1、概念 释放者是指引起同种个体或异种个体发生一定反应的某些 形态、结构或行为型,释放者使信息发送方和接收方都能受 益。 2、特点 醒目和容易辨认。
十二、释放者
统计学中的回归分析方法

统计学中的回归分析方法统计学是一门应用科学,可以帮助我们理解和解释数据。
在统计学中,回归分析是一种常用的方法,用于研究变量之间的关系以及预测未来的趋势。
回归分析是一种基于概率论和数理统计的方法,用于描述和模拟数据的线性关系。
通过回归分析,我们可以确定一个或多个自变量与因变量之间的数学关系。
这使得我们能够根据已有的数据预测未来的趋势和结果。
回归分析的核心概念是回归方程。
回归方程是用于描述自变量与因变量之间关系的数学公式。
在简单线性回归中,回归方程可以用y = a+ bx来表示,其中y是因变量,x是自变量,a和b是回归方程的参数。
通过回归方程,我们可以计算自变量对因变量的影响程度。
回归的目标是找到最适合数据的回归方程,并通过该方程对未知数据做出预测。
回归分析有不同的类型。
简单线性回归是最基本的形式,用于研究两个变量之间的关系。
多元线性回归则用于研究多个自变量对因变量的影响。
此外,还有逻辑回归用于处理二元分类问题,和多项式回归适用于非线性关系。
回归分析还可以帮助我们评估各个变量对因变量的相对重要性。
通过计算回归方程中各个参数的显著性,我们可以确定哪些自变量对因变量的影响更为显著。
在回归分析中,误差的处理也是非常重要的。
误差代表了回归模型无法解释的数据波动。
最小二乘法是一种常用的方法,用于最小化回归模型的总体误差。
除了简单的回归分析,还有一些衍生的方法可以扩展回归模型的适用范围。
岭回归和Lasso回归是用于应对多重共线性问题的方法。
弹性网络回归则是将岭回归和Lasso回归进行结合,取两种方法的优点。
回归分析在许多领域都有广泛的应用。
在经济学中,回归分析常用于研究经济指标之间的关系。
在市场营销中,回归模型可以用于预测销量和分析市场趋势。
在医学研究中,回归分析可以帮助研究人员研究疾病和治疗方法之间的关系。
总之,统计学中的回归分析是一种强大的工具,用于研究变量之间的关系和预测未来的趋势。
通过回归分析,我们可以理解数据并做出有意义的预测。
第二章 一元线性回归模型 知识点
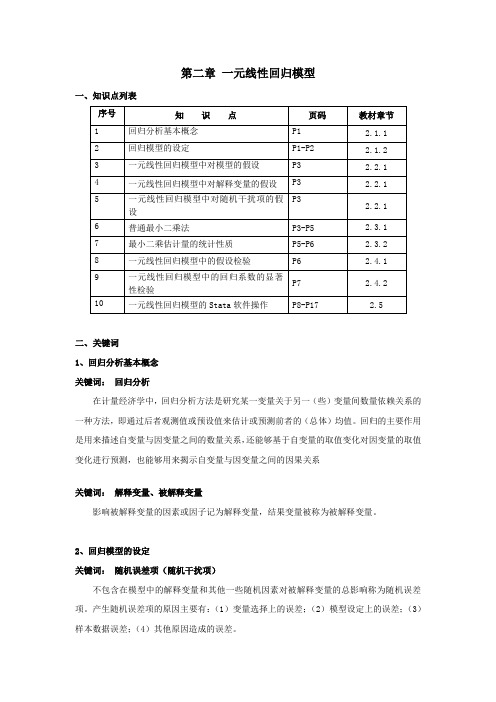
第二章一元线性回归模型一、知识点列表二、关键词1、回归分析基本概念关键词:回归分析在计量经济学中,回归分析方法是研究某一变量关于另一(些)变量间数量依赖关系的一种方法,即通过后者观测值或预设值来估计或预测前者的(总体)均值。
回归的主要作用是用来描述自变量与因变量之间的数量关系,还能够基于自变量的取值变化对因变量的取值变化进行预测,也能够用来揭示自变量与因变量之间的因果关系关键词:解释变量、被解释变量影响被解释变量的因素或因子记为解释变量,结果变量被称为被解释变量。
2、回归模型的设定关键词:随机误差项(随机干扰项)不包含在模型中的解释变量和其他一些随机因素对被解释变量的总影响称为随机误差项。
产生随机误差项的原因主要有:(1)变量选择上的误差;(2)模型设定上的误差;(3)样本数据误差;(4)其他原因造成的误差。
关键词:残差项(residual )通过样本数据对回归模型中参数估计后,得到样本回归模型。
通过样本回归模型计算得到的样本估计值与样本实际值之差,称为残差项。
也可以认为残差项是随机误差项的估计值。
3、一元线性回归模型中对随机干扰项的假设 关键词:线性回归模型经典假设线性回归模型经典假设有5个,分别为:(1)回归模型的正确设立;(2)解释变量是确定性变量,并能够从样本中重复抽样取得;(3)解释变量的抽取随着样本容量的无限增加,其样本方差趋于非零有限常数;(4)给定被解释变量,随机误差项具有零均值,同方差和无序列相关性。
(5)随机误差项服从零均值、同方差的正态分布。
前四个假设也称为高斯马尔科夫假设。
4、最小二乘估计量的统计性质关键词:普通最小二乘法(Ordinary Least Squares ,OLS )普通最小二乘法是通过构造合适的样本回归函数,从而使得样本回归线上的点与真实的样本观测值点的“总体误差”最小,即:被解释变量的估计值与实际观测值之差的平方和最小。
ββ==---∑∑∑nn n222i i 01ii=111ˆˆmin =min ()=min ()i i i i u y y y x关键词:无偏性由于未知参数的估计量是一个随机变量,对于不同的样本有不同的估计量。
回归分析在统计学中的作用

回归分析在统计学中的作用统计学作为一门应用广泛的学科,主要研究数据的收集、整理、分析和解释,以便对现象和问题进行理解和预测。
在统计学中,回归分析是一种常用的数据分析方法,被广泛应用于各个领域,如经济学、社会学、医学和环境科学等。
本文将探讨回归分析在统计学中的作用,并展示其在实际问题中的应用。
一、回归分析的概念和原理回归分析是一种用于分析自变量与因变量之间关系的统计方法。
其基本原理是通过建立数学模型,揭示自变量对因变量的影响程度和趋势。
在回归分析中,自变量可以是一个或多个变量,而因变量则是所要预测或解释的变量。
二、回归分析的种类和应用1.简单线性回归简单线性回归是回归分析中最基础的方法之一,它研究的是只有一个自变量与一个因变量之间的关系。
在实际应用中,可以利用简单线性回归来分析两个变量之间的相关性,并通过拟合直线来预测因变量的取值。
2.多元回归多元回归是一种比简单线性回归更为复杂的分析方法,它研究的是多个自变量与一个因变量之间的关系。
多元回归可以帮助人们了解多个影响因素对结果的综合影响,并提供更准确的预测和解释。
3.非线性回归除了线性关系,回归分析也可以研究非线性关系。
非线性回归用来分析自变量与因变量之间的非线性关系,并通过拟合非线性曲线来预测因变量的取值。
4.时间序列分析时间序列分析是回归分析的一种特殊形式,它专门用于研究时间上的变化和趋势。
时间序列回归可以帮助人们预测未来的趋势和变化,并对过去的数据进行解释。
三、回归分析的应用案例1.经济学中的回归分析在经济学中,回归分析被广泛应用于研究宏观经济和微观经济问题。
例如,经济学家可以利用回归分析研究GDP与产出、失业率、通货膨胀等因素之间的关系,以及对未来经济发展的预测。
2.医学中的回归分析医学研究中常常需要考察自变量对生物指标或健康结果的影响。
例如,医学研究者可以利用回归分析来研究生活方式与血压、血糖或心血管疾病等之间的关系,并为疾病的预防和治疗提供科学依据。
数据分析中的回归分析与预测模型

数据分析中的回归分析与预测模型在当今信息爆炸的时代,数据已经成为了一种重要的资源。
随着大数据技术的发展,数据分析也逐渐成为了许多行业中不可或缺的一环。
而在数据分析的过程中,回归分析与预测模型是两个重要的工具。
回归分析是一种通过建立数学模型来描述变量之间关系的方法。
它的基本思想是,通过观察已知的自变量和因变量的取值对,建立一个数学模型,然后用这个模型来预测未知的因变量取值。
回归分析可以用来探索变量之间的关系、预测未来的趋势以及评估变量之间的影响程度。
预测模型是一种通过利用已知的数据来推断未知数据的方法。
它基于已有的数据,通过建立一个数学模型,来预测未来的趋势或者未知变量的取值。
预测模型可以应用于各种领域,如金融、市场营销、医疗等。
通过预测模型,企业可以更好地了解市场需求,制定合理的销售策略;医疗机构可以预测疾病的发生概率,提前采取相应的防控措施。
回归分析和预测模型之间有着紧密的联系。
回归分析可以作为预测模型的一种方法,通过建立回归方程来预测未知的因变量取值。
而预测模型则可以通过回归分析的结果来进行优化和调整。
两者相辅相成,共同为数据分析提供了强大的工具。
在进行回归分析和预测模型时,我们需要注意一些问题。
首先,选择合适的自变量和因变量。
自变量应该与因变量之间存在一定的相关性,否则建立的模型将无法准确预测。
其次,我们需要选择合适的回归方法和模型。
常见的回归方法有线性回归、多项式回归、逻辑回归等,每种方法都有其适用的场景。
最后,我们需要对模型进行评估和验证。
通过比较模型的预测结果与真实值,我们可以评估模型的准确性和可靠性。
回归分析和预测模型在实际应用中有着广泛的应用。
在金融领域,回归分析可以用来预测股票价格的变化趋势,帮助投资者做出合理的投资决策。
在市场营销领域,预测模型可以用来预测用户的购买行为,帮助企业制定个性化的推广策略。
在医疗领域,回归分析可以用来预测疾病的发生概率,帮助医生制定个性化的治疗方案。
新中式风格的发现趋势

新中式风格的发现趋势
1. 回归中式元素:在建筑、室内设计中,越来越多地使用传统中式的元素,如明式家具、徽州建筑等。
传统的中式设计与现代设计风格的完美结合,让中式风格焕发出新的光彩。
2. 简约化:新中式设计注重砍繁就简,简化造型,以达到统一性、和谐性和美感。
3. 材质选用:新中式设计强调材料的真实性和质感,追求自然的美感。
青色石板、黑色板岩、绿色花岗岩等原生态材料,都是中式风格设计的常用材料。
4. 色彩运用:主要以红、黄、黑、绿、蓝为基础色,通过巧妙的搭配和运用,让整个设计更加和谐统一。
5. 灯光装饰:中式设计注重灯光的设计与运用。
通过巧妙设计的灯光,可以让建筑物或房间在夜间更加美观,更有历史文化的感觉。
6. 圆形造型:在中式风格中,圆形造型被广泛运用,比如“天坛”、“将军庙”、墙壁、置物架等。
7. 纹饰设计:中式设计的纹饰通常采用云、龙、凤等传统图案,通过特殊的造型和色彩的运用,使整个设计更富有中国传统文化的韵味。
总的来说,新中式设计比传统的中式设计更为简约、现代化。
传统文化与现代设计的合二为一,引起了更多年轻人的关注和欣赏,使中式文化的传承得以延续。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1趋中回归现象
当某些被试在一个变量上的取值远离群体均值(特别低或特别高),这些被试在同一个变量上的另一次观测值或在其它相关的变量上的观测值,往往会比较靠近均值。
这就是所谓的趋中回归(regression toward the mean)现象。
其实,“趋中回归”并不是什么新概念,它就是当年英国生物学家兼统计学家Galton所说的“回归”(regression)。
他根据人体身高具有遗传性却不会出现两极分化的事实,得出如下结论:高个子人群的子代平均身高虽然高于子代总平均身高(遗传的影响),但低于他们父代的平均身高;矮个子人群的子代平均身高虽然低于子代总平均身高,但高于他们父代的平均身高。
就是说,子代的身高有向平均值靠拢的趋向,Galton用“回归”一词来描述子代身高与父代身高的这种关系。
不过,现在统计中通常所说的“回归”一词,已经没有多少原始含义,只是沿用成习,人们继续使用这个词而已。
这样一来,当需要考虑Galton所说的回归时,为了避免混淆,使用“趋中回归”一词。
(本文中,如果只说“回归”,指的是通常统计中的回归,“回归”与“趋中回归”是两个不同的但又关联的概念。
)趋中回归是一种非常普遍的现象。
例如,一个球队在上一届联赛中表现出色,在下一届联赛的表现往往不如上一届;一个走红的文学作品(小说、电影或电视剧等),其续集(如果有的话)往往令人失望;高考状元在大学期间的成绩很难保持名列前茅;在一个场合表现得非常聪明(或愚笨)的学生在另一个场合往往表现得没那么聪明(或愚笨),等等。
然而,这种司空见惯的趋中回归现象,所引起的结果经常被错误地解释[1]。
