第六章 结构振动特征值问题的矩阵摄动法
结构动力学中的特征值反问题

南京航空航天大学博士学位论文结构动力学中的特征值反问题姓名:***申请学位级别:博士专业:一般力学与力学基础指导教师:***20060601南京航空航天大学博士学位论文摘要本文研究了结构动力学中的特征值反问题,包括弹簧-质点系统振动反问题、离散梁振动反问题、阻尼振动系统的振动反问题以及振动杆结构探伤问题。
全文主要包括以下内容:首先,研究了弹簧-质点系统的振动反问题。
对二自由度简单连接度弹簧-质点系统分别通过加刚性约束、弹性约束和质量摄动得到修改系统,研究了利用原系统和修改系统的两组特征值(频率)和修改量识别系统的物理参数问题,给出了解的表达式。
对于多自由度简单连接度弹簧-质点系统,研究了增容修改系统的频率反问题。
提出了由多自由度简单连接弹簧-质点系统的四个和五个特征对(频率和模态)识别系统物理参数的振动反问题,分别研究了解的存在性,给出了解的表达式、相应算法和算例。
提出并研究了一类混合连接弹簧-质点系统的振动反问题,提出了利用三个特征对(频率和模态)以及部分系统物理参数识别系统其它物理参数的振动反问题,研究了解的存在性,给出了解的表达式、相应算法和模型算例。
其次,研究了有限差分离散梁振动反问题,利用有限差分法得到振动梁的弹簧-质点-刚杆模型,质量矩阵为对角矩阵而刚度矩阵为对称五对角矩阵。
提出了基于三个特征对的频率模态反问题,研究了解的存在性,给出了解存在惟一的充要条件和解的表达式、数值算法和算例。
再次,研究了阻尼振动系统中的二次特征值反问题。
研究了阻尼弹簧-质点系统的物理参数识别,包括:由全部频率信息模态识别阻尼振动系统的结构物理参数;由部分频率模态信息识别比例阻尼振动系统的结构物理参数;由两对频率模态信息识别比例阻尼振动系统的结构物理参数;由频率模态信息识别非比例阻尼振动系统的结构物理参数。
对每种提法分别研究了问题解的存在性,给出了数值算法,并对每种问题给出了阻尼振动模型算例。
最后,研究了振动杆结构探伤的特征值反问题。
《结构力学课件》矩 阵 位 移 法

将(17—21)及(17—25) T F 式代入上式得: e
K
T
e
T e
e
F
T
K
T e
e 另 [T]T[ K ] [I]=[K]e 则 用结分点块式表示为:
{F}e=[K]e{}e
e Fi e F j e Kii e K ji e e Kij i e Ke jj j
• 注:1) F , 为结构坐标的杆端力和杆端位移。 • 2) Kij e 表示单元e 的j端三个位移分别产生单位位移时在i 端各力 • 分量分别产生的力。 • 3) Kii , Kij , K ji , K jj 分别为单元在结构整体坐标中刚度。
e e
返回 下一张 上一张 小结图17-4来自返回 下一张 上一张 小结
• 17.1.6 引入支承条件,求结点位移
• 已知上例支承条件 1 =0,连同已获得的[K],以及各结点 荷载值(M1、M2、及M3=0)一起代入基本方程(7—6)式中,得:
4i1 2i 1 0 2i1 4i1 4i 2 2i 2 0 0 2i 2 2 4i 2 3 M1 M 2 0
{
矩阵位移法是以位移法为力学原理,应用矩阵理论,以电子 计算机为工具的结构分析方法。 有限单元法包含两个基本环节:一是单元分析;一是整体分析。
在矩阵位移法中:单元分析的任务是建立单元刚度方程,形 成单元刚度矩阵——讨论任意坐标系中单元刚度方程的通用形式; 整体分析的任务是将单元及合成整体,由单元刚度矩阵按照 刚度集成规则形成整体刚度矩阵,建立整体结构的位移法基本方 程,从而求解。 直接由单元刚度矩阵导出整体刚度矩阵的集成规则,是矩阵 位移法的核心内容。
高等结构振动学-第6章-结构振动特征值问题的矩阵摄动法

)
({u0(s)}T [K1]{u1(i)} (0i){u0(s)}T [M1]{u1(i)}
1(i){u0(s)}T [M 0 ]{u1(i)} 1(i){u0(s)}T [M1]{u0(i)})
(6-29)
当 i s 时, ci(2) 的确定如下:
n
以
{u
(i 0
)
}T
)}
所以,代入(6-8)式得:
{u1(i)}
n s 1
(i ) 0
1
( s ) 0
({u0(s)}T [K1]{u0(i)} (0i){u0(s)}T [M1]{u0(i)}){u0(s)}
si
1 2
({u0(i)}T
[M1]{u0(i)}){u0(i)}
故一阶摄动解为:
(6-22) (6-23)
)}
{u0(i
)
}T
[M1
]{u1(i)
}
{u1(i
)}T
[
M
1
]{u0(i
)})
(6-32)
故特征向量的二阶摄动解为:
{u2(i)}
n s 1
(i) 0
1
( s ) 0
({u0(s)}T [K1]{u1(i)}
si
(i 0
){u0( s
)}T
[
M
1]{u1(i
)}
{u (i) (s) 10
n
(i 0
)
[
M
0
]
c (1) s
{u 0( s
)
}
(i) 0
结构动态设计的矩阵摄动理论(陈塑寰著)PPT模板

05 第3章 重频结构振动分析 的矩阵摄动理论
第3章 重频结构振动分析的矩阵摄动理论
3.1 引言
1
3.2 重频模态的摄动理
论
2
3.3 重频模态一阶摄动
3
的近似模态展开法
3.4 重频模态一阶摄动
计算的高精度模态展开法
4
3.5 利用重频模态计算
5
重频模态导数的精确方法
3.6 计算模态向量一阶
摄动的胡海昌方法
结构动态设计的矩阵摄动理论(陈 塑寰著)
演讲人
2 0 2 x - 11 - 11
01 序
序
02 前言
前言
03 第1章 结构振动分析的有 限元方法
第1章 结 构振动分析 的有限元方 法
01 1 .1 引言
02 1 .2 离 散 系 统 的
hamilton变分原理
03 1 .3 建 立 结 构 振动 04 1 .4 单 元 力 学 特性
法
2.3.2 和 rayleigh商相 结合的摄动法
2.3.3 数值 例子
第2章 孤立特征值的矩阵摄动理论
2.4 振型一阶导数的高精度截尾模态展开法
01
2.4.1 计算振 型一阶导数的 wangb.p.方法
02
03
2.4.2 计算振 型一阶导数的高 精度截尾模态展 开法
2.4.3 数值例 子
第2章 孤立特征 值的矩阵摄动理论
1.11.1 中心差分
法
1.11.2 wilson-
θ方法
1.11.3 newmar
k方法
04 第2章 孤立特征值的矩阵 摄动理论
第2章 孤立特征值的矩阵摄动理论
2.1 引言
2.3 摄动法的改进
结构力学(I)-结构静力分析篇6 矩阵位移法解析

FP 结点
1,2,3 ----结构结点编码(总码) (1,2,3) ----结点位移编码
1 2 ----杆端结点编码(局码)
1 2 ----单元编码
1
1
3(5,6)FP
2 2
2
1
1(1,2)
2(3,4)
单元方向 1 2
11 / 105
第六章 矩阵位移法 §6-2 单元刚度方程
建立单元的结点力和结点位移之间关系的过 程称单元分析,形成的方程称单元刚度方程。
6EI l2 2 EI l
12EI l3
6EI l2 12 EI l3
6EI l2
6 EI l2 2 EI l
6EI l2 4 EI l
1 2 3 4
e
刚度方程
18 / 105
第六章 矩阵位移法
12 EI
l3 6EI
k
e
l2
12EI l3
6 EI l2
位移法 是先求结点位移,再换算成力,该法的计 算自动化和通用性强,目前广为采用。
6 / 105
第六章 矩阵位移法
二、基本假设和基本原理
线弹性、小变形。满足叠加原理、功能原理
三、结构矩阵分析的基本思路
化整为零
(单元分析)
集零为整
(结点力平衡、位移协调)
7 / 105
第六章 矩阵位移法
四、拟解决的问题
6EI l2
1
4EI l
2
6EI l2
3
2EI l
4
F3e
12EI l3
1
6EI l2
2
12EI l3
3
6EI l2
4Hale Waihona Puke F4e6EI l2
6《结构动力学》-第六章
x2
x3
k4
x4
k5
x5
m2
k3
m3
m4
m5
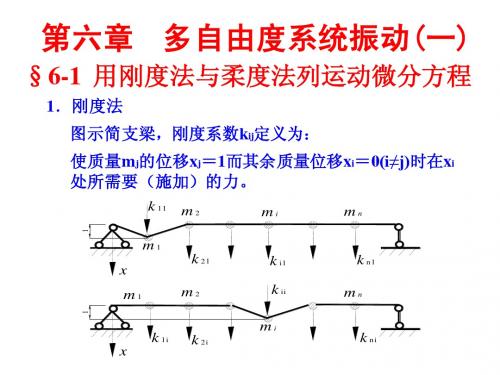
解:首先用力使m1产生单位位移,并用力使其余质量不动, 首先用力使 产生单位位移,并用力使其余质量不动, 则需要给m 的力为k 的弹性力和, 则需要给 1的力为 1与k2的弹性力和,即k11=k1+k2。此时 m2需加力为 2,沿x的负方向,即k21=-k2,其余质量不必 需加力为k 的负方向, 的负方向 施加任何力, 施加任何力,即k31=k41=k51=0。 。 用类似方法可得其余刚度系数,于是有: 用类似方法可得其余刚度系数,于是有:
m2上加单位力,各质量的位移分别为: 上加单位力,各质量的位移分别为:
a12 = 1 k1 a 22 = 1 1 + k1 k 2 a 32 = a 22 = 1 1 + k1 k 2
〈例〉求图示三自由度系统的刚度矩阵和柔度矩阵。 求图示三自由度系统的刚度矩阵和柔度矩阵。
k1
m1
x1 k2
x2
x3 m3
LL
用矩阵符号可写成: 用矩阵符号可写成:
LL
mn &&n = −k n1 x1 − k n 2 x2 − LL − k nn xn + Fn (t ) x
& [M ]{X& }+ [K ]{X } = {F (t )}
〈例〉求图示五自由度系统的刚度矩阵。 求图示五自由度系统的刚度矩阵。
k1
m1
x1 k2
或写成: 或写成:
& {X } + [A][M ]{X& } = {0}
在刚度矩阵[K]非奇异条件下,柔度矩阵 与刚度矩 在刚度矩阵 非奇异条件下,柔度矩阵[A]与刚度矩 非奇异条件下 存在如下的互逆关系: 阵[K]存在如下的互逆关系: 存在如下的互逆关系
振动分析矩阵迭代法

1 2
2
333Y3(0)
1 3
2
...
这些惯性力产生的挠度是
v (1) 1
~ff
( I
0)
~f
*
m
112Y1(
0)
223Y2(
0)
1 2
2
2
333Y3(0)
1 3
...
(4) 1
1.000 17.121
0.320 5.287
v v (4)
(5)
1
1
1.000 17.082
0.653 11.121 0.650 11.082
0.306 5.182 0.303 5.159
12
max(v1(s1) )
(s)
max(v1 )
v(4) 11
v(5) 11
210.77
缺点:柔度矩阵是满阵,与窄带刚度矩阵相 比的运算相比会使计算效率降低。
补充:基于刚度矩阵的动力矩阵: E m1K 由于收敛于最高阶阵型,所以实际应用不大。
逆迭代法
基本思路:逆迭代法是利用是利用刚度矩阵窄 带性质的首选方法,因为其是使用刚度矩 阵的逆矩阵,所以此法向最低阵型收敛。 为保证刚度矩阵K的窄带性质,不形成动力 矩阵E,而是把假定的位移向量和质量举证 结合,然后求解基于刚度的平衡联立方程 组得到改进的位移向量,解方程组是常采 用LU分解法。
用迭代法反复进行迭代,就可以得到体系 的最低频率和相应的阵型。
迭代收敛性的证明:
Stodola法和Holzer法 Stodola法是先假定初始振型并不断迭代调整
第六章 摄动方法

t a, b 可以是无穷区间,或闭区间, 1 ,设 f t
为连续函数; F 对 t 连续,对其余变量在其变化范 围内解析,则该问题称为摄动问题 P , 0 时对应的问题称为退化问题 P0 ,若 P 问题的解 u t, 当 0 时,对 t a, b 有一致渐近幂级数,即
" i i 1
(10)
第二步:将所有的项都按小参数(这里是 a )展开,使
每一项都可写成一个 a 的幂级数。利用 sin x 的展开
式,上式中的第二项为:
a sin ai ai i 0
1
a i i a a i a a a … i i 0 3! i 0
1 1 1 cos t cos3t t sin t 192 16 192
注意到,上面的求解都是形式上的。设
t , i t i
i 0
(12)
由此可得一阶近似:
t, 0 t 1 t
0
第六章 摄动方法
摄动方法是一种重要的应用数学方法,它在力学,物 理和众多的工程学科中有着广泛的应用。 工程技术中归纳出来的数学模型,其中不少是含有小 参数的,且方程的准确解难以获得。
利用计算机进行数值积分,虽然可以给
出定解问题的数值解,但很难给出物理现象的 全貌和一般规律,利用摄动法可以求得解析形 式的近似解,对物理系统进行相当精确的定量 和定性讨论。这里,主要讨论正则摄动方法 和奇异摄动方法。
§1 正则摄动方法
例1:已知初值问题
dy 2 1 y dx y 0 0
(1)
的解
yy
0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 结构振动特征值问题的矩阵摄动法§6.1 概述工程振动问题中经常遇到结构有小改动的情形,例如结构的制造误差、结构的小修改设计、对结构参数改变进行灵敏度分析等。
这些情况都有一个共同的特点,就是结构的参数仅发生很小的变化。
结构参数的小变化所引起的结构振动特性变化问题,对工程结构优化设计有重要意义。
经典的方法是每修改一次方案就需要求解一次结构的固有特性,即求解广义特征值问题。
这对于大型结构的振动分析,是非常麻烦的。
我们希望能找到一种能够利用修改前结构的固有特性信息,且计算量小的方法,来解决上述问题。
矩阵摄动法就是这种结构特征值重分析和灵敏度快速分析的计算方法。
§6.2 孤立特征值的摄动法对离散系统特征值问题,假定已经得到了其特征对的解:}]{[}]{[)(00)(0)(00i i i u M u K λ=(6-1)][],[00M K 分别为参数未变化的原结构刚度矩阵和质量矩阵,第i 个特征值2)(0)(0)(i i ωλ=,)(0i ω为第i 阶固有频率,}{)(0i u 为第i 阶特征向量(固有模态)。
结构参数的变化或修改设计一般通过刚度矩阵和质量矩阵的改变反映出来。
即][][][10M M M ε+= (6-2) ][][][10K K K ε+= (6-3)ε称为小参数。
先看)(i 0λ是单根的情形。
上标)(i 代表第i 个根,下标0)(代表参数未变化的原结构。
从物理意义上知道,绝大多数情况下,质量阵和刚度阵只有小变化时,特征值和特征向量也只有小量变化,根据摄动理论,特征值和特征向量按小参数ε展开为:+++=+++=)(22)(1)(0)()(22)(1)(0)(}{}{}{}{i i i i i i i i u u u u λεελλλεε (6-4)代入方程(6-1),略去)(2εO 以上的项,比较ε同次幂的系数,得到:}]{[}]{[)(00)(0)(00i i i u M u K λ= (6-5)}]{[}]{[}]{[}]{[}]{[)(00)(1)(01)(0)(10)(0)(01)(10i i i i i i i i u M u M u M u K u K λλλ++=+(6-6) }]{[}]{[}]{[}]{[}]{[}]{[}]{[)(00)(2)(01)(1)(10)(1)(11)(0)(20)(0)(11)(20i i i i i i i i i i i i u M u M u M u M u M u K u K λλλλλ++++=+(6-7))(i 1λ、)(i 2λ、}{)(1i u 、}{)(2i u 分别是特征值与特征向量的第一阶摄动和第二阶摄动。
因此,只要解出了原系统的特征值和特征向量,并知道了质量阵和刚度阵的改变量][1M 、][1K ,就可以求出特征值的摄动解。
【一阶摄动】由展开定理,∑==+++=ns s s i u c u c u c u c u 1)(0)1()3(0)1(3)2(0)1(2)1(0)1(1)(1}{}{}{}{}{ (6-8)代入(6-6)式}]{[}]{[}{][}]{[}{][)(00)(1)(01)(01)(0)1(0)(0011)(0)1(0i i i i ns s s i ins s s u M u M u c M u K u c K λλλ++=+⋅∑∑== (6-9)方程两边乘以Ts u }{)(0并利用正交性公式: isi Ts s is i T s u M u u K u δλδ==}]{[}{}]{[}{)(00)(0)(0)(00)(0 (6-10)得到:is i i T s i i s i T s s s u M u c u K u c δλλλλ)(1)(01)(0)(0)(0)1(01)(0)(0)1(}]{[}{}]{[}{++=+ (6-11)即:}]{[}{}]{[}{)()(01)(0)(001)(0)(1)(0)(0)1(i T s i i T s is i s i s u M u u K u c λδλλλ-=+- (6-12)当i s =时,)(0)(0s i λλ=,1=is δ}]{[}{}]{[}{)(01)(0)(0)(01)(0)(1i T i i i T i i u M u u K u λλ-= (6-13)当i s ≠时,0=is δ})]{[}{}]{[}({1)(01)(0)(0)(01)(0)(0)(0)1(i T s i i T s s i s u M u u K u c λλλ--=(6-14) 根据振型的正交性:1}]{[}{)()(=i T i u M u (6-15)将(6-4)式代入1}){}{}({])[]([}){}{}({)(22)(1)(010)(22)(1)(0=++⋅+++i i i T i i i u u u M M u u u εεεεε (6-16)展开并比较ε的同次幂项,有:1}]{[}{)(00)(0=i T i u M u(6-17)0}]{[}{}]{[}{}]{[}{)(01)(0)(00)(1)(10)(0=++i T i i T i i T i u M u u M u u M u (6-18) 0}]{[}{}]{[}{}]{[}{}]{[}{}]{[}{)(01)(1)(11)(0)(00)(2)(10)(1)(20)(0=++++i T i i Ti i T i i T i i T i u M u u M u u M u u M u u M u (6-19)用][}{0)(0M u Ti 前乘(6-8)式,根据正交性,有:}]{[}{)(10)(0)1(i T i i u M u c = (6-20)转置得到:}]{[}{)(00)(1)1(i T i i u M u c = (6-21)代入(6-18)式,得到:}]{[}{21)(01)(0)1(i T i i u M u c -= (6-22)所以,代入(6-8)式得:}}){]{[}({21}}){]{[}{}]{[}({1}{)(0)(01)(0)(0)(01)(0)(0)(01)(01)(0)(0)(1i i T i s i T s i i T s nis s s i i u u M u u u M u u K u u ---=∑≠=λλλ (6-23)故一阶摄动解为:}}){]{[}({21}}){]{[}{}]{[}({1}{}]{[}{}]{[}{)(0)(01)(0)(0)(01)(0)(0)(01)(01)(0)(0)(1)(01)(0)(0)(01)(0)(1i i T i s i T s i i T s nis s s i i i T i i i T i i u u M u u u M u u K u u u M u u K u ---=-=∑≠=λλλλλ(6-24) 【二阶摄动】同样根据展开定理:∑==ns s s i u c u 1)(0)2()(2}{}{ (6-25) 代入(6-7)式,得:}]{[}]{[}]{[}]{[}{][}]{[}{][)(00)(2)(01)(1)(10)(1)(11)(0)(01)2(0)(0)(11)(01)2(0i i i i i i i i s ns s i i s ns su M u M u M u M u c M u K u c K λλλλλ++++=+∑∑==(6-26)上式两端左乘T s u }{)(0,并利用正交性,得到:}]{[}{}]{[}{}]{[}{}]{[}{)()(01)(0)(1)(10)(0)(1)(11)(0)(0)(11)(0)(2)(0)(0)2(i T s i i T s i i T s i i T s is i s i s u M u u M u u M u u K u c λλλδλλλ---=+- (6-27)当i s =时,)(0)(0s i λλ=,1=is δ,特征值的二阶摄动解为:}]{[}{}]{[}{}]{[}{}]{[}{)(01)(0)(1)(10)(0)(1)(11)(0)(0)(11)(0)(2i T i i i T i i i T i i i T i i u M u u M u u M u u K u λλλλ---= (6-28)当i s ≠时,0=is δ})]{[}{}]{[}{}]{[}{}]{[}({1)(01)(0)(1)(10)(0)(1)(11)(0)(0)(11)(0)(0)(0)2(i T s i i T s i i Ts i i T s s i s u M u u M u u M u u K u c λλλλλ----=(6-29)当s i =时,)2(i c 的确定如下:以][}{0)(0M u Ti 乘∑==ns s s i u c u 1)(0)2()(2}{}{,根据正交性得到:}]{[}{)(20)(0)2(i T i i u M u c = (6-30)转置得:}]{[}{)(00)(2)2(i T i i u M u c = (6-31)代入到(6-18)式,得到:})]{[}{}]{[}{}]{[}({21)(01)(1)(11)(0)(10)(1)(i T i i T i i T i s i u M u u M u u M u c ++-=(6-32)故特征向量的二阶摄动解为:}}){]{[}{}]{[}{}]{[}({21}{})]{[}{}]{[}{}]{[}{}]{[}({1}{)(0)(01)(1)(11)(0)(10)(1)(0)(01)(0)(1)(10)(0)(1)(11)(0)(0)(11)(01)(0)(0)(2i i T i i T i i T i s i T s i i Ts i i T s i i T s nis s s i i u u M u u M u u M u u u M u u M u u M u u K u u ++-⋅----=∑≠=λλλλλ (6-33)§6.3 退化系统特征值的摄动当系统有重频时,称为退化系统。
退化系统特征值的摄动有两个特点。
即:参数变化后,原来的一组特征值由重特征值变为非重特征值;参数变化后,特征向量可能产生跳跃。
即)1,,1,(}{}{}{)(0)()(-++=-=m i i i j u u u j j j ∆(m 为重频数) (6-34)不再是一个小量。
下面以一个简单的例子来说明。
图示的两自由度系统,其运动方程为:()⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+----+++⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡0043)(43)(434002132323232121x x k k k k k k k k k x x m m (6-35)记:2ωλ=,则(i ) 当k k k k ===321m k2321==λλ ⎥⎦⎤⎢⎣⎡=1001][φ (6-36)(ii ) 当k k k k k k ==+=3211,δ⎥⎦⎤⎢⎣⎡==+=1001][23223211φλδλm kmk k (6-37) (iii ) 当k k k k k k ==+=2133,δ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-==+=21232321][23223231φλδλm kmk k (6-38) 由此看到,对退化系统,当参数有小的变化时,有时特征向量会发生突变的跳跃现象。
