中学数学(高中)学科竞赛集锦 (14)
高中数学竞赛赛题精选(带答案)

高中数学竞赛赛题精选(带答案)高中数学竞赛是中学生竞赛中最重要的一部分,它不仅需要智力,还需要充分发挥数学能力和思维能力。
以下是一些高中数学竞赛赛题的精选和解答。
1. 设$a_n=x^n$+5的前n项和为S(n),求S(n+1)-S(n)的值。
解:S(n+1)-S(n)=(x^n+1+5)-(x^n+5)=(x^n+1)-(x^n)=x^n(x-1)。
由于$a_n=x^n+5$,所以S(n)=a_0+a_1+...+a_n=(x^0+5)+(x^1+5)+...+(x^n+5)=(x^0+x^1+...+x^n)+5(n+1),因此S(n+1)-S(n)=x^n(x-1)=(S(n+1)-S(n)-5(n+2))/(x^0+x^1+...+x^n)。
2. 已知函数f(x)=sin(x)+cos(x),0≤x≤π/2,求f(x)在[0,π/4]上的最小值。
解:f(x)=sin(x)+cos(x)=√2sin(x+π/4),当0≤x≤π/4时,x+π/4≤π/2,sin(x+π/4)不小于0,因此f(x)的最小值由sin(x+π/4)的最小值决定。
sin(x+π/4)的最小值为-√2/2,因此f(x)的最小值为-1。
3. 已知正整数n,设P(n)是n的质因数分解中所有质因数加起来的和,Q(n)是n的数字分解中所有数位加起来的和。
给定P(n)+Q(n)=n,求最小的n。
解:P(n)的范围是2到9×log_10n之间,因此可以枚举P(n)和Q(n),判断它们之和是否等于n。
当P(n)取到最小值2时,Q(n)的最大值为9log_10n,因此n的最小值为11。
4. 已知函数f(x)=2cos^2x-3cosx+1,x∈[0,2π],求f(x)的最小值。
解:由于f(x)=2cos^2x-3cosx+1=2(cosx-1/2)^2-1/2,因此f(x)的最小值为-1/2,且取到最小值的x为0或2π。
5. 已知正整数n,求使得3^n的末2位是9的最小正整数n。
高中数学竞赛试题及答案

高中数学竞赛试题及答案一、选择题(每题3分,共15分)1. 下列哪个数不是有理数?A. πB. √2C. 1/3D. -3.142. 若函数f(x) = 2x^2 + 3x + 1,求f(-2)的值。
A. -1B. 3C. 5D. 73. 一个圆的半径为5,它的面积是多少?A. 25πB. 50πC. 75πD. 100π4. 已知等差数列的首项为3,公差为2,求第5项的值。
A. 11B. 13C. 15D. 175. 以下哪个是二次方程x^2 - 5x + 6 = 0的根?A. 2B. 3C. -2D. -3二、填空题(每题4分,共20分)6. 一个三角形的内角和为______度。
7. 若a,b,c是三角形的三边,且a^2 + b^2 = c^2,则此三角形是______三角形。
8. 一个正六边形的内角为______度。
9. 将一个圆分成4个扇形,每个扇形的圆心角为______度。
10. 若sinθ = 1/2,且θ在第一象限,则cosθ = ______。
三、解答题(每题10分,共65分)11. 证明:对于任意实数x,等式e^x ≥ x + 1成立。
12. 解不等式:2x^2 - 5x + 3 > 0。
13. 已知数列{an}的通项公式为an = 3n - 2,求前n项和Sn。
14. 求函数y = x^3 - 3x^2 + 2x的极值点。
15. 已知椭圆的方程为x^2/a^2 + y^2/b^2 = 1(a > b > 0),求椭圆的焦点坐标。
四、附加题(10分)16. 一个圆内接正六边形的边长为a,求圆的半径。
答案一、选择题1. A2. B3. B4. C5. A二、填空题6. 1807. 直角8. 1209. 9010. √3/2三、解答题11. 证明:设g(x) = e^x - (x + 1),则g'(x) = e^x - 1。
当x < 0时,g'(x) < 0,当x > 0时,g'(x) > 0。
高中数学竞赛试题汇总

高中数学竞赛试题汇总高中数学竞赛模拟试题一一试一、填空题(共8小题,8×7=56分)1、已知点(x,y)在直线x+2y=3上移动,当2x+4y取最小值时,点(x,y)与原点的距离是。
2、设f(n)为正整数n(十进制)的各数位上的数字的平方之和,比如记f1(n)=f(n),fk+1(n)=f(fk(n)),f(123)=12+22+32=14.k=1,2,3.则f2010(2010)=。
3、如图,正方体ABCD-A1B1C1D1的二面角度数是。
4、在1,2.2010中随机选取三个数,能构成递增等差数列的概率是。
5、若正数a,b,c满足abc=-(b+ca+ca+b),则ba+c的最大值是。
6、在平面直角坐标系xoy中,给定两点M(-1,2)和N(1,4),点P在X轴上移动,当∠MPN取最大值时,点P的横坐标是。
7、已知数列a,a1,a2.an。
满足关系式(3-an+1)(6+an)=18且a=3,则∑(i=1 to n)ai的值是。
8、函数f(x)=sinx+tanxcosx+tanxcosx+cotxsinx+cotx的最小值为。
二、解答题(共3题,14+15+15=44分)9、设数列{an}满足条件:a1=1,a2=2,且an+2=an+1+an (n=1,2,3.),求证:对于任何正整数n,都有:na(n+1)≥1+(n/2)(an)2,3.10、已知曲线M:x2-y2=m,x>0,m为正常数.直线l与曲线M的实轴不垂直,且依次交直线y=x、曲线M、直线y=-x于A、B、C、D4个点,O为坐标原点。
1)若|AB|=|BC|=|CD|,求证:△AOD的面积为定值;2)若△BOC的面积等于△AOD面积的1/3,求证:|AB|=|BC|=|CD|。
11、已知α、β是方程4x2-4tx-1=0(t∈R)的两个不等实根,函数f(x)=2x-t的定义域为[α,β]。
求证:2α+1<2β+1.Ⅰ)求函数g(t)=max{f(x)}-min{f(x)};Ⅱ)证明:对于u1,u2,u3∈(0,π),若sinu1+sinu2+sinu3=1/2,则1113+g(tanu1)g(tanu2)g(tanu3)<6.二试考试时间:150分钟总分:200分)一、(本题50分)如图,O1和O2与△ABC的三边所在的三条直线都相切,E,F,G,H为切点,并且EG、FH的延长线交于P点。
高中数学竞赛试题及参考答案
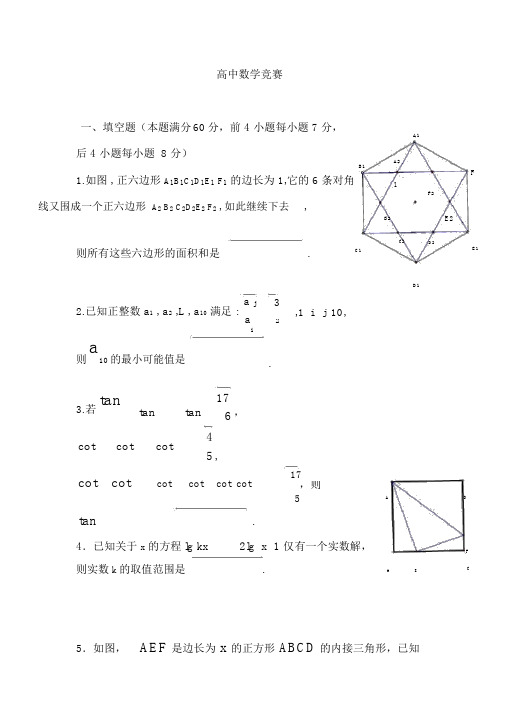
高中数学竞赛一、填空题(本题满分60分,前 4 小题每小题 7 分,后 4 小题每小题 8 分)B11.如图 , 正六边形A1B1C1D1E1F1的边长为 1,它的 6 条对角线又围成一个正六边形A2 B2 C2D2E2 F2,如此继续下去,A1A2F 1F2B2E2则所有这些六边形的面积和是.C12.已知正整数 a1 , a2 ,L, a10满足 :a j3, a,1 i j 102i则a10 的最小可能值是.C2D2D1E13.若tantan tan17,6cot cot cot 4 ,5cot cot cot cot cot cot17,则5tan.4.已知关于x的方程lg kx2lg x 1 仅有一个实数解,A DF则实数 k 的取值范围是.B E C 5.如图,AEF 是边长为 x 的正方形ABCD的内接三角形,已知AEF 90 ,AE a, EF b, a b ,则x.6.方程2m 3n3n 12m 13的非负整数解m,n.7.一个口袋里有 5 个大小一样的小球,其中两个是红色的,两个是白色的,一个是黑色的,依次从中摸出 5 个小球,相邻两个小球的颜色均不相同的概率是. (用数字作答)8.数列a n定义如下:a11,a2 2, a n2 n1an 1n.若2n2na n , n 1,2,L2a m20112,则正整数 m 的最小值为.2012二、解答题9.(本题满分 14分)如图,在平行四边形ABCD中,AB x , BC1,对角线 AC 与 BD 的夹角BOC 45 ,记直线 AB 与 CD 的距离为h(x).求 h(x) 的表达式,并写出x的取值范围.D C 10.(本题满分 14分)给定实数a 1,求函数OA B(a sin x)(4sin x)f ( x)的最小值.1 sin x11 .(本题满分16分)正实数x, y, z满足9xyz xy yz zx4 ,求证:4(1)xyyzzx3 ;(2)xyz2.12.( 本 题 满 分16 分 ) 给 定 整 数 n( 3) , 记f (n)为 集 合1,2,L,2 n1的满足如下两个条件的子集 A 的元素个数的最小值:(a)1 A, 2n1 A ;(b) A 中的元素(除 1 外)均为 A 中的另两个(可以相同)元素的和.( 1)求 f (3) 的值;(2)求证: f (100)108 .上海市高中数学竞赛答案1、9 32、9243、114、 ,0U4a 25、 6、3,0, 2,2 a 2 (a b)27 28 4025 59OB 2OC21(AB2BC 2)1( x2 1)2 22OBCBC2OB2OC 22OB OC cos BOC OB2OC22OB OC1OB OC x21522SABCD 4SOBC 41OB OC sin BOC22OB OC x21 2AB h( x)x21 2h(x)x2110 2xx210x1OB 2OC 22OB OC1( x21)2x21222x11x21h( x)x211x21142x10(a sin x)(4 sin x)3(a 1)f ( x)1 sin xa 21 sin x1 sin x1 a7 0 3(a1) 233(a 1)f ( x) 1 sin xa 2 2 3(a 1) a 21 sin xsin x3(a 1) 11,1f min ( x)23(a1)a267y3(a 1)a3(a1)2“ ”t3t0, 3(a1)f min ( x) f (1) 23(a 1) a 2 5(a 1)2 22 3(a 1) a2, 1 a7 ; f min (x)3145(a 1) ,a 7 .23xy yz zx111t333xyyz zx 2xyz3( xy)( yz)( zx)2434 9xyz xy yz zx 9t 33t2所以3t23t 23t20 ,而 3t 23t20,所以 3t20,即t2,3从而xyyz zx4( 10分)3.(2)又因为( x y z)23(xy yz zx) ,所以( x y z)2 4 ,故 x y z 2 .( 16分)12.解(1)设集合A1,2,L ,2 3 1 ,且A满足(a),( b).则1 A,7 A.由于1, m,7 m 2,3,L ,6 不满足 (b) ,故A 3 .又 1,2,3,7 , 1,2,4,7 , 1,2,5,7 , 1,2,6,7 , 1,3,4,7 , 1,3,5,7 , 1,3,6,7 ,1,4,5,7 , 1,4,6,7 , 1,5,6,7 都不满足(b),故A 4.而集合 1,2,4,6,7满足 (a),( b) ,所以f(3) 5 .( 6 分)(2)首先证明f (n 1) f (n)2,n3,4,L.①事实上,若A1,2,L,2 n 1,满足 (a),( b) ,且A的元素个数为 f (n) .令 B A U 2n 12, 2n 1 1 ,由于2n 122n1,Bf (n)22n 122(2n1), 2n 1 11(2 n 12)BL,2n 11B(a),( b)1,2,f (n1)B f (n)210f (2n) f (n)n1, n3,4,LA1,2,L,2 n1(a),( b)Af (n)B A U2(2n 1), 22 (2n1),L ,2 n (2n1),22 n12(2n1)22 (2 n1)L2n (2 n1)22 n1 B1,2,L,2 2n1B f (n)n 12k 1(2 n1)2k (2n1)2k (2n1), k0,1,L , n1 22n12n (2 n1)(2 n1)B(a),( b)f (2n)B f (n)n 114f (2 n1) f (n)n 3f (100) f (50)50 1 f (25)25151f (12)12377 f (6) 6192f (3) 3 1 99 10816。
中学数学(高中)学科竞赛集锦 (24)
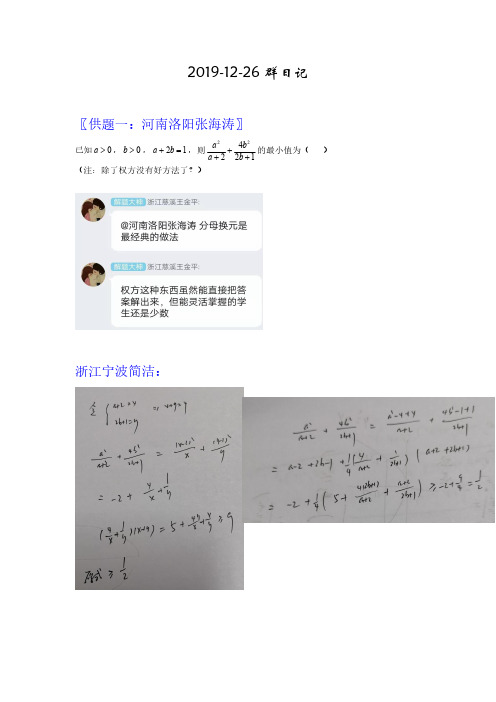
2019-12-26群日记
〖供题一:河南洛阳张海涛〗
已知0a >,0b >,21a b +=,则22
4221a b a b +++的最小值为()(注:除了权方没有好方法了?)
浙江宁波简洁:
浙江金华周江波
胡不归
〖供题二:江西九江陶智(群题征解)〗
〖供题三:浙江宁波于楠〗
〖供题四:江西九江陶智〗(昨天的折线距离再补一个解析)
浙江宁波王国勇(换元或平移坐标系)
〖供题五:浙江台州方敏〗
浙江东阳郭扬文:
供题六:浙江温州卢宇
解题人:江苏苏州崔锋
文献提供
供题7:广东东莞彭曦
此题延伸:
供题人自答:
横空出世惊为天人无数人膜拜叹服的解答——浙江温州林熙皓
居然还有后续:
供题8:浙江省杭州市颜米司
解题人1:浙江杭州罗彪
解题人2:浙江义乌李耀华
解题人3:浙江兰溪张昊
供题9:山西运城王丽
解题人:浙江兰溪张昊
供题10:浙江衢州颜志荣
解题人1:浙江绍兴高飞
解题人2:浙江绍兴赵灿
供题11:浙江杭州李磊
解题人:浙江义乌鲁明明
供题12:福建漳州林晓峰
江西九江陶智提问:
与此题计算量差不多解几题还有没有?(浙江考题范围内)
供题13:浙江绍兴李宇轩
折线距离的题型补充:。
高中数学竞赛中平面几何涉及的定理

1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足不L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆) 圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)ss为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和三角形△都是正三角形,则由线段AD、BE、CF的重心构成的三角形也是正三角形。
高中数学竞赛试题及解题答案

高中数学竞赛试题及解题答案在高中数学竞赛中,试题是考察学生数学思维和解决问题的能力的重要手段。
下面将为大家提供一部分高中数学竞赛试题及解题答案,希望能够帮助大家更好地理解和应用数学知识。
一、整数与多项式试题1:已知多项式P(x)满足P(x)=x^3-5x^2+ax+b,其中a、b均为整数。
若多项式P(x)除以(x-1)得到余数4,则多项式P(x)除以(x+2)的余数为多少?解题思路:我们知道,多项式f(x)除以x-a的余数等于把a带入f(x)中所得到的值。
那么,题目中给出了P(x)除以(x-1)的余数为4,即P(1)=4,我们可以将1代入P(x)中,得到一个方程。
同理,题目要求求解P(x)除以(x+2)的余数,即P(-2)=?根据题意,我们有以下方程:P(1) = 4,即1^3 - 5(1^2) + a(1) + b = 4P(-2) = ?,即(-2)^3 - 5((-2)^2) + a(-2) + b = ?解题步骤:1. 代入P(1)的方程求解:1 - 5 + a + b = 4化简得 a + b = 82. 代入P(-2)的方程求解:-8 - 20 - 2a + b = ?化简得 -2a + b = ?将两个方程合并求解可得:-2a + b = a + b - 16当两边消去b时,可得:-2a = a - 16a = -8将a代入第一个方程a + b = 8,可得:-8 + b = 8b = 16因此,通过计算可得多项式P(x)除以(x+2)的余数为-16。
试题2:已知整数序列a1, a2, a3, ...,其中a1 = 1,a2 = 2,an = an-1 + an-2(n ≥ 3)。
求证:对于任意正整数n,任务子序列a1, a2, ..., an中必定存在一个数可以被11整除。
解题思路:根据题意,我们需要证明对于任意正整数n,序列a1, a2, ..., an中必定存在一个数可以被11整除。
竞赛数学高中试题及答案

竞赛数学高中试题及答案试题一:多项式问题题目:已知多项式 \( P(x) = x^3 - 3x^2 + 2x - 5 \),求 \( P(2) \) 的值。
解答:将 \( x = 2 \) 代入多项式 \( P(x) \) 中,得到:\[ P(2) = 2^3 - 3 \times 2^2 + 2 \times 2 - 5 = 8 - 12 + 4 -5 = -5 \]试题二:几何问题题目:在直角三角形 ABC 中,角 C 是直角,若 \( AB = 10 \) 且\( AC = 6 \),求斜边 BC 的长度。
解答:根据勾股定理,直角三角形的斜边 \( BC \) 可以通过以下公式计算:\[ BC = \sqrt{AB^2 - AC^2} = \sqrt{10^2 - 6^2} = \sqrt{100 - 36} = \sqrt{64} = 8 \]试题三:数列问题题目:给定数列 \( a_n = 2n - 3 \),求数列的前 5 项。
解答:根据数列公式 \( a_n = 2n - 3 \),我们可以计算出前 5 项:\[ a_1 = 2 \times 1 - 3 = -1 \]\[ a_2 = 2 \times 2 - 3 = 1 \]\[ a_3 = 2 \times 3 - 3 = 3 \]\[ a_4 = 2 \times 4 - 3 = 5 \]\[ a_5 = 2 \times 5 - 3 = 7 \]数列的前 5 项为:-1, 1, 3, 5, 7。
试题四:概率问题题目:一个袋子里有 5 个红球和 3 个蓝球,随机抽取 2 个球,求抽到一个红球和一个蓝球的概率。
解答:首先计算总的可能组合数,即从 8 个球中抽取 2 个球的组合数:\[ \text{总组合数} = \binom{8}{2} = \frac{8 \times 7}{2} = 28 \]然后计算抽到一个红球和一个蓝球的组合数:\[ \text{有利组合数} = \binom{5}{1} \times \binom{3}{1} = 5 \times 3 = 15 \]所以,抽到一个红球和一个蓝球的概率为:\[ P = \frac{\text{有利组合数}}{\text{总组合数}} =\frac{15}{28} \]试题五:函数问题题目:若函数 \( f(x) = x^2 - 4x + 4 \),求 \( f(x) \) 的最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年1月9日截屏〖供题一:贵州六盘水罗勇〗
浙江诸暨杨岸杰
〖供题二:项成天〗求数列(){}n n 312⋅+的前n 项和浙江宁波简洁
〖供题三:河南洛阳张海涛〗
浙江宁波简洁
〖供题四:天津冯晨〗
浙江宁波简洁
〖供题五:四川成都李鑫〗(第3小题)
河南郑州万方
〖供题六:江苏苏州崔峰〗
浙江丽水廖忠龙
四川南充张涛
浙江台州蔡利兵
〖供题七:江西九江陶智〗
〖供题八:黑龙江大庆王启民〗问:已知椭圆14
:22=+y x C ,P(0,m )是y 轴正半轴上一动点,若以P 为圆心任意长为半径的圆与椭圆C 至多有两个交点,则m 的取值范围是()浙江宁波刘念
浙江宁波刘念(点差法)
〖供题九:浙江杭州魏朝翰〗
(利用最大角原理解)
〖供题十:浙江台州方敏〗问:斜线段AB与平面α所成的角为60°,B为斜足,点P是平面α上的动点且满足∠PAB=60°,则动点P的轨迹是()
A、直线
B、抛物线
C、椭圆
D、双曲线的一支
浙江台州张学军
〖供题十一:浙江兰溪薛小君〗
〖供题十二:四川南充张涛〗
浙江台州陈益
〖供题十三:浙江宁波茹威豪〗问:多项式函数的解析式能不能变形算出对称轴呀?或者对称中心。
