北航数学建模——数学模型12
北航线性系统理论完整版答案

1-1 证明:由矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=12-n 1-n n- - - -1 0 1 0 00 0 1 0a a a a A可知A 的特征多项式为nn n n n n n n n n nn n n n a a a a a a a a a a a a a a a a a a a a a a a A I ++++++=+++++=+++=++=+=-+λλλλλλλλλλλλλλλλλλλλλλλ1-3-32-21-11-3-3122-2-1-n 13-n 2-n 21-1n 12-n 1-n 12-n 1-n n1- )1(-)1(- 00 0 1- )1(-)1(- 0 00 1-1 0 1- 0 00 1-若i λ是A 的特征值,则00 0 0 1 10 1- 0 0 0 1-111n 1-n i 12-n 1-n n =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=++++=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--ni n i n i i i i i a a a a a a a λλλλλλλλ 所以[]Ti i 1-n i 2 1 λλλ 是属于i λ的特征向量。
1-7 解:由于()ττ--t e t g =,,可知当τ<t 时,()0≠τ,t g ,所以系统不具有因果性。
又由于()()0 ,,ττ-=t g t g ,所以系统是时不变的。
1-8 解:容易验证该系统满足齐次性与可加性,所以此系统是线性的。
由于()()t 0 t ⎩⎨⎧>≤-=-=ααββαβαt u t u P u Q P 而()()⎩⎨⎧+>+≤-=⎩⎨⎧>≤=βαβαβααβαβ t 0 t t 0 t t u t u Q u P Q ,故u P Q u Q P αββα≠,所以系统是时变的。
又因为()()()()()⎩⎨⎧>≤=⎩⎨⎧>≤=ααααα,,T T t u t u P u P P T T min t 0 min t t 0 t 而()()()()()()()⎩⎨⎧>≤=⎩⎨⎧>≤=ααααα,,,,T T t u T T t u P u P P P T T T min t 0 min t min t 0 min t ,故()()u P P P u P P T T T αα=,所以系统具有因果性。
2012年北航数模获奖名单
何泽文10091071 郭维薇10091030 数学与系统科学学院 孙海燕 冉令可10051218 王宁10051266 航空科学与工程学院 孙海燕 骆斐10171101 杨烈10171111 仪器科学与光电工程学院 刘超 王梦仑10091226 岳喜春10061075 吴俣10231023 苏澄10091228 苏腾飞10091211 王天宇10091219 裴壮39241115 刘真39085111 陈冰影10171031 彭龙10091234 罗汉10231030 赵乐文10231012 熊伟10021051 李娜10091203 李佳宝10091213 刘伟10031019 冯向南10091216 李水华10061073 党尚10231019 居飞10091223 孟繁超10091207 刘松涛10091235 邹秦萌39241107 张雨春39093112 周航10011034 段潇楠10091212 唐锐10151194 朱恺轶10031004 曲前伟10231031 安琪10091029 王昱10091208 智伟10151096
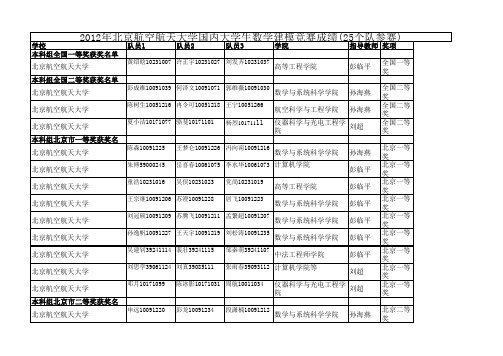
2012年北京航空航天大学国内大学生数学建模竞赛成绩(25个队参赛)
学校 队员1 本科组全国一等奖获奖名单 黄绍晗10231007 北京航空航天大学 本科组全国二等奖获奖名单 彭成维10091039 北京航空航天大学 陈树生10051216 北京航空航天大学 夏小洁10171077 北京航空航天大学 本科组北京市一等奖获奖名单 陈森10091225 北京航空航天大学 朱博59000245 北京航空航天大学 童浩10231016 北京航空航天大学 王宗继10091206 北京航空航天大学 刘冠硕100航空航天大学 吴建钊39241114 北京航空航天大学 刘思学39061124 北京航空航天大学 邓月10171099 北京航空航天大学 本科组北京市二等奖获奖名单 申远10091220 北京航空航天大学 安朝 10231026 北京航空航天大学 戴文轩10231003 北京航空航天大学 徐齐瑞10231025 北京航空航天大学 郑擎擎10091052 北京航空航天大学 陈安琪10091236 北京航空航天大学 张元昊10171011 北京航空航天大学 队员2 队员3 学院 指导教师 奖项 彭临平 全国一等奖 全国二等奖 全国二等奖 全国二等奖 北京一等奖 北京一等奖 北京一等奖 北京一等奖 北京一等奖 北京一等奖 北京一等奖 北京一等奖 北京一等奖 北京二等奖 北京二等奖 北京二等奖 北京二等奖 北京二等奖 北京二等奖 北京二等奖
北京工业大学工程数学-实验1-数学建模入门

d1100101010011000过河的方式有两种过河次数为奇数时船从此岸划向彼岸过河次数为偶数时船从彼岸划向此岸所以则状态ks随决策kd变化的规律为??kdkksks11????因此设计安全过河方案归结为求决策序列21ddddn??使状态ssk?按状态转移律由初始状态??11111?s经n步达到??00001??ns
我们将人,猫,鸡,米在岸上的情况,依次用四维向量S表示,即S(人,猫,鸡,米),并将这些向量称为状态,则第k次渡河前的状态记为 。
当一物在此岸时,相应分量记为1,在彼岸时记为0。例如(1,1,1,1)表示它们都在此岸,(0,1,1,0)表示猫和鸡在此岸,人和米在彼岸。由于问题中的限制条件,有些状态是允许的,有些状态是不允许的。安全渡河条件下的状态称为允许状态。对本问题而言,允许状态集合为:
(1,0,0,0)
(1,0,0,1)
(1,0,1,0)
(1,1,0,0)
(1,0,0,0)
(1,0,1,0)
1
2
3
4
5
6
7
8
(1,1,1,1)
(0,1,0,1)
(1,1,0,1)
(0,0,0,1)
(1,1,0,1)
(0,0,1,0)
(1,0,1,0)
(0,0,0,0)
(1,0,1,0)
(1,0,0,0)
(2)甲乙两站之间有汽车想通,每隔10分钟甲乙两站相互发一趟车,但发车时刻不一定相同。甲乙两站之间有一中间站丙,某人每天在随机时刻到达丙站,并搭乘最先经过丙站的那趟车,结果发现100天中约有90天到达甲站,大约10天到达乙站。问开往甲乙两站的汽车经过两站的时刻表是如何安排的?
数学建模答案 (3)

一、解释下列词语,并举例说明(每小题满分5分,共15分)1.模型答:为了某种特定的目的将原型的某一部分信息简化、压缩、提炼而构成的原型替代物。
如地图。
苯分子图等。
2.数学模型答:由数字、字母、或其他数学符号组成的,描述现实对象(原型)数量规律的数学结构。
3.抽象模型答:通过人们对原型的反复认识,将获取的知识以经验的形式直接存储在大脑中的模型称之谓思维模型。
从实际的人、物、事和概念中抽取所关心的共同特性,忽略非本质的细节把这些特性用各种概念精确地加以描述。
二、简答题(每小题满分8分,共24分)1.模型的分类按照模型替代原型的方式,模型可以简单分为形象模型和抽象模型两类。
形象模型:直观模型,物理模型,分子模型等;抽象模型:思维模型,符号模型,数学模型等。
2.数学建模的基本步骤(1) 建模准备:确立建模课题的过程;(2) 建模假设:根据建模的目的将原型进行抽象,简化.有目的性的原则。
简明性原则,真实性原则和全面性原则。
(3) 构造模型:在模型假设的基础上,进一步分析建模假设的各条款,选择恰当的数学工具和构造模型的方法对其进行表征,构造出根据已知条件和数据,分析模型的特征和模型的结构特点,设计或选择求解模型的数学刻画实际问题的数学模型;(4) 模型求解:构造数学模型之后,方法和算法,并借助计算机完成对模型的求解;(5) 模型分析:根据建模的目的的要求,对模型求解的数字结果,或进行稳定性分析,或进行系统参数的灵敏度分析,或进行误差分析等;(6) 模型检验:模型分析符合要求之后,还必须回到客观中去对模型进行检验,看它是否符合客观实际;(7) 数学应用:模型应用是数学建模的宗旨,将其用于分析,研究和解决实际问题,充分发挥建模在生产和科研中的特殊作用。
3.数学模型的作用数学模型的根本作用在于他将客观原型化繁为简,化难为易,便于人们采用定量的方法去分析和解决实际问题。
正应为如此,数学建模在科学发展,科学预见,科学预测,科学管理,科学决策,驾控市场乃至个人高效工作和生活等众多方面发挥着特殊的重要作用。
Matlab北航教程 第六章

1)产生连线:鼠标从一模块出口拖至另一 模块入口 2)分支线:鼠标指向分叉点,[ctrl]+鼠标 拖动 3)连线的折曲:光标指向待折点,shift+ 鼠标拖动 4)折点的移动:选中折线,将光标指向待 移折点,用鼠标拖动 5)信号线标识:双击信号线 4.对模型注释:双击模型窗空白处,填写注 释内容
四、常用模块组 1.信号(信源)模块组 2.连续模块组 3.离散模块组 4.表格模块组 5.数学运算模块组 6.非连续模块组 块组 10.其它模块组:COMM,DSP,Dial&Gauges Nonlinear Control Design, Power System Virtual Reality,SimMechanic,Real-Time
反之地建模,因而流程清晰。 4.仿真精细,贴近实际。提供了丰富的模 拟实际物理器件和过程的模块。如“死 区”、“库仑摩擦”、“饱和”等模块。 二、SIMULINK仿真集成环境 1.进入SIMULINK环境 点击simulink图标;指令窗中运行simulink 指令。此时即打开库浏览器。 2.进入模型窗 在库浏览器上点击“新建”或“打开”图 标。图形窗口是用户完成建模和调试的主 要场所。典型的windows用户界面 3.常用项简介
五、仿真参数配置 就是对【simulation;simulation parameter】 的设置。 1.仿真算法设置——求解器的选择 连续系统一般问题:ode45变步长 连续系统刚性问题:ode15s变步长 离散系统:discrete方法定步长,步长值 可以人工确定,也可自动确 定。 2.仿真区间设定:人工确定或利用stop根据 情况随机结束仿真。 3.输入输出设置:选定tout,yout可将仿真 结果输出到工作空间
【format;signal dimentions】用数字表示多 路信号线中信号的数目 【format;port data types】标明端口数据 类型 CH 2 SIMULINK模型的建立 一、simulink模型的特点 1.视觉上为实现各种功能的模块及连线构成 1. 的图。 2.文件上是扩展名为MDL的ASCII码文件 3.在数学上是一组微分方程和差分方程 4.在本质上模拟物理器件或过程的动态特性 二、 simulink模型的结构
北航 计算理论 第二章 计算模型

2.1 图灵机模型
与图灵机等价的计算模型:
寄存器机 Lambda演算
2.1 图灵机模型
Church-Turning论题:
一切直觉上能行可计算的函数都可用图 灵机计算,反之亦然。
作业
1. 设计一台图灵机,接受由a和b组成的, 且a与b出现次数相同的字符串。举正反例 给出识别过程。长度大于5.
2.1 图灵机模型
给出串0011的识别过程。
q00011 ┣xq1011 ┣x0q111 ┣xq20y1
┣q2x0y1 ┣xq00y1 ┣xxq1y1
┣xxyq11 ┣xxq2yy ┣xq2xyy
┣xxq0yy ┣xxyq3y ┣xxyyq3B
┣xxyyBq4B
2.1 图灵机模型
给出串0010的识别过程:
δ(q0,1) = (q1,(1,R)),
δ(q0,B) = (q1,(B, R)),
δ(q1,0) = (q0, 0, L),
δ(q1, 1) = (q0, 1, L), δ(q1, B) = (q0, B, L).
考虑输入串01,10,…
2.1 图灵机模型
对输入串的不接受:
拒绝状态
不停机
2.1 图灵机模型
应用实例1:自然数及其运算
输入带上0的个数表示自然数
n: 0n
函数的参数以1分隔。 f(n1,n2…,nk)的参数表示为:0n1 10n21…10nk
m+n
0m10n 0m+n 思路:将输入带上的中间的1改为0,将最后 的0改为B。 若m为0则直接将1改为B即可。
数学建模在航空航天工程中的应用及创新

数学建模在航空航天工程中的应用及创新航空航天工程是一门复杂而又高度技术化的领域,数学建模在其中扮演着重要的角色。
通过数学建模,工程师们能够更好地理解和解决航空航天领域中的问题,并且为创新提供了强有力的支持。
首先,数学建模在航空航天工程中的应用主要体现在飞行力学方面。
在飞行器的设计和研发过程中,飞行力学是一个关键的环节。
通过数学建模,我们可以利用力学原理和方程来描述和分析飞行器在空气中的运动。
例如,我们可以使用牛顿力学的运动方程来模拟飞行器的受力和运动轨迹,从而预测飞行器在不同条件下的性能和飞行特性。
这对于改进设计、提高飞行器的稳定性和安全性非常重要。
其次,数学建模还在航空航天工程中的结构分析和优化中发挥了重要作用。
在飞行器的结构设计中,我们需要考虑到各种因素,如材料的力学性能、结构的强度和刚度等。
通过数学建模,我们可以建立数学模型来描述和分析飞行器的结构特性,并通过数值计算和优化算法来寻找最佳的结构设计。
这样可以提高飞行器的性能和效率,减少材料的使用量和重量,从而降低成本和能耗。
另外,数学建模还在航空航天工程中的控制系统设计中发挥了重要作用。
在飞行器的控制系统中,我们需要设计和优化各种控制算法和策略,以实现对飞行器的精确控制和稳定性。
通过数学建模,我们可以建立飞行器的动力学模型,并使用控制理论和方法来分析和设计控制系统。
这样可以提高飞行器的操纵性和安全性,确保飞行器在各种工况下都能保持稳定和可控。
此外,数学建模还在航空航天工程中的数据分析和决策支持中发挥了重要作用。
在航空航天领域中,我们需要处理和分析大量的数据,如飞行数据、传感器数据等。
通过数学建模,我们可以使用统计学和数据分析方法来处理和分析这些数据,从而提取有用的信息和知识,并支持决策和优化。
例如,我们可以使用回归分析来建立飞行器性能和参数之间的关系模型,以帮助优化设计和运行。
总之,数学建模在航空航天工程中的应用不仅提供了理论基础和工具,还为创新提供了强有力的支持。
数学模型在航空航天中的应用

数学模型在航空航天中的应用航空航天是现代科技领域中最为重要的一个部门之一,它的发展不仅深刻影响了我们的生活和工作,而且也成为了各国竞争能力和影响力的重要标志。
在实践过程中,航空航天面临着诸多的挑战,如飞行稳定性、能源效率、空中交通管制、飞行指令编码等等,而这些挑战均可以通过数学模型的应用来解决。
一、数学模型在航空航天中的基本应用航空航天中的数学模型最基本的应用涉及到气动和结构特性的计算和分析。
例如,研究航空器在飞行中制造的气动力,可以使用不同的方法建立复杂的数学模型,其中包括有限元方法、计算流体动力学、数值模拟方法等等。
同时,这些数学模型还可以用来分析飞行器的性能,如提高航空器的燃油效率和降低噪音水平等。
近年来,随着数据科学和人工智能技术的进步,数学模型在航空航天中的应用进一步扩展。
例如,可以使用机器学习算法来对航空器的气动性能进行优化,将数据分析与数学建模紧密结合起来,以有效提高飞行器的性能和效率。
此外,数学模型在航空航天中也可以用来建立相应的仿真和测试系统。
这些系统可以模拟各种情况下的飞行特性和设计参数,以帮助工程师更好地评估设计的准确性和性能。
通过这种方法,可以在设计阶段发现和解决潜在的问题,减少实验和测试带来的成本和风险。
二、数学模型在航空航天中的新应用现代航空航天领域正在经历着快速发展和变化,而数学模型作为经典的建模方法也不断更新和改进。
在这样的背景下,数学模型在航空航天中的应用也会得到进一步的拓展和创新。
一种新的应用方法是使用深度学习技术进行自适应控制和优化。
这种方法可以学习和调整针对特定问题和数据的优化策略,以适应各种复杂的场景和变化。
例如,可以将深度学习算法应用于飞行器的自主导航和控制中,从而提高飞行器的适应性和敏捷度。
除了深度学习,量子计算技术也被广泛研究和应用于航空航天。
量子计算能够通过高效的计算算法解决很多常规计算机上取得困难的问题,从而在设计优化和飞行控制上具有广泛的应用潜力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
变量和参量: 饲养时间 t(天),生猪重w(t)(kg), 售价p(t)元/kg 售猪所获得的总收益R(t)(元), t 天内饲料的总花费C(t)(元), 最终获得的净收益P(t)(元)。 猪的现价 p0(元/kg),售价日减少量 r(元/kg), 猪的初重w0(kg),猪的日增重量 g(kg/天), 每天饲料的花费 k(元),前期投入k0(元)。
关于猪的重量增加和价格降低是线性函数 的假设不总是成立的。
但是我们确信,如果没有什么意外,在短时间内 它们的变化率 w’ 和 p’ 的变化就不会太大。 短时间内模型有关函数线性的假设是近似成立的。 这时如果参数发生较大的变化,例如g或r有5% 的改变 令 g = (1.9,2,2.1) , r = (0.057, 0.06, 0.063) 将他们配成不同的组合代入模型中,并且使用计 算机绘出净收益随时间变化的图像,
V=ad/(b+d) =7.83d/(75.60+d)
例 2. 生猪饲养
一头重量是100kg的猪, 在上一周每天增重约2kg。 五天前售价为7.8元/kg, 现在售价为7.5元/kg 饲养每天需花费7.1元。 前期投入约500元 求出售猪的最佳时间。
假设 1.出售前,猪每天增重相同。 2.猪的售价每天降低的数量相同 3.用于猪饲料的花费每天不变 4.猪在饲养和出售期间内不再有其 他的花费
增重率 g 对售猪时间 t 的影响.
重量 w(t)=200 + g t 净收益 P(t)=(7.5-0.06t)(100+gt)-(500+7.1t) 最大值点 t = (7.5g–13.1)/(0.12g)
-5% -1% +1% +5%
g 5.04 1.98 2 2.02 t 5.04 7.37 7.92 8.46 % -36.6 - 6.94 0 6.82
1 26 .41 0.06 0.214 4 8 36 10 257 .52
当模型的参数 r 和 g 在我们设定的数值附近变 化时, 尽管生猪出售的最优时间会有很大的变化, 但所得到的净收益的变化是不大的。 这两个参数每改变1% 的大小, 仅使得净收益有 0.214% 和 0.432% 的变化。 绝对的数值为 257.32元×0.214% = 0.55元 和 257.32元×0.432% = 1.11元的变化。 在前面关于关于生猪生长和销售情况线性变化 的假设下 对参数所作的估计虽然不是完全准确的,但是 是可靠的。
建议这位农民可以放心地继续饲养一周。 在这期间是不会错过最佳售猪的时间的。 在这一周的后期每天要观察生猪增重和出售价 格的情况,判断是否需要出售。 在周末净收益的动态仍旧看好, 可以依据所得到的数据重新估计w0, w’, p0和 p’, 再用模型继续分析计算。
问题1. 在售猪问题中,对每天的饲养花费 做灵敏度分析。 分别考虑对最佳售猪时间和相应收益的影 响。 如果有新的饲养方式,每天的饲养花费为 9元,会使猪按3.5kg/天增重。 那么是否值得改变饲养方式? 求出使饲养方式值得改变的最小的增重率。
2.1 10.51 32.7
r,g 的变化对售猪的时间的影响是灵敏的
将上面的分析过程进一步数学化, 如果参数 r 改变了△r, 将导致售猪的时间 t 有△t的改变量。 则它们的相对改变量的比值是 △t / t 与△r / r 之比。 令△r→ 0,按照导数的定义,则有
t r dt r r t dr t
参数
人数 nk,教室距离 Lk,门宽 D. 速度v,间隔 d,疏散时间 Tk
模型
T1=(n1d+L1)/v T2=(n2d+L1+L2+D )/v T12=(n2d+L1+L2+D )/v, [(n1+ n2+1 )d+L1] /v,
(L2+D)≥(n1+1)d (L2+D)<(n1+1)d
教室门口的时间。
5.人体厚度相同w
继续讨论
1. T=(nd+L)/v, v增, 则T减; d增, 则 T增. 2. 多行行进 3.令d=0, 则有T=L/v, 疏散时间与人数无关! 假设中忽略了人体的厚度!! 4.考虑厚度的影响 T=(n(d+w)+L)/v, 若v*为可能最快的速度 v=v*, d=0, 则 T* = (nw+L)/v* 最短 合理吗?
模型的稳健性分析 我们组建数学模型总是希望力求完美, 但有时是不可能达到的。 确切的说我们应尽力使得所构建的模型接近完美 一个数学模型称为稳健的, 即使这个模型不完全精确,但其结果仍是可信的。 一个好的数学模型有较好的稳健性 是指虽然它给出的答案并不是完全精确的, 但是足够近似的从而可以在实际问题中应用。 在数学模型问题中关于模型稳健性的讨论是必要的。
四. 建模问题与数学问题的处理
问题的叙述:原始、粗糙、不规范。 问题的假设:问题的研究手段。 问题的分析:推理正确,符合实际情况 问题的标准:与实际情况差异不大 或结论可信。 问题的答案:不确定、不封闭。
2. 参数 r, g 的变化对净收益 P 的影响 固定g=2kg,令r 在0.06附近变化, 可得出售时间t为5.28和10.23。 分别代入模型 P(t)=(0.65-0.01t)(200+gt)-0.45t 可得最优净收益为131.2,135.8 与原来的净收益133.2只相差约2美元 相对改变了1.5%和1.95%
它表明,生猪的日增重每增加 1%,将导致售猪时 间要延长6.89%。 参数值的变化对于售猪的最优时间的影响是很灵 敏的。 如果要得到准确的生猪最优的出售时间, 需要求更加准确地估计参数 r 和 g 的数值。
2. 参数 r, g 的变化对净收益 P 的影响
固定生猪日增重量 g = 2 kg, 价格变化 r 在对售猪得到的净收益的影响。有 P(t,r) = (7.5 – r t) (100 + 2 t) - (500 + 7.1 t) = 250 + (7.9–100 r) t– 2 r t2 由于随着r 的不同最优售猪的时间会发生变化 模型为t = (7.9 -100 r)/(4 r)。
w0=100, g=2, p0=7.5, r=0.06, k=7.1, k0=500 P(t) = R(t) – C(t) = (7.5-0.06 t)(100 + 2 t)-(500+ 7.1 t) P(t) = 250 + 1.9t – 0.12 t2.
问题:求售猪的时间t使净收益P(t)最高 P(t) = 250 + 1.9t – 0.12 t2. 则有 t = 1.9 / (2×0.12) 得 t =7.9≈8(天) P(8)=250+1.9×7.9-0.12×7.92= 257.52 结论: 饲养8天然后出售, 净收益最高为257.52元 结论可靠吗?
分析 1.参数r,g的变化对售猪时间 t 的影响 价格变化率 r 对售猪时间t 的影响.
价格 p(t)=7.5 – r t, 净收益 P(t) = (7.5-rt)(100+2t)-(500+4.1t) 最大值点 t = (7.9-100r)/(4r) -5% -1% +1% +5% r 0.057 0.0594 0.06 0.0606 0.063 t 9.74 8.25 7.92 7.59 6.34 % 23 4.17 -4.15 -19.8
我们称这个极限值为模型值 t 随参数 r 变化 的灵敏度,记为 S(t,r)。
由于售猪时间与增重量的关系为 t = (7.5g–13.1)/(0.12 g)。 故可以算出在 g = 2 附近,t 关于 g 的灵敏度为
dt g S (t , g ) dg t
g 2
13.1 2 6.89 0.12 4 7.92
继续修改假设
1.单排教室,直走道,一个出口。 2.人员撤离时, 单行、有序、间隔 均匀、匀速地撤出。 3.忽略列队的时间和第一个人到达 教室门口的时间。 4. 人体厚度相同 5. 行进速度与队列的密度有关 v=v(d)
模型
T=[n(d+w)+L]/v(d), 其中 v=v(d)应满足 d 增, 则v 增; 若d→∞,则 v=v*. 若d=0, 则 v=0. 这时存在唯一的间隔 d* 和相应的 速度 v*, 使得疏散的时间最短?
245
240
235
0
5
10
15
可以看出, 当猪的增重量g<2,售价的减少量r>0.06时 生猪的最优出售时间均处于8天之前, 其最优的净收益值均低于参数组(2,0.06)时 的净收益257.52元。 但是差别很小,不超过2元。
如果在这段时间内内 w’ 和 p’ 不能近似为定常的数值, 可以直接使用净收益值 P(t) = w(t) p(t) – (k0 + k t) 每天的改变量来判断生猪出售的时间。 我们分别用△P,△w 和 △p表示净收益,生猪重量和出 售的价格的日改变量, 则近似地有如下的关系: △P = P(t+1) – P(t) = △w×p(t)+w(t)×△p - k +△w×△p ≈ △w×p(t) + w(t)×△p﹣k 式中第一项代表由于生猪增重而增加的收益。 第二项代表因价格下降而受到的经济损失。 这个模型告诉我们, 只要预测下一天售猪所增加的收益大于饲养的费用,就应 暂不卖出,继续饲养。
