2018-2019学年度北师大版必修三习题:课下能力提升(四) Word版含答案
【最新】2018-2019学年度高中数学北师大版必修三习题:课下能力提升(十五) -含答案

一、选择题1.“某彩票的中奖概率为1100”意味着( ) A .买100张彩票就一定能中奖B .买100张彩票能中一次奖C .买100张彩票一次奖也不中D .购买彩票中奖的可能性为11002.抛掷一枚骰子两次,用随机模拟方法估计上面的点数和为7的概率,共进行了两次试验,第一次产生了60组随机数,第二次产生了200组随机数,那么这两次估计的结果相比较( )A .第一次准确B .第二次准确C .两次的准确率相同D .无法比较3.下列结论正确的是( )A .事件A 发生的概率P (A )满足0<P (A )<1B .事件A 发生的概率P (A )=0.999,则事件A 是必然事件C .用某种药物对患有胃溃疡的500 名病人进行治疗,结果有380人有明显的疗效,现有胃溃疡的病人服用此药,则估计有明显疗效的可能性为76%D .某奖券的中奖率为50%,则某人购买此奖券10张,一定有5张中奖4.给出下列三个命题,其中正确命题的个数为( )①设有一批产品,已知其次品率为0.1,则从中任取100件,必有10件是次品;②做7次抛硬币的试验,结果3次出现正面朝上,则硬币出现正面朝上的概率是37;③随机事件发生的频率就是这个随机事件发生的概率.A .0B .1C .2D .35.在给病人动手术之前,外科医生会告知病人或家属一些情况,其中有一项是说这种手术的成功率大约是99%,下列解释正确的是( )A .100个手术有99个手术成功,有1个手术失败B .这个手术一定成功C .99%的医生能做这个手术,另外1%的医生不能做这个手术D .这个手术成功的可能性是99%二、填空题6.一个口袋装有除颜色外其他均相同的白球、红球共100个,若摸出一个球为白球的概率为34,则估计这100个球内,有白球________个. 7.在200件产品中,有192件一级品,8件二级品,则下列事件:。
2017-2018学年高二数学北师大版必修三习题:课下能力提升(一) Word版

一、选择题1.现从80件产品中随机抽出10件进行质量检验,下列说法正确的是( )A.80件产品是总体B.10件产品是样本C.样本容量是80D.样本容量是102.下列调查时,必须采用“抽样调查”的是( )A.调查某城市今年7月份的温度变化情况B.调查某一品牌5万瓶化妆品是否符合质量标准C.调查我国所有城市中哪些是第一批沿海开放城市D.了解全班50名学生100米短跑的成绩3.下列哪个问题不宜用普查( )A.为了缓解城市的交通情况,某市准备出台限制私家车的政策,为此要进行民意调查B.对你所在学校的学生最喜欢的体育活动情况的调查C.某轮胎厂要对一个批次轮胎的寿命进行调查D.对上海市常住人口家庭收入情况的调查4.为了调查北京市2015年家庭的收入情况,在该问题中总体是( )A.北京市B.北京市的所有家庭的收入C.北京市的所有人口D.北京市的工薪阶层5.下列调查中属于抽样调查的是( )①每隔5年进行一次人口普查;②某商品的质量优劣;③某报社对某个事件进行舆论调查;④高考考生的身体检查.A.②③ B.①④C.③④ D.①②6.下面的各事件中,适合抽样调查的有________.①调查除夕之夜我国有多少人观看中央电视台春节联欢晚会;②调查某工厂生产的一万件西服中有无不合格产品;③评价一个班级升学考试的成绩;④调查当今中学生中,对交通法规的了解情况;⑤调查山东省初中生每人每周的零花钱数.7.随着人们健康意识的提高,有色食品的质量引起消费者的特别关注,检验员为了检查彩色豆腐是否具有染色现象,应采用__________的方法检验.8.某地区发现了新型流感病毒,在病毒发作区,对与病毒携带者亲密接触的人要进行检查,所采用的方法是________.三、解答题9.有人说“如果抽样方法设计得好,用样本进行视力调查与对24 300名学生进行视力普查的结果会差不多,而且对于教育部门掌握学生视力状况来说,因为节省了人力、物力和财力,抽样调查更可取”,你认为这种说法有道理吗?为什么?10.为了了解高一一班语文老师的教学情况,从全班50名同学中抽取了成绩在前10名的10名同学进行问卷调查,这种抽样方法合理吗?为什么?答案1. 解析:选D 在该问题中,80件产品的质量是总体,所以A错误;所抽取的10件产品的质量是样本,所以B错误;总体容量是80,所以C错误;样本容量是10,所以D正确.2. 解析:选B 调查化妆品是否符合质量标准,具有“破坏性”,必须使用抽样调查.3. 答案:C4. 答案:B5. 解析:选A ①④为普查,②③为抽样调查.6. 答案:①②④⑤7. 解析:这是破坏性的检验,不可能进行普查,应当采取抽样调查的方法进行检验,对随机抽取的部分产品进行检验,根据得到的检验结果,就可以得到这批产品是否具有染色现象,因为同一批豆腐,从中随机抽取一部分代表全体产品的质量是合理的.答案:抽样调查8. 答案:普查9. 解:这种说法有道理,因为一个好的抽样方法能够保证调查结果接近于普查的结果,因此只要根据误差的要求取合适的样本进行调查会和普查的结果差不多,而且抽样调查还可以节省人力、物力和财力.10. 解:这种抽样方法不合理,它不具有随机性,不能保证每个个体被抽到的机会相等,并且成绩的好坏也可能会影响到对老师印象的偏见.在抽样时,一定要做到随机性,尽量避免人为的主观因素的影响.。
2017-2018学年高中数学北师大版必修三习题 课下能力提升(十九) Word版 含答案

一、选择题1.在区间[0,3]上任取一点,则此点落在区间[2,3]上的概率是( ) A.13 B.12 C.23 D.342.如图,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率为23,则阴影区域的面积为( )A.43B.83C.23D .无法计算 3.有四个游戏盘,如果撒一粒黄豆落在阴影部分,则可中奖.小明希望中奖,他应当选择的游戏盘为( )4.A 是圆上的一定点,在圆上其他位置任取一点B ,连接A 、B 两点,它是一条弦,则它的长度大于等于半径长度的概率为( )A.12B.23C.32D.145.在区间[0,1]内任取两个数,则这两个数的平方和也在[0,1]内的概率是( ) A.π4 B.π10 C.π20 D.π40二、填空题6.函数f (x )=x -2,x ∈[-5,5],那么任取一点x 0∈[-5,5],使f (x 0)≤0的概率是________. 7.圆上的任意两点间的距离大于圆的内接正三角形边长的概率是________.8.已知点P 是边长为4的正方形内任一点,则P 到四个顶点的距离均大于2的概率是________.三、解答题9.在△ABC 内任取一点P ,求△ABP 与△ABC 的面积之比大于23的概率.10.甲、乙两人约定晚6点到晚7点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若他早到则不需等待.求甲、乙两人能见面的概率.答 案1. 解析:选A 区间[2,3]长度为1,总区间[0,3]的长度为3,∴P =13.2. 解析:选B 由几何概型的公式知:S 阴影S 正方形=23,又:S 正方形=4,∴S 阴影=83. 3. 解析:选A A 游戏盘的中奖概率为38,B 游戏盘的中奖概率为13,C 游戏盘的中奖概率为2r 2-πr 22r 2=4-π4,D 游戏盘的中奖概率为r 2πr 2=1π,A 游戏盘的中奖概率最大. 4. 解析:选B 如图,当取点落在B 、C 两点时,弦长等于半径;当取点落在劣弧上时,弦长小于半径;当取点落在优弧上时,弦长大于半径.所以弦长超过半径的概率P =360°-120°360°=23.5. 解析:选A 设在[0,1]内取出的数为a ,b ,若a 2+b 2也在[0,1]内,则有0≤a 2+b 2≤1.如图,试验的全部结果所构成的区域为边长为1的正方形,满足a 2+b 2在[0,1]内的点在14单位圆内(如阴影部分所示),故所求概率为14π1=π4.6. 解析:由f (x 0)≤0得x 0-2≤0,x 0≤2,又x 0∈[-5,5],∴x 0∈[-5,2].设使f (x 0)≤0为事件A ,则事件A 构成的区域长度是2-(-5)=7,全部结果构成的区域长度是5-(-5)=10,则P (A )=710.答案:7107. 解析:如图所示,从点A 出发的弦中,当弦的另一个端点落在劣弧B C 上的时候,满足已知条件,当弦的另一个端点在劣弧A B 或劣弧A C 上的时候不能满足已知条件.又因为△ABC是正三角形,所以弦长大于正三角形边长的概率是13.答案:138. 解析:如图所示,边长为4的正方形ABCD ,分别以A 、B 、C 、D 为圆心,并以2为半径画圆截正方形ABCD 后剩余部分是阴影部分.则阴影部分的面积是42-4×14×π×22=16-4π,所以所求概率是16-4π16=1-π4.答案:1-π49. 解:设P 点、C 点到AB 的距离分别为d P 、d C , 则S △ABP =12AB ·d P ,S △ABC =12AB ·d C ,所以S △ABP S △ABC =d P d C ,要使d P d C >23, 只需使P 点落在某条与AB 平行的直线的上方,当然P 点应在△ABC 之内,而这条与AB 平行的直线EF 与AB 的距离要大于d C 的23.由几何概率公式,得P =S △CEF S △ABC =⎝ ⎛⎭⎪⎫3-232=19. 10. 解:用x 轴、y 轴分别表示甲、乙两人到达约定地点的时间.若甲早到,当y -x ≤30时,两人仍可见面;若乙早到,则两人不可能见面,因此,必须有x ≤y . 如图,事件A “两人可以见面”的可能结果是阴影部分的区域.故P (A )=12×602-12×302602=38.。
北师大版高中英语必修3全册课下能力提升含答案编辑版.doc

2017-2018学年北师大版高中英语必修3全册课下能力提升训练Unit 7 课下能力提升(一)Ⅰ.单词拼写1.We have p________ him to accept our ideas.2.You've been in prison six times ________ (根据) to our records.3.They a________for the late departure of this flight.4.She hopes to get a job on the local newspaper and ________ (最终) works for The Times.5.Many experts think the common ________ (祖先) lived at least seven million years ago.6.The v________ took months and first brought him to Moscow, then westward.7.She was a very brave girl and everyone who knew her admired her ________ (精神).8.All CEOs love a good wellprepared 90minute l________.Ⅱ.完成句子1.不久你就会意识到是你错了。
It will not be ________________ you ________ you are wrong.2.他为让我们等待数小时而向我们道歉。
He __________________ having kept us waiting for hours.3.有很多乘客正在公共汽车站等车。
There were many passengers ________________ the bus at the bus stop.4.我们不得不求助于老师,因为只有老师才能说服他不再上网。
2019-2020学年度北师大版数学必修四习题:课下能力提升(二十五)

——教学资料参考参考范本——2019-2020学年度北师大版数学必修四习题:课下能力提升(二十五)______年______月______日____________________部门一、选择题1.(重庆高考)=( )A .-B .-12C. D.322.在△ABC 中,若sin(B +C)=2sin Bcos C ,那么这个三角形一定是( )A .锐角三角形B .钝角三角形C .直角三角形D .等腰三角形3.(湖南高考)函数f(x)=sin x -cos 的值域为 ( )A .[-2,2]B .[-,]C .[-1,1] D.⎣⎢⎡⎦⎥⎤-32,324.已知sin αcos α=,0<α<,则cos 的值为( )A. B .-15C. D .±15二、填空题5.函数y =sin xcos +cos xsin 的最小正周期T =________.6.在△ABC 中,A ,B 为锐角,且sin A =,sin B =,则A +B =________.7.(大纲全国卷)当函数y=sin x-cos x(0≤x<2π)取最大值时,x=________.8.设α,β,γ∈,且sin α+sin γ=sin β,cos β+cosγ=cos α,则β-α等于________.三、解答题9.已知函数f(x)=4cos xsin-1.(1)求f(x)的最小正周期;(2)求f(x)在区间上的最大值和最小值.10.已知0<β<,<α<,cos=,sin=,求sin(α+β)的值.答案1.解析:选C 原式=sin(30°+17°)-sin 17°cos 30°cos 17°=sin 30°cos 17°+cos 30°sin 17°-sin 17°cos 30°cos 17°==.2.解析:选D ∵sin(B+C)=2sin Bcos C,∴sin Bcos C+cos Bsin C=2sin Bcos C即cos Bsin C=sin Bcos C,sin(B-C)=0又-π<B-C<π,∴B-C=0,B=C.3.解析:选 B f(x)=sin x-cos(x+)=sin x-cos x+sin x =sin(x-),∵sin(x-)∈[-1,1],∴f(x)值域为[-,].4.解析:选 C ∵cos(-α)=(cos cos α+sin ·sin α)=cos α+sin α,∴[cos(-α)]2=(sin α+cos α)2=1+2sin αcos α=1+2×=.∵0<α<,∴-<-α<0,-<-α<,∴cos(-α)>0.∴cos(-α)=.5.解析:y=sin(x+x+)=sin(2x+),∴T==π.答案:π6.解析:∵A,B为锐角,∴cos A==,cos B==.∴cos(A+B)=cos Acos B-sin Asin B=×-×=.又0<A+B<π,∴A+B=.答案:π47.解析:y=sin x-cos x=2sin(x-),由0≤x<2π⇔-≤x-<可知-2≤2sin(x-)≤2,当且仅当x-=时即x=取得最大值.答案:5π68.解析:由条件知sin β-sin α=sin γ,①cos β-cos α=-cos γ,②由①2+②2得2-2(sin βsin α+cos αcos β)=1.∴cos(β-α)=,又由①知sin β>sin α,∴β>α,β-α∈(0,).∴β-α=.答案:π39.解:(1)∵f(x)=4cos xsin(x +)-1 =4cos x(sin x +cos x)-1 =sin 2x +cos 2x =2sin(2x +), ∴f(x)的最小正周期为π. (2)∵-≤x≤,∴-≤2x+≤.∴当2x +=,即x =时,f(x)取得最大值2; 当2x +=-,即x =-时,f(x)取得最小值-1. 10.解:∵<α<, ∴-<-α<0.∴sin(-α)=- =-. 又∵0<β<, ∴<+β<π,∴cos(+β)=- =-.∴sin(α+β)=-cos(+α+β) =-cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫3π4+β-⎝ ⎛⎭⎪⎫π4-α=-coscos -sinsin ⎝ ⎛⎭⎪⎫π4-α=-×-×=.。
2019-2020学年高中数学北师大版必修三习题:课下能力提升(十六) Word版含答案

一、选择题1.下面是古典概型的是( )A .任意抛掷两粒骰子,所得的点数之和作为基本事件B .为求任取一个正整数,该正整数平方值的个位数字是1的概率,将取出的正整数作为基本事件C .从甲地到乙地共有n 条路线,求某人正好选中最短路线的概率D .抛掷一枚均匀硬币至首次出现正面为止2.下列对古典概型的说法中正确的是( )①试验中所有可能出现的基本事件只有有限个;②每个事件出现的可能性相等;③每个基本事件出现的可能性相等;④基本事件总数为n ,随机事件A 若包含k 个基本事件,则P (A )=k n.A .②④B .①③④C .①④D .③④3.在5张卡片上分别写上数字1,2,3,4,5,然后将它们混合后,再任意排成一行,则得到的五位数能被2或5整除的概率是( )A .0.2B .0.4C .0.6D .0.84.从1,2,3,4这四个数字中,任取两个不同的数字构成一个两位数,则这个两位数大于30的概率为( )A.12B.13C.14D.155.4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( )A.13B.12C.23D.34二、填空题6.三张卡片上分别写上字母E ,E ,B ,将三张卡片随机地排成一行,恰好排成英文单词BEE 的概率为________.7.(江苏高考)从1,2,3,4这四个数中一次随机地取两个数,则其中一个数是另一个数的两倍的概率是________.7.(江苏高考)从1,2,3,4这四个数中一次随机地取两个数,则其中一个数是另一个数的两倍的概率是________.8.将一枚质地均匀的硬币先后抛掷三次,恰好出现一次正面向上的概率是________.三、解答题9.设b 和c 分别是先后抛掷一枚骰子得到的点数,求方程x 2+bx +c =0有实根的概率.10.(山东高考)袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;(2)向袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.答 案1. 解析:选C 对于A ,所得点数之和为基本事件,个数虽有限但不是等可能发生的;对于B ,D ,基本事件的个数都是无限的;只有C 是古典概型.2. 解析:选B ②中所说的事件不一定是基本事件,所以②不正确;根据古典概型的特点及计算公式可知①③④正确.3. 解析:选C 一个五位数能否被5整除关键看其个位数字,而由1,2,3,4,5组成的五位数中,1,2,3,4,5出现在个位是等可能的.所以个位数字的基本事件有1,2,3,4,5,“能被2或5整除”这一事件中含有基本事件2,4,5,概率为35=0.6. 4. 解析:选 A 从1,2,3,4这四个数字中,任取两个不同的数字,可构成12个两位数:12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43,其中大于30的有:31,32,34,41,42,43共6个,所以所得两位数大于30的概率为P =612=12. 5. 解析:选C 从4张卡片中随机抽取2张,对应的基本事件有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),故基本事件总数n =6.且每个基本事件发生的可能性相等.设事件A =“取出的2张卡片上的数字之和为奇数”,则A 中所含的基本事件为:(1,2),(1,4),(2,3),(3,4),故m=4,综上可知所求事件的概率P (A )=m n =23. 6. 解析:三张卡片的排列方法有EEB ,EBE ,BEE ,共3种.且等可能出现,则恰好排成英文单词BEE 的概率为13. 答案:137. 解析:采用枚举法:从1,2,3,4这四个数中一次随机取两个数,基本事件为:{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},共6个,符合“一个数是另一个数的两倍”的基本事件有{1,2},{2,4},共2个,所以所求的概率为13. 答案:138. 解析:所有的基本事件为(正,正,正),(正,正,反),(正,反,正),(正,反,反),(反,正,正),(反,正,反),(反,反,正),(反,反,反),共8组.设“恰好出现1次正面向上”为事件A ,则A 包含(正,反,反),(反,正,反),(反,反,正),共3个基本事件,所以P (A )=38. 答案:389. 解:设事件A 为“方程x 2+bx +c =0有实根”,则 A ={(b ,c )|b 2-4c ≥0,b ,c =1,2,…,6}.而(b ,c )共有(1,1)(1,2)(1,3)(1,4)(1,5)(1,6),(2,1)(2,2)(2,3)(2,4)(2,5)(2,6),(3,1)(3,2)(3,3)(3,4)(3,5)(3,6),(4,1)(4,2)(4,3)(4,4)(4,5)(4,6),(5,1)(5,2)(5,3)(5,4)(5,5)(5,6),(6,1)(6,2)(6,3)(6,4)(6,5)(6,6),共36组.其中,可使事件A 成立的有(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(4,4),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共19组.故事件A 的概率为P (A )=1936. 10. 解:(1)标号为1,2,3的三张红色卡片分别记为A ,B ,C ,标号为1,2的两张蓝色卡片分别记为D ,E ,从五张卡片中任取两张的所有可能的结果为:(A ,B ),(A ,C ),(A ,D ),(A ,E ),(B ,C ),(B ,D ),(B ,E ),(C ,D ),(C ,E ),(D ,E ),共10种.由于每一张卡片被取到的机会均等,因此这些基本事件的出现是等可能的.从五张卡片中任取两张,这两张卡片颜色不同且它们的标号之和小于4的结果为:(A ,D ),(A ,E ),(B ,D ),共3种.所以这两张卡片颜色不同且它们的标号之和小于4的概率为310. (2)记F 为标号为0的绿色卡片,从六张卡片中任取两张的所有可能的结果为:(A ,B ),(A ,C ),(A ,D ),(A ,E ),(A ,F ),(B ,C ),(B ,D ),(B ,E ),(B ,F ),(C ,D ),(C ,E ),(C ,F ),(D ,E ),(D ,F ),(E ,F ),共15种.由于每一张卡片被取到的机会均等,因此这些基本事件的出现是等可能的.从六张卡片中任取两张,这两张卡片颜色不同且它们的标号之和小于4的结果为:(A ,D ),(A ,E ),(B ,D ),(A ,F ),(B ,F ),(C ,F ),(D ,F ),(E ,F ),共8种.8 15.所以这两张卡片颜色不同且它们的标号之和小于4的概率为。
2019-2020学年高中数学北师大版必修三习题:课下能力提升(六) Word版含答案

一、选择题1.下列说法不.正确的是( )A.频率分布直方图中每个小矩形的高就是该组的频率B.频率分布直方图中各个小矩形的面积之和等于1C.频率分布直方图中各个小矩形的宽一样大D.频率分布折线图是依次连接频率分布直方图的每个小矩形上端中点得到的2.样本容量为100的频率分布直方图如图所示.根据样本的频率分布直方图估计样本数据落在[6,10)内的频数为a,样本数据落在[2,10)内的频率为b,则a,b分别是( )A.32,0.4 B.8,0.1 C.32,0.1 D.8,0.43.将一个容量为50的样本数据分组后,分组与频数如下:[12.5,15.5),3;[15.5,18.5),8;[18.5,21.5),9;[21.5,24.5),11;[24.5,27.5),10;[27.5,30.5),6;[30.5,33.5),3.则估计小于30的数据大约占总体的( )A.94% B.6% C.92% D.12%4.为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图所示).已知图中从左到右的前3个小组的频率之比为1∶2∶3,第2小组的频数为12,则抽取的学生人数为( )A.46 B.48 C.50 D.605.设矩形的长为a,宽为b,其比满足b:a=5-12≈0.618,这种矩形给人以美感,称为黄金矩形.黄金矩形常应用于工艺品设计中.下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:甲批次:0.598 0.625 0.628 0.595 0.639乙批次:0.618 0.613 0.592 0.622 0.620根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是( ) A.甲批次的总体平均数与标准值更接近B.乙批次的总体平均数与标准值更接近C.两个批次总体平均数与标准值接近程度相同D.两个批次总体平均数与标准值接近程度不能确定二、填空题6.(广东高考)由正整数组成的一组数据x1,x2,x3,x4,其平均数和中位数都是2,且标准差等于1,则这组数据为________.(从小到大排列)7.《中华人民共和国道路交通安全法》规定;车辆驾驶员血液酒精浓度在20~80 mg/100 mL(不含80)之间,属于酒后驾车;血液酒精浓度在80 mg/100 mL(含80)以上时,属醉酒驾车.据《法制晚报》报道,2011年2月15日至2月28日,全国查处酒后驾车和醉酒驾车共28 800人,如图是对这28 800人酒后驾车血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为________.8.一组数据中的每一个数据都减去80,得一组新数据,若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是________,________.三、解答题9.有一个容量为50的样本,数据的分组及各组的频数如下:[25,30),3;[30,35),8;[35,40),9;[40,45),11;[45,50),10;[50,55),5;[55,60],4.(1)列出样本的频率分布表;(2)画出频率分布直方图及频率分布折线图.10.某校为了了解甲、乙两班的数学学习情况,从两班各抽出10名学生进行数学水平测试,成绩如下(单位:分):甲班:82 84 85 89 79 80 91 89 79 74 乙班:90 76 86 81 84 87 86 82 85 83 (1)求两个样本的平均数; (2)求两个样本的方差和标准差; (3)试分析比较两个班的学习情况.答 案1. 解析:选A 频率分布直方图的每个小矩形的高=频率组距. 2. 解析:选A 由于样本数据落在[6,10)内的频率为0.08×4=0.32,则a =100×0.32=32;由于样本数据落在[2,6)内的频率为0.02×4=0.08,则样本数据落在[2,10)内的频率b =0.08+0.32=0.4.3. 解析:选C 由样本的频率分布估计总体的分布.小于30.5的样本频数为3+8+9+11+10+6=47,所以其频率为4750=94%.小于27.5的样本频数为3+8+9+11+10=41,所以其频率为4150=82%.因此小于30的样本频率应在82%~94%之间,满足条件的只有92%.4. 解析:选B 前3个小组的频率和为1-0.037 5×5-0.012 5×5=0.75.又因为前3个小组的频率之比为1∶2∶3,所以第2小组的频率为26×0.75=0.25.又知第2小组的频数为12,则120.25=48,即为所抽样本的人数. 5. 解析:选A x 甲=0.598+0.625+0.628+0.595+0.6395=0.617,x 乙=0.618+0.613+0.592+0.622+0.6205=0.613,∴x 甲与0.618更接近.6. 解析:设x 1≤x 2≤x 3≤x 4,根据已知条件得到x 1+x 2+x 3+x 4=8,且x 2+x 3=4,所以x 1+x 4=4,又因为14x 1-2+x 2-2+x 3-2+x 4-2]=1,所以(x 1-2)2+(x 2-2)2=2,又因为x 1,x 2,x 3,x 4是正整数,所以(x 1-2)2=(x 2-2)2=1,所以x 1=1,x 2=1,x 3=3,x 4=3.答案:1,1,3,37. 解析:(0.01×10+0.005×10)×28 800=4 320.答案:4 3208. 解析:由题意得原来数据的平均数是80+1.2=81.2,方差不变,仍是4.4. 答案:81.2 4.49. 解:(1)频率分布表如下:(2)频率分布直方图、频率分布折线图如下图所示:10. 解:(1)x甲=110(82+84+85+89+79+80+91+89+79+74)=83.2,x乙=110(90+76+86+81+84+87+86+82+85+83)=84.(2)s2甲=110[(82-83.2)2+(84-83.2)2+(85-83.2)2+(89-83.2)2+(79-83.2)2+(80-83.2)2+(91-83.2)2+(89-83.2)2+(79-83.2)2+(74-83.2)2]=26.36,s2乙=110[(90-84)2+(76-84)2+(86-84)2+(81-84)2+(84-84)2+(87-84)2+(86-84)2+(82-84)2+(85-84)2+(83-84)2]=13.2,∴s甲=26.36≈5.13,s乙=13.2≈3.63.(3)由于x甲<x乙,则甲班比乙班平均水平低.由于s甲>s乙,则甲班没有乙班稳定.∴乙班的总体学习情况比甲班好.。
2018-2019学年度北师大版必修2课下能力提升:(三)Word版含解析
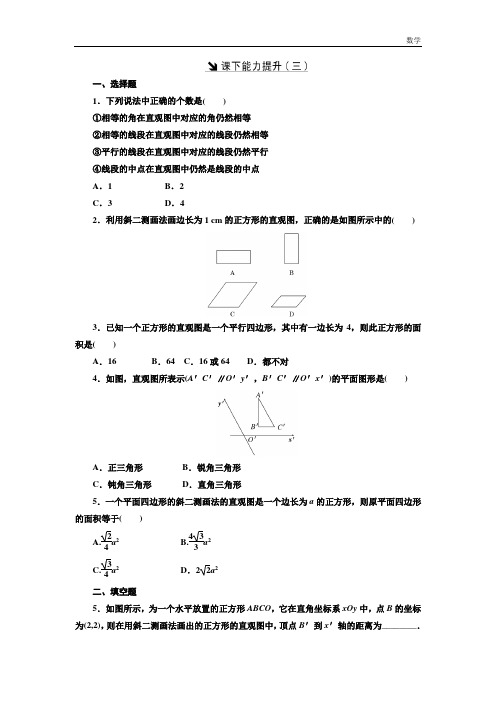
一、选择题1.下列说法中正确的个数是()①相等的角在直观图中对应的角仍然相等②相等的线段在直观图中对应的线段仍然相等③平行的线段在直观图中对应的线段仍然平行④线段的中点在直观图中仍然是线段的中点A.1B.2C.3 D.42.利用斜二测画法画边长为1 cm的正方形的直观图,正确的是如图所示中的()3.已知一个正方形的直观图是一个平行四边形,其中有一边长为4,则此正方形的面积是()A.16B.64 C.16或64D.都不对4.如图,直观图所表示(A′C′∥O′y′,B′C′∥O′x′)的平面图形是()A.正三角形B.锐角三角形C.钝角三角形D.直角三角形5.一个平面四边形的斜二测画法的直观图是一个边长为a的正方形,则原平面四边形的面积等于()A.24a2 B.433a2C.34a2D.22a2二、填空题5.如图所示,为一个水平放置的正方形ABCO,它在直角坐标系xOy中,点B的坐标为(2,2),则在用斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为________.6.水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为________.8.如图所示是水平放置的△ABC在直角坐标系中的直观图,其中D是AC的中点,原△ACB中,∠ACB≠30°,则原图形中与线段BD的长相等的线段有________条.三、解答题9.画出一个正三棱台的直观图(尺寸:上、下底面边长分别为1 cm、2 cm,高为2 cm).10.用斜二测画法得到一水平放置的三角形为直角三角形ABC,AC=1,∠ABC=30°,如图所示,试求原图的面积.答案1. 解析:选B只有③④正确.2. 解析:选D正方形的直观图应是平行四边形,且相邻两边的边长之比为2∶1.3. 解析:选C当其中在x′轴上的边长为4时,正方形面积为16;当其中在y′轴上的边长为4时,正方形面积为64.4. 解析:选D由A′C′∥O′y′,B′C′∥O′x′,∠A′C′B′=45°知对应的平面图形为直角三角形.5. 解析:选D由题意知,平行四边形的直观图为对应在直角坐标系下的图形为:∴平行四边形的面积为S′=2×12×a×22a=22a2.6. 解析:在直观图中,A′B′C′O′是有一个角为45°且长边为2,短边为1的平行四边形,∴B′到x′轴的距离为22.答案:2 27. 解析:由于直观图中,∠A′C′B′=45°,则在原图形中∠ACB=90°,AC=3,BC =4,则斜边AB=5,故斜边AB上的中线长为2.5.答案:2.58. 解析:先按照斜二测画法把直观图还原为真正的平面图形,然后根据平面图形的几何性质找与线段BD长度相等的线段,把△ABC还原后为直角三角形,则D为斜边AC的中点,∴AD=DC=BD.答案:29. 解:(1)画轴,以底面△ABC的垂心O为原点,OC所在直线为y轴,平行于AB的直线为x轴,建立平面直角坐标系,以上底面△A′B′C′的垂心O′与O的连线为z轴,建立空间坐标系.(2)画下底面,在xOy平面上画△ABC的直观图,在y轴上量取OC=33cm,OD=36cm.过D作AB∥x轴,且AB=2 cm,以D为中点,连接AC、BC,则△ABC为下底面三角形的直观图.(3)画上底面,在z轴上截取OO′=2 cm,过O′作x′轴∥x轴,y′轴∥y轴,在y′轴上量取O′C′=36cm,O′D′=312cm,过D′作A′B′∥x′轴,A′B′=1 cm,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题
1.下面哪种统计图没有数据信息的损失,所有的原始数据都可以从该图中得到( ) A.条形统计图 B.茎叶图
C.扇形统计图 D.折线统计图
2.某班学生在课外活动中参加文娱、美术、体育小组的人数之比为3∶1∶6,则在扇形统计图中表示参加体育小组人数的扇形圆心角是( )
A.108° B.216° C.60° D.36°
3.如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的频率为( )
A.0.2 B.0.4 C.0.5 D.0.6
4.某同学对高一(1)班和高一(2)班两个班级今年的获奖情况进行了统计,制成两个统计图(如图所示),你认为哪个图比较恰当( )
A.①恰当 B.②恰当 C.①②都恰当 D.①②都不恰当
5.2013年某学科能力测试共有12万考生参加,成绩采用15级分,测试成绩分布图如下:试估计成绩高于11级分的人数为( )
A.8 000 B.10 000 C.20 000 D.60 000
二、填空题
6.某校高一(1)班有50名学生,综合素质评价“运动与健康”方面的等级统计如图所示,
则该班“运动与健康”评价等级为A的人数是________.
7.在如图所示的茎叶图中,甲、乙两组数据的中位数分别是________,________.
8.某校为了了解学生的睡眠情况,随机调查了50名学生,得到他们在某一天各自的睡眠时间的数据,结果用如图所示的条形图表示.根据条形图可得这50名学生这一天平均每人的睡眠时间为________ h.
三、解答题
9.某赛季甲、乙两名篮球运动员每场比赛得分原始记录如下:
甲运动员的得分:13,23,8,26,38,16,33,14,28,39;
乙运动员的得分:49,24,12,31,50,44,15,25,36,31.
用茎叶图将甲、乙运动员的成绩表示出来.
10.某地农村某户农民年收入如下(单位:元):
土地收入打工收入养殖收入其他收入
4 320 3 600 2 357 843
请用不同的统计图来表示上面的数据.
答案
1. 解析:选B 所有的统计图中,仅有茎叶图完好无损地保存着所有的数据信息.
2. 解析:选B 参加体育小组人数占总人数的6
3+1+6
=60%,则扇形圆心角是360°×60%=216°.
3. 解析:选B 由茎叶图可知数据落在区间[22,30)内的频数为4,所以数据落在区间[22,30)
内的频率为4
10
=0.4.
4. 解析:选 B 图②较恰当.由图②我们可以很清楚地看出运动类的获奖次数(1)班比(2)班多一些,而学习类的获奖次数(1)班比(2)班少一些.
5. 解析:选B 由题意结合条形图分析得成绩高于11级分的考生数的百分比大约为(2.3+3+0.9+1.7)%=7.9%,所以考生大约为:7.9%×120 000=9480(人).故最接近的人数为10 000.
6. 解析:由扇形图可知:评价等级为A的人数占总人数的38%,由此可知高一(1)班的50名学生中有50×38%=19人在该等级中.
答案:19
7. 解析:甲组数据为:28,31,39,42,45,55,57,58,66,中位数为45;
乙组数据为:29,34,35,42,46,48,
53,55,67,中位数为46.
答案:45 46
8. 解析:法一:要确定这50名学生的平均睡眠时间,就必须计算其总睡眠时间.总睡眠时间为5.5×0.1×50+6×0.3×50+6.5×0.4×50+7×0.1×50+7.5×0.1×50=27.5+90+130+35+37.5=320.
故平均睡眠时间为320÷50=6.4 (h).
法二:根据图形得平均每人的睡眠时间为
t=5.5×0.1+6×0.3+6.5×0.4+7×0.1+7.5×0.1=6.4(h).
答案:6.4
9. 解:制作茎叶图的方法是:将所有的两位数的十位数字作为“茎”,个位数字作为“叶”,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出,共茎的叶一般按从大到小(或从小到大)的顺序同行列出.
甲、乙运动员的得分茎叶图如图.
10. 解:用条形统计图表示,如图所示.
用折线统计图表示,如图所示.
用扇形统计图表示,如图所示.。
