非参数假设检验补充例题
非参数假设检验.pptx

计算每分钟内通过收费站的汽车为0辆、1辆、2辆、3 辆、4辆或更多的概率。
第12页/共43页
e 各概率乘以观测总数n=100,便得到理论频数 ,具体结果见下表: i ei
计算 2统计量的值:
2 (14.96 10)2 (28.42 26)2 (27.0 35)2
H0 :汽车通过收费站的辆数服从泊松分布; H1 :不服从泊松分布。
观测值分为5组,且有 u0 10,u1 26,u2 35,u4 5
第11页/共43页
回忆泊松分布
P{X x} e x , x 0,1, 2,
x!
其中 为泊松分布的期望值,是未知的,需要用样
本观测值来估计。由于100分钟内观测到190辆汽车, 所以平均每分钟观测到190/100=1.9辆汽车,故
第9页/共43页
计算 2统计量的值:
2 6 (ui ei )2
i1
ei
(27 25)2 (18 25)2 (15 25)2 (24 25)2
25
25
25
25
(36 25)2 (30 25)2 12
25
25
在本例的情况下, 统2 计量的自由度为m-1=6-1=5。
第8页/共43页
解:本例中的观测值以月为组,共分为m=6组,
每 月的销售台数即为观测的频v数i ,观测的总次
数为n=150。现欲检验是否服从(离散的)均匀 分布,即每月的销售量是否为
ei
nPi
150 6
25(台),
Pi
1 6
,i
1,
,6
为此,设
H0 :洗衣机销售量服从均匀分布;
H1 :并不服从均匀分布;
非参数检验

举例
书上P88,例3.3.7
二、秩和检验法
符号检验法的缺点:没有充分利用数据 符号检验法的缺点 没有充分利用数据 本身提供的信息, 本身提供的信息,而且必须在数据成对时 使用。 使用。 如果两样本数据不成对, 如果两样本数据不成对,则可用秩和检 验法。 验法。
秩和检验法
秩和检验法的做法: 秩和检验法的做法: 建立H 将两组数据依从小到大次序( 建立 0和H1;将两组数据依从小到大次序( 秩号)排列成表,如果有两个以上重复的数, 秩号)排列成表,如果有两个以上重复的数,则 取秩号平均数作为其秩。 取秩号平均数作为其秩。 取样本容量小的一组(样本容量相同时, 取样本容量小的一组(样本容量相同时,取平 均数小的一组),其数据个数记为n 则另一组数 ),其数据个数记为 均数小的一组),其数据个数记为 1,则另一组数 据个数记为n 据个数记为 2,将样本容量小的一组所对应的秩 相加称为该组的秩和( 记为T。 相加称为该组的秩和(Sum of Ranks),记为 。 ) 记为
计算出
npi 查表得: 查表得:1.35<9.448 接受H 认为盒中5种球的个数相等 种球的个数相等。 接受 0,认为盒中 种球的个数相等。
χ
2
∑( f =
i
− npi )
2
= 1.35
拟合优度检验举例2 拟合优度检验举例2
书P82,例3.3.5
二、列联表的独立性检验
独立性检验是对两个总体,或两组资料, 独立性检验是对两个总体,或两组资料, 或一总体的两种指标(分类、特性、 或一总体的两种指标(分类、特性、特征 等之间的独立性所进行的检验。因此, )等之间的独立性所进行的检验。因此, 若设X和 是两个总体 是两个总体( 若设 和Y是两个总体(或一个总体的两个 指标),则其假设应为: ),则其假设应为 指标),则其假设应为: H0:两总体 与Y相互独立 两总体X与 相互独立 H1:两总体 与Y不独立 两总体X与 不独立
第6章 非参数检验

第六章非参数检验在前面的章节中我们介绍了多种假设检验的方法,例如单个总体的t检验、基于两个独立样本的t检验、基于两个匹配样本的t检验、方差分析等。
在这些检验都需要对总体的分布特征作出某些假设(例如在t检验和方差分析中都需要假设总体服从正态分布),然后根据检验统计量的抽样分布对总体参数(如均值、比率等)进行检验。
这类检验方法称为参数检验。
我们前面强调过,在需要的假设条件不满足的情况下,特别是小样本的情况下,t检验、F检验都是不适用的。
那么,如何检验数据是否来自正态分布或者其他分布?在参数检验假设条件不满足的情况下如何对相应的问题进行分析?非参数检验方法可以帮助我们回答这类问题。
在这一章中,我们将首先简要说明非参数检验的概念和优缺点,然后介绍几种常见的非参数检验方法及其在SPSS中的实现方法。
第一节非参数检验概述非参数检验(nonparametric tests)也称为与总体分布无关的检验(distribution free tests),与参数检验相比,在非参数检验中不需要对总体分布的具体形式作出严格假设,或者只需要很弱的假设。
大部分非参数检验都是针对总体的分布进行的检验,但也可以对总体的某些参数进行检验。
与参数检验相比,非参数检验主要有以下几个方面的特点:(1)非参数检验不需要严格假设条件,因而比参数检验有更广泛的适用面。
(2)非参数检验几乎可以处理包括定类数据和定序数据在内的所有类型的数据,而参数检验通常只能用于定量数据的分析。
(3)虽然对于满足参数检验的假设条件的数据也可以采用非参数检验法进行分析,但在参数检验和非参数检验都可以使用的情况下,由于非参数检验没有充分利用样本内所有的数量信息,因此其检验的功效(power)要低于参数检验方法。
也就是说,在备择假设为真的情况下,采用参数检验方法拒绝原假设的概率要高于非参数检验的方法,从而更容易发现显著的差异。
在假设检验中,犯取伪错误的概率记为β,则1-β越大,意味着当备择假设为真时,拒绝原假设的概率越大,检验的判别能力就越好;1-β越小,意味着当备择假设为真时,拒绝原假设的概率越小,检验的判别能力就越差。
统计软件实践习题数据-非参数部分

统计软件实践数据(SPSS非参数部分)第一章单样本非参数检验1.1 2 检验例1.某企业大批连续生产某产品,要求不合格率不大于5%。
现从产品总体中,抽取100个进行检查,不合格品有12个,试以5%的显著性水平检验该批产品的不合格率是否为5%。
例2.某金融机构的货款偿还类型有A、B、C、D四种,各种的预期偿还率为80%、12%、7%和1%。
在一段时间的观察记录中,A型按时偿还的有380笔,B型有69笔,C型有43笔,D型有8笔。
问在5%显著性水平上,这些结果与预期的是否一致。
例3.两种不同牌号的茶哪个更好。
今有30人组成的品茶专家组,对A、B两种不同牌号的茶进行6种味道的检验。
凡专家认为优者被记录下来,如下表示。
1.2 K-S 检验例1.《数理统计与管理》论文作者服从洛特卡分布。
例2.公共交通设施适合性的研究——公共汽车到达时间是否服从正态分布公共汽车按计划每15分钟通过一个商店旁。
然而,由于交通条件,乘客数目等的影响,汽车实际到达的时间有很大的不同。
通过一天的随机观察,获得的数据如下表示。
比计划提前到达的为负值,取大的整数,如提前一分10秒到达,记为-1;比计划晚到的为正值,也取大的整数,如迟到1分10秒,记作+2。
公共汽车到达时间是否服从3σ=的正态分布。
例3.某大街在一年内的交通事故按星期日、星期一、星期二、星期六分为七类进行统计,记录如下表。
试问:事故的发生是否与星期几有关?1.3 符号检验例1.广告对商品促销是否起作用。
例2.生产过程是否需要调整某企业生产一种钢管,规定和度的中位数为10米。
现随机地从正在生产的生产线上选取10根进行测量,结果为:9.8, 10.1, 9.7, 9.9, 9.8, 10.0, 9.7, 10.0, 9.9, 9.8例3.领导者的领导水平是可以训练的为验证领导者是可以训练的,根据人的聪明程度、人品、受教育状况等,随机抽取出12个人配对成6对,每对中有一人随机选择受训,记作T,另一人则不受训记作经过一段时间后,按被设计好的问题评价他们的领导水平,结果如下表示。
非参数统计题目及答案

1.人们在研究肺病患者的生理性质时发现,患者的肺活量与他早在儿童时期是否接受过某种治疗有关,观察3组病人,第一组早在儿童时期接受过肺部辐射,第二组接受过胸外科手术,第三组没有治疗过,现观察到其肺活量占其正常值的百分比如下:这一经验是否可靠。
解:H 0:θ2≤θ1≤θ3 H 1:至少有一个不等式成立可得到 N=15由统计量H=)112+N N (∑=Ki i N R 1i 2-3(N+1)=)(1151512+(32×6.4+29×5.8+59×11.8)-3×(15+1)=5.46查表(5,5,5)在P(H ≥4.56)=0.100 P(H ≥5.66)=0.0509 即P (H ≥5.46)﹥0.05 故取α=0.05, P ﹥α ,故接受零假设即这一检验可靠。
2.关于生产计算机公司在一年中的生产力的改进(度量为从0到100)与它们在过去三年中在智力投资(度量为:低,中等,高)之间的关系的研究结果列在下表中:值等等及你的结果。
(利用Jonkheere-Terpstra 检验) 解:H 0:M 低=M 中=M 高 H 1:M 低﹤M 中﹤M 高U 12=0+9+2+8+10+9+10+2+10+10+8+0.5+3=82.5 U 13=10×8=80U 23=12+9+12+12+12+11+12+11=89 J=∑≤jijUi =82.5+80+89=251.5大样本近似 Z=[]72)32()324121i 222∑∑==+-+--ki i i ki n n N N n N J ()(~N (0,1)求得 Z=3.956 Ф(3.956)=0.9451取α=0.05 , P >α,故接受原假设,认为智力投资对改进生产力有帮助。
非参数统计题目及答案

1.人们在研究肺病患者的生理性质时发现,患者的肺活量与他早在儿童时期是否接受过某种治疗有关,观察3组病人,第一组早在儿童时期接受过肺部辐射,第二组接受过胸外科手术,第三组没有治疗过,现观察到其肺活量占其正常值的百分比如下:这一经验是否可靠。
解:H 0:θ2≤θ1≤θ3 H 1:至少有一个不等式成立可得到 N=15由统计量H=)112+N N (∑=Ki i N R 1i 2-3(N+1)=)(1151512+(32×6.4+29×5.8+59×11.8)-3×(15+1)=5.46查表(5,5,5)在P(H ≥4.56)=0.100 P(H ≥5.66)=0.0509 即P (H ≥5.46)﹥0.05 故取α=0.05, P ﹥α ,故接受零假设即这一检验可靠。
2.关于生产计算机公司在一年中的生产力的改进(度量为从0到100)与它们在过去三年中在智力投资(度量为:低,中等,高)之间的关系的研究结果列在下表中:值等等及你的结果。
(利用Jonkheere-Terpstra 检验) 解:H 0:M 低=M 中=M 高 H 1:M 低﹤M 中﹤M 高U 12=0+9+2+8+10+9+10+2+10+10+8+0.5+3=82.5 U 13=10×8=80U 23=12+9+12+12+12+11+12+11=89 J=∑≤jijUi =82.5+80+89=251.5大样本近似 Z=[]72)32()324121i 222∑∑==+-+--ki i i ki n n N N n N J ()(~N (0,1)求得 Z=3.956 Ф(3.956)=0.9451取α=0.05 , P >α,故接受原假设,认为智力投资对改进生产力有帮助。
非参数统计十道题
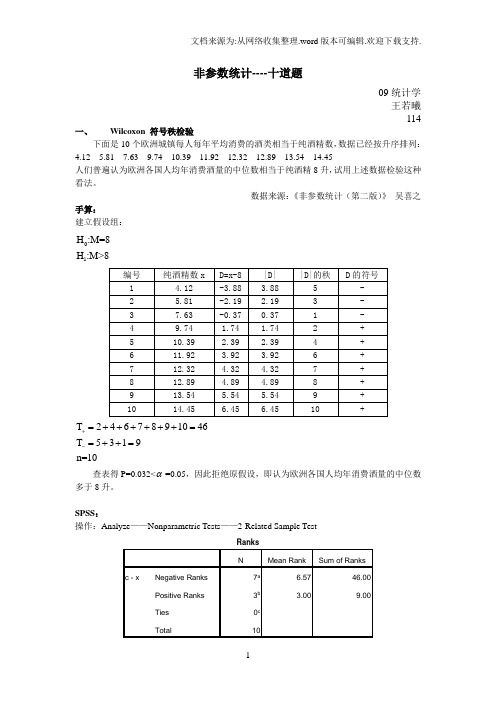
非参数统计----十道题09统计学 王若曦114一、 Wilcoxon 符号秩检验下面是10个欧洲城镇每人每年平均消费的酒类相当于纯酒精数,数据已经按升序排列: 4.12 5.81 7.63 9.74 10.39 11.92 12.32 12.89 13.54 14.45 人们普遍认为欧洲各国人均年消费酒量的中位数相当于纯酒精8升,试用上述数据检验这种看法。
数据来源:《非参数统计(第二版)》 吴喜之手算:建立假设组:01H :M=8H :M>8T 2467891046T 5319n=10+-=++++++==++=查表得P=0.032<α=0.05,因此拒绝原假设,即认为欧洲各国人均年消费酒量的中位数多于8升。
SPSS :操作:Analyze ——Nonparametric Tests ——2-Related Sample TestRanksNMean RankSum of Ranksc - xNegative Ranks 7a 6.57 46.00 Positive Ranks 3b 3.009.00Ties 0c Total10由输出结果可知,单侧精确显著性概率P=0.032<=0.05,因此拒绝原假设,即认为欧洲各国人均年消费酒量的中位数多于8升。
与手算结果相同。
R语言:> x=c(4.12,5.81,7.63,9.74,10.39,11.92,12.32,12.89,13.54,14.45)> wilcox.test(x-8,alt="greater")Wilcoxon signed rank testdata: x - 8V = 46, p-value = 0.03223alternative hypothesis: true location is greater than 0由输出结果可知,P=0.03223<α=0.05,因此拒绝原假设,即认为欧洲各国人均年消费酒量的中位数多于8升。
卡方检验例题

卡方检验例题卡方检验是一种用来检验观察值与理论值之间差异的方法,是一种常用的非参数假设检验方法。
在本篇文档中,我们将为大家介绍卡方检验的基本概念以及一个具体的例题解析。
基本概念在了解卡方检验之前,我们需要先了解一下以下几个基本概念:•观察值:指实际调查或实验中得到的某一类别的数量。
•理论值:指在该种情况下,如果服从某种假设分布所得到的某一类别的数量。
•卡方值:衡量观察值和理论值之间差异的统计量,计算方式为将观察值与理论值的差异平方后除以理论值,然后将所有类别的结果相加得到。
•自由度:指随机变量可以自由取得的值的数目减1。
卡方检验的原假设为两组数据之间没有差异,备择假设为两组数据之间有差异。
例题解析现在我们来看一个具体的例题:在一个蓝球和红球各10个的盒子里,随机抽出了10个球,结果出现了7个蓝球和3个红球。
问你,能否认为这个盒子里的蓝球和红球数量相等?解析:根据题意,我们可以得出观察值为7和3,理论值应该是5和5,如果两组数据之间没有差异,那么我们可以使用卡方检验来检验。
首先,我们需要列出以下的交叉列表格:颜色实际数量预期数量实际数量-预期数量差异平方差异平方/预期数量蓝色7 5 2 4 0.8红色 3 5 -2 4 0.8总计10 10 8 1.6然后,我们可以根据卡方检验公式来计算卡方值:$X^2=\\sum_{i=1}^{n} \\frac{(O_i-E_i)^2}{E_i}$其中,O i为观察值,E i为理论值,n为类别总数。
代入数据后计算得:$X^2=\\frac{(7-5)^2}{5}+\\frac{(3-5)^2}{5}=1.6$接下来,我们需要确定自由度。
自由度的计算公式为:自由度=类别总数-1。
在本例中,我们有2个类别,因此自由度为1。
最后,我们需要根据自由度和显著性水平(通常为0.05或0.01)查找卡方分布表来确定临界值。
在自由度为1,显著性水平为0.05时,临界值为3.84;在显著性水平为0.01时,临界值为6.63。
