大学物理综合练习答案PPT课件
合集下载
《大学物理》的习题训练与详细解答三PPT课件
（3）T1T2 T3
（4）不能确定
T2 2 m我们知道对于相同的弹簧，
k
m，k相同，周期T自然也相等.
与弹簧放置位置无关!
答案为(2)
.
15
4.水平面上有一轻弹簧振子，当它作无阻尼自由振动时， 一块橡胶泥正好竖直落在该振动物体上，设此时刻： （1）振动物体正好通过平衡位置，（2）振动物体正好 在最大位移处。则：
谐振动的振动曲线。则（1）和（2）合成振动的振幅为
，初周相为
，周期为
，试在图
中画出合振动的曲线。
.
13
答 案 为 ： 1cm;,T12s
3
.
14
3.轻弹簧k的一端固定，另一端系一物体m。将系统按图 2所示三种情况放置，如果物体作无阻尼的简谐振动，则 它们振动周期的关系是：
（1）T1T2 T3
（2）T1T2 T3
T 2 ,初始位相为：；某时刻的周相为(t )
从题目我们可以知道：
T=1s;初位相为23；t
2s时周相为14；周相为32 对应的
3
3
t 振 动 方 程 x = 0 . 0 2 c o s 2 ( t +1 3 )米 的 振 子 在 初 始
时 刻 及 t = 0 . 2 5 , 0 . 5 ， 1 . 0 秒 各 时 刻 的 矢 量 位 置 。
大学物理Ⅳ-习题课3
练习十 机械振动（一）
1。质量为0.01千克的小球与弹簧组成的系统的振动规律为:
x=0.1cos2(t+13)米，t以秒计。则该振动的周期为——————，
初位相为———————；t 2秒时的周期为————————；周相为
323对 谐振 应动 的的 时运 刻动 t 方__程 ___为 ___： ___x_ . Acos(t)
《大学物理》习题答案10,匡乐满主编,北京邮电大学出版社PPT文档共23页
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路，那么，任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远，吾将上下而求索。——屈原 75、内外相应，言行相称。——韩非
《大学物理》习题答案10,匡乐满主编,北 京邮电大学出版社
31、园日涉以成趣，门虽设而常关。 32、鼓腹无所思。朝起暮归眠。 33、倾壶绝余沥，窥灶不见烟。
34、春秋满四泽，夏云多奇峰，秋月 扬明辉 ，冬岭 秀孤松 。 35、丈
71、既然我已经踏上这条道路，那么，任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远，吾将上下而求索。——屈原 75、内外相应，言行相称。——韩非
《大学物理》习题答案10,匡乐满主编,北 京邮电大学出版社
31、园日涉以成趣，门虽设而常关。 32、鼓腹无所思。朝起暮归眠。 33、倾壶绝余沥，窥灶不见烟。
34、春秋满四泽，夏云多奇峰，秋月 扬明辉 ，冬岭 秀孤松 。 35、丈
大学物理作业答案PPT课件
精选PPT课件
习题答案
1
精选PPT课件
2.2一自由落体在最后1S内通过了其全程距离的一 半．试求出该落体下落的距离及所用时间
设该落体下落的距离为h,所用的时间为t 由题意可知
即
得
所以
2
精选PPT课件
2.3一钢球从一建筑物的屋顶由静止开始自由下 落．建筑物内一观察者站在高度为1.3 M的窗前， 发现钢球从窗的最上端落至最下端用了1/8S．钢 球继续下落，2.0 S后，与水平地面发生完全弹性 碰撞并上升至窗的最下端，试求该建筑物的高度
（A）终极速度 v = mg/R
（B ）
精选PPT课件
（C）
（D）
9
精选PPT课件
3.10. 水流冲击涡轮机的碟状叶片，冲击前后水 的速率均为V，如图所示．单位时间撞击叶片的 水量是常量 。求水施加在叶片上的力。
设水施加在叶片上的力为F 则 所以
10
精选PPT课件
3.11. 所谓的汤川(YUKAWA)势具有如下形式：
（A）设质点在最低点的速度为v 则在最低点时，有 （1） 又由能量守恒定律可知 （2）
13
精选PPT课件
3.14
由上述（1）（2）式可得
所以当
时
可得
（B）在（A）中情形下
将
代入（2）式可得
质点运动到最低点时的速度为
将
代入（2）式中可得
即
所以质点下落时一部分的重力势能转化为弹性势 能并且相对于同一 个 弹性势能大于重力势能，所 以 v比悬线为非弹性是的速度要小
当
时， 由于t=f(θ) 在此区间内递增
所以当 sin θ = 2/3 时
当
பைடு நூலகம்时，
习题答案
1
精选PPT课件
2.2一自由落体在最后1S内通过了其全程距离的一 半．试求出该落体下落的距离及所用时间
设该落体下落的距离为h,所用的时间为t 由题意可知
即
得
所以
2
精选PPT课件
2.3一钢球从一建筑物的屋顶由静止开始自由下 落．建筑物内一观察者站在高度为1.3 M的窗前， 发现钢球从窗的最上端落至最下端用了1/8S．钢 球继续下落，2.0 S后，与水平地面发生完全弹性 碰撞并上升至窗的最下端，试求该建筑物的高度
（A）终极速度 v = mg/R
（B ）
精选PPT课件
（C）
（D）
9
精选PPT课件
3.10. 水流冲击涡轮机的碟状叶片，冲击前后水 的速率均为V，如图所示．单位时间撞击叶片的 水量是常量 。求水施加在叶片上的力。
设水施加在叶片上的力为F 则 所以
10
精选PPT课件
3.11. 所谓的汤川(YUKAWA)势具有如下形式：
（A）设质点在最低点的速度为v 则在最低点时，有 （1） 又由能量守恒定律可知 （2）
13
精选PPT课件
3.14
由上述（1）（2）式可得
所以当
时
可得
（B）在（A）中情形下
将
代入（2）式可得
质点运动到最低点时的速度为
将
代入（2）式中可得
即
所以质点下落时一部分的重力势能转化为弹性势 能并且相对于同一 个 弹性势能大于重力势能，所 以 v比悬线为非弹性是的速度要小
当
时， 由于t=f(θ) 在此区间内递增
所以当 sin θ = 2/3 时
当
பைடு நூலகம்时，
吉林大学大学物理作业答案综合练习题(下)(二)
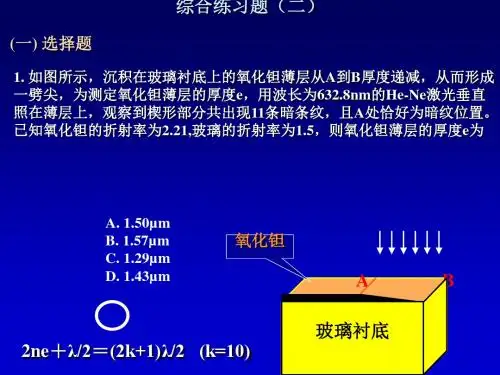
A. 1.50µm B. 1.57µm C. 1.29µm D. 1.43µm
氧化钽
A
B
玻璃衬底 玻璃衬底
2ne＋λ/2＝(2k+1)λ/2 (k=10)
2.物体在周期性外力作用下发生受迫振动，且周期性外力的频率与物体固 有频率相同。若忽略阻力，在稳定情况下，物体的运动表现出如下特点
A. 物体振动频率与外力驱动力的频率不同， 振幅呈现有限值； B. 物体振动频率与外力驱动力的频率相同， 振幅呈现有限值； C. 物体振动频率与外力驱动力的频率不同， 振幅趋于无限大； D. 物体振动频率与外力驱动力的频率相同， 振幅趋于无限大；
固有长度l0
3.两飞船，在自己的静止参照系中测得各自的长度均为100m。飞船1上的 仪器测得飞船1的前端驶完飞船2的全长需5/3×10-7s。两飞船的相对速度 的大小是（ ）
同地钟——固有时间t
0
A.
c/ 6
B.
C.
c/2
l t0
D.
c/ 2
2c / 5
l l0
v2 1 2 c
v
4.光子A的能量是光子B的两倍。则光子A的动量是光子B的（ A.1/4 B.1 C. D.2 倍。
l 0 . 5 m m 解：
e e 3 9 0 0 n m 5 2 2
2 2n
l
1 . 71 0r a d
4
4.一平面透射光栅，当用白光垂直照射时，能在30°衍射方向上观察到600nm的第 二级干涉主极大，并能在该处分辨△λ=0.05nm的两条光谱线，但在此30°方向上却 测不到400nm的第三级主极大，计算此光栅的缝宽a和缝距b以及总缝数N 。
大学物理上册全章节及习题ppt课件
大学物理上册 全章节PPT及 习题
• 6、切向加速度和法向加速度
dv at dt
d dt
v2 an
2 2 a a a t n
• 7、角速度和角加速度
d d 2 2 d t dt
an 2r
v r
at r
a a v u a e • 8、相对运动 v
e x i n 质点系的动能定理: W W E E k k 0
五、保守力的功 势能
保守力的功： F d势能： E p kx l 2 Mm 引力势能： E G p W ( E E ) E 保 pb pa p r
• 9、牛顿第二定律
2 d v d r F m a m m2 dt dt
第二章
一、牛顿三定律
质点动力学
牛顿第一定律：惯性定律 d v 牛顿第二定律 Fm m a d t 牛顿第三定律：作用力与反作用力 二、动量定理 动量守恒定律 t2 质点动量定理 m v v d I 2-m 1 Ft
六、功能原理 机械能守恒定律
ex in 功能原理： W W E E nc 0
0
动能和势能之和 ——机械能
机械能守恒 E E0
第三章 刚体力学
一、定轴转动定律
1）受力分析
M J
质点：牛顿第二定律 F ma 2）列方程： 刚体：转动定律 M J 无滑动条件：a R
固有长度
相对静止时测得棒的长度叫固有长度，相对棒长 方向运动时，测得长度要变短，长度只沿运动方向 收缩。
二、洛仑兹变换 x ut x' 2 2 1 u / c 洛 仑 y' y 兹 变 z 'z u 换 t 2 x 式 c t 1 u2 / c2
• 6、切向加速度和法向加速度
dv at dt
d dt
v2 an
2 2 a a a t n
• 7、角速度和角加速度
d d 2 2 d t dt
an 2r
v r
at r
a a v u a e • 8、相对运动 v
e x i n 质点系的动能定理: W W E E k k 0
五、保守力的功 势能
保守力的功： F d势能： E p kx l 2 Mm 引力势能： E G p W ( E E ) E 保 pb pa p r
• 9、牛顿第二定律
2 d v d r F m a m m2 dt dt
第二章
一、牛顿三定律
质点动力学
牛顿第一定律：惯性定律 d v 牛顿第二定律 Fm m a d t 牛顿第三定律：作用力与反作用力 二、动量定理 动量守恒定律 t2 质点动量定理 m v v d I 2-m 1 Ft
六、功能原理 机械能守恒定律
ex in 功能原理： W W E E nc 0
0
动能和势能之和 ——机械能
机械能守恒 E E0
第三章 刚体力学
一、定轴转动定律
1）受力分析
M J
质点：牛顿第二定律 F ma 2）列方程： 刚体：转动定律 M J 无滑动条件：a R
固有长度
相对静止时测得棒的长度叫固有长度，相对棒长 方向运动时，测得长度要变短，长度只沿运动方向 收缩。
二、洛仑兹变换 x ut x' 2 2 1 u / c 洛 仑 y' y 兹 变 z 'z u 换 t 2 x 式 c t 1 u2 / c2
大学物理综合练习答案
解:当物体滑至前端到达 台面 滑道 x时摩擦力可表示为 x L S m xg i (0 x L) f L mg i ( x L) 则全过程摩擦力的功为： S L m L A f f dl xg dx mg dx mg ( S ) L 2 0 L 动能定理：
。
t
dr t2 t i dt dV V i 2j 2m dt 0m 2j
V
2t 3 t t2 t3 dr i 2 j dt r i 2 tj i 2 tj 6m 3 0 0 2m
a dV / dt V dV / dx
3.飞轮作加速运动时，轮边缘上一点的运动方程为S=0.1t3(SI),飞轮 半径为2m.当此点的速率V= 30m/s时,其切向加速度为a 6m/s2 ， 2 dS t 法向加速度为an= 450m/s2 V 。 V 0.3t 2 dV
d负电荷负电荷在点电荷q的电场中选取以q为中心半径为r的球面上一点p处作电势零点则与点电荷q距离为r的两块面积均为s的金属平板a和b彼此平行放置板间距离为dd远小于板的线度设a板带电量q精选课件12两块面积均为s的金属平板a和b彼此平行放置板间距离为dd远小于板的线度设a板带电量q一无限大均匀带电平面a其附近放一与它平行的有一定厚度的无限大平面导体板b已知a上的电荷面密度为则在导体板b的两个表面1和2上的感应电荷面密度为
作用在质点上的力对原点的力矩 M
( r P ) 即： k 或L r P r mV 12k Kg m2 s1 。 r F 3k N m
Y
。
t
dr t2 t i dt dV V i 2j 2m dt 0m 2j
V
2t 3 t t2 t3 dr i 2 j dt r i 2 tj i 2 tj 6m 3 0 0 2m
a dV / dt V dV / dx
3.飞轮作加速运动时，轮边缘上一点的运动方程为S=0.1t3(SI),飞轮 半径为2m.当此点的速率V= 30m/s时,其切向加速度为a 6m/s2 ， 2 dS t 法向加速度为an= 450m/s2 V 。 V 0.3t 2 dV
d负电荷负电荷在点电荷q的电场中选取以q为中心半径为r的球面上一点p处作电势零点则与点电荷q距离为r的两块面积均为s的金属平板a和b彼此平行放置板间距离为dd远小于板的线度设a板带电量q精选课件12两块面积均为s的金属平板a和b彼此平行放置板间距离为dd远小于板的线度设a板带电量q一无限大均匀带电平面a其附近放一与它平行的有一定厚度的无限大平面导体板b已知a上的电荷面密度为则在导体板b的两个表面1和2上的感应电荷面密度为
作用在质点上的力对原点的力矩 M
( r P ) 即： k 或L r P r mV 12k Kg m2 s1 。 r F 3k N m
Y
吉林大学大学物理练习册综合练习一答案
R1
R2O
λ1 r P
λ2
D. 0
9. 真空中一半径为 的球面均匀带电 ，在球心 处有一 真空中一半径为R的球面均匀带电 的球面均匀带电Q，在球心O处有一 带电量为q的点电荷 如图所示。 的点电荷， 带电量为 的点电荷，如图所示。设无穷远处为电 势零 则在球内离球心O距离为 距离为r的 点处电势为 点，则在球内离球心 距离为 的P点处电势为
二、填空题 x = 6 t − t 2 ( SI) ,则在 由0至4 s的 1. 一质点的运动方程为 则在t由 至 的 则在 时间间隔内， 时间间隔内，质点的位移大小为 8m ，在t由0到4 s 由 到 的时间间隔内质点走过的路程为 10m 。 2. 半径为 半径为30cm的飞轮 从静止开始以 的飞轮,从静止开始以 的飞轮 从静止开始以0.5rad/s2的匀角加速 度转动， 度转动，则飞轮边缘上一点在飞轮转过 240°时的切向 ° 法向加速度的大小a 加速度的大小 at＝ 0.15 m/s2 ， 法向加速度的大小 n ＝ 0.4π m/s2 。 3．一定量的理想气体处于热动平衡状态时，此热力学 ．一定量的理想气体处于热动平衡状态时， 系统不随时间变化的三个宏观量是____________, 系统不随时间变化的三个宏观量是 P,V ,T 2 1 而随时间不断变化的微观量是_________________. 而随时间不断变化的微观量是 υ, 2 mυ , mυ等
m dMf = rµ gdm = rµ g 2 2π rdr πR
mg 2 Mf = ∫ rµ 2 2πrdr = mgµ R 3 πR 0
R
1 2 − Mf θ = 0 − Iω0 2
n =θ
3Rω = 2π 16πµ g
2 0
3. 一卡诺热机 可逆的 ，当高温热源的温度为 一卡诺热机(可逆的 当高温热源的温度为127oC, 低温 可逆的)， 热源温度为27 时 其每次循环对外作净功8000J。今维 热源温度为 oC时，其每次循环对外作净功 。 持低温热源的温度不变，提高高温热源温度， 持低温热源的温度不变，提高高温热源温度，使其每次 循环对外作净功10000J 。若两个卡诺循环都工作在相同 循环对外作净功 的两条绝热线之间，试求： 的两条绝热线之间，试求： (1) 第二个循环热机的效率； 第二个循环热机的效率； (2) 第二个循环的高温热源的温度。 第二个循环的高温热源的温度。 T1 − T2 A 解： = η = ⇒Q2 = 24000J T1 Q2 + A 两循环工作在相同的两条绝热线之间， 两循环工作在相同的两条绝热线之间，且低温热源的 温度不变， 不变。 温度不变，故Q2不变。
大学物理第1章习题解答(全)ppt课件
2 t
23 23 t t 0 3 3
1-24 一质点在半径为0.10m 的圆周上运动， 3 2 4 t 其角位置为 ，式中 的单位为 rad ， t的单位为s。求： （1）在 t=2.0s时质点的法向加速度和切向 加速度。 （2）当切向加速度的大小恰等于总加速度大 小的一半时， 值为多少？ （3）t为多少时，法向加速度和切向加速度 相等？ d 2 3 得： 12 t 2 4 t 解 （1）由 dt
（2）加速度的大小和方向。 解：（1）速度的分量式为 dx dy v 10 60 t v 15 40 t x y dt dt
v ( t ) v v 10 60 t 15 40 t
2 2 x y 2 2
v ( t ) v v 10 60 t 15 40 t
解 （1）由参数方程
x 2 . 0 t , y 19 . 0 2 . 0 t
2
消去t得质点的轨迹方程：
y 19 . 0 0 . 50 x
(2)
2
t1 1 .0 s
t2 2 .0 s
r r r 2 1 v 2 . 0 i 6 . 0 j t t t 2 1
dv d 2 2 2 a (v v ) 3 . 58 m s tt 1 x y dt dt
a a a 1 . 79 m s n
2 2 t
2
(4)
t 1 . 0 s时质点的速度大小为
2 2 1 v v v 4 . 47 m s x y
2
a a a 72 . 1 m s
设 a与 x 轴正向的夹角为
23 23 t t 0 3 3
1-24 一质点在半径为0.10m 的圆周上运动， 3 2 4 t 其角位置为 ，式中 的单位为 rad ， t的单位为s。求： （1）在 t=2.0s时质点的法向加速度和切向 加速度。 （2）当切向加速度的大小恰等于总加速度大 小的一半时， 值为多少？ （3）t为多少时，法向加速度和切向加速度 相等？ d 2 3 得： 12 t 2 4 t 解 （1）由 dt
（2）加速度的大小和方向。 解：（1）速度的分量式为 dx dy v 10 60 t v 15 40 t x y dt dt
v ( t ) v v 10 60 t 15 40 t
2 2 x y 2 2
v ( t ) v v 10 60 t 15 40 t
解 （1）由参数方程
x 2 . 0 t , y 19 . 0 2 . 0 t
2
消去t得质点的轨迹方程：
y 19 . 0 0 . 50 x
(2)
2
t1 1 .0 s
t2 2 .0 s
r r r 2 1 v 2 . 0 i 6 . 0 j t t t 2 1
dv d 2 2 2 a (v v ) 3 . 58 m s tt 1 x y dt dt
a a a 1 . 79 m s n
2 2 t
2
(4)
t 1 . 0 s时质点的速度大小为
2 2 1 v v v 4 . 47 m s x y
2
a a a 72 . 1 m s
设 a与 x 轴正向的夹角为
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
单位为10-2m/s，则该时刻P点的速度为
： (B)
V 25.1i 18.8 j
V
R
二、填空题：
1.在x轴上作变加速直线运动的质点,已知其初速度为V0, 初位置为x0,
加速度a=Ct2(其中C为常量)，则其速度与时间的关系为
V=
V0
1 3
Ct
3
.
运动方程为 x=x0V0tFra bibliotek1 12
Ct 4
。
径向外跑去，当人离转台中心2m时，转台的角速度为
3 19
/s
.
0
2 n
2
1 10
5
/s
角动量守恒：
L0
J00
1200
5
L J'' (1200 80 22)'
8.一可绕定轴转动的飞轮，在20N·m的总力矩作用下，在10s内转速
由零均匀地增加到8rad/s，飞轮的转动惯量J= 25Kg·m2 。
M J d dt
求：(1) (2)
陨石下落过程中，万有引力的功是 陨石落地的速度大小是 V 2Gmh
R(R h)
A GmM ( 1 r2
动能定理
1 ) GmMh
r1
R(R h)
。
。
4.质量为0.25Kg 的质点，受力 F t i (SI) 的作用，式中t为时间。t=0
时该质点以
位置矢量是
F ma
V
ra232mFjtm3im/tsi的2t j速r0dddVtr度。0t通 2t过m20t mti坐id2标tjd原2VtjdV点，r则V6t该m3 i2质tm2 2i点tj 2任j23t意3ddirt时 2刻tj 的
6.一转台绕竖直固定光滑轴转动，每10s转一周，转台对轴的转动惯
量为1200Kg·m2。质量为80Kg的人开始时站在台的中心，随后沿半
动，绕过盘的边缘挂有质量为m长为l的匀质柔软绳索。设绳与圆盘
无相对滑动，试求当圆盘两侧绳长之差为S时，绳的加速度大小
解：设任意时刻左右两侧的绳长为x1、x2，
其质量为
m l
x1
、
m l
x2
，且a1= a2=a
T2
m l
x2 g
m l
x2a
m l
x1 g
T1
m l
x1a
(T1
T2 )R
J
(1 MR2 2
g(2S L)
2.质量为m、长为L的匀质细棒，一端悬挂在O点上，可绕水平轴无
摩擦地转动，在同一悬挂点，有一长为l的轻绳悬一质量也为m的小
球。当小球悬线偏离竖直方向某一角度时，将小球由静止释放。小
球在悬挂点正下方与静止的棒发生完全弹性碰撞。问当绳长l为多少
时，小球与棒碰后，小球刚好静止（略去空气阻力） O
的功以及物体的初速V0 。
L
V0
解:当物体滑至前端到达
x时摩擦力可表示为
f
滑道
m
xg
i
L
mg i
x (0 x L)
( x L)
L
台面
S
则全过程摩擦力的功为：
Af
f dl
L
0
m L
xg
dx
S
L
mg
dx
mg(
S
L) 2
动能定理：
Af
Ek
0
1 2
mV02
V02 g(2S L)
V0
2.质量m=1Kg的物体，在坐标原点处从静止出发在水平面内沿X轴
运动，其所受合力方向与运动方向相同，合力大小为F=3+2x(SI)，
那么物体在开始运动的3m内，合力所做功W=
其速率V=
6m/s
。
a F /m 3 2x
a dV / dt V dV / dx
18J
F
dr;且 03x(3=32mx)时i d，x i
此物体，另一端穿过桌面中心的孔，该物体原以角速度在距孔为R
的圆周上转动，今将绳从小孔缓慢往下拉，则物体：
F
(E) 角动量不变，动能、动量都改变
4时.一刻刚刚FM体x体以r上0每F一 分点0动钟P量(的6改0位转变) 置；绕矢Z轴角量动做为量匀rL速不3转变i ：动4EL（kjJ125J沿k 2(Z轴10正2动m方能)向改，）变若T。；速设度某
如图。若在转动过程中细线被拉断，套管将沿着杆滑动。在套管滑
动过程中，该系统转动的角速度与套管离轴的距离x的函数关系是
什么？(已知杆本身对OO’的转动惯量为
1 3
ml
2 ，滑动面光滑)
10
8
Mdt Jd
0
0
J 10 M 25Kg m2 8
7.如图所示，质点P的质量为2Kg，位置矢量为
r
，速度为
V
，它
受到力
F
作用，这三个矢量均在OXY面内，且r=3.0m,
V=4.0m/s，
F=2N，则该质点对原点O的角动量
作用在质点上的力对原点的力矩
M
L
r
或mLV (rrrPmP)
3.飞轮作加速运动时，轮边缘上一点的运动方程为S=0.1t3(SI),飞轮
半径为2m.当此点的速率V= 30m/s时,其切向加速度为at 6m/s2 ，
法向加速度为an= 450m/s2 V。2
R
V dS 0.3t 2 dt
t
at
dV dt
0.6t
5. 一陨石从距离地面高h处由静止开始落向地面，忽略空气阻力，
V sin r 12Kg m2
即 ：k r mV
12k
Kg
m2
F 3k N m
s1 ;
s1
。
Y V
O
F
V 30
30 P r
X
三、计算题：
1.传送机通过滑道将长为L、质量为M的匀质物体以速度V0向右送上 水平台面，物体前端在台面上滑动S距离(S>L)后停下来。若滑道摩
擦不计，物体与台面间摩擦系数为，试计算台面对物体的摩擦力
m R
l
R2 )
a
S
N
a R l R x1 x2
S x1 x2
a
(
1 2
mgS M m)l
T1 T1
m' g
T2
Mg T2
m l
x1
m l
x2
4. 在一水平放置的质量为m长度为l的匀质细杆上套着一质量也为m
的套管B(可看作质点)，套管用细线拉住，它到竖直的光滑固定轴
OO’的距离为0.5l，杆和套管所组成的系统以角速度0绕OO’轴转动,
解：取小球、杆、地球为系统，做受力分析，有： 内力：mg 外力：T、N ，均不做功，无力矩产生
m L
l
T mg
m
角动量守恒： mVl 1 mL2
mg
3
机械能守恒：
1 2
mV
2
1 2
(1 3
mL2
)
2
V为碰撞前小球的速率，为碰撞后细棒的角速度
l 3L 3
3. 质量为M的匀质圆盘，可绕通过盘中心垂直于盘的固定光滑轴转
之 综合一
一、选择题：
1.对于沿曲线运动的物体，以下几种说法中哪一种是正确的 ：
(B) 法向加速度必不为零（拐点处除外）
2.质点做曲线运动， r 表示径矢，S表示路程，at表示切向加速度，
下列表达式中 ： (D) 只有(3)是对的
(3) dS / dt V
3.有一个小物块，置于一个光滑的水平桌面上，有一绳其一端连结