陶文铨 数值传热学 第二版 第五章 5-2
ANSYSCFD流体工程师认证考试大纲

一考试目标与要求ANSYS CFD(Computational Fluid Dynamics)流体工程师认证考试,是针对从事工程设计的工程师应具备的流体力学和传热学分析知识与ANSYS CFD软件应用能力而实施的技能考核与认证。
认证考试的面向对象包括航空、航天、船舶、车辆、机械、能源、化工、电子、兵器、核能等专业领域的在校本科生及研究生,以及企事业单位从事流体和热设计及分析工作的工程技术人员。
通过认证考试,可以督促考生深入掌握工程流体力学和传热学分析技能并提高软件应用的熟练度,可以帮助考生提高工程实践技能以增强就业能力。
该认证考试的成绩也可以为相关企事业单位提供招聘用人参考。
通过中级认证考试的人员,可以认为其比较系统地掌握了流体力学和传热学分析的基本概念和基本原理,能熟练使用ANSYS CFD软件完成几何建模、网格划分、设置边界条件、设置求解参数、结果后处理等工作,能通过流体力学和传热学基础理论和工程经验知识来确认仿真模型与工程问题的等效性,并能对计算结果进行准确解读和评价。
二考试内容和分值权重ANSYS CFD流体工程师认证考试的题型为选择题,包括单选题和多选题。
考试要求考生具备一定的流体力学、传热学基础知识,并对有限体积法的数值计算过程和相关处理技巧有一定了解。
要求考生可以利用基础理论,将工程实际中的流动和传热问题转化为CFD仿真问题,并能够熟练应用ANSYS CFD软件进行快速、准确的建模和计算。
1.理论基础部分(30%)●流体力学基础1.了解流体的宏观性质与微观结构,连续介质假设及其适用条件,流体的粘性、可压缩性、热膨胀性、表面张力,牛顿流体、非牛顿流体,作用在流体上的质量力与表面力;2.了解流体静力学基本方程及其应用,了解静压强、等压面的概念,了解平面与曲面上流体作用力,流体的相对平衡;3.了解拉格朗日法与欧拉法对流体运动的描述及其之间的联系,了解流线、迹线、涡量、涡管等概念;4.了解连续性方程(雷诺输运定理),动量方程(流体的受力、应力张量),能量方程(热力学定律),本构关系,状态方程等流体力学方程组及其定解条件;5.了解量纲分析与流动相似理论,流体力学中的无量纲量及其物理意义、相似原理的应用;6.了解无粘流、粘性流体的概念及其控制方程的区别;7.了解粘性流体的流动状态:层流、湍流,了解雷诺数的概念;8.了解边界层的概念,了解边界层的分离,湍流的发生,层流到湍流的转捩等现象;9.了解声速和马赫数的概念,了解激波的形成,拉瓦尔喷管的流动特征;●传热学基础1.了解传热学的研究目标,了解热量传递的三种基本方式2.了解温度场、导热系数等概念;了解具有内热源的导热微分方程,以及单值性条件的基本概念;3.了解稳态传热和非稳态传热的概念及其区别;4.了解对流换热,牛顿冷却公式与换热系数;5.了解自然对流和强制对流的概念及其区别;6.了解凝结与沸腾换热等伴随有相变的对流换热现象;7.了解热辐射的本质和特点,了解黑体、灰体、漫射体、发射率、吸收率等基本概念,了解斯蒂芬-玻尔兹曼常数;●有限体积法1.了解对计算区域进行空间离散化的意义,了解流体力学控制方程离散化的方法和意义;2.了解显式方法和隐式方法各自的形式和特点;3.了解对扩散项和对流项的各种离散格式的处理方法、精度和稳定性;4.了解不同类型的网格特点及生成方法,从而针对不同的问题选择合理的网格类型,了解网格疏密度分布的控制策略,了解壁面附近边界层网格的控制策略,了解网格质量的评判标准;5.了解分离式求解方法中常用的SIMPLE算法的压力修正思想和方法。
传热学第四版杨世铭陶文铨第五章2

y = 薄层 —— 流动边界层
或 速度边界层
— 边界层厚度
定义:u/u=0.99 处离壁的距离为边界层厚度
小:空气外掠平板,u=10m/s
边界层内:平均速度梯度很大;y=0处的速度梯度最大
2020/3/19
5
R 青岛科技大学热能与动力工程
由牛顿粘性定律:
速度梯度大,粘滞应力大
边界层外: u 在 y 方向不变化, u/y=0
传热学
第五章 对流换热
§5-1 对流换热概述及其数学描述 §5-2 对流换热过程的边界层微分方程组 §5-3 比拟理论 §5-4 相似原理与量纲分析 §5-5 强制对流换热 §5-6 自然对流换热
2020/3/19
1
R 青岛科技大学热能与动力工程
§5-2 边界层微分方程
问题的提出 高度非线性
偏微分方程 ➢ 控制微分方程组 难以得到分 ➢ 边界条件
0 y :
2020/3/19
0(1)、0()表示数量级为1和 , 1>> 。“~” — 相当于
10
R 青岛科技大学热能与动力工程
对流换热微分方程组的简化
➢ 二维、稳态、无内热源、层流、忽略体积力
u
x
v y
0
( u
u
u x
v
u ) y
Fx
p x
(
2u x2
2u y 2
)
(
v
u
v x
v
v ) y
求解以上方程组可得到速度场和温度 T T 均匀温度
场,利用傅立叶定律可以得到壁面处
的热流密度。
2020/3/19
2
R 青岛科技大学热能与动力工程
数值传热学陶文铨主编第二版习题答案
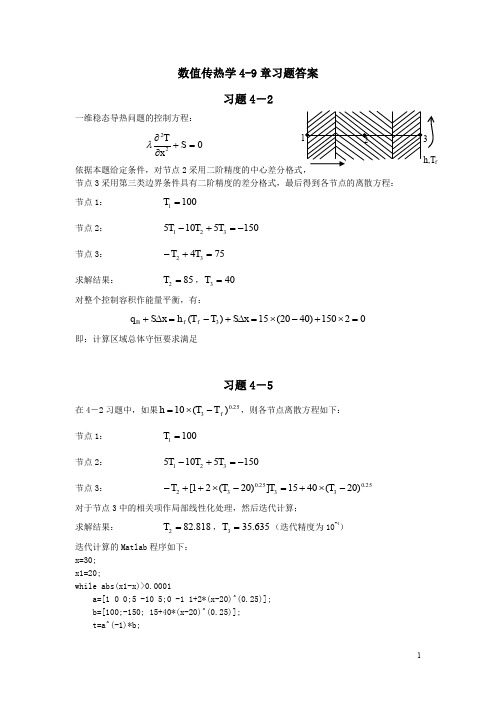
依据本题给定条件,对节点 2 采用二阶精度的中心差分格式, 节点 3 采用第三类边界条件具有二阶精度的差分格式,最后得到各节点的离散方程: 节点 1: 节点 2: 节点 3: 求解结果:
T1 100
5T1 10T2 5T3 150 T2 4T3 75
T2 85 , T3 40
习题 4-12 的 Matlab 程序
%代数方程形式 AiTi=CiTi+1+BiTi-1+Di mdim=10;%计算的节点数 x=linspace(1,3,mdim);%生成 A、C、B、T 数据的基数; A=cos(x);%TDMA 的主对角元素 B=sin(x);%TDMA 的下对角线元素 C=cos(x)+exp(x); %TDMA 的上对角线元素 T=exp(x).*cos(x); %温度数据 %由 A、B、C 构成 TDMA coematrix=eye(mdim,mdim); for n=1:mdim coematrix(n,n)=A(1,n); if n>=2 coematrix(n,n-1)=-1*B(1,n); end if n<mdim coematrix(n,n+1)=-1*C(1,n); end end %计算 D 矢量 D=(coematrix*T')'; %由已知的 A、B、C、D 用 TDMA 方法求解 T %消元 P(1,1)=C(1,1)/A(1,1); Q(1,1)=D(1,1)/A(1,1); for n=2:mdim P(1,n)=C(1,n)/(A(1,n)-B(1,n)*P(1,n-1)); Q(1,n)=(D(1,n)+B(1,n)*Q(1,n-1))/(A(1,n)-B(1,n)*P(1,n-1)); end %回迭 Tcal(1,mdim)=Q(1,mdim); for n=(mdim-1):-1:1 Tcal(1,n)=P(1,n)*Tcal(1,n+1)+Q(1,n); end Tcom=[T;Tcal]; %绘图比较给定 T 值和计算 T 值 plot(Tcal,'r*') hold on plot(T)
沈阳建筑大学加试《传热学》2020年考研专业课复试大纲

2020年硕士研究生考试
同等学力加试传热学科目考试大纲
一、考查目标
按全国硕士研究生入学考试要求为沈阳建筑大学招收建筑设备与环境、供暖通风与空调专业硕士研究生而设置的专业课程考试科目。
其中,传热学是属招生学校自行命题的性质。
它的考查目标是高等学校优秀本科毕业生能达到的及格或及格以上水平,以保证被录取者具有基本的传热理论知识并有利于招生学校在专业上择优选拔。
传热学考试的目标在于考查考生对传热学基本概念、基本理论的掌握和分析求解基本问题的能力。
考生应能:
1. 准确地把握定义的物理量以及它们的量纲;
2. 正确理解基本概念和基本规律;
3. 正确应用基本理论知识分析和处理实际传热问题;
4. 掌握基本计算方法,准确完成传热问题的定量计算。
二、考试形式与试卷结构
(一)试卷满分及考试时间
传热学满分为100分,考试时间为2小时。
(二)答题方式
答题方式为闭卷、笔试。
(三)试卷内容结构。
《传热学》杨世铭-陶文铨-第五章对流传热理论基础

h(tw t f ) W m2
第五章 对流换热
3
4 表面传热系数(对流换热系数)
h Φ ( A(tw t )) W (m2 C)
—— 当流体与壁面温度相差1度时、每单位壁面面 积上、单位时间内所传递的热量
如何确定h及增强换热的措施是对流换热的核心问题
Q导热 + Q对流 = U热力学能
Q导热
2t x2
dxdy+
2t y2
dxdy
单位时间内、 沿 x 方向热对流传递
到微元体的净热量:
Qx
(qm )in (h
1 u2 2
gz)in
(qm )in (h)in
dyu cpt
Q对流,x
Qx"
Qx"dx
Qx"
dy
Q"y y
dy
c p
(vt) y
dydx
c p
t
v y
v
t y
dydx
第五章 对流换热
27
Q导热
2t x2
dxdy+
2t y2
dxdy
Q对流
cp u
t x
t
u x
dxdy
c
p
v
10
(5) 流体的热物理性质:
热导率 [W (m C)]
密度 [kg m3]
比热容 c [J (kg C)] 动力粘度 [N s m2 ]
运动粘度 [m2 s] 体胀系数 [1 K]
传 热 学30页PPT

水,M2 20oC
图0-1 传热学与热力学的区别
(2) 传热学以热力学第一定律和第二定律为基础,即 始终从高温热
源向低温热院传递,如果没有能量形式的转化,则 始终是守恒的
3 传热学应用实例
自然界与生产过程到处存在温差 传热很普遍
a 人体为恒温体。若房间里气体的温度在夏天和 冬天都保持20度,那么在冬天与夏天、人在房间里所 穿的衣服能否一样?为什么? b 夏天人在同样温度(如:25度)的空气和水中的感 觉不一样。为什么? c 北方寒冷地区,建筑房屋都是双层玻璃,以利于保 温。如何解释其道理?越厚越好?
tw2
t r
Φ
tw1
tw2
t R
A
R
A
r
导热热阻 单位导热热阻
t
dx
tw1
dt
Q
tw2
0
tw1
Q
A
x
tw2
图0-2 导热热阻的图示
例 题 1-1
例题 1-1 一块厚度δ =100 mm 的平板, 两侧表面分别维 持在 tw 130 oC ,0 tw 210 oC .0试求下列条件下的热流密度。
(2)物质的属性:可以在固体、液体、气体中发生 (3)导热的特点:a 必须有温差;b 物体直接接触;c
依靠分子、原子及自由电子等微观粒子热运动而传递 热量;d 在引力场下单纯的导热只发生在密实固体 中。
(4) 一维稳态导热及其导热热阻 如图0-2所示,稳态 q = const。
q
tw1
q — 热流密度 Wm2 h — 表面传热系数 W (m 2K)
(完整版)数值传热学陶文铨主编第二版习题答案
数值传热学4-9章习题答案习题4-2一维稳态导热问题的控制方程:022=+∂∂S xTλ依据本题给定条件,对节点2节点3采用第三类边界条件具有二阶精度的差分格式,最后得到各节点的离散方程:节点1:1001=T 节点2:1505105321-=+-T T T 节点3:75432=+-T T 求解结果:,852=T 403=T 对整个控制容积作能量平衡,有:2150)4020(15)(3=⨯+-⨯=∆+-=∆+x S T T h x S q f f B 即:计算区域总体守恒要求满足习题4-5在4-2习题中,如果,则各节点离散方程如下:25.03)(10f T T h -⨯=节点1:1001=T 节点2:1505105321-=+-T T T 节点3:25.03325.032)20(4015])20(21[-⨯+=-⨯++-T T T T 对于节点3中的相关项作局部线性化处理,然后迭代计算;求解结果:,(迭代精度为10-4)818.822=T 635.353=T 迭代计算的Matlab 程序如下:x=30;x1=20;while abs(x1-x)>0.0001a=[1 0 0;5 -10 5;0 -1 1+2*(x-20)^(0.25)]; b=[100;-150; 15+40*(x-20)^(0.25)]; t=a^(-1)*b;x1=x;x=t(3,1);endtcal=t习题4-12的Matlab程序%代数方程形式A i T i=C i T i+1+B i T i-1+D imdim=10;%计算的节点数x=linspace(1,3,mdim);%生成A、C、B、T数据的基数;A=cos(x);%TDMA的主对角元素B=sin(x);%TDMA的下对角线元素C=cos(x)+exp(x); %TDMA的上对角线元素T=exp(x).*cos(x); %温度数据%由A、B、C构成TDMAcoematrix=eye(mdim,mdim);for n=1:mdimcoematrix(n,n)=A(1,n);if n>=2coematrix(n,n-1)=-1*B(1,n);endif n<mdimcoematrix(n,n+1)=-1*C(1,n);endend%计算D矢量D=(coematrix*T')';%由已知的A、B、C、D用TDMA方法求解T%消元P(1,1)=C(1,1)/A(1,1);Q(1,1)=D(1,1)/A(1,1);for n=2:mdimP(1,n)=C(1,n)/(A(1,n)-B(1,n)*P(1,n-1));Q(1,n)=(D(1,n)+B(1,n)*Q(1,n-1))/(A(1,n)-B(1,n)*P(1,n-1)); end%回迭Tcal(1,mdim)=Q(1,mdim);for n=(mdim-1):-1:1Tcal(1,n)=P(1,n)*Tcal(1,n+1)+Q(1,n);endTcom=[T;Tcal];%绘图比较给定T值和计算T值plot(Tcal,'r*')hold onplot(T)n gin th a r e 结果比较如下,由比较可知两者值非常切合(在小数点后8位之后才有区别):习题4-14充分发展区的温度控制方程如下:)(1rTr r r x T uc p ∂∂∂∂=∂∂λρ对于三种无量纲定义、、进行分析如下w b w T T T T --=Θ∞∞--=ΘT T T T w ww T T T T --=Θ∞1)由得:wb wT T T T --=Θww b T T T T +Θ-=)(由可得:T x T x T x T T T x T w b w w b ∂∂Θ-+∂∂Θ=∂+Θ-∂=∂∂)1(])[(rT r T T r T T T r T w w b w w b ∂∂Θ-+∂Θ∂-=∂+Θ-∂=∂∂)1()(])[(由与无关、与无关以及、的表达式可知,除了均匀的情况外,该无量b T r Θx x T ∂∂rT∂∂w T 纲温度定义在一般情况下是不能用分离变量法的;2)由得:∞∞--=ΘT T T T w ∞∞+Θ-=T T T T w )(由可得:T xT x T T T x T w w ∂∂Θ=∂+Θ-∂=∂∂∞∞])[(rT r T T r T T T r T w w w ∂∂Θ+∂Θ∂-=∂+Θ-∂=∂∂∞∞∞)(])[(由与无关、与无关以及、的表达式可知,在常见的四种边界条件中除了b T r Θx x T ∂∂rT ∂∂轴向及周向均匀热流的情况外,有,则该无量纲温度定义是可以用分const q w =0=∂∂rT w离变量法的;3)由得:wwT T T T --=Θ∞ww T T T T +Θ-=∞)(由可得:T xT x T T T x T w w w ∂∂Θ-=∂+Θ-∂=∂∂∞)1(])[(r T T r T T T r T w w w -+∂Θ∂-=∂+Θ-∂=∂∂∞∞1()(])[(同2)分析可知,除了轴向及周向均匀热流const q w =温度定义是可以用分离变量法的;习题4-181)采用柱坐标分析,写出统一的稳态柱坐标形式动量方程:S r r r r r r x x w r v r r r u x +∂∂∂∂+∂∂∂∂+∂∂∂∂=∂∂+∂∂+∂∂(1)(1)()(1)(1)(θφλθφλφλφρθφρφρ、和分别是圆柱坐标的3个坐标轴,、和分别是其对应的速度分量,其中x r θu v w 是管内的流动方向;x 对于管内的层流充分发展有:、,;0=v 0=w 0=∂∂xu并且方向的源项:x x pS ∂∂-=方向的源项:r r pS ∂∂-=方向的源项:θθ∂∂-=pr S 1由以上分析可得到圆柱坐标下的动量方程:方向:x 0)(1)(1=∂∂-∂∂∂∂+∂∂∂∂x pu r r r u r r r θλθλ方向:r 0=∂∂r p 方向:θ0=∂∂θp 边界条件:,R r =0=u ,;对称线上,0=r 0=∂∂r u 0=∂∂θu 不考虑液体的轴向导热,并简化分析可以得到充分发展的能量方程为:)(1(1θλθλρ∂∂∂∂+∂∂∂∂=∂∂Tr r r T r r r x T uc p 边界条件:,;,R r =w q r T =∂∂λ0=r 0=∂∂rT,πθ/0=0=∂∂-θλT2)定义无量纲流速:dxdp R uU 2-=λ并定义无量纲半径:;将无量纲流速和无量纲半径代入方向的动量方程得:R r /=ηx 0))1((1)1((122=∂∂-∂-∂∂∂+∂-∂∂∂xp U dx dp R R R R U dx dp R RR R θληλθηηλληηη上式化简得:011(1(1=+∂∂∂∂+∂∂∂∂θηθηηηηηU U 边界条件:,1=η0=U ,;对称线上,0=η0=∂∂ηU 0=∂∂θU定义无量纲温度:λ/0R q T T b-=Θ其中,是折算到管壁表面上的平均热流密度,即:;0q Rq q wπ=0由无量纲温度定义可得:bT Rq T +Θ=λ0将表达式和无量纲半径代入能量方程得:T η(1)(100θληλθηηλληηηρ∂Θ∂∂∂+∂Θ∂∂∂=∂∂R q R R R R q R R R x T uc b p 化简得:(1))1(1)(10θηθηηηηηρ∂Θ∂∂∂+∂Θ∂∂∂=∂∂x T u c q R b p 由热平衡条件关系可以得:mm m b m p b p p RU U q R u u R q A u u dx dT A u c x T u c x T uc 020221221)(===∂∂=∂∂ππρρρ将上式代入式(1)可得:)1(1)(12θηθηηηηη∂Θ∂∂∂+∂Θ∂∂∂=m U U 边界条件:,;,0=η0=∂Θ∂η1=ηR q q w πη10==∂Θ∂,;,0=θ0=∂Θ∂θπθ=0=∂Θ∂θ单值条件:由定义可知: 且: 0/0=-=ΘλR q T T b b b ⎰⎰Θ=ΘAAb UdAUdA 即得单值性条件:=Θ⎰⎰AA UdAUdA 3)由阻力系数及定义有:f Re 228)(21/Re ⎪⎭⎫ ⎝⎛=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=D D U D u u dx dp D f e m e m me νρ且:m W b m W b m W R q T T D T T q Nu ,0,,0~2)/(2Θ=-=-=λλ5-21.一维稳态无源项的对流-扩散方程如下所示: (取常物性)xx u 22∂∂Γ=∂∂φφρ边界条件如下:LL x x φφφφ====,;,00上述方程的精确解如下: 11)/(00--=--⋅Pe L x Pe L e e φφφφΓ=/uL Pe ρ2.将分成20等份,所以有:L ∆=P Pe 20 1 2 3 4 5 6……………………… 17 18 19 20 21对于中心差分、一阶迎风、混合格式和QUICK 格式分别分析如下:1)中心差分中间节点: 2)5.01()5.01(11-∆+∆++-=i i i P P φφφ20,2 =i 2)一阶迎风中间节点: ∆-∆++++=P P i i i 2)1(11φφφ20,2 =i 3)混合格式当时,中间节点: 1=∆P 2)5.01()5.01(11-∆+∆++-=i i i P P φφφ 20,2 =i 当时,中间节点: 10,5=∆P 1-=i i φφ20,2 =i 4)QUICK 格式*12111)35(8122121⎥⎦⎤⎢⎣⎡---++++++=+--∆∆-∆∆+∆i i i i i i i P P P P P φφφφφφφ2≠i*1111)336(8122121⎥⎦⎤⎢⎣⎡--++++++=+-∆∆-∆∆+∆i i i i i i P P P P P φφφφφφ2=i 数值计算结果与精确解的计算程序如下:%except for HS, any other scheme doesnt take Pe<0 into consideration %expression of exact solutiony=dsolve('a*b*Dy=c*D2y','y(0)=y0,y(L)=yL','x')y=subs(y,'L*a*b/c','t')y=simple(subs(y,'a*b/c*x','t*X'));ysim=simple(sym(strcat('(',char(y),'-y0)','/(yL-y0)')))y=sym(strcat('(',char(ysim),')*(yL-y0)','+y0'))% in the case of Pe=0y1=dsolve('D2y=0','y(0)=y0,y(L)=yL','x')y1=subs(y1,'-(y0-yL)/L*x','(-y0+yL)*X')%grid Pe number tt=[1 5 10];%dimensionless length m=20;%mdim is the number of inner node mdim=m-1;X=linspace(0,1,m+1);%initial value of variable during calculation y0=1;yL=2;%cal exact solution for n=1:size(tt,2) t=m*tt(1,n); if t==0 yval1(n,:)=eval(y1); else yval1(n,:)=eval(y); end end%extra treatment because max number in MATLAB is 10^308if max(isnan(yval1(:))) yval1=yval1'; yval1=yval1(:);indexf=find(isnan(yval1)); for n=1:size(indexf,1) if rem(indexf(n,1),size(X,2))==0 yval1(indexf(n),1)=yL; else yval1(indexf(n),1)=y0; endendyval1=reshape(yval1,size(X,2),size(yval1,1)/size(X,2));yval1=yval1';end%CD solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([0.5*(1-0.5*t)],1,mdim);c(n,:)=repmat([0.5*(1+0.5*t)],1,mdim);d(n,1)=0.5*(1+0.5*tt(1,n))*y0;d(n,mdim)=0.5*(1-0.5*tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval2=TDMA(a,b,c,d,mdim);yval2=[repmat([1],size(tt,2),1),yval2,repmat([2],size(tt,2),1)]; Fig(1,X,yval1,yval2,tt);title('CD Vs. Exact Solution')% FUS solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([1/(2+t)],1,mdim);c(n,:)=repmat([(1+t)/(2+t)],1,mdim);d(n,1)=(1+tt(1,n))/(2+tt(1,n))*y0;d(n,mdim)=1/(2+tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval3=TDMA(a,b,c,d,mdim);yval3=[repmat([1],size(tt,2),1),yval3,repmat([2],size(tt,2),1)]; Fig(2,X,yval1,yval3,tt);title('FUS Vs. Exact Solution')% HS solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);if t>2b(n,:)=repmat([0],1,mdim);c(n,:)=repmat([1],1,mdim);d(n,1)=y0;elseif t<-2b(n,:)=repmat([1],1,mdim);c(n,:)=repmat([0],1,mdim);d(n,mdim)=yL;elseb(n,:)=repmat([0.5*(1-0.5*t)],1,mdim);c(n,:)=repmat([0.5*(1+0.5*t)],1,mdim);d(n,1)=0.5*(1+0.5*t)*y0;d(n,mdim)=0.5*(1-0.5*t)*yL;endendc(:,1)=0;b(:,mdim)=0;% numerical cal by using TDMA subfuctionyval4=TDMA(a,b,c,d,mdim);yval4=[repmat([1],size(tt,2),1),yval4,repmat([2],size(tt,2),1)]; Fig(3,X,yval1,yval4,tt);title('HS Vs. Exact Solution')%QUICK Solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([1/(2+t)],1,mdim);c(n,:)=repmat([(1+t)/(2+t)],1,mdim);d(n,1)=(1+tt(1,n))/(2+tt(1,n))*y0;d(n,mdim)=1/(2+tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval5=zeros(size(tt,2),mdim);yval5com=yval5+1;counter=1;%iterativewhile max(max(abs(yval5-yval5com)))>10^-10if counter==1yval5com=TDMA(a,b,c,d,mdim);endfor nn=1:size(tt,2)for nnn=1:mdimif nnn==1d(nn,nnn)=((6*yval5com(nn,nnn)-3*y0-3*yval5com(nn,nnn+1))*tt(1,nn))/(8*(2+tt(1,nn)))+((1+tt(1,nn))/(2+tt(1,nn))*y0);elseif nnn==2d(nn,nnn)=((5*yval5com(nn,nnn)-3*yval5com(nn,nnn+1)-yval5com(nn,nnn-1)-y0)*tt(1,nn))/(8*(2+tt(1,nn)));elseif nnn==mdimd(nn,nnn)=((5*yval5com(nn,nnn)-3*yL-yval5com(nn,nnn-1)-yval5com(nn,nnn-2))*tt(1,nn))/(8*(2+tt(1,nn)))+(1/(2+tt(1,nn))*yL);elsed(nn,nnn)=((5*yval5com(nn,nnn)-3*yval5com(nn,nnn+1)-yval5com(nn,nnn-1)-yval5com(nn,nnn-2))*tt(1,nn))/(8*(2+tt(1,nn)));endendendyval5=TDMA(a,b,c,d,mdim);temp=yval5;yval5=yval5com;yval5com=temp;counter=counter+1;endyval5=yval5com;yval5=[repmat([1],size(tt,2),1),yval5,repmat([2],size(tt,2),1)];Fig(4,X,yval1,yval5,tt);title('QUICK Vs. Exact Solution')%-------------TDMA SubFunction------------------function y=TDMA(a,b,c,d,mdim)%form a b c d resolve yval2 by using TDMA%eliminationp(:,1)=b(:,1)./a(:,1);q(:,1)=d(:,1)./a(:,1);for n=2:mdimp(:,n)=b(:,n)./(a(:,n)-c(:,n).*p(:,n-1));q(:,n)=(d(:,n)+c(:,n).*q(:,n-1))./(a(:,n)-c(:,n).*p(:,n-1));end%iterativey(:,mdim)=q(:,mdim);for n=(mdim-1):-1:1y(:,n)=p(:,n).*y(:,n+1)+q(:,n);end%-------------ResultCom SubFunction------------------function y=ResultCom (a,b,c)for n=1:max(size(c,2))y(2*n-1,:)=a(n,:);y(2*n,:)=b(n,:);end%-------------Fig SubFunction------------------function y=Fig(n,a,b,c,d)figure(n);plot(a,b);hold onplot(a,c,'*');str='''legend(';for n=1:size(d,2)if n==size(d,2)str=strcat(str,'''''Pe=',num2str(d(1,n)),''''')''');elsestr=strcat(str,'''''Pe=',num2str(d(1,n)),''''',');endendeval(eval(str));a n d A l l t h i n g s i n t h ei r b e i n g a r e g 13精确解与数值解的对比图,其中边界条件给定,。
《传热学》杨世铭-陶文铨-第六章单相对流传热
(2)各特征数之间存在着函数关系,如常物性流体外略平板对
流换热特征数: Nu f (Re, Pr)
特征数方程:无 量纲量之间的函
数关系
第五章 对流换热
3
4 物理现象相似的条件
• 同名的已定特征数相等 • 单值性条件相似:初始条件、边界条件、几何条件、物理条件
实验中只需测量各特征数所包含的物理量,避免了测量的盲 目性——解决了实验中测量哪些物理量的问题
试验数据的整理形式:
Nu c Ren Nu c Ren Pr m Nu c(Gr Pr)n
第五章 对流换热
23
§6-3 内部流动强制对流换热实验关联式
一. 管槽内强制对流流动和换热的特征
内部强制对流在工 程上有大量应用: 暖气管道、各类热 水及蒸汽管道、换 热器等
第五章 对流换热
24
1 管槽内强迫对流换热的特点及几个重要的物理量
4 Ac P
Ac —— 过流断面面积,m2 P —— 湿周,m
第五章 对流换热
17
c 特征速度:Re数中的流体速度
流体外掠平板或绕流圆柱:取来流速度 u
管内流动:取截面上的平均速度 um
流体绕流管束:取最小流通截面的最大速度 umax
第五章 对流换热
18
2 常见无量纲(准则数)数的物理意义及表达式
使用特征数关联式时,必须与其定性温度一致
第五章 对流换热
16
b 特征长度:包含在相似特征数中的几何长度;
应取对于流动和换热有显著影响的几何尺度
如:管内流动换热:取直径 d
流体在流通截面形状不规则的槽道中流动:取当量直径作 为特征尺度:
当量直径(de) :过流断面面积的四倍与湿周之比称为当量直
数值传热学
课程编号:S201E045数值传热学学时:32 学分: 2 开课时间:春季授课单位:机械工程任课教师:李汛一、课程内容简介本教程的目的是使学生掌握一种能够预测传热与传质、流体流动过程的数值方法,用以解决工程实际中大量存在的,而用解析方法难以解决的传热与流体流动问题。
本课程的特点是:它强烈地以物理上的依据为基础,而不只是以数学推演为基础。
学生在学习数值方法的同时,可以加深对基本物理过程的认识和理解。
物理的手段将使学生掌握通用的评定准则。
他们应用这些准则就可以对现有的以及未来的数值方法做出评判。
课程由三部分组成,每部分分成三章,共九章。
前三章是预备性的知识,其中包括对数学与数值方法的基本讨论。
此外,这一部分还概述了本课程所特有的方法。
第四到第六章包含着数值方法的主要推演。
最后的三章则致力于解释和应用。
第一章是绪论。
第二章中概述并讨论了有关的物理现象和微分方程。
在这一章中尤为重要的是,从物理意义的观点来分析这些方程的抛物型或椭圆型特性。
在第三章中提出了数值解的概念,其中描述了构成数值方法的一般步骤。
以这一部分内容为基础,本书进一步系统地提出了形式为四项基本法则的一般准则。
这些基本法则构成本书其余部分中数值方法推演过程的准绳。
数值方法的构成开始于第四章,它通过三个步骤进行。
第四章处理热传导。
第五章集中讨论对流与热传导的相互作用;这时认为:流场是已知的。
最后,在第六章中处理速度场本身的计算。
最后三章用于对前面的方法的解释和应用。
This course is primarily aimed at to help the students to mastery a numerical method which is able to predict the process of heat and mass transfer and fluid flow and with which to solve the complex engineering problems, to which the analytical method can find no way out.An important characteristic of the numerical method to be developed here is that they strongly based on the physical consideration, not just on mathematical manipulation. A significant of this strategy is that the student, while learning about the numerical method, develops a deeper understanding of, and insight into, the underlying physical process. Further, the physical approach will equip the students with general criteria with which to judge other existing and future numerical methods.The course is consisted of three different parts with three chapters each. The first three chapters constitute the preparatory phase. Here,a preliminary discussion about the mathematical and numerical aspect is included, and the particular philosophy of the course is outlined. Chapters 4-6 contain the main development of the numerical method. The last three chapters are devoted to elucidations and applications.The first chapter is introduction. In Chapter 2, the related physical phenomena and differential equations are outlined and discussed. Of special importance in that chapter is the examination of the parabolic or elliptic nature of these equations from a physically meaningful viewpoint.The concept of numerical solution is developed in Chapter 3, where the common procedures of constructing numerical methods are described. This introductory material is used to formulate general criteria in the form of four basic rules. These rules form the guideposts for the development of the numerical method in the rest of this book.The construction of the numerical method begins in Chapter 4. It is carried out in three stages. Heat conduction (i.e., the general problem without the convection term) is treated in Chapter 4. Chapter 5 concentrates on the interaction of convection and conduction with the flow field regarded as given. Finally, the calculation of the velocity field itself is dealt with in Chapter 6.As to the last three chapters, as mentioned above, are devoted to elucidations and applications of the previous methods.二、先修课程流体力学、传热学三、教材Numerical Heat Transfer and Fluid Flow, by S.V. Patankar, McGraw-Hill Company, 1980四、主要参考书目及文献1、《数值传热学》(第二版),陶文铨著,西安交通大学出版社,20012、《计算传热学的近代进展》,陶文铨著,科学出版社,2000在燃烧问题中,高温气流和与之相邻的液体或固体物质之间存在着一个相分界面。
数值传热学绪论热流问题的数值计算课件01
注意
1.4数值传热学及常用的数值方法
1.4.1数值传热学求解问题的基本思想:
把原来在空间与时间坐标中连续的物理量的场 ,用一系列有限个离散点(称为节点)上的值 的集合来代替,通过一定的原则建立起这些离 散点上变量值之间关系的代数方程(称为离散 方程),求解的建立起来的代数方程以获得所 求解变量的近似值。如图1-7所表示(见下页) 。
1.3控制方程的数学分类及基对数值 解的影响
1.3.1偏微分方程的3种类型
双曲型(hyperbolic); 抛物型(parabolic); 椭圆型(elliptic).
1.3.2椭圆型方程
描写物理学中一类稳态问题,这种物理问 题的变量与时间无关而需要在空间的一个 闭区域内来求解。如图1-4所示。各节点上 的代数方程必须联立求解,而不能先解得 区域中某一部分上的值后再去确定其余地 区上的值。
u-动量方程:
v-动量方程:
w-动量方程:
流体的第2 分子黏度
流体的动力粘度
矢量形式为:
其中
为3个动量方程的广义
源项,其表达式为:
对粘性为常数的不可压缩流体
于是式(1-6)简化成为:
1.1.3能量守恒方程
对图1-1所示的微元体应用能量守恒定 律:
[微元体内热力学能的增加率]=[进 入微元体的净热流量]+[体积力与表 面力对微元体做的功]
再引入导热Fourier定律,可得出用流 体比焓h及温度T表示的能量方程:
导热系数
耗散函数
流体的内 热源
为由于粘性作用机械能转换为热能 的部分,其计算式如下:
对不可压流体有:
1.1.4控制方程的通用形式
1.1.5几点说明:
1. 式(1-4)是三维非稳态Navier-Stokes方程 ,无论对层流或湍流都是适用的。
