【数学】2011年北京市各区一模试题分类解析(19):创新题
北京市西城区2011年高三4月一模数学(理科)试题(WORD精校版)

开始是否i < 输出S结束2i S S =+1i i =+①1,1S i ==北京市西城区2011年高三一模试卷 数 学(理科) 2011. 4一、选择题:本大题共8小题,每小题5分,共40分. 在每小题列出的四个选项中,选出符合题目要求的一项. 1. 已知集合{5}A x x =∈<Z ,{20}B x x =-≥,则A B 等于 (A )(2,5)(B )[2,5)(C ){2,3,4}(D ){3,4,5}2.下列给出的函数中,既不是奇函数也不是偶函数的是 (A )2xy =(B )2y x x =-(C )2y x = (D )3y x =3. 设3log 2=a ,3log 4=b ,5.0=c ,则 (A )a b c <<(B )b c a <<(C )c a b <<(D )b a c <<4.设向量(1,sin )θ=a ,(3sin ,1)θ=b ,且//a b ,则cos2θ等于 (A )31-(B )32-(C )32 (D )31 5. 阅读右侧程序框图,为使输出的数据为31, 则①处应填的数字为 (A )4 (B )5 (C )6 (D )76.已知函数①x x y cos sin +=,②x x y cos sin 22=,则下列结论正确的是(A )两个函数的图象均关于点(,0)4π-成中心对称 (B )两个函数的图象均关于直线4x π=-成中心对称(C )两个函数在区间(,)44ππ-上都是单调递增函数(D )两个函数的最小正周期相同 7.已知曲线1:(0)C y x x=>及两点11(,0)A x 和22(,0)A x ,其中210x x >>.过1A ,2A 分别作x 轴的垂线,交曲线C 于1B ,2B 两点,直线12B B 与x 轴交于点33(,0)A x ,那么 (A )312,,2x x x 成等差数列 (B )312,,2x x x 成等比数列 (C )132,,x x x 成等差数列 (D )132,,x x x 成等比数列8.如图,四面体OABC 的三条棱OC OB OA ,,两两垂直,2==OB OA ,3=OC ,D 为四面体OABC 外一点.给出下列命题.①不存在点D ,使四面体ABCD 有三个面是直角三角形 ②不存在点D ,使四面体ABCD 是正三棱锥③存在点D ,使CD 与AB 垂直并且相等④存在无数个点D ,使点O 在四面体ABCD 的外接球面上 其中真命题的序号是(A )①② (B )②③ (C )③ (D )③④二、填空题:本大题共6小题,每小题5分,共30分.9. 在复平面内,复数2i1i-对应的点到原点的距离为_____.10.如图,从圆O 外一点P 引圆O 的切线PA 和割线PBC ,已知22PA =,4PC =, 圆心O 到BC 的距离为3,则圆O 的半径为_____.11.已知椭圆:C cos ,()2sin x y θθθ=⎧∈⎨=⎩R 经过点1(,)2m ,则m =______,离心率e =______.12.一个棱锥的三视图如图所示,则这个棱锥的体积为_____.13.某展室有9个展台,现有3件展品需要展出,要求每件展品独自占用1个展台,并且3件展品所选用的展台既不在两端又不相邻,则不同的展出方法有______种;如果进一步要求3件展品所选用的展台之间间隔不超过两个展位,则不同的展出方法有____种.14.已知数列{}n a 的各项均为正整数,对于⋅⋅⋅=,3,2,1n ,有1135,2n n n n n n kk a a a a a a +++⎧⎪=⎨⎪⎩为奇数为偶数.其中为使为奇数的正整数,,当111a =时,100a =______;若存在*m ∈N ,当n m >且n a 为奇数时,n a 恒为常数p ,则p 的值为______. 三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题满分13分)设ABC ∆中的内角A ,B ,C 所对的边长分别为a ,b ,c ,且54cos =B ,2=b . (Ⅰ)当35=a 时,求角A 的度数;(Ⅱ)求ABC ∆面积的最大值. 16.(本小题满分13分)甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为11,,23p .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为14. (Ⅰ)求甲乙二人中至少有一人破译出密码的概率; (Ⅱ)求p 的值;(Ⅲ)设甲、乙、丙三人中破译出密码的人数为X ,求X 的分布列和数学期望EX .PABCO• OABDC正(主)视图俯视图侧(左)视图344333如图, ABCD 是边长为3的正方形,DE ⊥平面ABCD ,DE AF //,AF DE 3=,BE 与平面ABCD 所成角为060.(Ⅰ)求证:AC ⊥平面BDE ; (Ⅱ)求二面角D BE F --的余弦值;(Ⅲ)设点M 是线段BD 上一个动点,试确定点M 的位置,使得//AM 平面BEF ,并证明你的结论.18. (本小题满分14分)已知函数2(1)()a x f x x -=,其中0a >. (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若直线10x y --=是曲线()y f x =的切线,求实数a 的值; (Ⅲ)设2()ln ()g x x x x f x =-,求()g x 在区间[1,e]上的最大值.(其中e 为自然对数的底数)19. (本小题满分14分)已知抛物线22(0)y px p =>的焦点为F ,过F 的直线交y 轴正半轴于点P ,交抛物线于,A B 两点,其中点A 在第一象限.(Ⅰ)求证:以线段FA 为直径的圆与y 轴相切;(Ⅱ)若1FA AP λ= ,2BF FA λ= ,1211[,]42λλ∈,求2λ的取值范围.A BCD F E定义=),,,(21n a a a τ12231||||||n n a a a a a a --+-++- 为有限项数列{}n a 的波动强度. (Ⅰ)当(1)nn a =-时,求12100(,,,)a a a τ ;(Ⅱ)若数列,,,a b c d 满足()()0a b b c -->,求证:(,,,)(,,,)a b c d a c b d ττ≤;(Ⅲ)设{}n a 各项均不相等,且交换数列{}n a 中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列{}n a 一定是递增数列或递减数列.北京市西城区2011年高三一模试卷参考答案及评分标准数学(理科) 2011.4一、选择题:本大题共8小题,每小题5分,共40分.题号 1 2 3 4 5 6 7 8 答案CBADBCAD二、填空题:本大题共6小题,每小题5分,共30分.9. 2 10. 2 11. 415±,3212. 12 13. 60,48 14.62;1或5 注:11题,13题,14题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分. 15.(本小题满分13分) 解:(Ⅰ)因为54cos =B ,所以53sin =B . ……………………2分 因为35=a ,2=b ,由正弦定理B b A a sin sin =可得21sin =A . …………………4分因为b a <,所以A 是锐角,所以o30=A . ……………………6分(Ⅱ)因为ABC ∆的面积ac B ac S 103sin 21==, ……………………7分 所以当ac 最大时,ABC ∆的面积最大.因为B ac c a b cos 2222-+=,所以ac c a 58422-+=. ……………………9分 因为222a c ac +≥,所以8245ac ac -≤, ……………………11分 所以10≤ac ,(当10a c ==时等号成立) ……………………12分 所以ABC ∆面积的最大值为3. ……………………13分16.(本小题满分13分)解:记“甲、乙、丙三人各自破译出密码”分别为事件321,,A A A ,依题意有12311(),(),(),23P A P A P A p ===且321,,A A A 相互独立.(Ⅰ)甲、乙二人中至少有一人破译出密码的概率为121()P A A -⋅1221233=-⨯=. …………………3分(Ⅱ)设“三人中只有甲破译出密码”为事件B ,则有()P B =123()P A A A ⋅⋅=121(1)233pp -⨯⨯-=, …………………5分 所以1134p -=,14p =. ……………………7分(Ⅲ)X 的所有可能取值为3,2,1,0. ……………………8分所以1(0)4P X ==, (1)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅111312111423423424=+⨯⨯+⨯⨯=, (2)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅11312111112342342344=⨯⨯+⨯⨯+⨯⨯=, (3)P X ==P 123()A A A ⋅⋅=111123424⨯⨯=. ……………………11分 X 分布列为:X 0 1 23 P14 1124 14 124……………………12分所以,1111113()012342442412E X =⨯+⨯+⨯+⨯=. ……………………13分17.(本小题满分13分)(Ⅰ)证明: 因为DE ⊥平面ABCD ,所以AC DE ⊥. ……………………2分 因为ABCD 是正方形, 所以BD AC ⊥,从而AC ⊥平面BDE . ……………………4分 (Ⅱ)解:因为DE DC DA ,,两两垂直,所以建立空间直角坐标系xyz D -如图所示.因为BE 与平面ABCD 所成角为060,即60DBE ∠=, ………………5分 所以3=DBED. 由3=AD 可知36DE =,6AF =. ………………6分则(3,0,0)A ,(3,0,6)F ,(0,0,36)E ,(3,3,0)B ,(0,3,0)C ,所以(0,3,6)BF =- ,(3,0,26)EF =-, ………………7分设平面BEF 的法向量为=n (,,)x y z ,则00BF EF ⎧⋅=⎪⎨⋅=⎪⎩n n ,即3603260y z x z ⎧-+=⎪⎨-=⎪⎩, 令6z =,则=n (4,2,6). …………………8分因为AC ⊥平面BDE ,所以CA 为平面BDE 的法向量,(3,3,0)CA =-,xyBCAEzDFx M所以613cos ,133226CA CA CA ⋅〈〉===⨯n n n . …………………9分 因为二面角为锐角,所以二面角D BE F --的余弦值为1313. ………………10分 (Ⅲ)解:点M 是线段BD 上一个动点,设(,,0)M t t .则(3,,0)AM t t =-,因为//AM 平面BEF ,所以AM ⋅n 0=, …………………11分即4(3)20t t -+=,解得2=t . …………………12分 此时,点M 坐标为(2,2,0),13BM BD =,符合题意. …………………13分18. (本小题满分14分) 解:(Ⅰ)3(2)()a x f x x -'=,(0x ≠), ……………3分 在区间(,0)-∞和(2,)+∞上,()0f x '<;在区间(0,2)上,()0f x '>.所以,()f x 的单调递减区间是(,0)-∞和(2,)+∞,单调递增区间是(0,2). ………4分(Ⅱ)设切点坐标为00(,)x y ,则002000030(1)10(2)1a x y x x y a x x -⎧=⎪⎪⎪--=⎨⎪-⎪=⎪⎩ ……………7分(1个方程1分)解得01x =,1a =. ……………8分 (Ⅲ)()g x =ln (1)x x a x --,则()ln 1g x x a '=+-, …………………9分 解()0g x '=,得1e a x -=,所以,在区间1(0,e)a -上,()g x 为递减函数,在区间1(e ,)a -+∞上,()g x 为递增函数. ……………10分当1e1a -≤,即01a <≤时,在区间[1,e]上,()g x 为递增函数,所以()g x 最大值为(e)e e g a a =+-. ………………11分当1ee a -≥,即2a ≥时,在区间[1,e]上,()g x 为递减函数,所以()g x 最大值为(1)0g =. ………………12分当11<e<e a -,即12a <<时,()g x 的最大值为(e)g 和(1)g 中较大者;(e)(1)e e 0g g a a -=+->,解得ee 1a <-, 所以,e1e 1a <<-时,()g x 最大值为(e)e e g a a =+-, …………………13分e2e 1a ≤<-时,()g x 最大值为(1)0g =. …………………14分综上所述,当e 0e 1a <<-时,()g x 最大值为(e)e e g a a =+-,当e e 1a ≥-时,()g x 的最大值为(1)0g =.19. (本小题满分14分) 解:(Ⅰ)由已知(,0)2pF ,设11(,)A x y ,则2112y px =, 圆心坐标为112(,)42x p y +,圆心到y 轴的距离为124x p+, …………………2分 圆的半径为1121()2224FAx p px +=⨯--=, …………………4分 所以,以线段FA 为直径的圆与y 轴相切. …………………5分(Ⅱ)解法一:设022(0,),(,)P y B x y ,由1FA AP λ= ,2BF FA λ=,得111101(,)(,)2p x y x y y λ-=--,22211(,)(,)22p px y x y λ--=-, …………………6分所以1111101,()2px x y y y λλ-=-=-,221221(),22p px x y y λλ-=-=-, …………………8分 由221y y λ=-,得222221y y λ=. 又2112y px =,2222y px =,所以 2221x x λ=. …………………10分 代入221()22p p x x λ-=-,得22121()22p p x x λλ-=-,2122(1)(1)2px λλλ+=+, 整理得122p x λ=, …………………12分代入1112px x λ-=-,得122222p p p λλλ-=-, 所以12211λλλ=-, …………………13分 因为1211[,]42λλ∈,所以2λ的取值范围是4[,2]3. …………………14分 解法二:设),(),,(2211y x B y x A ,:2pAB x my =+, 将2p x my =+代入22y px =,得2220y pmy p --=, 所以212y y p =-(*), …………………6分由1FA AP λ= ,2BF FA λ=,得111101(,)(,)2p x y x y y λ-=--,22211(,)(,)22p px y x y λ--=-, …………………7分 所以,1111101,()2px x y y y λλ-=-=-,221221(),22p px x y y λλ-=-=-, …………………8分 将122y y λ-=代入(*)式,得2212p y λ=, …………………10分所以2122p px λ=,122p x λ=. …………………12分代入1112px x λ-=-,得12211λλλ=-. …………………13分因为1211[,]42λλ∈,所以2λ的取值范围是4[,2]3. …………………14分 20.(本小题满分13分)(Ⅰ)解:12100122399100(,,,)||||||a a a a a a a a a τ=-+-++- ………………1分222299198=+++=⨯= . ………………3分(Ⅱ)证明:因为(,,,)||||||a b c d a b b c c d τ=-+-+-,(,,,)||||||a c b d a c c b b d τ=-+-+-,所以(,,,)(,,,)||||||||a b c d a c b d a b c d a c b d ττ-=-+-----. ……………4分 因为()()0a b b c -->,所以a b c >>,或a b c <<.若a b c >>,则(,,,)(,,,)||||a b c d a c b d a b c d a c b d ττ-=-+--+--||||c b c d b d =-+---当b c d >>时,上式()2()0c b c d b d c b =-+---=-<, 当b d c ≥≥时,上式()2()0c b d c b d d b =-+---=-≤, 当d b c >>时,上式()0c b d c d b =-+---=,即当a b c >>时,(,,,)(,,,)0a b c d a c b d ττ-≤. ………………6分若a b c <<,则(,,,)(,,,)||||a b c d a c b d b a c d c a b d ττ-=-+--+--,||||0b c c d b d =-+---≤.(同前)所以,当()()0a b b c -->时,(,,,)(,,,)a b c d a c b d ττ≤成立. ……………7分(Ⅲ)证明:由(Ⅱ)易知对于四个数的数列,若第三项的值介于前两项的值之间,则交换第二项与第三项的位置将使数列波动强度减小或不变.(将此作为引理)下面来证明当12a a >时,{}n a 为递减数列.(ⅰ)证明23a a >.若231a a a >>,则由引理知交换32,a a 的位置将使波动强度减小或不变,与已知矛盾.若2a a a >>31,则1212212121(,,)||||||||(,,)a a a a a a a a a a a a a a ττ=-+->-+-=3333,与已知矛盾. 所以,321a a a >>. ………………9分 (ⅱ)设12(32)i a a a i n >>>≤≤- ,证明1i i a a +>.若i i i a a a >>+-11,则由引理知交换1,+i i a a 的位置将使波动强度减小或不变,与已知矛盾. 若i i i a a a >>-+11,则211211(,,,)(,,,)i i i i i i i i a a a a a a a a ττ--+--+=,与已知矛盾. 所以,1+>i i a a . …………11分 (ⅲ)设121n a a a ->>> ,证明1n n a a ->. 若1n n a a ->,考查数列121,,,,n n a a a a - ,则由前面推理可得122n n n a a a a -->>>> ,与121n a a a ->>> 矛盾. 所以,1n n a a ->. ……………12分 综上,得证.同理可证:当12a a <时,有{}n a 为递增数列. ………………13分。
【数学】2011年北京市各区二模试题分类解析(19):创新题

十九、创新题1、(2011丰台二模理14).如图所示,∠AOB =1rad ,点A l ,A 2,…在OA 上,点B 1,B 2,…在OB 上,其中的每一个实线段和虚线段的长均为1个长度单位,一个动点M 从O 点出发,沿着实线段和以O 为圆心的圆弧匀速运动,速度为l 长度单位/秒,则质点M 到达A 3点处所需要的时间为__秒,质点M 到达A n 点处所需要的时间为_(1),2(3),2n n n n a n n n +⎧⎪⎪=⎨+⎪⎪⎩为奇数,为偶数._秒.2、(2011顺义二模理14).给定集合A ,若对于任意A b a ∈,,有A b a ∈+,且A b a ∈-,则称集合A 为闭集合,给出如下四个结论:①集合{}4,2,0,2,4--=A 为闭集合;②集合{}Z k k n n A ∈==,3|为闭集合; ③若集合21,A A 为闭集合,则21A A ⋃为闭集合;④若集合21,A A 为闭集合,且R A R A ⊆⊆21,,则存在R c ∈,使得()21A A c ⋃∉. 其中正确结论的序号是______ ②④__________________. 3、(2011昌平二模文14)给出定义:若2121+≤<-m x m (其中m 为整数),则m 叫做离实数x 最近的整数,记作m x =}{,在此基础上给出下列关于函数}{)(x x x f -=的四个命题: ①函数y =)(x f 的定义域为R ,最大值是21;②函数y =)(x f 在]1,0[上是增函数;③函数y =)(x f 是周期函数,最小正周期为1;④函数y =)(x f 的图象的对称中心是(0,0). 其中正确命题的序号是___①③_______4、(2011朝阳二模文8)已知点P 是ABC ∆的中位线EF 上任意一点,且//EF BC . 设ABC ∆,PBC ∆,PCA ∆,PAB ∆的面积分别为S ,1S ,2S ,3S ,记11S S λ=,22SSλ=,33S Sλ=,定义123()(, , )M P λλλ=.当23λλ⋅取最大值时,则()M P 等于(A) (A )111(,,)244 (B )111(,,)442 (C )111(,,)333 (D )111(,,)222OA 1A 2A 3 A 4B 1 B 2 B 3 B 4 AB5、(2011丰台二模文14)如图所示,已知正方形ABCD 的边长为1,以A 为圆心,AD 长为半径画弧,交BA 的延长线于P 1,然后以B 为圆心,BP 1长为半径画弧,交CB 的延长线于P 2,再以C 为圆心,CP 2长为半径画弧,交DC 的延长线于P 3,再以D 为圆心,DP 3长为半径画弧,交AD 的延长线于P 4,再以A 为圆心,AP 4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是_8__,画出第n 道弧时,这n 道弧的弧长之和为_(1)4n n +π6、(2011顺义二模文14)给定集合A ,若对于任意A b a ∈,,有A b a ∈+,且A b a ∈-,则称集合A 为闭集合,给出如下三个结论:①集合{}4,2,0,2,4--=A 为闭集合;②集合{}Z k k n n A ∈==,3|为闭集合; ③若集合21,A A 为闭集合,则21A A ⋃为闭集合;其中正确结论的序号是____②______. 7、1、(2011朝阳二模理20)(本小题满分14分)对于正整数, a b ,存在唯一一对整数q 和r ,使得a bq r =+,0r b <≤. 特别地,当0r =时,称b 能整除a ,记作|b a ,已知{1, 2, 3,,23}A =⋅⋅⋅.(Ⅰ)存在q A ∈,使得201191 (091)q r r =+<≤,试求,q r 的值;(Ⅱ)求证:不存在这样的函数:{1,2,3}f A →,使得对任意的整数12,x x A ∈,若AB C D P 1 P 2P 3P 4P 512||{1,2,3}x x -∈,则12()()f x f x ≠;(Ⅲ)若B A ⊆,12)(=B card (()card B 指集合B 中的元素的个数),且存在,a b B ∈,b a <,|b a ,则称B 为“和谐集”. 求最大的m A ∈,使含m 的集合A 的有12个元素的任意子集为“和谐集”,并说明理由. (Ⅰ)解:因为201191229=⨯+,所以22,9q r ==. ……………………………………2分(Ⅱ)证明:假设存在这样的函数:{1,2,3}f A →,使得对任意的整数,x y ,若||{1,2,3}x y -∈,则()()f x f y ≠.设(1)f a =,{1,2,3}a ∈,(2)f b =,{1,2,3}b ∈,由已知a b ≠, 由于|31|2,|32|1-=-=,所以(3)(1)f f ≠,(3)(2)f f ≠. 不妨令(3)f c =,{1,2,3}c ∈,这里c a ≠,且c b ≠, 同理,(4)f b ≠,且(4)f c ≠,因为{1,2,3}只有三个元素,所以(4)f a =. 即(1)(4)f f =,但是|41|3-=,与已知矛盾.因此假设不成立,即不存在这样的函数:{1,2,3}f A →,使得对任意的整数,x y ,若||{1,2,3}x y -∈,则()()f x f y ≠. ……………………………………8分(Ⅲ)当8m =时,记}16,,2,1|7{⋅⋅⋅=+=i i M ,}4,3,2,1|)7(2{=+=i i N 记P =M N C ,则12)(=P card ,显然对任意116i j <≤≤,不存在3n ≥,使得7(7)j n i +=+成立. 故P 是非“和谐集”,此时{8,9,10,11,12,13,14,15,17,19,21,23}P =.同样的,当9,10,11,12m =时,存在含m 的集合A 的有12个元素的子集为非“和谐集”.因此7m ≤. ……………………………………10分 下面证明:含7的任意集合A 的有12个元素的子集为“和谐集”. 设}7,,,,{1121a a a B ⋅⋅⋅=,若1,14,21中之一为集合B 的元素,显然为“和谐集”.现考虑1,14,21都不属于集合B ,构造集合}16,8,4,2{1=B ,}12,6,3{2=B ,}20,10,5{3=B ,}18,9{4=B ,}22,11{5=B ,}23,19,17,15,13{='B .以上54321,,,,B B B B B 每个集合中的元素都是倍数关系.考虑B B '⊆的情况,也即B '中5个元素全都是B 的元素,B 中剩下6个元素必须从54321,,,,B B B B B 这5个集合中选取6个元素,那么至少有一个集合有两个元素被选,即集合B 中至少有两个元素存在倍数关系.综上所述,含7的任意集合A 的有12个元素的子集B 为“和谐集”,即m 的最大值为7. ……………………………………14分 2、(2011丰台二模理20).(本小题共13分)用[]a 表示不大于a 的最大整数.令集合{1,2,3,4,5}P =,对任意k P ∈和N*m ∈,定义51(,)[i f m k ==∑,集合{|N*,}A m k P =∈∈,并将集合A 中的元素按照从小到大的顺序排列,记为数列{}n a . (Ⅰ)求(1,2)f 的值; (Ⅱ)求9a 的值;(Ⅲ)求证:在数列{}n a中,不大于m 00(,)f m k 项. 解:(Ⅰ)由已知知(1,2)f =++++ 110002=++++=.所以(f =. ………………4分(Ⅱ)因为数列{}n a是将集合{N*,}A m k P =∈∈中的元素按从小到大的顺序排成而成,<<<<<<<<<<‥‥所以9a =.………………8分(Ⅲ)任取12,*m m ∈N ,12,k kP ∈,若m m =,则必有1212,m m k k ==. 即在(Ⅱ)表格中不会有两项的值相等.对于m 1m 的数不大于m 则1m m ≤1m ≤,所以1m =,同理,第二行共有2m 的数不大于m 2m =,第i 行共有i m 的数不大于m i m =.所以,在数列{}n a 中,不大于m 51[i m =∑项,即00(,)f m k 项.………………13分3、(2011海淀二模理20)(本小题共13分)对于数列12n A a a a :,,,,若满足{}0,1(1,2,3,,)i a i n ∈=⋅⋅⋅,则称数列A 为“0-1数列”.定义变换T ,T 将“0-1数列”A 中原有的每个1都变成0,1,原有的每个0都变成1,0. 例如A :1,0,1,则():0,1,1,0,0,1.T A 设0A 是“0-1数列”,令1(),k k A T A -=12k =,,3,.(Ⅰ) 若数列2A :1,0,0,1,0,1,1,0,1,0,0,1. 求数列10,A A ;(Ⅱ) 若数列0A 共有10项,则数列2A 中连续两项相等的数对至少有多少对?请说明理由; (Ⅲ)若0A 为0,1,记数列k A 中连续两项都是0的数对个数为k l ,1,2,3,k =⋅⋅⋅.求k l 关于k 的表达式.解:(Ⅰ)由变换T 的定义可得1:0,1,1,0,0,1A …………………………………2分0:1,0,1A …………………………………4分(Ⅱ) 数列0A 中连续两项相等的数对至少有10对 …………………………………5分 证明:对于任意一个“0-1数列”0A ,0A 中每一个1在2A 中对应连续四项1,0,0,1,在0A 中每一个0在2A 中对应的连续四项为0,1,1,0,因此,共有10项的“0-1数列”0A 中的每一个项在2A 中都会对应一个连续相等的数对, 所以2A 中至少有10对连续相等的数对. …………………………………………………………8分 (Ⅲ) 设k A 中有k b 个01数对,1k A +中的00数对只能由k A 中的01数对得到,所以1k k l b +=,1k A +中的01数对有两个产生途径:①由k A 中的1得到; ②由k A 中00得到,由变换T 的定义及0:0,1A 可得k A 中0和1的个数总相等,且共有12k +个,所以12kk k b l +=+, 所以22kk k l l +=+,由0:0,1A 可得1:1,0,0,1A ,2:0,1,1,0,1,0,0,1A 所以121,1l l ==, 当3k ≥时,若k 为偶数,222k k k l l --=+ 4242k k k l l ---=+2422l l =+上述各式相加可得122421(14)11222(21)143k k kk l ---=++++==--,经检验,2k =时,也满足1(21)3k k l =-若k 为奇数,222k k k l l --=+ 4242k k k l l ---=+312l l =+上述各式相加可得12322(14)112221(21)143k k kk l ---=++++=+=+-,经检验,1k =时,也满足1(21)3k k l =+所以1(21),31(21),3kk k k l k ⎧+⎪⎪=⎨⎪-⎪⎩为奇数为偶数……4、(2011西城二模理20).(本小题满分13分)若m A A A ,,,21 为集合2}(,,2,1{≥=n n A 且)n ∈*N 的子集,且满足两个条件: ①12m A A A A =;②对任意的A y x ⊆},{,至少存在一个},,3,2,1{m i ∈,使}{},{x y x A i = 或}{y . 则称集合组m A A A ,,,21 具有性质P .如图,作n 行m 列数表,定义数表中的第k 行第l 列的数为⎩⎨⎧∉∈=)(0)(1l l kl A k A k a .(Ⅰ)当4n =时,判断下列两个集合组是否具有性质P ,如果是请画出所对应的表格,如果不是请说明理由;集合组1:123{1,3},{2,3},{4}A A A ===; 集合组2:123{2,3,4},{2,3},{1,4}A A A ===.(Ⅱ)当7n =时,若集合组123,,A A A 具有性质P ,请先画出所对应的7行3列的一个数表,再依此表格分别写出集合123,,A A A ;(Ⅲ)当100n =时,集合组12,,,t A A A 是具有性质P 且所含集合个数最小的集合组,求t 的值及12||||||t A A A ++的最小值.(其中||i A 表示集合i A 所含元素的个数)(Ⅰ)解:集合组1具有性质P . ………………1分所对应的数表为:………………3分集合组2不具有性质P . ………………4分 因为存在{{2,3}1,2,3,4}⊆, 有123{2,3}{2,3},{2,3}{2,3},{2,3}A A A ===∅,与对任意的A y x ⊆},{,都至少存在一个{1,2,3}i ∈,有}{},{x y x A i = 或}{y 矛盾,所以集合组123{2,3,4},{2,3},{1,4}A A A ===不具有性质P . ………………5分(Ⅱ)……………7分123{3,4,5,7},{2,4,6,7},{1,5,6,7}A A A ===. ………………8分 (注:表格中的7行可以交换得到不同的表格,它们所对应的集合组也不同) (Ⅲ)设12,,,t A A A 所对应的数表为数表M ,因为集合组12,,,t A A A 为具有性质P 的集合组, 所以集合组12,,,t A A A 满足条件①和②,由条件①:12t A A A A =,可得对任意x A ∈,都存在{1,2,3,,}i t ∈有i A x ∈,所以1=xi a ,即第x 行不全为0,所以由条件①可知数表M 中任意一行不全为0.………………9分由条件②知,对任意的A y x ⊆},{,都至少存在一个{1,2,3,,}i t ∈,使}{},{x y x A i = 或}{y ,所以yi xi a a ,一定是一个1一个0,即第x 行与第y 行的第i 列的两个数一定不同.所以由条件②可得数表M 中任意两行不完全相同. ………………10分 因为由0,1所构成的t 元有序数组共有2t 个,去掉全是0的t 元有序数组,共有21t-个,又因数表M 中任意两行都不完全相同,所以10021t≤-,所以7t ≥.1 1 1 1 1 1 1 1 1 11 1 0 0 0 00 0 0 0 0 01 1 0 0 00 1 1 0 0 1又7t =时,由0,1所构成的7元有序数组共有128个,去掉全是0的数组,共127个,选择其中的100个数组构造100行7列数表,则数表对应的集合组满足条件①②,即具有性质P .所以7t =. ………………12分 因为12||||||t A A A +++等于表格中数字1的个数,所以,要使12||||||t A A A +++取得最小值,只需使表中1的个数尽可能少,而7t =时,在数表M 中,1的个数为1的行最多7行; 1的个数为2的行最多2721C =行;1的个数为3的行最多3735C =行; 1的个数为4的行最多4735C =行;因为上述共有98行,所以还有2行各有5个1,所以此时表格中最少有722133543552304+⨯+⨯+⨯+⨯=个1. 所以12||||||t A A A +++的最小值为304. ………………14分5、(2011昌平二模文20) (本小题满分14分)已知函数)()(2R x a ax x x f ∈+-=,在定义域内有且只有一个零点,存在21x x 0<<, 使得不等式)x (f )x (f 21>成立. 若*N n ∈,)(n f 是数列}{n a 的前n 项和.(I )求数列{}n a 的通项公式;(II )设各项均不为零的数列{}n c 中,所有满足01<⋅+k k c c 的正整数k 的个数称为这个数列{}n c 的变号数,令nn a c 41-=(n 为正整数),求数列{}n c 的变号数; (Ⅲ)设61n +=n a T (2≥n 且*n ∈N ),使不等式 321)1)...(1()1(30732+∙++∙+≤n T T T m n 恒成立,求正整数m 的最大值. 解:(I )∵)(x f 函数在定义域内有且只有一个零点40042===-=∆∴a a a a 或得 ……1分当a =0时,函数2)(x x f =在),0(+∞上递增 故不存在210x x <<, 使得不等式)()(21x f x f >成立 …… 2分 综上,得44)(,42+-==x x x f a …….3分442+-=∴n n S n⎩⎨⎧≥-==-=∴-2,521,11n n n S S a n n n …………4分(II )解法一:由题设⎪⎩⎪⎨⎧≥--=-=2n ,5n 2411n ,3c n 3n ≥ 时,0)3n 2)(5n 2(83n 245n 24c c n 1n >--=---=-+ 3n ≥∴时,数列{}n c 递增 031c 4<-=由505241≥>--n n 得 可知0a a 54<⋅即3n ≥时,有且只有1个变号数; 又3c ,5c ,3c 321-==-= 即0c c ,0c c 3221<⋅<⋅ ∴此处变号数有2个综上得数列{}n c 共有3个变号数,即变号数为3 ……9分解法二:由题设⎪⎩⎪⎨⎧≥--=-=2n 5n 2411n 3c n 当2n ≥时,令03272529201<--⋅--<⋅+n n n n c c n n 得4229272523==<<<<n n n n 或解得或即 又5c ,3c 21=-= 1n =∴时也有0c c 21<⋅ 综上得数列{}n c 共有3个变号数,即变号数为3 …………9分(Ⅲ)2≥n 且*n ∈N 时,121+=n T n321)1211)...(711)(511(307+∙++++≤n n m 可转化为 3211222122...9107856307+∙++∙-∙∙≤n n n n n m . 设=)(n g 3211222122...9107856+∙++∙-∙∙n n n n n , 则当2≥n 且*n ∈N ,3211222...910785652132421222...9107856)()1(+∙++∙∙+∙++∙++∙∙=+n n n n n n n n n g n g2423n n +==+24124n n +=>===+. 所以)()1(n g n g >+,即当n 增大时,)(n g 也增大. 要使不等式321)1)...(1)(1(30732+∙+++≤n T T T m n 对于任意的*n ∈N 恒成立,只需 min )(307n g m ≤即可.因为3576775671)2()(min =∙=∙=g n g , 所以3576307≤m . 即 71535180=≤m 所以,正整数m 的最大值为5.6、(2011朝阳二模文20)(本小题满分14分)对于整数, a b ,存在唯一一对整数q 和r ,使得a bq r =+,0||r b <≤. 特别地,当0r =时,称b 能整除a ,记作|b a ,已知{1, 2, 3, , 23}A =⋅⋅⋅.(Ⅰ)存在q A ∈,使得201191q r =+(091)r <≤,试求q ,r 的值;(Ⅱ)若B A ⊆,12)(=B card (()card B 指集合B 中的元素的个数),且存在,a b B ∈,b a <,b a ,则称B 为“谐和集”.请写出一个含有元素7的“谐和集”0B 和一个含有元素8的非“谐和集”C ,并求最大的m A ∈,使含m 的集合A 有12个元素的任意子集为“谐和集”,并说明理由.(Ⅰ)解:因为201191q r =+,所以201191229=⨯+. ………………………2分又因为q A ∈,所以22, 9q r ==. ……………………………4分(Ⅱ)含有元素7的一个“和谐集”0{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}B =.…5分含有元素8的一个非“和谐集”{8,9,10,11,12,13,14,15,17,19,21,23}C =.…7分 当8m =时,记{7|1, 2, , 16}M i i =+=⋅⋅⋅,{2(7)|1, 2, 3, 4}N i i =+=,记P =M N C ,则12)(=P card .显然对任意116i j <≤≤,不存在3n ≥,使得7(7)j n i +=+成立. 故P 是非“和谐集”,此时{8, 9, 10, 11, 12, 13, 14, 15, 17, 19, 21, 23}P =.同理,当9, 10, 11, 12m =时,存在含m 的集合A 的有12个元素的子集为非“和谐集”. 因此7m ≤. …………………………………………………10分 下面证明:含7的任意集合A 的有12个元素的子集为“和谐集”.设1211{, , , , 7}B a a a =⋅⋅⋅,若1,14,21中之一为集合B 的元素,显然为“和谐集” . 现考虑1,14,21都不属于集合B ,构造集合1{2, 4, 8, 16}B =,2{3, 6, 12}B =, 3{5, 10, 20}B =,4{9, 18}B =,5{11, 22}B =,{13, 15, 17, 19, 23}B '=.…12分以上54321,,,,B B B B B 每个集合中的元素都是倍数关系.考虑B B '⊆的情况,也即B '中5个元素全都是B 的元素,B 中剩下6个元素必须从54321,,,,B B B B B 这5个集合中选取6个元素,那么至少有一个集合有两个元素被选,即集合B 中至少有两个元素存在倍数关系.综上,含7的任意集合A 的有12个元素的子集B 为“和谐集”,即m 的最大值为7. …………………………………………7、(2011西城二模文20)(本小题满分13分)若函数)(x f 对任意的x ∈R ,均有)(2)1()1(x f x f x f ≥++-,则称函数)(x f 具有性质P .(Ⅰ)判断下面两个函数是否具有性质P ,并说明理由.①(1)xy a a =>; ②3y x =. (Ⅱ)若函数)(x f 具有性质P ,且(0)()0f f n ==(2,n >n ∈*N ),求证:对任意{1,2,3,,1}i n ∈-有()0f i ≤;(Ⅲ)在(Ⅱ)的条件下,是否对任意[0,]x n ∈均有0)(≤x f .若成立给出证明,若不成立给出反例.(Ⅰ)证明:①函数)1()(>=a a x f x具有性质P . ……………1分 111(1)(1)2()2(2)x x x x f x f x f x a a a a a a-+-++-=+-=+-, 因为1>a ,1(2)0x a a a+->, ……………3分 即)(2)1()1(x f x f x f ≥++-,此函数为具有性质P .②函数3)(x x f =不具有性质P . ……………4分 例如,当1x =-时,(1)(1)(2)(0)8f x f x f f -++=-+=-, 2()2f x =-, ……………5分所以,)1()0()2(-<+-f f f ,此函数不具有性质P .(Ⅱ)假设)(i f 为(1),(2),,(1)f f f n -中第一个大于0的值, ……………6分 则0)1()(>--i f i f ,因为函数()f x 具有性质P ,所以,对于任意n ∈*N ,均有(1)()()(1)f n f n f n f n +-≥--,所以0)1()()2()1()1()(>--≥≥---≥--i f i f n f n f n f n f ,所以()[()(1)][(1)()]()0f n f n f n f i f i f i =--+++-+>, 与0)(=n f 矛盾,所以,对任意的{1,2,3,,1}i n ∈-有()0f i ≤. ……………9分(Ⅲ)不成立. 例如2()()x x n x f x xx -⎧=⎨⎩为有理数,为无理数. ……………10分 证明:当x 为有理数时,1,1x x -+均为有理数,222(1)(1)2()(1)(1)2(112)2f x f x f x x x x n x x x -++-=-++---++-=, 当x 为无理数时,1,1x x -+均为无理数,22)1()1()(2)1()1(222=-++-=-++-x x x x f x f x f所以,函数)(x f 对任意的x ∈R ,均有)(2)1()1(x f x f x f ≥++-,即函数)(x f 具有性质P . ……………12分 而当],0[n x ∈(2n >)且当x 为无理数时,0)(>x f .所以,在(Ⅱ)的条件下,“对任意[0,]x n ∈均有0)(≤x f ”不成立.……………13分(其他反例仿此给分.如()()0()1x x f x ⎧=⎨⎩为有理数为无理数,()()0()1x x f x ⎧=⎨⎩为整数为非整数,2()()0()x x f x x ⎧=⎨⎩为整数为非整数,等.)。
2011年西城区初三一模试题答案Word版_题库_初中数学新_更新_二模试题

北京市西城区2011年初三一模试卷数学答案及评分标准 2011. 5一、选择题(本题共32分,每小题4分) 题号 1 2 3 4 5 6 7 8答案A C ABC CD B二、填空题(本题共16分,每小题4分)91011 12()23-x y8①③5,n 511题阅卷说明:全对得4分,仅填①或③得2分,其余情况均不得分. 三、解答题(本题共30分,每小题5分) 13.解:原式 =13234122+-⨯- ………………………………………………………4分 =12-. …………………………………………………………………………5分14.解:302(1)33.x x x +>⎧⎨-+⎩,≥ 由①得3x >-. ………………………………………………………………………1分 由②得x ≤1.…………………………………………………………………………3分∴ 原不等式组的解集是3-<x ≤1. ………………………………………………4分 ∵ 31>,∴ 3x =不是该不等式组的解.………………………………………………… 5分 15.解:(1)如图1.设直线l 的解析式为y kx b =+(k ,b 为常数且k ≠0).∵ 直线l 经过点(0,2)B ,点(1,1)P ,∴ 2, 1.b k b =⎧⎨+=⎩ 解得 1,2.k b =-⎧⎨=⎩①②图∴ 直线l 的解析式为2y x =-+. ……………………………………………2分(2)∵ 直线l 的解析式为2y x =-+,∴ 点A 的坐标为(2,0).………………………………………………………3分 ∵ 点P 的坐标为(1,1), ∴ 12AOP P S OA y ∆=⨯⨯=12112⨯⨯=.………………………………………5分 16. 证明:如图2.(1)∵ BF 平分ABC ∠,∴ ABF CBF ∠=∠.………………1分 在△ABF 与△CBF 中,,,,AB CB ABF CBF BF BF =⎧⎪∠=∠⎨⎪=⎩∴ △ABF ≌△CBF . ………………………………………………………2分∴ AF CF =.………………………………………………………………3分(2)∵ AF CF =,∴ FCA FAC ∠=∠.……………………………………………………… 4分∵ AF ∥DC , ∴ FAC DCA ∠=∠.∴ FCA DCA ∠=∠,即CA 平分DCF ∠. ………………………………5分 17. 解:由题意,2214202b a b a ∆=-⨯=-=.…………………………………………1分 ∴ 22b a =. ………………………………………………………………………2分∴ 原式222211ab a a b =-++- ……………………………………………………3分2222ab a b a =+- 2222222a a a a a a a ⋅==+-.…………………………………………………4分 ∵ 0a ≠,∴ 原式2222a a==.………………………………………………………………5分18. 解:(1)初三学生步行骑车乘公交车其它方式图………………………………………………………………………………4分 阅卷说明:每空1分.(2)72.………………………………………………………………………………5分 四、解答题(本题共20分,每小题5分)19.解:设抢修车每小时行驶x 千米,则吉普车每小时行驶x 5.1千米.151154 1.5x x-=.………………………………………………………………………2分 解得20x =. ………………………………………………………………………3分经检验,20x =是原方程的解,并且符合题意. ………………………………4分 ∴ 1.530x =.答:抢修车每小时行驶20千米,吉普车每小时行驶30千米.………………………5分 20.解:如图3.(1)由题意,点A 与点A ',点B 与点B '分别关于直线MN 对称,∴AM A M '=,BN B N '=. ………………………………………………1分 设BN B N x '==,则9CN x =-. ∵ 正方形ABCD , ∴ o 90C ∠=.∴ 222CN B C B N ''+=.∵ C B '=3,∴ 222(9)3x x -+=.解得5x =.∴ 5BN =.……………………………………………………………………2分(2)∵ 正方形ABCD ,∴ AD ∥BC ,o 90A ∠=.∵ 点M ,N 分别在AD ,BC 边上, ∴ 四边形ABNM 是直角梯形. ∵ '5BN B N ==,9BC =,∴ 4NC =. ∴ 4sin 15∠=,4tan 13∠=. ∵ 1290∠+∠=︒,2390∠+∠=︒, ∴ 31∠=∠. ∴ 4sin 3sin 15∠=∠=. 人数 人数人数 人数 人数300991329图在Rt △ DB P '中,∵90 D ∠=︒,6DB DC B C ''=-=,4sin 35DB PB '∠==', ∴ 152PB '=. ∵ 9A B AB ''==,∴ 32A P AB PB ''''=-=. ∵ 43∠=∠, ∴ 4tan 4tan 33∠=∠=. 在Rt △ A MP '中,∵ 90 A A '∠=∠=︒,32A P '=,4tan 43A M A P '∠==', ∴ 2A M '=.…………………………………………………………………4分 ∴ 1163()(25)9222ABNM S AM BN AB =+⨯=⨯+⨯=梯形.…………………5分 21.(1)证明:连接BO .(如图4)∵ AB =AD ,∴ ∠D =∠ABD .∵ AB =AO ,∴ ∠ABO =∠AOB .又∵ 在△OBD 中,∠D +∠DOB +∠ABO +∠ABD =180°,∴ ∠OBD =90°.∴ BD ⊥BO .…………………………………………………………………1分∵ 点B 在⊙O 上,∴ BD 是⊙O 的切线 . ……………………………………………………2分(2)解:∵ ∠C =∠E ,∠CAF =∠EBF ,∴ △ACF ∽△BEF . ………………………………………………………3分∵ AC 是⊙O 的直径,点B 在⊙O 上,∴ ∠ABC =90°.∵ 在Rt △BFA 中,∠ABF =90°,cos ∠BFA =32=AF BF , ∴24()9BEF ACF S BF S AF ∆∆==.………………………………………………………4分 图又∵ BEF S ∆=8 ,∴ ACF S ∆=18 . ……………………………………………………………5分22.解:(1)1∶2,121 .……………………………………………………………………2分(2)正三角形或正六边形.…………………………………………………………4分(3)如图5. …………5分阅卷说明:第(2)问全对得2分,仅填正三角形或正六边形得1分,其余情况均不得分;第(3)问其它符合题意的图形同样给分.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.(1)证明:∵ 2360a b c ++=,∴12362366b a b c ca a a a++==-=-. ………………………………………1分 ∵ a >0,c <0,∴0c a <,0ca ->. ∴ 1023b a +>. ……………………………………………………………2分(2)解:∵ 抛物线经过点P 1(,)2m ,点Q (1,)n ,∴ 11 ,42.a b c m a b c n ⎧++=⎪⎨⎪++=⎩ ① ∵ 2360a b c ++=,a >0,c <0,∴ 223a b c +=-,223ab c =--.∴ 1112111()42424312b c m a b c a a a a +=++=+=+-=-<0.………3分2(2)33a an a b c a c c c =++=+--+=->0.………………………4分∴ 0mn <.…………………………………………………………………5分 ② 由a >0知抛物线2y ax bx c =++开口向上. ∵ 0m <,0n >,图图∴ 点P 1(,)2m 和点Q (1,)n 分别位于x 轴下方和x 轴上方.∵ 点A ,B 的坐标分别为A 1(,0)x ,B 2(,0)x (点A 在点B 左侧), ∴ 由抛物线2y ax bx c =++的示意图可知,对称轴右侧的点B 的横坐标2x 满足2112x <<.(如图6所示)………………………………………6分∵ 抛物线的对称轴为直线2b x a =-,由抛物线的对称性可1222x x ba+=-,由(1)知123b a -<, ∴12123x x +<. ∴ 12221332x x <-<-,即116x <.…………………………………… 7分24.解:(1)∠AOB= 30 °,α= 60 °.…………………………………………………2分(2)∵ A (23,2),B (4,0),△OAB 绕点O 顺时针旋转α角得到△OCD ,(如图7)∴ OA =OB=OC=OD=4.由(1)得 30BOC AOB ∠=︒=∠.∴ 点C 与点A 关于x 轴对称,点C 的坐标为(23,2)-. ∵ 点C ,D ,F 落在同一反比例函数ky x=(k ≠0)的图象上, ∴ 43C C k x y =⋅=-.∵ 点F 是由点A 沿x 轴负方向平移m 个单位得到, ∴ 2F y =,43232F x -==-,点F 的坐标为(23,2)-.……………3分 ∴ 点F 与点A 关于y 轴对称,可设经过点A ,B ,F 的抛物线的解析式为2y ax c =+.∴ 2 (23)2, 160.a c a c ⎧+=⎪⎨+=⎪⎩ 解得1 ,2 8.a c ⎧=-⎪⎨⎪=⎩∴ 所求抛物线的解析式为2182y x =-+. …………………………………4分(3)满足条件的点P 的个数为 5 .………………………………………………5分 抛物线2182y x =-+的顶点为(0,8)M .∵ △EFG 是由△OAB 沿x 轴负方向平移m 个单位得到,∴ 43m FA ==,43E O x x m =-=-,∠FEG=∠AOB=30°. ∴ 点E 的坐标为(43,0)-.可得直线EF 的解析式为343y x =+. ∵ 点H 的横坐标是方程2314832x x +=-+的解,整理,得2323240x x +-=.解得 1243,233x x ==-. ∴ 点H 的坐标为4316(,)33.由抛物线的对称性知符合题意的1P 点的坐标为4316(,)33-.……………6分 可知△AFM 是等边三角形,∠MAF= 60°. 由A ,M 两点的坐标分别为A (23,2),(0,8)M , 可得直线AM 的解析式为38y x =-+.过点H 作直线AM 的平行线l ,设其解析式为3y x b =-+(b ≠8).将点H 的坐标代入上式,得1643333b =-⨯+. 解得283b =,直线l 的解析式为2833y x =-+.∵ 直线l 与抛物线的交点的横坐标是方程 22813832x x -+=-+的解.整理,得236380x x -+=.解得124323,33x x ==. ∴ 点2P 2322(,)33满足HAM AM P S S ∆∆=2,四边形2P MFA 的面积与四边形MFAH 的面积相等.(如图8)……………………………………………7分点2P 关于y 轴的对称点3P 也符合题意,其坐标为3P 2322(,)33-.………8分综上所述,位于直线EF 上方的点P 的坐标分别为1P 4316(,)33-, 2P 2322(,)33,3P 2322(,)33-. 25.解:(1)如图9,∠APE= 45 °. ……………………2分(2)解法一:如图10,将AE 平移到DF ,连接BF ,EF . ……………………3分则四边形AEFD 是平行四边形. ∴ AD ∥EF ,AD=EF .∵ 3AC BD =,3CD AE =, ∴3=BD AC ,3==DF CDAE CD . ∴ AC CD BD DF =.……………………………………………………4分 ∵ ∠C =90°,∴ 18090BDF C ∠=︒-∠=︒. ∴ ∠C=∠BDF .∴ △ACD ∽△BDF .………………5分∴3AD ACBF BD ==,∠1=∠2. ∴ 3EF AD BF BF==.∵ ∠1+∠3=90°, ∴ ∠2+∠3=90°. ∴ BF ⊥AD .∴ BF ⊥EF .…………………………………………………………6分∴ 在Rt △BEF 中,3tan 3BF BEF EF ∠==. ∴ ∠APE =∠BEF =30°.…………………………………………7分解法二:如图11,将CA 平移到DF ,连接AF ,BF ,EF .………………3分则四边形ACDF 是平行四边形.图图9∵∠C=90°,∴四边形ACDF是矩形,∠AFD=∠CAF= 90°,∠1+∠2=90°.∵在Rt△AEF中,3 tan33AE AEAF CD∠===,在Rt△BDF中,3 tan13BD BDDF AC∠===,∴3130∠=∠=︒.∴∠3+∠2=∠1+∠2=90°,即∠EFB =90°.∴∠AFD=∠EFB.…………………4分又∵32DF AFBF EF==,∴△ADF∽△EBF.………………………………………………5分∴∠4=∠5.…………………………………………………………6分∵∠APE+∠4=∠3+∠5,∴∠APE=∠3=30°.………………………………………………7分图11。
【数学】2011年北京市各区一模试题分类解析(8):极坐标、参数方程

达人教育 010 - 63261009 教师一对一 您身边的考试专家 - 1 - 八、极坐标、参数方程1(2011西城一模理11).已知椭圆:C c o s,()2sin x y θθθ=⎧∈⎨=⎩R 经过点1(,)2m ,则m =__415±____,离心率e =____322(2011东城一模理10)已知曲线C 的参数方程为2cos ,sin x y θθ=+⎧⎨=⎩(θ为参数),则曲线上C的点到直线3440x y -+=的距离的最大值为 3 .3(2011朝阳一模理3).极坐标方程4cos ρθ=化为直角坐标方程是(A )(A )22(2)4x y -+= (B )224x y +=(C )22(2)4x y +-= (D )22(1)(1)4x y -+-=4(2011丰台一模理11).已知圆M :x 2+y 2-2x -4y +1=0,则圆心M 到直线43,31,x t y t =+⎧⎨=+⎩(t 为参数)的距离为2 .5(2011海淀一模理3). 在极坐标系下,已知圆C 的方程为2cos ρθ=,则下列各点在圆C 上的是 AA .1,3π⎛⎫-⎪⎝⎭B . 1,6π⎛⎫ ⎪⎝⎭C .32,4π⎛⎫ ⎪⎝⎭ D . 52,4π⎛⎫ ⎪⎝⎭6(2011门头沟一模理9).极坐标方程2ρ=化为直角坐标方程是 224x y += .7(2011石景山一模理11).在平面直角坐标系xOy 中,已知圆5cos 1,:5sin 2x C y θθ=-⎧⎨=+⎩(θ为参数)和直线46,:32x t l y t =+⎧⎨=--⎩ (t 为参数),则圆C 的普通方程为 22(1)(2)25x y ++-= ,直线l 与圆C 的位置关系是 相交 .。
2011年北京市海淀区【理科】数学一模试卷(含答案)

海淀区2011年高三年级第二学期期中练习数 学 (理科) 2011.4选择题 (共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1、已知集合{}30<<∈=x x A R ,{}42≥∈=x x B R ,则=B AA. {}32<<x xB. {}32<≤x x C. {}322<≤-≤x x x 或 D. R2.已知数列{}n a 为等差数列,n S 是它的前n 项和.若21=a ,123=S ,则=4S A .10 B .16 C .20 D .243. 在极坐标系下,已知圆C 的方程为2cos ρθ=,则下列各点在圆C 上的是 A .1,3π⎛⎫- ⎪⎝⎭B . 1,6π⎛⎫⎪⎝⎭C.34π⎫⎪⎭D .54π⎫⎪⎭4.执行如图所示的程序框图,若输出x 的值为23,则输入的x 值为A .0B .1C .2D .11 5.已知平面l = αβ,m 是α内不同于l 的直线,那么下列命题中 错误..的是 A .若β//m ,则l m // B .若l m //,则β//m C .若β⊥m ,则l m ⊥ D .若l m ⊥,则β⊥m 6. 已知非零向量,,a b c 满足++=a b c 0,向量,a b 的夹角为120,且||2||=b a ,则向量a 与c 的夹角为A .︒60B .︒90C .︒120D . ︒1507.如果存在正整数ω和实数ϕ使得函数)(cos )(2ϕω+=x x f (ω,ϕ为常数)的图象如图所示(图象经过点(1,0)),那么ω的值为A .1B .2C . 3 D. 48.已知抛物线M :24y x =,圆N :222)1(r y x =+-(其中r 为常数,0>r ).过点(1,0)的直线l 交圆N 于C 、D 两点,交抛物线M 于A 、B 两点,且满足BD AC =的直线l 只有三条的必要条件是A .(0,1]r ∈B .(1,2]r ∈C .3(,4)2r ∈D .3[,)2r ∈+∞非选择题(共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9.复数3i1i-+= . 10.为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为1s ,2s ,3s ,则它们的大小关系为 .(用“>”连接)11.如图,A ,B ,C 是⊙O 上的三点,BE 切⊙O 于点B , D 是CE 与⊙O的交点.若︒=∠70BAC ,则=∠CBE ______;若2=BE ,4=CE ,则=CD .12.已知平面区域}11,11|),{(≤≤-≤≤-=y x y x D ,在区域D 内任取一点,则取到的点位于直线y kx =(k R ∈)下方的概率为____________ .13.若直线l 被圆22:2C x y +=所截的弦长不小于2,则在下列曲线中:①22-=x y ② 22(1)1x y -+= ③ 2212x y += ④ 221x y -= 与直线l 一定有公共点的曲线的序号是 . (写出你认为正确的所有序号)14.如图,线段AB =8,点C 在线段AB 上,且AC =2,P 为线段CB 上一动点,点A 绕点C 旋转后与点B 绕点P 旋转后重合于点D .设CP =x ,△CPD 的面积为()f x .则()f x 的定义域为 ; '()f x 的零点是 .ACP BD 乙丙甲三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15. (本小题共13分)在ABC ∆中,内角A 、B 、C 所对的边分别为,,a b c ,已知1tan 2B =,1tan 3C =,且1c =. (Ⅰ)求tan A ; (Ⅱ)求ABC ∆的面积.16. (本小题共14分)在如图的多面体中,EF ⊥平面AEB ,AE EB ⊥,//AD EF ,//EF BC ,24BC AD ==,3EF =,2AE BE ==,G 是BC 的中点.(Ⅰ) 求证://AB 平面DEG ;(Ⅱ) 求证:BD EG ⊥;(Ⅲ) 求二面角C DF E --的余弦值.17. (本小题共13分)某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为23.现有10件产品,其中6件是一等品,4件是二等品. (Ⅰ) 随机选取1件产品,求能够通过检测的概率;(Ⅱ)随机选取3件产品,其中一等品的件数记为X ,求X 的分布列; (Ⅲ) 随机选取3件产品,求这三件产品都不能通过检测的概率.18. (本小题共13分)已知函数()ln f x x a x =-,1(), (R).ag x a x+=-∈ (Ⅰ)若1a =,求函数()f x 的极值;(Ⅱ)设函数()()()h x f x g x =-,求函数()h x 的单调区间;(Ⅲ)若在[]1,e (e 2.718...=)上存在一点0x ,使得0()f x <0()g x 成立,求a 的取值范围.A DF E BG C19. (本小题共14分)已知椭圆2222:1x y C a b+= (0)a b >>经过点3(1,),2M 其离心率为12.(Ⅰ)求椭圆C 的方程;(Ⅱ)设直线1:(||)2l y kx m k =+≤与椭圆C 相交于A 、B 两点,以线段,OA OB 为邻边作平行四边形OAPB ,其中顶点P 在椭圆C 上,O 为坐标原点.求OP 的取值范围.20. (本小题共13分)已知每项均是正整数的数列A :123,,,,n a a a a ,其中等于i 的项有i k 个(1,2,3)i =⋅⋅⋅, 设jj k k k b +++= 21 (1,2,3)j = ,12()m g m b b b nm =+++-(1,2,3)m =⋅⋅⋅.(Ⅰ)设数列:1,2,1,4A ,求(1),(2),(3),(4),(5)g g g g g ;(Ⅱ)若数列A 满足12100n a a a n +++-= ,求函数)(m g 的最小值.海淀区高三年级第二学期期中练习数 学(理)答案及评分参考 2011.4选择题 (共40分)一、选择题(本大题共8小题,每小题5分,共40分)非选择题 (共110分)二、填空题(本大题共6小题,每小题5分. 共30分.有两空的题目,第一空3分,第二空2分)9.12i - 10. s 1>s 2>s 3 11. 70 ; 3 12.1213. ① ③ 14. (2,4); 3 三、解答题(本大题共6小题,共80分) 15.(共13分) 解:(I )因为1tan 2B =,1tan 3C =,tan tan tan()1tan tan B CB C B C ++=-,………………1分代入得到,1123tan()111123B C ++==-⨯ . …………………3分 因为180A B C =-- , …………………4分所以t A B=-. …………………5分(II )因为0180A << ,由(I )结论可得:135A = . …………………7分 因为11tan tan 023B C =>=>,所以090C B <<< . …………8分 所以sin B =sin C =. …………9分由sin sin a cA C=得a = …………………11分所以ABC ∆的面积为:11sin 22ac B =. ………………13分16. (共14分)解:(Ⅰ)证明:∵//,//AD EF EF BC , ∴//AD BC .又∵2BC AD =,G 是BC 的中点, ∴//AD BG ,∴四边形ADGB 是平行四边形,∴ //AB DG . ……………2分 ∵AB ⊄平面DEG ,DG ⊂平面DEG ,∴//AB 平面DEG . …………………4分 (Ⅱ) 解法1证明:∵EF ⊥平面AEB ,AE ⊂平面AEB ,∴EF AE ⊥,又,AE EB EB EF E ⊥= ,,EB EF ⊂平面BCFE ,∴AE ⊥平面BCFE . ………………………5分过D 作//DH AE 交EF 于H ,则DH ⊥平面BCFE . ∵EG ⊂平面BCFE , ∴DH EG ⊥. ………………………6分∵//,//AD EF DH AE ,∴四边形AEHD 平行四边形, ∴2EH AD ==,∴2EH BG ==,又//,EH BG EH BE ⊥,∴四边形BGHE 为正方形,∴BH EG ⊥, ………………………7分又,BH DH H BH =⊂ 平面BHD ,DH ⊂平面BHD ,∴EG ⊥平面BHD . ………………………8分 ∵BD ⊂平面BHD ,∴BD EG ⊥. ………………………9分H A DFEB G C解法2∵EF ⊥平面AEB ,AE ⊂平面AEB ,BE ⊂平面AEB ,∴EF AE ⊥,EF BE ⊥, 又AE EB ⊥, ∴,,EB EF EA 两两垂直. ……………………5分以点E 为坐标原点,,,EB EF EA 分别为,,x y z 轴建立如图的空间直角坐标系.由已知得,A (0,0,2),B (2,0,0), C (2,4,0),F (0,3,0),D (0,2,2), G (2,2,0). …………………………6分∴(2,2,0)EG = ,(2,2,2)BD =-,………7分 ∴22220BD EG ⋅=-⨯+⨯=, ………8分∴BD EG ⊥. …………………………9分(Ⅲ)由已知得(2,0,0)EB =是平面EFDA 的法向量. …… ………………10分设平面DCF 的法向量为(,,)x y z =n ,∵(0,1,2),(2,1,0)FD FC =-=,∴00FD n FC n ⎧⋅=⎪⎨⋅=⎪⎩ ,即2020y z x y -+=⎧⎨+=⎩,令1z =,得(1,2,1)=-n . ……………………12分 设二面角C DF E --的大小为θ,则cos cos ,EB =<>== θn …………………………13分 ∴二面角C DF E --的余弦值为 …………………………14分 17. (共13分)解:(Ⅰ)设随机选取一件产品,能够通过检测的事件为A …………………………1分事件A 等于事件 “选取一等品都通过检测或者是选取二等品通过检测”…………2分151332104106)(=⨯+=A p …………………………4分 (Ⅱ) 由题可知X 可能取值为0,1,2,3.30463101(0)30C C P X C ===,21463103(1)10C C P X C ===,12463101(2)2C C P X C ===,03463101(3)6C C P X C ===. (8)分……………9分(Ⅲ)设随机选取3件产品都不能通过检测的事件为B ……………10分事件B 等于事件“随机选取3件产品都是二等品且都不能通过检测” 所以,3111()()303810P B =⋅=. ……………13分18. (共13分)解:(Ⅰ)()f x 的定义域为(0,)+∞, ………………………1分 当1a =时,()ln f x x x =-,11()1x f x x x-'=-= , ………………………2分 (3)分所以()f x 在1x =处取得极小值1. ………………………4分 (Ⅱ)1()ln ah x x a x x+=+-, 22221(1)(1)[(1)]()1a a x ax a x x a h x x x x x +--++-+'=--==………………………6分 ①当10a +>时,即1a >-时,在(0,1)a +上()0h x '<,在(1,)a ++∞上()0h x '>, 所以()h x 在(0,1)a +上单调递减,在(1,)a ++∞上单调递增; ………………………7分 ②当10a +≤,即1a ≤-时,在(0,)+∞上()0h x '>, 所以,函数()h x 在(0,)+∞上单调递增. ………………………8分 (III )在[]1,e 上存在一点0x ,使得0()f x <0()g x 成立,即 在[]1,e 上存在一点0x ,使得0()0h x <,即 函数1()ln ah x x a x x+=+-在[]1,e 上的最小值小于零. ………………………9分由(Ⅱ)可知①即1e a +≥,即e 1a ≥-时, ()h x 在[]1,e 上单调递减,所以()h x 的最小值为(e)h ,由1(e)e 0e a h a +=+-<可得2e 1e 1a +>-, 因为2e 1e 1e 1+>--,所以2e 1e 1a +>-; ………………………10分 ②当11a +≤,即0a ≤时, ()h x 在[]1,e 上单调递增,所以()h x 最小值为(1)h ,由(1)110h a =++<可得2a <-; ………………………11分 ③当11e a <+<,即0e 1a <<-时, 可得()h x 最小值为(1)h a +, 因为0ln(1)1a <+<,所以,0ln(1)a a a <+< 故(1)2ln(1)2h a a a a +=+-+>此时,(1)0h a +<不成立. ………………………12分综上讨论可得所求a 的范围是:2e 1e 1a +>-或2a <-. (13)分19. (共14分)解:(Ⅰ)由已知可得222214a b e a -==,所以2234a b = ① ……………1分 又点3(1,)2M 在椭圆C 上,所以221914a b+= ② ……………2分 由①②解之,得224,3a b ==.故椭圆C 的方程为22143x y +=. ……………5分 (Ⅱ) 当0k =时,(0,2)P m 在椭圆C上,解得2m =±,所以||OP ……6分 当0k ≠时,则由22,1.43y kx m x y=+⎧⎪⎨+=⎪⎩ 消y 化简整理得:222(34)84120k x kmx m +++-=,222222644(34)(412)48(34)0k m k m k m ∆=-+-=+->③ ……………8分设,,A B P 点的坐标分别为112200(,)(,)(,)x y x y x y 、、,则012012122286,()23434km mx x x y y y k x x m k k =+=-=+=++=++. ……………9分 由于点P 在椭圆C 上,所以2200143x y +=. ……………10分 从而222222216121(34)(34)k m m k k +=++,化简得22434m k =+, 经检验满足③式. ………11分又||OP ===== ………………………12分因为102k <≤,得23434k <+≤,有2331443k ≤<+,OP ≤. ………………………13分 综上,所求OP的取值范围是. ………………………14分 (Ⅱ)另解:设,,A B P 点的坐标分别为112200(,)(,)(,)x y x y x y 、、, 由,A B在椭圆上,可得2211222234123412x y x y ⎧+=⎨+=⎩①②………………………6分 ①—②整理得1213()()4(x x x x y y -++-+③ ………………………7分 由已知可得OP OA OB=+,所以120120x x x y y y +=⎧⎨+=⎩④⑤……………………8分 由已知当1212y y k x x -=- ,即1212()y y k x x -=-⑥ ………………………9分把④⑤⑥代入③整理得0034x ky =- ………………………10分与22003412x y +=联立消0x 整理得202943y k =+ ……………………11分 由22003412x y +=得2200443x y =-, 所以220024||3O P k =++ ……………………12分 因为12k ≤,得23434k ≤+≤,有2331443k ≤≤+,OP ≤. ………………………13分 所求OP的取值范围是. ………………………14分 20. (共13分)解:(1)根据题设中有关字母的定义,12342,1,0,1,0(5,6,7)j k k k k k j ======12342,213,2103,4,4(5,6,7,)m b b b b b m ==+==++====112123123412345(1)412(2)423,(3)434,(4)444,(5)45 4.g b g b b g b b b g b b b b g b b b b b =-⨯=-=+-⨯=-=++-⨯=-=+++-⨯=-=++++-⨯=-(2)一方面,1(1)()m g m g m b n ++-=-,根据“数列A 含有n 项”及j b 的含义知1m b n +≤, 故0)()1(≤-+m g m g ,即)1()(+≥m g m g ① …………………7分另一方面,设整数{}12max ,,,n M a a a = ,则当m M ≥时必有m b n =,所以(1)(2)(1)()(1)g g g M g M g M ≥≥≥-==+=所以()g m 的最小值为(1)g M -. …………………9分 下面计算(1)g M -的值:1231(1)(1)M g M b b b b n M --=++++--1231()()()()M b n b n b n b n -=-+-+-++-233445()()()()M M M M k k k k k k k k k k =----+----+----++- 23[2(1)]M k k M k =-+++-12312(23)()M M k k k Mk k k k =-++++++++123()n M a a a a b =-+++++123()n a a a a n =-+++++ …………………12分 ∵123100n a a a a n ++++-= , ∴(1)100,g M -=-∴()g m 最小值为100-. …………………13分说明:其它正确解法按相应步骤给分.。
2011中考北京东城一模数学答案
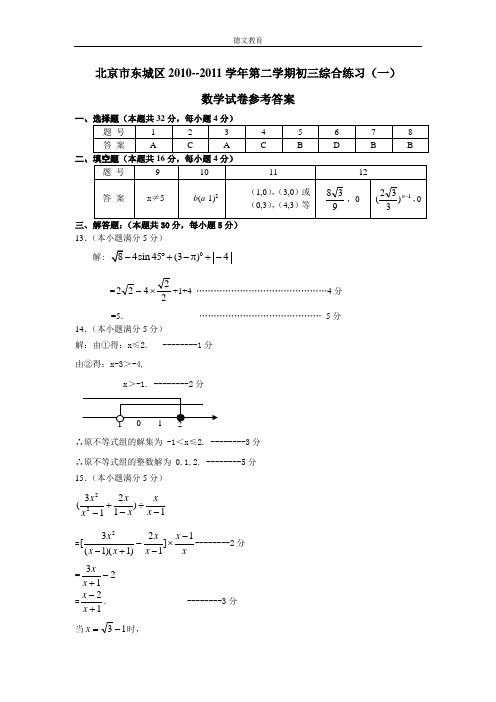
北京市东城区2010--2011学年第二学期初三综合练习(一)数学试卷参考答案一、选择题(本题共32分,每小题4分)13.(本小题满分5分)解:4sin 45(3)4︒+-π+-=22422⨯-+1+4 ………………………………………4分=5. …………………………………… 5分 14.(本小题满分5分) 解:由①得:x ≤2. --------1分 由②得:x-3>-4,x>-1. --------2分∴原不等式组的解集为 -1<x ≤2. --------3分 ∴原不等式组的整数解为 0,1,2. --------5分 15.(本小题满分5分) 1)1213(22-÷-+-x x xx x x=xx x x x x x1]12)1)(1(3[2-⨯--+---------2分=213-+x x=12+-x x . --------3分当13-=x 时,3133312-=-=+-x x .--------5分16.(本小题满分5分)证明:∵AC 是∠DAE 的平分线, ∴∠1=∠2. -------1分又∵AD ∥EC ,∴∠2=∠3. ------2分 ∴∠1=∠3.∴AE=CE. --------3分 在△ABE 和△CBE 中, , ∠AEB=∠CEB , ,∴△ABE ≌△CBE. --------4分 ∴AB=CB. ------5分17.(本小题满分5分)解:设小明家2月份用气x 立方米,则去年12月份用气(x +10) 立方米.-------1分 根据题意,得%251096109690⨯+=+-x x x . ----------------3分解这个方程,得x =30. ---------------4分 经检验,x =30是所列方程的根.答:小明家2月份用气30立方米. -----------------5分 18.(本小题满分5分)证明:(1)∵四边形ABCD 是平行四边形, ∴∠B=∠D.又AE ⊥BC ,AF ⊥CD , ∴∠AEB=∠AFD.∴∠BAE=∠DAF.---------2分 (2)在Rt △ABE 中,sin ∠BAE=53,AE=4,可求 AB=5. ---------3分又∵∠BAE=∠DAF ,ABCDE2 31ABCDEF∴ sin ∠DAF=sin ∠BAE=53.在Rt △ADF 中,AF=524, sin ∠DAF =53,可求DF=518-------4分∵ CD=AB=5. ∴CF=5-518=57. …………………………………………5分四、解答题(本题共20分,每小题5分)19.(本小题满分5分)解:(1)0.6;36;------------2分(2)72°;补全图如下:------------4分(3)1500×0.6=900.答:学生中“比较了解”的人数约为900人 ------------5分 20.(本小题满分5分) (1)证明:在⊙O 中,OD ⊥AB ,CB ⊥AB ,∴AM =MB ,OD ∥BC . …………………1分 ∴AD =DC . ……………2分(2)∵DE 为⊙O 切线,∴OD ⊥DE ……………3分∴四边形MBED 为矩形.∴DE ∥AB. ……………4分 ∴MB=DE =2,M D=BE =EC =1.连接OB.在R t △OBM 中,OB 2=OM 2+BM 2. 解得 OB=25 . …………………5分21.(本小题满分5分)解:(1)∵点A (1,6),B (a ,3)在反比例函数y =xk 2的图象上,∴ k 2=1×6=6. --------1分 ∴ a ×3=6,a =2.60%比较了解不太了解2%18%MOA BCDE∴B (2,3).由点A (1,6),B (2,3)也在直线y=k 1x+b 上, 得⎩⎨⎧=+=+,32,611b k b k 解得k 1=-3.∴k 1=-3, k 2=6. -----------------2分 (2) 设点P 的坐标为(m,n ). 依题意,得21×3(m +2+m -2)=18,m =6. -----------------3分∴ C (6,3),E (6,0). ∵ 点P 在反比例函数y =x6的图象上,∴ n =1. ------------------4分 ∴PE :PC =1:2 . ------------------5分22.(本小题满分5分)解: (1)设AD =x ,由题意得,BG=x -2,CG=x-3. 在Rt △BCG 中,由勾股定理可得 222(2)(3)5x x -+-=. 解得 6x =. --------------2分(2)参考小萍的做法得到四边形AEGF ,∠EAF=60°,∠EGF=120°,∠AEG=∠AFG= 90°,AE=AF=AD=4. 连结EF ,可得 △AEF 为等边三角形. ∴ EF=4.∴ ∠FEG=∠EFG= 30°. ∴ EG=FG.在△EFG中,可求,E G =∴△EFG 的周长=. --------------5分五、解答题:(本题共22分,第23题7分,第24题7分,第25题8分) 23.(本小题满分7分)GF EDCBA解: 由方程(m -1)x 2-(2m -1)x +2+xm=0可得)1(22)1(4)12()12(2-⨯-⨯--±--=m m m m x =)1(2)32(12)1(2)32()12(2-+±-=--±-m m m m m m111-=m x ,.22=x∵21,x x 均为正整数,m 也是整数, ∴m =2. ----------3分 (2)由(1)知x 2-3x +2+x2=0.∴x 2-3x +2= -x2.画出函数y = x 2-3x +2,y = -x2的图象,---------6分由图象可知,两个函数图象的交点个数是1. ---------7分24. (本小题满分7分)(1)△EPF 为等边三角形. --------------1分 (2)设BP=x ,则CP =6-x.由题意可 △BEP28x .△CFP的面积为2)2x -.△ABC的面积为. 设四边形AEPF 的面积为y. ∴y =-28x 2)2x --=2-+-.自变量x 的取值范围为3<x <6. --------------4分 (3)可证△EBP ∽△PCF.∴B P B EC FC P=.设BP=x , 则 (6)8x x -=.解得 124,2x x ==.∴ PE 的长为4或 --------------7分25.(本小题满分8分)解:(1)依题意,可知 C(0,8),则B(4,0) 将A(-2,0),B(4,0)代入 y=ax 2+bx +8,⎩⎨⎧=++=+-.08416,0824b a b a 解得⎩⎨⎧=-=.2,1b a配方得y,顶点D (1,9). ---------3分(2)假设满足条件的点存在,依题意设,由求得直线的解析式为, 它与轴的夹角为. 过点P 作PN ⊥y 轴于点N.依题意知,∠NPO=30°或∠NPO=60°. ∵PN=2,∴ON=332或23.∴存在满足条件的点,的坐标为(2,332 )和(2,23).-----------6分(3)由上求得.当抛物线向上平移时,可设解析式为. 当时,. 当时,.或.由题意可得m 的范围为.∴ 抛物线最多可向上平移72个单位. -----------8分228y x x ∴=-++2(1)9x =--+P (2)P t ,(08)(19)C D ,,,C D 8y x =+x 45 P P (80)(412)E F -,,,228(0)y x x m m =-+++>8x =-72y m =-+4x =y m =720m ∴-+≤12m ≤072m ∴<≤。
北京市东城区2011届高三一模数学(理)试题及答案
东城区2010-2011学年度综合练习(一)高三数学 (理科)学校_____________班级_______________姓名______________考号___________ 本试卷分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)一、本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)“2x >”是“24x >”的(A )充分非必要条件 (B )必要非充分条件 (C )充要条件(D )既不充分也不必要条件(2)已知数列{}n a 为等差数列,且12a =,2313a a +=,那么则456a a a ++等于(A )40 (B )42 (C )43 (D )45(3)已知函数()f x 对任意的x ∈R 有()()0f x f x +-=,且当0x >时,()ln(1)f x x =+,则函数()f x 的大致图像为(A )(B )(C ) (D )(4)已知平面上不重合的四点P ,A ,B ,C 满足0PA PB PC ++= ,且AB AC m AP +=,那么实数m 的值为(A )2 (B )3 (C )4 (D )5(5)若右边的程序框图输出的S 是126,则条件①可为A .5n ≤B .6n ≤C .7n ≤D .8n ≤(6)已知(,)2απ∈π,1tan()47απ+=,那么ααcos sin +的值为(A )51-(B )57(C )57- (D )43(7)已知函数31)21()(x x f x-=,那么在下列区间中含有函数)(x f 零点的是(A ))31,0( (B ))21,31((C ))32,21( (D ))1,32((8)空间点到平面的距离定义如下:过空间一点作平面的垂线,这个点和垂足之间的距离叫做这个点到这个平面的距离.已知平面α,β,γ两两互相垂直,点A ∈α,点A 到β,γ的距离都是3,点P 是α上的动点,满足P 到β的距离是到P 到点A 距离的2倍,则点P 的轨迹上的点到γ的距离的最小值是 (A ) 33- (B )323- (C )36-(D )340 50 60 70 80 90 体重(kg)频率A第Ⅱ卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分。
2011年北京市各区一模数学试题分类解析(16):复数
十六、复数1(2011西城一模理9). 在复平面内,复数2i1i-对应的点到原点的距离为__2___. 2(2011西城一模文9). 若复数(1i)(1i)a ++是纯虚数,则实数a 等于___1 ___. 3(2011东城一模理9)如果2(i)(1i)m m ++是实数,那么实数m = 1- . 4(2011东城一模文1)已知复数z 满足(1i)2z -=,则z 等于(A )1i + (B )1i - (C )1i -+ (D )1i -- 5.(2011朝阳一模理9)复数13i z =+,21i z =-,则12z z 等于 1+2i .6(2011海淀一模理9).复数3i1i-+= 12i - .7(2011门头沟一模理1).在复平面内,复数1ii+对应的点位于 (A )第一象限 (B )第二象限 (C )第三象限(D )第四象限8(2011石景山一模理2).若17()2ia bi ab i+=+∈-,R ,i 是虚数单位,则乘积ab 的值是( C ) A . 15- B . 3 C .3- D .59(2011朝阳一模文9).已知i 为虚数单位,则3i1i+-= 12i + .10(2011丰台文6).程序框图如图所示,若输入a 的值是虚数单位i ,则输出的结果是(A)(A) -1 (B) i -1 (C) 0 (D) - i11(2011海淀一模文9). 计算21i=+_____1i - _____________.12(2011石景山一模文2).若17()2ia bi ab i+=+∈-,R ,i 是虚数单位,则乘积ab 的值是( C ) A . 15- B . 3 C .3- D .5。
2011年北京市平谷区数学一模试卷及答案
平谷区2010~2011学年度第二学期初三第一次统一练习数学试卷(120分钟)2011.4一、选择题(本题共8个小题,每小题4分,共32分)在下列各题的四个备选答案中,只有一个是正确的.1.9-的相反数是A.19 B.19- C.9- D.92.北京市2010年暨“十一五”期间国民经济和社会发展统计公报显示,2010年末,全市共有公共图书馆25个,总藏量44 510 000册.将44 510 000用科学记数法表示应为A.810451.4⨯ B.710451.4⨯ C.61051.44⨯ D.8104451.0⨯3.如图,已知AB∥CD,∠C=35°,BC平分∠ABE,则∠ABE的度数是A.17.5° B.35° C.70° D.105°4.下列运算正确的是A .224236x x x =·B .22231x x -=-C .2222233x x x ÷= D .224235x x x += 5.某男子排球队20名队员的身高如下表:则此男子排球队20名队员的身高的众数和中位数分别是(单位:cm )A .186,186B .186,187C .208,188D .188,1876.把多项式8822++x x 分解因式,结果正确的是A .()242+xB .()242+xC .()222-xD .7.如图,一个可以自由转动的转盘被等分成6了 相应的颜色,转动转盘,转盘停止后,指针指向红色区域的概率是 A.16B.13C.12D.238.如图,AB 是O ⊙的直径,弦2cm BC =,F 是弦BC 的中点,60ABC ∠=°.若动点E 以2cm/s 的速度从A 点出发沿着 A B A →→方向运动,设运动时间为()(03)t s t <≤,连结EF ,当BEF △是直角三角形时,t (s )的值为A .47 B .1 C .47或1 D .47或1 或49 二、填空题(本题共16分,每小题4分)9.在函数y =x 的取值范围是 .10.已知113x y -=,则代数式21422x xy yx xy y----的值为 .11.如图,⊙O 是△ABC 的外接圆,OD ⊥AB 于点D 、交⊙O 于点E , ∠C =60°, 如果⊙O 的半径为2,那么OD = .12.如图所示,直线1+=x y 与y 轴交于点1A ,以1OA 为边作正方形111C B OA 然后延长11B C 与直线1+=x y 交于点2A ,得到第一个梯形211A OC A ;再以21A C 为边作正方形2221C B A C ,同样延长22B C 与直线1+=x y 交于点3A 得到第二个梯形3212A C C A ;,再以32A C 为边作正方形3332C B A C ,延长33B C ,得到第三个梯形;……则第2个梯形3212A C C A 的面积是 ;第n (n 是正整数)个梯形的面积是 (用含n 的式子表示).三、解答题(本题共30分,每小题5分)13.计算:︒+⎪⎭⎫⎝⎛----30tan 6213220111.14.求不等式组⎪⎩⎪⎨⎧-≤--x x x x 22158)2(3>的整数解. 15.已知:如图,C F 、在BE 上,A D AC DFBF EC ∠=∠=,∥,.A B C FE DABOD CE求证:△ABC ≌DEF .16.已知0342=--x x ,求4)1)(1()1(22--+--x x x 的值. 17.列方程或方程组解应用题:服装厂为红五月歌咏比赛加工300套演出服.在加工60套后,采用了新技术,使每天的工作效率是原来的2倍,结果共用9天完成任务.求该厂原来每天加工多少套演出服.18.在平面直角坐标系中,A 点坐标为(04),,C 点坐标为(100),. (1)如图①,若直线AB OC ∥,AB 上有一动点P ,当P 点的坐标为 时,有PO PC =;(2)如图②,若直线AB 与OC 不平行, 在过点A 的直线4y x =-+上是否存在点P ,使90OPC ∠=︒,若有这样的点P ,求出它的坐标.若没有,请简要说明理由.四、解答题(本题共20分,第19题5分,20题5分,第21题6分,第22题4分)19.已知,如图,梯形ABCD 中,AD ∥BC ,∠A =90°,∠C =45°,BE ⊥DC 于E ,BC =5,AD :BC =2:5.求ED 的长.20.如图,在ABC △中,AB AC =,AE平分ABC ∠交AE 于点M ,经过B M ,两点的O ⊙点G ,交AB 于点F ,FB 恰为O ⊙的直径. (1)求证:AE 与O ⊙相切;(2)当14cos 3BC C ==,时,求O ⊙的半径.21.小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:(2)扇形统计图中,表示短信费的扇形的圆心角为多少度? (3)请将表格补充完整; (4)请将条形统计图补充完整.22.一种电讯信号转发装置的发射直径为31km .现要求:在一边长为30km 的正方形城区选择若干个安装点,每个点安装一个这种转发装置,使这些装置转发的信号能完全覆盖这个城市.问: (1)能否找到这样的4个安装点,使得这些点安装了这种转发装置后能达到预设的要求?在图1中画出安装点的示意图,并用大写字母M 、N 、P 、Q 表示安装点;(2)能否找到这样的3个安装点,使得在这些点安装了这种转发装置后能达到预设的要求?在图2中画出示意图说明,并用大写字母M 、N 、P 表示安装点,用计算、推理和文字来说明你的理由. 五、解答题 (本题共22分,第23图BC D图BCD题7分,第24题7分,第25题8分) 23.已知二次函数)0a (23bx ax y 2≠-+=的图象经过点(10),,和(30)-,,反比例函数xk =1y (x >0)的图象经过点(1,2).(1)求这两个二次函数的解析式,并在给定的直角坐标系中作出这两个函数的图象;(2)若反比例函数xk=1y (0x >)的图象与二次函数)0a (23bx ax y 2≠-+=)的图象在第一象限内交于点00()A x y ,,0x 落在两个相邻的正整数之间.请你观察图象写出这两个相邻的正整数; (3)若反比例函数2ky x=(00k x >>,)的图象与二次函数)0a (23bx ax y 2≠-+=的图象在第一象限内的交点为A ,点A 的横坐标0x 满足023x <<,试求实数k 的取值范围.24.已知点A ,B 分别是两条平行线m ,n 上任意两点,C 是直线n 上一点,且∠ABC=90°,点E 在AC 的延长线上,BC =k AB (k ≠0).(1)当k =1时,在图(1)中,作∠BEF =∠ABC ,EF 交直线m 于点F .,写出线段EF 与EB 的数量关系,并加以证明;(2)若k ≠1,如图(2),∠BEF =∠ABC ,其它条件不变,探究线段EF 与EB 的数量关系,并说明理由.25.已知:抛物线k k x k kx y ++++=22)2(32经过坐标原点. (1)求抛物线的解析式和顶点B 的坐标;(2)设点A 是抛物线与x 轴的另一个交点,试在y 轴上确定一点P ,使PA +PB 最短,并求出点P 的坐标;(3)过点A作AC∥BP交y轴于点C,求到直线AP、AC、CP距离相等的点的坐标.平谷区2010~2011学年度第二学期初三第一次统一练习 数学试卷参考答案及评分参考 2011.4一、选择题(本题共8个小题,每小题4分,共32分)二、填空题(本题共16分,每小题4分)三、解答题(本题共30分,每小题5分)13.解:︒+⎪⎭⎫⎝⎛----30tan 6213220111=3362321⨯+-- …………………………………………………………………….4分=1- ………………………………………………………………………………………5分 14.解:由3(x x --≤得,1x -≥………………………………………………….1 分由1522x x -> 得,2x <……………………………………………………. 2分12x -<∴≤. ……………………………………………………………………4分∴不等式组的整数解是.1,0,1- . ………….. ……………………………………………5分15.证明:AC DF ∥,ACE DFB ∴∠=∠ (1)分 ∴ACB DFE ∠=∠. …………………………….2分又BF EC =,BF CF EC CF ∴-=-,即BC EF =. (3)分在△ABC 与△DEF 中,⎪⎩⎪⎨⎧=∠=∠∠=∠,,,EF BC DFE ACB D A …………………………………………………………………4分ABC DEF∴△≌△.………………………………………………………………………5分16.解:4)1)(1()1(22--+--x x x=4)1()12(222---+-x x x …………………………….…………………………...2分=142--x x …………………………………………….……………………………..4分 ∴原式=1)4(2--x x =213=-…………………….………………………………5分17.解:设服装厂原来每天加工x 套演出服.……………………………………….1分 根据题意,得AB C FE D603006092x x-+=. ………………………………………………….2分 解 得20x =.………………………………………………………………………3分 经检验,20x =是原方程的根.………………………………………………………..4分 答:服装厂原来每天加工20套演出服.……………………………………………….5分 18.解:(1)(54),……………………………………………………………………….2分(2)设(4)P x x -+,,连接OP PC ,,过P 作PE OC ⊥于E ,PN OA ⊥于N ,……………………………………3分因为222(4)OP x x =+-+,22(4)(10)P Cx x =-++-, 22O P P CO C +=,所以22222(4)(4)(10)10x x x x +-++-++-=.2980x x -+=,11x=,28x=. (4)分所以P坐标(,或(84)-,.………………………………………………………....5分四、解答题(本题共20分,第19题5分,20题5分,第21题6分,第22题4分)19.解:作DF⊥BC于F,EG⊥BC于G. ……………………………………………1分∵∠A=90°,AD∥BC∴四边形ABFD是矩形.∵BC=5,AD:BC=2:5.∴ AD=BF=2. ………………………………………..2分∴ FC=3.在Rt△DFC中,∵∠C=45°,∴ DC=23.…………………………………………3分在Rt△BEC中,∴EC=225……………………………………………….……………………………....4分∴DE =2222523=-……………………………………………………………….5分20.解:(1)证明:连结OM ,则OM OB =. ∴ 12∠=∠. ∵ BM 平分ABC ∠. ∴ 13∠=∠. ∴ 23∠=∠. ∴ OM BC ∥.∴ AMO AEB ∠=∠.…………………………..1分 在ABC △中,∵ AB AC =,AE 是角平分线, ∴AE BC ⊥.………………………………………………………………………..….2分 ∴ 90AEB ∠=°. ∴ 90AMO ∠=°. ∴ OM AE ⊥. ∴AE与O⊙相切.………………………………………………………………………3分(2)解:在ABC △中,AB AC =,AE 是角平分线,∴12BE BC ABC C =∠=∠,. ∵14cos 3BC C ==,, ∴2=BE ,.31cos =∠ABC在ABE △中,90AEB ∠=°, ∴6cos BEAB ABC==∠.………………………………………………………………….4分设O ⊙的半径为r ,则6AO r =-. ∵OM BC ∥, ∴AOM ABE △∽△.∴OM AOBE AB =. ∴ 626r r -=.解得32r =.∴O⊙的半径为32.………………………………………………………….5分 21.解:(1)总话费125元………….1分 (2)72°……………………..2分H (3)基本话费50;………….3分长途话费45;……………4分 短信费 25………………...5分 (4)……………………………6分22.解:(1)(2分) (2)(画图正确给1分)(2)图2(图案设计不唯一)将原正方形分割成如图2中的3个矩形,使得BE=OD=OC .将每个装置安装在这些矩形的对角线交点处,设AE x =,则30ED x =-,15DH =.由BE=OD ,得22223015(30)x x +=+-,22515604x ∴==,30.231BE ∴=≈<,即如此安装3个这种转发装置,也能达到预设要求. ···· 4分 或:将原正方形分割成如图2中的3个矩形,使得31BE =,H 是CD 的中点,将每个装置安装在这些矩形的对角线交点处,则AE ==30DE =∴ 318.2615)61-(3022<≈+=DO ,如此装三个这个转发装置,能达到预设要求.ADCB图1PQ M N五、解答题 (本题共22分,第23题7分,第24题7分,第25题8分) 23.解:(1)把(10),,和(30)-,分别代入 解方程组,得.1b ,21a ==………………1分 ∴抛物线解析式为23212-+=x x y …...2分 ∵ 反比例函数x k=1y 的图象经过点(1,2),∴ k =2. ∴ x2y 1= ……………….…...3分(2)正确的画出二次函数和反比例函数在第一象限内的图象 ……………………….4分由图象可知,这两个相邻的正整数为1与2. ………………………………………5分(3)由函数图象或函数性质可知:当2<x <3时,对y=23212-+x x ,y 随着x 的增大而增大,对y 2=xk (k >0),y 2随着x 的增大而减小.因为A (x 0,y 0)为二次函数图象与反比例函数图象的交点,所以当x 0=2时,由反比例函数图象在二次函数的图象上方,得y 2>y. 即2k >2322212-+⨯, 解得k>5. …………………………………………………………………………6分同理,当x 0=3时,由二次函数的图象在反比例函数图象上方的,得y>y 2,即2333212-+⨯>3k ,解得k <18. 所以k的取值范围为5<k<18. ………………………………………………7分 24.解:(1)正确画出图形………………………………………….…………..1分EF EB =.证明:如图(1),在直线m 上截取AM AB =,连结ME BC kAB =,1k =,BC AB ∴=.90ABC ∠=,45CAB ACB ∴∠=∠=.m n ∥,45MAE ACB CAB ∴∠=∠=∠=,90FAB ∠=. AE AE =,MAE BAE ∴△≌△. ····· 3分 EM EB ∴=,AME ABE ∠=∠.……………………………4分90BEF ABC ∠=∠=,180FAB BEF ∴∠+∠=. 180ABE EFA ∴∠+∠=.又180AME EMF ∠+∠=,EMF EFA ∴∠=∠. EM EF ∴=.EF EB ∴=.…………………….………………………………..5分 (2)1EF EB k=.说明:如图(2),过点E 作EM m ⊥,EN AB ⊥,垂足为M N ,. .m n ∥,90ABC ∠=,图A B CM EN mn F M90MAB ∴∠=.∴四边形MENA 为矩形.ME NA ∴=,90MEN ∠=.90BEF ABC ∠=∠=,MEF NEB ∴∠=∠.MEF NEB ∴△∽△. ··················· 6分 ME EF EN EB ∴=.AN EFEN EB∴=. 在Rt ANE △和Rt ABC △中,tan EN BCBAC k AN AB∠===, 1EF EB k∴=. ………………………………………………………………………………7分25.解:(1)∵ 抛物线k k x k kx y ++++=22)2(32经过坐标原点,∴ k k +2=0. 解得 1,021-==k k .∵ 0≠k ,∴ 1-=k ∴ x x y 322+-=…1分 ∴ ()3,3B . ………………………….2分 (2)令0=y ,得x x 322+-=0,解得 32,021==x x . ∴ ()0,32A ………..3分 ∴点A 关于y 轴的对称点A '的坐标为()0,32-. 联结B A ',直线B A '与y 轴的交点即为所求点P. 可求得直线B A '的解析式:233+=x y . ∴ ()2,0P ……………………………4分(3)到直线AP 、AC 、CP 距离相等的点有四个.如图,由勾股定理得4===AC PA PC ,所以△PAC 为等边三角形. 易证x 轴所在直线平分∠PAC ,BP 是△PAC 的一个外角的平分线.作∠PCA 的平分线,交x 轴于1M 点,交过A 点的平行线于y 轴的直线于2M 点,作△PAC 的∠PCA 相邻外角的平分线,交2AM 于3M 点,反向延长C 3M 交x 轴于4M 点.可得点1234M M M M ,,,就是到直线AP 、AC 、CP 距离相等的点.可证△AP 2M 、△AC 3M 、 △PC 4M 均为等边三角形.可求得:①332331==OP OM ,所以点M 1的坐标为⎪⎪⎭⎫ ⎝⎛0,332;…………5分②42==AM AP ,所以点M 2的坐标为()4,32;………………………………....6分 ③点M 3与点M 2关于x 轴对称,所以点M 3的坐标为()4,32-;………………..…..7分④点4M 与点A 关于y 轴对称,所以点4M 的坐标为()0,32-. 综上所述,到直线AP 、AC 、CP 距离相等的点的坐标分别为⎪⎪⎭⎫⎝⎛0,3321M ,()4,322M ,()4,323-M ,()0,324-M .…………………………….. 8分。
2011北京海淀一模、西城一模、东城一模、丰台一模经典试题汇编(含答案)
学而思韩春成老师题库资料分享【2011海淀区一模】8.如图,在Rt ABC △中,∠C =90°,AB =5cm ,BC =3cm ,动点P 从点A 出发, 以每秒1cm 的速度,沿A →B →C 的方向运动,到达点C 时停止.设2y PC =, 运动时间为t 秒,则能反映y 与t 之间函数关系的大致图象是答案:A12.如图,矩形纸片ABCD中,AB BC =第一次将纸片折叠,使点B 与点D 重合,折痕与BD 交于点1O ;设1O D 的中点为1D ,第二次将纸片折叠使点B 与点1D 重合,折痕与BD 交于点2O ;设21O D 的中点 为2D ,第三次将纸片折叠使点B 与点2D 重合,折痕与BD交于点3O ,… .按上述方法折叠,第n 次折叠后的折痕与BD 交于点n O ,则1BO = ,n BO = .…第一次折叠 第二次折叠 第三次折叠 … 答案:2 ,12332n n -- C A B DBADCBA BAD BAD学而思韩春成老师题库资料分享24.已知平面直角坐标系xOy 中, 抛物线2(1)y ax a x =-+与直线y kx =的一个公共点为(4,8)A .(1)求此抛物线和直线的解析式;(2)若点P 在线段OA 上,过点P 作y 轴的平行线交(1)中抛物线于点Q ,求线段PQ 长度的最大值;(3)记(1)中抛物线的顶点为M ,点N 在此抛物线上,若四边形AOMN 恰好是梯形,求点N 的坐标及梯形AOMN 的面积.解:(1)由题意,可得8164(1)a a =-+及84k =,解得1,2a k ==,所以,抛物线的解析式为22y x x =-,直线的解析式为2y x =. ………2分(2)设点P 的坐标为4(,2)(0)t t t ≤≤,可得点Q 的坐标为2(,2)t t t -,则 2222(2)4(2)4PQ t t t t t t =--=-=--+所以,当2t =时,PQ 的长度取得最大值为4. ……………………4分 (3)易知点M 的坐标为(1,-1).过点M 作直线OA 的平行线交抛物线于点N ,如图所示,四边形AOMN 为梯形.直线MN 可看成是由直线所以直线MN 的方程为2y x b =-.因为点M 在直线y MN 的方程为23y x =-,将其代入22y x x =- 2232x x x -=-即 2430x x -+= 解得 11x =,23x =易得 11y =-,23y =(备图1)(备图2)学而思韩春成老师题库资料分享所以,直线MN 与抛物线的交点N 的坐标为(3,3). …………5分如图,分别过点M 、N 作y 轴的平行线交直线OA 于点G 、H , 显然四边形MNHG 是平行四边形.可得点G (1,2),H (3,6).113(10)[2(1)]222OMG S MG =⨯-⨯=⨯--=△113(43)(63)222ANH S NH =⨯-⨯=⨯-=△(31)236MNHG S NH =-⨯=⨯=△所以,梯形AOMN 的面积9OMG MNHG ANH AOMN S S S S =++=△△△梯形. ………7分 25.在Rt △ABC 中,∠ACB =90°,tan ∠BAC =12. 点D 在边AC 上(不与A ,C 重合),连结BD ,F 为BD 中点. (1)若过点D 作DE ⊥AB 于E ,连结CF 、EF 、CE ,如图1. 设CF kEF =,则k = ; (2)若将图1中的△ADE 绕点A 旋转,使得D 、E 、B 三点共线,点F 仍为BD 中点,如图2所示.求证:BE -DE =2CF ;(3)若BC =6,点D 在边AC 的三等分点处,将线段AD 绕点A 旋转,点F 始终为BD中点,求线段CF 长度的最大值.解:(1)k =1; ……………………….……………………………2分(2)如图2,过点C 作CE 的垂线交BD 于点G ,设BD 与AC 的交点为Q .由题意,tan ∠BAC =12, ∴12BC DE AC AE ==. ∵ D 、E 、B 三点共线, ∴ AE ⊥DB .∵ ∠BQC =∠AQD ,∠ACB =90°,BCA DEFBDEA FC BAC1图2图备图2图BD EA FCGQ∴∠QBC=∠EAQ.∵∠ECA+∠ACG=90°,∠BCG+∠ACG=90°,∴∠ECA=∠BCG.∴BCG ACE△∽△.∴12 BC GBAC AE==.∴GB=DE.∵F是BD中点,∴F是EG中点.在Rt ECG△中,12CF EG=,∴2BE DE EG CF-==. ….……………………………5分(3)情况1:如图,当AD=13AC时,取AB的中点M,连结MF和CM,∵∠ACB=90°,tan∠BAC=12,且BC= 6,∴AC=12,AB=.∵M为AB中点,∴CM=∵AD=13 AC,∴AD=4.∵M为AB中点,F为BD中点,∴FM=12AD= 2.∴当且仅当M、F、C三点共线且M在线段CF上时CF最大,此时CF=CM+FM=2+分情况2:如图,当AD=23AC时,取AB的中点M,连结MF和CM,类似于情况1,可知CF的最大值为4+………………………7分综合情况1与情况2,可知当点D在靠近点C的三等分点时,线段CF的长度取得最大值为4+……………………….……………………………8分B【2011西城区一模】8.如图,点A 在半径为3的⊙O 内,,P 为⊙O 上一点, 当∠OP A 取最大值时,P A 的长等于( ).A .32B C D .答案:B12. 如图1,小正方形ABCD 的面积为1,把它的各边延长一倍得到新正方形1111D C B A ,正方形1111D C B A 的面积为 ;再把正方形1111D C B A 的各边延长一倍得到正方形2222D C B A (如图2),如此进行下去,正方形D C B A 的面积为 .(用含有n 的式子表示,n 为正整数)图1 图2 答案:5,n524.如图1,平面直角坐标系xOy 中,A ,B (4,0).将△OAB 绕点O 顺时针旋转α角(0°<α<90°)得到△OCD (O ,A ,B 的对应点分别为O ,C ,D ),将△OAB 沿x 轴负方向...平移m 个单位得到△EFG (m >0,O ,A ,B 的对应点分别为E ,F ,G ),α,m 的值恰使点C ,D ,F 落在同一反比例函数ky x=(k ≠0)的图象上.诶你 (1)∠AOB= °,α= °;(2)求经过点A ,B ,F 的抛物线的解析式;(3)若(2)中抛物线的顶点为M ,抛物线与直线EF 的另一个交点为H ,抛物线上的点P 满足以P ,M ,F ,A 为顶点的四边形的面积与四边形MF AH 的面积相等 (点P 不与点H 重合),请直接写出满足条件的点P 的个数,并求位于直线EF解:(1)∠AOB= 30 °,α= 60 °.…………………………………………………2分 (2)∵A ,B (4,0),△OAB 绕点O 顺时针旋转α角得到△OCD ,(如图7)∴ OA =OB=OC=OD=4.由(1)得 30BOC AOB ∠=︒=∠.∴ 点C 与点A 关于x 轴对称,点C的坐标为2)-. ∵ 点C ,D ,F 落在同一反比例函数ky x=(k ≠0)的图象上, ∴C C k x y =⋅=-∵ 点F 是由点A 沿x 轴负方向平移m 个单位得到,∴ 2F y =,F x ==-F的坐标为(-.……………3分 ∴ 点F 与点A 关于y 轴对称,可设经过点A ,B ,F 的抛物线的解析式为2y ax c =+.∴22, 160.a c a c ⎧+=⎪⎨+=⎪⎩ 解得1 ,2 8.a c ⎧=-⎪⎨⎪=⎩∴ 所求抛物线的解析式为2182y x =-+. …………………………………4分(3)满足条件的点P 的个数为 5 .………………………………………………5分抛物线2182y x =-+的顶点为(0,8)M .∵ △EFG 是由△OAB 沿x 轴负方向平移m 个单位得到,∴m FA ==,E O x x m =-=-,∠FEG=∠AOB=30°. ∴ 点E的坐标为(-. 可得直线EF的解析式为4y =+.∵ 点H 21482x x +=-+的解,整理,得23240x +-=.解得 12x x ==-∴ 点H 的坐标为16)3.由抛物线的对称性知符合题意的1P 点的坐标为16()3.……………6分 可知△AFM 是等边三角形,∠MAF= 60°.由A ,M 两点的坐标分别为A ,(0,8)M ,可得直线AM 的解析式为8y =+.过点H 作直线AM 的平行线l ,设其解析式为y b =+(b ≠8).将点H 的坐标代入上式,得163b =+.解得283b =,直线l 的解析式为283y =+.∵ 直线l 与抛物线的交点的横坐标是方程 2281832x +=-+的解.整理,得2380x -+=.解得12x x =.∴ 点2P 22)3满足HA M AM P S S ∆∆=2,四边形2P MFA 的面积与四边形MF AH 的面积相等.(如图8)……………………………………………7分点2P 关于y 轴的对称点3P 也符合题意,其坐标为3P 22()3.………8分综上所述,位于直线EF 上方的点P 的坐标分别为1P 16()3,2P 22)3,3P 22()3.25.在Rt △ABC 中,∠C =90°,D ,E 分别为CB ,CA 延长线上的点,BE 与AD 的交点为P .(1)若BD=AC ,AE=CD ,在图1中画出符合题意的图形,并直接写出∠APE 的度数;(2)若AC ,CD ,求∠APE 的度数.解:(1)如图9,∠APE= 45°. ……………………2分(2)解法一:如图10,将AE平移到DF,连接BF,EF (3)则四边形AEFD是平行四边形.∴AD∥EF,AD=EF.∵AC,CD,∴3=BDAC,3==DFCDAECD.∴AC CDBD DF=.……………………………………………………4分∵∠C=90°,∴18090BDF C∠=︒-∠=︒.∴∠C=∠BDF.∴△ACD∽△BDF.………………5分∴AD ACBF BD=1=∠2.∴EF ADBF BF=.∵∠1+∠3=90°,∴∠2+∠3=90°.∴BF⊥AD .∴BF⊥EF.…………………………………………………………6分∴在Rt△BEF中,tanBFBEFEF∠==.∴∠APE=∠BEF =30°.…………………………………………7分解法二:如图11,将CA平移到DF,连接AF,BF,EF.………………3分则四边形ACDF是平行四边形.∵∠C=90°,∴四边形ACDF是矩形,∠AFD=∠CAF= 90°,∠1+∠2=90°.∵在Rt△AEF中,tan3AE AEAF CD∠===在Rt△BDF中,tan1BD BDDF AC∠==∴3130∠=∠=︒.∴∠3+∠2=∠1+∠2=90°,即∠EFB =∴∠AFD=∠EFB. (4)又∵DF AFBF EF=∴△ADF∽△EBF.………………………………………………5分∴∠4=∠5.…………………………………………………………6分∵∠APE+∠4=∠3+∠5,∴∠APE=∠3=30°.………………………………………………7分【2011东城区一模】8. 如图,在矩形ABCD 中,AB =5,BC =4,E 、F 分别是AB 、AD 的中点.动点R 从点B 出发,沿B →C →D →F 方向运动至点F 处停止.设点R 运动的路程为x ,EFR △的面积为y ,当y 取到最大值时,点R 应运动到A .BC 的中点处B .C 点处C .CD 的中点处 D .D 点处答案:B .12. 如图,直线x y 33=,点1A 坐标为(1,0),过点1A 作x 轴的垂线交直线于点1B ,以原点O 为圆心,1OB 长为半径画弧交x 轴于点2A ;再过点2A 作x轴的垂线交直线于点2B ,以原点O 为圆心,2OB 长为半径画弧交x 轴于点3A ,…,按此做法进行下去,点4A 的坐标为( , );点n A ( , ).答案:938,0;1)332(-n ,024. 等边△ABC 边长为6,P 为BC 边上一点,∠MPN =60°,且PM 、PN 分别于边AB 、AC交于点E 、F .(1)如图1,当点P 为BC 的三等分点,且PE ⊥AB 时,判断△EPF 的形状; (2)如图2,若点P 在BC 边上运动,且保持PE ⊥AB ,设BP =x ,四边形AEPF 面积的y ,求y 与x 的函数关系式,并写出自变量x 的取值范围;(3)如图3,若点P 在BC 边上运动,且∠MPN 绕点P 旋转,当CF =AE =2时,求PE 的长.图1 图2 图3解:(1)△EPF 为等边三角形. --------------1分(2)设BP=x ,则CP =6-x.由题意可 △BEP 2x . △CFP 2)x -.△ABC 的面积为. 设四边形AEPF 的面积为y.∴ y =2x 2)x -=2+-自变量x 的取值范围为3<x <6. --------------4分(3)可证△EBP ∽△PCF.∴BP BECF CP=. 设BP=x , 则 (6)8x x -=. 解得 124,2x x ==.∴ PE 的长为4或 --------------7分25. 如图,已知二次函数y=ax 2+bx +8(a ≠0)的图像与x 轴交于点A (-2,0),B ,与y 轴交于点C ,tan ∠ABC =2.(1)求抛物线的解析式及其顶点D 的坐标; (2)设直线CD 交x 轴于点E .在线段OB的垂直平分线上是否存在点P ,使得经过点P 的直线PM 垂直于直线CD ,且与直线OP 的夹角为75°?若存在,求出点P 的坐标;若不存在,请说明理由;(3)过点B 作x 轴的垂线,交直线CD 于点F ,将抛物线沿其对称轴向上平移,使抛物线与线段EF 总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?解:(1)依题意,可知 C(0,8),则B(4,0)将A(-2,0),B(4,0)代入 y=ax 2+bx +8,⎩⎨⎧=++=+-.08416,0824b a b a 解得⎩⎨⎧=-=.2,1b a 228y x x ∴=-++配方得y2(1)9x =--+,顶点D (1,9). ---------3分 (2)假设满足条件的点P 存在,依题意设(2)P t ,,由(08)(19)C D ,,,求得直线CD 的解析式为8y x =+,它与x 轴的夹角为45 . 过点P 作PN ⊥y 轴于点N.依题意知,∠NPO=30°或∠NPO=60°.∵PN=2,∴ON=332或23. ∴存在满足条件的点P ,P 的坐标为(2,332 )和(2,23).-----------6分 (3)由上求得(80)(412)E F -,,,.当抛物线向上平移时,可设解析式为228(0)y x x m m =-+++>. 当8x =-时,72y m =-+. 当4x =时,y m =.720m ∴-+≤或12m ≤.由题意可得m 的范围为072m ∴<≤.∴ 抛物线最多可向上平移72个单位. -----------8分【2011朝阳区一模】8.已知二次函数y=ax 2+bx 的图象经过点A (-1,1),则ab 有 A .最大值 1 B .最大值2 C .最小值0 D .最小值41- 答案:D .分析:因为图象经过A 点,所以1a b -=,即1a b =+,所以2(1)ab b b b b =+=+21124b ⎛⎫=+- ⎪⎝⎭,当12b =-时,ab 有最小值为14-.12.如图,P 为△ABC 的边BC 上的任意一点,设BC=a ,当B 1、C 1分别为AB 、AC 的中点时,B 1C 1=a 21, 当B 2、C 2分别为BB 1、CC 1的中点时,B 2C 2=a 43,当B 3、C 3分别为BB 2、CC 2的中点时,B 3C 3=a 87,当B 4、C 4分别为BB 3、CC 3的中点时,B 4C 4=a 1615, 当B 5、C 5分别为BB 4、CC 4的中点时,B 5C 5=______, ……当B n 、C n 分别为BB n-1、CC n-1的中点时,则B n C n = ;设△ABC 中BC 边上的高为h ,则△PB n C n 的面积为______(用含a 、h 的式子表示).答案:a 3231, a n n 212-, ah n n 12212+- 分析:由题意知,B 5C 5∥BC ,555212AB AB -=,根据相似的性质,可得到B 5C 5=3132a , 同理可得到B n C n =a nn 212-.因为△ABC 中BC 边上的高为h ,所以△PB n C n 中B n C n 边上的高为h n 21,△PB n C n 的面积为ah h a n n n n n 122122121221+-=⨯-⨯. 24.已知抛物线()13)2(2++-+-=m x m x y .(1)求证:无论m 为任何实数,抛物线与x 轴总有交点;(2)设抛物线与y 轴交于点C ,当抛物线与x 轴有两个交点A 、B (点A 在点B 的 左侧)时,如果∠CAB 或∠CBA 这两角中有一个角是钝角,那么m 的取值范围 是 ;(3)在(2)的条件下,P 是抛物线的顶点,当△P AO 的面积与△ABC 的面积相等时,求该抛物线的解析式.B B (第12题图)解: (1)证明:∵()()()131422+⨯-⨯--=∆m m ……………………………………1分()042≥+=m ………………………………………………………… 2分∴无论m 为任何实数,抛物线与x 轴总有交点.(2) m <-1且m≠-4. ………………………………………………………………… 3分(3)解:令()013)2(2=++-+-=m x m x y ,解得x 1=m+1,x 2=-3. …………………………………………………………4分可求得顶点()⎪⎪⎭⎫⎝⎛+-44,222m m P . ①当A(m+1,0)、B(-3,0)时, ∵ABC PAO S S ∆∆=,∴()()()()13421441212+⨯--=+⨯+m m m m …………………………………5分 解得16-=m .∴45182---=x x y .……………………………………………………………6分 ②当A(-3,0)、B(m+1,0)时,同理得()()()[]13421443212+-⨯+=+⨯⨯m m m .…………………………7分 解得58-=m . ∴595182---=x x y .…………………………………………………………8分 25.已知:△ABC 和△ADE 都是等腰直角三角形,∠ABC =∠ADE =90°,点M 是CE 的中点,连接BM .(1)如图①,点D 在AB 上,连接DM ,并延长DM 交BC 于点N ,可探究得出BD 与BM 的数量关系为 ;(2)如图②,点D 不在AB 上,(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.图①图②解:(1)BD=2BM. ………………………………………………………………2分(2)结论成立.证明:连接DM,过点C作CF∥ED,与DM的延长线交于点F,连接BF,可证得△MDE≌△MFC.………………………………… 3分∴DM=FM, DE=FC.∴AD=ED=FC.由已知∠ADE=90°,∠ABC=90°,可证得∠1=∠2, ∠3=∠4.……………………………4分∵CF∥ED,∴∠1=∠FCM.∴∠BCF=∠4+∠FCM =∠3+∠1=∠3+∠2=∠BAD.∴△BCF≌△BAD. …………………………………………………………………………5分∴BF=BD,∠5=∠6.∴∠DBF=∠5+∠ABF=∠6+∠ABF=∠ABC=90°.∴△DBF是等腰直角三角形. ………………………………………………………………6分∵点M是DF的中点,则△BMD是等腰直角三角形.∴BD=2BM. ……………………………………………………………………………… 7分N M L图3图2图12n-1B 2C 2A CB1C 1C 1B 1CBA【2011丰台区一模】8. 一电工沿着如图所示的梯子NL 往上爬,当他爬到中点M 处时,由于地面太滑,梯子沿墙面与地面滑下,设点M 的坐标为(x ,y )(x>0),则y 与x 之间的函数关系用图象表示大致是A .B .C .D .答案:C12.已知在△ABC 中,BC=a.如图1,点B 1 、C 1分别是AB 、AC 的中点,则线段B 1C 1的长是_______;如图2,点B 1 、B 2 ,C 1 、C 2分别是AB 、AC 的三等分点,则线段B 1C 1 + B 2C 2的值是__________;如图3, 点12......、、、n B B B ,12......、、、n C C C 分别是AB 、AC 的(n+1)等分点,则线段B 1C 1 + B 2C 2+……+ B n C n 的值是 ______.答案:1,2a a ,12naDC B A A B C DA B C D x24.已知:如图,在□ EFGH 中,点F 的坐标是(-2,-1),∠EFG=45°. (1)求点H 的坐标;(2)抛物线1C 经过点E 、G 、H ,现将1C 向左平移使之经过点F ,得到抛物线2C ,求抛物线2C 的解析式;(3)若抛物线2C 与y 轴交于点A ,点P 在抛物线2C 的对称轴上运动.请问:是否存在以AG 为腰的等腰三角形AGP ?若存在,求出点P 的坐标;若不存在,请说明理由.解:(1)∵在□ABCD 中∴EH=FG=2 ,G (0,-1)即OG=1………………………1’ ∵∠EFG=45°∴在Rt △HOG 中,∠EHG=45° 可得OH=1∴H (1,0)……………………………………………………2’ (2)∵OE=EH-OH=1 ∴E (-1,0),设抛物线1C 解析式为1y =2ax +bx+c∴代入E 、G 、H 三点,∴a =1 ,b=0,,c=-1 ∴1y =2x -1……………………………………………………3’依题意得,点F 为顶点,∴过F 点的抛物线2C 解析式是2y =2(+2x )-1…………4’(3)∵抛物线2C 与y 轴交于点A ∴A (0,3),∴AG=4 情况1:AP=AG=4过点A 作AB ⊥对称轴于B ∴AB=2在Rt △PAB 中,BP=∴1P(-2,3+或2P(-2,3-……………………………6’ 情况2:PG=AG=4 同理可得:3P(-2,-1+或4P(-2,-1-…………………8’∴P 点坐标为(-2,3+或(-2,3-或(-2,-1+或(-2,-1-.25.已知:在△ABC 中,BC=a ,AC=b ,以AB 为边作等边三角形ABD. 探究下列问题:(1)如图1,当点D 与点C 位于直线AB 的两侧时,a=b=3,且∠ACB=60°,则CD= ;(2)如图2,当点D 与点C 位于直线AB 的同侧时,a=b=6,且∠ACB=90°,则CD= ;(3)如图3,当∠ACB 变化,且点D 与点C 位于直线AB 的两侧时,求 CD 的最大值及相应的∠ACB 的度数.图1 图2 图3解:(1)33;…………………………………………1’(2)2363 ; …………………………………………2’(3)以点D 为中心,将△DBC 逆时针旋转60°,则点B 落在点A ,点C 落在点E.联结AE,CE ,∴CD=ED ,∠CDE=60°,AE=CB= a , ∴△CDE 为等边三角形,∴CE=CD. …………………………………………4’当点E 、A 、C 不在一条直线上时,有CD=CE<AE+AC=a +b ; 当点E 、A 、C 在一条直线上时, CD 有最大值,CD=CE=a +b ;此时∠CED=∠BCD=∠ECD=60°,∴∠ACB=120°,……………………7’ 因此当∠ACB=120°时,CD 有最大值是a +b .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
十九、创新题1.(2011朝阳一模理8)定义区间(, )a b ,[, )a b ,(, ]a b ,[, ]a b 的长度均为d b a =-,多个区间并集的长度为各区间长度之和,例如, (1, 2)[3, 5) 的长度(21)(53)d =-+-=. 用[]x 表示不超过x 的最大整数,记{}[]x x x =-,其中x ∈R .设()[]{}f x x x =⋅,()1g x x =-,若用123,,d d d 分别表示不等式()()f x g x >,方程()()f x g x =,不等式()()f x g x <解集区间的长度,则当02011x ≤≤时,有 (B )(A )1231, 2, 2008d d d === (B )1231, 1, 2009d d d === (C )1233, 5, 2003d d d === (D )1232, 3, 2006d d d ===2.(2011朝阳一模理14)对于各数互不相等的整数数组),,,,(321n i i i i (n 是不小于3的正整数),对于任意的,{1,2,3,,}p q n ∈ ,当q p <时有q p i i >,则称p i ,q i 是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为该数组的“逆序数”,则数组(2,4,3,1)中的逆序数等于 4 ;若数组123(,,,,)n i i i i 中的逆序数为n ,则数组11(,,,)n n i i i - 中的逆序数为232n n - .3(2011丰台一模理8).对于定义域和值域均为[0,1]的函数f (x ),定义1()()f x f x =,21()(())f x f f x =,…,1()(())n n f x f f x -=,n =1,2,3,….满足()n f x x =的点x ∈[0,1]称为f 的n 阶周期点.设12,0,2()122,1,2x x f x x x ⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩则f 的n 阶周期点的个数是(C)(A) 2n (B) 2(2n -1) (C) 2n(D) 2n 24(2011丰台一模理14).将全体正奇数排成一个三角形数阵: 13 57 9 11 13 15 17 19……按照以上排列的规律,第n 行(n ≥3)从左向右的第3个数为.n 2-n +5 .5(2011海淀一模理14).如图,线段AB =8,点C 在线段AB 上,且A C =2,P 为线段C B 上一动点,点A 绕点C 旋转后与点B 绕点P 旋转后重合于点D .设C P =x , △C PD 的面积为()f x .则()f x 的定义域为 (2,4) ; '()f x 的零点是 3 .6(2011门头沟一模理14).设S 为非空数集,若,x y S ∀∈,都有,,x y x y xy S +-∈,则称S为封闭集.下列命题①实数集是封闭集;②全体虚数组成的集合是封闭集; ③封闭集一定是无限集;④若S 为封闭集,则一定有0S ∈;⑤若,S T 为封闭集,且满足S U T ⊆⊆,则集合U 也是封闭集, 其中真命题是 ①④ .7(2011石景山一模理13).已知两定点)0,1(-M ,)0,1(N ,若直线上存在点P ,使得4=+PN PM ,则该直线为“A 型直线”.给出下列直线,其中是“A 型直线”的是 ① ④ .①1+=x y ②2=y ③3+-=x y ④32+-=x y8(2011朝阳一模文14).对于各数互不相等的整数数组),,,,(321n i i i i (n 是不小于2的正整数),对于任意,{1,2,3,,}p q n ∈ ,当q p <时有q p i i >,则称p i ,q i 是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为该数组的“逆序数”,则数组(2,4,3,1)中的逆序数等于 4 .9(2011丰台文8).若函数()f x 满足条件:当12, [1,1]x x ∈-时,有1212|()()|3||f x f x x x -≤-成立,则称()f x ∈Ω.对于函数3()g x x =,1()2h x x =+,有(C)(A) ()g x ∈Ω且()h x ∉Ω (B) ()g x ∉Ω且()h x ∈Ω (C) ()g x ∈Ω且()h x ∈Ω (D) ()g x ∉Ω且()h x ∉Ω10(2011丰台文14).用[x ]表示不超过x 的最大整数,如[1.8]=1.对于下面关于函数2()([])f x x x =-的四个命题:①函数()y f x =的定义域为R ,值域为[0,1]; ②函数()y f x =的图象关于y 轴对称; ③函数()y f x =是周期函数,最小正周期为1; ④函数()y f x =在(0,1)上是增函数.其中正确命题的序号是③④ .(写出所有正确命题的序号)11(2011海淀一模文14).如图,线段AB =8,点C 在线段AB 上,且A C =2,P 为线段C B 上一动点,点A 绕点C 旋转后与点B 绕点P 旋转后重合于点D .设C P =x , △C PD 的面积为()f x .则()f x 的定义域为____(2,4) ,____;()f x 的最大值为_ 22_______.解答1(2011西城一模理20).(本小题满分13分)定义=),,,(21n a a a τ12231||||||n n a a a a a a --+-++- 为有限项数列{}n a 的波动强度.(Ⅰ)当(1)nn a =-时,求12100(,,,)a a a τ ;(Ⅱ)若数列,,,a b c d 满足()()0a b b c -->,求证:(,,,)(,,,)a b c d a c b d ττ≤; (Ⅲ)设{}n a 各项均不相等,且交换数列{}n a 中任何相邻两项的位置,都会使数列的波动强度增加,求证:数列{}n a 一定是递增数列或递减数列.(Ⅰ)解:12100122399100(,,,)||||||a a a a a a a a a τ=-+-++- ………………1分222299198=+++=⨯= . (3)分(Ⅱ)证明:因为(,,,)||||||a b c d a b b c c d τ=-+-+-,A C P BD(,,,)||||||a c b d a c c b b d τ=-+-+-,所以(,,,)(,,,)||||||||a b c d a c b d a b c d a c b d ττ-=-+-----. (4)分因为()()0a b b c -->,所以a b c >>,或a b c <<.若a b c >>,则(,,,)(,,,)||||a b c d a c b d a b c d a c b d ττ-=-+--+--||||c b c d b d =-+---当b c d >>时,上式()2()0c b c d b d c b =-+---=-<,当b d c ≥≥时,上式()2()0c b d c b d d b =-+---=-≤, 当d b c >>时,上式()0c b d c d b =-+---=,即当a b c >>时,(,,,)(,,,)0a b c d a c b d ττ-≤. (6)分若a b c <<,则(,,,)(,,,)||||a b c d a c b d b a c d c a b d ττ-=-+--+--,||||0b c c d b d =-+---≤.(同前)所以,当()()0a b b c -->时,(,,,)(,,,)a b c d a c b d ττ≤成立. …………………7分(Ⅲ)证明:由(Ⅱ)易知对于四个数的数列,若第三项的值介于前两项的值之间,则交换第二项与第三项的位置将使数列波动强度减小或不变.(将此作为引理)下面来证明当12a a >时,{}n a 为递减数列.(ⅰ)证明23a a >.若231a a a >>,则由引理知交换32,a a 的位置将使波动强度减小或不变,与已知矛盾. 若2a a a >>31,则1212212121(,,)||||||||(,,)a a a a a a a a a a a a a a ττ=-+->-+-=3333,与已知矛盾.所以,321a a a >>. ………………………9分(ⅱ)设12(32)i a a a i n >>>≤≤- ,证明1i i a a +>.若i i i a a a >>+-11,则由引理知交换1,+i i a a 的位置将使波动强度减小或不变,与已知矛盾.若i i i a a a >>-+11,则211211(,,,)(,,,)i i i i i i i i a a a a a a a a ττ--+--+=,与已知矛盾. 所以,1+>i i a a . …………………11分(ⅲ)设121n a a a ->>> ,证明1n n a a ->. 若1n n a a ->,考查数列121,,,,n n a a a a - ,则由前面推理可得122n n n a a a a -->>>> ,与121n a a a ->>> 矛盾.所以,1n n a a ->. …………………12分综上,得证.同理可证:当12a a <时,有{}n a 为递增数列. ……………………13分2(2011西城一模文20).(本小题满分13分)将n ,,3,2,1 这n 个数随机排成一列,得到的一列数n a a a ,,,21 称为n ,,3,2,1 的一个排列.定义=),,,(21n a a a τ||||||13221n n a a a a a a -+-+-- 为排列n a a a ,,,21 的波动强度.(Ⅰ)当3=n 时,写出排列321,,a a a 的所有可能情况及所对应的波动强度; (Ⅱ)当10=n 时,求1210(,,,)a a a τ 的最大值,并指出所对应的一个排列; (Ⅲ)当10=n 时,在一个排列中交换相邻两数的位置称为一次调整,若要求每次调整时波动强度不增加,问对任意排列1210,,,a a a ,是否一定可以经过有限次调整使其波动强度降为9;若可以,给出调整方案,若不可以,请给出反例并加以说明.解:(Ⅰ)3=n 时,排列321,,a a a 的所有可能为1,2,3;1,3,2;2,1,3;2,3,1;3,1,2;3,2,1. (2)分2)3,2,1(=τ;3)2,3,1(=τ;3)3,1,2(=τ;3)1,3,2(=τ;3)2,1,3(=τ;2)1,2,3(=τ. ………………4分(Ⅱ)1210(,,,)a a a τ= 1223910||||||a a a a a a -+-++- 上式转化为1223910a a a a a a ±±±±±±± ,在上述18个±中,有9个选正号,9个选负号,其中110,a a 出现一次,239,,,a a a 各出现两次.………………6分所以1210(,,,)a a a τ 可以表示为9个数的和减去9个数的和的形式, 若使1210(,,,)a a a τ 最大,应使第一个和最大,第二个和最小. 所以1210(,,,)a a a τ 最大为:(10109988776)(112233445)49++++++++-++++++++=. (8)分所对应的一个排列为:5,7,1,8,2,9,3,10,4,6.(其他正确的排列同等给分) ………9分(Ⅲ)不可以.例如排列10,9,8,7,1,2,3,4,5,6,除调整1,2外,其它调整都将使波动强度增加,调整1,2波动强度不变. ……………11分所以只能将排列10,9,8,7,1,2,3,4,5,6调整为排列10,9,8,7,2,1,3,4,5,6. 对于排列10,9,8,7,2,1,3,4,5,6,仍然是除调整2,1外,其它调整都将使波动强度增加,所以仍只能调整1,2两个数字.如此不断循环下去,不可能经过有限次调整使其波动强度降为9. ……………13分3(2011东城一模理20) (本小题共14分)对于)2(≥∈n n *N ,定义一个如下数阵:⎪⎪⎪⎪⎪⎭⎫⎝⎛=nn n n n n nna a a a a a a a a A212222111211 其中对任意的n i ≤≤1,n j ≤≤1,当i 能整除j 时,1=ij a ;当i 不能整除j 时,0=ij a .设nj j j ni ija a a aj t +++==∑= 211)(.(Ⅰ)当6=n 时,试写出数阵66A 并计算∑=61)(j j t ;(Ⅱ)若][x 表示不超过x 的最大整数,求证:∑=nj j t 1)(∑==ni in1][;(Ⅲ)若∑==nj j t nn f 1)(1)(,dx xn g n⎰=11)(,求证:()1()()1g n f n g n -<<+.(Ⅰ)解:依题意可得,⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=10001000000100010010010101011111166A .14423221)(61=+++++=∑=j j t .(Ⅱ)解:由题意可知,)(j t 是数阵nn A 的第j 列的和,因此∑=nj j t 1)(是数阵nn A 所有数的和.而数阵nn A 所有数的和也可以考虑按行相加.对任意的n i ≤≤1,不超过n 的倍数有i 1,i 2,…,i i n][.因此数阵nn A 的第i 行中有][in 个1,其余是0,即第i 行的和为][in.所以∑=nj j t 1)(∑==ni in 1][. (Ⅲ)证明:由][x 的定义可知,ini n i n≤<-][1, 所以∑∑∑===≤<-ni ni ni in i nn i n 111][.所以∑∑==≤<-ni ni i n f i111)(11.考查定积分dx xn⎰11,将区间],1[n 分成1-n 等分,则dx xn⎰11的不足近似值为∑=ni i21,dx xn⎰11的过剩近似值为∑-=111n i i.所以∑=ni i 21dx xn⎰<11∑-=<111n i i.所以111-∑=ni i)(n g <∑=<ni i11.所以<-1)(n g ∑=<-ni n f i 1)(11<≤∑=ni i111)(+n g .所以()1()()1g n f n g n -<<+. 4(2011东城一模文20)(本小题共13分)对于)2(≥∈n n *N ,定义一个如下数阵:⎪⎪⎪⎪⎪⎭⎫⎝⎛=nn n n n n nna a a a a a a a a A212222111211 其中对任意的n i ≤≤1,n j ≤≤1,当i 能整除j 时,1=ij a ;当i 不能整除j 时,0=ij a .(Ⅰ)当4n =时,试写出数阵44A ;(Ⅱ)设nj j j ni ija a a aj t +++==∑= 211)(.若][x 表示不超过x 的最大整数,求证:∑=nj j t 1)(∑==ni in1][.解:(Ⅰ)依题意可得,4411110101001001A ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭……………………4分(Ⅱ)由题意可知,)(j t 是数阵nn A 的第j 列的和,因此∑=nj j t 1)(是数阵nn A 所有数的和.而数阵nn A 所有数的和也可以考虑按行相加.对任意的n i ≤≤1,不超过n 的倍数有i 1,i 2,…,i in][.因此数阵nn A 的第i 行中有][in 个1,其余是0,即第i 行的和为][in .所以∑=nj j t 1)(∑==ni in 1][.……………………13分 5(2011丰台一模理20).(本小题共13分)已知123{(,,,,)n n S A A a a a a == ,0i a =或1,1,2,,}i n = (2)n ≥,对于,n U V S ∈,(,)d U V 表示U 和V 中相对应的元素不同的个数.(Ⅰ)令(0,0,0,0,0)U =,存在m 个5V S ∈,使得(,)2d U V =,写出m 的值;(Ⅱ)令0(0,0,0,,0)n W =个,若,n U V S ∈,求证:(,)(,)(,)d U W d V W d U V +≥;(Ⅲ)令123(,,,,)n U a a a a = ,若n V S ∈,求所有(,)d U V 之和.解:(Ⅰ)2510C =; ………3分(Ⅱ)证明:令123(,,)n u a a a a =……,123(,,)n v b b b b =……∵0i a =或1,0i b =或1;当0i a =,0i b =时,||i a +||0i b =||i i a b =- 当0i a =,1i b =时,||i a +||1i b =||i i a b =- 当1i a =,0i b =时,||i a +||1i b =||i i a b =- 当1i a =,1i b =时,||i a +||2i b =||0i i a b ≥-= 故||i a +||i b ||i i a b ≥-∴(,)(,)d u w d v w +=123()n a a a a ++ ++123()n b b b b +++ ++123(||||||)n a a a a =++ |++|123(||||||)n b b b b +++ |++|112233(||||||)n n a b a b a b a b ≥-+-+-- |++|(,)d u v = ………8分(Ⅲ)解:易知n S 中共有2n 个元素,分别记为(1,2,,2)nk v k = 123(,,)n v b b b b =……∵0i b =的k v 共有12n -个,1i b =的k v 共有12n -个.∴21(,)nk k d u v =∑=1111111122(2|0|2|1|2|0|2|120|21|)n n n n n n n n a a a a a a -------+-+-+--- |++|+|=12n n - ……13分∴21(,)nk k d u v =∑=12n n - . 法二:根据(Ⅰ)知使(,)k d u v r =的k v 共有rn C 个∴21(,)nk k d u v =∑=012012nn n n n C C C n C ++++21(,)nkk d u v=∑=12(1)(2)0n n n n nnn n C n C n C C --+-+-++两式相加得 21(,)nkk d u v=∑=12n n -6(2011丰台文20).(本小题共13分)已知123{(,,,,)n n S A A a a a a == ,0i a =或1,1,2,,}i n = (2)n ≥,对于,n U V S ∈,(,)d U V 表示U 和V 中相对应的元素不同的个数.(Ⅰ)如果(0,0,0,0)U =,存在m 个4V S ∈,使得(,)2d U V =,写出m 的值; (Ⅱ)如果0(0,0,0,,0)n W =个,,n U V S ∈,求证:(,)(,)(,)d U W d V W d U V +≥.解:(Ⅰ)6. ……………………4分(Ⅱ)证明:令123(,,,,)n U a a a a = ,123(,,,,)n V b b b b = .∵0i a =或1,0i b =或1;当0i a =,0i b =时,||i a +||0i b =||i i a b =-; 当0i a =,1i b =时,||i a +||1i b =||i i a b =-; 当1i a =,0i b =时,||i a +||1i b =||i i a b =-; 当1i a =,1i b =时,||i a +||2i b =||0i i a b ≥-=. 故||i a +||i b ||i i a b ≥-.∴(,)(,)d U W d V W +=123()n a a a a ++ ++123()n b b b b +++ ++123(||||||)n a a a a =++ |++|123(||||||)n b b b b +++ |++|112233(||||||)n n a b a b a b a b ≥-+-+-- |++|(,)d U V = ……………- 11 - ………13分法二:记U V 、中对应项同时为0的项的个数为p ,对应项同时为1的项的个数为q ,则对应项一个为1,一个为0的项的个数为n p q --;()p q N p q n ∈+≤、,. (,)d U W 即是U 中1的个数,(,)d V W 即是V 中1的个数,(,)d U V 是U V 、中对应项一个为1,一个为0的项的个数.于是有(,)d U V n p q =--.U V 、中1一共有2()q n p q +--个,即(,)(,)d U W d V W n p q +=-+. 所以有(,)(,)(,)20d U W d V W d U V q +-=≥,于是(d U +≥. ……………………13分。
