卷积积分图解法
合集下载
卷积积分及零状态响应的卷积计算法.
t
e RC
RCT
T RC t
e RCT 0
RC T RC
(t 0)
u0T T RC
e
t T
t
e RC
ε(t)
➢卷积积分的图解
求f(t)与h(t)的卷积,实质上是求一个新函数
f()h(t)在 由0到t的区间内的定积分。根据定积分的 几何意义,函数在0到t区间内的定积分值,决定于被积 函数f()h(t)的曲线在该区间内与 轴之间所限定的面
§4-6 卷积积分及零状态响 应的卷积计算法
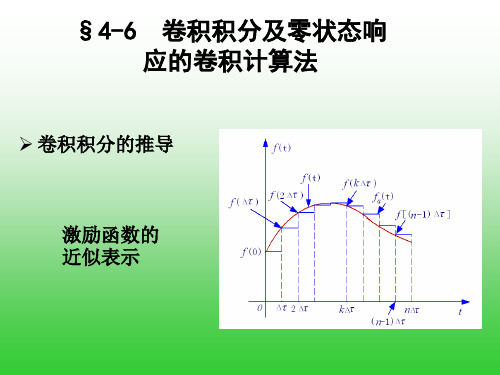
➢ 卷积积分的推导
激励函数的 近似表示
f (t) fa (t) f (0)ε(t) ε(t )
f ( )ε(t ) ε(t 2 )
f (2 )ε(t 2 ) ε(t 3 )
f (n 1) ε(t (n 1) ) ε(t n )
解: [e tε(t)] ε(t) t e ε( )ε(t )d 0
t ed 0
1 e t
0
(t 0)
(t 0)
1 1 e t ε(t)
例2 设图示RC串联电路中电压源的电压
t
u(t) u0e T ε(t)
求零状态响应电压uC(t)。
解: 用卷积积分公式求uC(t),应先求冲激响应
如按
t
r(t) h( ) f (t ) d h(t) f (t)
0
当 0<t <1 时
计算。
r(t ) te ε( )d t e d 1 et
0
0
当 t >1时
r(t ) t e ε( )d t 1
t e d e(t1) et t 1 返回
注意ቤተ መጻሕፍቲ ባይዱ分上、下限
卷积积分基础

f
(i 2
j
)
(t
)
f (t)
f1(1) (t)
f (1) 2
(t
)
d dt
f1(t)
t
f2 ()d
常数信号(直流信号) f (t) E ( t ) 经微分后为零,需特殊考虑, 不能用微分性质
15
三、与冲激函数或阶跃函数的卷积
f (t) (t) f (t)
f (t) (t) ( ) f (t )d f (t)
1 1
2
1
1 2
(t
)d
3t 3 4 16
7
r(t) e(t) h(t) e( )h(t )d
h(t )
e( )
t
(3) 1 t 3 2
e(t) h(t) 3 t 3 4 16
(4) 3 t 3
e( )
2
h(t )
t
e(t) h(t) 1 1 1 (t )d
t2
4
t 4
1 16
( 1 t 1) 2
r(t) e(t) h(t)
r(t)
43
t
3 16
(1 t 3) 2
t2
t
3
( 3 t 3)
4 2 4 2
0
其它
t
卷积结果所占的时宽等于两个函数各自时宽的总和
10
P842 14(1) f (t) u(t) u(t 1),求s(t) f (t) f (t)
(1) t 0时, s(t) 0
(2)
0 t 1时,
s(t)
t
d t
0
(3)
1 t 2时,
s(t)
1
卷积计算(图解法)

(1) n<0
x(m) m 0 4 h(n-m) m n-6 n0
y(n) = x(n) ∗ h(n) = 0
x(m) m
(2)在0≤n≤4区间上
0
4 h(n-m) m
n-6 0 n 4
∴ y(n) = ∑ x(m)h(n − m) = ∑1⋅ a
m=0 n m=0
n
n
n−m
=a
n
m=0
∑a
−m
1− a =a −1 1− a
n
−( n+1)
1− a =1− a
1+n
x(m)
(3)在4<n≤6区间上
m 0 4 h(n-m) m n-6 0
1+n
∴ y(n) = ∑x(m)h(n − m)
m=0
4
= ∑1⋅ a
m=0 n
4
n−m
=a
n
m=0
∑a
n−4
4
−m
4 6 n
1− a a −a =a = −1 1− a 1− a
−(1+4)
x(m) m 0 4 h(n-m) m 0 n-6
7
(4)在6<n≤10区间上
∴ y(n) = =
m=n−6
∑x(m)h(n − m)
=a
n m=n−6 −( 4+1)
n
m=n−6
∑1⋅ a
n
n
n−m
∑a
=
4
−m
6
n
10
=a
a
−( n−6)
−a −1 1− a
a
n−4
−a 1− a
综合以上结果, 可归纳如下: 综合以上结果,y(n)可归纳如下: 可归纳如下
电路原理课件-卷积积分

3
7) t≥7时,
y(t ) 0
注意:积分上下限应由被 积函数存在的时域范围的 上下限确定。
卷积积分在电路分析中的应用
例1、电路如图所示,uS=15e-0.25t(t)V。采用卷积计算uC。
解:以uC为响应,求单位阶跃响应
uC (0 ) uC (0 ) 0
uCf 40 1 0.5V 40 40
t t
t t
t 0
d dt t t
卷积积分上下限分析
t
0
r t h t f t f t h t
卷积符合交换律
δ t f t δ f t dτ τ τ
k 0
f (t ) f a (t )
f ( k ) ( t k ) ( t ( k 1) )
k 0 n 1
k 0 n 1
k 0
n 1
(t k ) (t (k 1) ) f (k )
例2、电路如图,R=10,L=1H,激励uS的波形如图 所示,求零状态响应i(t)。
解:以电流i 为响应,求单位阶跃响应为:
R t 1 g( t ) (1 e L ) ( t ) R 0.1(1 e 10 t ) ( t )
则单位冲激响应为:
dg( t ) h (t ) e 10 t ( t ) dt
40 40 RC 0.05 1s 40 40
uC ( t ) uCf (1 e ) ( t ) 0.5(1 e t ) ( t )V
t
单位阶跃响应为:
g(t ) 0.5(1 e t ) (t )
7) t≥7时,
y(t ) 0
注意:积分上下限应由被 积函数存在的时域范围的 上下限确定。
卷积积分在电路分析中的应用
例1、电路如图所示,uS=15e-0.25t(t)V。采用卷积计算uC。
解:以uC为响应,求单位阶跃响应
uC (0 ) uC (0 ) 0
uCf 40 1 0.5V 40 40
t t
t t
t 0
d dt t t
卷积积分上下限分析
t
0
r t h t f t f t h t
卷积符合交换律
δ t f t δ f t dτ τ τ
k 0
f (t ) f a (t )
f ( k ) ( t k ) ( t ( k 1) )
k 0 n 1
k 0 n 1
k 0
n 1
(t k ) (t (k 1) ) f (k )
例2、电路如图,R=10,L=1H,激励uS的波形如图 所示,求零状态响应i(t)。
解:以电流i 为响应,求单位阶跃响应为:
R t 1 g( t ) (1 e L ) ( t ) R 0.1(1 e 10 t ) ( t )
则单位冲激响应为:
dg( t ) h (t ) e 10 t ( t ) dt
40 40 RC 0.05 1s 40 40
uC ( t ) uCf (1 e ) ( t ) 0.5(1 e t ) ( t )V
t
单位阶跃响应为:
g(t ) 0.5(1 e t ) (t )
2-3-卷积积分

− 2t
= 6∫ e
0
t
− 2τ
dτ ε (t ) = 3(1 − e
) ε (t )
f1 (t ) ∗ f 3 (t ) = =
∫
∞
−∞
f1 (τ ) f 3 (t − τ )dτ
∫
∞
−∞
3e ε (τ ) ⋅ 2ε (t − τ − 2)dτ
− 2τ
=6
∫
t −2
e
− 2τ
0
dτ = 3(1 − e
问:
y2 (t ) = [ f (t − t1 )ε (t − t1 )]∗ [h(t − t 2 )ε (t − t 2 )]
y1 (t ) = [ f (t − t0 )ε (t − t0 )]∗ [h(t )ε (t )]
2)反因果信号 )
=
t
y (t ) = [ f (t )ε (− t )]∗ [h(t )ε (t )]
∫
(1)翻转 ) (2)平移 ) (3)相乘 ) (4)积分 )
f1 (τ ) → f1 (−τ )或 : f2 (τ ) → f2 (−τ )
f1(−τ ) → f1(t −τ )或f2 (−τ ) → f2 (t −τ )
f1 ( t − τ ) f 2 (τ )或f 2 ( t − τ ) f1 (τ )
(1)
=
-1 0
1 t o t0 t o t 0-1 t 0 t 0+1 t
图 2.2 – 3 例2.2 - 3图 图
例2.4-3 周期性单位冲激序列
δ T (t ) =
试求
f (t ) = f0 (t ) ∗ δ T (t )
∞ m = −∞
m = −∞
= 6∫ e
0
t
− 2τ
dτ ε (t ) = 3(1 − e
) ε (t )
f1 (t ) ∗ f 3 (t ) = =
∫
∞
−∞
f1 (τ ) f 3 (t − τ )dτ
∫
∞
−∞
3e ε (τ ) ⋅ 2ε (t − τ − 2)dτ
− 2τ
=6
∫
t −2
e
− 2τ
0
dτ = 3(1 − e
问:
y2 (t ) = [ f (t − t1 )ε (t − t1 )]∗ [h(t − t 2 )ε (t − t 2 )]
y1 (t ) = [ f (t − t0 )ε (t − t0 )]∗ [h(t )ε (t )]
2)反因果信号 )
=
t
y (t ) = [ f (t )ε (− t )]∗ [h(t )ε (t )]
∫
(1)翻转 ) (2)平移 ) (3)相乘 ) (4)积分 )
f1 (τ ) → f1 (−τ )或 : f2 (τ ) → f2 (−τ )
f1(−τ ) → f1(t −τ )或f2 (−τ ) → f2 (t −τ )
f1 ( t − τ ) f 2 (τ )或f 2 ( t − τ ) f1 (τ )
(1)
=
-1 0
1 t o t0 t o t 0-1 t 0 t 0+1 t
图 2.2 – 3 例2.2 - 3图 图
例2.4-3 周期性单位冲激序列
δ T (t ) =
试求
f (t ) = f0 (t ) ∗ δ T (t )
∞ m = −∞
m = −∞
计算卷积的方法.ppt

' t
dg ( t ) r ( t ) e ( t ) h ( t ) e ( t ) dt
de (t) *g(t) dt
e ( t ) e ( t ) u ( t )
de ( t ) d ( e ( t ) u ( t ))de ( t ) u ( t ) e ( t ) ( t ) dt dt dt
方法一:
h (t )
t
e( )
0
*
0
h(t ) 非零值下限是- 卷积分下限是零 u( ) 非零值下限是 0
h(t ) 非零值上限是 t 卷积分上限是 t u( ) 非零值上限是
若两个函数的左边界分别为tl1,tl2,右边界分别为 tr1,tr2,积分的 下限为max[tl1,tl2];积分的上限为min[tr1,tr2].
f f ( ) f ( t ) d 1 2 1 2 f
0 t-2 1
t
3 . if 1 t 2
1
b ab 2 ab 2 t a ( t ) d ( t ) 0 t 0 2 4 4
t
a t-2 0 t 1
ab (2 t 1 ) 4
2.各分段内卷积积分限的确定 。
分解成单位阶跃分量之和
f (t1 )
f( t t ) 1 1 f ( 0)
t1
t1
u ( t ) g ( t ) DaHarma ln tegr
*.Duharmal integral
r(t) e(0 )g(t) e ( )g(t )d 0
1
b ab 2 1 f f a ( t ) d ( t ) 1 2 0 02 4
dg ( t ) r ( t ) e ( t ) h ( t ) e ( t ) dt
de (t) *g(t) dt
e ( t ) e ( t ) u ( t )
de ( t ) d ( e ( t ) u ( t ))de ( t ) u ( t ) e ( t ) ( t ) dt dt dt
方法一:
h (t )
t
e( )
0
*
0
h(t ) 非零值下限是- 卷积分下限是零 u( ) 非零值下限是 0
h(t ) 非零值上限是 t 卷积分上限是 t u( ) 非零值上限是
若两个函数的左边界分别为tl1,tl2,右边界分别为 tr1,tr2,积分的 下限为max[tl1,tl2];积分的上限为min[tr1,tr2].
f f ( ) f ( t ) d 1 2 1 2 f
0 t-2 1
t
3 . if 1 t 2
1
b ab 2 ab 2 t a ( t ) d ( t ) 0 t 0 2 4 4
t
a t-2 0 t 1
ab (2 t 1 ) 4
2.各分段内卷积积分限的确定 。
分解成单位阶跃分量之和
f (t1 )
f( t t ) 1 1 f ( 0)
t1
t1
u ( t ) g ( t ) DaHarma ln tegr
*.Duharmal integral
r(t) e(0 )g(t) e ( )g(t )d 0
1
b ab 2 1 f f a ( t ) d ( t ) 1 2 0 02 4
信号与系统-23-§卷积积分

3.相乘:f1( ) f2 (t )
4.乘积的积分:
f1(
).
f2(t
)d
课堂练习
f1(t)=(t-1)2, f2(t)=δ(t-4),请分别用公式 法及作图法计算: y (t) = f1(t)* f2(t)
卷积计算小结
由于信号存在时间的局限性,卷积积分中积 分限的确定非常关键。
函数式复杂时,用图形分段求出积分限方便准确。
f1( )
f2
(t
)d
为f1(t)与f2(t)的卷积,记为f(t)= f1(t)*f2(t)
yzs(t)
f ( )h(t ) d f (t) * h(t)
二、卷积的计算
f
t
f1
f 2 t
d
1. f1(t) f1( ),
2. f2 (t) f2 ( ) 倒置 f2 ( ) 时延t f2 (t )
§2.3 卷积积分
• 卷积积分
• 卷积的图解法
Yun Liu, Information College, Zhongkai University of Agriculture and Engineering
一、卷积积分
1.信号的时域分解
任意信号f(t)可表示为f源自tftd
2 .任意信号作用下的零状态响应
积分
f (t) LTI系统 yzs(t)
本质
零状态
δ(t) 由时不变性: δ(t -τ)
由齐次性: f (τ)δ(t -τ)
由叠加性:
f
( ) (t
) d
‖
f (t)
h(t) h(t -τ)
f (τ) h(t -τ)
f
( )h(t ) d
卷积积分的运算

§2.5 卷积积分的运算和图解
y(t) x(t) h(t) x( )h(t )d
1)将x(t)和h(t)中的自变量由t改为,成为函数的自 变量; 2)把其中一个信号翻转、平移;
h( ) 翻转h( ) 平移th(( t)) h(t )
3)将x() 与h(t )相乘;对乘积后的图形积分。
例11:画出下列系统的模拟图
y(t) 5 y(t) 3 y(t) 3x(t) x(t)
例:引入辅助函数q(t)
q(t) 5q(t) 3q(t) x(t) 利用微分特性法 y(t) 3q(t) q(t)
q(t) x(t) 5q(t) 3q(t)
例12:根据系统的模拟图写出其微分方程模型
et
d
r t
d
et
rt
et
rt
et
T rt
rt de(t)
dt
t
r(t) e(t)dt
rt et rt et T
例10:试用系统模拟图来表示下列方程所描述的LTI系统
a2 y(t) a1 y(t) a0 y(t) b2 x(t) b1 x(t) b0 x(t) a2 y(t) b2 x(t) b1 x(t) b0 x(t) a1 y(t) a0 y(t)
y(t )
1 a2
[b2 x(t )
b1 x(t )
b0 x(t )
a1
y(t)
a0
y(t )]
y(t )
1 a2
[b2 x(t )
b1 x(1) (t )
b0 x(2) (t ) a1 y(1) (t ) a0 y(2) (t )]
根据该式,可直接画出系统模拟图
y(t)
y(t) x(t) h(t) x( )h(t )d
1)将x(t)和h(t)中的自变量由t改为,成为函数的自 变量; 2)把其中一个信号翻转、平移;
h( ) 翻转h( ) 平移th(( t)) h(t )
3)将x() 与h(t )相乘;对乘积后的图形积分。
例11:画出下列系统的模拟图
y(t) 5 y(t) 3 y(t) 3x(t) x(t)
例:引入辅助函数q(t)
q(t) 5q(t) 3q(t) x(t) 利用微分特性法 y(t) 3q(t) q(t)
q(t) x(t) 5q(t) 3q(t)
例12:根据系统的模拟图写出其微分方程模型
et
d
r t
d
et
rt
et
rt
et
T rt
rt de(t)
dt
t
r(t) e(t)dt
rt et rt et T
例10:试用系统模拟图来表示下列方程所描述的LTI系统
a2 y(t) a1 y(t) a0 y(t) b2 x(t) b1 x(t) b0 x(t) a2 y(t) b2 x(t) b1 x(t) b0 x(t) a1 y(t) a0 y(t)
y(t )
1 a2
[b2 x(t )
b1 x(t )
b0 x(t )
a1
y(t)
a0
y(t )]
y(t )
1 a2
[b2 x(t )
b1 x(1) (t )
b0 x(2) (t ) a1 y(1) (t ) a0 y(2) (t )]
根据该式,可直接画出系统模拟图
y(t)
