matlab小论文
Matlab的应用-论文.docx

MATLAB在控制系统中的应用结课论文所在学院:信息工程学院专业名称:自动化10-3学生姓名:王思嘉学号代码: 1005130315指导教师:崔新忠MATLAB在控制系统中的应用1 MATLAB简介MATLAB是Mathworks公司开发的一种集数值计算、符号计算和图形可视化三大基本功能于一体的功能强大、操作简单的优秀工程计算应用软件。
MATLAB不仅可以处理代数问题和数值分析问题,而且还具有强大的图形处理及仿真模拟等功能。
从而能够很好的帮助工程师及科学家解决实际的技术问题。
MATLAB的含义是矩阵实验室(Matrix Laboratory),最初主要用于方便矩阵的存取,其基本元素是无需定义维数的矩阵。
经过十几年的扩充和完善,现已发展成为包含大量实用工具箱(Toolbox)的综合应用软件,不仅成为线性代数课程的标准工具,而且适合具有不同专业研究方向及工程应用需求的用户使用。
MATLAB最重要的特点是易于扩展。
它允许用户自行建立完成指定功能的扩展MATLAB函数(称为M文件),从而构成适合于其它领域的工具箱,大大扩展了MATLAB的应用范围。
目前,MATLAB已成为国际控制界最流行的软件,控制界很多学者将自己擅长的CAD方法用MATLAB加以实现,出现了大量的MATLAB配套工具箱,如控制系统工具箱(control systems toolbox),系统识别工具箱(system identification toolbox),鲁棒控制工具箱(robust control toolbox),信号处理工具箱(signal processing toolbox)以及仿真环境SIMULINK等。
2 MATLAB在控制系统中的应用1.稳定性分析模块:包含系统的稳定性的判断和显示闭环系统所有的特征根,很直观地显示系统的稳定性判断是否正确,快捷地表示已知系统的稳定性。
2.时域分析响应模块:包括了一阶系统、典型二阶系统、任意阶系统三个主要界面,可以通过此界面绘制时域的响应曲线并且计算相关参数。
运用MATLAB软件进行潮流计算论文

摘要本文运用MATLAB软件进行潮流计算,对给定题目进行分析计算,再应用DDRTS软件,构建系统图进行仿真,最终得到合理的系统潮流。
潮流计算是电力系统最基本最常用的计算。
根据系统给定的运行条件,网络接线及元件参数,通过潮流计算可以确定各母线的电压幅值和相角,各元件流过的功率,整个系统的功率损耗。
潮流计算是实现电力系统安全经济发供电的必要手段和重要工作环节。
因此,潮流计算在电力系统的规划计算,生产运行,调度管理及科学计算中都有着广泛的应用。
首先,画出系统的等效电路图,在计算出各元件参数的基础上,应用牛顿—拉夫逊Newton-Raphson法以及MATLAB软件进行计算对给定系统图进行了四种不同负荷下的潮流计算,经过调节均得到符合电压限制及功率限制的潮流分布。
其次,牛顿—拉夫逊Newton-Raphson法具有较好的收敛性,上述计算过程经过四到五次迭代后均能收敛。
根据运算结果,分析各支路损耗和系统总损耗。
最后,应用DDRTS软件,构建系统图,对给定负荷重新进行分析,潮流计算后的结果也能满足相应的参数要求。
关键词:牛顿-拉夫逊法MATLAB DDRTS 潮流计算目录1.摘要 (2)2.题目原始资料 (2)3.题目分析 (5)4.题目求解 (6)1)根据题意要求画出等值电路 (6)2)读程序画出拉夫逊法的流程图 (7)3)变电所负荷为题目所给数据进行求解 (8)4)编写程序并运行 (10)5)具体调压调损耗过程 (10)1.改变变压器变比调压 (10)2.改变发电机机端电压调压 (12)3.负荷按照一定比例变化的潮流计算分析 (15)4.轮流断开支路双回线中的一条的潮流计算 (19)5.仿真并比较 (26)6.设计心得 (28)7.参考文献 (29)一、 题目原始资料:1.系统图:两个发电厂分别通过变压器和输电线路与四个变电所相连。
变电所1变电所2母线2、发电厂资料:母线1和2为发电厂高压母线,发电厂一总装机容量为(300MW ),母线3为机压母线,机压母线上装机容量为(100MW),最大负荷和最小负荷分别为50MW和20MW;发电厂二总装机容量为(200MW )。
matlab论文

利润最大化问题摘要公司是以营利为目的而存在,公司要想在变化的市场中利润最大化,就得在销售收入和成本之间找到平衡点。
本文通过公司调查市场得到的数据,包括成本、售价和预期销售量、广告费和销售增长因子之间的关系进行分析,试图为公司的运营找到最好的广告费用投入和出售价格,从而使公司利润最大化。
针对问题,本文采用了MATLAB首先由散点图推测售价和预期销售量之间线性关系,广告费用和销售增长因子之间存在二次多项式的关系。
通过题目提供的数据编程拟合得出以上两个关系式的系数。
再通过,销售利润=销售收入-销售成本推算出销售利润和售价、广告费用的恒等式,最后用fminsearch找到利润最大值。
关键词:利润最大化MATLAB 拟合一、问题重述公司是以营利为目的而存在,公司要想在变化的市场中利润最大化,就得在销售收入和成本之间找到平衡点。
要想获得最大利润就必须调查市场,再分析由市场得到数据,确定销售价格和广告费用的投入,最终利润的最大化,为今后公司的生产与销售提供依据。
二、问题分析本文为了确定是利润最大化的销售价格、广告费用投入,再根据题目提供的数据,从以下步骤讨论分析问题:1、为了减少变量,可以充分挖掘销售价格和预期销售量之间的关系、广告费的投入和销售增长因子之间的关系。
2、用MATLAB拟合出以上两个关系式的系数,再用销售价格的代数式表示预期销售量、广告费用的投入的代数式表示销售增长因子。
3、利用销售利润=销售收入-销售成本计算出最佳的销售价格和广告费用投入、最大利润。
三、模型假设本文假设有市场得到的数据是能代表市场的,近期公司所从事的行业不会有大的波动。
四、符号说明sj :销售价格;ggfy :广告费用投入;yqxsl :预期销售量;xszzyz :销售增长因子;profit :利销售润;fmin :最大利润的相反数;u :对应销售价格和广告费用投入;tggfy :广告费用投入变量取点;tyqxsl :预期销售量取点;tsj :销售价格取点;txszzyz :销售增增长因子取点。
毕业设计(论文)基于matlab的数字基带通信系统仿真
基于matlab的数字基带通信系统仿真1.课程设计的目的(1)增加对仿真软件的认识,学会对各种软件的操作和使用方法(2)加深理解数字基带通信系统的概念(3)初步掌握系统的设计方法,培养独立工作能力2.设计方案论证2.1数字基带传输系统在数字传输系统中,其传输的对象通常是二进制数字信号,它可能是来自计算机、电传打字机或其它数字设备的各种数字脉冲,也可能是来自数字终端的脉冲编码调制(PCM)信号。
这些二进制数字信号的频带范围通常从直流和低频开始,直到某一频率m f ,我们称这种信号为数字基带信号。
在某些有线信道中,特别是在传输距离不太远的情况下,数字基带信号可以不经过调制和解调过程在信道中直接传送,这种不使用调制和解调设备而直接传输基带信号的通信系统,我们称它为基带传输系统。
而在另外一些信道,特别是无线信道和光信道中,数字基带信号则必须经过调制过程,将信号频谱搬移到高频处才能在信道中传输,相应地,在接收端必须经过解调过程,才能恢复数字基带信号。
我们把这种包括了调制和解调过程的传输系统称为数字载波传输系统。
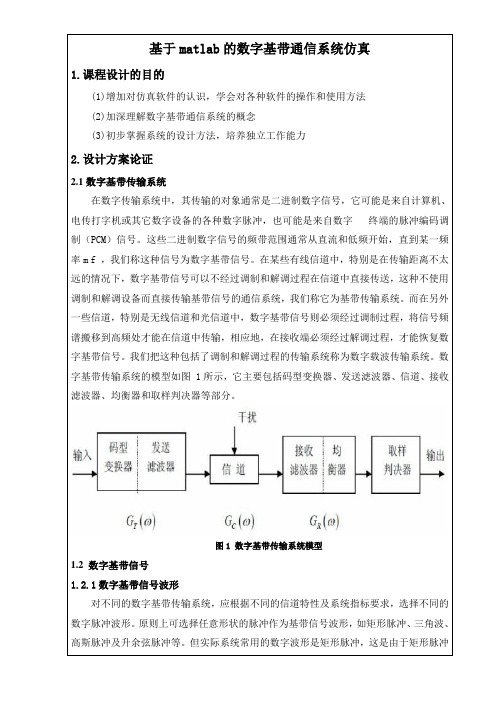
数字基带传输系统的模型如图 1所示,它主要包括码型变换器、发送滤波器、信道、接收滤波器、均衡器和取样判决器等部分。
图1 数字基带传输系统模型1.2 数字基带信号1.2.1数字基带信号波形对不同的数字基带传输系统,应根据不同的信道特性及系统指标要求,选择不同的数字脉冲波形。
原则上可选择任意形状的脉冲作为基带信号波形,如矩形脉冲、三角波、高斯脉冲及升余弦脉冲等。
但实际系统常用的数字波形是矩形脉冲,这是由于矩形脉冲纤数字传输系统中的线路传输码型。
此外,CMI 码和曼彻斯特码一样都是将一位二进制码用一组两位二进制码表示,因此称其为1B2B 码。
(5)4B/3T 码4B/3T 码是1B/1T 码的改进型它把4 个二进制码元变换为3个三进制码元。
显然,在相同信息速率的条件下,4B/3T 码的码元传输速率要比1B/1T 码的低,因而提高了系统的传输效率。
MATLAB论文【范本模板】

本科课程设计题目:连续时间信号傅里叶级数分析及MATLAB实现院系:信息工程学院姓名:周莎莎学号:1434140161专业:通信工程年级:2014 级指导教师:温金芳职称:讲师完成日期:2016年6月目录摘要 (I)A BSTRACT (II)绪论 01MATLAB简介 (1)1.1MATLAB语言功能 (1)1。
2MATLAB语言特点 (1)2 连续时间周期信号的傅里叶级数 (2)2。
1连续时间周期信号的分解 (2)2.1.1三角形式的傅里叶级数 (2)2。
1。
2指数形式的傅里叶级数 (3)2.2连续时间周期信号的傅里叶综合 (3)2.3吉布斯现象 (4)3连续时间周期信号的频谱分析 (6)3.1单边与双边频谱关系 (6)3。
2以单边幅度频谱为例,研究脉冲宽度与频谱的关系 (7)3.3以单边幅度频谱为例,研究脉冲周期与频谱的关系 (8)4 典型周期脉冲的频谱 (10)4.1周期方波脉冲频谱的MATLAB实现 (10)4。
1。
1周期方波脉冲双边频谱的MATLAB实现 (10)4.1.2 周期方波脉冲单边频谱的MATLAB实现 (12)4.2周期三角波脉冲频谱的MATLAB实现 (14)4。
2。
1 周期三角波双边频谱的MATLAB实现 (15)4。
2。
2 周期三角波单边频谱的MATLAB实现 (16)5小结 (18)致谢 (19)参考文献 (20)附录 (21)摘要MATLAB目前已发展成为由MATLAB 语言、MATLAB 工作环境、MATLAB 图形处理系统、MATLAB 数学函数库和MATLAB 应用程序接口五大部分组成的集数值计算、图形处理、程序开发为一体的功能强大的系统。
本次课程设计则在深入研究连续时间信号傅里叶级数分析理论知识的基础上,利用MATLAB强大的图形处理功能、符号运算功能以及数值计算功能,通过MATLAB编程进行图形功能仿真,从而实现连续时间周期信号频域分析的仿真波形,包括以下内容:用MATLAB实现周期信号的傅里叶级数分解与综合的波形;用MATLAB 实现周期信号的单边频谱及双边频谱的波形与分析;用MATLAB实现典型周期信号的频谱的波形。
MATLAB简易计算器论文

MATLAB简易计算器论文概述:计算器是一种用于执行基本数学运算的设备或工具。
随着计算机技术的不断发展,计算器在工程、科学和教育领域中被广泛使用。
为了满足各种计算需求,研究人员开发了各种类型的计算器。
其中,MATLAB简易计算器是一种基于MATLAB编程语言编写的计算器,以提供基本数学运算和数据分析功能。
背景:MATLAB是一种用于数值计算、数据可视化和编程的高级技术计算语言和环境。
它提供了丰富的功能和工具包,可用于各种科学、工程和统计应用。
自诞生以来,MATLAB已成为学术、工业和商业界广泛使用的标准计算工具。
简易计算器设计:MATLAB简易计算器是基于MATLAB的开发,使用MATLAB编程语言和MATLAB的计算和可视化功能。
它提供了实现基本数学运算的功能,包括加法、减法、乘法和除法。
此外,它还可以执行一些高级计算和数据分析功能,如求平方根、求幂、求和等。
用户可以通过简单的输入,使用MATLAB简易计算器进行数学运算。
用户可以输入表达式,例如“2+3”、“4-2”、“5*6”和“8/2”,然后在计算器界面上点击“计算”按钮以获得结果。
计算器会返回计算结果,并在界面上显示出来。
因为MATLAB具有图形化用户界面的特性,所以MATLAB简易计算器还可以显示计算结果的图表,例如直方图、散点图和线图。
这些图表可以帮助用户更直观地理解数据的分布和关系。
应用:MATLAB简易计算器可以广泛应用于各种领域,包括科学、工程和教育。
在科学领域,它可以用于数据分析、建模和仿真。
在工程领域,它可以用于电路设计、信号处理和控制系统。
在教育领域,它可以用于教学和学生练习。
优点和局限:与其他计算器相比,MATLAB简易计算器具有以下优点:(1)使用MATLAB编程语言进行开发,具有强大的计算和可视化功能;(2)提供了简单易用的用户界面,使用户能够轻松进行数学运算;(3)可以用于高级计算和数据分析,满足更复杂的需求。
然而,MATLAB简易计算器也存在一些局限:(1)需要MATLAB软件的支持,因此在没有安装MATLAB的计算机上无法运行;(2)对于大型数据集的处理,可能会遇到性能问题;(3)对于一些特殊的数学运算,可能需要自己编写MATLAB脚本。
关于matlab的毕业论文
关于matlab的毕业论文Matlab在毕业论文中的应用毕业论文是大学生完成学业的重要一环,对于学生来说,选择一个合适的主题和合适的工具是至关重要的。
在当今科技发达的时代,计算机软件的应用已经成为毕业论文中不可或缺的一部分。
而Matlab作为一种强大的科学计算软件,在毕业论文中的应用也越来越广泛。
首先,Matlab在数据分析和处理方面有着得天独厚的优势。
毕业论文往往需要大量的数据分析和处理工作,而Matlab提供了丰富的数据处理函数和工具箱,可以高效地完成这些任务。
例如,对于需要进行统计分析的数据,Matlab提供了统计工具箱,可以进行各种统计分析和建模。
对于需要进行图像处理的数据,Matlab提供了图像处理工具箱,可以实现图像的滤波、边缘检测等功能。
这些功能的使用可以大大提高数据处理的效率和准确性。
其次,Matlab在数学建模方面也有着独特的优势。
毕业论文中的数学建模是一个重要的环节,通过数学模型可以对研究对象进行定量分析和预测。
而Matlab提供了丰富的数学建模工具和函数,可以轻松地实现各种数学模型的建立和求解。
例如,对于需要进行优化问题的研究,Matlab提供了优化工具箱,可以实现各种优化算法的求解。
对于需要进行微分方程求解的研究,Matlab提供了微分方程工具箱,可以实现各种微分方程的求解。
这些功能的使用可以使得数学建模更加简单和高效。
此外,Matlab在可视化方面也有着独特的优势。
毕业论文中的结果展示是一个重要的环节,通过合适的可视化方式可以更好地展示研究结果和结论。
而Matlab提供了强大的可视化工具,可以实现各种图表和图像的绘制。
例如,对于需要展示数据分析结果的研究,Matlab提供了各种绘图函数,可以绘制出直方图、散点图等图表。
对于需要展示图像处理结果的研究,Matlab提供了图像显示函数,可以展示出图像的处理前后对比。
这些功能的使用可以使得研究结果更加直观和易于理解。
综上所述,Matlab在毕业论文中的应用是不可忽视的。
MATLAB 结课小论文
基于MATLAB的控制系统分析摘要MATLAB具有强大的图形处理功能、符号运算功能和数值计算功能。
MATLAB 工具几乎涵盖了整个科学技术运算领域。
其中系统的仿真(Simulink)工具箱是从底层开发的一个完整的仿真环境和图形界面。
在这个环境中,用户可以完成面向框图系统仿真的全部过程,并且更加直观和准确地达到仿真的目标。
此次,以数字电路中的时序逻辑电路为线索来学习Simulink,了解了许多数字电路中常用模块的使用方法.时序电路中除具有逻辑运算功能的组合电路外,还必须有能够记忆电路状态的存储单元或延迟单元,这些存储或延迟单元主要由本次设计所用到的触发器来实现。
D触发器、RS触发器、JK触发器等这些时序逻辑电路中常用的器件在Simulink中都有相应的仿真模块,除此之外,用户还可以自行设计封装模块来一步一步完成更大的电路系统,实现更强大的逻辑功能。
关键词:MATLAB、Simulink、时序电路1 Matlab内容简介MATLAB拥有了更丰富的数据类型和结构,更好的面向对象的快速精美的图形界面,更多的数学和数据分析资源,MATLAB工具几乎涵盖了整个科学技术运算领域。
在大部分大学里,应用代数、数理统计、自动控制、数字信号处理、模拟与数字通信、时间序列分析、动态系统仿真等课程的教材都把MATLAB作为必不可少的内容。
在国际学术界,MATLAB被确认为最准确可靠的科学计算标准软件,在许多国际一流的学术刊物上都可以看到MATLAB在各个领域里的应用。
2系统的稳定性分析稳定是控制系统的重要性能,也是系统能够正常运行的首要条件。
在分析控制系统时,首先遇到的问题就是系统的稳定性。
对线性系统来说,如果一个系统的所有几点都位于左半s 平面,则该系统是稳定的。
对于离散系统来说,如果一个系统的全部极点都在单位圆内,则该系统可以被认为是稳定的。
由此可见,线性系统的稳定性完全取决于系统的极点在根平面上的位置。
判断一个线性系统稳定性的一种最有效的方法是直接求出系统所用的极点,然后根据极点的分布情况来确定系统的稳定性。
MATLAB课程论文要求(含论文模板)
2019年秋学期《matlab 》课程论文写作要求:(作为期末考查方式占课程分数20%)论文主题:自选跟matlab 相关的主题。
也可参考以下列表领域选择其中某一主题:1.利用matlab 进行选择结构程序设计2.利用matlab 进行循环结构程序设计3..matlab 的高层绘图操作4.利用matlab 进行GUI 设计5. matlab 符号计算基础与符号微积分6.matlab 与方程符号求解7.利用simulink 进行系统仿真8.利用matlab 进行电路分析9.利用matlab 进行信号处理10.利用matlab 进行图像处理11.其他与本课程相关即可。
论文要求:1.字数不得低于2000 字,但不得超过5000 字。
2.必须要附有论文里实例源文件。
(M 文件、MDL 文件或fig 文件)3.格式要求按杂志期刊论文投稿格式要求来撰写(参考文后附录)。
4.论文正文中必须包含图、表格。
特此通告:课程论文若有以下情况之一,无论平时成绩如何,整个课程作不及格处理。
1.雷同论文。
如有同学论文雷同,全部作为不及格处理。
2.完全拷贝网上论文或教材章节的论文。
3.没有上交源文件。
4.没有上交课程论文。
论文上交:上交清单:(1)word 版论文(2)源文件(M文件、MDL文件或fig文件)(3)论文打印版本(请学习委员收集齐后给我上交)XXXX(中文标题:二号黑体,居中)作者(作者名:四号仿宋体,居中)摘要:(五号黑体,缩进两格)xxxxx(摘要内容:五号楷体)关键词:(五号黑体,缩进两格)词1,词2,词3(五号宋体)0 引言(四号宋体,顶格)xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxx......(正文:五号宋体,每段首行缩进两格)1 XXXXX(四号宋体,顶格)xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxx......(正文:五号宋体,每段首行缩进两格)1.1 XXXX(五号黑体,顶格)1.1.1 xxxx(五号楷体,顶格)xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxx.........(正文:五号宋体,每段首行缩进两格)图图1 XXX(图名:小五号宋体,居中列于图下)1.1.2 xxxx(五号楷体,顶格)xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxx.........(正文:五号宋体,每段首行缩进两格)表1 XXXX (表题:小五号黑体,居中排于表格上方)参考文献:(五号黑体,顶格)[1] xx (英文摘要:六号Times New Roman,缩进两格)[2] xxx (中文摘要:六号宋体,缩进两格)xxx(对照英文格式:六号Times New Roman,缩进两格)[3] xxx (中文摘要:六号宋体,缩进两格)xxx(对照英文格式:六号Times New Roman,缩进两格)[4] xxx。
matlab 论文
《MATLAB语言》课程论文基于MATLAB在高等数学基础部分中的应用姓名:**学号:********专业:********班级:********指导老师:******学院:************完成日期:2010.12.03MATLAB在高等数学基础部分中的应用(姓名 12010245280 2010级自动化1班)[摘要]计算机的发明是二十世纪四十年代的事情,经过几十年的发展,它已经成为一门复杂的工程技术学科,它的应用从国防、科学计算,到家庭办公、教育娱乐,无所不在。
它的分类从巨型机、大型机、小型机,到工作站、个人电脑,五花八门。
但是,无论怎样尖端,怎样高科技,从它诞生之日起,在许多人心目中它就是一部机器,一部冰冷的高速运算的机器。
从ENIAC揭开计算机时代的序幕,到UNIVAC成为迎来计算机时代的宠儿,不难看出这里发生了两个根本性的变化:一是计算机已从实验室大步走向社会,正式成为商品交付客户使用;二是计算机已从单纯的军事用途进入公众的数据处理领域,真正引起了社会的强烈反响。
随着计算机的日趋普及和计算机技术的发展.汁算机辅助教学逐渐称为一种重要的教学方式,Matlab是MathWorks公司出品的一款著名数学软件.是当今国际上科学界(尤其是自动控制领域)最具影响力、也是最有活力的软件。
它起源丁-矩阵运算,并已经发展成一种高度集成的计算机语言。
它提供r强大的科学运算、灵活的程序没计流程、高质肇的图形可视化与界面设计、便捷的与其他程序和语言接f1的功能:Matlab语言在各国高校与研究单位起着重大的作用。
应用Matlab进行高等数学的计算机辅助教学。
能够加深我们对所学高等数学知识的理解。
并应用数学软件进行计算,把我们从繁琐的计算中解脱出来。
MATLAB 和Mathematica、Maple并称为三大数学软件。
它在数学类科技应用软件中在数值计算方面首屈一指。
MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于MATLAB在傅里叶变换中的应用樊(学号:)(学院专业班)摘要:MATLAB自推出以来就受到广泛的关注,其强大的扩转功能为各个领域的应用提供了有力的工具。
信号处理箱就是其中之一。
在信号处理工具箱中,MATLAB提供了滤波器分析、滤波器实现、模拟滤波器设计、模拟滤波器变换、滤波器离散化、线性系统变换等方面的函数命令。
应用MATLAB作数值计算,针对当自变量的信号“时间”或“频率”取连续值或离散值时形成的五种情况作出相应的计算及频谱曲线。
关键词:傅里叶变换;周期;频率;MATLAB。
1.引言MATLAB 是国际上公认的优秀、可靠的科学计算和仿真的标准软件。
它在许多科学领域中成为计算机辅助设计和分析、算法研究的基本工具。
在傅里叶变换中,应用MATLAB作数值计算,可以很容易的作出相对应的计算及频谱曲线,大大提高了计算效率。
2.傅里叶变换傅里叶变换就是建立以时间为自变量的“信号”与以频率为自变量之间的某种变化关系。
所以,当自变量“时间”或“频率”取连续值或离散值时,就形成了几种不同形式的傅里叶变换,如表1傅里叶变换形式所示。
表 1傅里叶变换形式3.连续时间、连续频率------福利叶变换这就是连续时间非周期信号x(t)福利叶变换关系,所得到的是连续的非周期的频率密集度函数()X jΩ.其变换对为:正变换:()()j tX j x t e dt-Ω∞Ω=-∞⎰(1)逆变换:1()()2j tX t x j e d π-Ω∞=ΩΩ-∞⎰ (2) 例 1 分析如图 1时域信号及其频谱图 所示的矩形脉冲信号()f t (非周期信号)在Ω=-40~40rad/s 区间的频谱。
(a )采样密 (b )采样稀,有频率泄漏图 1时域信号及其频谱图根据离散时间信号[]x n 的Z 变换定义: ()[]n x z x n z +∞--∞=∑,矩形脉冲信号的频谱为:F(j )=()j t f t e dt -Ω∞Ω-∞⎰按MATLAB 作数值计算的要求,它不能计算无限区间,根据信号波形的情况,将积分上下限定为0~10s ,并将t 分成N 等份,用求和代替积分。
这样,10111()()()1MM NN b b z n b z Y z H z X z a z n a z ----+++==+++ (3)可写为12121F(j )=()[(),(),,()][,,,]n Nj t j t j t j t i n i f t e t f t f t f t e e e t -Ω-Ω-Ω-Ω=Ω∆=⋅⋅⋅⋅⋅⋅∆∑ (4)这说明求和的问题可以用()f t 行向量乘以n j t e -Ω列向量来实现,式中t ∆是t 的增量,在程序中用dt 表示。
由于求一系列不同Ω(程序中用Ω用W 表示)处的F 值,都用同一公式,这就可以利用matlab 中的元素群运算能力。
类似地也可以得到傅里叶逆变换的数值计算式。
MATLAB 源程序如下: clear,tf=10; N=input;dt=10/N;t=[1:N]*dt; f=[ones(1,N/2),zeros(1,N/2)]; wf=input; Nf=input;w1=linspace(0,wf,Nf) ;dw=wf/(Nf-1); F1=f*exp(-j*t'*w1)*dt; w=[-fliplr(w1),w1(2:Nf)]; F=[fliplr(F1),F1(2:Nf)]; subplot(1,2,1), plot(t,f,'linewidth',1.5), grid onset(gcf,'color','w') axis([0,10,0,1.1]) subplot(1,2,2),plot(w,abs(F),'linewidth',1.5) grid on程序运行结果:若时间分隔的点数N=256,需求得频率宽度wf=40,需求的频率点数Nf=64,所得结果所示。
若取时间分隔的点数N=64,频数宽度=40,频谱点数Nf=256,则得结果所示。
此时采取采样周期为dt=10/64s ,对应的采样频率fs=1/dt=6.4Hz 或s Ω=40.2124rad/s 。
从图中可以看出高频频谱以s Ω/2处为基准线的转迭,出现频率泄露。
4. 连续时间、离散频率----傅里叶级数设()x t 代表一个周期为0T 的周期性连续时间函数,()x t 课展开成傅里叶级数,其傅里叶级数的系数为0()X jk Ω,0()X jk Ω是离散频率的非周期函数,()x t和0()X jk Ω组成的变换对为:正变换:000/20/21()()T jk t T X jk x t e dt T -Ω-Ω=⎰(5)逆变换:00()()jk tX t x jk e ∞Ω-∞=Ω∑ (6)式中,002/T πΩ=为离散频率相邻两谱线之间的频率间隔,k 为谐波序号。
5. 离散时间、连续频率----序列傅里叶变换如果信号()x n 是非周期且绝对可和,则它的离散时间傅里叶变换对数为: 正变换: ()()j j n X e x n e ωω∞-∞=∑ (7)逆变换: 1()()2j j n x n X e e d πωωπωπ-=⎰ (8)在时域上市离散序列,而在频域上是连续函数,即具有连续的频谱。
这里的ω为数字频域,它与模拟角频率Ω的关系为:T ω=Ω,其中T 为模拟信号()()x n x nT =的抽样时间间隔。
值得注意的是,对于序列傅里叶变换,如果()x n 为无限长,那么就不能用MATLAB 直接利用式1211112()111N N r r r H z p z p z p z---=++⋅⋅⋅+---来计算()j X e ω,只可以用它对表达式()j X e ω在[0,]π频率点上求值,在画出它的幅度和相位(或者实部和虚部)。
如果()x n 为有限长,那么就可直接用MATLAB ,根据式1211112()111N N r r r H z p z p z p z---=++⋅⋅⋅+---,在任意频率对()j X e ω进行数值计算。
例2求/3()(0.9)j n x n e π=,010n ≤≤的离散时间傅里叶变换。
MATLAB 源程序如下: n=0:10;x=(0.9*exp(j*pi/3)).^n; k=-200:200;w=(pi/100)*k;X=x*(exp(-j*pi/100)).^(n'*k); magX=abs(X);angX=angle(X); subplot(2,1,1);plot(w/pi,magX);grid axis([-2,2,0,8])xlabel('frequency in pi units');ylabel('|X|'); title('Magnitude Part')subplot(2,1,2);plot(w/pi,angX/pi);grid axis([-2,2,-1,1])xlabel('frequency in pi units');ylabel('Radians/pi'); title('Angle part')程序运行结果如图2所示。
6. 离散时间、离散频率----离散傅里叶级数设()x n 是周期为N 的周期序列,则()x n 的离散傅里叶级数只有N 个独立的谐波成分,数字基数为02/N ωπ=谐波成分为2/,1,2,,1k N k N π=-。
k 次谐波的系数大小为()X k 。
()x n 与()X k 的变换对数为:图 2副频和相频特性曲线正变换: 1()[()]()N nkN n X K DFS X n x n W -===∑ 0,1,2,,1k N =- (9)逆变换: 11()[()]()N nk Nk X n IDFS X k x k WN--===∑ 0,1,2,,1n N =- (10)式中,2jnk NNW π-。
可以看出谐波系数()X k 也是一个以N 为周期的周期序列。
7. 离散时间、离散频率----离散傅里叶变换如果时域序列()x n 是有限长的,长度为N ,它的频谱可以通过离散傅里叶变换(DFT )来获得,其变换对为:正变换: 10()[()]()N nk N n X k DFT x n x n W -===∑ 0,1,2,,1k N =- (11)逆变换:11()[()]()N nk Nk x n IDFS X k K k WN--===∑ 0,1,2,,1n N =- (12)由DFT 变换对可以看出,DFT 是对有限长序列频谱的离散化,通过DFT 是对域有限长度系列与频域有限长度相对应,从而可再频域用计算机进行信号处理。
更重要的是DFT 有多个快速算法(FFT ),可使信号处理速度提高好几倍,是数字信号的实时处理得以实现。
例3用FFT 计算先练两个序列的卷积。
()sin(0.4)()N x n n R n =,()0.9()n M h n R M =并测试直接卷积和快速卷积的时间。
用圆周卷积(FFT )替代线性卷积的计算方框图如图3所示。
图 3快速卷积方框图按照该方框图很容易编写出如下MATLAB 程序: xn=sin(0.4*[1:15]); hn=0.9.^(1:20); tic,yn=conv(xn,hn); toc,M=length(xn); N=length(hn); nx=1:M;nh=1:N;L=pow2(nextpow2(M+N-1)); tic,Xk=fft(xn,L); Hk=fft(hn,L); Yk=Xk.*Hk; yn=ifft(Yk,L) toc,subplot(2,2,1),stem(nx,xn,'.'),ylabel('x(n)'); subplot(2,2,2),stem(nh,hn,'.');subplot(2,1,2),ny=1:L;stem(ny,real(yn),'.'),ylabel('y(n)'图 4 ()x n ,()h n 及其线性卷积波形8.结语通过本次设计,学习和掌握了MATLAB软件在傅里叶变换中的应用,分析了连续时间、连续频率傅里叶变换,连续时间、离散频率序列傅里叶变换,离散时间、离散频率离散傅里叶级数。
从中学到了MATLAB软件对傅里叶变换的可视化编写程序,及其各种MATLAB表达式的表示,及相关函数的了解。
参考文献:[1] 刘勍,温志贤.MATLAB基础及应用[M].南京:东南大学出版社:江建中,2011.[2] 唐向红,岳恒立,郑雪峰.MATLAB及在电子信息类课程中的应用(第2版)[M].北京:电子工业出版社:韩同平,2010.。
